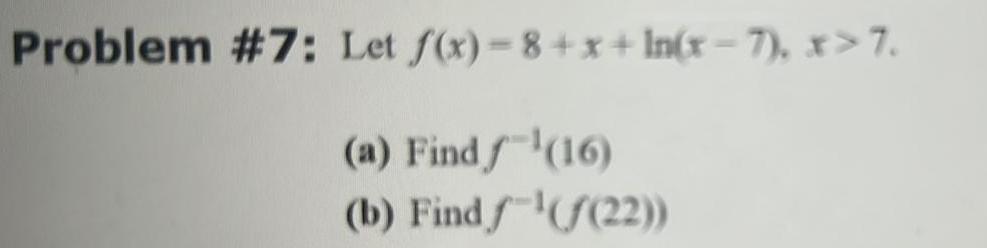Application of derivatives Questions and Answers

Calculus
Application of derivativesFor the following alternating series 0 6 0 6 5 3 5 n 1 an 0 6 0 6 7 7 how many terms do you have to go for your approximation your partial sum to be within 0 000000110 7 from the conver value of that series

Calculus
Application of derivativesThe bell tower of the cathedral in Pisa Italy leans 5 6 from the vertical A tourist stands 104 m from its base with the tower leaning directly toward her She measures the angle of elevation to the top of the tower to be 29 5 Find the length of the tower to the nearest meter

Calculus
Application of derivativesSolve the triangle using the Law of Sines Assume c 80 ZA 49 and LB 25 Round lengths to two decimal places a b 20 A b C a B

Calculus
Application of derivativesUse the Law of Sines to find the indicated side x Assume c 25 7 Round your answer to one decimal place A 52 70 B
Calculus
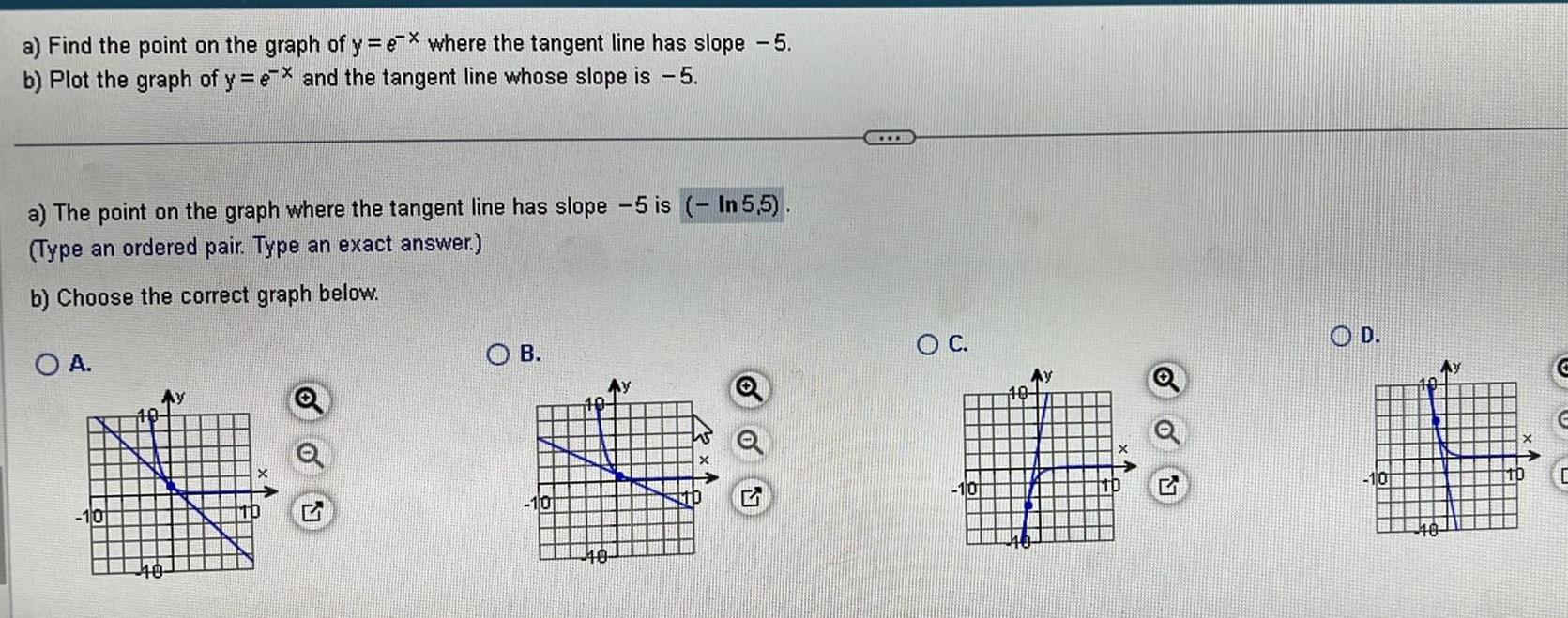
Application of derivativesa Find the point on the graph of y ex where the tangent line has slope 5 b Plot the graph of y ex and the tangent line whose slope is 5 a The point on the graph where the tangent line has slope 5 is In 5 5 Type an ordered pair Type an exact answer b Choose the correct graph below O A 40 OB 10 40 O C 10 10 Ay O D 10 C

Calculus
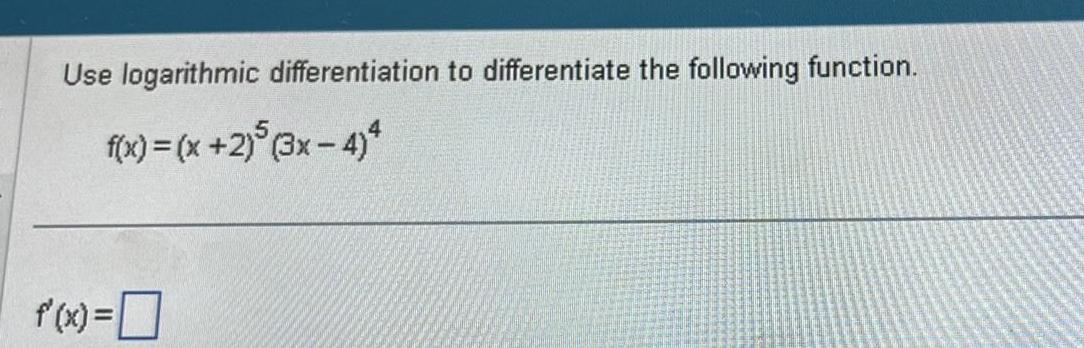
Application of derivativesUse logarithmic differentiation to differentiate the following function f x x 2 5 3x 4 4 f x 0
Calculus
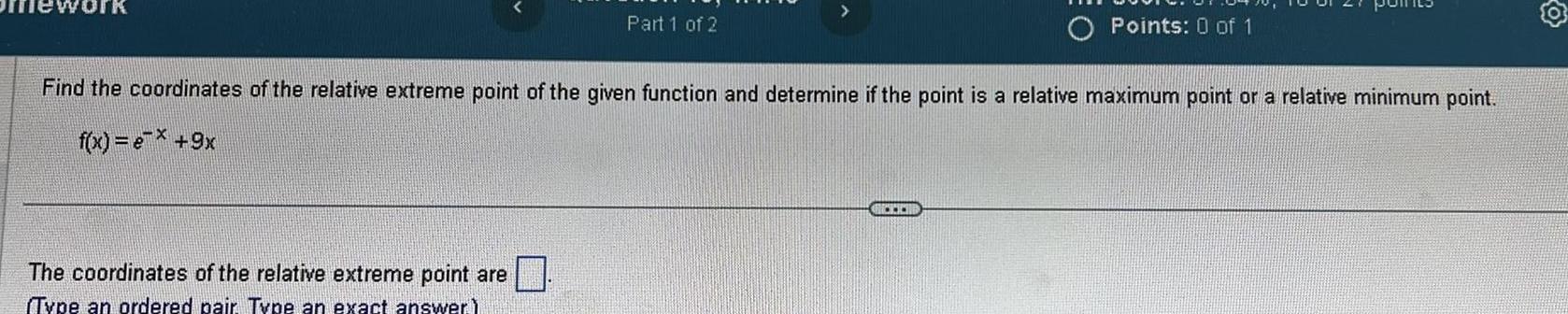
Application of derivativesPart 1 of 2 The coordinates of the relative extreme point are Type an ordered pair Type an exact answer Find the coordinates of the relative extreme point of the given function and determine if the point is a relative maximum point or a relative minimum point f x e 9x O Points 0 of 1 E
Calculus
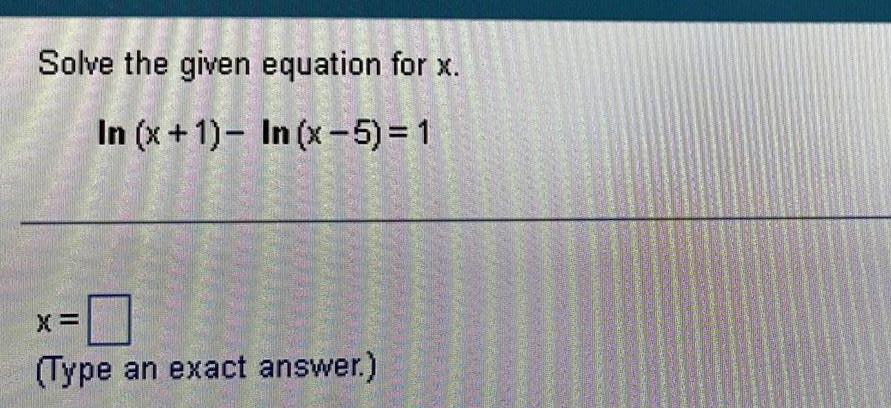
Application of derivativesSolve the given equation for x In x 1 In x 5 1 X Type an exact answer

Calculus
Application of derivativesDifferentiate the following function 4 In 5x x y d 4 dx ln 5x In 176 5x Q X

Calculus
Application of derivativesThe velocity of a parachutist during free fall is f t 82 1 e 0 12t meters per second Answer the following questions using the graph Recall that acceleration is the derivative of velocity a What is the approximate velocity when t 4 seconds m sec C 80 70 60 50 40 30 20 10 0 0 fft fath 10 20 30 o
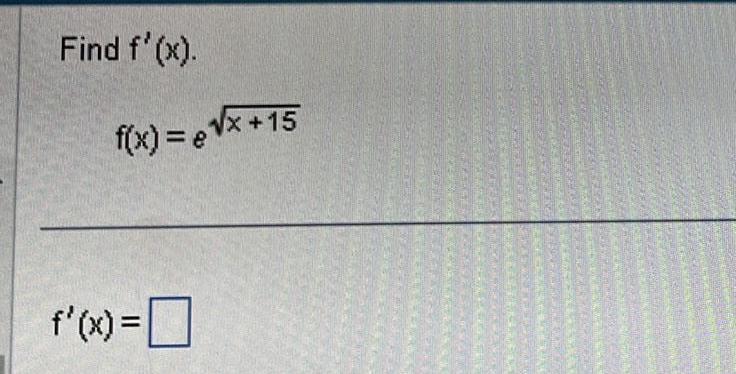
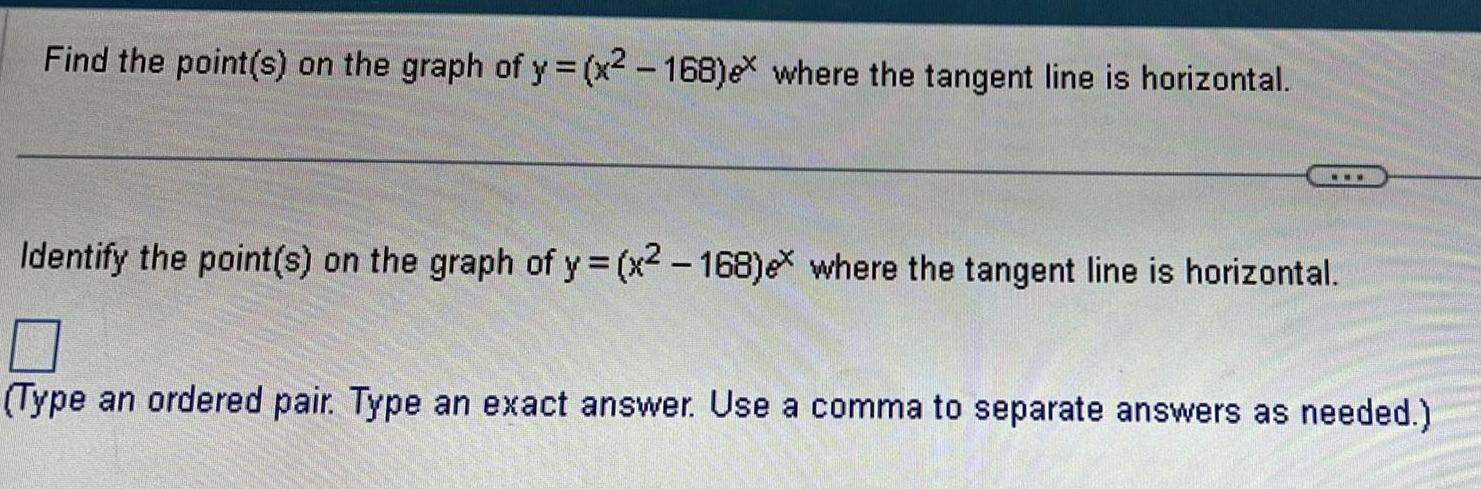
Calculus
Application of derivativesFind the point s on the graph of y x 168 ex where the tangent line is horizontal www Identify the point s on the graph of y x2 168 ex where the tangent line is horizontal 0 Type an ordered pair Type an exact answer Use a comma to separate answers as needed

Calculus
Application of derivativesFind the equation of the tangent line to the curve y et 1 8eX at What is the equation of the line tangent to the curve at 0 3 at 0 7 2
Calculus
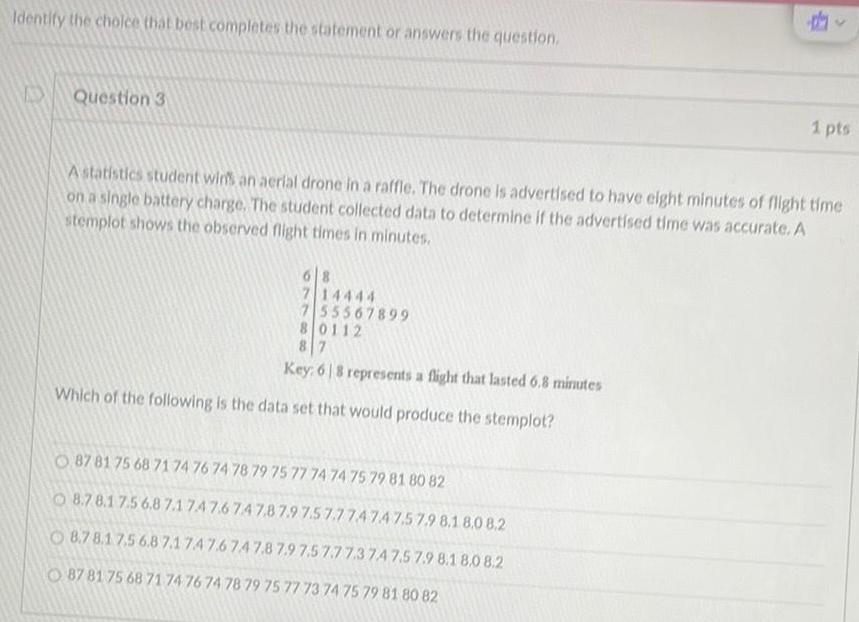
Application of derivativesIdentify the choice that best completes the statement or answers the question Question 3 714444 7 55567899 80112 87 Key 68 represents a flight that lasted 6 8 minutes Which of the following is the data set that would produce the stemplot dy A statistics student wins an aerial drone in a raffle The drone is advertised to have eight minutes of flight time on a single battery charge The student collected data to determine if the advertised time was accurate A stemplot shows the observed flight times in minutes O87 81 75 68 71 74 76 74 78 79 75 77 74 74 75 79 81 80 82 8 7 8 1 7 5 6 8 7 1747 6 747 8 7 9 7 5 7 7 7474 7 5 7 9 8 1 8 0 8 2 8 7 8 1 7 5 6 8 7 1 7 4 7 6 7 4 7 8 7 9 7 5 7 7 7 3 74 7 5 7 9 8 1 8 0 8 2 87 81 75 68 71 74 76 74 78 79 75 77 73 74 75 79 81 80 82 1 pts
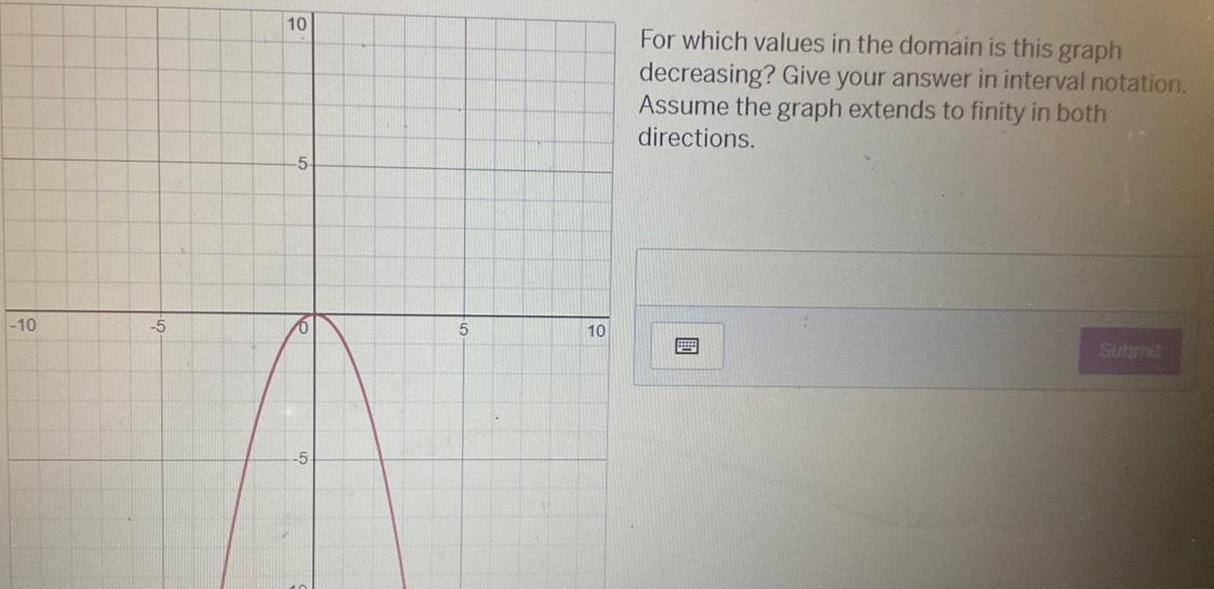
Calculus
Application of derivatives10 5 10 5 5 5 10 For which values in the domain is this graph decreasing Give your answer in interval notation Assume the graph extends to finity in both directions
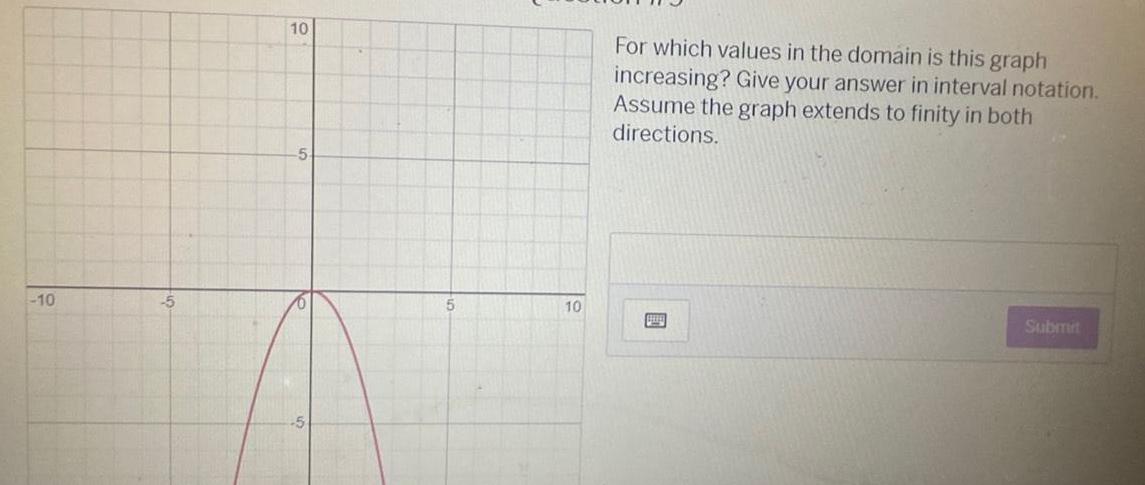
Calculus
Application of derivatives10 5 10 5 5 10 For which values in the domain is this graph increasing Give your answer in interval notation Assume the graph extends to finity in both directions Submit
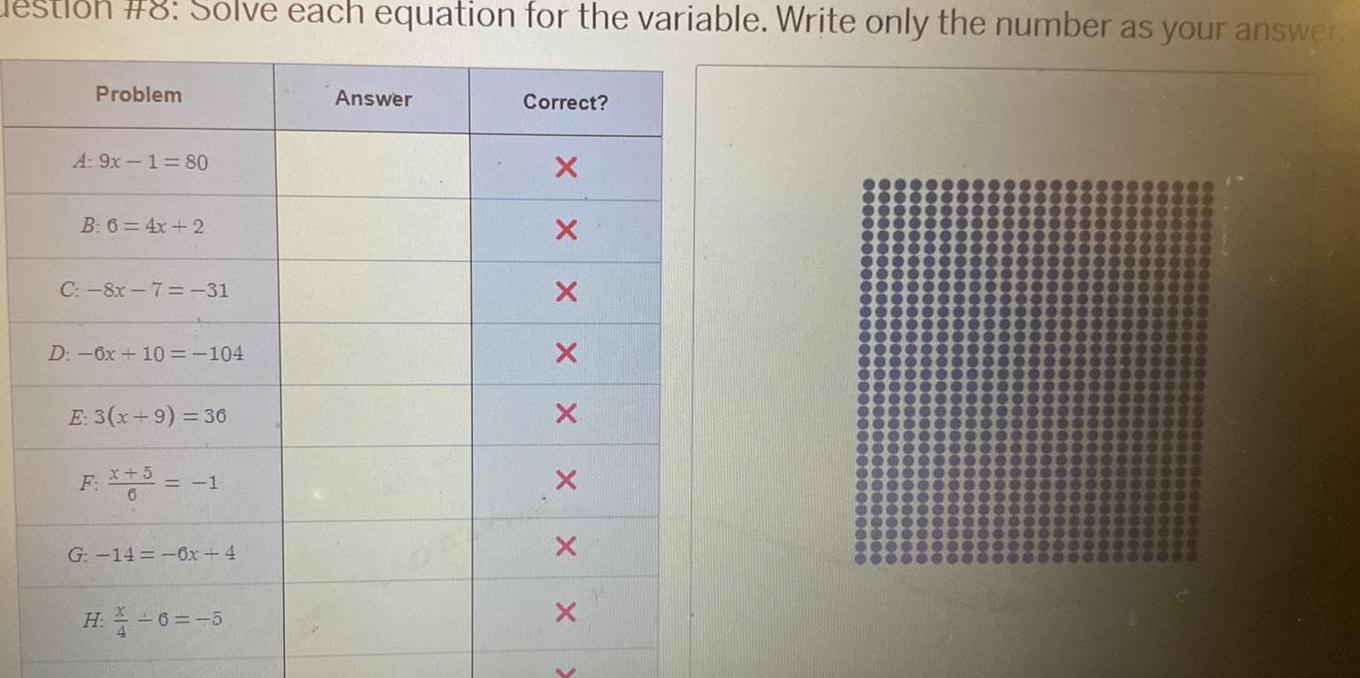
Calculus
Application of derivativesstlon 8 Solve each equation for the variable Write only the number as your answer Problem A 9x180 B 6 4x 2 C 8x 7 31 D 6x 10 104 E 3 x 9 36 F 5 1 G 14 6x 4 H 6 5 Answer Correct X X X X X X X X V

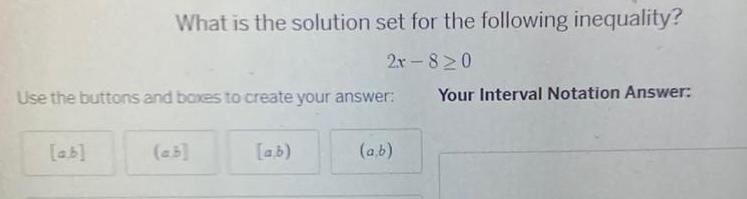
Calculus
Application of derivativesWhat is the solution set for the following inequality 2r 820 Use the buttons and boxes to create your answer ab a b a b Your Interval Notation Answer
Calculus
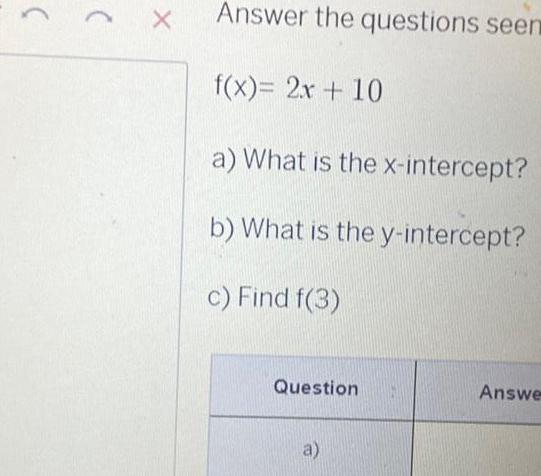
Application of derivativesX Answer the questions seen f x 2x 10 a What is the x intercept b What is the y intercept c Find f 3 Question a Answe
Calculus
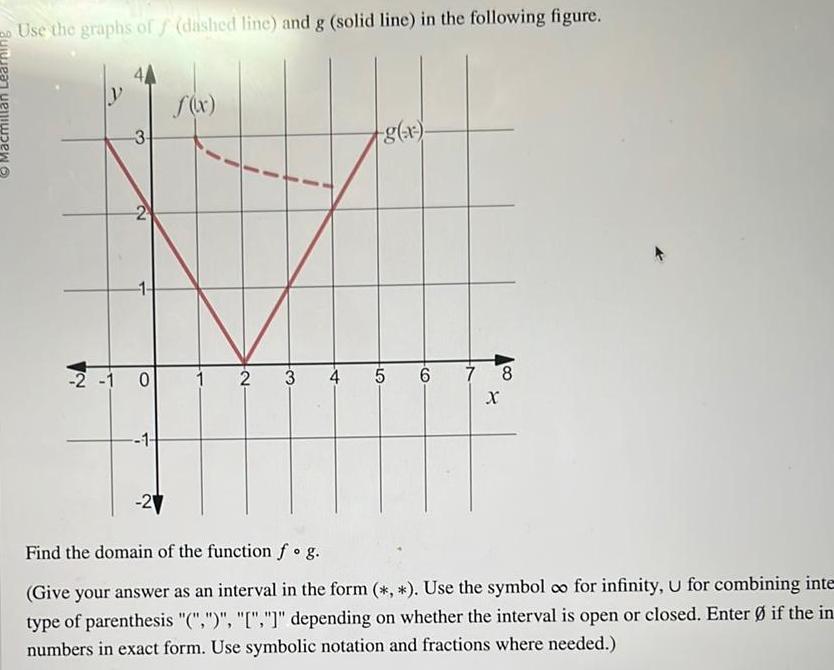
Application of derivativesMacmillan Lear Use the graphs of f dashed line and g solid line in the following figure a 2 1 3 2 1 0 1 2 f x 1 N 2 1 T 3 1 4 g x 5 6 7 X 8 Find the domain of the function f o g Give your answer as an interval in the form Use the symbol oo for infinity U for combining inte type of parenthesis depending on whether the interval is open or closed Enter if the in numbers in exact form Use symbolic notation and fractions where needed

Calculus
Application of derivativesA group of friends wanted to take a 10 day backpacking trip to Wyoming They checked the weather forecast for their destination s daily low temperatures The dotplot below shows the daily low temperatures in degrees Fahrenheit for their 10 day trip Delly Low Tempente What is the interpretation of the dot above 46 in the dotplot The dot above 46 represents the last day of the trip and about 70 of the days should be cooler than 41 degrees O The dot above 46 represents the warmest day of the trip and about 60 of the days should be cooler than 41 degrees O The dot above 46 represents the last day of the trip and about 60 of the days should be cooler than 41 degrees The dot above 46 represents the warmest day of the trip and about 70 of the days should be cooler than 41 degrees
Calculus
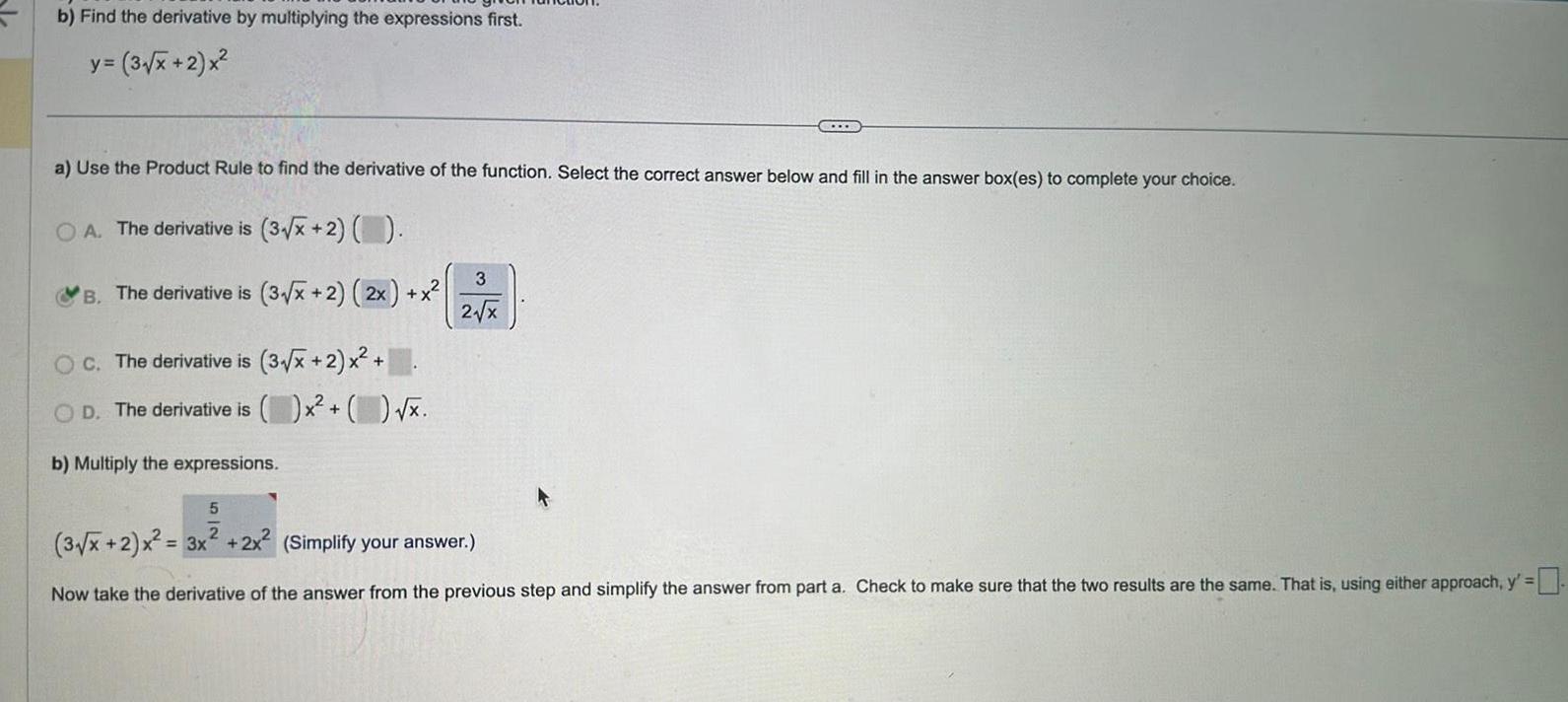
Application of derivativesb Find the derivative by multiplying the expressions first y 3 x 2 x a Use the Product Rule to find the derivative of the function Select the correct answer below and fill in the answer box es to complete your choice OA The derivative is 3 x 2 B The derivative is 3 x 2 2x x OC The derivative is 3 x 2 x D The derivative is b Multiply the expressions x x TULE 3 2 x 5 2 3 x 2 x 3x 2x 2 Simplify your answer Now take the derivative of the answer from the previous step and simplify the answer from part a Check to make sure that the two results are the same That is using either approach y


Calculus
Application of derivativesThe equ 6200 R v V can be used to determine the heart rate R of a person whose heart pumps 6200 milliliters mL of blood per minute and v milliliters of blood per beat Complete parts a through c below a Find the rate of change of heart rate with respect to v the output per beat R v 6200 b Find the heart rate at v 90 mL per beat The heart rate is beats min Round to two decimal places as needed STO Heart rate 100 100 Output per beat 200
Calculus
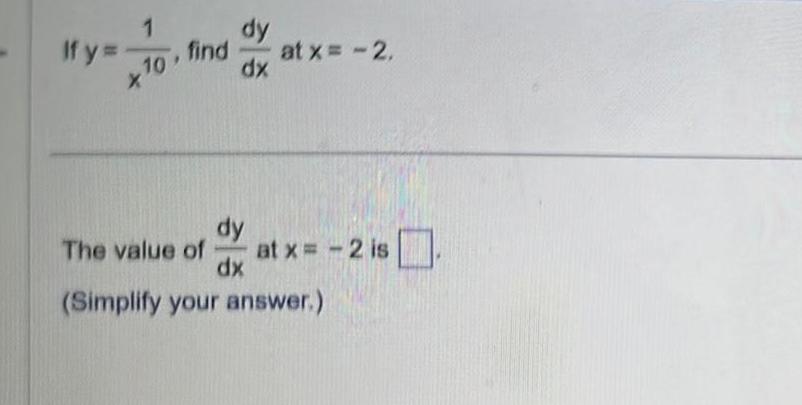
Application of derivativesIf y 1 10 X dy find dx at x 2 The value of dy dx Simplify your answer at x 2 is
Calculus
Application of derivativesFor the polynomial below 3 is a zero g x x 9x 24x 18 Express g x as a product of linear factors g x 0


Calculus
Application of derivativesPrevious Solve the given equation If there are more than one solution separate 75 44
Calculus
Application of derivatives25 4 Question 26 a b 25 40 answered Simplify 80x6y to the form a b Quectio

Calculus
Application of derivativesMultiply and simplify completely 3xy 10 Your answer will be in the form A B where A and B are expressions Enter your expressions for A and B in the boxes below A B 6x1026
Calculus
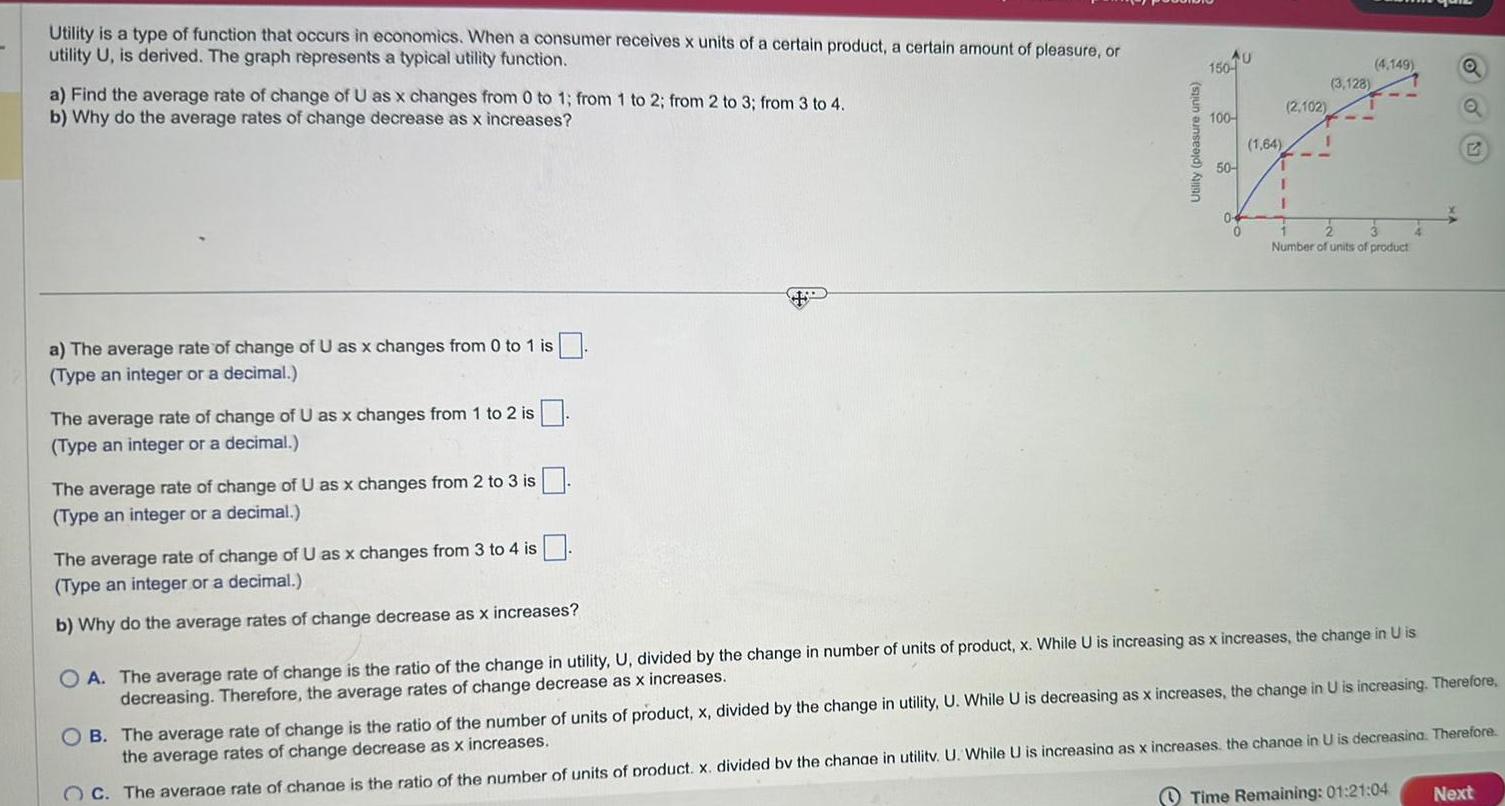
Application of derivativesUtility is a type of function that occurs in economics When a consumer receives x units of a certain product a certain amount of pleasure or utility U is derived The graph represents a typical utility function a Find the average rate of change of U as x changes from 0 to 1 from 1 to 2 from 2 to 3 from 3 to 4 b Why do the average rates of change decrease as x increases a The average rate of change of U as x changes from 0 to 1 is Type an integer or a decimal The average rate of change of U as x changes from 1 to 2 is Type an integer or a decimal The average rate of change of U as x changes from 2 to 3 is Type an integer or a decimal The average rate of change of U as x changes from 3 to 4 is Type an integer or a decimal b Why do the average rates of change decrease as x increases Utility pleasure units AU 150 100 50 2 102 3 128 1 64 1 1 4 149 2 3 Number of units of product OA The average rate of change is the ratio of the change in utility U divided by the change in number of units of product x While U is increasing as x increases the change in U is decreasing Therefore the average rates of change decrease as x increases Q Q Time Remaining 01 21 04 G OB The average rate of change is the ratio of the number of units of product x divided by the change in utility U While U is decreasing as x increases the change in U is increasing Therefore the average rates of change decrease as x increases OC The average rate of change is the ratio of the number of units of product x divided by the change in utilitv U While U is increasing as x increases the change in U is decreasing Therefore Next
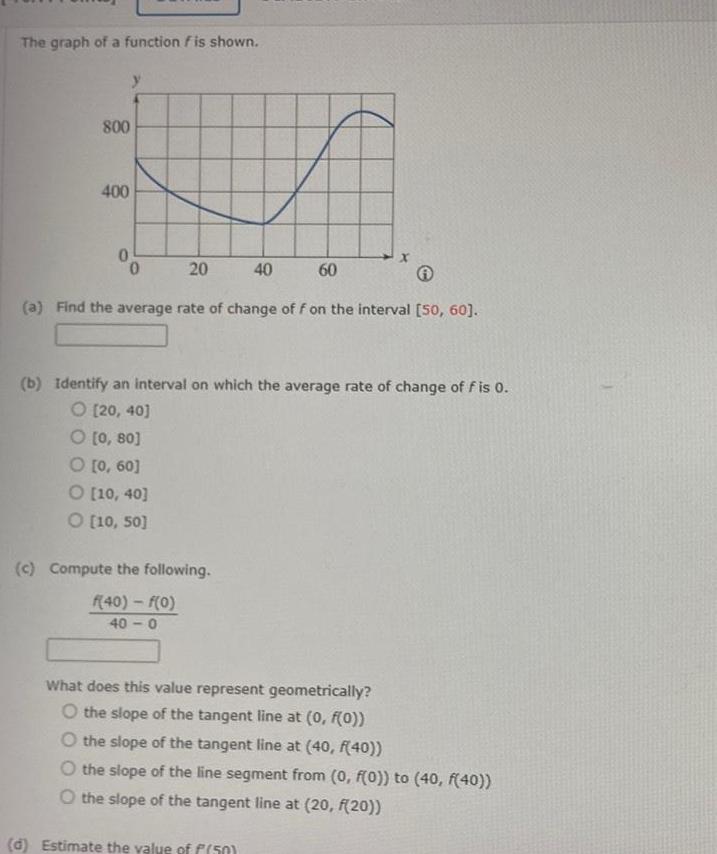
Calculus
Application of derivativesThe graph of a function f is shown 800 400 0 0 20 40 c Compute the following f 40 f 0 40 0 60 a Find the average rate of change of f on the interval 50 60 b Identify an interval on which the average rate of change of f is 0 O 20 40 O 0 80 O 0 60 O 10 40 O 10 50 X What does this value represent geometrically O the slope of the tangent line at 0 f 0 d Estimate the value of f 50 O the slope of the tangent line at 40 f 40 O the slope of the line segment from 0 f 0 to 40 f 40 O the slope of the tangent line at 20 f 20
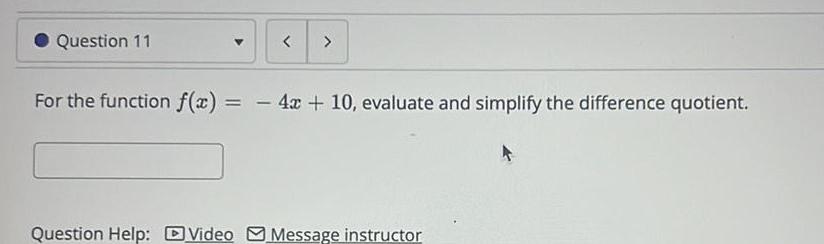
Calculus
Application of derivativesQuestion 11 For the function f x 4x 10 evaluate and simplify the difference quotient Question Help Video Message instructor

Calculus
Application of derivatives5t 98 6 where T is the temperature in degrees Fahrenheit at time t in hours 2 The temperature T of a person during an illness is given by T t a Find the rate of change of the temperature with respect to time b Find the temperature at t 1 hr c Find the rate of change of the temperature at t 1 hr a Find the rate of change of the temperature with respect to time T t AT 1 102 98 0


Calculus
Application of derivativesa Graph the function f x 2x 9x 10 b Draw a tangent line to the graph at the point whose x coordinate is 3 O A b Choose the correct graph of the tangent line OA Ay Q OA f 3 Q Simplify your answer O B B There is no solution O B Ay Ay Q D c f x d Select the correct choice below and if necessary fill in the answer box to complete your choice O C O C Ay Q G O D O D Q Time Remaining 01 18 52 Next
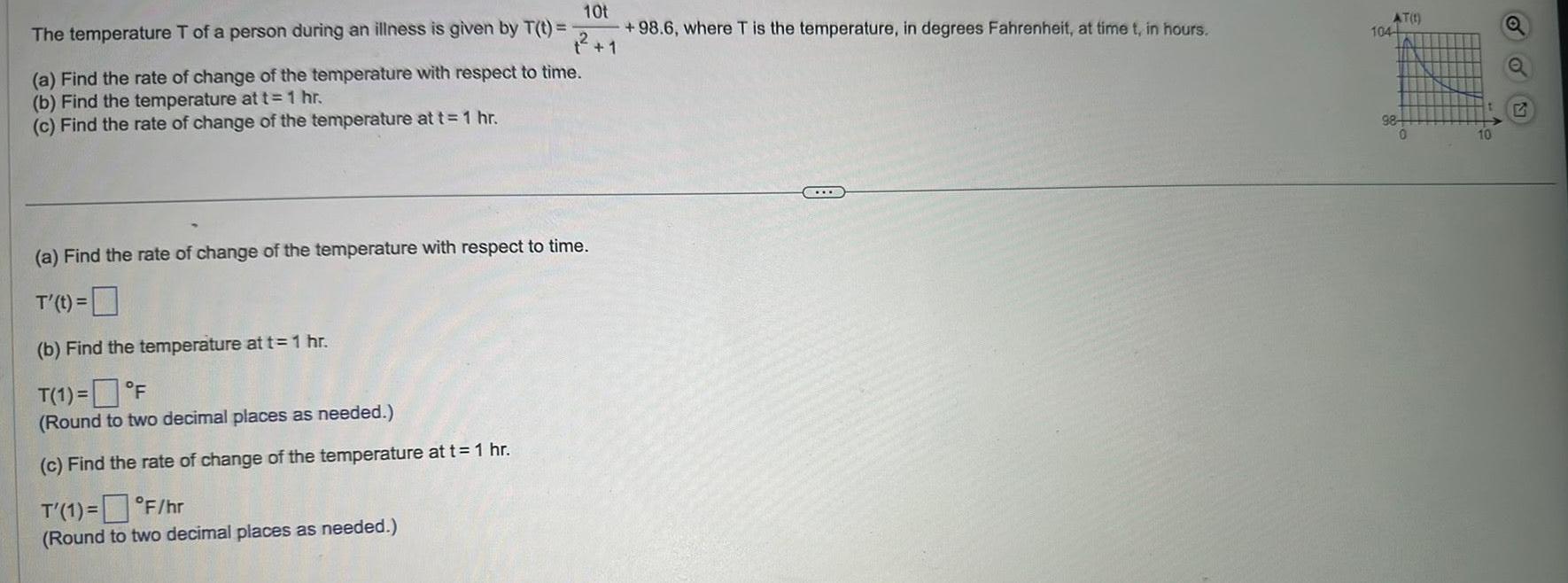
Calculus
Application of derivatives10t 1 The temperature T of a person during an illness is given by T t a Find the rate of change of the temperature with respect to time b Find the temperature at t 1 hr c Find the rate of change of the temperature at t 1 hr a Find the rate of change of the temperature with respect to time T t b Find the temperature at t 1 hr T 1 F Round to two decimal places as needed c Find the rate of change of the temperature at t 1 hr T 1 F hr Round to two decimal places as needed 98 6 where T is the temperature in degrees Fahrenheit at time t in hours AT 1 104 98 0 10 Q
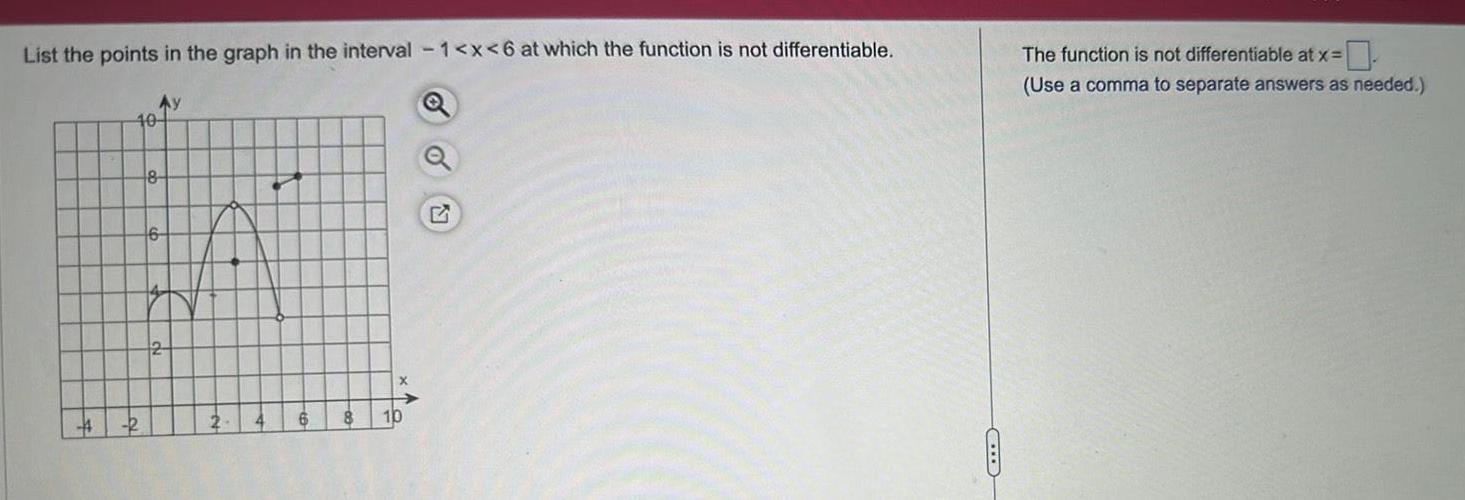
Calculus
Application of derivativesList the points in the graph in the interval 1 x 6 at which the function is not differentiable Ay 40 R 8 4 6 8 10 SOU The function is not differentiable at x Use a comma to separate answers as needed
Calculus
Application of derivativesSuppose that a fashion company determines that the cost in dollars of producing x cellphone cases is given by C x 0 05x 60x Find result to the company C 301 C 300 Simplify your answer 301 300 Interpret the significance of this result to the company Choose the correct answer below OA It represents the additional cost to produce one more item after making 300 items B It represents the average cost of producing 301 items C It represents the additional cost to produce one item after the fixed costs have been paid D It represents the average cost per item to produce 300 items C 301 C 300 301 300 and interpret the significance of this
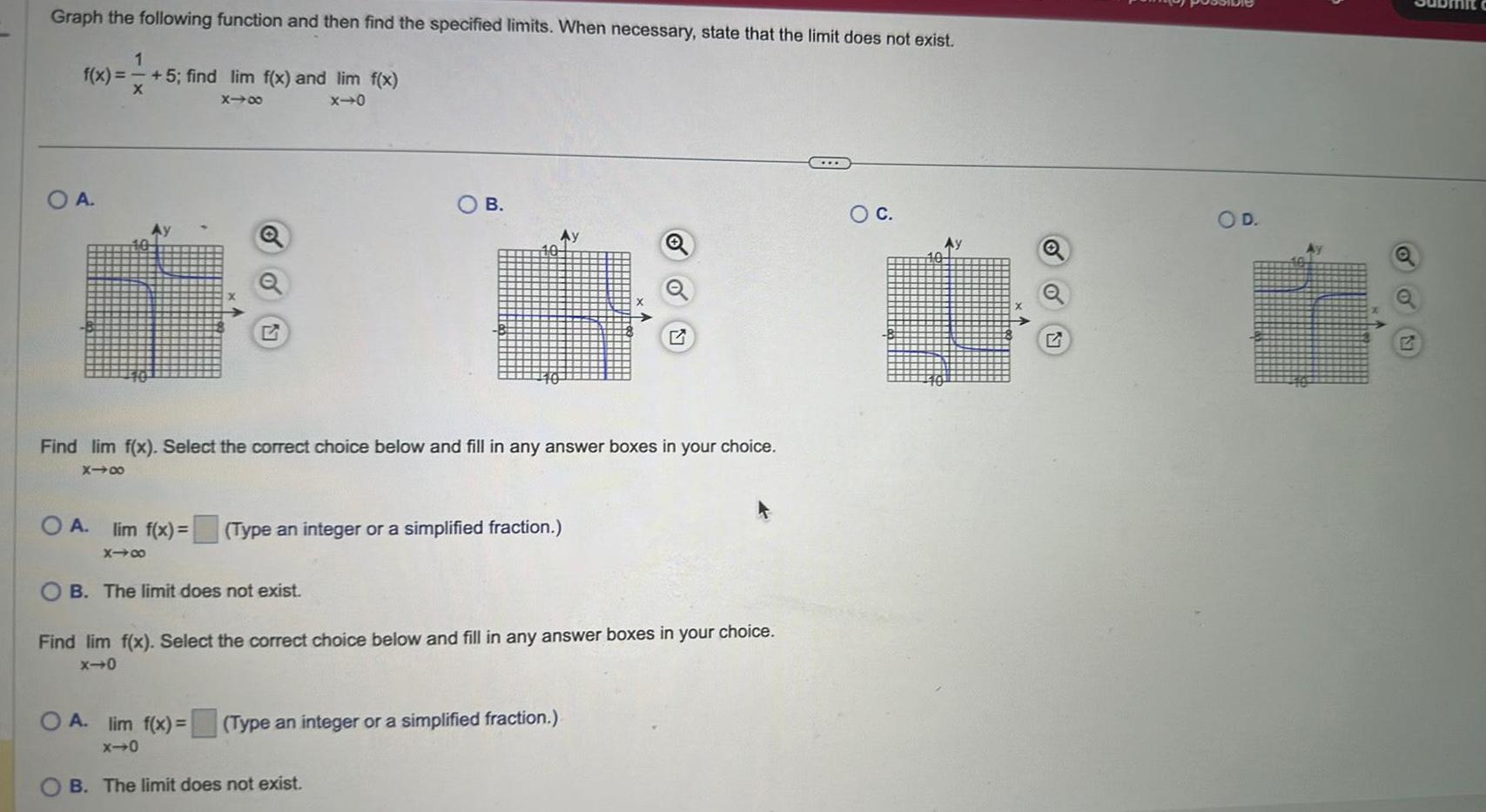
Calculus
Application of derivativesGraph the following function and then find the specified limits When necessary state that the limit does not exist 1 f x 5 find lim f x and lim f x X 818 x 0 OA OA lim f x x48 Find lim f x Select the correct choice below and fill in any answer boxes in your choice 818 OB The limit does not exist B Type an integer or a simplified fraction O A lim f x x 0 Find lim f x Select the correct choice below and fill in any answer boxes in your choice x 0 Q Type an integer or a simplified fraction B The limit does not exist O C Q O D Ay 1
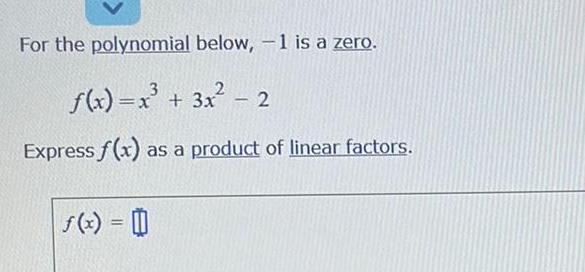
Calculus
Application of derivativesFor the polynomial below 1 is a zero 3 f x x 3x 2 Express f x as a product of linear factors f x
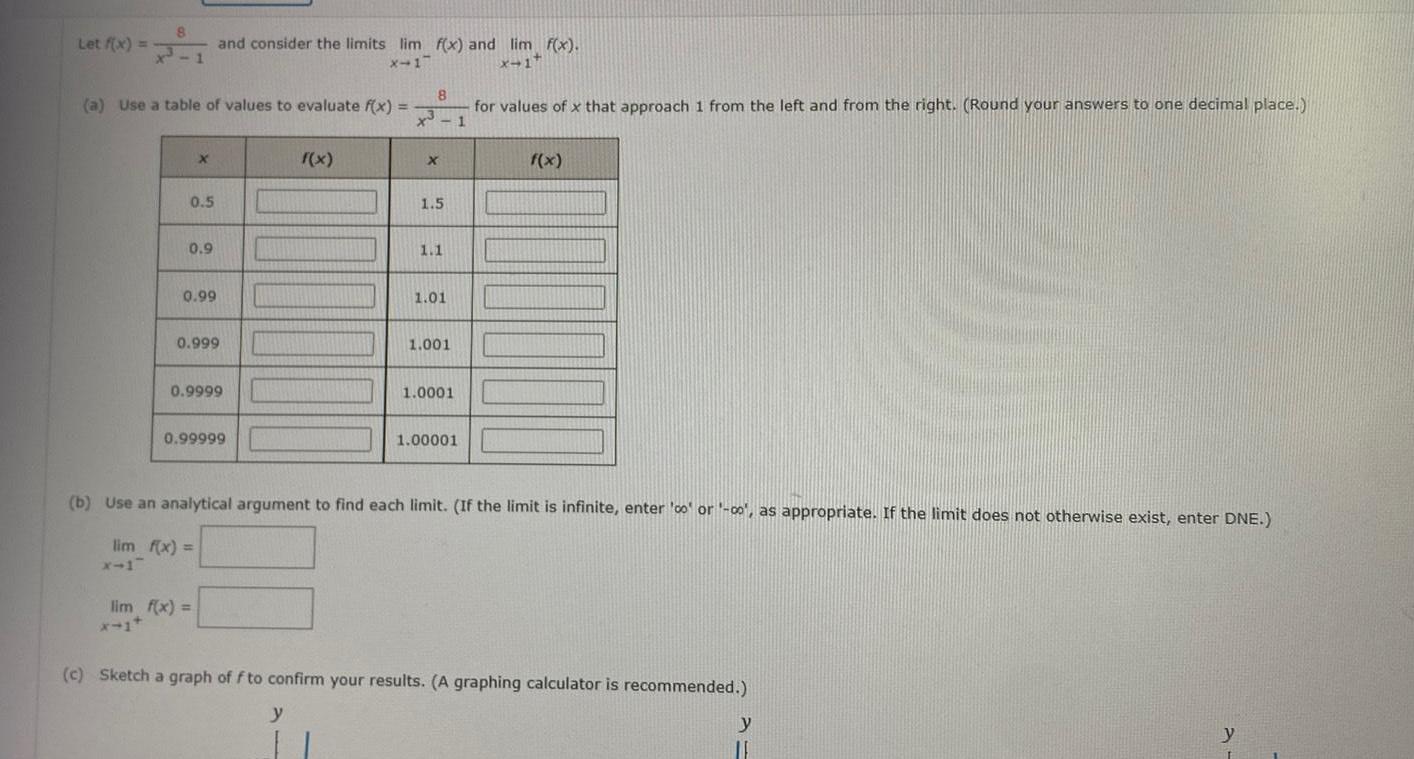
Calculus
Application of derivativesLet f x a Use a table of values to evaluate f x 3 X 0 5 0 9 0 99 and consider the limits lim f x and lim f x X 17 x 1 0 999 0 9999 0 99999 lim f x f x 8 X 1 5 1 1 1 01 1 001 1 0001 for values of x that approach 1 from the left and from the right Round your answers to one decimal place 1 1 00001 f x b Use an analytical argument to find each limit If the limit is infinite enter co or 00 as appropriate If the limit does not otherwise exist enter DNE lim f x c Sketch a graph of f to confirm your results A graphing calculator is recommended y y y
Calculus
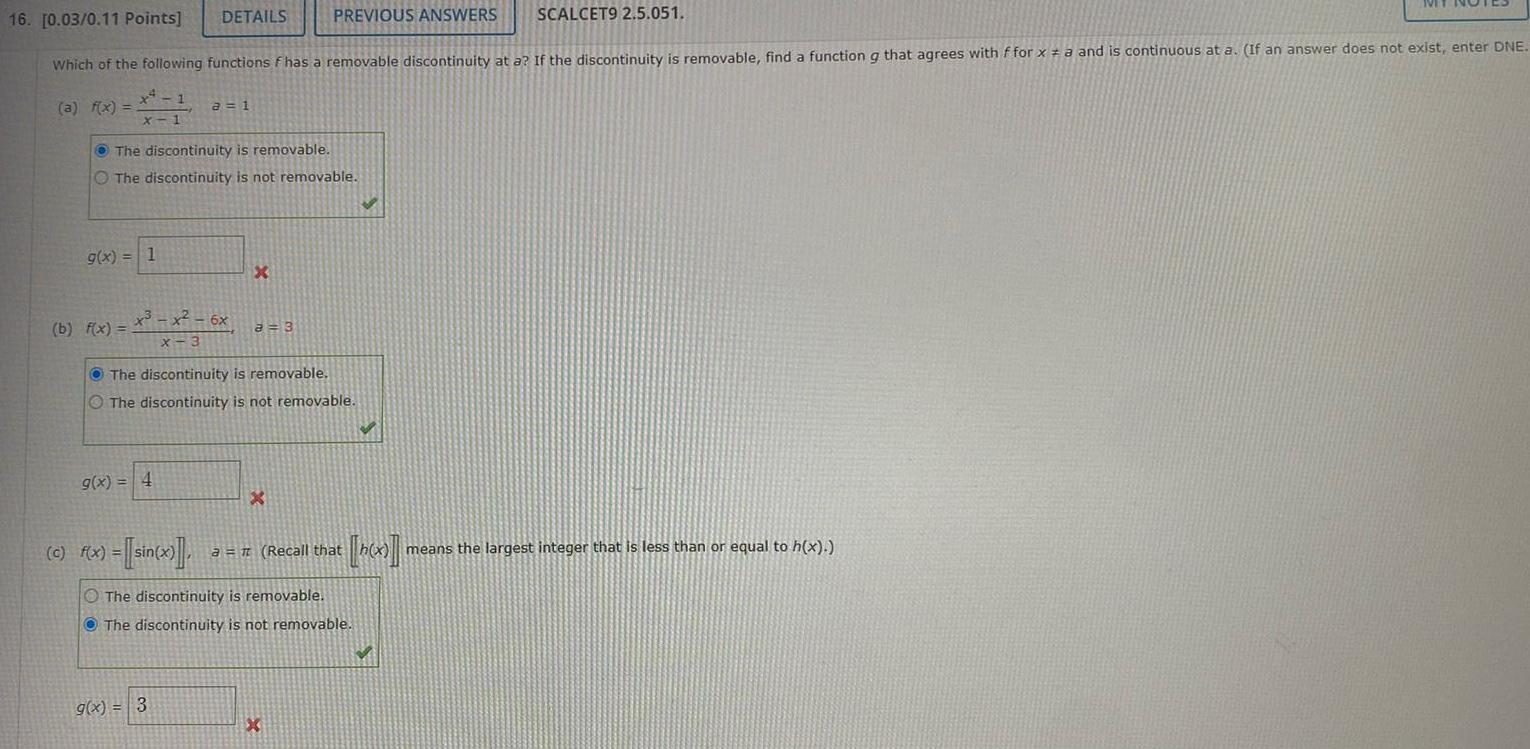
Application of derivativesa f x 16 0 03 0 11 Points Which of the following functions f has a removable discontinuity at a If the discontinuity is removable find a function g that agrees with f for x a and is continuous at a If an answer does not exist enter DNE 1 X 1 g x 1 b f x DETAILS The discontinuity is removable The discontinuity is not removable a 1 x x 6x X 3 g x 4 g x 3 X PREVIOUS ANSWERS SCALCET9 2 5 051 a 3 The discontinuity is removable The discontinuity is not removable X c f x sin x a Recall that The discontinuity is removable The discontinuity is not removable IVIT means the largest integer that is less than or equal to h x

Calculus
Application of derivativesDivide 19x 6x 20 1 2x 3 Write your answer in the following form Quotient 19x 6x 20 2x 3 0 X 2x 3 0 2 Remainder x 2x 3
Calculus
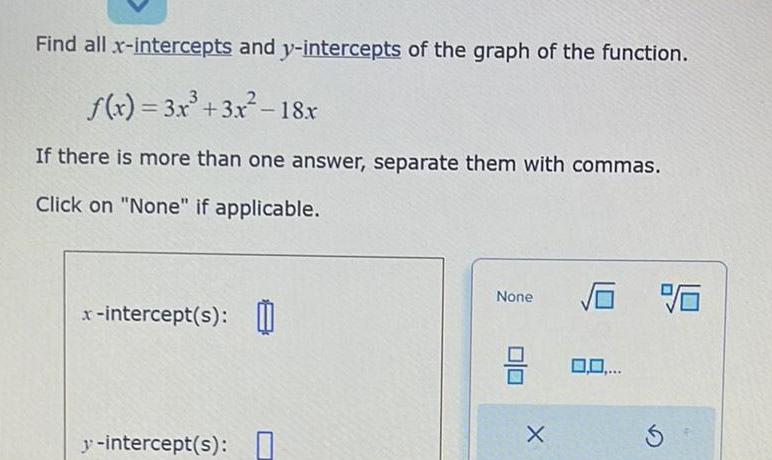
Application of derivativesFind all x intercepts and y intercepts of the graph of the function f x 3x 3x 18x If there is more than one answer separate them with commas Click on None if applicable x intercept s y intercept s None 3 X 0 0

Calculus
Application of derivativesExplain what it means to say that lim f x 8 and X 3 X 3 O As x approaches 3 from the right f x approaches 8 As x approaches 3 from the left f x approaches 5 O As x approaches 3 from the left f x approaches 8 As x approaches 3 from the right f x approaches 5 O As x approaches 3 f x approaches 5 but f 3 8 O As x approaches 3 f x approaches 8 but f 3 5 lim f x 5 In this situation is it possible that lim f x exists Explain X 3 O Yes f x could have a hole at 3 8 and be defined such that f 3 5 O Yes f x could have a hole at 3 5 and be defined such that f 3 8 Yes if f x has a vertical asymptote at x 3 it can be defined such that lim f x 8 lim f x 5 and lim f x exists X 3 X 3 X 3 No lim f x cannot exist if lim f x lim f x X 3