Application of derivatives Questions and Answers
Calculus
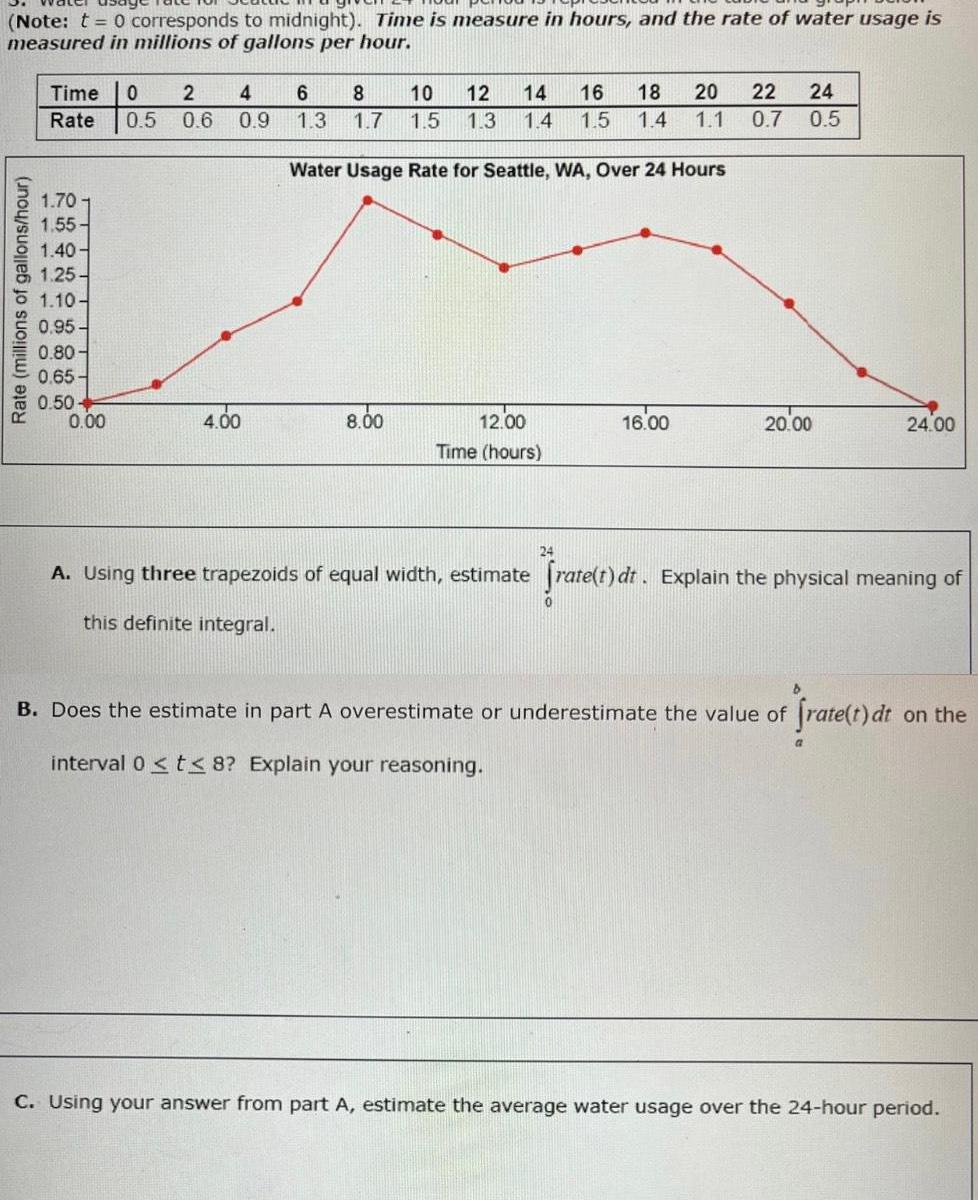
Application of derivativesNote t 0 corresponds to midnight Time is measure in hours and the rate of water usage is measured in millions of gallons per hour Rate millions of gallons hour Time 0 Rate 0 5 1 70 1 55 1 40 1 25 1 10 0 95 0 80 0 65 0 50 0 00 2 0 6 4 0 9 4 00 6 8 1 3 1 7 10 12 14 16 18 20 22 24 1 5 1 3 1 4 1 5 1 4 1 1 0 7 0 5 Water Usage Rate for Seattle WA Over 24 Hours 8 00 12 00 Time hours 16 00 20 00 24 00 24 A Using three trapezoids of equal width estimate frate t dt Explain the physical meaning of fratel t dt this definite integral B Does the estimate in part A overestimate or underestimate the value of frate t dt on the interval 0 t 8 Explain your reasoning a C Using your answer from part A estimate the average water usage over the 24 hour period
Calculus
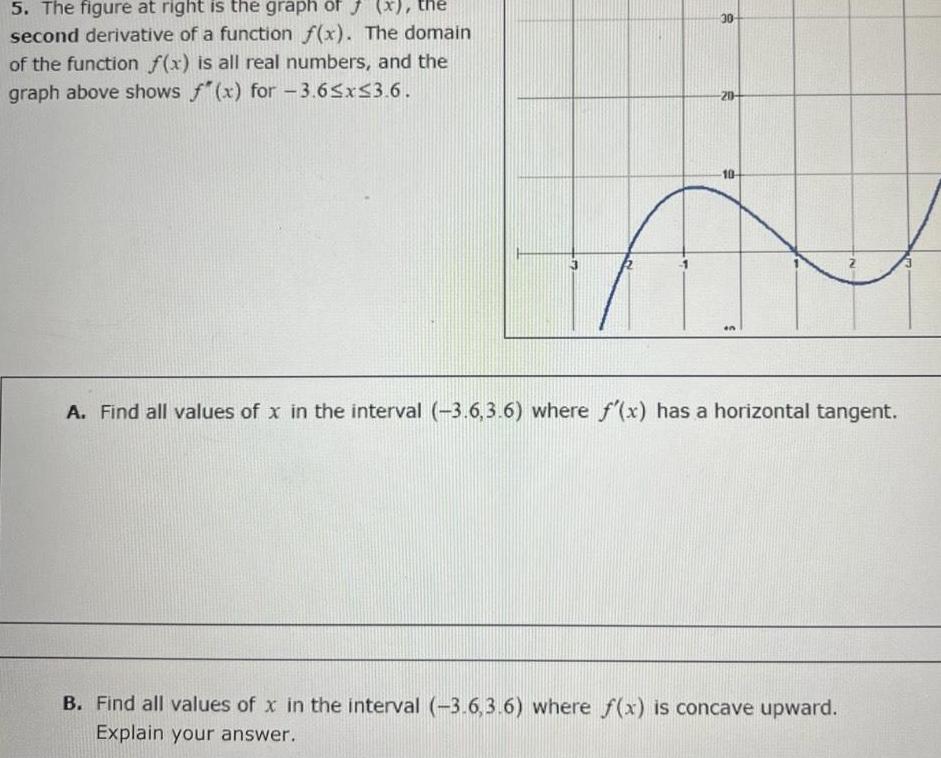
Application of derivatives5 The figure at right is the graph of f x the second derivative of a function f x The domain of the function f x is all real numbers and the graph above shows f x for 3 6 x 3 6 30 20 10 A Find all values of x in the interval 3 6 3 6 where f x has a horizontal tangent B Find all values of x in the interval 3 6 3 6 where f x is concave upward Explain your answer

Calculus
Application of derivativesHow many critical points does the function f x x 1 6 x 5 have O A 6 OB 13 O C 1 OD 7 OE 3
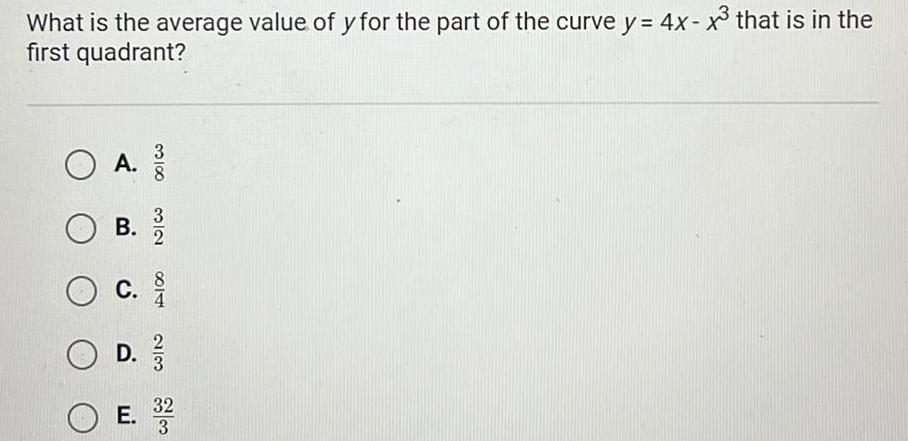
Calculus
Application of derivativesWhat is the average value of y for the part of the curve y 4x x that is in the first quadrant O A B 3 2 O c D 2 3 E 3 2 2

Calculus
Application of derivativesThe slope of the line normal to the graph of y 2 ln sec x at x is OA 2 OB 1 2 OC 2 D nonexistent E OE 1 2

Calculus
Application of derivativesIn an experiment to study the growth of bacteria a medical student measured 5000 bacteria at time 0 and 8000 at time 10 minutes Assuming that the number of bacteria grows exponentially how many bacteria will be present after 30 minutes A 14000 bacteria B 29333 bacteria C 24332 bacteria D 20480 bacteria E 17830 bacteria
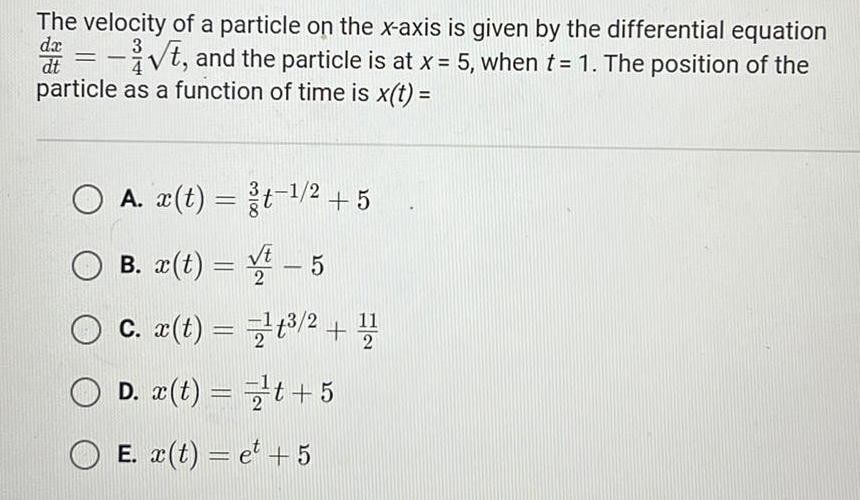
Calculus
Application of derivativesThe velocity of a particle on the x axis is given by the differential equation 3 da t and the particle is at x 5 when t 1 The position of the dt particle as a function of time is x t O A x t gt 2 5 B x t t 5 c x t 1 12 D x t t 5 E x t et 5
Calculus
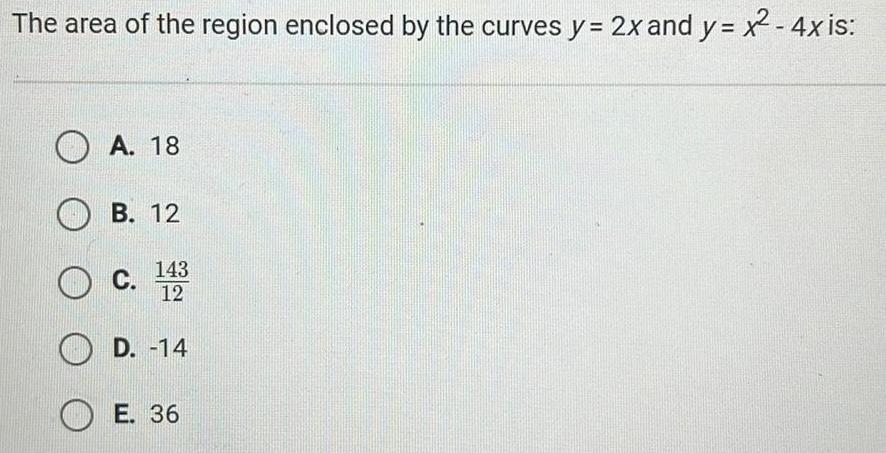
Application of derivativesThe area of the region enclosed by the curves y 2x and y x 4x is A 18 B 12 143 O C 12 D 14 E 36
Calculus
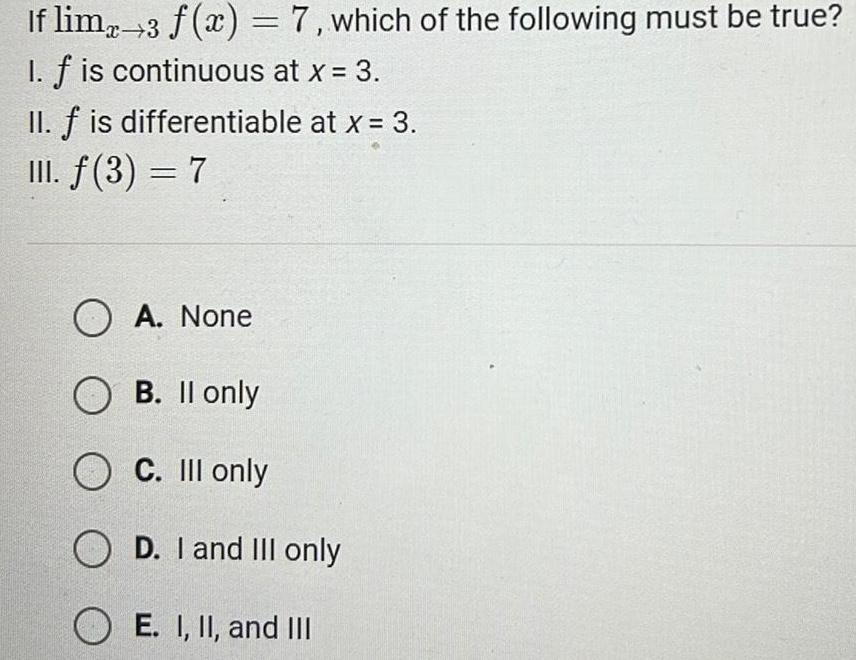
Application of derivativesIf limx 3 f x 7 which of the following must be true I f is continuous at x 3 II f is differentiable at x 3 III f 3 7 OA None O B II only O C III only OD I and III only OE I II and III

Calculus
Application of derivativesWhich of the following is a right hand endpoint Riemann sum approximation to f f x dx with six equal subdivisions A 1 5 2 f 2 5 f 3 3 5 4 O B O c f 1 f 1 5 f 2 f 2 5 f 3 f 3 5 f 1 f 1 5 f 2 f 2 5 f 3 f 3 5 O D f 1 f 1 5 f 2 f 2 5 f 3 f 3 5 E 1 5 f 2 f 2 5 3 f 3 5 f 4
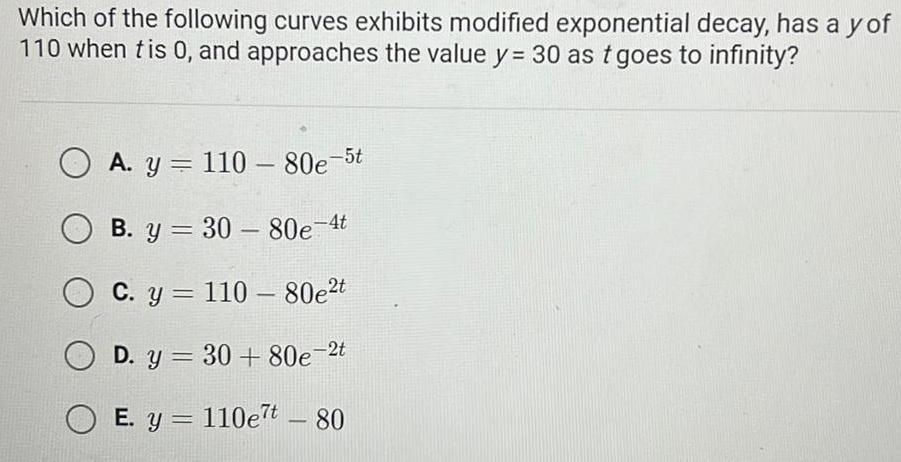
Calculus
Application of derivativesWhich of the following curves exhibits modified exponential decay has a y of 110 when tis 0 and approaches the value y 30 as t goes to infinity OA y 110 80e 5t B y 30 80e 4t OC y 110 80e t OD y 30 80e 2t OE y 110e t 80

Calculus
Application of derivativesThe rate of change of P with respect to tis directly proportional to 10 and inversely proportional to the cube root of P The differential equation that models this situation is O A d OB c de dt k 10 t 1 T kv P 10 t 10 t P dP O D dt k 10 t VP O E k 10 t P
Calculus
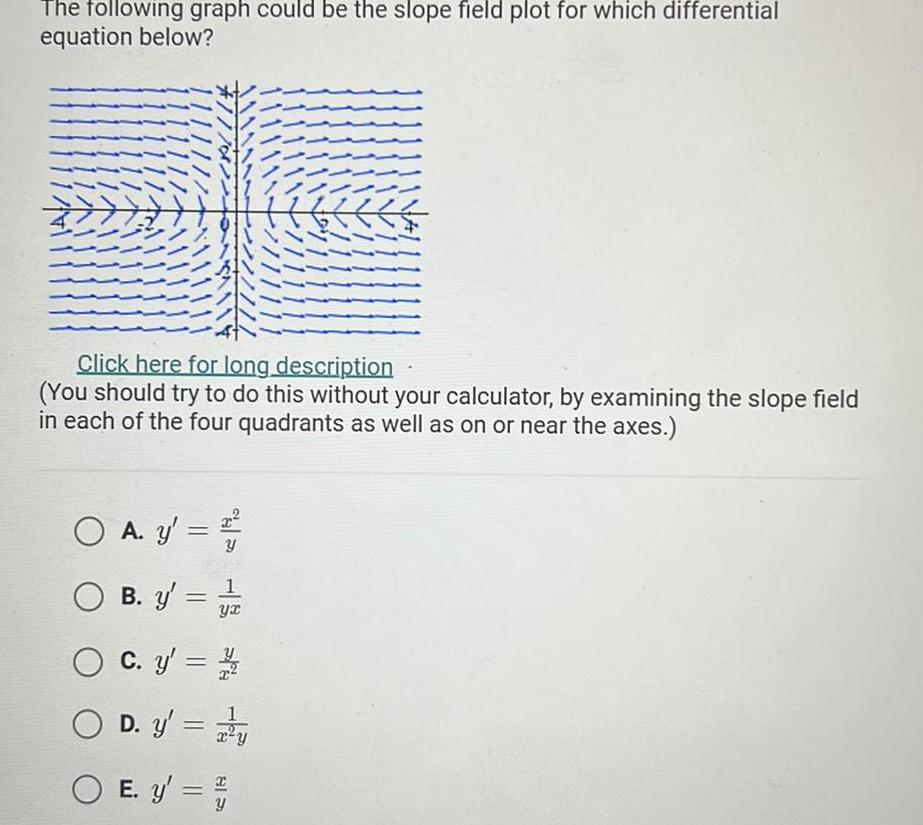
Application of derivativesThe following graph could be the slope field plot for which differential equation below X 2 O A y Y Click here for long description You should try to do this without your calculator by examining the slope field in each of the four quadrants as well as on or near the axes O B y 1 yx O O D y O E y C y 1 2 1111111 Go I 1 1 1 1 1 1 1 1 1 11 11

Calculus
Application of derivativesSolve the following differential equation with initial conditions y e 2t 10e t y 0 1 y 0 0 The solution is 5 4t O A y e e 3t O B y e 2t 54 2 O C y 4e 2t 16e t 6t 19 OD y e 2t e4t 1 O E y 2t e t 2t 4t 8

Calculus
Application of derivativeshe acceleration of a particle moving along the x axis at time tis given by a t 6t 2 If the velocity is 25 when t 3 and the position is 10 when t 1 the position x t A t t 4t 6 B 36t 4t2 77t 55 O c 9t 1 D t3 t 9t 20 OE 3t 2t 4
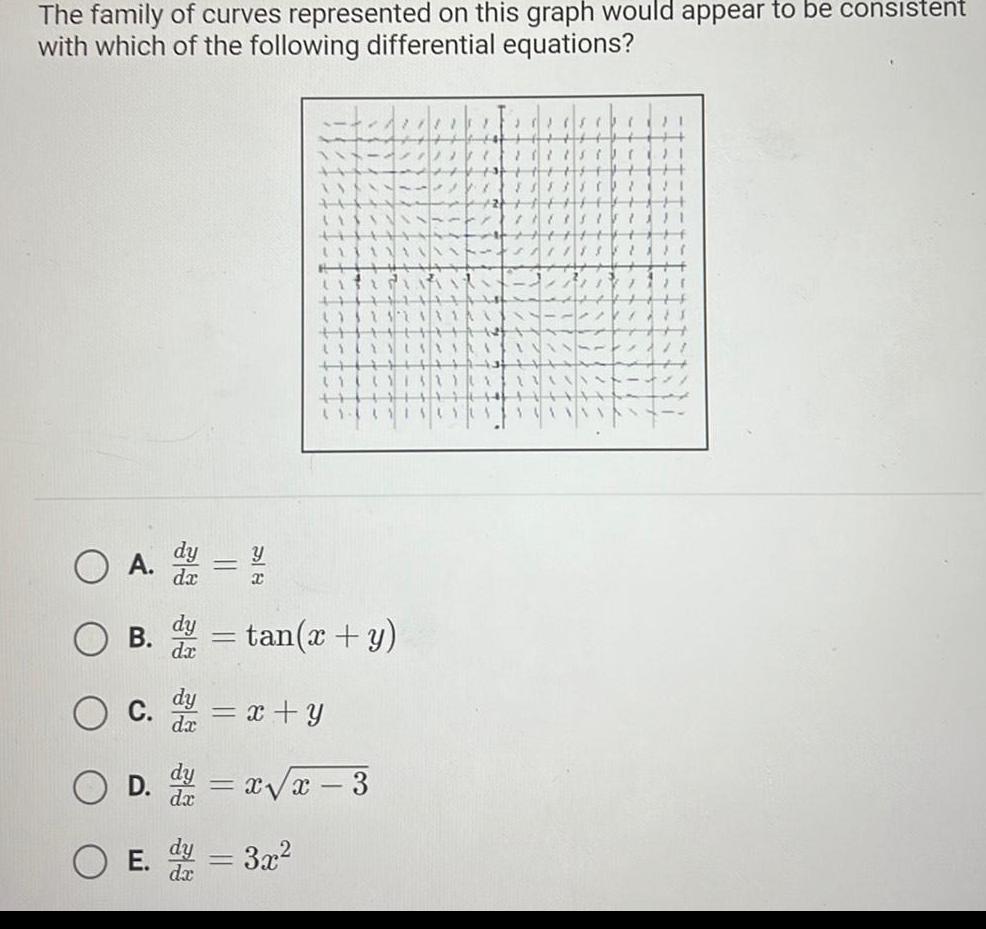
Calculus
Application of derivativesThe family of curves represented on this graph would appear to be consistent with which of the following differential equations A d B D da Y Te tan x y d x y x x 3 E d 3x

Calculus
Application of derivativesLet f be the function defined by f x X Which of the following statements is true OA fis discontinuous at x 0 B fis an odd function O c f 0 0 OD f x 0 for x 0 E fhas a relative maximum x for for x 0 x 0

Calculus
Application of derivativesFor the following function make a table of slopes of secant lines and make a conjecture about the slope of the tangent line at the indicated point f x 11 cos x at x RIN x 2 Complete the table below Round the final answer to three decimal places as needed Round all intermediate values to four decimal places as needed Slope of secant line Interval T
Calculus
Application of derivativesWhich of the following differential equations is are not separable 1 t yt 1 dt II d y dx 3xy III dy y yx da O A I only O B II only O C III only D II and III dy dx OE I and III
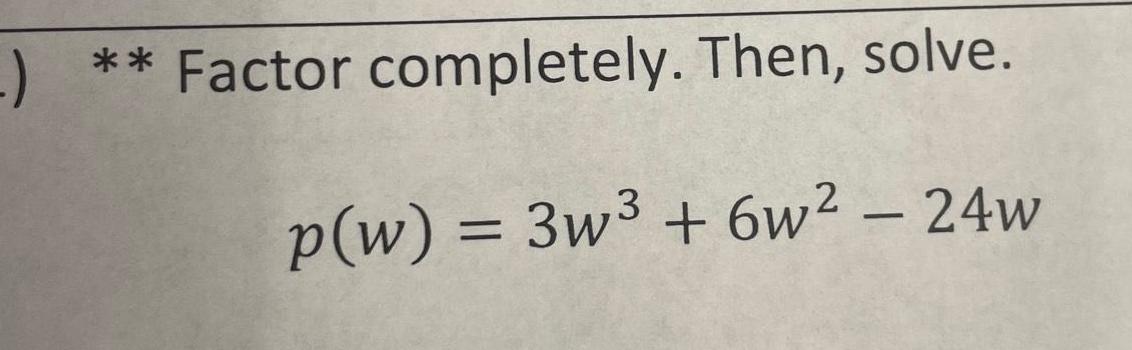

Calculus
Application of derivatives9 Discontinuities at 0 and 3 but continuous from the right at 0 and from the left at 3

Calculus
Application of derivativesIf x 2xy y 2 at the point 1 1 dy is da A 0 1 OB B 2 O C 12 2 OD nonexistent OE
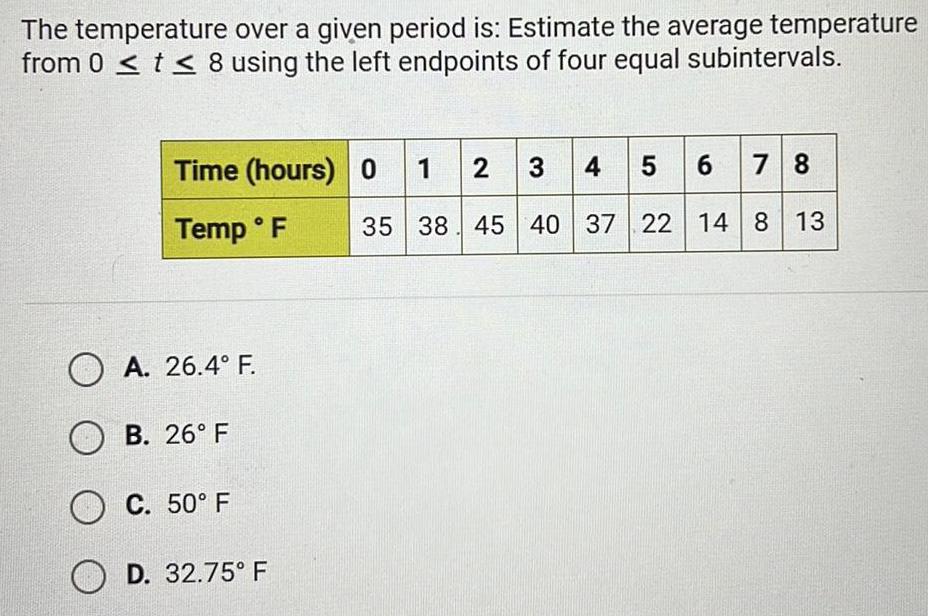
Calculus
Application of derivativesThe temperature over a given period is Estimate the average temperature from 0 t 8 using the left endpoints of four equal subintervals Time hours 0 1 2 3 4 5 6 7 8 Temp F 35 38 45 40 37 22 14 8 13 A 26 4 F B 26 F C 50 F OD 32 75 F

Calculus
Application of derivativesLet f be a polynomial function with degree greater than 2 If a b and f a f b 1 which of the following must be true for at least one value of x between a and b I f x 0 11 f x 0 III f x 0 OA None OB I only O C II only OD I and II only OE I II and III

Calculus
Application of derivativesConsider the position function s t 4 9t 29t 17 Complete the following table with the appropriate average velocities and then make a conjecture about the value of the instantaneous velocity at t 4 Complete the following table Type exact answers Type integers or decimals Time Interval Average Velocity 4 5 4 4 1 4 4 01 4 4 001 4 4 0001

Calculus
Application of derivativesThe slope of the line normal to the curve ex x 2 10 at the point 0 3 is OA O B 6 O C 6 O D 6 OE Undefined

Calculus
Application of derivatives2 Which of the following equations is perpendicular to the graph of 4x 3y 10 A 3x 4y 10 B 4x 3y 10 C 3x 4y 12 1 D 3y 12 4
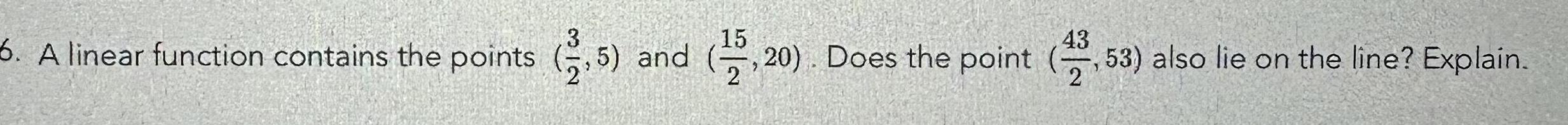
Calculus
Application of derivatives3 6 A linear function contains the points 2 5 and 15 20 Does the point 43 53 also lie on the line Explain 2

Calculus
Application of derivatives4 Line 1 passes through the points 2 5 and 6 k and is perpendicular to the line given by y 1 x 1 5 Find the value of k

Calculus
Application of derivatives1 Write the equation of the line that is perpendicular to y 5x and passes through 7 2

Calculus
Application of derivativesThe position of an object moving vertically along a line is given by the function s t 4 9t2 26t 17 Find the average velocity of the object over the following intervals a 0 7 b 0 4 c 0 1 d 0 h where h 0 is a real number

Calculus
Application of derivativesO A 2 ln sin 0 2 4 C OB In sin 0 2 4 C O c 2 ln cos 0 2 4 C O D In cos 0 2 4 C OE None of these s

Calculus
Application of derivativesg x x 2x 1 What is the slope of the tangent line to the curve g x at the point 2 1 O A 1 OB 5 OC 8 OD 14 OE E

Calculus
Application of derivativesz 2 x y is an equation for the tangent plane to z f x y at the point 0 0 Which of the following is the linear approximation for f 0 02 0 01 O2 03 1 97 1 99 O2 01

Calculus
Application of derivativesSuppose z 1 2x 3y is an equation for the tangent plane to z f x y at 0 0 Then we also know that select all that apply Of 1 1 0 Ofz 0 0 2 Of 0 0 3 Of 0 0 1 The vector n 2 3 1 is orthogonal to the tangent plane


Calculus
Application of derivativesda In 12x 4 dx 1 12x O A OB OC None of the above O D 12 12x 4 OE X 1 12x 4
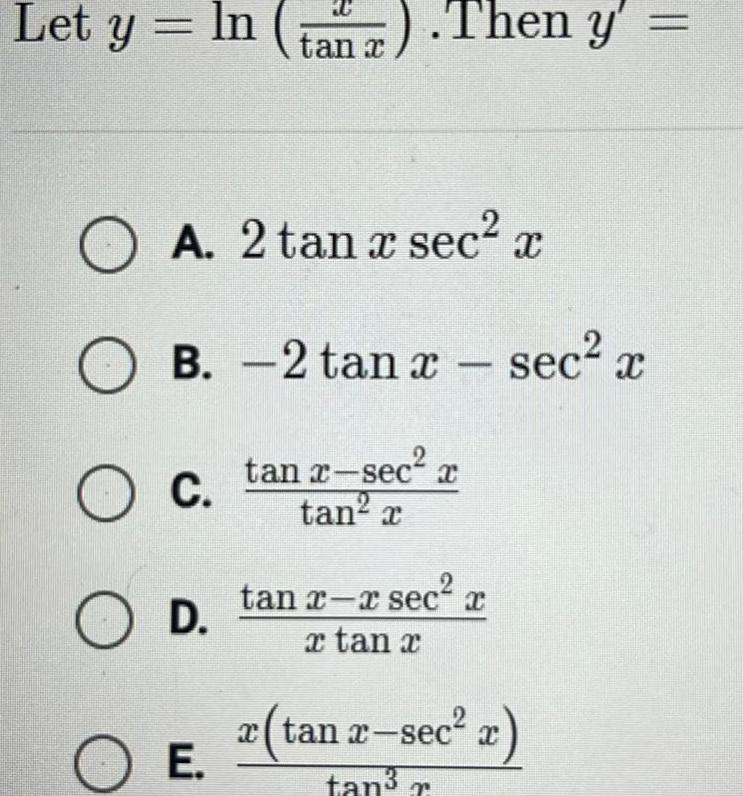
Calculus
Application of derivativesLet y In t tan a OA 2 tan x sec x O C B 2 tanx sec x tan x secr tan a O D OE Then y tan x x sec x a tan x sec x x tan x sec tan r

Calculus
Application of derivativesThe curve y x log3 x 5 has points of inflection at x OA In 3 5 B There are no points of inflection O c 10 O D D 10 In 3 OE 5

Calculus
Application of derivativesda A 2 In 2 In x 2 2 x In 2 In x 2 O B B O C In 2 2 X O D D 2 In 2 2 In x 2 X O E In 2 2 In x 2 X

Calculus
Application of derivativesLet f x 1 x if x 0 2x 1 if x 0 Evaluate f 3 and f 6 f 3 8 f 6 If you have had difficulty with these problems you should look at Sections 1 1 1 3 of y

Calculus
Application of derivativesO A 22 In 2 In x 2 B In 2 In x 2 In 2 2 I OB O C OD In 2 2 ln x 2 O E In 2 2 In x 2

Calculus
Application of derivatives3000 young trout are introduced into a large fish pond The number of trout still alive after tyears is modeled by the formula N t 3000 0 9 What is the rate of population decrease when the number of trout in the pond reaches 2000 A Approximately 520 trout per year B Approximately 211 trout per year C Approximately 2000 trout per year D Approximately 494 trout per year OE None of the above
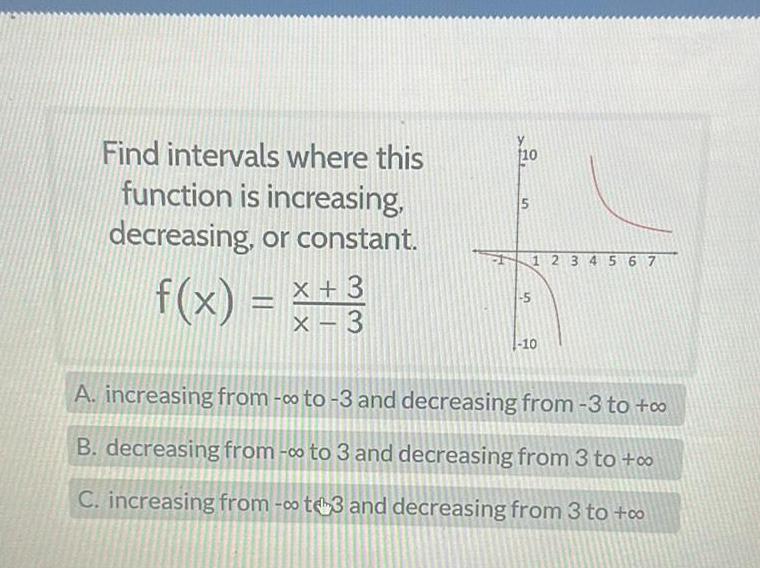
Calculus
Application of derivativesFind intervals where this function is increasing decreasing or constant 3 f x x 3 10 5 1 1 2 3 4 5 6 7 5 10 A increasing from to 3 and decreasing from 3 to o B decreasing from to 3 and decreasing from 3 to o C increasing from t3 and decreasing from 3 to co
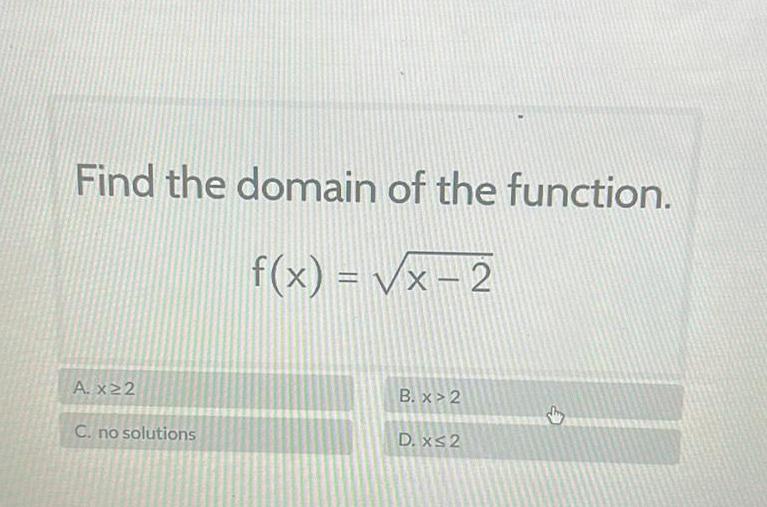
Calculus
Application of derivativesFind the domain of the function f x x 2 A x22 C no solutions B x 2 D x 2

Calculus
Application of derivativesda O A O O B O c x 3 x ln 2 1 3x O D None of the above 1 O E x In 2

Calculus
Application of derivativesdx O A OB B e3r 1 e z 1 2 2 1 e 1 x 1 2 O c 1 1 2 O D 3 D 2 1 2 E 3 1 x 1 2
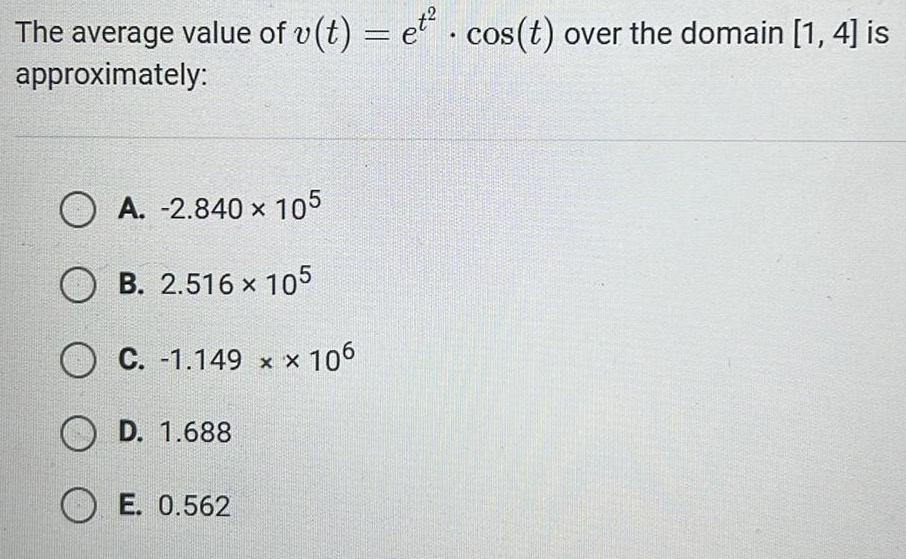
Calculus
Application of derivativesThe average value of v t et cos t over the domain 1 4 is approximately OA 2 840 105 OB 2 516 x 105 O C 1 149 x x 106 OD 1 688 OE 0 562