Application of derivatives Questions and Answers

Calculus
Application of derivativesIf fis continuous for all x which of the following integrals necessarily have the same value cb a f x dxII f x a da III cb 1 f x d ll I 0 ab c 1 f x c dx a c OA I and II only B I and III only OC II and III only D I II and III E No two necessarily have the same value
Calculus
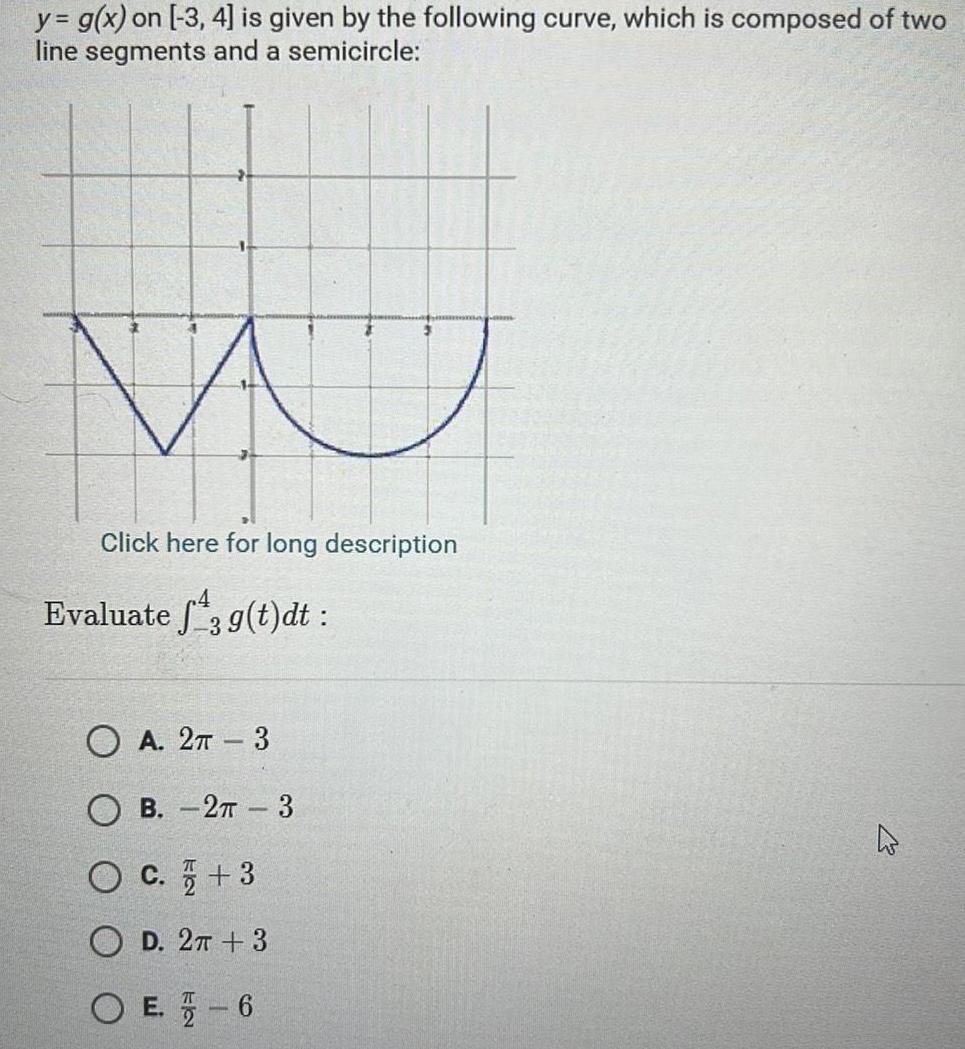
Application of derivativesy g x on 3 4 is given by the following curve which is composed of two line segments and a semicircle Click here for long description Evaluate f3 g t dt OA 2 3 OB 2 3 O C 3 OD 2T 3 OE 6 W

Calculus
Application of derivativesThe function g x 12x sin x is the first derivative of f x If f 0 2 what is the value of f 2 O A 2 5 OB 8T2 2 OC 32 2 OD 30T 2 OE 47 8
Calculus
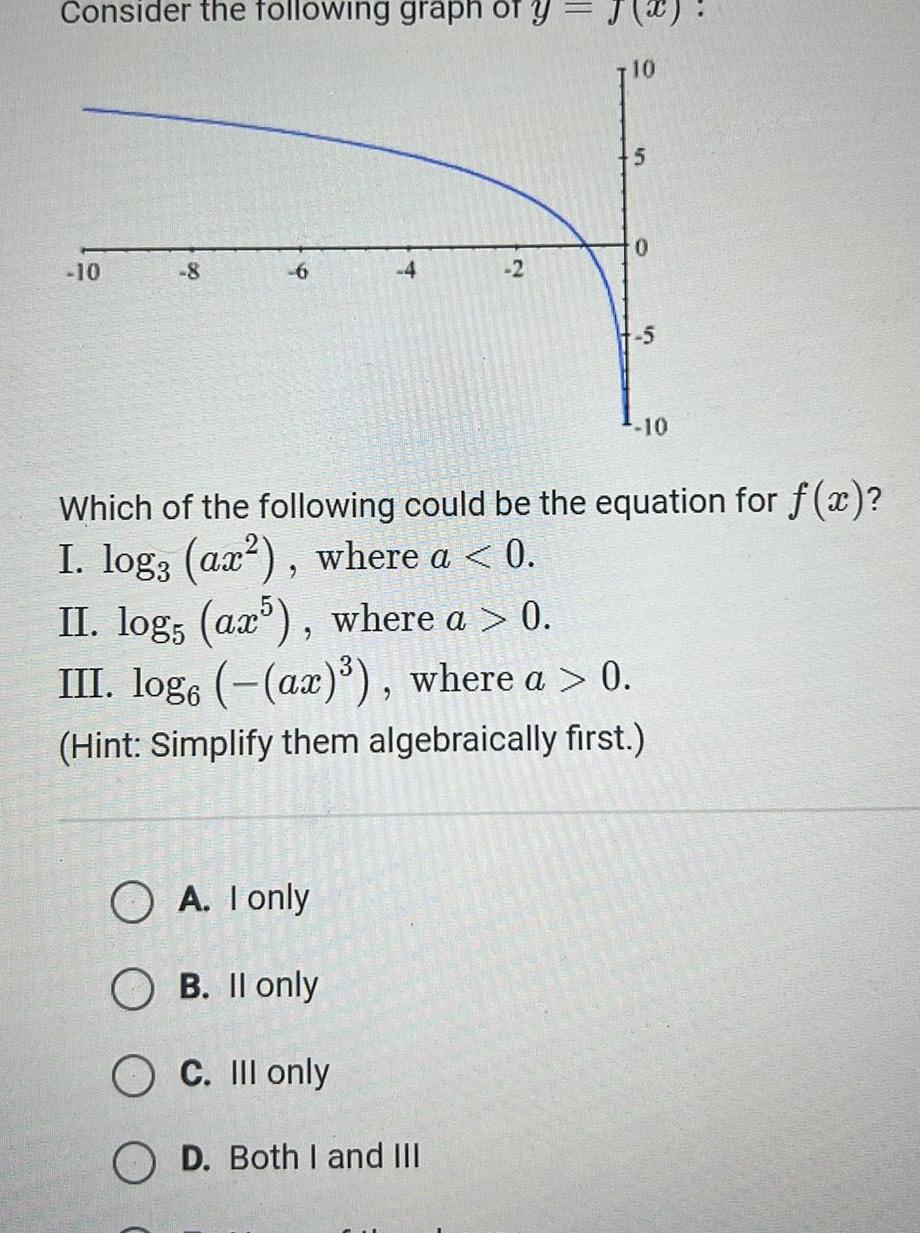
Application of derivativesConsider the following graph of y 10 8 6 4 O A I only OB II only O C III only 2 D Both I and III 10 5 0 5 Which of the following could be the equation for f x I log ax where a 0 II logs ax5 where a 0 III log ax where a 0 Hint Simplify them algebraically first 10

Calculus
Application of derivativesSuppose f x sin cos x On any interval where the inverse function y f x exists the derivative of f x with respect to x is OA B C D E 1 COS cos y where x and y are related by the equation X sin cos y 1 sin y cos cos y x sin cos y where x and y are related by the equation 1 sin y cos COS y 2 X sin cos y 1 cos TC TT COS X equation x where x and y are related by the equation where x and y are related by the equation satisfy the sin cos y 1 sin x cos cos x X sin cos y where x and y are related by the equation

Calculus
Application of derivativesWhat is the area bounded by y x and y 3x A 5 OB 8 O C OD 25 OE 11 2 72

Calculus
Application of derivativesConsider the function f x 100 of the following are true I lim f x 70 XIX II lim f x 70 118 III lim f x 100 18 IV lim f x 100 118 V lim f x 100 x 0 12000 400 3000a 12000 400 3000a OA I and V only B I and IV only OC II and III only OD III and V only OE I IV and V only where 0 a 1 Which
Calculus
Application of derivativesSuppose f x Find the slope of the tangent line to the graph of y f x at 3 1 You get OA 972 1 O B 24 C 00062 D 1620 E 1 16 4x

Calculus
Application of derivativesA mass suspended from a spring is raised a distance of 5 cm above its resting position The mass is released at time t 0 and allowed to oscillate After one third of a second it is observed that the mass returns to its highest position which was 4 5 cm above its resting position What is the rate of change of the position of the mass at t 2 1 seconds Round your answer to three decimal places
Calculus
Application of derivativesAn isotope of sodium has a half life of 20 hours Suppose an initial sample of this isotope has mass 10 grams The amount of the isotope in grams remaining after thours is given by NOTE We re assuming exponential decay here Use the exponential decay function OA 10 965936329 B Both 10 1 035264924 and 10e 965936329t C 10e 965936329t D 10 1 035264924 t E Both 10 965936329 and 10e 965936329t

Calculus
Application of derivativesSuppose that y f x 2x x 0 Find a c 0 such that the tangent line to the curve y f x at x chas the same slope as the tangent line to the curve y f x at x c You get O A c B c 1 3 12 3 3 2 3 C c D c 1 E c 1 C 12

Calculus
Application of derivativesSolving the equation 33x 235 2 for x you get x O A 17 O B log3 5 O c log3 5 OD 7 O E 35
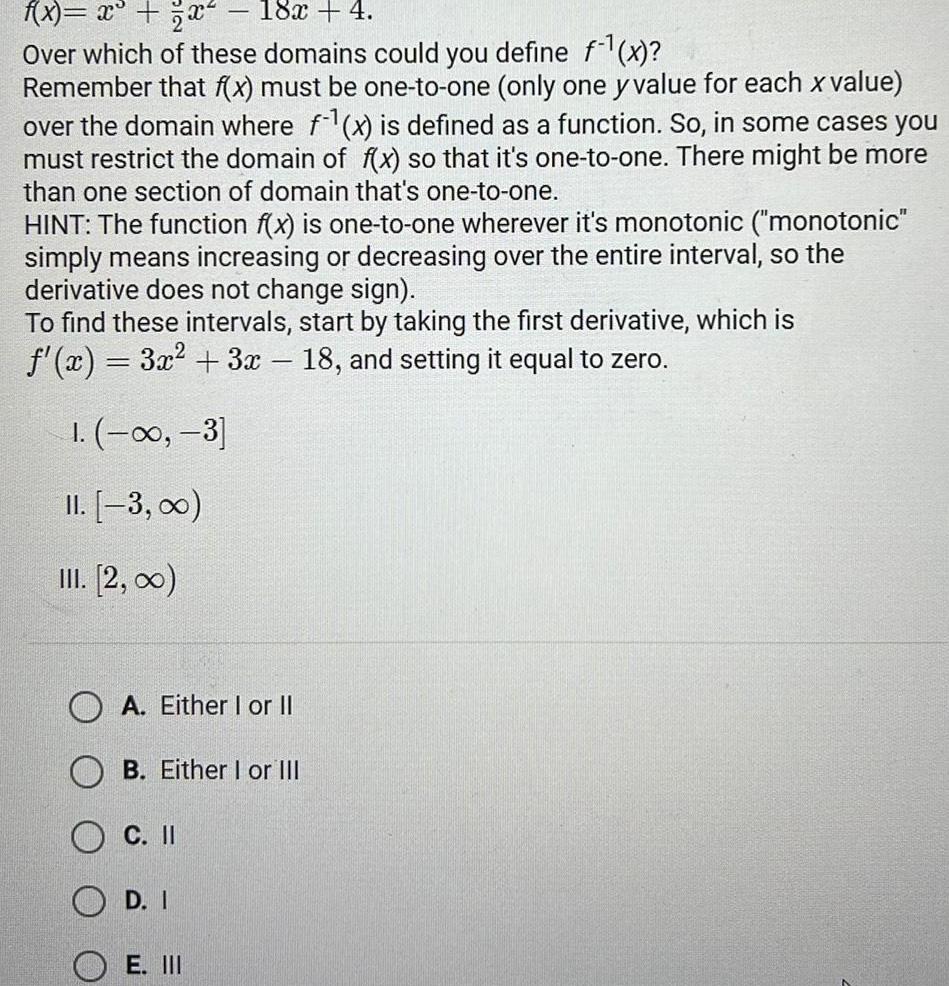
Calculus
Application of derivativesf x x x 18x 4 Over which of these domains could you define f x Remember that f x must be one to one only one y value for each x value over the domain where f x is defined as a function So in some cases you must restrict the domain of f x so that it s one to one There might be more than one section of domain that s one to one HINT The function f x is one to one wherever it s monotonic monotonic simply means increasing or decreasing over the entire interval so the derivative does not change sign To find these intervals start by taking the first derivative which is f x 3x 3x 18 and setting it equal to zero 1 3 II 3 III 2 00 OA Either I or II B Either I or III C II OD I E III
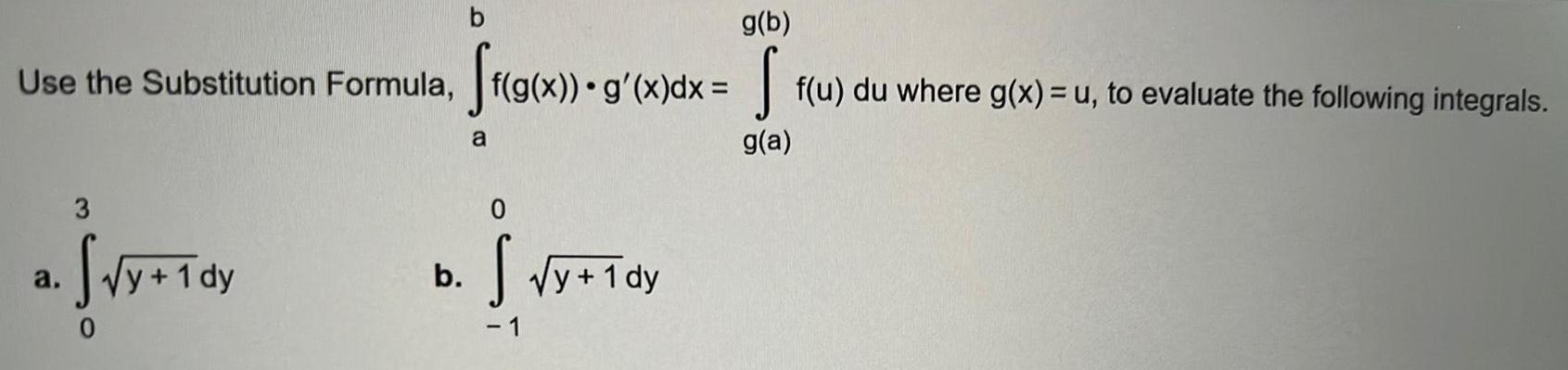
Calculus
Application of derivativesb g b Use the Substitution Formula ff g x g x dx f u du where g x u to evaluate the following integrals g a a y 1 dy b a 0 S y 1dy 1
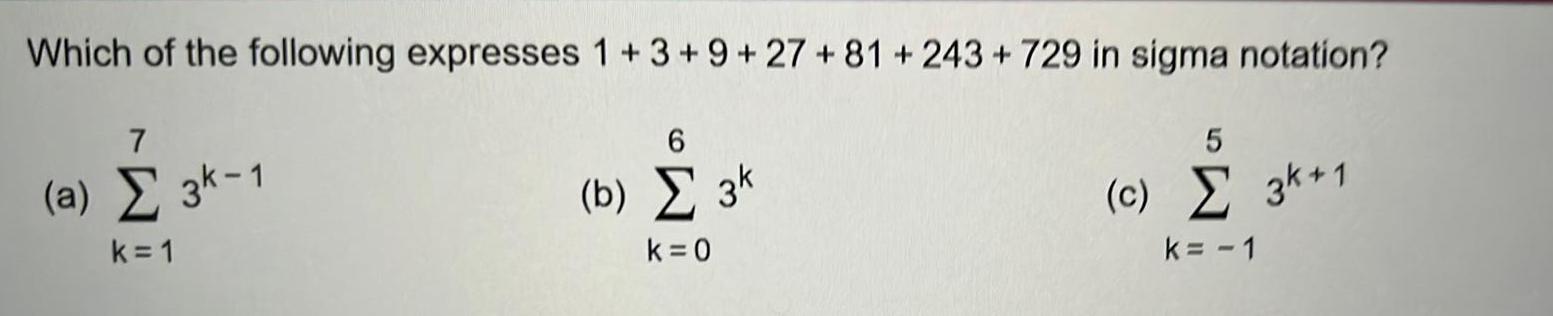
Calculus
Application of derivativesWhich of the following expresses 1 3 9 27 81 243 729 in sigma notation 7 a 3k 1 k 1 6 b 3k k 0 5 c 3k 1 k 1
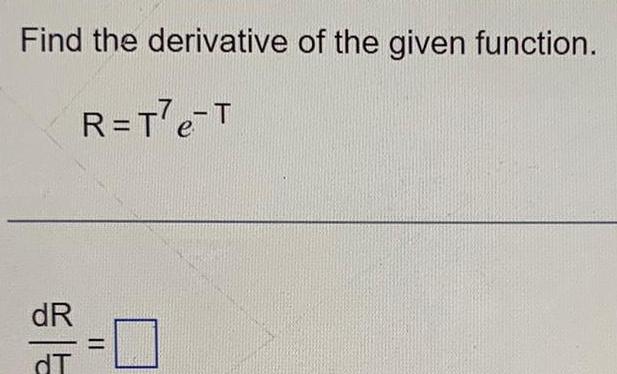
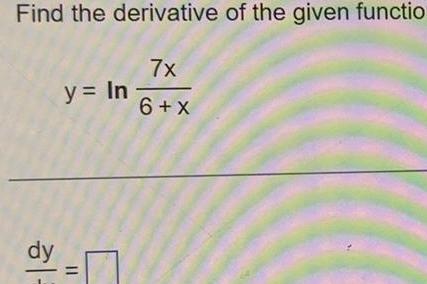
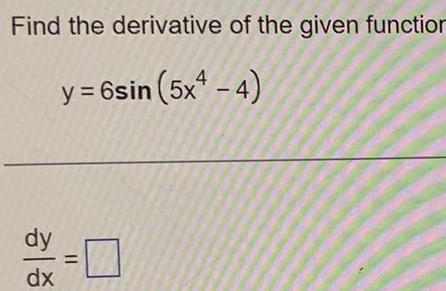
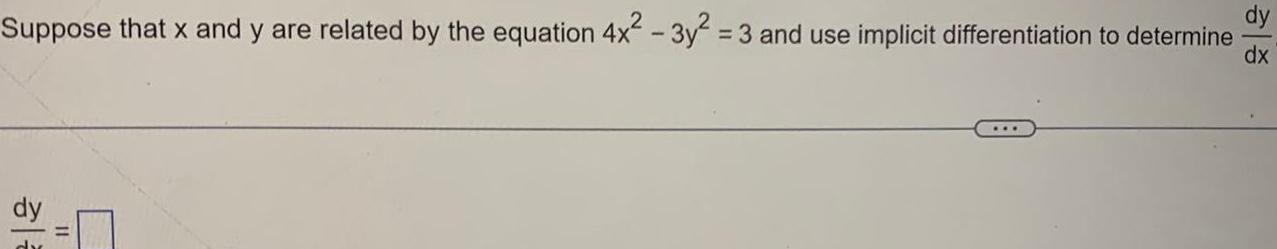
Calculus
Application of derivativesSuppose that x and y are related by the equation 4x 3y 3 and use implicit differentiation to determine dx dy dy 11


Calculus
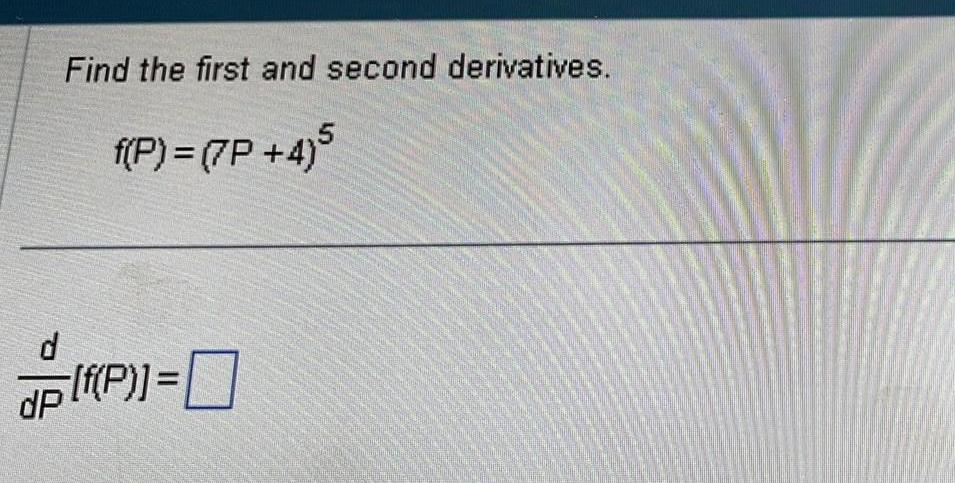
Application of derivativesFind the derivative of the following function 5x 8 f x f x 2 x 4x 9
Calculus
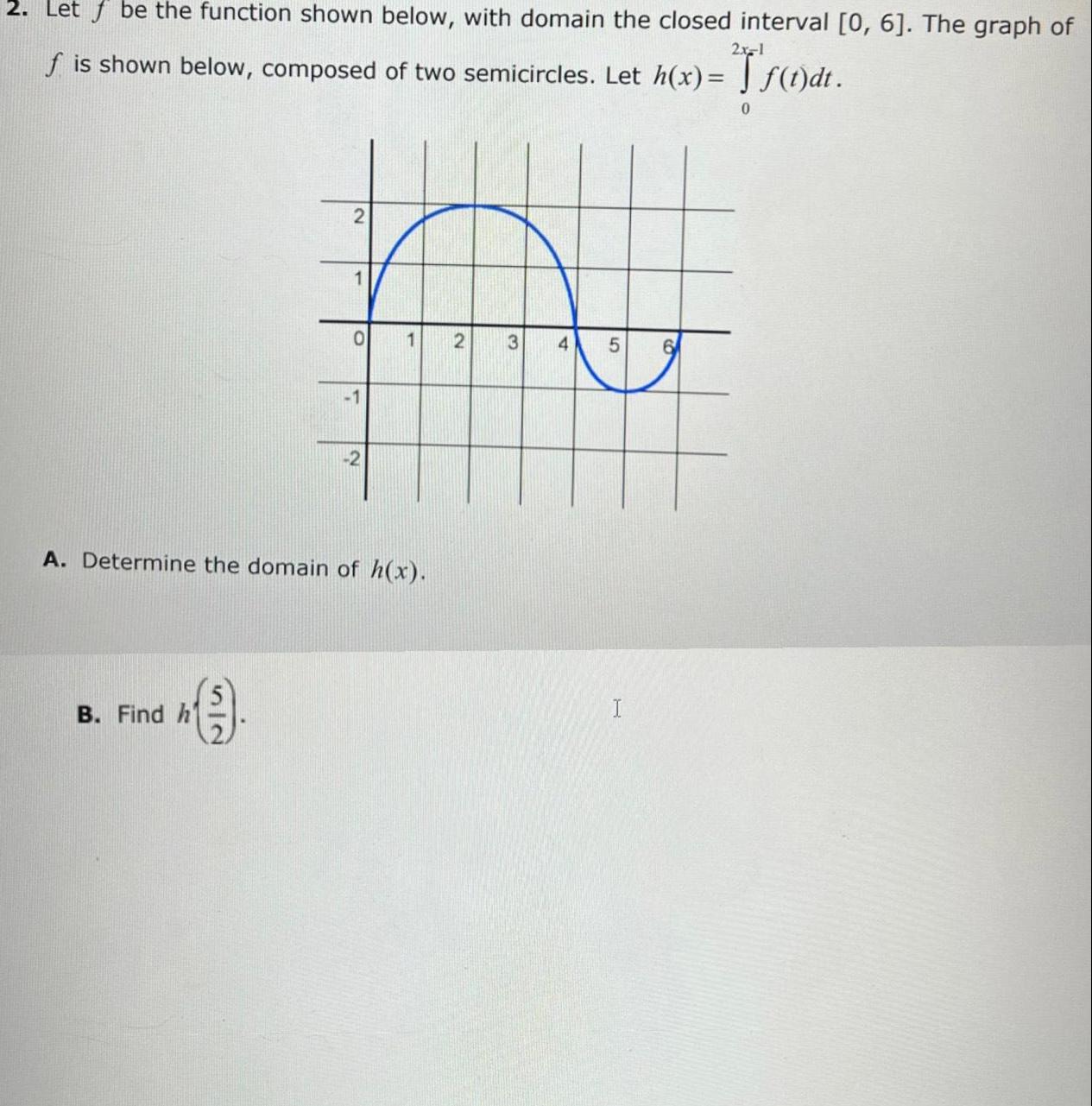
Application of derivatives2x 1 2 Let be the function shown below with domain the closed interval 0 6 The graph of f is shown below composed of two semicircles Let h x f t dt B Find h 1 9 O 1 2 A Determine the domain of h x 1 2 3 4 5 6 0
Calculus
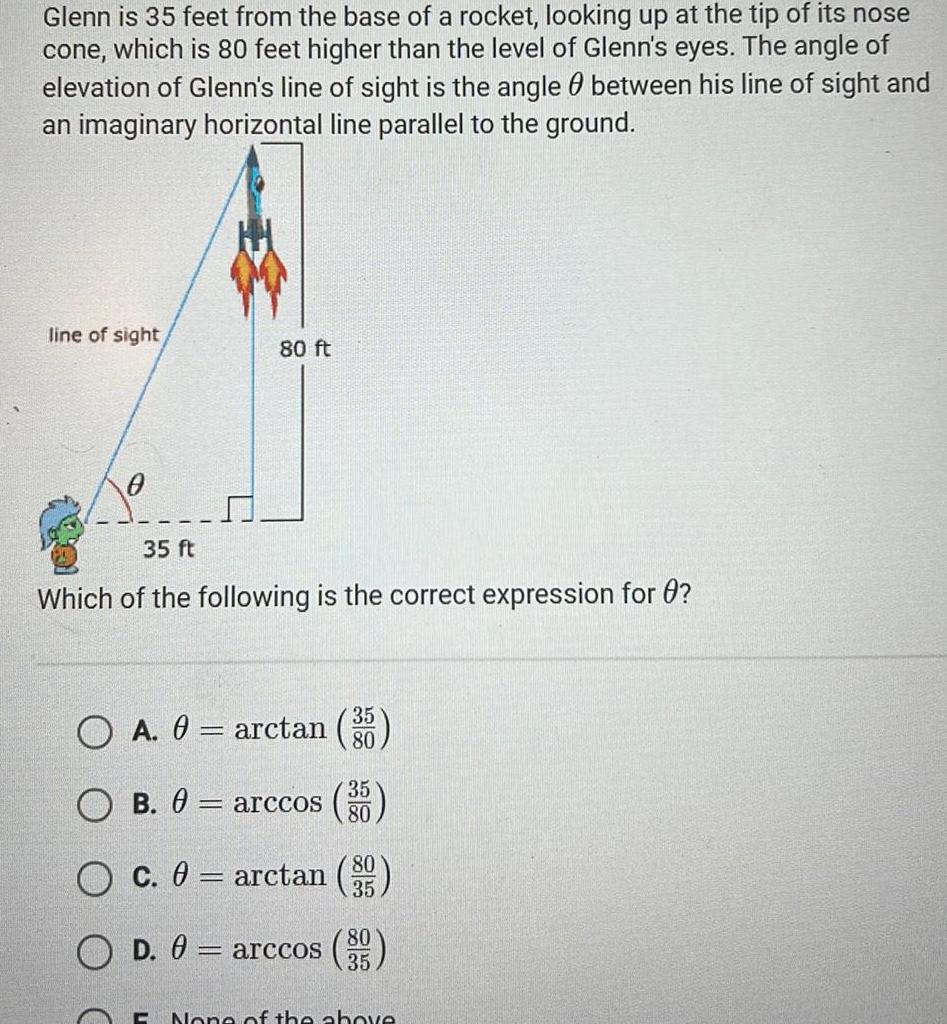
Application of derivativesGlenn is 35 feet from the base of a rocket looking up at the tip of its nose cone which is 80 feet higher than the level of Glenn s eyes The angle of elevation of Glenn s line of sight is the angle between his line of sight and an imaginary horizontal line parallel to the ground line of sight 80 ft 35 ft Which of the following is the correct expression for 0 O A 0 arctan g B 0 arccos O c 0 arctan O D 0 arccos 395 80 35 80 35 C None of the above

Calculus
Application of derivativesConsider the function f x x 4x 5 x 2 You have that f x 1 O A where x and y are related by the equation y x 4x 5 x 2 2y 4 for x 1 OB O C d da O E 1 2x 4 1 2x 4 for x 2 D 2y4 where x and y are related by the equation y x 4x 5 x 2 where x and y are related by the equation satisfy th equation x y 4y 5 x 1 1 2y 4

Calculus
Application of derivativesA tetrahedron has three mutually perpendicular faces and three mutually perpendicular edges of lengths 2 3 and 4 cm respectively Find its volume

Calculus
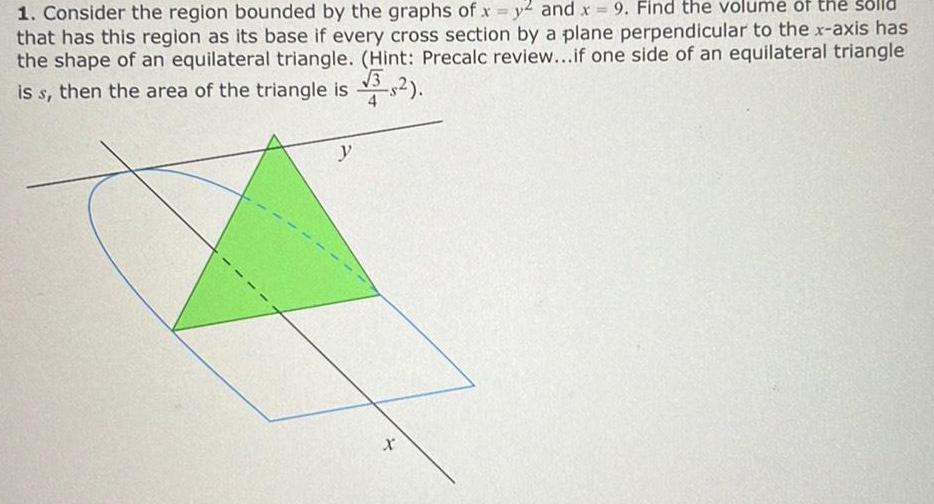
Application of derivatives4 A solid has as its base the region bounded by the curves y 21 2 and y x 1 Find the volume of the solid if every cross section of a plane perpendicular to the x axis is a trapezoid with lower base in the xy plane upper base equal to the length of the lower base and height equal to 2 times the length of the lower base
Calculus
Application of derivatives1 Consider the region bounded by the graphs of x y2 and x 9 Find the volume of the solld that has this region as its base if every cross section by a plane perpendicular to the x axis has the shape of an equilateral triangle Hint Precalc review if one side of an equilateral triangle 3 is s then the area of the triangle is 3 2 y X
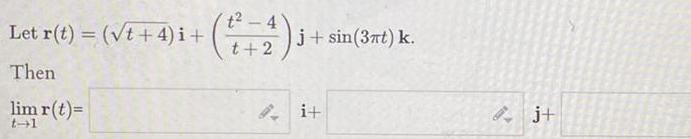

Calculus
Application of derivativesIf g x f x on the interval a b then the area between the curves for a x bis given by O A f f x g x dx O B f g x f x dx O c f A x dx OD Both f f x g x dx and o f x dx f g x dx ob E f f x dx f g x dx
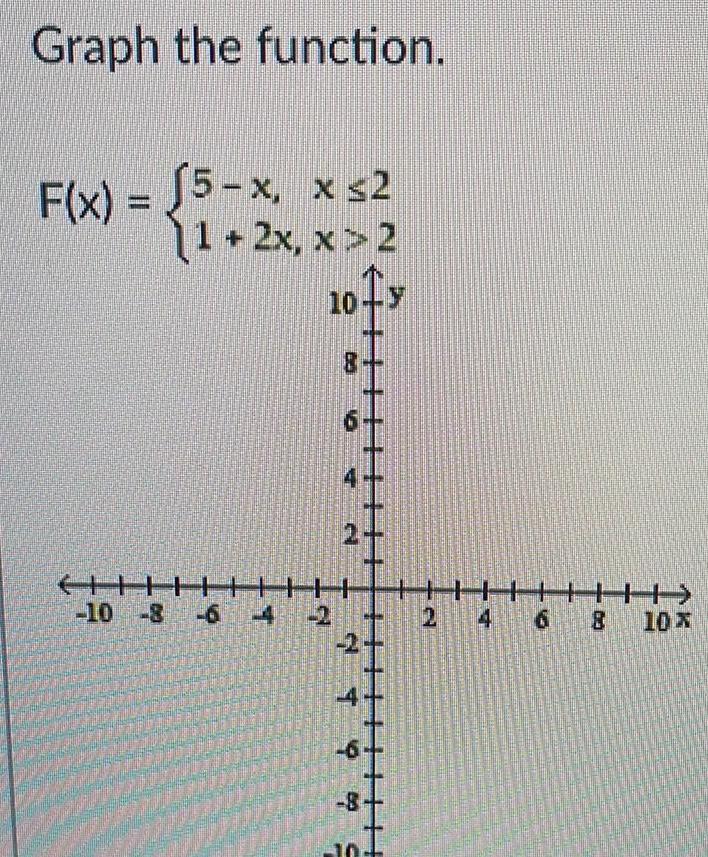
Calculus
Application of derivativesA child wanders slowly down a circular staircase from the top of a tower With z y z in feet and the origin at the base of the tower her position t minutes from the start is given by x 30 cost y 30 sint 90 5t a How tall is the tower height ft b When does the child reach the bottom time minutes c What is her speed at time t speed ft min d What is her acceleration at time t acceleration ft min2

Calculus
Application of derivativesFind r t and v t given acceleration initial velocity and initial position v t r t 1 a t t 1 v 0 6 6 r 0 0 0

Calculus
Application of derivativesFind v t given the acceleration and initial condition v t Usage To enter a vector for example x y z type x y z a t 4i v 0 j

Calculus
Application of derivativesFind the equation of the plane which passes through O and is parallel to 3y 2x z 6 y z 8 x

Calculus
Application of derivativesFind a vector n normal to the plane with the equation y 3x3z 4 n 3

Calculus
Application of derivativescertain chemical involved in the reaction changes at a rate that s inversely proportional to the product of the mass of the chemical present in grams and the time elapsed since the reaction began in seconds A The mass m m t of this chemical is modeled with what differential equation for time 12 1 second B The solution to the differential equation modeling the mass m of the chemical at time t seconds is m t 2kInt C for t 1 where k and C are undetermined constants Show how this equation is derived from your answer in part A C Suppose that the amount of this chemical involved in the reaction is 40 grams at time t 1 second and 30 grams at time t 10 seconds Find an explicit equation for the mass m of the chemical as a function of t for t 1 Your equation should not involve any unknown constants or any calculator numbers D According to your equation for m t in part Cat what time

Calculus
Application of derivatives3 9 Evaluate the limit and justify each step by indicating the appropriate Limit Law s 3 lim 4x 5x x 5 5 lim v 2v 2v 5 v 2 7 lim 9 u 2u 2 9 lim 1 2t5 5t 4 3 4 lim 2x 6x 9 x 3 3t 1 7t 5t 2 6 lim 8 lim x 5 2x 3x X 3 I
Calculus
Application of derivatives3 The slope of a curve is equal to y divided by 4 more than x at any point x y on the curve A Find a differential equation describing this curve B Solve the differential equation from part A C Suppose it s known that as x goes to infinity on the curve v goes to 1 Find the equation
Calculus
Application of derivatives4 Consider the functions f x x3 x4 1 and g x Let R denote the region in the first x 1 quadrant bounded by the curves y f x and y g x Find the exact volume of the solid that has R as its base if every cross section by a plane perpendicular to the x axis is a rectangle of height 3 Exact volume means no calculator numbers

Calculus
Application of derivatives2 A particle moves on a coordinate line with an acceleration at time seconds of et 2 m sec2 At 1 0 the particle is at the origin and its velocity is 4 m seci A Find a function v t that gives the velocity of the particle at time t B At what exact time is the velocity of the particle 0 m s C Set up an expression which may contain integrals but not absolute values to find the total distance traveled by the particle from time 0 to 1 6 You do not have to solve your

Calculus
Application of derivativesthe given nonlinear system and associated critica Point find the Jacobian Matnix and use eigenvalues to classify the critical point in terms of type an Stability Then wonite out the linearization to the system Show all your work dy 21 64 4x4 dt dx x 2x xy dt at 0 3
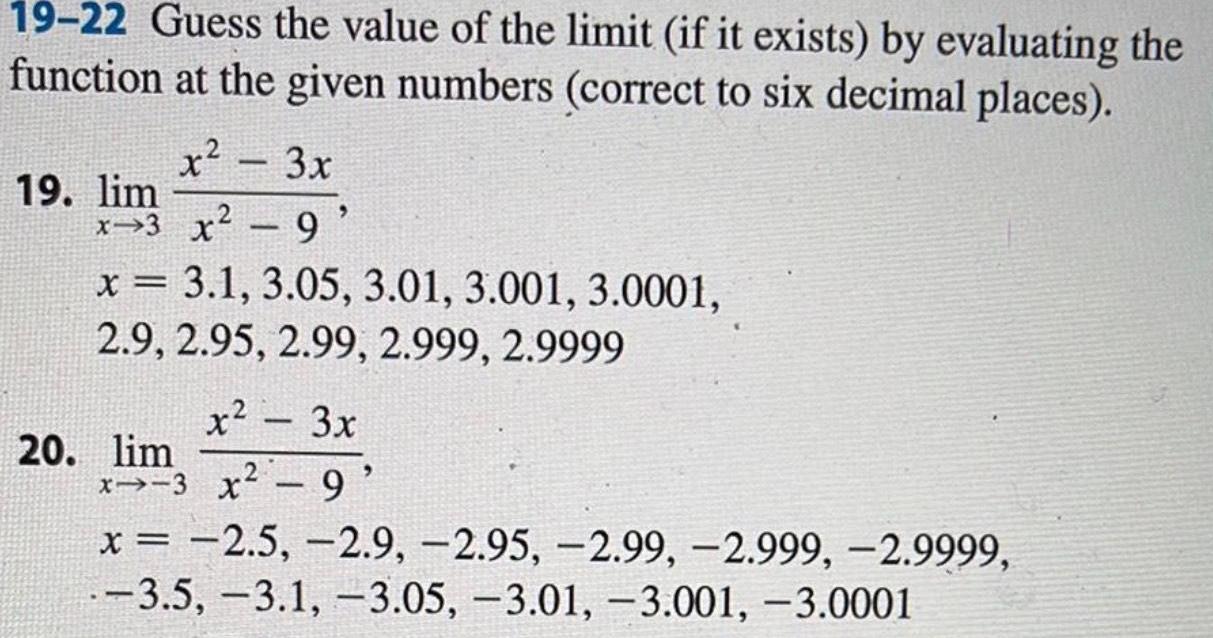
Calculus
Application of derivatives19 22 Guess the value of the limit if it exists by evaluating the function at the given numbers correct to six decimal places x 3x x 3 x 9 19 lim x 3 1 3 05 3 01 3 001 3 0001 2 9 2 95 2 99 2 999 2 9999 x 3x x3 x 9 20 lim x 2 5 2 9 2 95 2 99 2 999 2 9999 3 5 3 1 3 05 3 01 3 001 3 0001

Calculus
Application of derivatives12 A race car is running practice laps in preparation for an upcoming race To judge how the car is performing the crew takes measurements of the car s speed S t in miles per hour or mph every minute The measurements are given in the table below t minutes S t mph 0 201 1 205 208 214 218 212 219 223 220 221 217 218 216 3 5 6 7 8 10 11 12 A Use the trapezoid rule with 4 equal subdivisions to approximate the total distance the car traveled in miles over the first 12 minutes B Find one approximation for S 6 including the units Explain what this quantity means in the context of the problem
Calculus
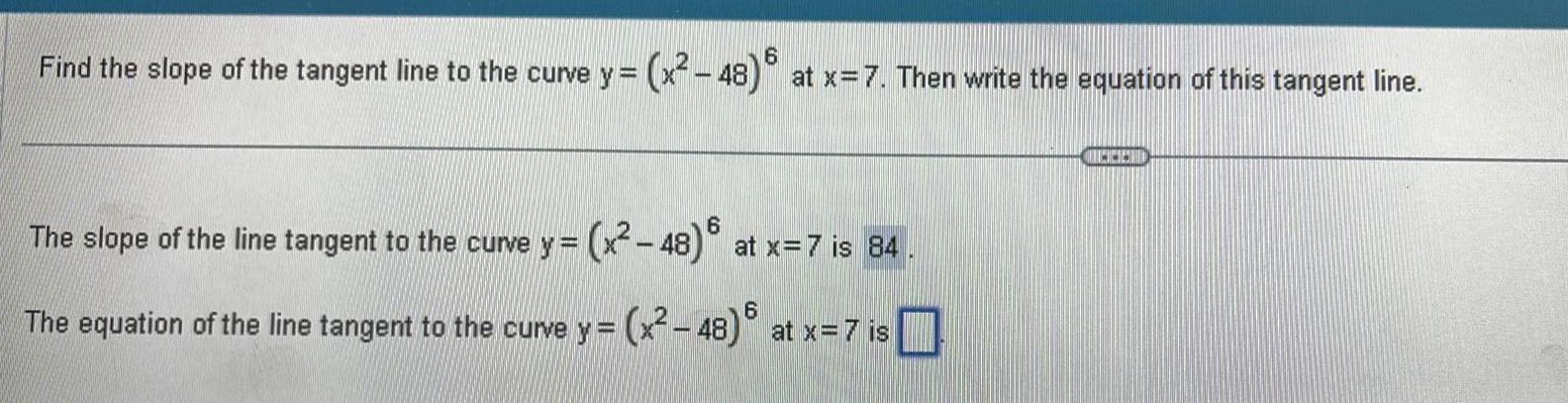
Application of derivatives6 Find the slope of the tangent line to the curve y x 48 at x 7 Then write the equation of this tangent line 6 x 48 at x 7 is 84 The slope of the line tangent to the curve y 6 The equation of the line tangent to the curve y x 48 at x 7 is CHCES
Calculus
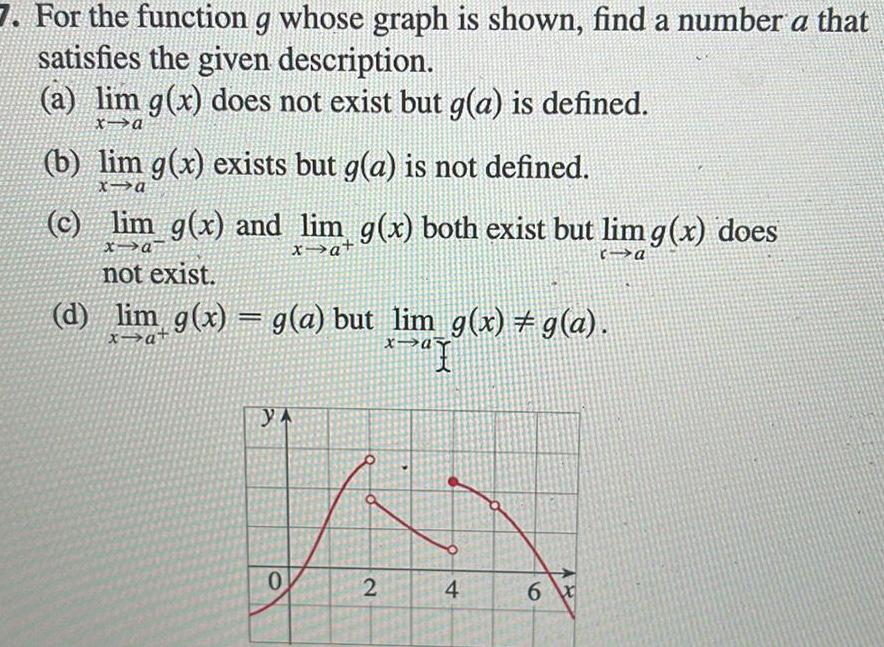
Application of derivatives7 For the function g whose graph is shown find a number a that satisfies the given description a lim g x does not exist but g a is defined x a b lim g x exists but g a is not defined x a c lim g x and lim g x both exist but lim g x does x a ca xa not exist d lim g x g a but lim g x g a x a x a YA 0 2 7 I 4 6x
Calculus
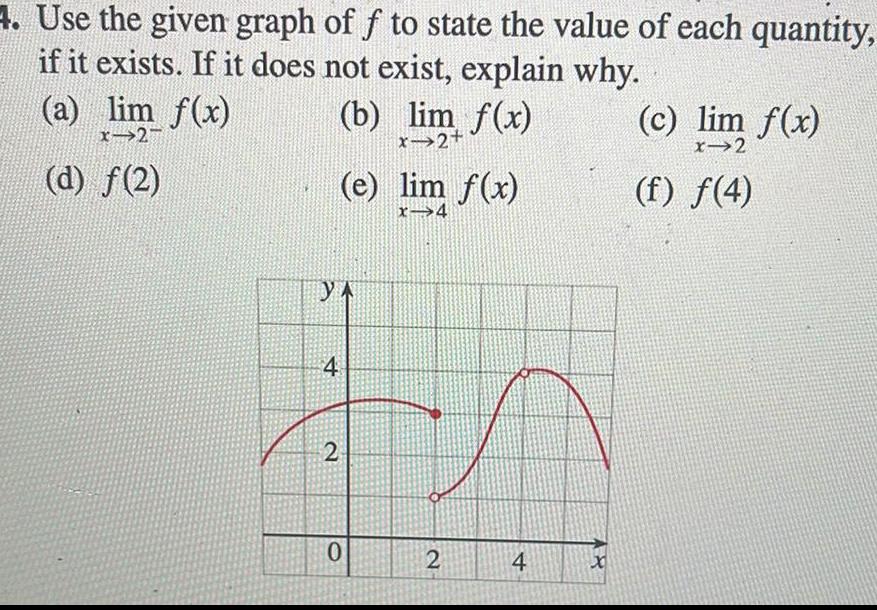
Application of derivatives4 Use the given graph of f to state the value of each quantity if it exists If it does not exist explain why a lim f x x 27 d f 2 b lim f x x 2 4 e lim f x x 4 YA 2 0 2 4 48 c lim f x x 2 f f 4
Calculus
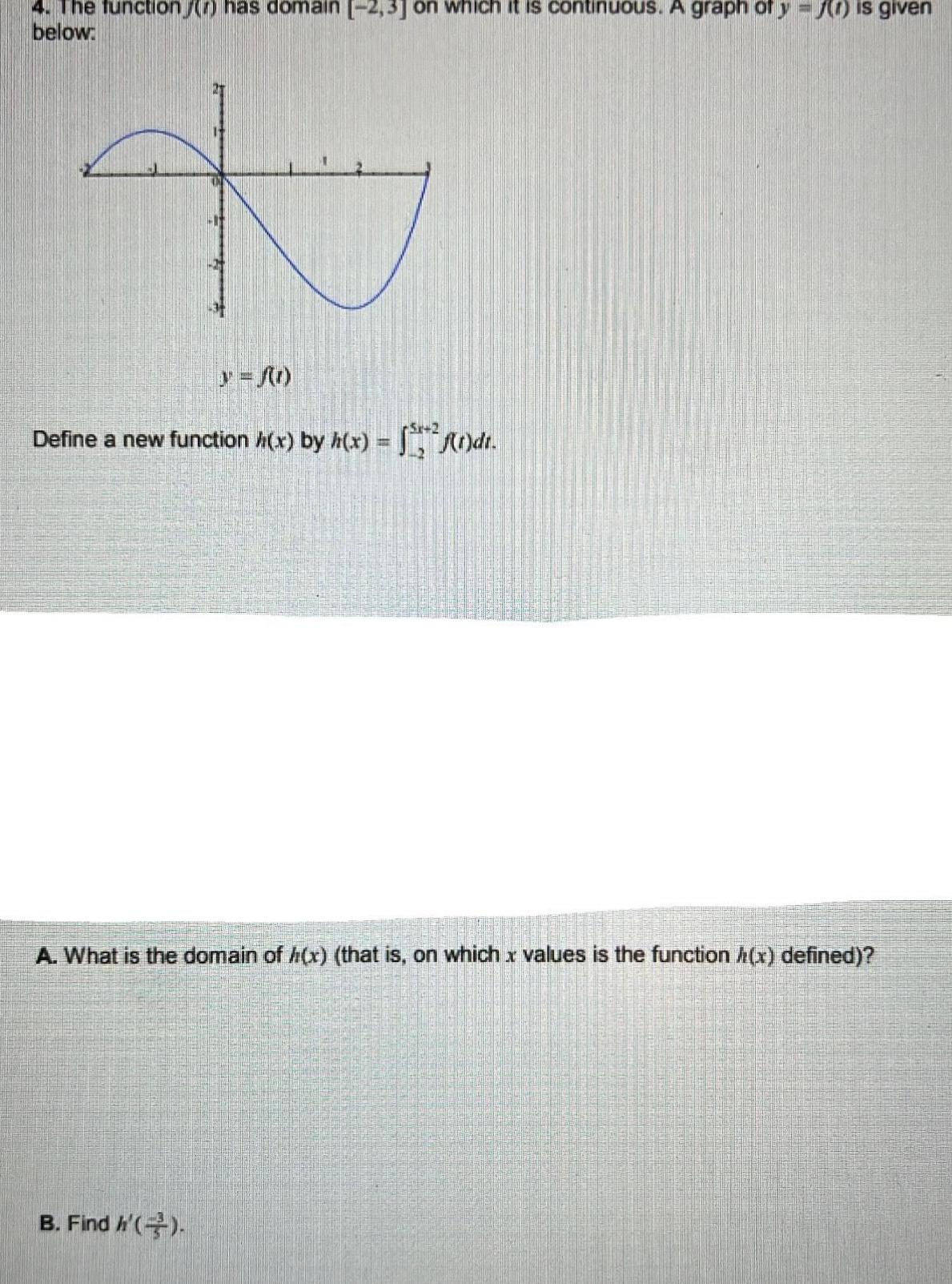
Application of derivatives4 The function has domain below IX B Find h y f 1 5x 2 which it is continuous A graph of y is given Define a new function h x by h x f t dt A What is the domain of x that is on which x values is the function x defined

Calculus
Application of derivativesbeginning of a race Velocities of the two cars during the race are given in the tables below where velocities are in miles per hour and times are in seconds Sappho s car timer velocity vs 0 1 2 4 5 6 7 8 9 10 0 20 35 48 85 93 99 106 Homer s Car time 0 1 2 4 6 7 8 10 velocity VII 0 18 43 68 79 86 93 95 96 A Use ten trapezoids to approximate the area between the curves y vs t and y vu 1 on the interval from 0 to 1 10 What definite integral are you approximating B If you haven t done so convert your answer from part A into units that make good common sense for the physical situation described Then explain what practical meaning this answer has for the physical situation