Application of derivatives Questions and Answers
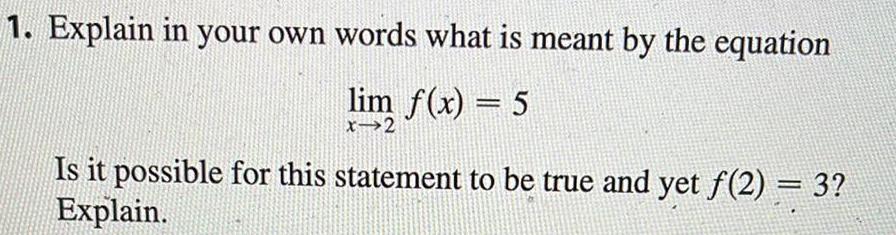
Calculus
Application of derivatives1 Explain in your own words what is meant by the equation lim f x 5 x 2 Is it possible for this statement to be true and yet f 2 3 Explain

Calculus
Application of derivativesIf a rock is thrown upward on the planet Mars with a velocity of 10 m s its height in meters t seconds later is given by y 10t 1 86t 1 a Find the average velocity over the given time intervals ii 1 1 5 iii 1 1 1 i 1 2 iv 1 1 01 v 1 1 001 b Estimate the instantaneous velocity when t 1

Calculus
Application of derivatives5 The deck of a bridge is suspended 275 feet above a river If a pebble falls off the side of the bridge the height in feet of the pebble above the water surface after t seconds is given by y 275 16t a Find the average velocity of the pebble for the time period beginning when t 4 and lasting i 0 1 seconds ii 0 05 seconds iii 0 01 seconds b Estimate the instantaneous velocity of the pebble after 4 seconds


Calculus
Application of derivativesUse limits to compute the derivative 3 f 0 where f x x 6x 2 0 Simplify your answer

Calculus
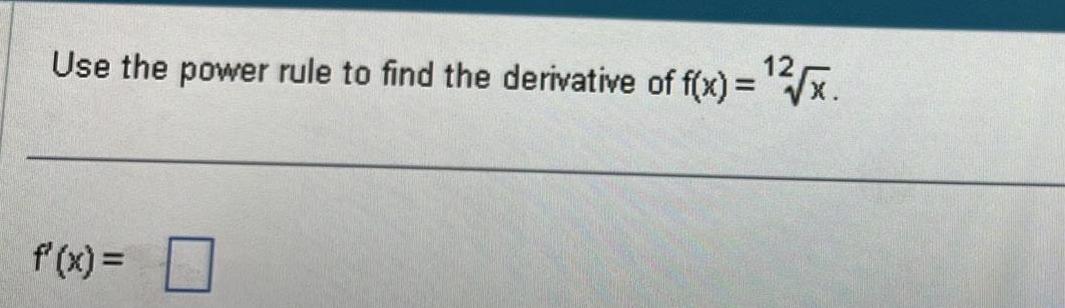
Application of derivativesFind the equation of the tangent line to the graph y f x at the given value of x f x 10x 8 x 6 What is the equation of the tangent line Type an equation CO
Calculus
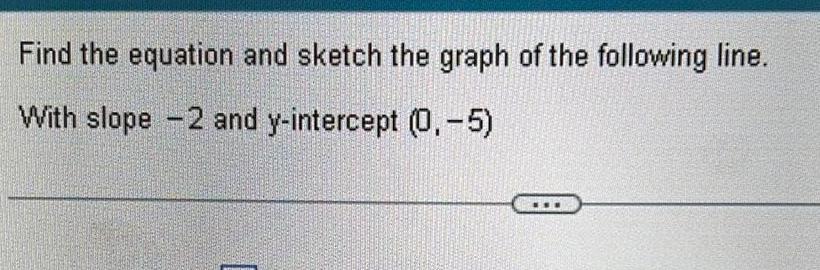
Application of derivativesFind the equation and sketch the graph of the following line With slope 2 and y intercept 0 5 www



Calculus
Application of derivativesWhat does the transformation f x f x do to the graph of f x reflects it across the y axis shrinks it vertically stretches it vertically reflects it across the x axis
Calculus
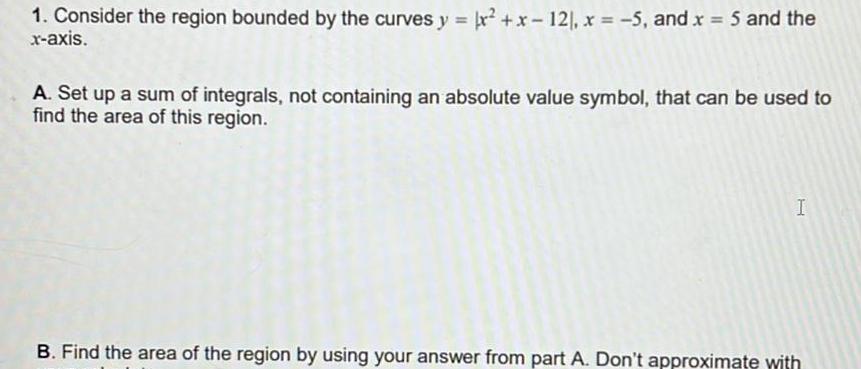
Application of derivatives1 Consider the region bounded by the curves y x x 12 x 5 and x 5 and the x axis A Set up a sum of integrals not containing an absolute value symbol that can be used to find the area of this region I B Find the area of the region by using your answer from part A Don t approximate with
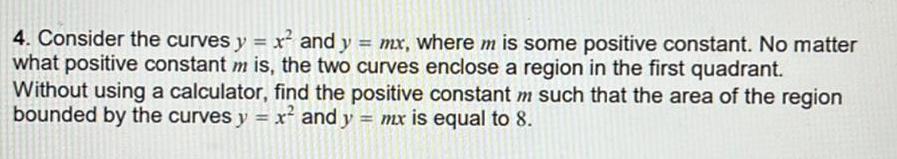
Calculus
Application of derivatives4 Consider the curves y x and y mx where m is some positive constant No matter what positive constant m is the two curves enclose a region in the first quadrant Without using a calculator find the positive constant m such that the area of the region bounded by the curves y x and y mx is equal to 8
Calculus
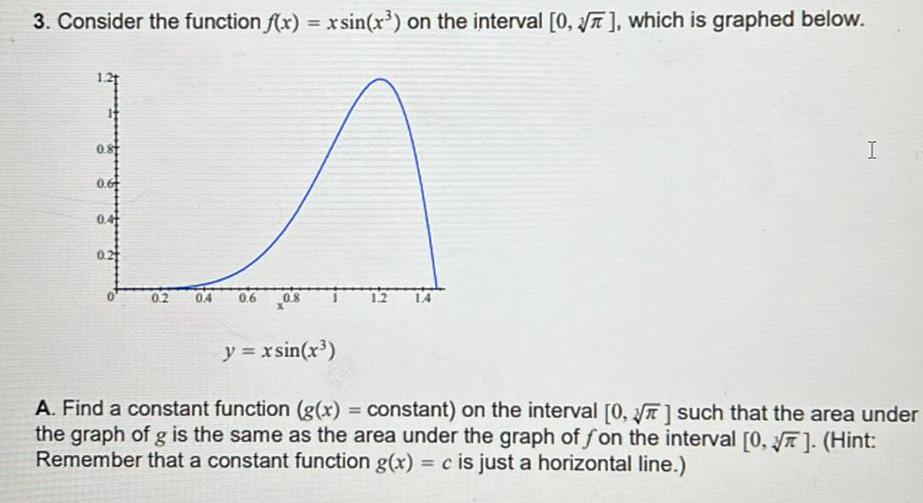
Application of derivatives3 Consider the function f x x sin x on the interval 0 which is graphed below 0 8 0 6 0 4 0 2 0 4 0 6 0 8 I y xsin x A Find a constant function g x constant on the interval 0 such that the area under the graph of g is the same as the area under the graph of fon the interval 0 Hint Remember that a constant function g x c is just a horizontal line

Calculus
Application of derivativessing of a certai is given b where P is in dollars and M x is marginal cost in dollars per unit A Suppose the marginal cost at a production level of 500 units is 10 per unit and the cost of producing 500 units is 12 000 that is M 500 10 and P 500 12000 Use a tangent line approximation to estimate the cost of producing only 497 units B Suppose the production schedule is such that the company produces five units each day That is the number of units produced is x 51 where is in days and 0 corresponds the beginning of production Write an equation for the cost of production P as a function of time t

Calculus
Application of derivativesFind the area of the region IN THE FIRST QUADRANT upper right quadrant bounded by the curves y sin x cos x y 2x cos x and y 4 4x Use the area to the left of curve y 4 4x You get O A 0 16165 OB 1 7281 OC 0 36974 O D 1 8467 OE 0 37859
Calculus
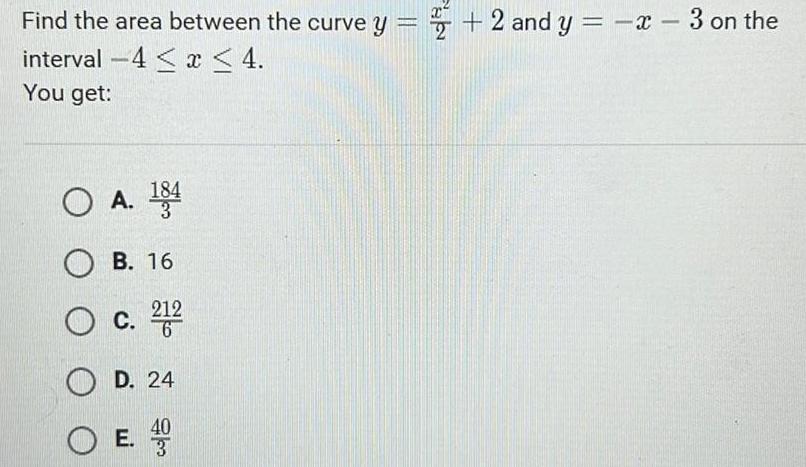
Application of derivativesFind the area between the curve y 2 and y x 3 on the interval 4 x 4 You get O A 184 OB 16 O c 212 OD 24 40 OE col
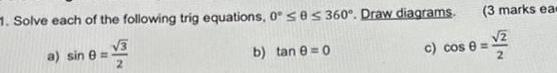
Calculus
Application of derivatives1 Solve each of the following trig equations 0 ses 360 Draw diagrams 3 b tan 0 0 a sin 3 marks eas 2 c cos 8

Calculus
Application of derivativesAssume that a couple invests 750 upon the birth of their daughter Assume that the investment earns 6 4 compounded annually What will the investment be worth on the daughter s 10th birthday The investment will be worth approximately on the daughter s 10th birthday Do not round until the final answer Then round to the nearest cent as needed
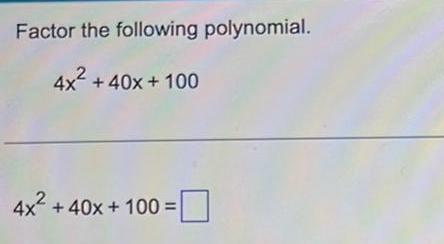

Calculus
Application of derivativesSuppose a 26 2 is expanded in descending powers of a Then the 5th term in the expansion is i 22 a 26 12 4 ii 12 a 26 12 1 a 26 5 iv 12 1 a 26 5 V None of the options
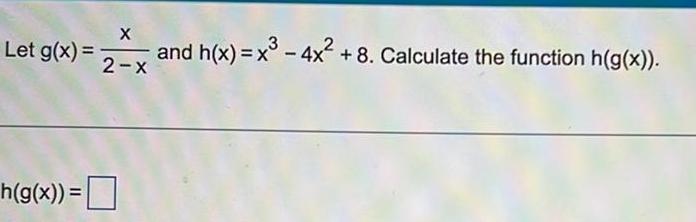
Calculus
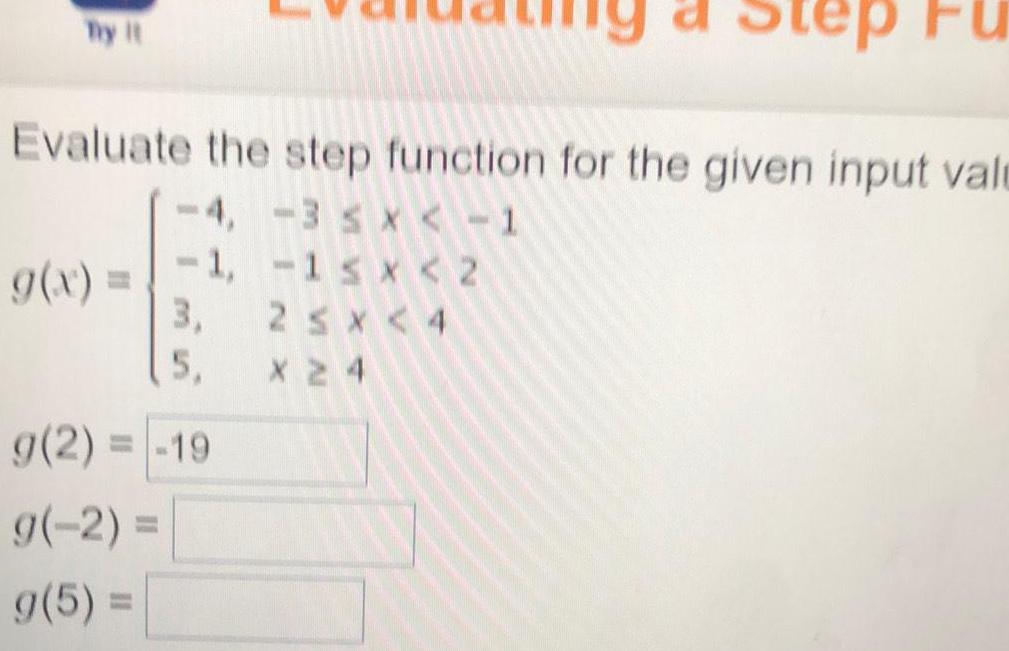
Application of derivativesTry it Evaluate the step function for the given input vale 4 3 x 1 1 1 x 2 2 x 4 X 24 g x a Step 3 5 g 2 19 g 2 g 5

Calculus
Application of derivatives1 point Find the Laplace transform F s L f t of the function f t est 10 h t 2 defined on the interval t 0 Here h t is the unit step function Heaviside F s L est 10h t 2 help formulas

Calculus
Application of derivativesThe volume of an open topped box with a square base is 245 cubic centimeters Find the height in centimeters of the box that uses the least amount of material OA 6 centimeters OB 3 centimeters OC 7 883 centimeters OD 2 centimeters OE 3 942 centimeters

Calculus
Application of derivativesX sin 2x 2 dx OA cos 2x 3 2 C OB 3 cos 2x 3 2 C OC cos 2x 3 2 C OD cos 2x 3 2 C E None of these This one can t be done using the metho substitution

Calculus
Application of derivativesx 4x 7 Ad O A 2 42 7 C O B 2 42 7 C O C C O E 2 5 x 4x 7 5 OD None of these This one can t be done using the method substitution 4 5 x 4x 7 5 C

Calculus
Application of derivatives1 point Consider the initial value problem y 9y 0 y 0 3 y 0 0 a Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation Denote the Laplace transform of y t by Y s Do not move any terms from one side of the equation to the other until you get to part b below b Solve your equation for Y s Y s L y t c Take the inverse Laplace transform of both sides of the previous equation to solve for y t y t help formulas

Calculus
Application of derivatives1 point Consider the rational function A Select ALL terms below that occur in the general form of the complete partial fraction decomposition of F s The capital letters A B C L denote constants B C D E F G H Hs I s 11 A s 6 Bs C s 6 s 11 2 Es F 5 6 G s 11 Ks L F s s 11 D s 6 5 2 s 6 2 s 11
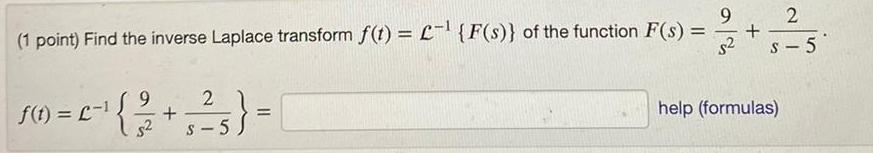
Calculus
Application of derivatives9 1 point Find the inverse Laplace transform f t L F s of the function F s 9 2 f t 1 2 5 1 5 5 2 S 5 help formulas
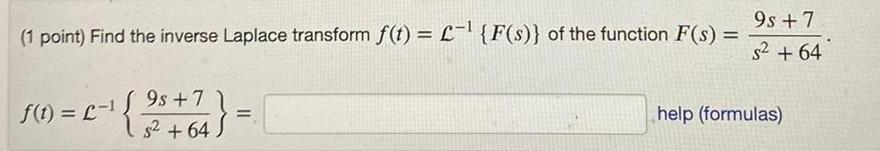
Calculus
Application of derivatives1 point Find the inverse Laplace transform f t L F s of the function F s 9s f 0 L 9 7 64 9s 7 s 64 help formulas
Calculus
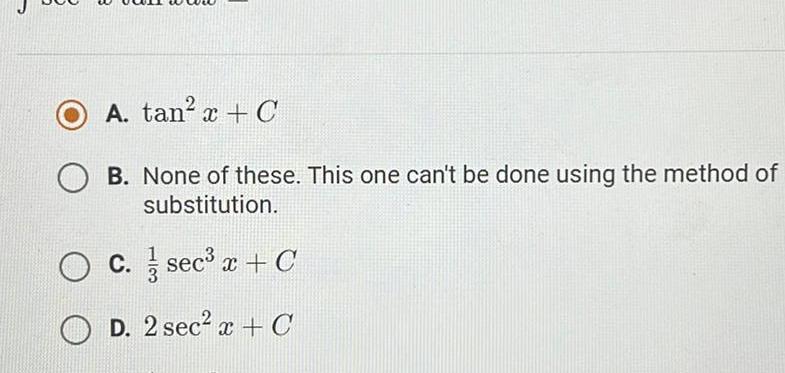
Application of derivativesA tan x C B None of these This one can t be done using the method of substitution OC sec x C D 2 sec x C

Calculus
Application of derivativesJx 2 x 2 dx 3 x 4x x 2x O B x 4x C O C c x 2x C O A 1312 O D 1 3 C x 4x C x 2x C O E None of the above

Calculus
Application of derivativesA particle s position in meters is given by the equation s t 5x sin 2x on the interval 1 4 minutes What is its instantaneous velocity at t 0 OA TT OB 3 O C 1 OD O E id3363061

Calculus
Application of derivativesA paperweight is thrown straight up with an initial upward velocity of 60 meters per second and an initial height of 6 meters The acceleration due to gravity of the object is given by a t 9 8 meters per second per second where tis in seconds The equation that describes the paperweight s velocity as a function of time tis A v t 4 9t 60 B v t 9 8t C c v t 4 9t 60 D v t 9 8t 60 E t 9 8t 60

Calculus
Application of derivativesThe absolute maximum value of f x x 12x on the closed interval 1 4 occurs at x OA 2 OB 0 OC 2 OD 4 E Cannot be determined
Calculus
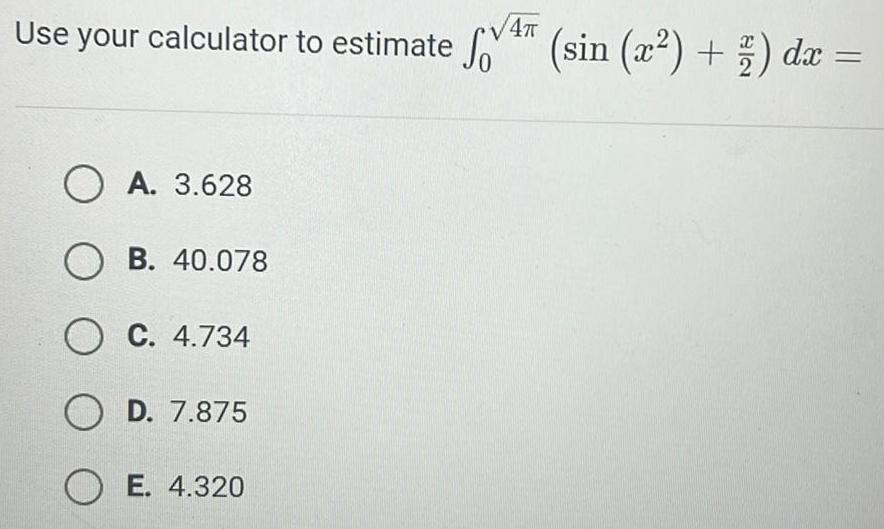
Application of derivativesUse your calculator to estimate 4 sin 22 dx 4 OA 3 628 OB 40 078 O C 4 734 OD 7 875 OE 4 320

Calculus
Application of derivativesThe population of ground squirrels in a public park is measured to be 100 The growth of the population over time can be modeled by P t 600 1 5e 0 5t with P representing the number of squirrels and t given in months after the initial population measurement According to this model what is the maximum number of squirrels the park can support
Calculus
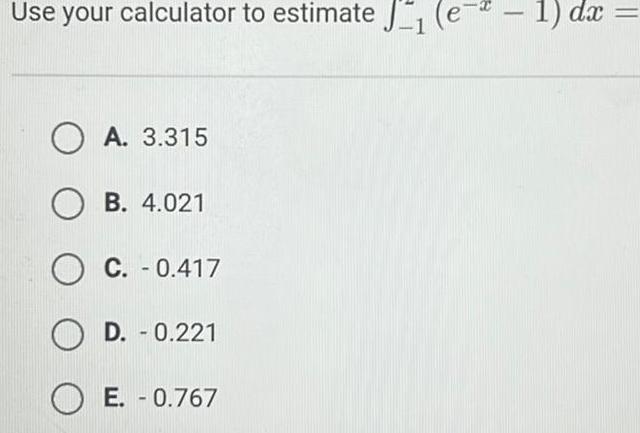
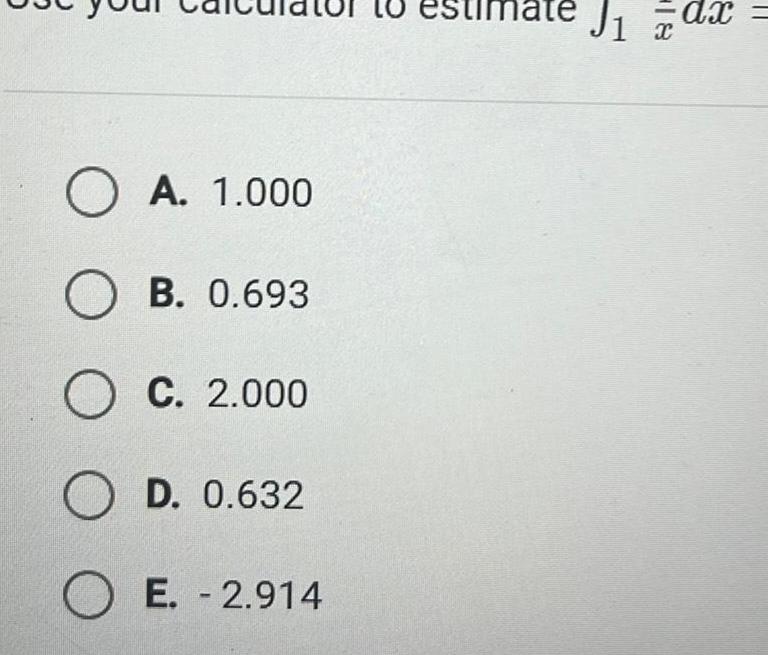
Application of derivativesUse your calculator to estimate OA 3 315 B 4 021 O C 0 417 OD 0 221 OE 0 767 1 dx

Calculus
Application of derivativesGiven that f x is continuous f x dx 7 f f x dx 3 and 4 S f x dx 2 Then f f x dx A 2 B 6 C 3 D 4 E O

Calculus
Application of derivativesGiven that fx dx 63 0 and 3 xdx A 121 5 OB 49 5 OC 256 5 OD 274 5 13 5 then f 3x 5x dx E Can t tell from the information given
Calculus
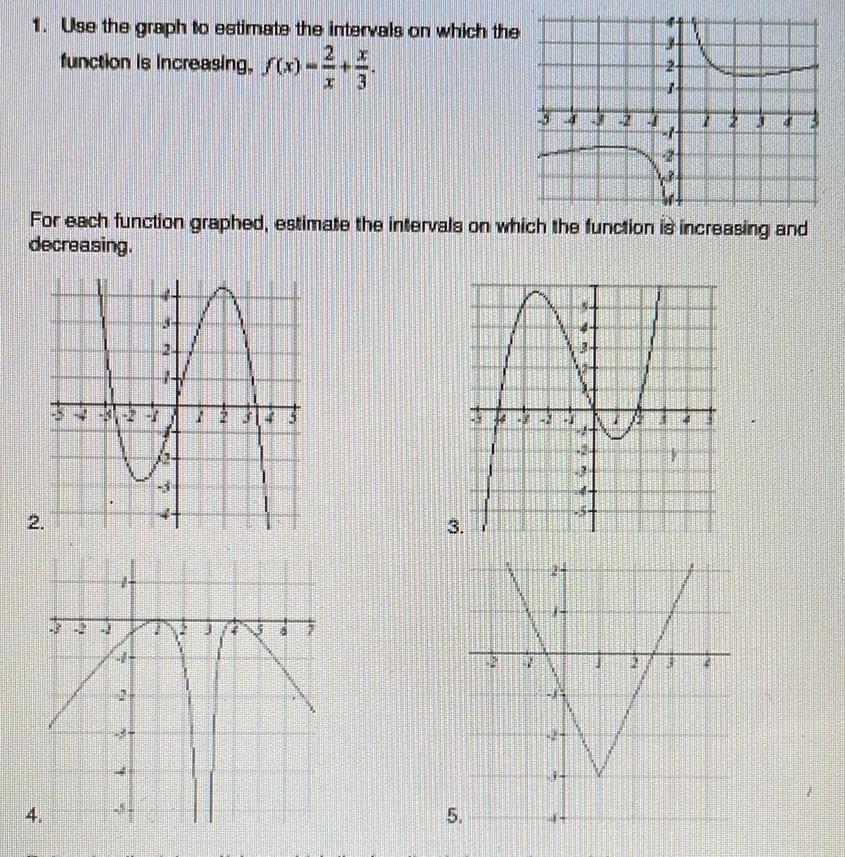
Application of derivatives1 Use the graph to estimate the intervals on which the 2 x function is increasing f x x 3 2 For each function graphed estimate the intervals on which the function is increasing and decreasing 4 4 4 B 6 my mi 5 EN P 220 SEN
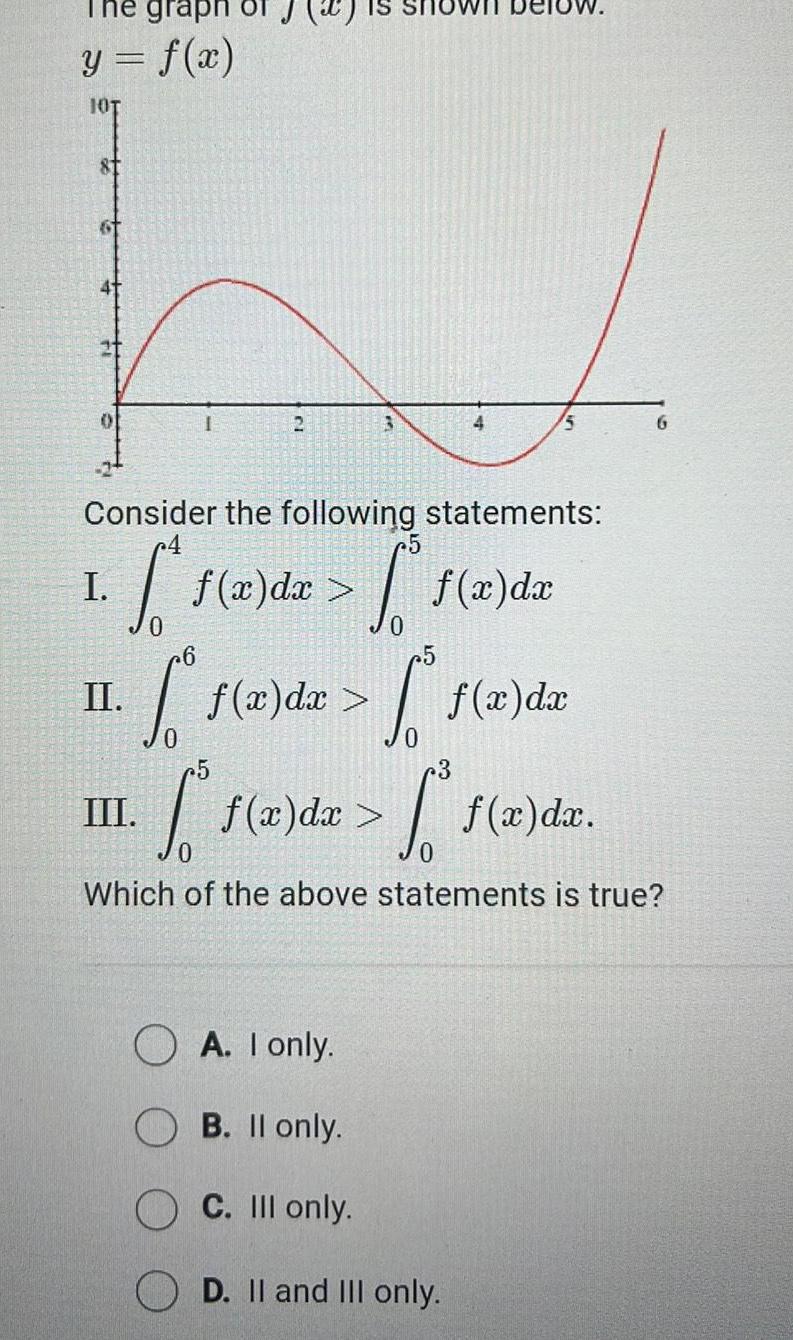
Calculus
Application of derivativesgraph y f x 10T 81 41 21 2 3 III 4 Consider the following statements 1 f x dx f x da I below 5 II 1 f z dz f z dz dx dx 5 OA I only B II only C III only D II and III only c5 3 f ar da f x d dx Which of the above statements is true 6

Calculus
Application of derivativesFind limx 6 x 12x 36 x 6 O A Does not exist OB 36 O C 0 OD CO O E co 8

Calculus
Application of derivativesFind lim 6 x 12x 36 x 6 O A Doe s not exist OB 36 O C O O D D 00 OE 8
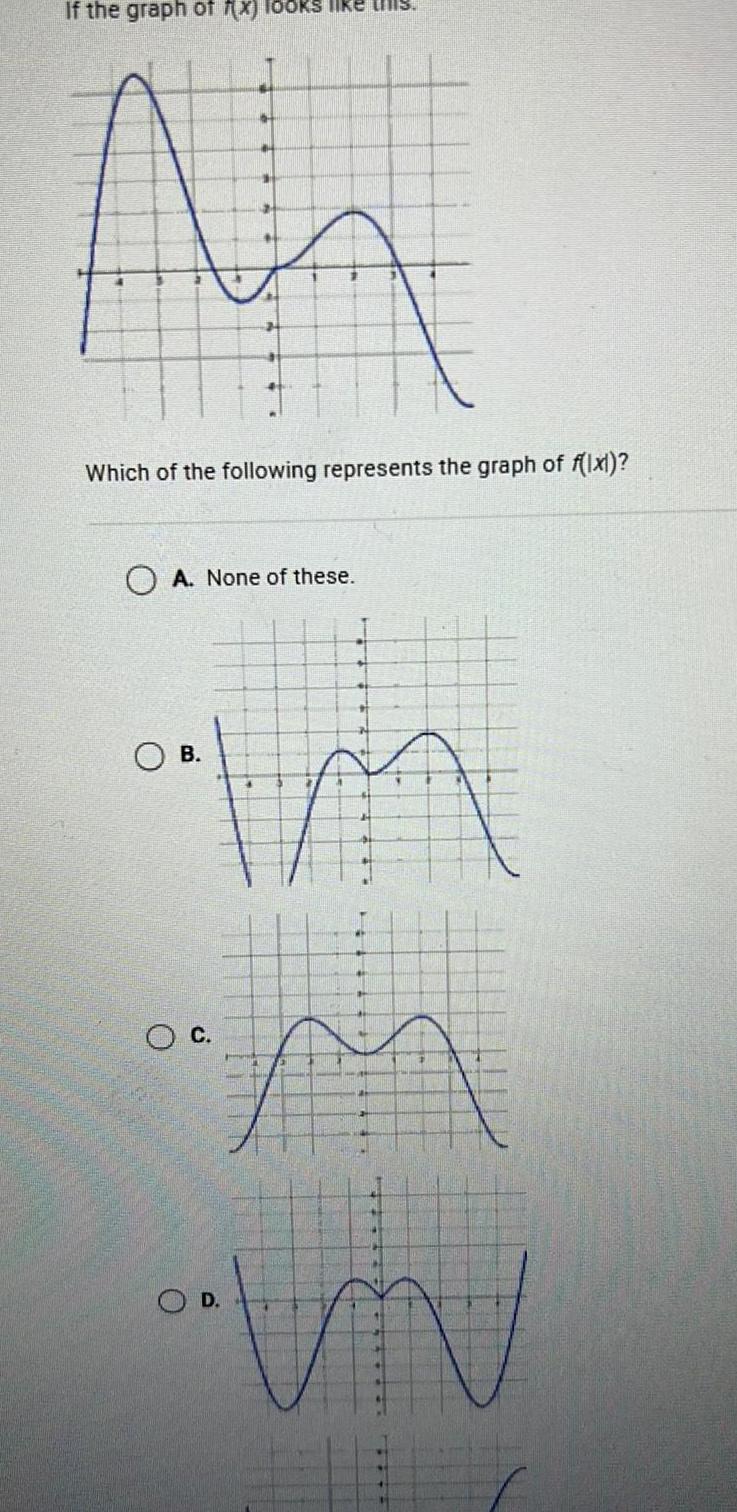
Calculus
Application of derivativesIf the graph of f x looks like M Which of the following represents the graph of f lxl A None of these B C m VV

Calculus
Application of derivativesA metai bar is heated and then allowed to cool Its temperature T in C is found to be T 5 25e 0 30t where t in min is the time of cooling Find the time rate of change temperature after 10 0 min After 10 0 minutes the time rate of change is degrees per minute Round to three decimal places as needed

Calculus
Application of derivativesThe vertical displacement y in cm of the end of an industrial robot arm for each cycle is y 3 2 Its vertical velocity for t 18s is cm s Round to the nearest tenth as needed tan 0 5t where t is the time in s Find its vertical velocity for t

Calculus
Application of derivativesFind the values of x for which the given function is concave up the values of x for which it is concave down and any points of inflection 3 y x 8x 8x 13 When is the graph of y concave up A 0 x 4 B x 0 C x 4 D x 0 and x 4