Application of derivatives Questions and Answers

Calculus
Application of derivativesHeat flows normal to isotherms curves along which the temperature is constant Find the line along which heat flows through the point 4 5 when the isotherm is along graph of 2x y 57 The equation of the line along which heat flows is y
Calculus
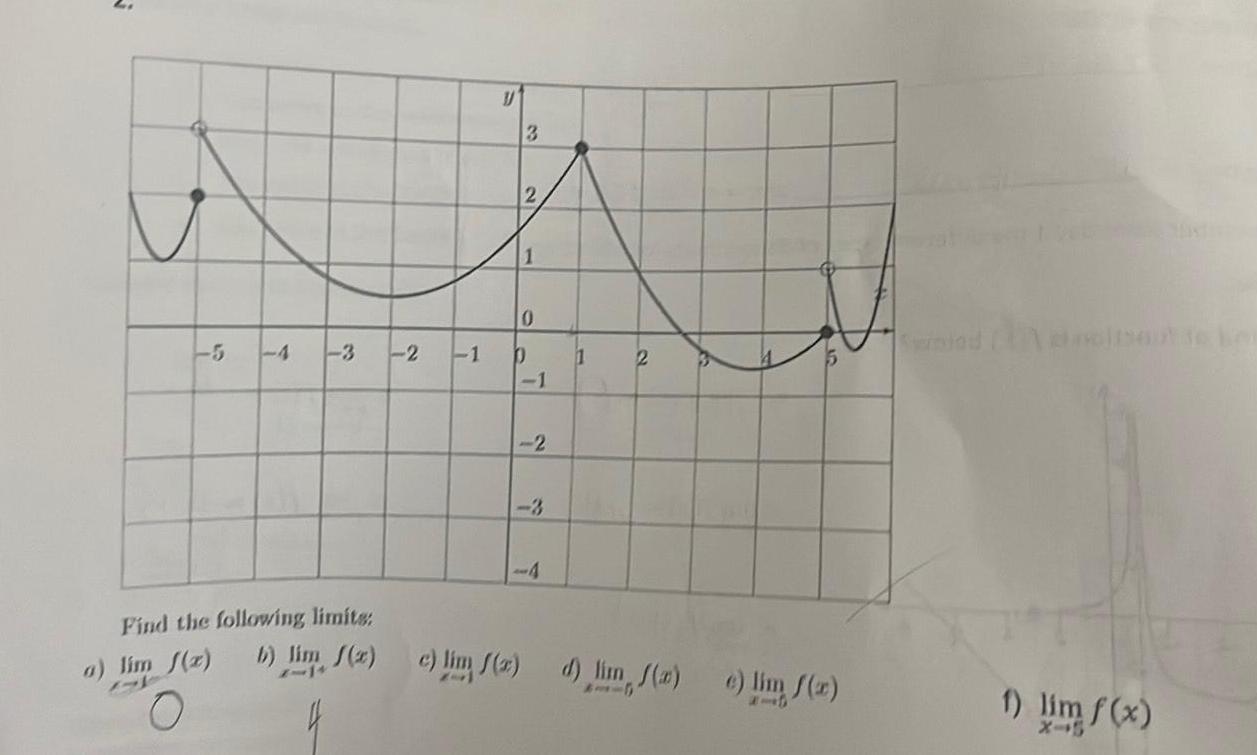
Application of derivativesv 20 3 Find the following limits a lim f x O U 3 2 0 2 1 P 1 2 b lim f x c lim f x 88 4 1 2 d lim f x e lim f x 1 lim f x X 5
Calculus
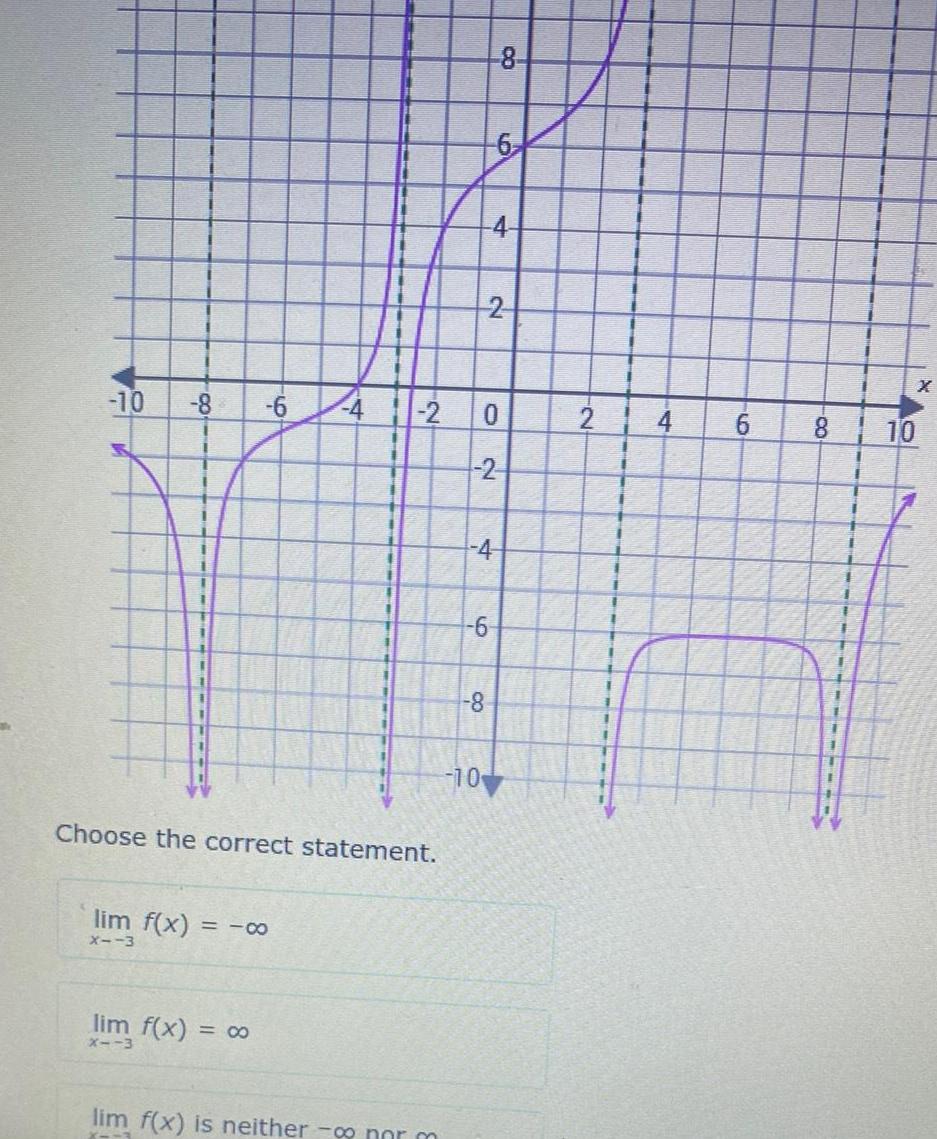
Application of derivativesF 10 8 6 lim f x 00 X 3 lim f x x 3 4 Choose the correct statement 2 lim f x is neither norm 8 6 8 4 0 2 10 2 4 6 2 I 1 4 6 8 10 O X

Calculus
Application of derivativesWhich points on the curve of x xy y2 5 have vertical tangent lines O A 1 2 O B 2 1 and 2 1 O C 0 5 O D 4 2 and 4 2 OE There are no vertical tangents to this curve
Calculus
Application of derivativesA particle moves along the x axis so that its velocity at any time v t 2n 5 t sin nt A Find the acceleration at any time t 6 points is given by B Find the minimum acceleration of the particle over the interval 0 3 12 points
Calculus
Application of derivatives3 Consider the function h x a 2x 1 5 b where a 0 and b 0 are constants A Find h x and h x 6 points B Show that his monotonic that is that either halways increases or remains constant or h always decreases or remains constant 12 points

Calculus
Application of derivatives1 The radius r of a sphere is increasing at a constant rate of 0 05 meters per second A At the time when the radius of the sphere is 12 meters what is the rate of increase in its volume 12 points B At the time when the volume of the sphere is 36 cubic meters what is the rate of increase in its surface area 15 points
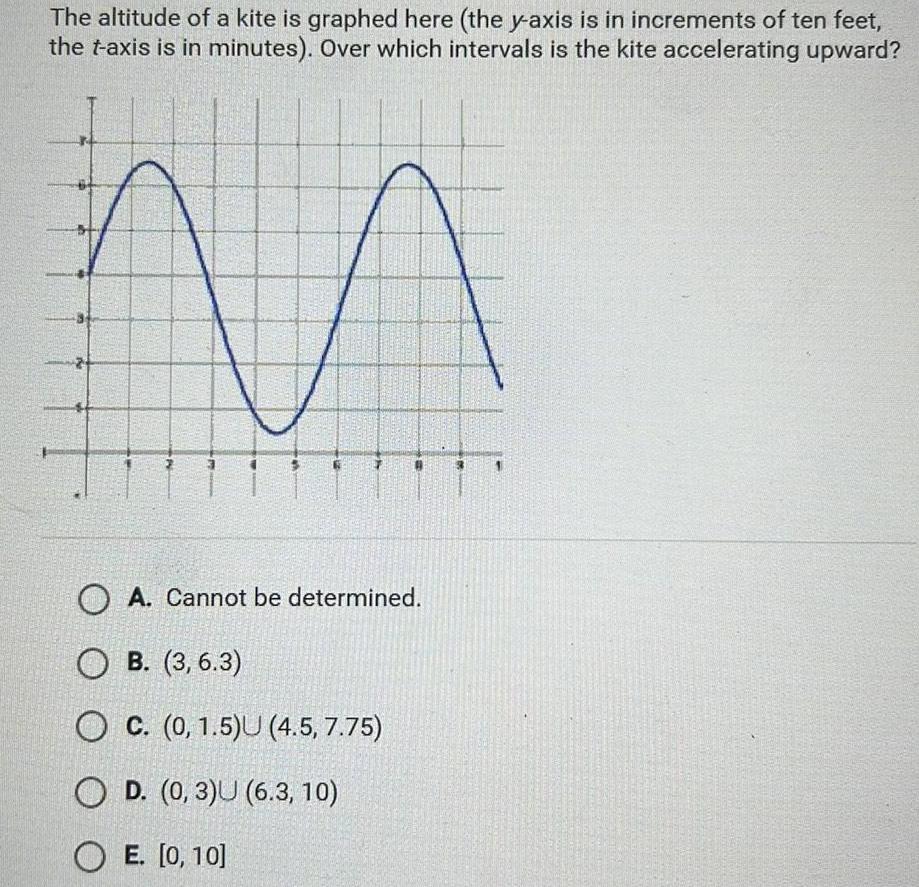
Calculus
Application of derivativesThe altitude of a kite is graphed here the y axis is in increments of ten feet the t axis is in minutes Over which intervals is the kite accelerating upward C N V O A Cannot be determined OB 3 6 3 OC 0 1 5 U 4 5 7 75 OD 0 3 U 6 3 10 OE 0 10
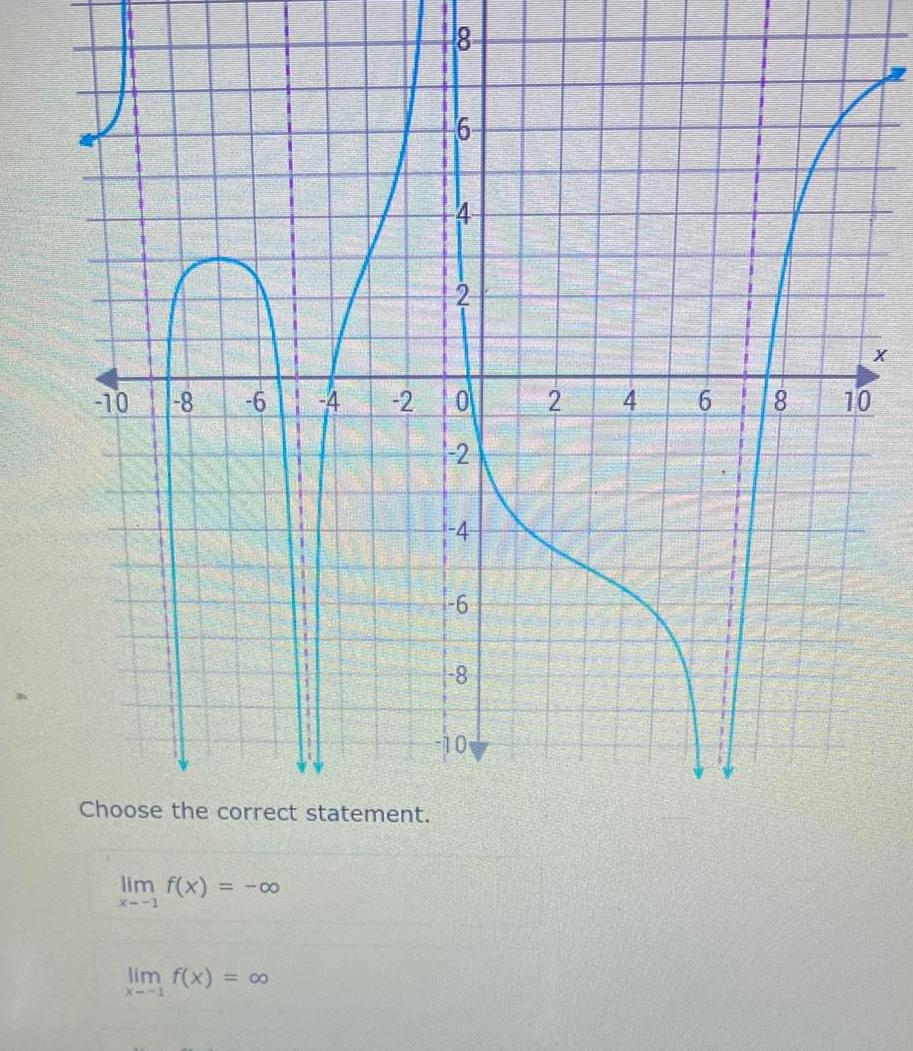
Calculus
Application of derivatives10 8 6 Choose the correct statement lim f x 00 x 1 x x 2 8 8 6 4 0 2 6 8 10 4 1 10
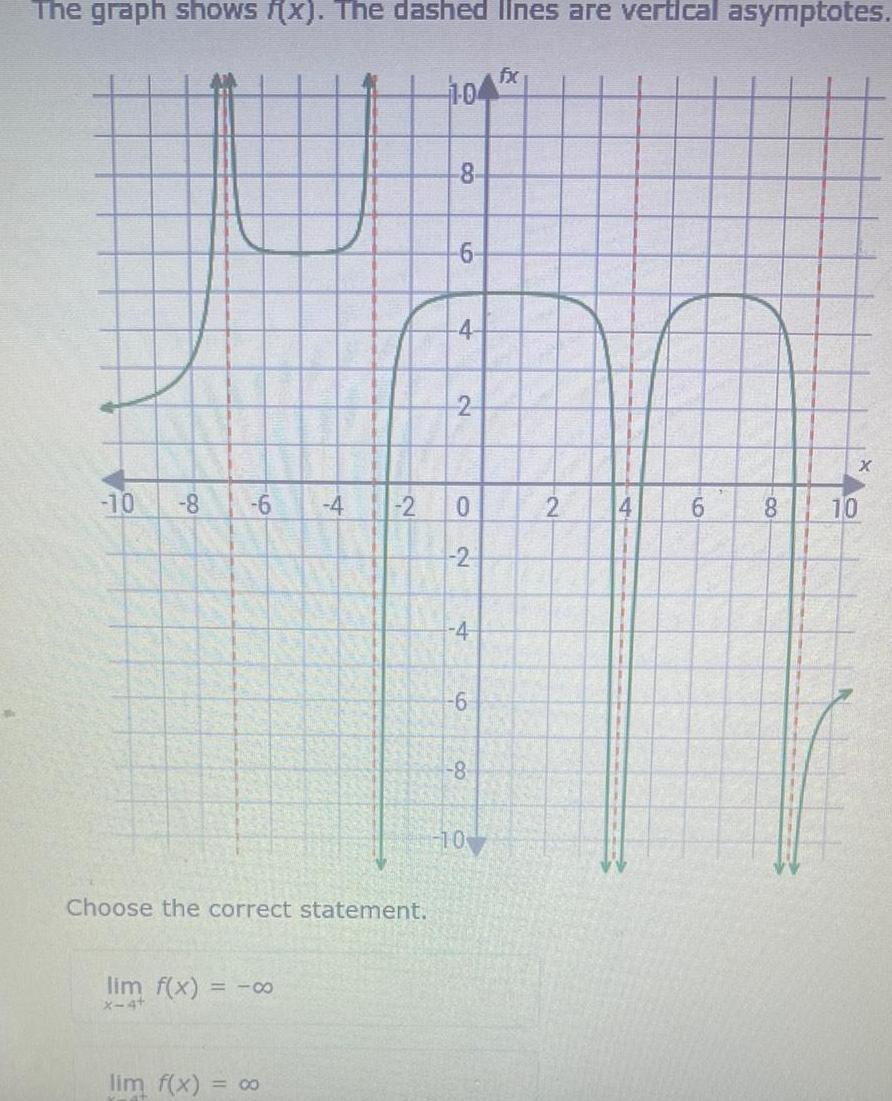
Calculus
Application of derivativesThe graph shows f x The dashed lines are vertical asymptotes 10 8 6 lim f x X 4 Choose the correct statement lim f x 4 00 2 1 04 8 6 4 2 0 2 4 6 8 10 fx 2 6 8 10 X
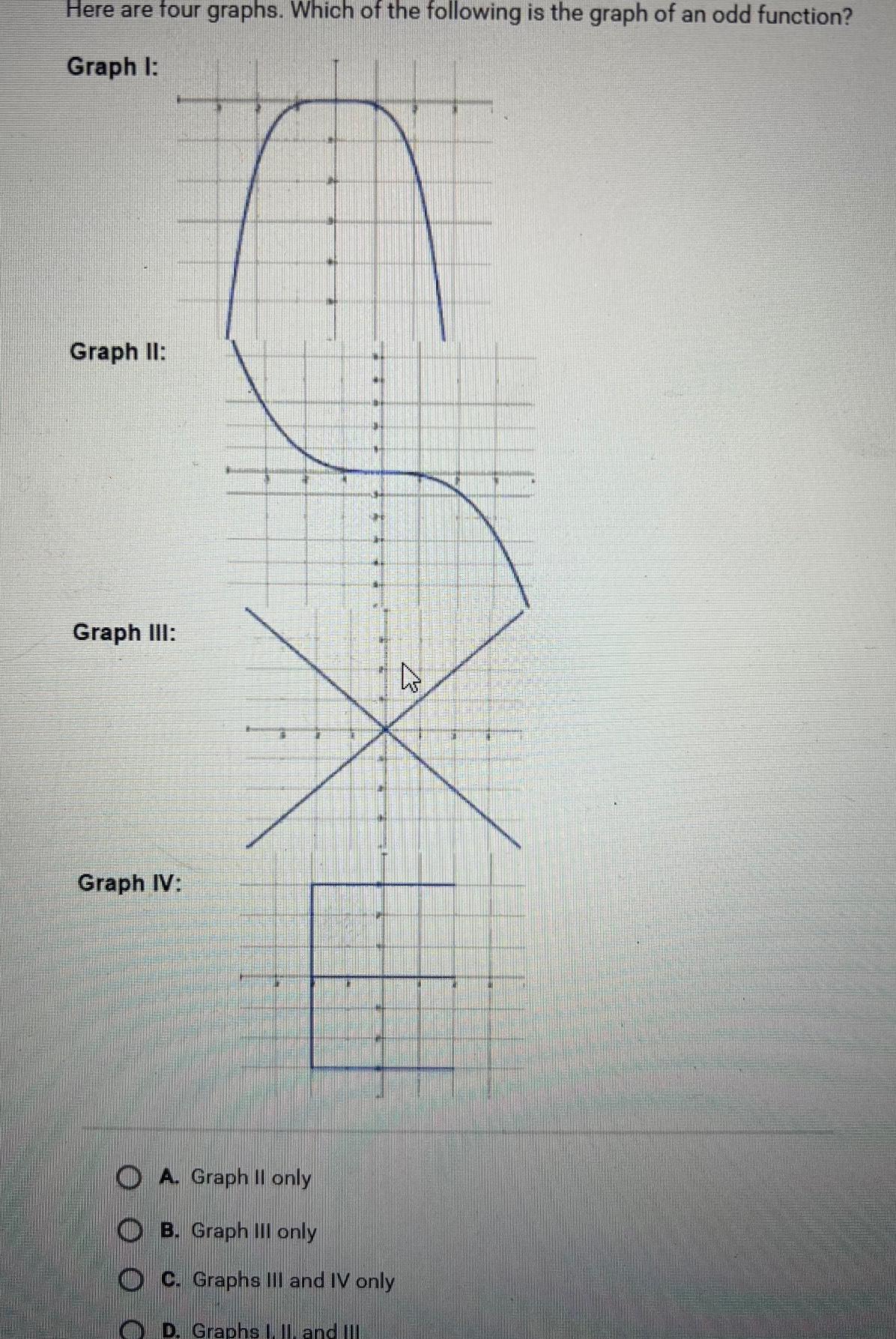
Calculus
Application of derivativesHere are four graphs Which of the following is the graph of an odd function Graph I Graph II Graph III Graph IV OA Graph II only OB Graph III only OC Graphs III and IV only D Graphs I II and III
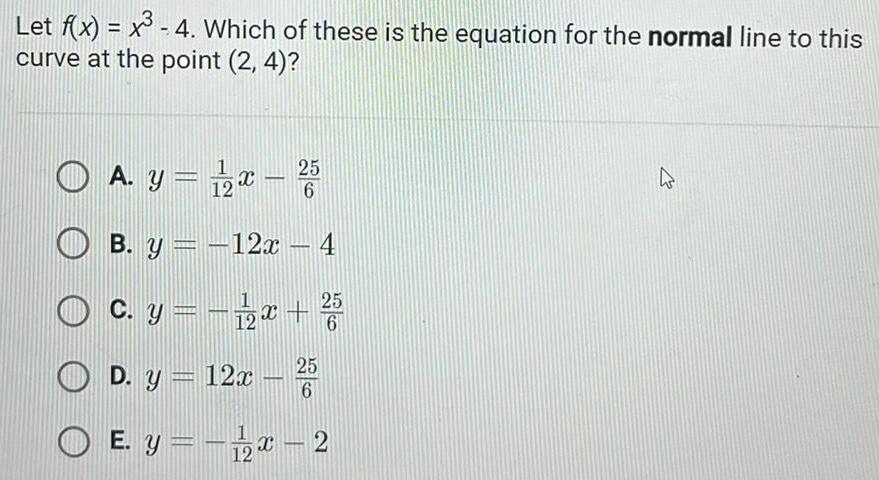
Calculus
Application of derivativesLet f x x 4 Which of these is the equation for the normal line to this curve at the point 2 4 O A y 1 2x 25 B y 12x 4 c y 1 2x 5 6 25 D y 12x 6 O E y x 2 12 4 27

Calculus
Application of derivatives2 Suppose a coin is dropped from the top of the Empire State building in New York which is 1 454 feet tall The position function for free falling objects is s t 16t vot Sor where vo is the initial velocity and so is the initial position A Determine the position and velocity functions for the coin B Determine the average velocity of the coin on the interval 1 3
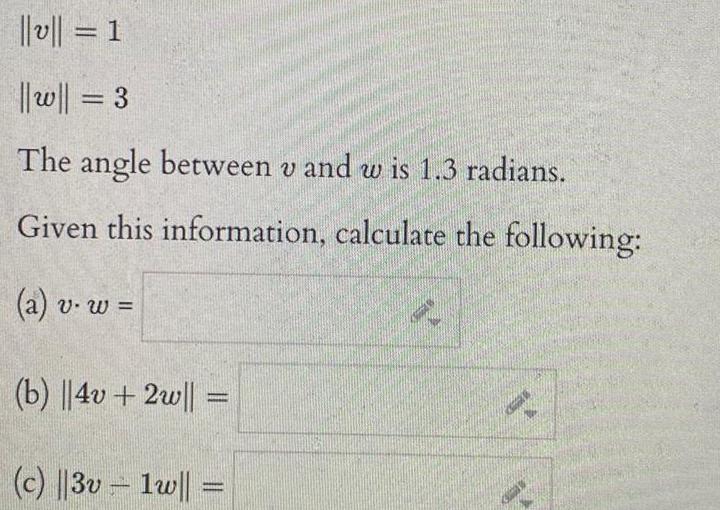
Calculus
Application of derivativesv 1 w 3 The angle between v and w is 1 3 radians Given this information calculate the following a v w b 4v 2w c 3v1w

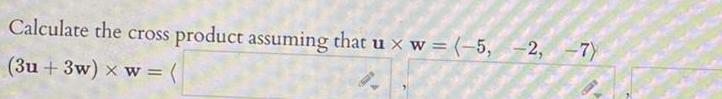
Calculus
Application of derivativesCalculate the cross product assuming that u x w 5 2 7 3u 3w x w CURS

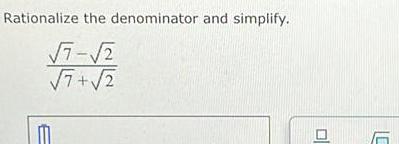

Calculus
Application of derivativesThe regions in the graph indicate whether a person is obese overweight borderline overweight normal weight or underweight The formula to find a person s body mass index BMI is as follows BMI 703W H The variable W represents weight in pounds The variable H represents height in inches 2 Body Mass Index BMI C 15 Obise 10 20 30 Males Overweigh Borderline Overv Normal Range Underweight 40 50 a Using the formula for BMI find a male s BMI if he is 20 years old 74 inches tall and weighs 234 pounds Round to the nearest integer as needed 60 70

Calculus
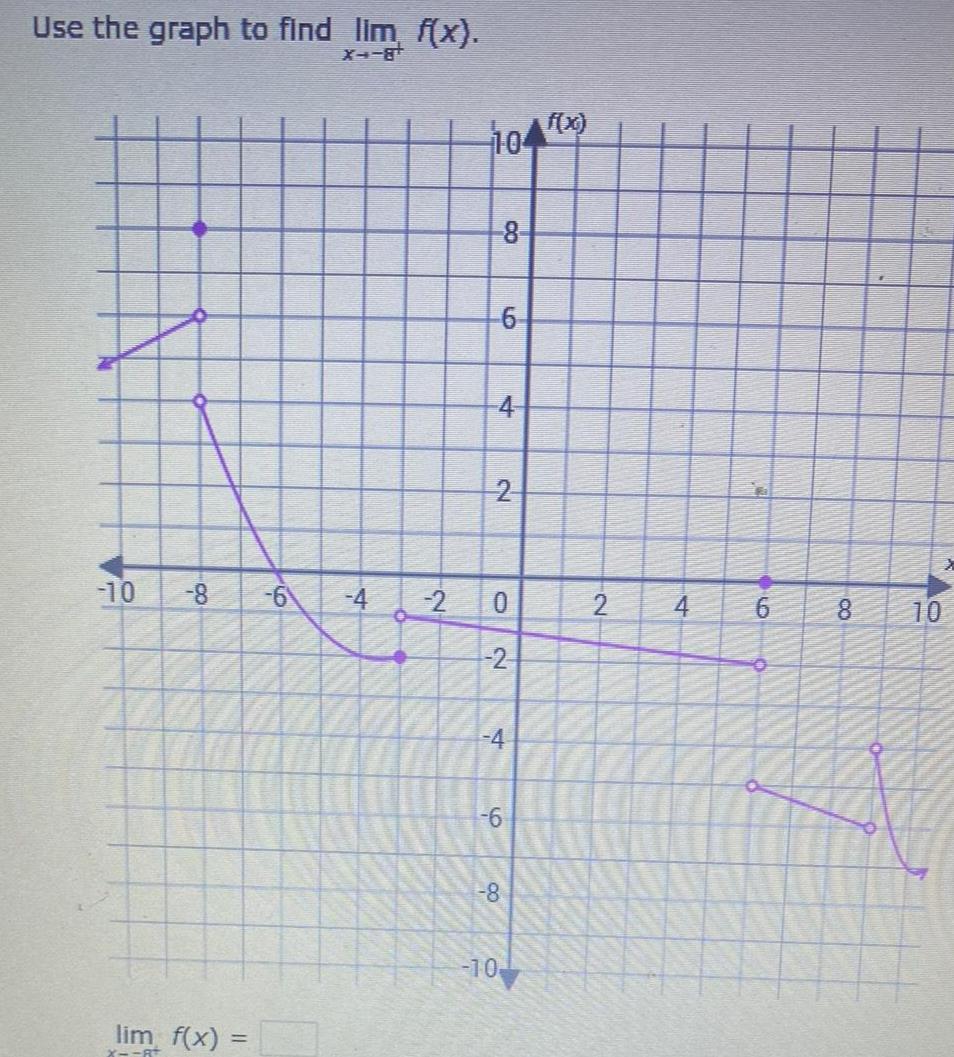
Application of derivativesUse the graph to find lim f x 10 8 6 4 lim f x X At 2 104 8 6 4 2 0 2 4 6 8 10 f x 2 4 6 O 8 10
Calculus
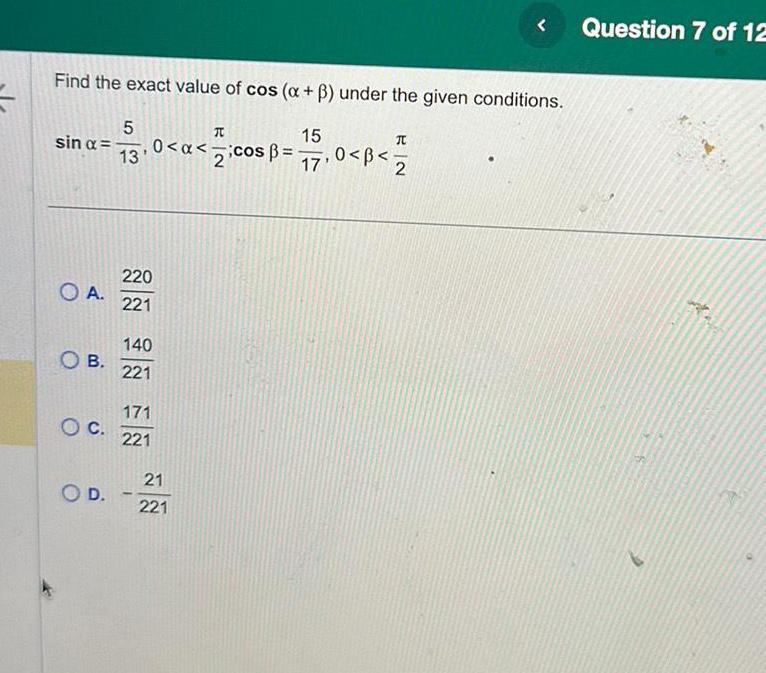
Application of derivativesFind the exact value of cos x under the given conditions 15 17 0 B sin OA OB 5 13 O D T 0 x cos 2 220 221 140 221 171 OC 221 21 221 Question 7 of 12

Calculus
Application of derivatives6 At a certain instant the base of a triangle is 5 inches and is increasing at the rate of 1 inch per minute At the same instant the height is 10 inches and is decreasing at the rate of 2 5 inches per minute Is the area of the triangle increasing or decreasing Justify your answer

Calculus
Application of derivatives1 A candy company needs a custom box for their truffles The box they ve chosen is in the shape of a cylinder with a hemisphere of the same radius on top The total volume of the box is v 1 2 4 y 7 where y is the height of the box and is the radius of the box Originally the candy box was designed to have a height of 6 inches and a radius of 2 inches but the shipper suggests that the boxes be made slightly shorter You now need to adjust the radius so that the height is reduced to 5 75 inches but the volume remains constant A Find the value of at the point r 2 y 6 I

Calculus
Application of derivativesEvaluate the following definite integral by interpretir 5 S 2 2 3x dx OA 24 OB 17 5 O C 12 5 OD 37 5 OE 75 0
Calculus
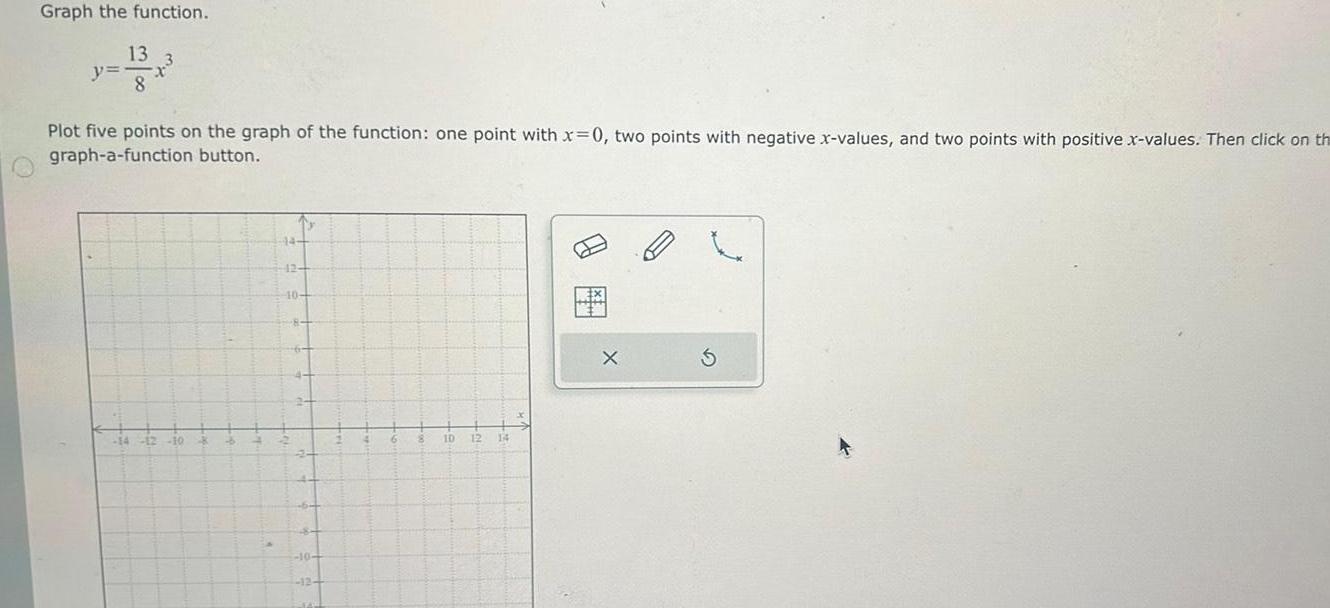
Application of derivativesGraph the function y 13 8 Plot five points on the graph of the function one point with x 0 two points with negative x values and two points with positive x values Then click on th graph a function button 14 12 10 12 10 12 14 X

Calculus
Application of derivativesLeila Dan and Reuben sent a total of 124 text messages over their cell phones during the weekend Dan sent 9 fewer messages than Leila Reuben sent 3 times as many messages as Dan How many messages did they each send Number of text messages Leila sent Number of text messages Dan sent Number of text messages Reuben sent 0 0 E X S

Calculus
Application of derivatives4 Suppose the point 4 is on the curve sinx siny C where C is a constant Use x y the tangent line approximation to find the y coordinate of the point on the curve with x coordinate 10 Be sure to show all your work

Calculus
Application of derivatives2 A boat is pulled into a dock by a rope with one end attached to the front of the boat and the other end passing through a ring attached to the dock at a point 5 feet higher than the front of the boat The rope is being pulled through the ring at the rate of 0 6 feet per second How fast is the boat approaching the dock when 13 feet of rope are out
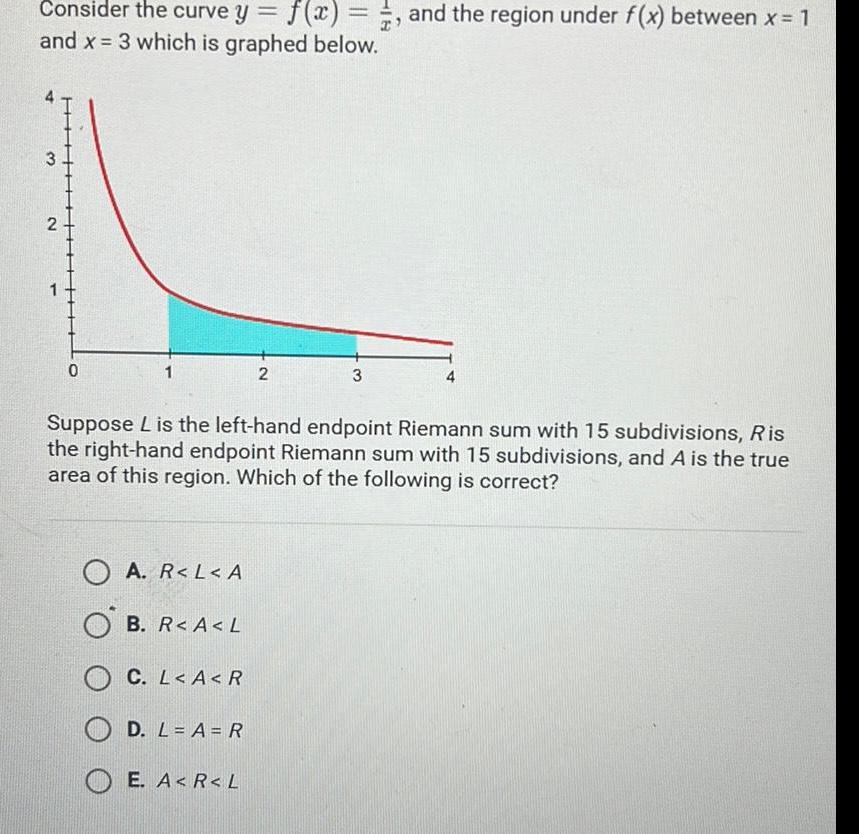
Calculus
Application of derivativesConsider the curve y f x and the region under f x between x 1 and x 3 which is graphed below 3 2 0 A R L A OB R A L C L A R Suppose L is the left hand endpoint Riemann sum with 15 subdivisions Ris the right hand endpoint Riemann sum with 15 subdivisions and A is the true area of this region Which of the following is correct D L A R 2 E A R L 3

Calculus
Application of derivatives1 At a certain instant the length of a rectangle is 3 inches and is increasing at the rate of 1 inch per minute At the same instant the width is 2 inches and is decreasing at the rate of 5 inches per minute Is the area increasing or decreasing

Calculus
Application of derivativesSolve each of the linear systems in Problems 13 through 20 to determine whether the critical point 0 0 is stable asymptot cally stable or unstable Use a computer system or graphing calculator to construct a phase portrait and direction field for the given system Thereby ascertain the stability or instabil ity of each critical point and identify it visually as a node a saddle point a center or a spiral point 15 dx dt 2x dy dt y
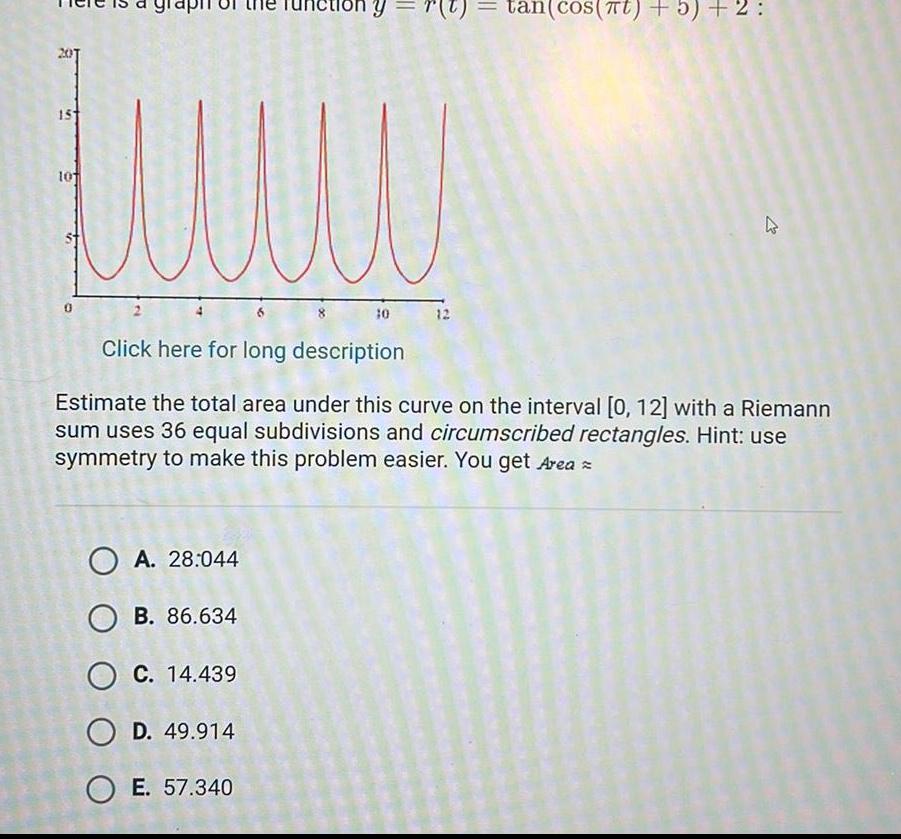
Calculus
Application of derivatives15 10 ny OA 28 044 OB 86 634 O C 14 439 OD 49 914 OE 57 340 10 12 tan cOS TU 3 2 27 Click here for long description Estimate the total area under this curve on the interval 0 12 with a Riemann sum uses 36 equal subdivisions and circumscribed rectangles Hint use symmetry to make this problem easier You get Area

Calculus
Application of derivatives1 The U S Post Office will accept a box for shipment only if the sum of the length and girth distance around is at most 108 inches Find the dimensions of the largest acceptable box with square ends air cargo fragile

Calculus
Application of derivativesYou re sunbathing on the island shown on the map below The island is six miles from shore at the closest point and the nearest store is a convenience store seven miles down the beach If you can row at 4 miles an hour and you can walk at 5 miles an hour where should you land to get a bag of tortilla chips in the least possible time Ignore tides currents and sharks No fair renting a helicopter a 7 miles

Calculus
Application of derivatives4 Given a right circular cone you put an upside down cone inside it so that its vertex is at the center of the base of the larger cone and its base is parallel to the base of the larger cone If you choose the upside down cone to have the largest possible volume what fraction of the volume of the larger cone does it occupy Let H and R be the height and radius of the large cone let h and be the height and radius of the small cone Use similar triangles to get an equation relating and r The formula for the volume of a cone is V r h
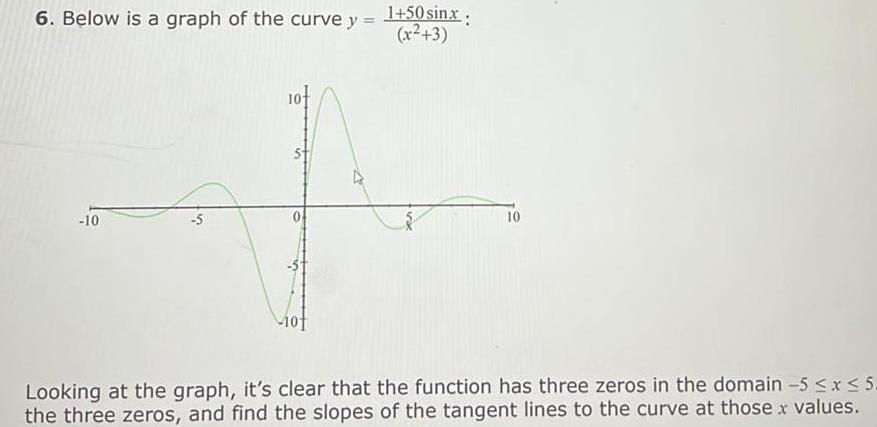
Calculus
Application of derivatives6 Below is a graph of the curve y 10 1 50sinx C x 3 10 Looking at the graph it s clear that the function has three zeros in the domain 5 x 5 the three zeros and find the slopes of the tangent lines to the curve at those x values
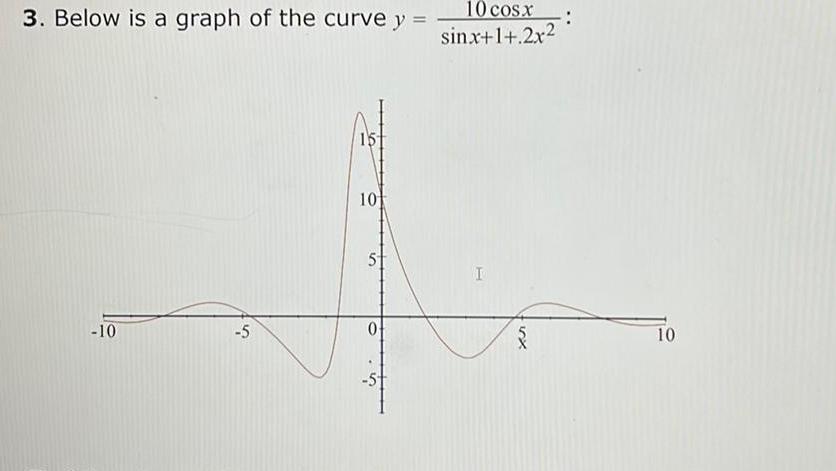
Calculus
Application of derivatives3 Below is a graph of the curve y 10 5 15 10 5 0 10 cosx sinx 1 2x2 I 3 10
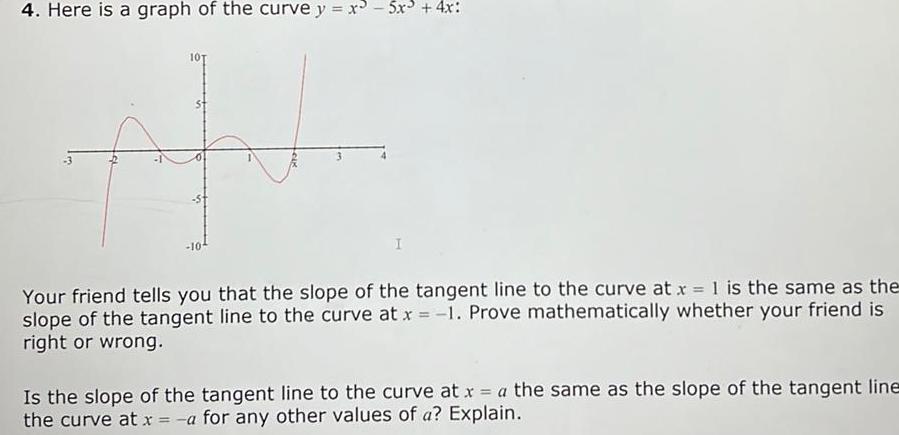
Calculus
Application of derivatives4 Here is a graph of the curve y x3 5x 4x 101 I Your friend tells you that the slope of the tangent line to the curve at x 1 is the same as the slope of the tangent line to the curve at x 1 Prove mathematically whether your friend is right or wrong Is the slope of the tangent line to the curve at x a the same as the slope of the tangent line the curve at x a for any other values of a Explain
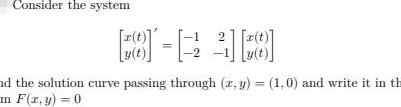
Calculus
Application of derivativesConsider the system 8 238 E nd the solution curve passing through x y 1 0 and write it in th m F x y 0

Calculus
Application of derivativesSally s anime club is selling brownies to raise money Instead of just aiming blindly Sally does some market research to try and maximize the club s prom E 4p2 10P 125 Where is the amount the club will earn from the bake sale and P is the price they charge for each brownie both measured in dollars A What price should the club charge for their brownies to maximize their profits B How much money should the club expect to make if they sell their brownies at this price
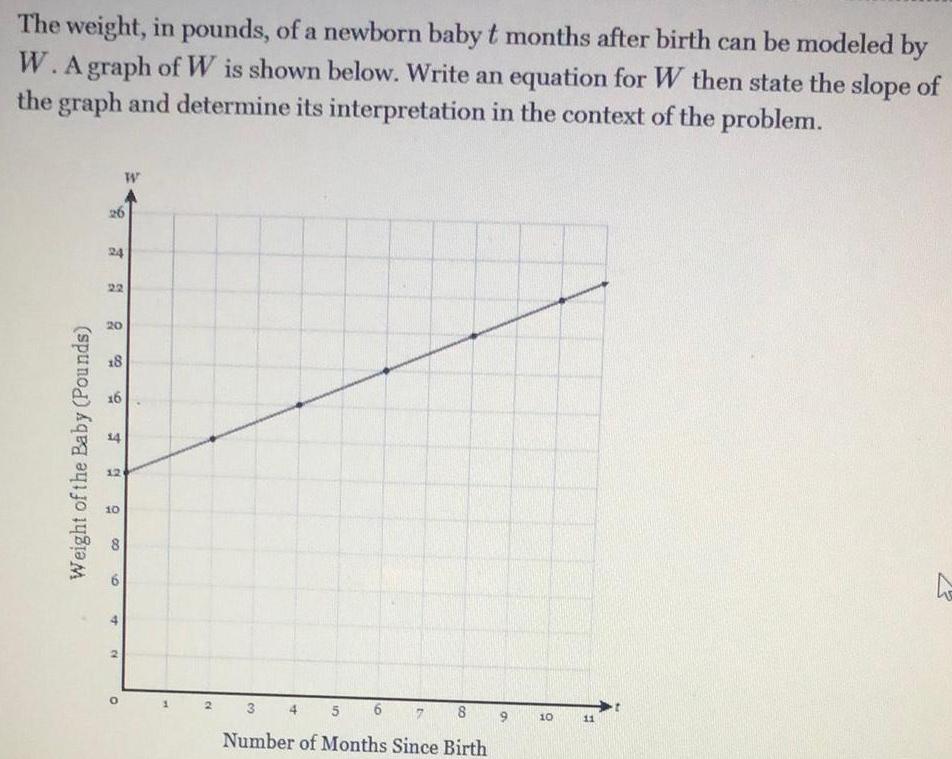
Calculus
Application of derivativesThe weight in pounds of a newborn baby t months after birth can be modeled by W A graph of W is shown below Write an equation for W then state the slope of the graph and determine its interpretation in the context of the problem Weight of the Baby Pounds 26 24 13 20 18 9 14 12 10 CO 4 W O 3 8 Number of Months Since Birth 10 11 ha

Calculus
Application of derivativesa c Use the criteria indicated to create a pair of 3 x 3 matrices D D where the entries of the matrix D are all integers 20 marks i d 1 5 d3 2 2 Create your own substitution cipher Then use it and the matrix D you created in a to encrypt the title of your favourite movie 20 marks ii Use the matrix D and the appropriate substitution cipher to decrypt the message from b 20 marks

Calculus
Application of derivativesThe derivative of y 1 sin x COS X is O A tan x O B O C O D O E 1 1 sin x sin x COS X sin x Cos x cos x sin x 1 sin x 2

Calculus
Application of derivativesThe slope of the tangent line to the graph y x at the point 1 is A 1 B 0 C 2 D 1 3 E Undefined
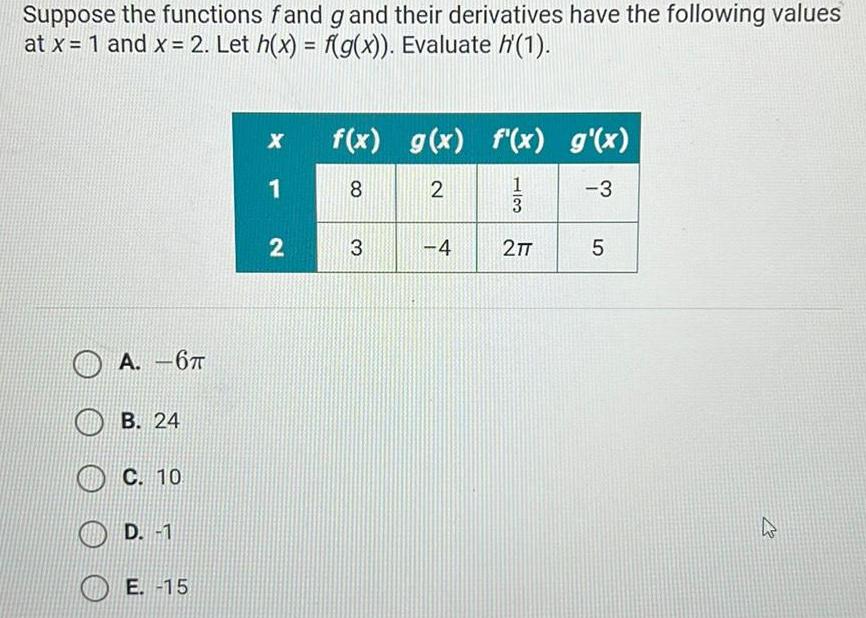
Calculus
Application of derivativesSuppose the functions fand g and their derivatives have the following values at x 1 and x 2 Let h x f g x Evaluate 1 A 6T B 24 C 10 D 1 E 15 X 1 2 f x g x f x g x 8 2 3 3 4 113 2TT LO 5 K

Calculus
Application of derivativesThe inflection point of the curve y 8x 24x 7x 3 is O A 1 23 OB 0 3 O C 1 21 OD 2 59 OE There is no point of inflection
Calculus
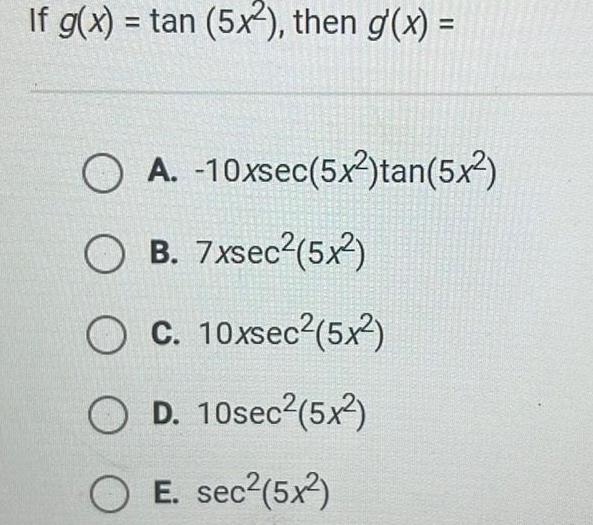
Application of derivativesIf g x tan 5x2 then g x O A 10xsec 5x tan 5x OB C 7xsec 5x 10xsec 5x OD 10sec 5x2 O E sec 5x O O
Calculus
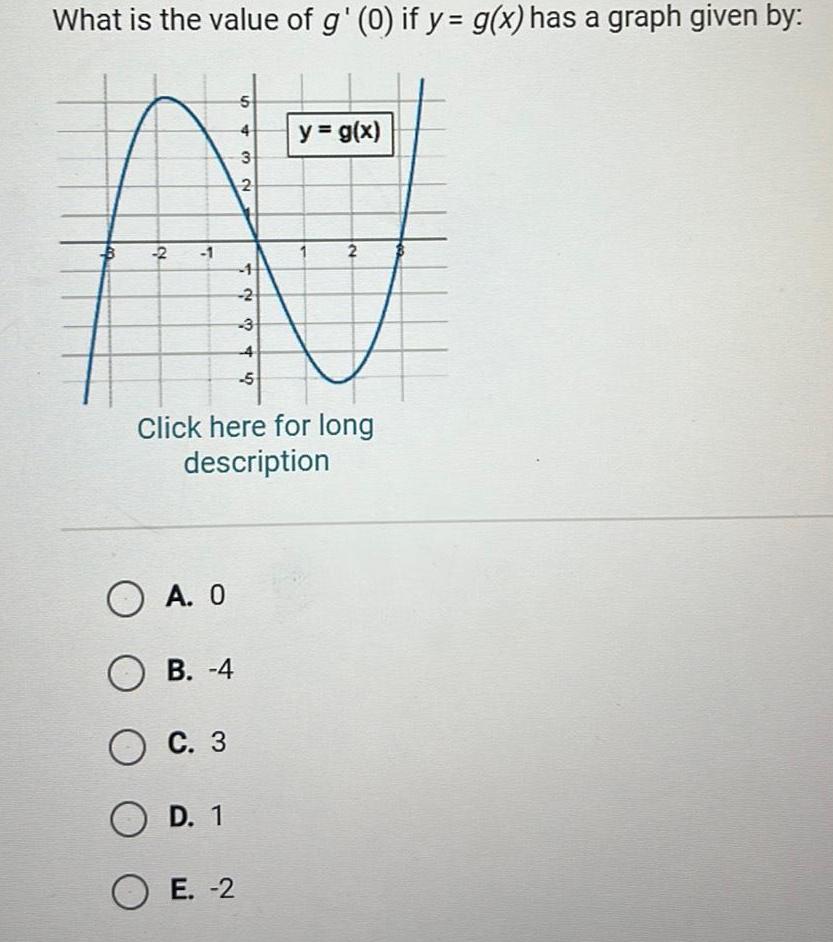
Application of derivativesWhat is the value of g 0 if y g x has a graph given by 2 1 10 OA O OB 4 O C 3 O D 1 OE 2 432 423 2 4 5 y g x 2 Click here for long description