Application of derivatives Questions and Answers
Calculus
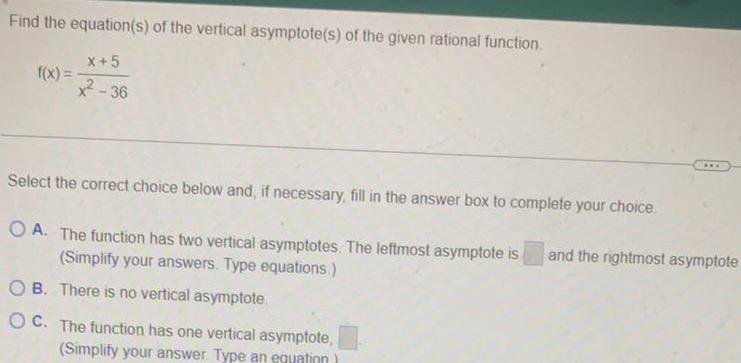
Application of derivativesFind the equation s of the vertical asymptote s of the given rational function f x X 5 36 Select the correct choice below and if necessary fill in the answer box to complete your choice OA The function has two vertical asymptotes The leftmost asymptote is Simplify your answers Type equations OB There is no vertical asymptote OC The function has one vertical asymptote Simplify your answer Type an equation www and the rightmost asymptote
Calculus
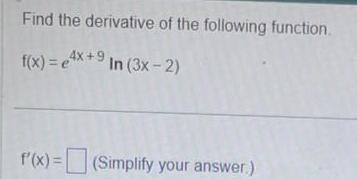
Application of derivativesFind the derivative of the following function f x 4x 9 In 3x 2 f x Simplify your answer

Calculus
Application of derivativesUse the second derivative test for local extrema to indicate any local extrema or saddle points of the following function f x y x y 3xy

Calculus
Application of derivativesUse the method of Lagrange multipliers to minimize 2 f x y x 4xy y subject to the constraint x y 16 You may assume a minimum exists

Calculus
Application of derivatives15 points Solve for the variable in each equation a 4 sin 0 10 b 2logg x log3 5 1

Calculus
Application of derivativesGiven that 6f 12g 18h 72 4f 3g 42h 248 and 2f g 22h 132 solve the system of equations using Gaussian elimination Select the correct answer below 2 4 6 O 2 6 4 O 4 2 6 infinitely many solutions

Calculus
Application of derivativesA world famous prix fixe menu includes the following choices Beverage choose one wine soft drink coffee tea milk juice or cappuccino First course no choice baguette bruschetta whole roasted garlic and butter Second course choose one quesadilla onion soup salad Caesar salad lettuce wedge spinach salad or romaine salad Third course choose one rib eye steak swordfish rack of lamb whitefish grilled chicken southern fried chicken lobster or vegetaria plate if you choose steak then choose one of the following fries mashed potatoes creamed corn spinach broccoli or grilled onions Fourth course choose one chocolate cake cinnamon tart apple tart pecan tart creme brulee mango sorbet or chocolate tart How many different choices are possible meals
Calculus
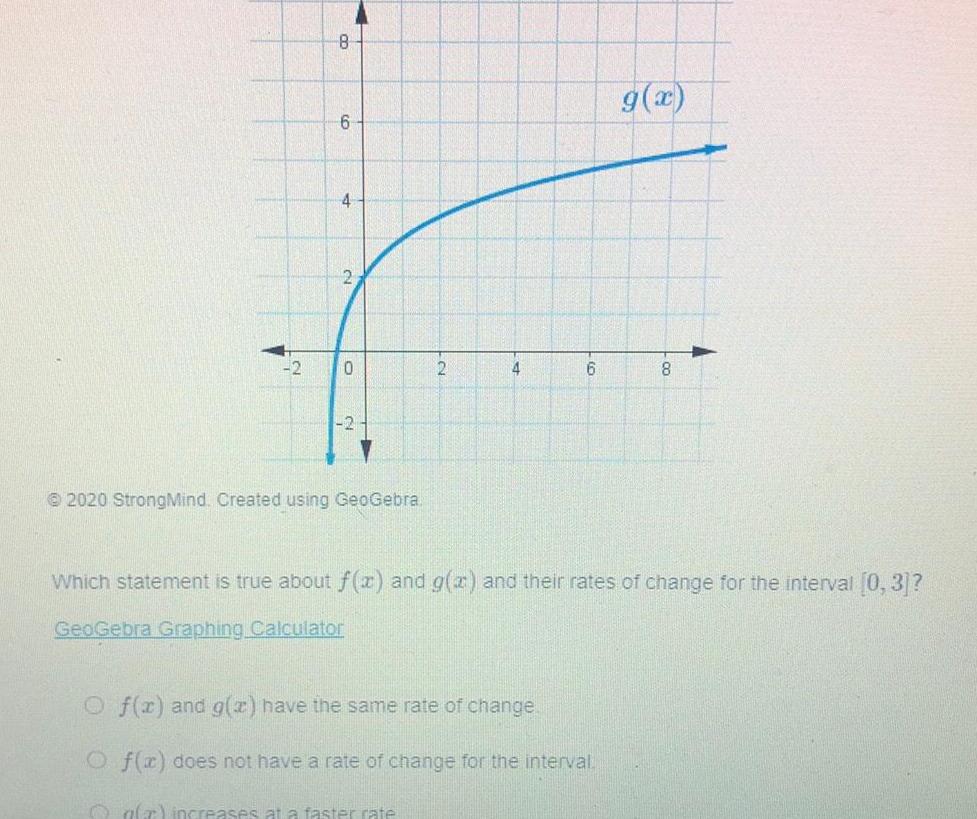
Application of derivatives2 8 6 4 2 0 2020 StrongMind Created using GeoGebra 6 g x Of x and g x have the same rate of change O f x does not have a rate of change for the interval ala increases at a faster rate 8 Which statement is true about f x and g x and their rates of change for the interval 0 3 GeoGebra Graphing Calculator

Calculus
Application of derivativesSome automobiles have four button locks To gain entry push four buttons in a particular order repeats allowed to unlock the door How ma different four digit codes are possible codes

Calculus
Application of derivativesON 4 2 points A population of punishers is described by the DTDS 1 1 density after t weeks FIND the general Solution of the DTDS if initially to
Calculus
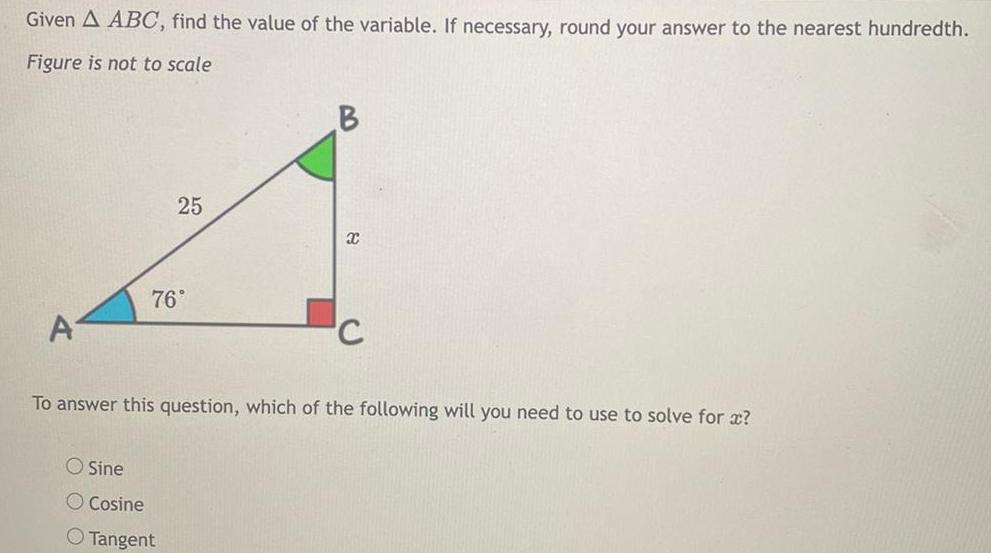
Application of derivativesGiven A ABC find the value of the variable If necessary round your answer to the nearest hundredth Figure is not to scale A 25 76 O Sine O Cosine O Tangent B X C To answer this question which of the following will you need to use to solve for x

Calculus
Application of derivativesClassify the problem as a permutation a combination or neither How many three digit numbers can be formed using the numerals 3 4 5 6 7 without repetition permutation O combination O neither Answer the given question
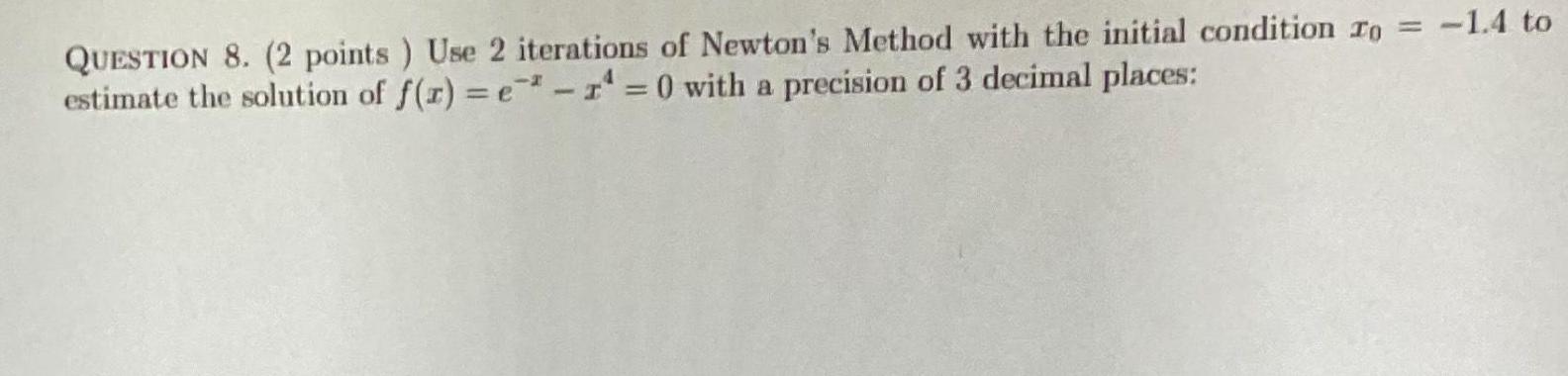
Calculus
Application of derivativesQUESTION 8 2 points Use 2 iterations of Newton s Method with the initial condition To 1 4 to estimate the solution of f x e r 0 with a precision of 3 decimal places
Calculus
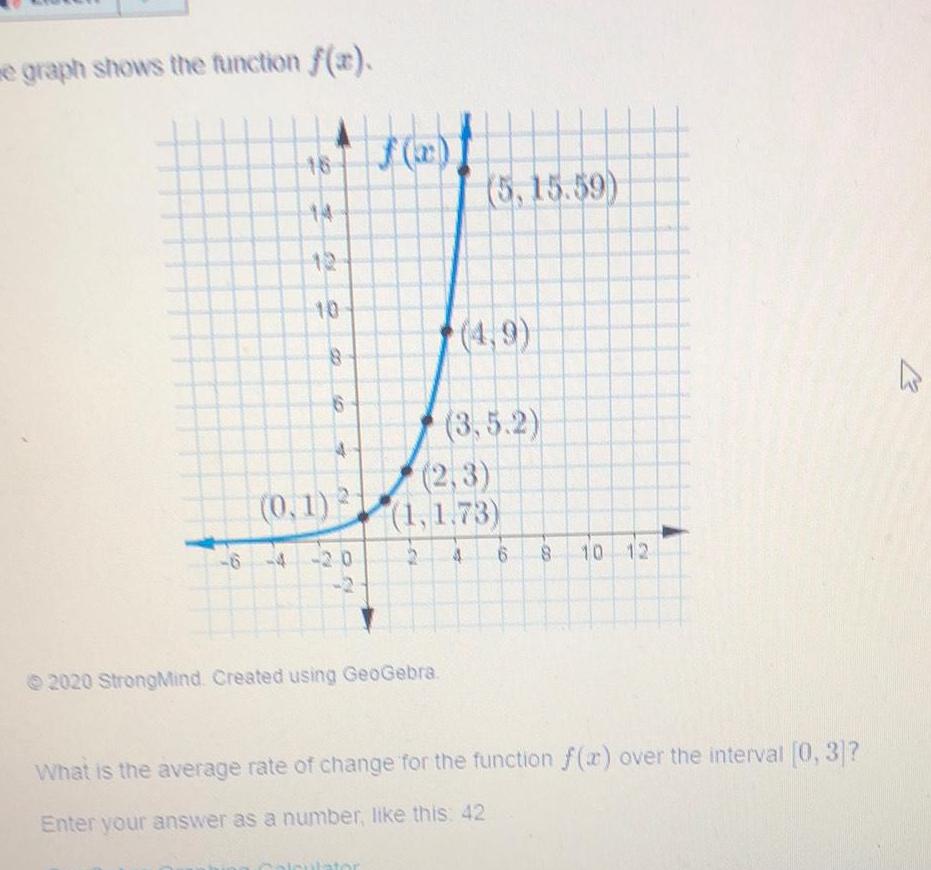
Application of derivativese graph shows the function f x 19 18 14 12 10 0 1 CO 6 4 20 2 5 15 59 2020 StrongMind Created using GeoGebra 4 9 3 5 2 2 3 1 1 73 2 4 6 8 10 12 What is the average rate of change for the function f x over the interval 0 3 Enter your answer as a number like this 42 E

Calculus
Application of derivativesCalculate the average rate of change of f x over the interval 1 x 3 I f x 4 2 877 3 2 270 2 0 423 1 2 728 O 5 546 What is the average rate of change for the function f x over the interval 1 x 3 00 0 2 524 0 2 524 2 728 0 423 O 1 364 1 2 3 4

Calculus
Application of derivativesUse the table to calculate the average rate of change of f x over the interval 0 4 x f x 1 2 4 3 2 1 0 1 2 3 4 4 8 16 32 64 128 256

Calculus
Application of derivatives5 2 points Consider the function f r r 12r 1 defined on the closed be and its Global absolute maximum and find its Global absolute minimum

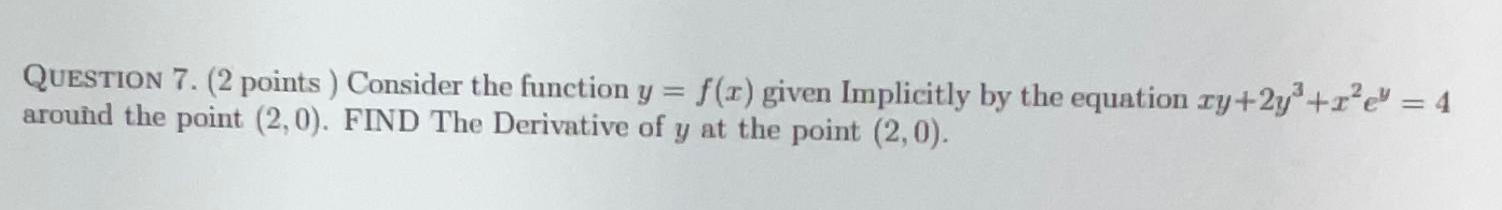
Calculus
Application of derivativesQUESTION 7 2 points Consider the function y f x given Implicitly by the equation ry 2y 1 e 4 around the point 2 0 FIND The Derivative of y at the point 2 0
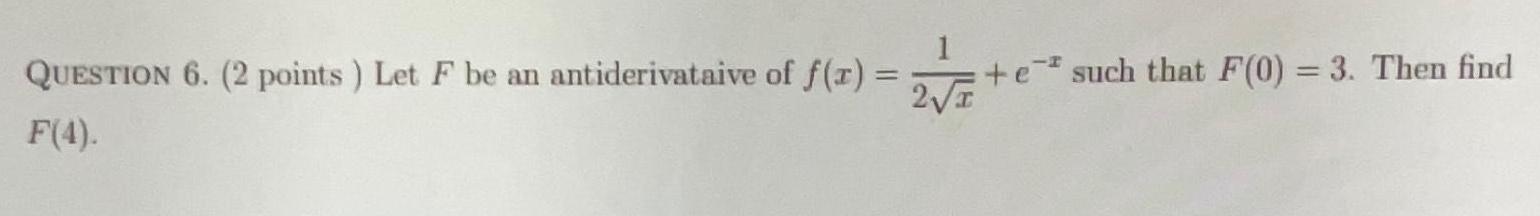
Calculus
Application of derivativesQUESTION 6 2 points Let F be an antiderivataive of f x 2 I F 4 e such that F 0 3 Then find

Calculus
Application of derivativesIn how many ways can seven books be arranged on a bookshelf ways OF

Calculus
Application of derivativesQUESTION 2 2 points Information on functions f x g r f r and g r for some r is given in the table Let h x gof x I f x f x g x g x Find h 1 and h 1 1 27 3 3 2 312 QUESTION 3 2 points Find the derivative of f x ln 3 5 2 3 cos x 22 11 x 2 4e 4 3 1 1 4
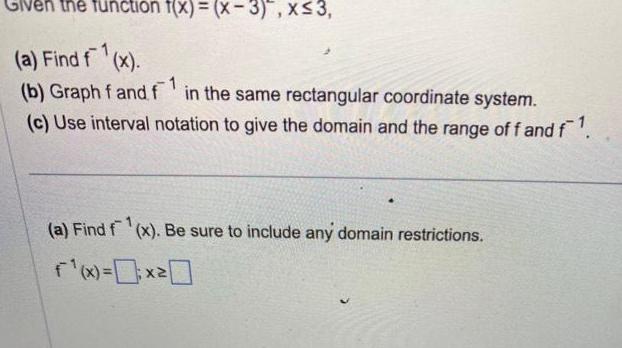
Calculus
Application of derivativesGiven the function f x x 3 x 3 a Find f x 1 1 b Graph f and f in the same rectangular coordinate system c Use interval notation to give the domain and the range of f and f a Find f x Be sure to include any domain restrictions f x 0 x 0

Calculus
Application of derivatives7 Find the term that does not contain x in the expansion of 10 4x 2x
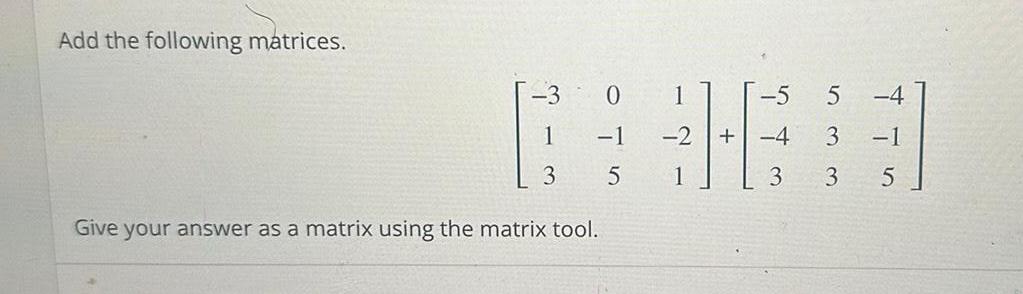
Calculus
Application of derivativesAdd the following matrices 1 3 0 1 5 Give your answer as a matrix using the matrix tool 2 1 5 4 3 5 3 3 1
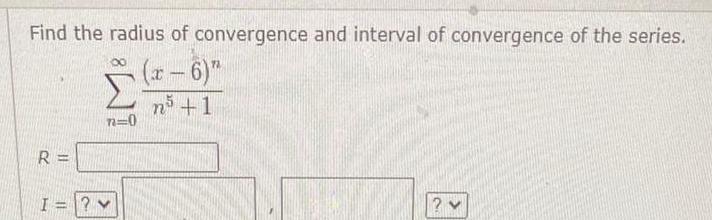
Calculus
Application of derivativesFind the radius of convergence and interval of convergence of the series x 6 n 1 R I n 0

Calculus
Application of derivativesFind the price p per unit that produces the maximum profit P if C x 25 16x and p 24 2x OA 16 OB 20 O C 22 O D 12
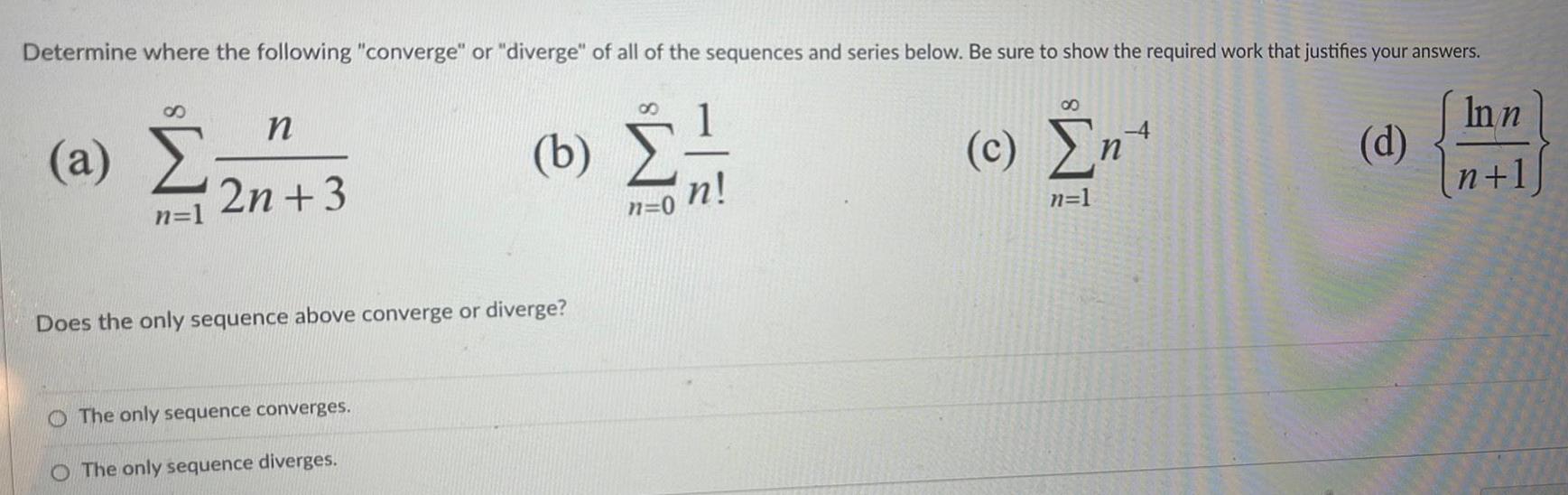
Calculus
Application of derivativesDetermine where the following converge or diverge of all of the sequences and series below Be sure to show the required work that justifies your answers S a n 1 n 2n 3 b n 0 Does the only sequence above converge or diverge The only sequence converges O The only sequence diverges n 8 c Ent n 1 d Inn n 1
Calculus
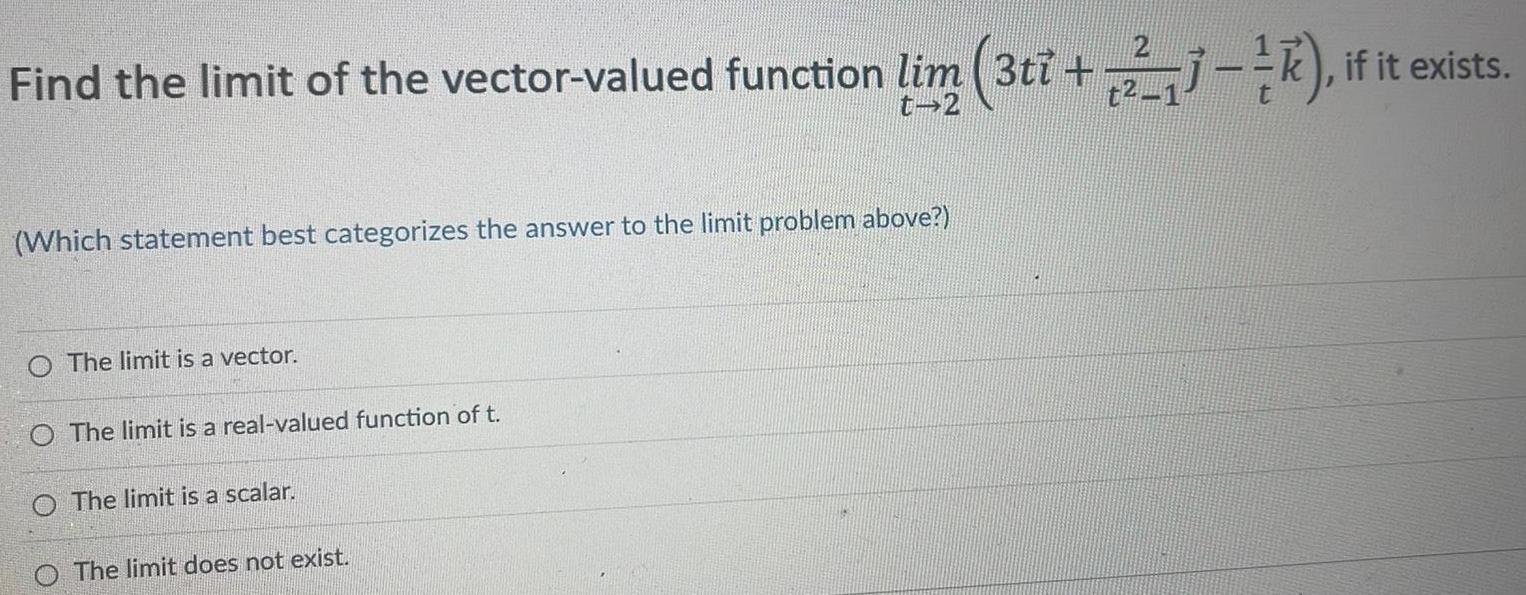
Application of derivativesFind the limit of the vector valued function lim 3ti 23 if it exists t2 t 2 Which statement best categorizes the answer to the limit problem above O The limit is a vector O The limit is a real valued function of t O The limit is a scalar The limit does not exist

Calculus
Application of derivativesa Create a table of values for the variables found in the given parametric equations below b Write the corresponding rectangular equation by eliminating the parameter c Sketch the curve represented by the parametric equations indicate the orientation of the cur x t 1 y t 3t 3 t 2 According to your table of values when x 0 what does y equal Enter this answer in the space provided

Calculus
Application of derivativesConsider the function f x sin x Write the fifth Maclaurin polynomial P5 x for sin x b Write the Maclaurin series representation in sigma notation for sim Use P5 x to approximate sin 0 8 to six decimal places a C Enter part c rounded to six decimal places in the space provided

Calculus
Application of derivativesGiven that u 3 4 2 and 1 2 3 find a u b uxi Enter the answer to part a in the space provided c the unit vector in the same direction as

Calculus
Application of derivativesFind the interval of convergence of the power series Express your answer in interval notation n 1 x 5 n n Do not skip any spaces when entering the interval of convergence

Calculus
Application of derivatives3 Consider the following system of linear equations 3Z X 2x 2y 5z X 2Z 1 2 0 a Write down the coefficient matrix A i e the matrix of coefficients of the above syster and determine A 0 4 2 2 4 b Show that AA and A A I where is the 3 x 3 identity matrix c Use A to solve the system d Evaluate Al by expanding by the second column e Use Cramer s rule to solve the above system
Calculus
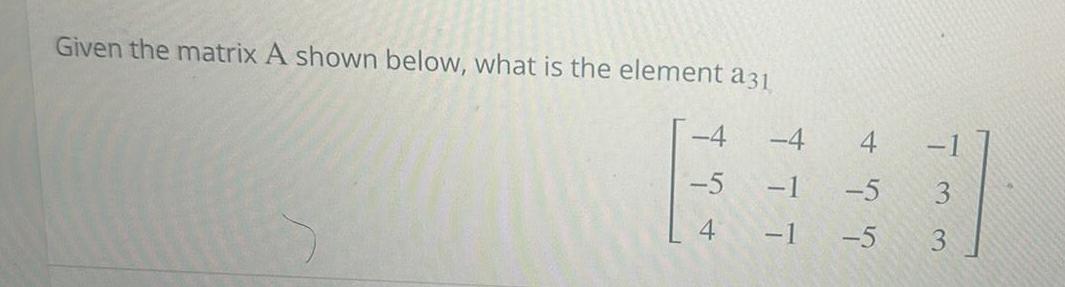
Application of derivativesGiven the matrix A shown below what is the element a31 4 5 4 4 1 5 1 5 3
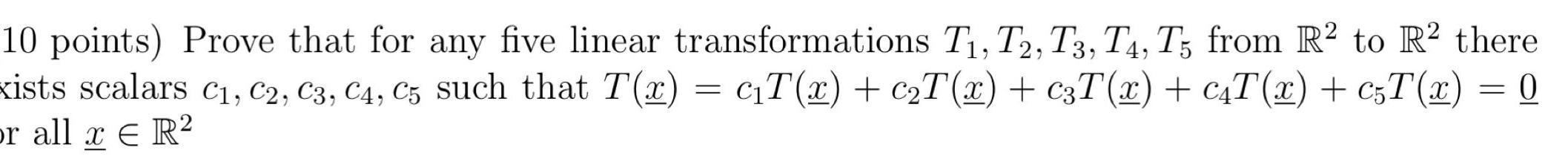
Calculus
Application of derivatives10 points Prove that for any five linear transformations T T2 T3 T4 T5 from R to R there xists scalars C C2 C3 C4 C5 such that T x c T x c T x c3T x c T x c5T x 0 or all x R E R2

Calculus
Application of derivativesA sample of 500 g of radioactive lead 210 decays to polonium 210 according to the function A t 500e 0 032t where t is time in years Find the amount of radioactive lead remaining after a 4 yr b 8 yr c 20 yr d Find the half life a The amount of radioactive lead remaining after 4 yr will be Round to the nearest integer as needed b The amount of radioactive lead remaining after 8 yr will be g Round to the nearest integer as needed c The amount of radioactive lead remaining after 20 yr will be Round to the nearest integer as needed g d The half life is about yr Round to two decimal places as needed g

Calculus
Application of derivativesThe average monthly temperature T m in degrees Celsius in a particular city varies according to the model T m 4 sin sin m 2 1 2 where m represents the months of the year and January begins at m 0 Between what months will the temperature be above 0 C O February and April January and July January and April January and May

Calculus
Application of derivativesQuestion 4 4 points Our goal is to estimate the value of In 0 9 using a Taylor polynomial a 1 point Write down the formula for the Taylor polynomial of degree 3 of a function f r centered at z a

Calculus
Application of derivatives9 End Behavior Give the equation of the horizontal asymptote of eac rational function If there is no horizontal asymptote state that fact 5x4 12x 120x 100 2x 20x 25 a b C 12x 25x 75x 125 100 2x3 7x 55x 125 4x3 125
Calculus
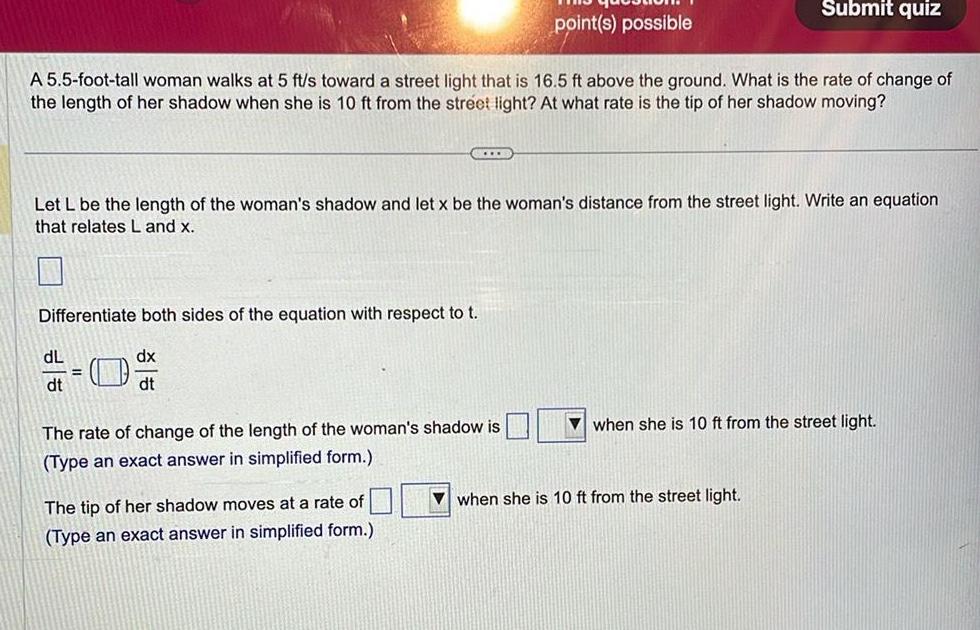
Application of derivativesA 5 5 foot tall woman walks at 5 ft s toward a street light that is 16 5 ft above the ground What is the rate of change of the length of her shadow when she is 10 ft from the street light At what rate is the tip of her shadow moving CLE Differentiate both sides of the equation with respect to t dx dt dL dt Let L be the length of the woman s shadow and let x be the woman s distance from the street light Write an equation that relates L and x point s possible The rate of change of the length of the woman s shadow is Type an exact answer in simplified form The tip of her shadow moves at a rate of Type an exact answer in simplified form Submit quiz when she is 10 ft from the street light when she is 10 ft from the street light

Calculus
Application of derivativesFind the average rate of change of y with respect to x from P to Q Then compare this with the instantaneous rate of change of y with respect to x at P by finding ma y 7 x P 3 20 Q 3 4 32 304 Enter the average rate of change of y with respect to x from point P to Q below mpo Type an integer or a decimal
Calculus
Application of derivatives2 The area of a circle increases at a rate of 6 cm s a How fast is the radius changing when the radius is 4 cm b How fast is the radius changing when the circumference is 2 cm a Write an equation relating the area of a circle A and the radius of the circle r Type an exact answer using it as needed
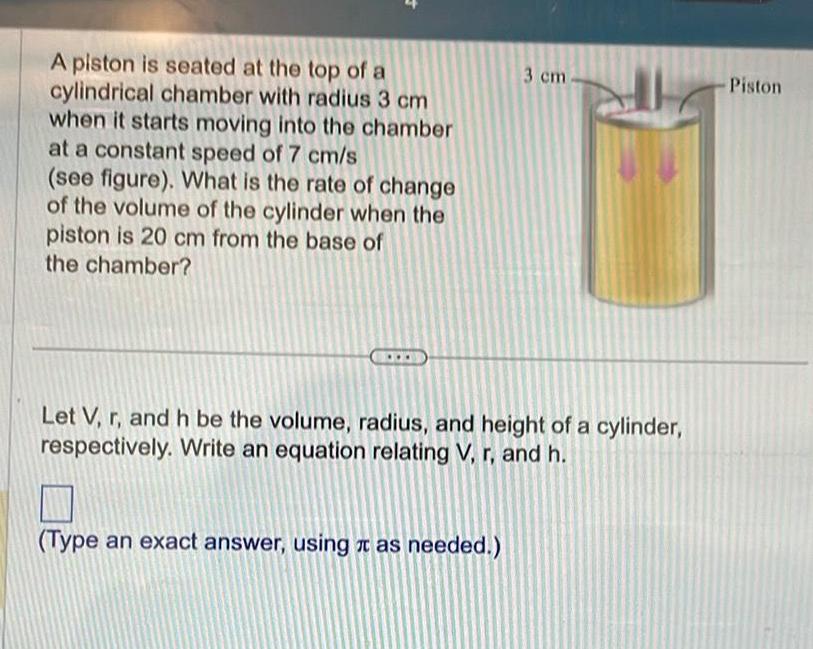
Calculus
Application of derivativesA piston is seated at the top of a cylindrical chamber with radius 3 cm when it starts moving into the chamber at a constant speed of 7 cm s see figure What is the rate of change of the volume of the cylinder when the piston is 20 cm from the base of the chamber 3 cm Let V r and h be the volume radius and height of a cylinder respectively Write an equation relating V r and h Type an exact answer using as needed Piston
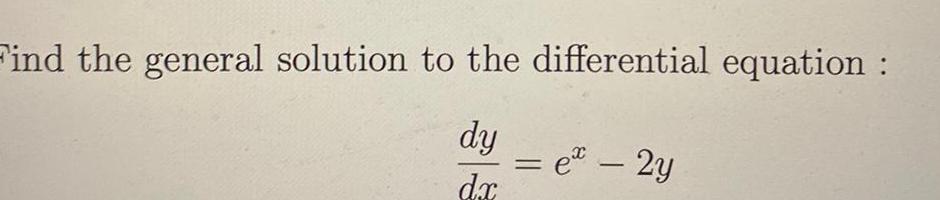
Calculus
Application of derivativesFind the general solution to the differential equation dy dx ex 2y

Calculus
Application of derivativesA 13 foot ladder is leaning against a vertical wall see figure when Jack begins pulling the foot of the ladder away from the wall at a rate of 0 5 ft s How fast is the top of the ladder sliding down the wall when the foot of the ladder is 5 ft from the wall 13 ft Let x be the distance from the foot of the ladder to the wall and let y be the distance from the top of the ladder to the ground Write an equation relating x and y

Calculus
Application of derivativesAn angler hooks a trout and reels in his line at 3 in s Assume the tip of the fishing rod is 13 ft above the water and directly above the angler and the fish is pulled horizontally directly toward the angler see figure Find the horizontal speed of the fish when it is 20 ft from the angler 13 ft Decreasing at 3 in s Let x be the horizontal distance from the angler to the fish and z be the length of the fishing line where both x and z are measured in inches Write an equation relating x and z

Calculus
Application of derivativesA rocket burns up at the rate of 5 tons min after falling out of orbit into the atmosphere If the rocket weighed 5400 tons before reentry express its weight w as a function of the time t in minutes of reentry Write the weight of the rocket as the function w t w t Simplify your answer Do not factor

Calculus
Application of derivativesA rectangle initially has dimensions 2 cm by 5 cm All sides begin increasing in length at a rate of 2 cm s At what rate is the area of the rectangle increasing after 16 s Let A b and h be the area base and height of a rectangle respectively Write an equation relating A b and h