Application of derivatives Questions and Answers

Calculus
Application of derivativesOnce Kate s kite reaches a height of 57 ft above her hands it rises no higher but drifts due east in a wind blowing 6 ft s How fast is the string running through Kate s hands at the moment that she has released 119 ft of string Let x be the horizontal distance from Kate to the kite and z be the length of the string Write an equation relating x and z

Calculus
Application of derivativesThe volume of a cube decreases at a rate of 0 2 ft min What is the rate of change of the side length when the side lengths are 7 ft Write an equation relating the volume of a cube V and an edge of the cube s
Calculus
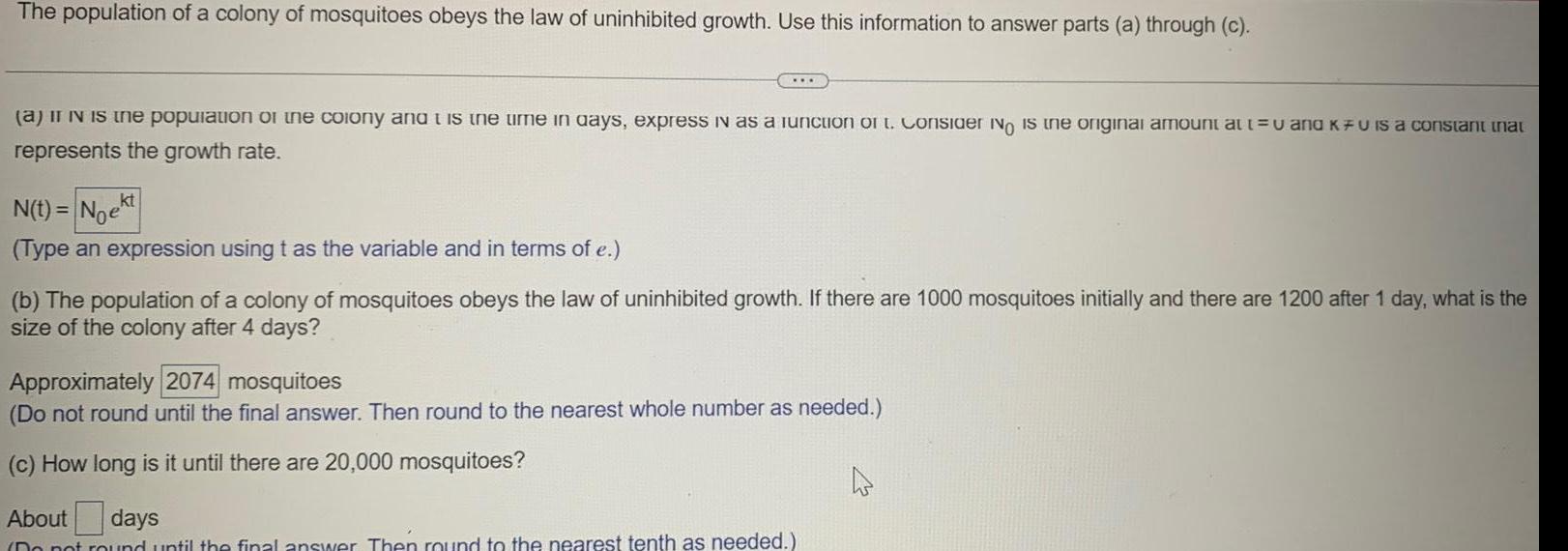
Application of derivativesThe population of a colony of mosquitoes obeys the law of uninhibited growth Use this information to answer parts a through c a it iN is the population of the colony and is the time in days express in as a function of t Consider No is the original amount at t u and KFU is a constant that represents the growth rate N t Noekt Type an expression using t as the variable and in terms of e b The population of a colony of mosquitoes obeys the law of uninhibited growth If there are 1000 mosquitoes initially and there are 1200 after 1 day what is the size of the colony after 4 days Approximately 2074 mosquitoes Do not round until the final answer Then round to the nearest whole number as needed c How long is it until there are 20 000 mosquitoes About days Do not round until the final answer Then round to the nearest tenth as needed 4

Calculus
Application of derivativesA thermometer reading 10 C is brought into a room with a constant temperature of 32 C If the thermometer reads 17 C after 2 minutes what will it read after being in the room for 4 minutes For 9 minutes C After 4 minutes the thermometer will read Do not round until the final answer Then round to the nearest hundredth as needed
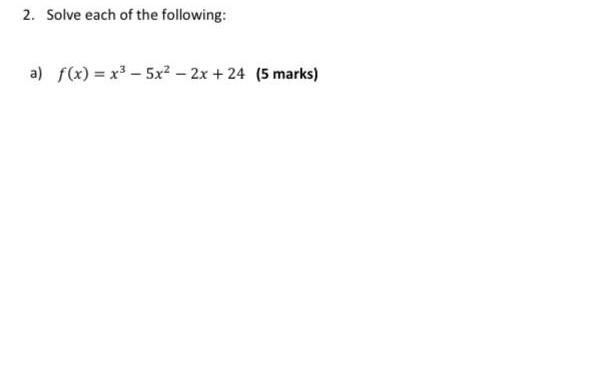

Calculus
Application of derivatives1 Given f x 3x and g x x 4 determine the expression for f g x 3 marks

Calculus
Application of derivativesDetermine the volume of the largest rectangular box in the first octant with three faces in the coordinate planes one vertex at the origin and its opposite vertex in the plane 3r 6y z 18 6 pts

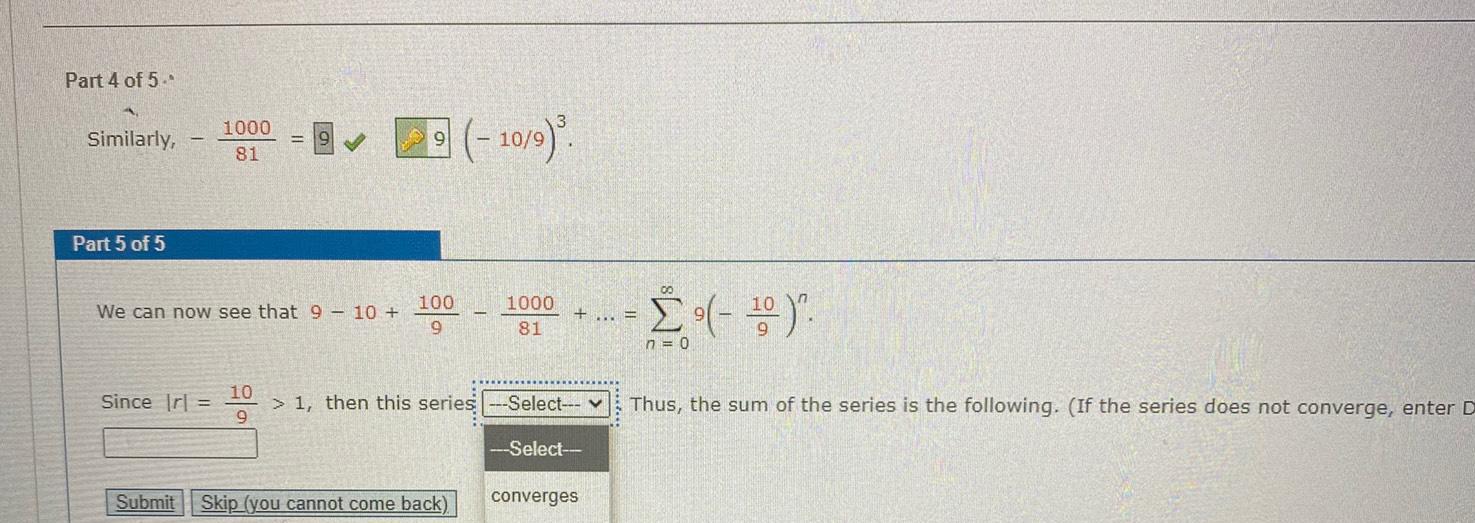
Calculus
Application of derivativesPart 4 of 5 Similarly Part 5 of 5 1000 81 Since Irl We can now see that 9 10 10 9 100 9 10 9 Submit Skip you cannot come back 1000 81 1 then this series Select Select converges 00 n 0 Thus the sum of the series is the following If the series does not converge enter D
Calculus
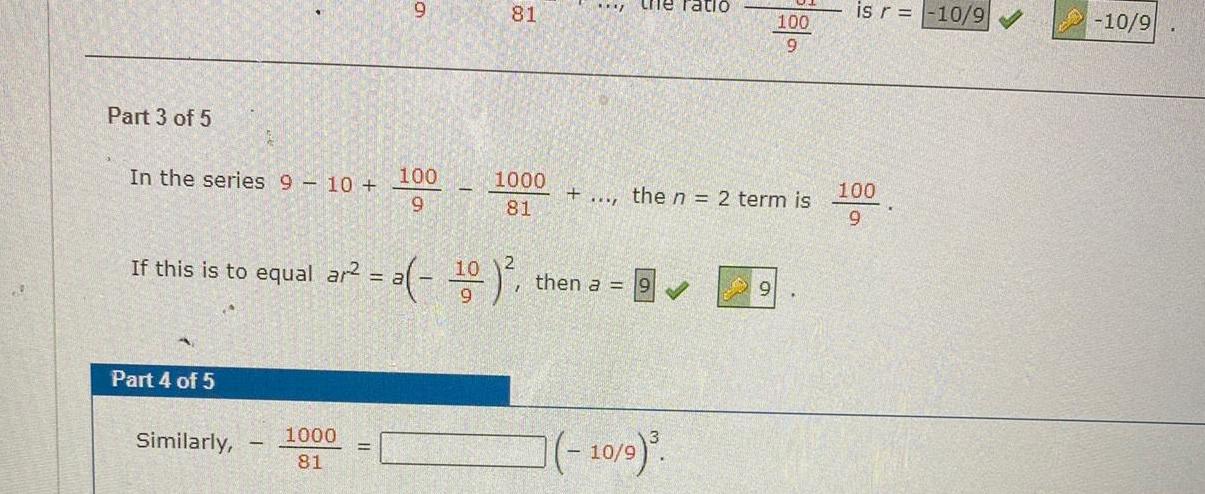
Application of derivativesPart 3 of 5 In the series 9 10 100 9 Part 4 of 5 9 Similarly 1000 81 81 1000 81 the ratiO If this is to equal ar a 10 a 10 then a P the n 2 term is 100 9 10 9 is r 10 9 100 9 10 9
Calculus
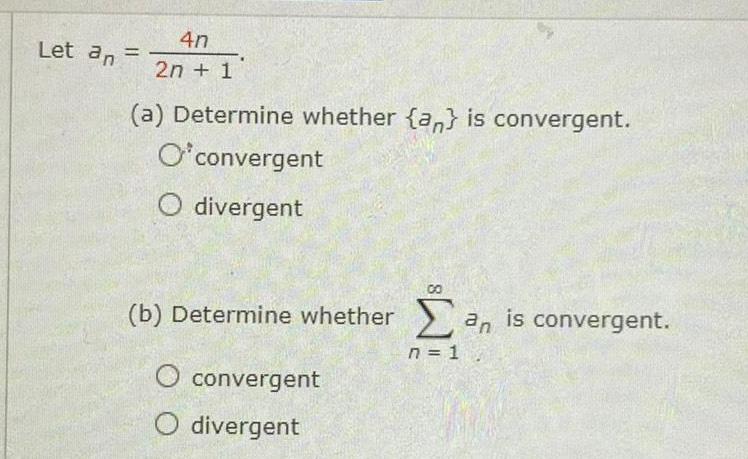
Application of derivativesLet an 4n 2n 1 a Determine whether a is convergent O convergent O divergent b Determine whether an is convergent n 1 convergent CO O divergent
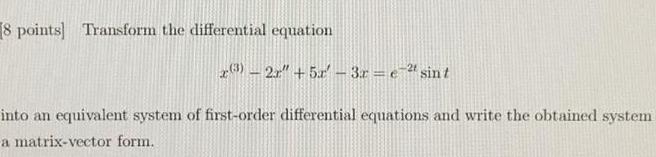
Calculus
Application of derivatives8 points Transform the differential equation 3 2r 5r 3r etsint into an equivalent system of first order differential equations and write the obtained system a matrix vector form
Calculus
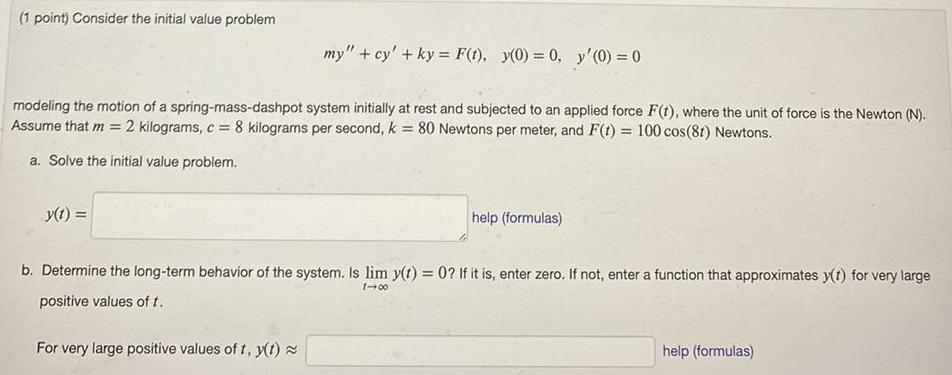
Application of derivatives1 point Consider the initial value problem my cy ky F t y 0 0 y 0 0 modeling the motion of a spring mass dashpot system initially at rest and subjected to an applied force F t where the unit of force is the Newton N Assume that m 2 kilograms c 8 kilograms per second k 80 Newtons per meter and F t 100 cos 8t Newtons a Solve the initial value problem y t help formulas b Determine the long term behavior of the system Is lim y t 0 If it is enter zero If not enter a function that approximates y t for very large positive values of t 1 00 For very large positive values of t y t help formulas
Calculus
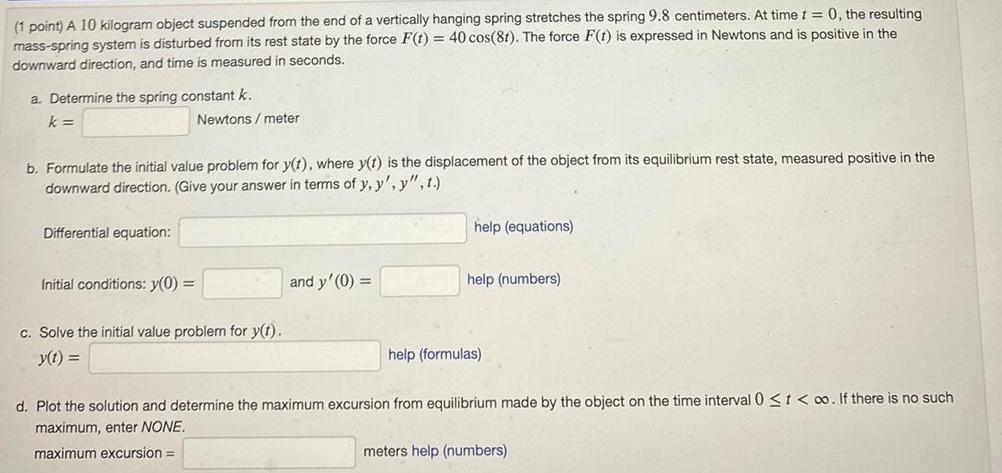
Application of derivatives1 point A 10 kilogram object suspended from the end of a vertically hanging spring stretches the spring 9 8 centimeters At time t 0 the resulting mass spring system is disturbed from its rest state by the force F t 40 cos 81 The force F t is expressed in Newtons and is positive in the downward direction and time is measured in seconds a Determine the spring constant k k b Formulate the initial value problem for y t where y t is the displacement of the object from its equilibrium rest state measured positive in the downward direction Give your answer in terms of y y y t Differential equation Newtons meter Initial conditions y 0 c Solve the initial value problem for y t y t and y 0 help equations help numbers help formulas d Plot the solution and determine the maximum excursion from equilibrium made by the object on the time interval 0 t o If there is no such maximum enter NONE maximum excursion meters help numbers

Calculus
Application of derivativesFind the centroid of the region bounded by the xy plane the cylinder x y 2401 and the 1 Assume the density of 8 x y z 1 Use symbolic notation and fractions where needed Express numbers in exact form Give your answer as point coordinates ins the form x J Z 0 0 100
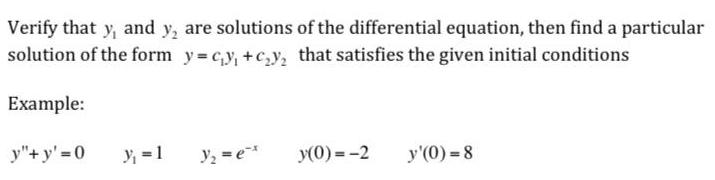
Calculus
Application of derivativesVerify that y and y are solutions of the differential equation then find a particular solution of the form y c y c y that satisfies the given initial conditions Example y y 0 y 1 y ex y 0 2 y 0 8
Calculus
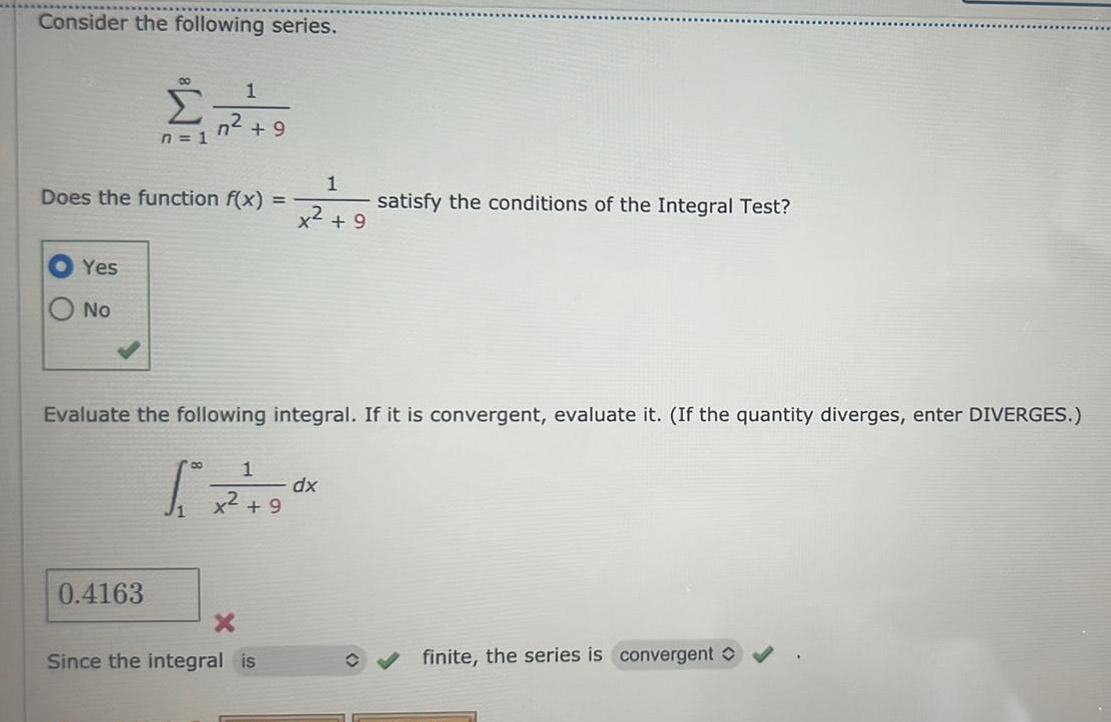
Application of derivativesConsider the following series Yes No 00 n 1 Does the function f x 1 n 9 0 4163 1 x 9 Evaluate the following integral If it is convergent evaluate it If the quantity diverges enter DIVERGES 80 1 5 x 2 9 9 X Since the integral is satisfy the conditions of the Integral Test dx finite the series is convergent
Calculus
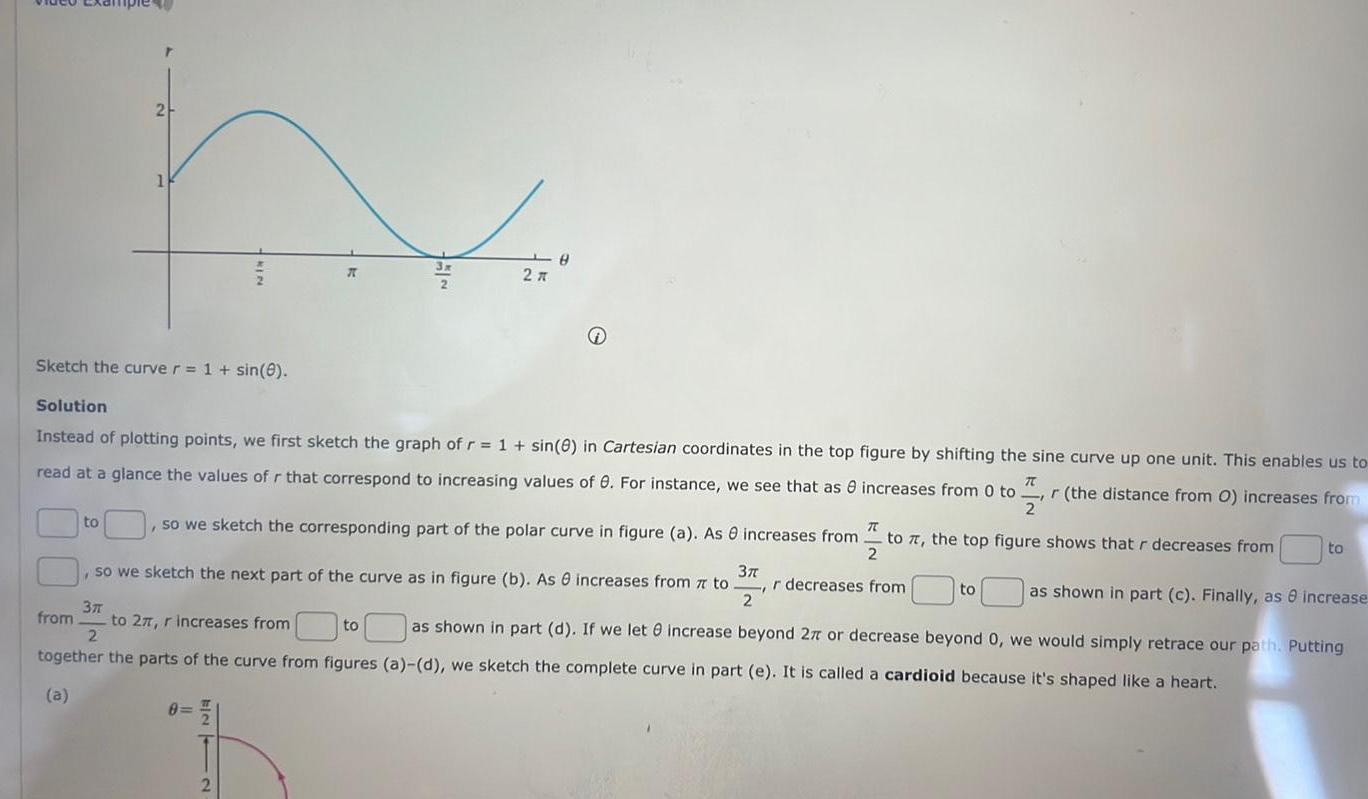
Application of derivativesSketch the curve r 1 sin 0 2 h to from Solution Instead of plotting points we first sketch the graph of r 1 sin 8 in Cartesian coordinates in the top figure by shifting the sine curve up one unit This enables us to read at a glance the values of r that correspond to increasing values of 0 For instance we see that as r the distance from O increases from 2 increases from 0 to 70 TC 2 so we sketch the corresponding part of the polar curve in figure a As increases from to 7 the top figure shows that r decreases from as shown in part c Finally as 8 increase as shown in part d If we let increase beyond 27 or decrease beyond 0 we would simply retrace our path Putting KIN 37 8 so we sketch the next part of the curve as in figure b As increases from 7 to r decreases from 2 8 2 x 2 8 3T 2 to 27 r increases from together the parts of the curve from figures a d we sketch the complete curve in part e It is called a cardioid because it s shaped like a heart a to to to

Calculus
Application of derivativesFind a polar equation for the curve represented by the given Cartesian equation Assume 0 0 2 3x 3 y
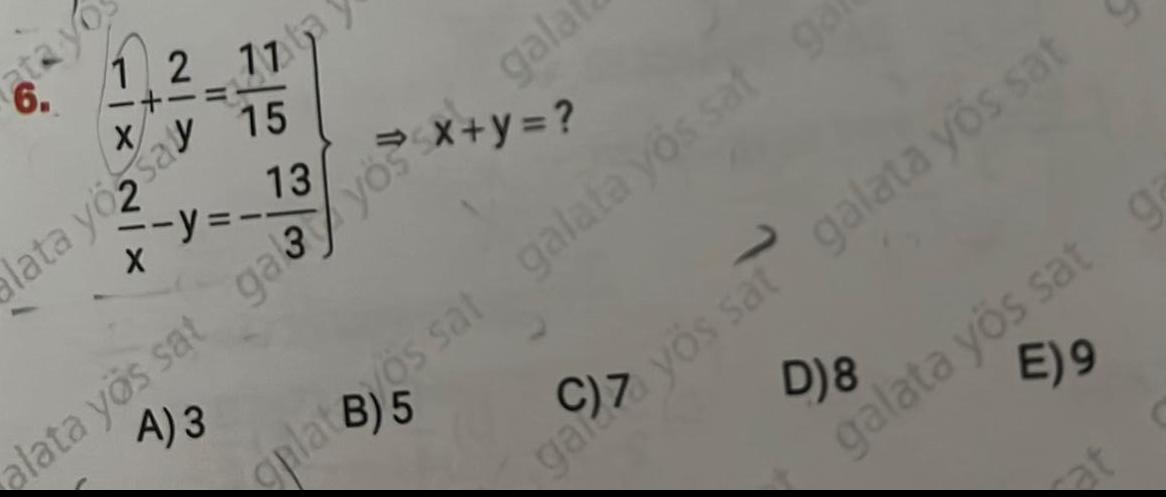
Calculus
Application of derivatives6 FIX 12 11 X lata you sa A 3 1767 13 D 8 galata y s sat E 9 gar a y s sat galata y s sat plats sat galata y s sat ga alata y s sat gale yogalaf

Calculus
Application of derivativesFind the maximum volume of a box that is resting on the xy plane with one vertex at the origin and the opposite vertex in the given plan 7x By 2z24

Calculus
Application of derivativesA tank initially contains 120 liters of pure water A mixture containing a concentration of y g liter of salt enters the tank at a rate of 3liters min and the well stirred mixture leaves the tank at the same rate Find an expression in terms of y for the amount of salt in the tank at any time t Also find the limiting amount of salt in the tank as t

Calculus
Application of derivativesTechnetium 99m is a radioactive substance used to diagnose brain diseases Its half life is approximately 6 hours Initially you have 220 mg of technetium 99m a Write an equation that gives the amount of technetium 99m remaining after t hours NOTE Round any values to four decimal places if required R t 220 e6t b Determine the number of hours needed for your sample to decay to 132 mg NOTE Round your answer to three decimal places It takes approximately hours for the sample to decay to 132 mg c Determine the concavity of the graph that models the quantity of technetium 99m using average rates of change over intervals of length 2 between t 0 and t 6 The graph is concavo

Calculus
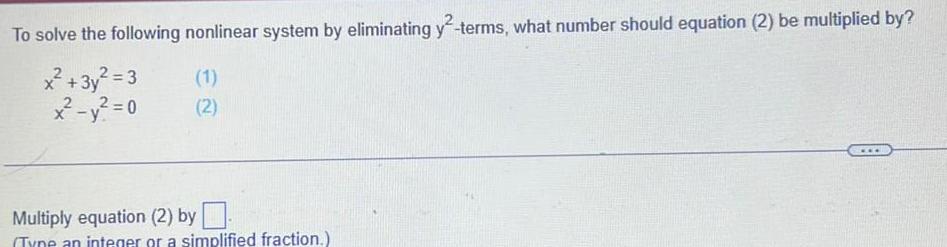
Application of derivativesTo solve the following nonlinear system by eliminating y terms what number should equation 2 be multiplied by x 3y 3 x y 0 1 2 Multiply equation 2 by Tyne an integer or a simplified fraction
Calculus
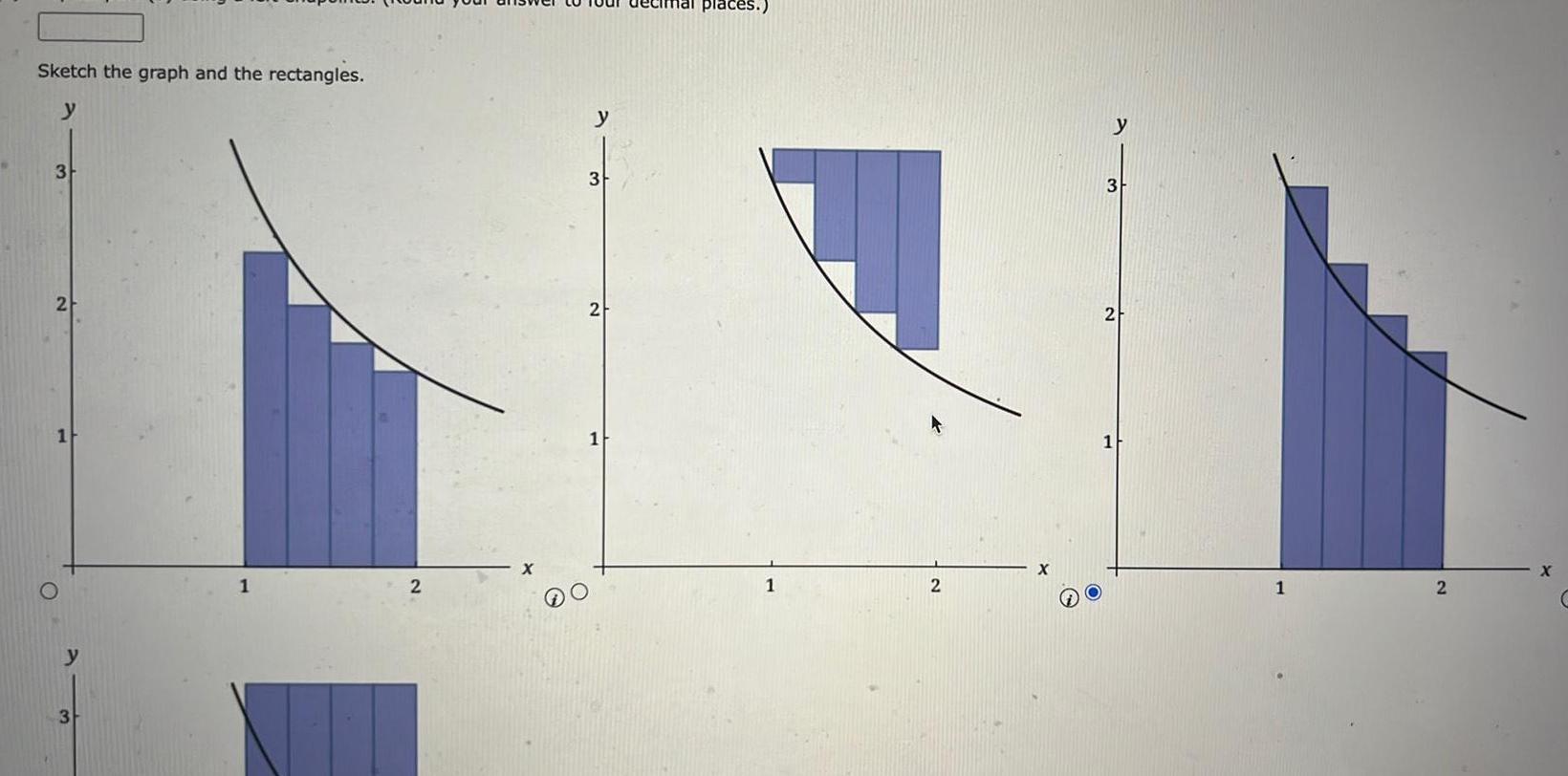
Application of derivativesSketch the graph and the rectangles y 3 2 O 3 2 y 3 2 mal places 1 2 y 3 2 1 1 2 X

Calculus
Application of derivativessquare is inscribed in a circle such that each corner touches the circle A Find a function that gives the area of the square as a function of the radius of the circle Simplify the function as much as possible and describe any symmetry in the function Make certain to show all the steps you use to come up with the function as well as describe your reasoning B State the domain and range of the function you came up with in part A keeping in mind all practical considerations
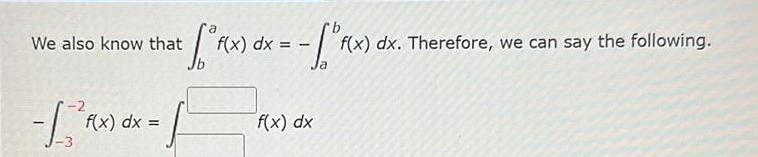
Calculus
Application of derivativesWe also know that I Rx it f x f x dx f x dx F F x f x dx f x dx Therefore we can say the following
Calculus
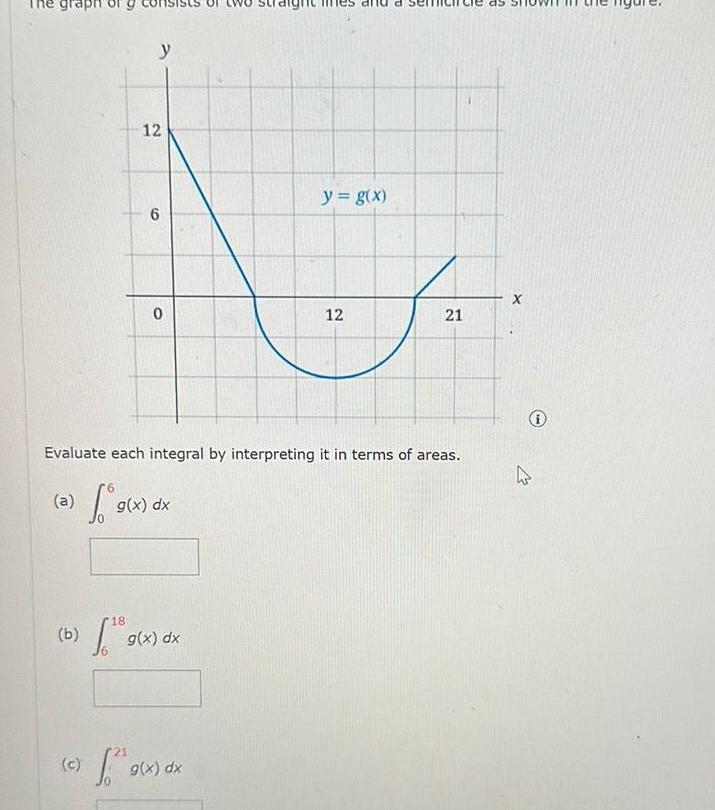
Application of derivativesgrap a b 18 g c y 12 6 1 9 0 Evaluate each integral by interpreting it in terms of areas g x dx g x dx y g x g x dx 12 21 X 4
Calculus
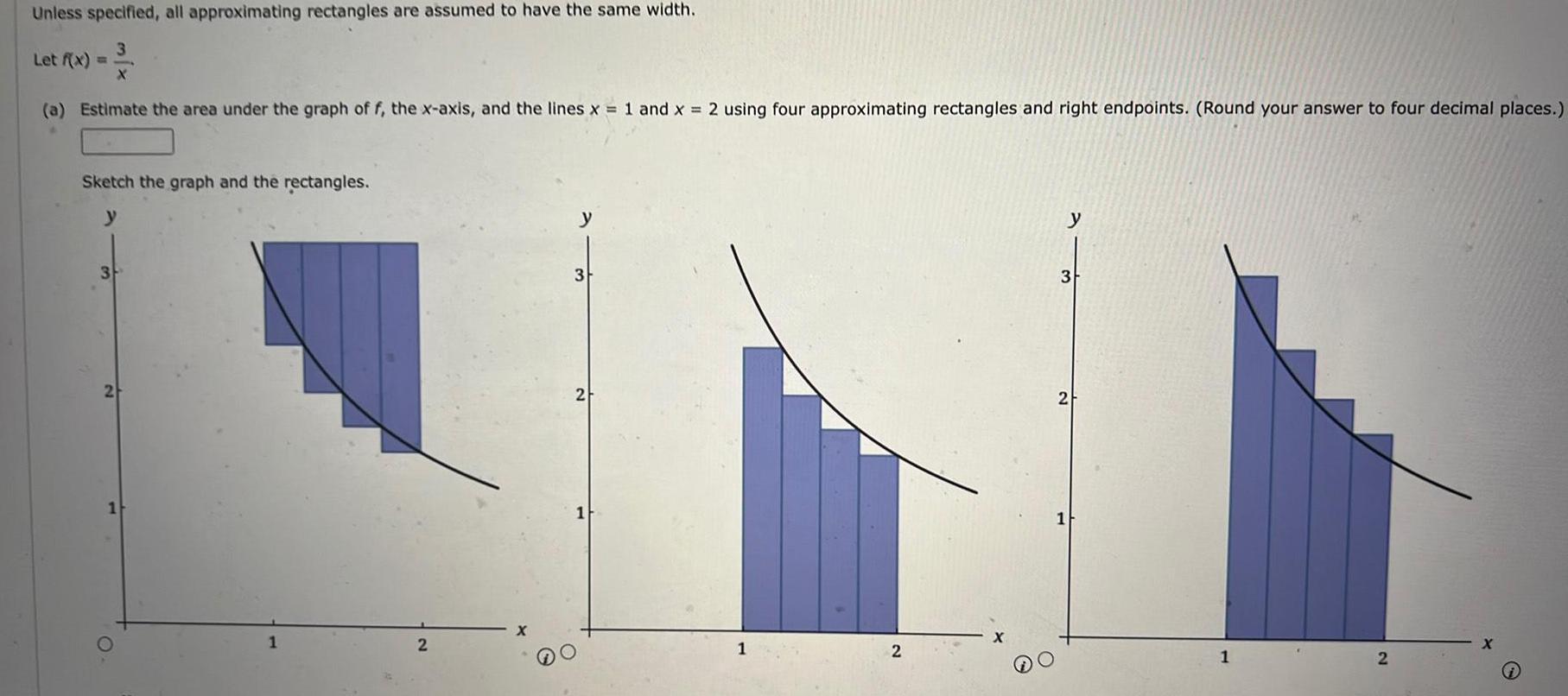
Application of derivativesUnless specified all approximating rectangles are assumed to have the same width Let f x X a Estimate the area under the graph of f the x axis and the lines x 1 and x 2 using four approximating rectangles and right endpoints Round your answer to four decimal places Sketch the graph and the rectangles y 3 2 O 2 3 2 1 1 2 y 3 2 1 2 X

Calculus
Application of derivativesFinding the Domain In Exercises 3 4 5 6 7 8 9 and 10 find the domain of the vector valued function 1 t 3 r t i j 3tk t 1 Answer 4 r t 4 t i t j 6tk 5 r t In ti e j tk

Calculus
Application of derivativesFinding the Domain In Exercises 3 4 5 6 7 8 2 and 10 find the domain of the vector valued function 3 r t i j3tk
Calculus
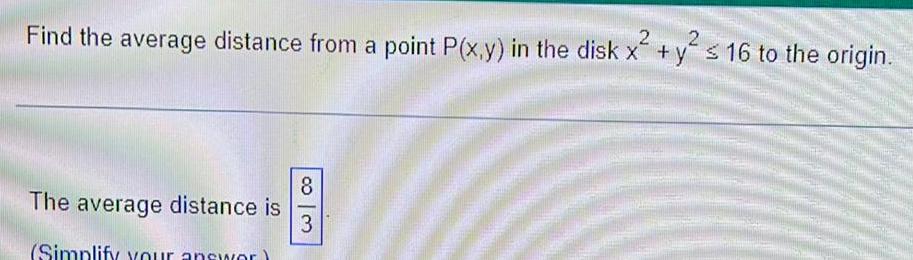
Application of derivatives2 2 Find the average distance from a point P x y in the disk x y 16 to the origin The average distance is Simplify your answer 8 1 3

Calculus
Application of derivativesFinding a Cross Product In Exercises 11 12 13 and 14 find u v and show that it is orthogonal to both u and v 11 u 4 1 0 v 6 3 0
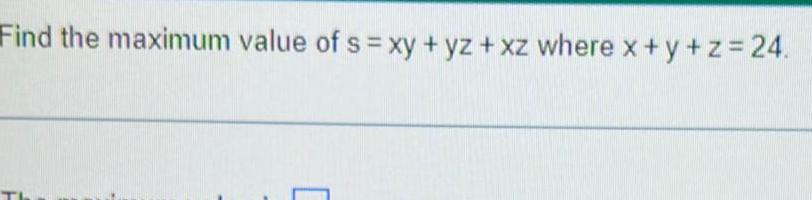
Calculus
Application of derivativesPart 1 of 2 We must solve 125 75 110e 1 30 In 15 22 t or 5 11 e 1 30 In 15 22 t 5 11 Part 2 of 2 Now we have the following Round your final answer to the nearest whole number 1 30 In 15 t t 11 30 In min
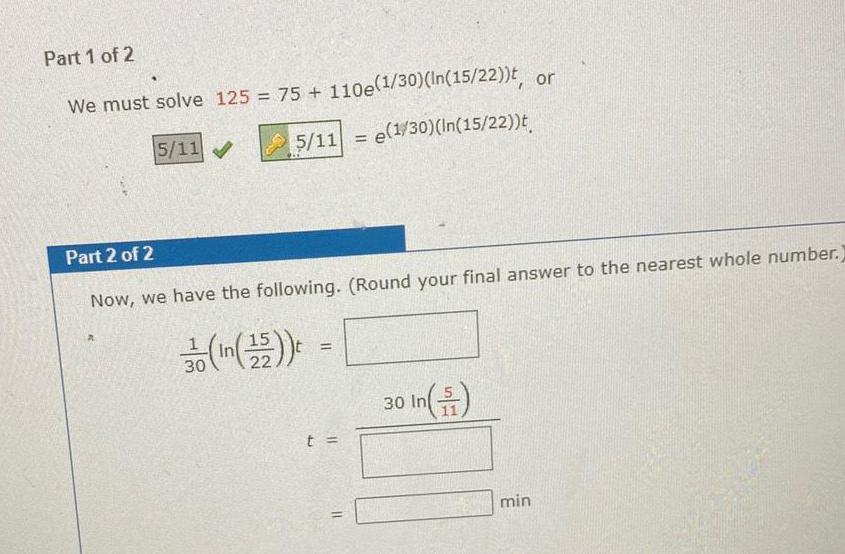
Calculus
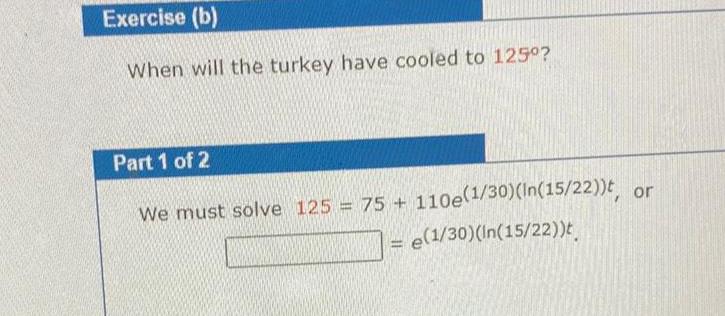
Application of derivativesExercise b When will the turkey have cooled to 125 Part 1 of 2 We must solve 125 75 110e 1 30 In 15 22 t or e 1 30 In 15 22 t
Calculus
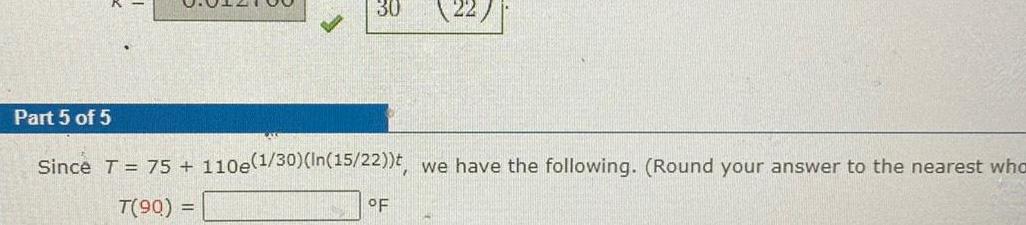
Application of derivatives30 Part 5 of 5 Since T 75 110e 1 30 In 15 22 t we have the following Round your answer to the nearest who T 90 F
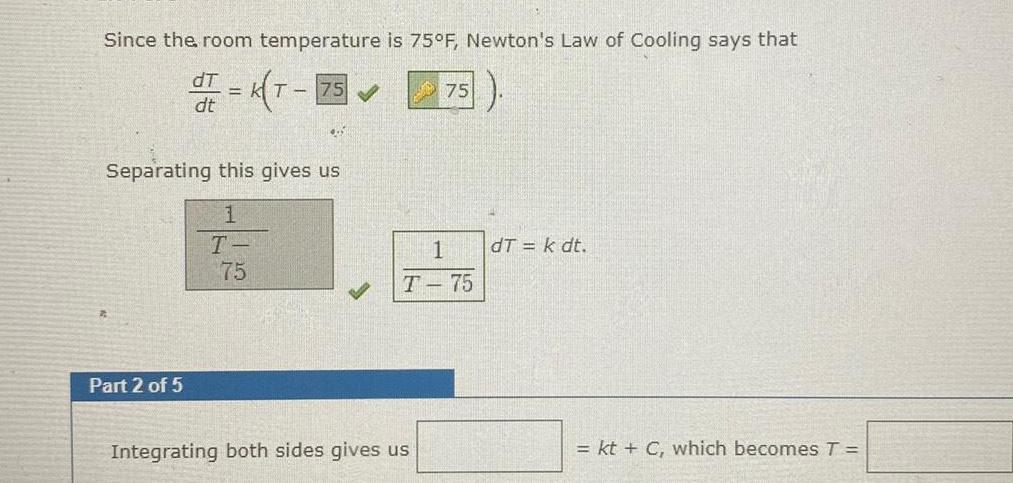
Calculus
Application of derivativesSince the room temperature is 75 F Newton s Law of Cooling says that dT dr K T 75 dt 455 Separating this gives us 1 T 75 Part 2 of 5 75 1 T 75 Integrating both sides gives us dT k dt kt C which becomes T
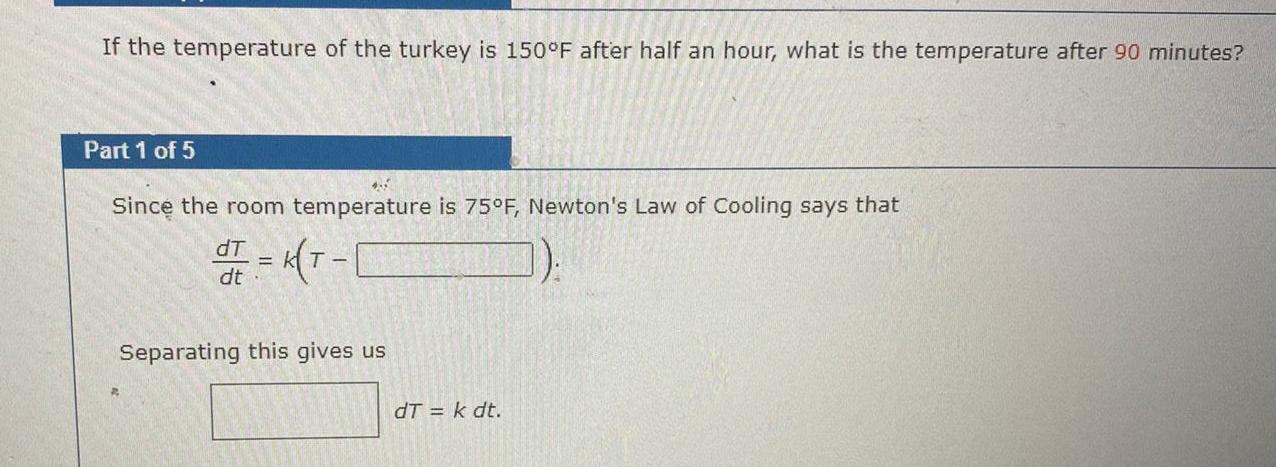
Calculus
Application of derivativesIf the temperature of the turkey is 150 F after half an hour what is the temperature after 90 minutes Part 1 of 5 Since the room temperature is 75 F Newton s Law of Cooling says that dT d K T 1 dt Separating this gives us dT k dt
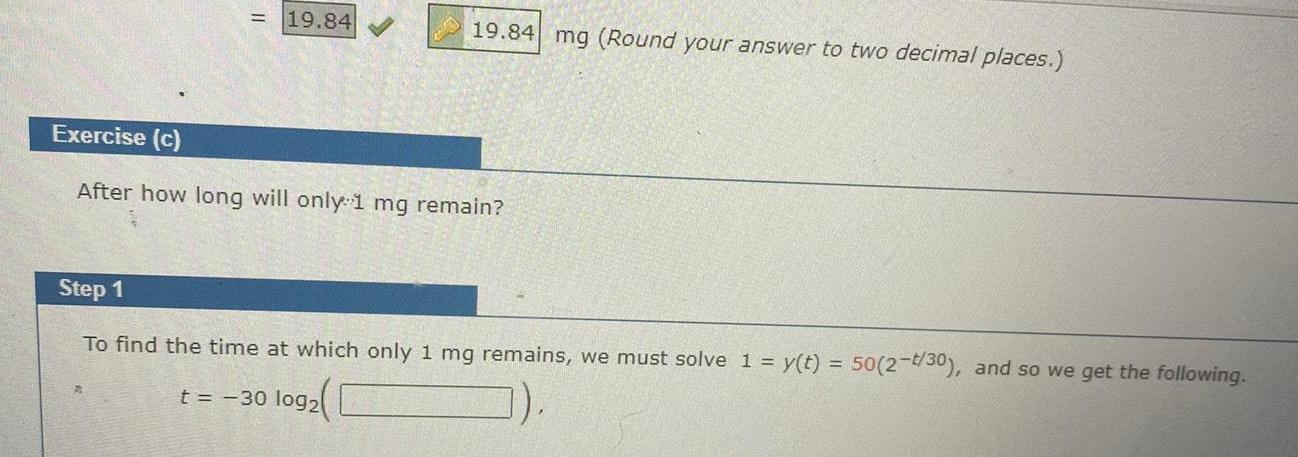
Calculus
Application of derivatives19 84 19 84 mg Round your answer to two decimal places Exercise c After how long will only 1 mg remain Step 1 To find the time at which only 1 mg remains we must solve 1 y t 50 2 t 30 and so we get the following t 30 log2
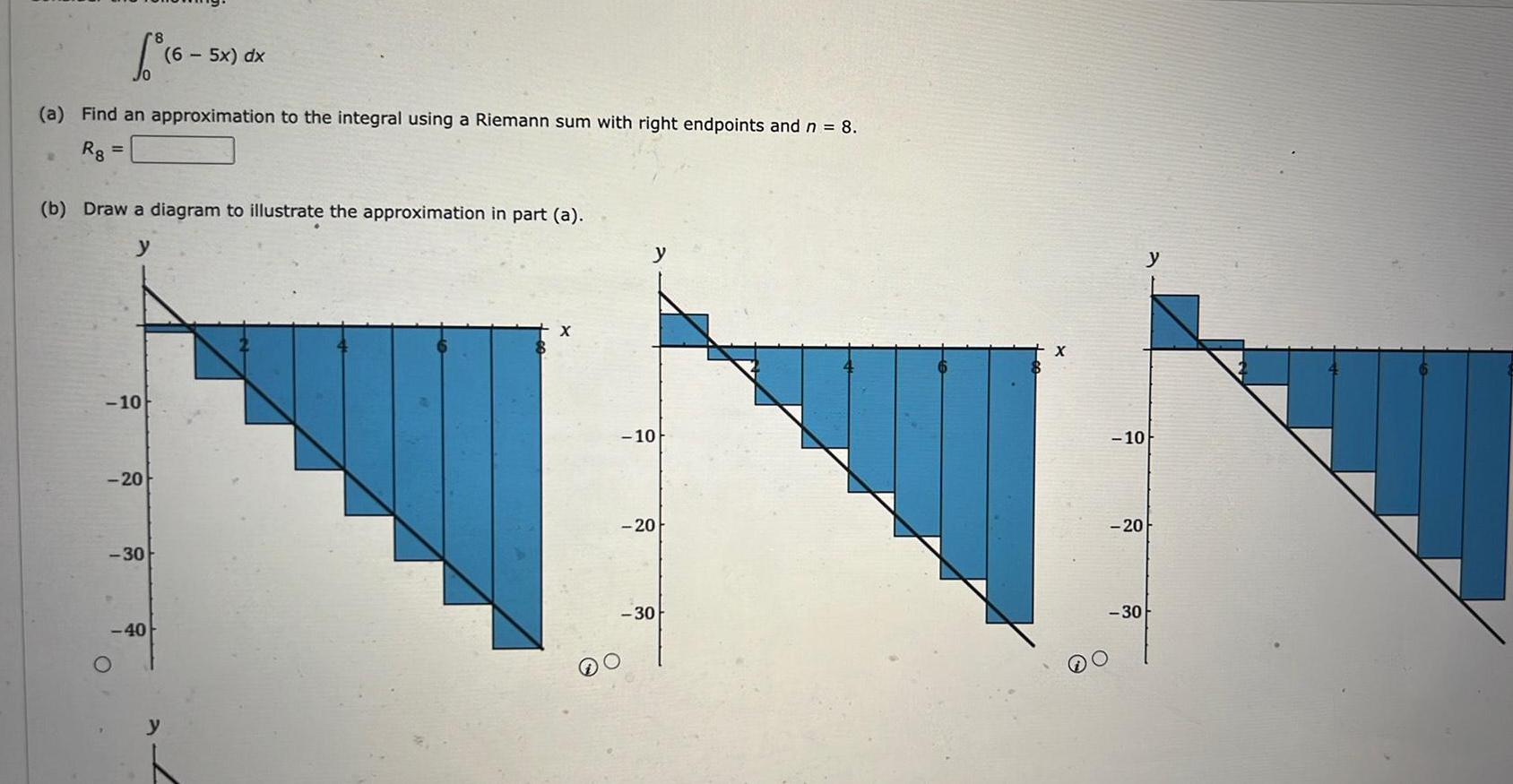
Calculus
Application of derivatives6 16 5 a Find an approximation to the integral using a Riemann sum with right endpoints and n 8 Rg b Draw a diagram to illustrate the approximation in part a y 10 20 6 5x dx 30 40 10 20 30 10 20 30 y

Calculus
Application of derivativesUse this definition with right endpoints to find an expression for the area under the graph of f as a limit Do not evaluate the limi f x 4 sin x 0 x A lim 816 w1
Calculus
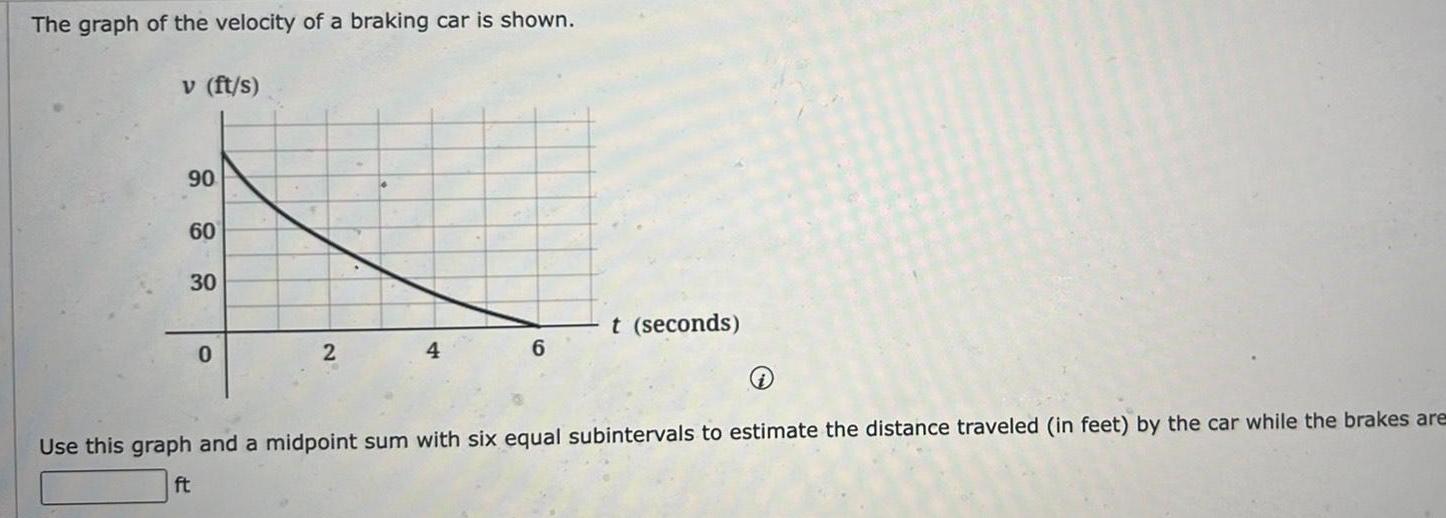
Application of derivativesThe graph of the velocity of a braking car is shown v ft s 90 60 30 0 2 4 6 t seconds Use this graph and a midpoint sum with six equal subintervals to estimate the distance traveled in feet by the car while the brakes are ft

Calculus
Application of derivatives1 Prove the following cos2x 1 sin2x cotx 2 Find all solution in 0 27 Sin 2x sin x 0

Calculus
Application of derivativesDetermine if the following equations represent a parabola an ellipse or a hyperbola x 1 4 y 3 45 100 49x 25y 294x100y 884 0 y 12y x 28 0 9x2 16y2 36x 96y 36 0 x 1 y 2 16 25 y 2 20 x 2 25 1 1 1 Parabola 2 Hyperbola 3 Ellipse