Application of derivatives Questions and Answers
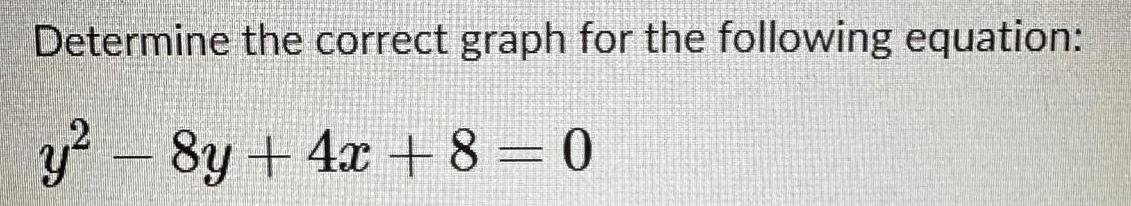
Calculus
Application of derivativesDetermine the correct graph for the following equation y 8y 4x 8 0
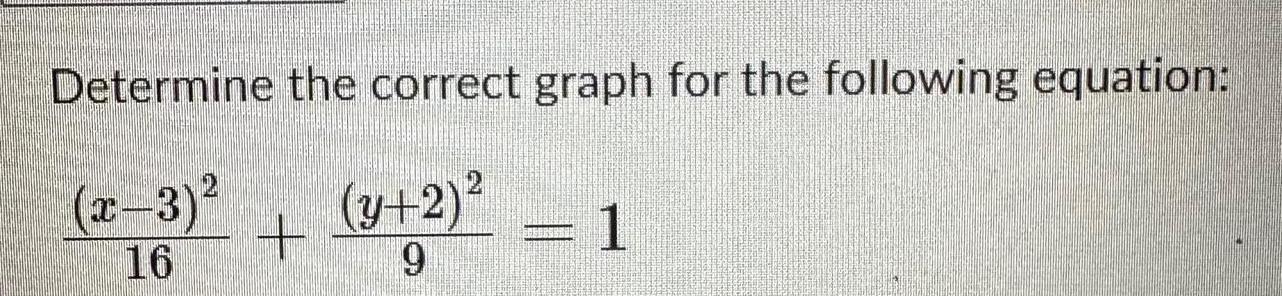
Calculus
Application of derivativesDetermine the correct graph for the following equation x 3 y 2 16 9 ERCORSERIE 1
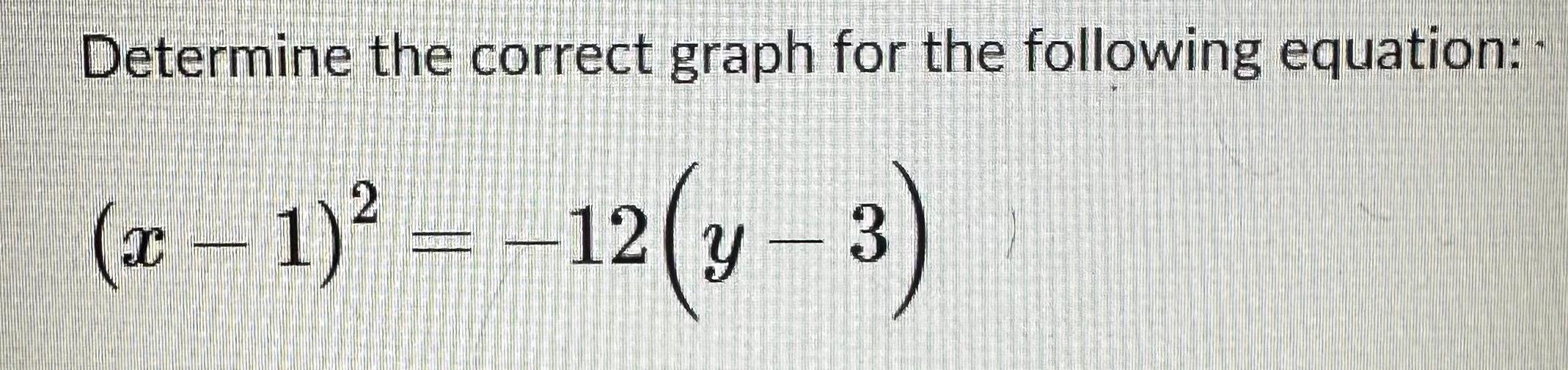
Calculus
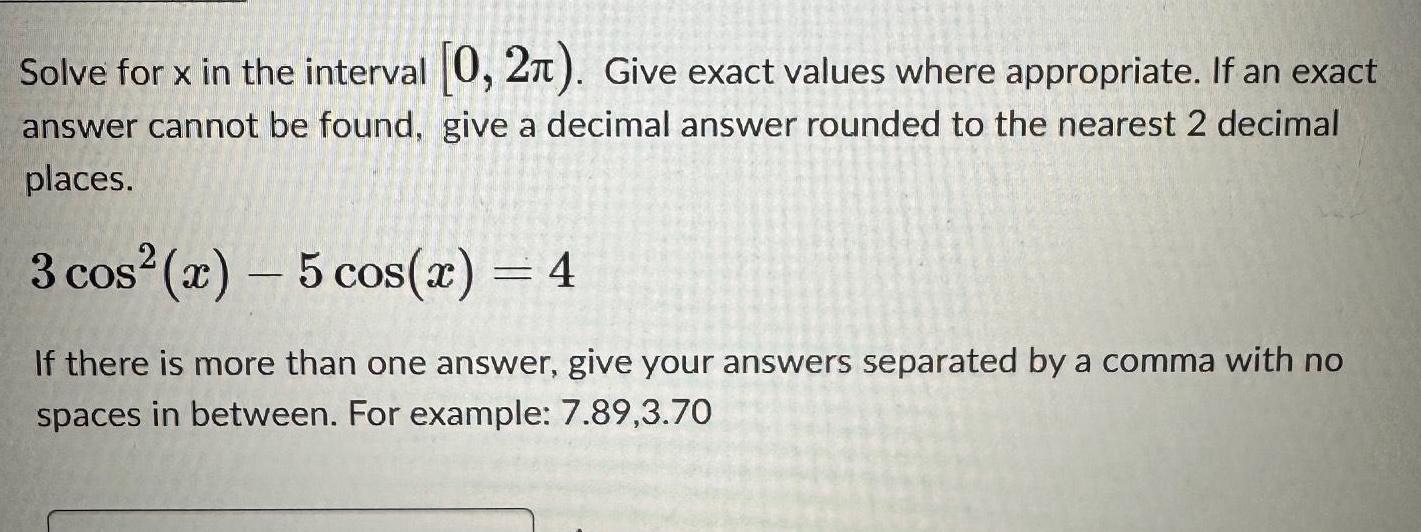
Application of derivativesSolve for x in the interval 0 2 Give exact values where appropriate If an exact answer cannot be found give a decimal answer rounded to the nearest 2 decimal places 3 cos x 5 cos x 4 If there is more than one answer give your answers separated by a comma with no spaces in between For example 7 89 3 70
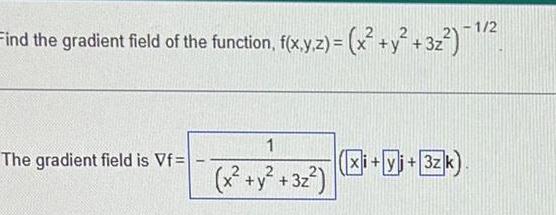
Calculus
Application of derivativesFind the gradient field of the function f x y z x y 3z 1 2 The gradient field is Vf 1 x y 3z xi yi 3zk

Calculus
Application of derivativesFind and dx dy 2 2 f x y 4x y 4x dx 4x y ax y ay 4x y Type an exact answer using radicals as needed Type an exact answer using radicals as needed
Calculus
Application of derivativesFind the maximum value of s xy yz xz where x y z 15 The maximum value is www

Calculus
Application of derivativesa The curvature of the helix r t a cost i a sin t j bt k a b 0 is k 2 a b The largest value x can have for a given value of b is What is the largest value x can have for a given value of ba

Calculus
Application of derivativesx 10x 12 x x 2 3x 3 Determine the correct partial fraction decomposition for the expression above Enter your answer as the sum of fractions with a constant in each numerator and with a linear expression in each denominator Provide your answer below

Calculus
Application of derivatives1 Consider the data below for a car tire with a leak Minutes after the leak began Pressure of air in the tire in kilopascals kPa 0 400 5 335 10 295 15 20 255 225 25 195 30 170 a Calculate the average rate of change over the 30 minute interval Explain the meaning of this rate using proper units
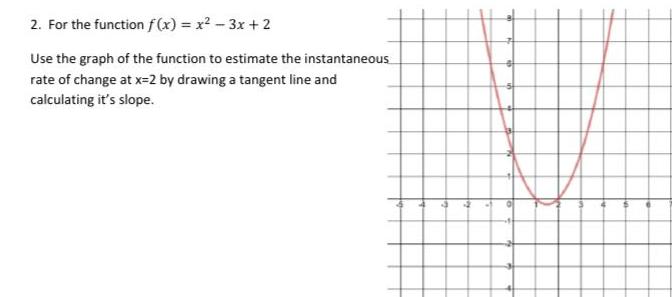
Calculus
Application of derivatives2 For the function f x x 3x 2 Use the graph of the function to estimate the instantaneous rate of change at x 2 by drawing a tangent line and calculating it s slope

Calculus
Application of derivatives4 What is the fundamental difference between average rate of change and instantaneous rate of change Use the concept of tangent and secant lines to explain

Calculus
Application of derivativesFind an equation of the curve that passes through the point 0 6 and whose slope at x y is y 36
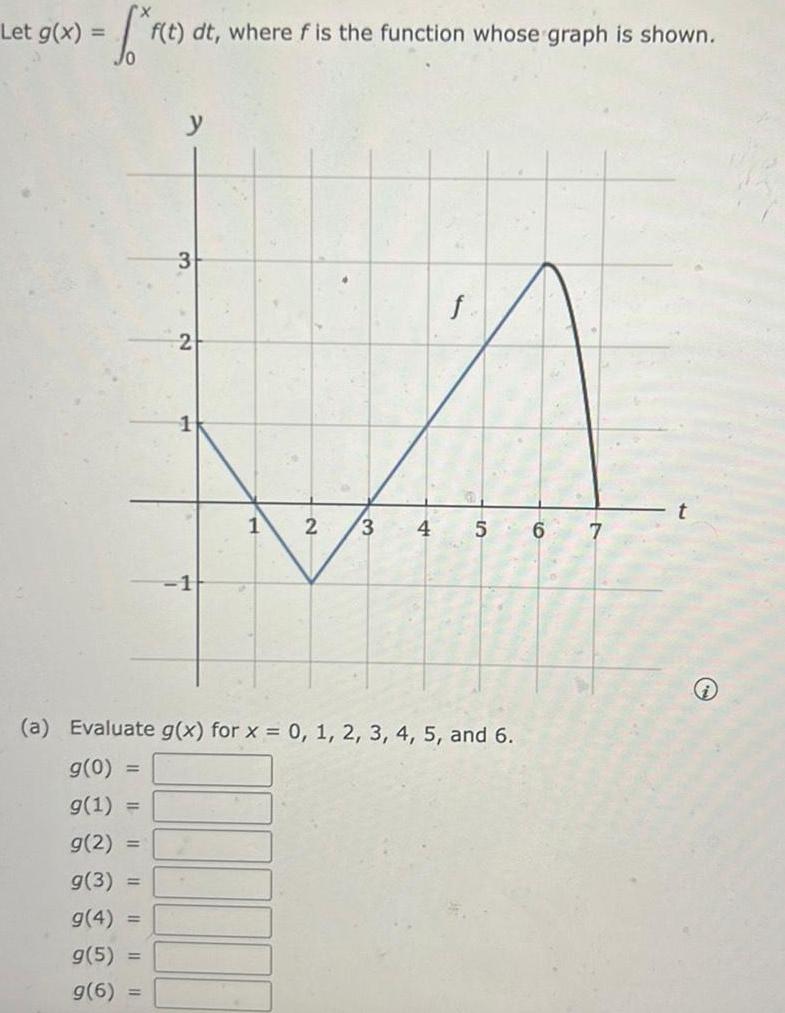
Calculus
Application of derivativesf f t f t dt where f is the function whose graph is shown Let g x 3 g 5 g 6 2 1 2 3 a Evaluate g x for x 0 1 2 3 4 5 and 6 g 0 g 1 g 2 g 3 g 4 f 4 5 6 7 t
Calculus
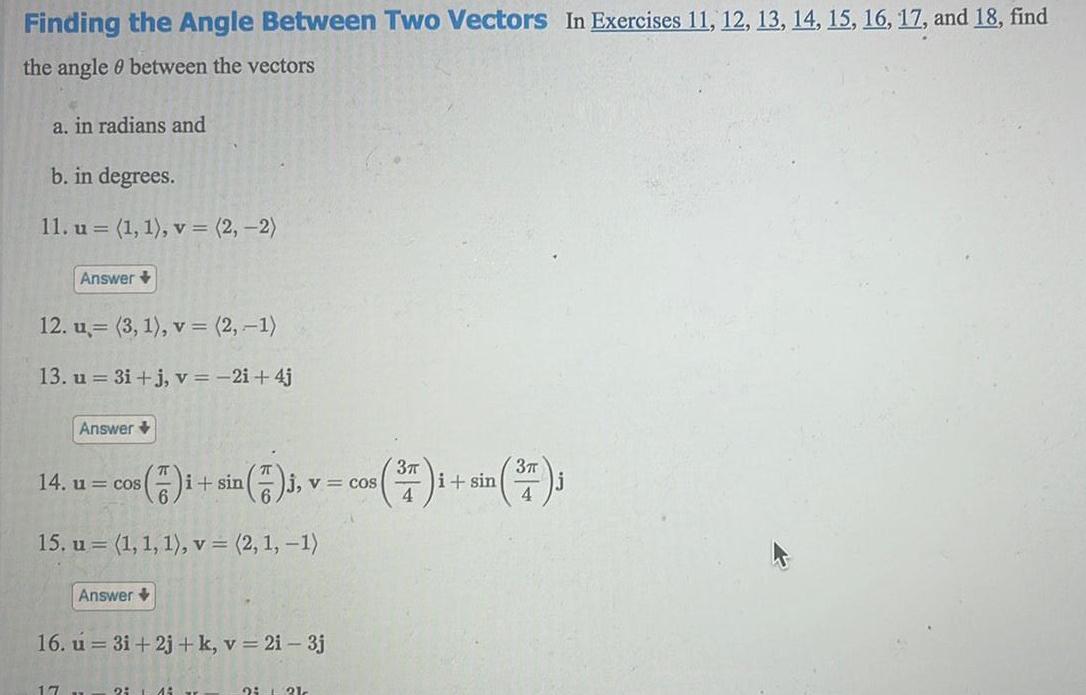
Application of derivativesFinding the Angle Between Two Vectors In Exercises 11 12 13 14 15 16 17 and 18 find the angle between the vectors a in radians and b in degrees 11 u 1 1 v 2 2 Answer 12 u 3 1 v 2 1 13 u 3i j v 2i 4j Answer 14 u cos 17 15 u 1 1 1 v 2 1 1 Answer i sin 2 14 j v 16 u 3i 2j k v 2i 3j 3 3 cos 377 1 sin 37 J 4 2 121
Calculus
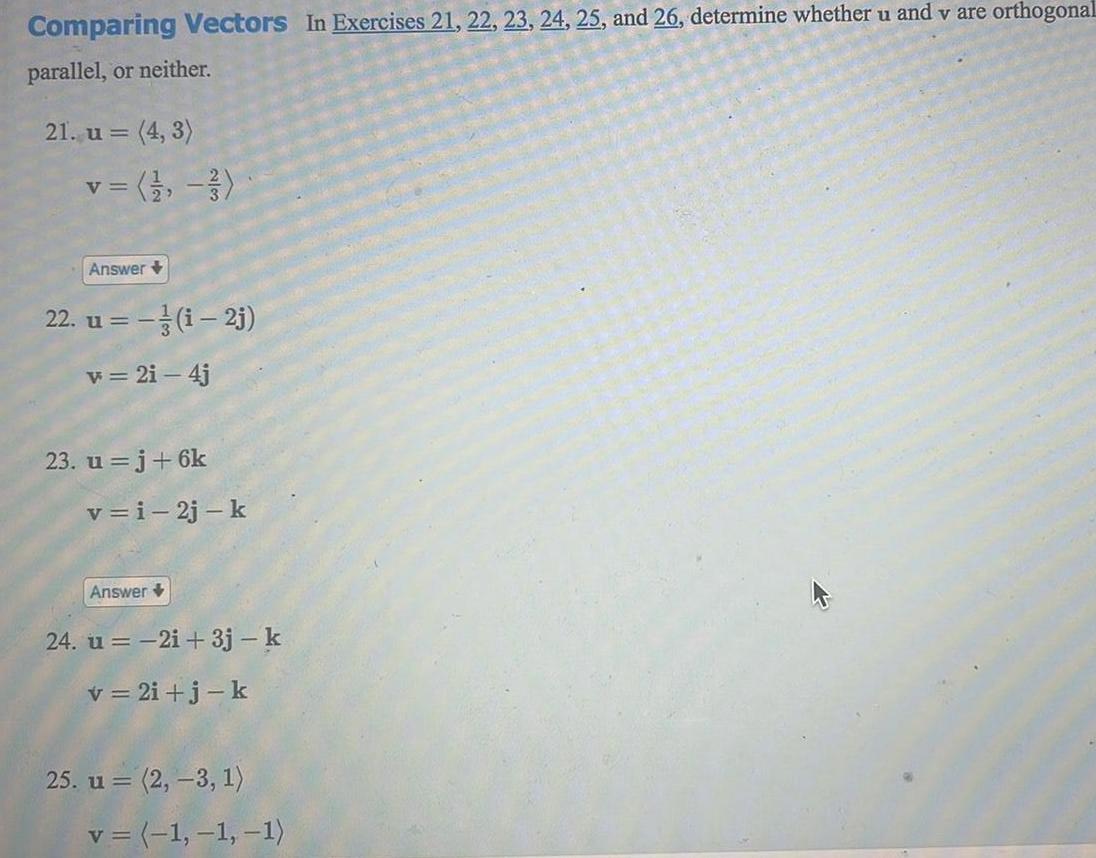
Application of derivativesComparing Vectors In Exercises 21 22 23 24 25 and 26 determine whether u and v are orthogonal parallel or neither 21 u 4 3 v 1 2 3 Answer 22 u i 2j v 2i 4j 23 u j 6k v i 2j k Answer 24 u 2i 3j k v 2i j k 25 u 2 3 1 v 1 1 1
Calculus
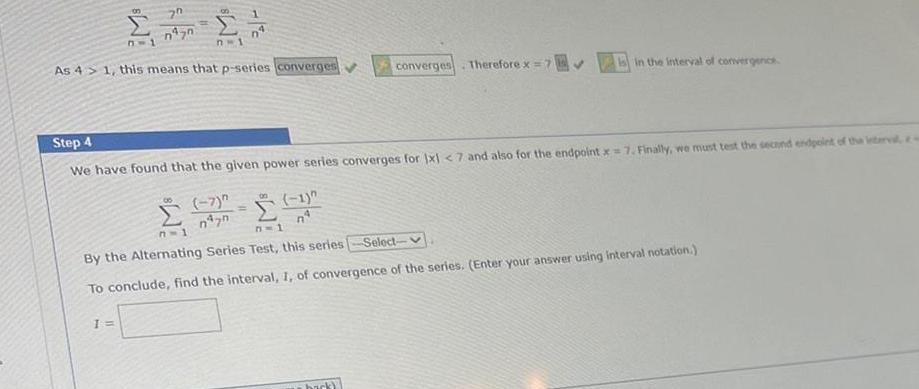
Application of derivatives8 7 1 70 1 n Lan n 1 As 4 1 this means that p series converges 09 7 07 Step 4 We have found that the given power series converges for 1x1 7 and also for the endpoint x 7 Finally we must test the second endpoint of the interval e 8 1 n converges Therefore x 7 in the interval of convergence n 1 7 1 By the Alternating Series Test this series Select To conclude find the interval 1 of convergence of the series Enter your answer using interval notation back

Calculus
Application of derivativesTherefore k 30 In 2 30 Step 4 Now remembering that In x n In x and that eln z z we have y t 50e t 30 In 2 mg

Calculus
Application of derivativesP 3 0 1 Points Find the solution of the differential equation that satisfies the given initial condition dp dt DETAILS 7 3 ad Help 7 Pt P 1 3 3 PREVIOUS 7 3 Read It X

Calculus
Application of derivativesDETAILS 9 0 1 Points PREVIOUS ANSW Find the area of the region that lies inside the first curve and outside the second curve r 16 sin 8 11 71 x r 8
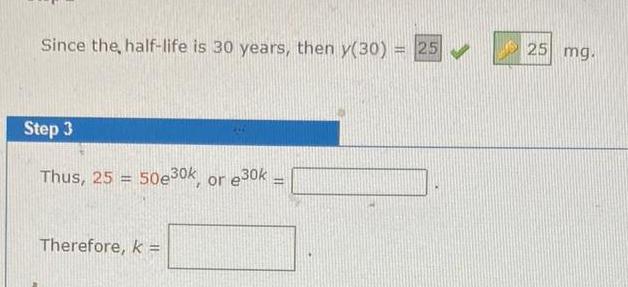
Calculus
Application of derivativesSince the half life is 30 years then y 30 25 Step 3 Thus 25 50e30k or 30k Therefore k H 25 mg
Calculus
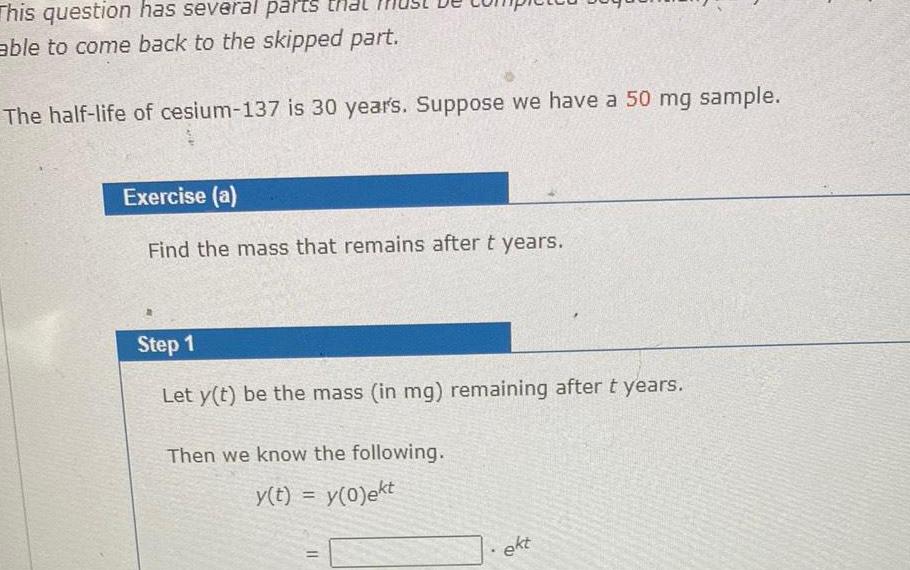
Application of derivativesThis question has several parts that able to come back to the skipped part The half life of cesium 137 is 30 years Suppose we have a 50 mg sample Exercise a Find the mass that remains after t years Step 1 Let y t be the mass in mg remaining after t years Then we know the following y t y 0 ekt ekt

Calculus
Application of derivativesSolve for x cos x cos 2x 0 0 2n X Select 3 correct answer s KO 4 60 03 Gla co No solution 02 2 W H 560 n
Calculus
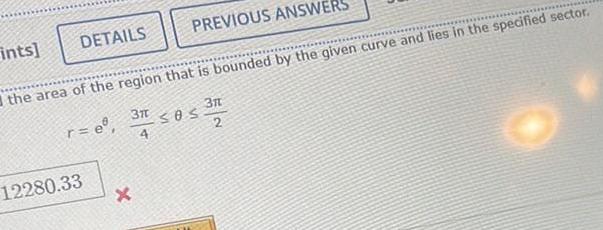
Application of derivativesPREVIOUS ANSWERS the area of the region that is bounded by the given curve and lies in the specified sector r e 3 t 4 Os 3128 2 DETAILS ints 12280 33 X
Calculus
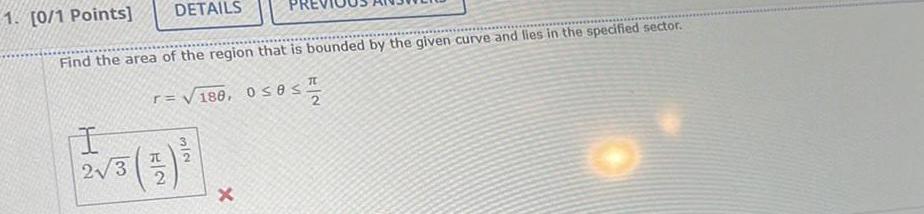
Application of derivatives1 0 1 Points DETAILS Find the area of the region that is bounded by the given curve and lies in the specified sector r 180 0 8 I 2 3 x T


Calculus
Application of derivativesX Select 4 correct answer s 4 3 00 11 57 12 03 017 No solution 12 13m 12 2 5 6

Calculus
Application of derivativesDetermine which of the following double identity replacements is the best accurate choice in solving the equation cos x cos 2x 0 cos x 2 cos x sin x 0 None of these O cos x cos r sin x 0 cos x 2 cos x 1 0 cos x 1 2 sin x 0 G
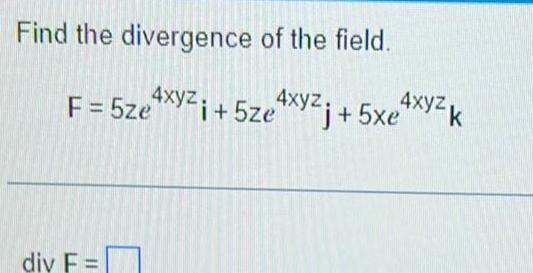
Calculus
Application of derivativesFind the divergence of the field F 5ze4xyzi 5ze i 5ze div F j 5x4xyzk
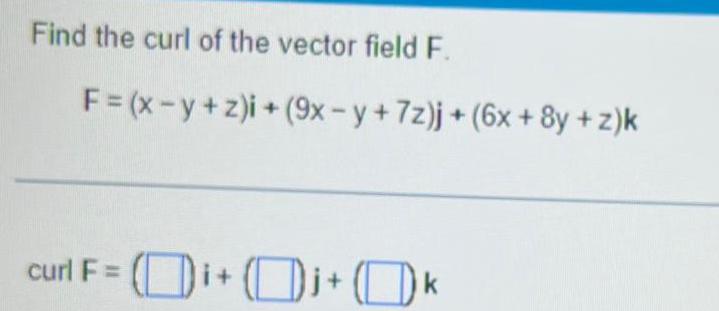
Calculus
Application of derivativesFind the curl of the vector field F F x y z i 9x y 7z j 6x 8y z k curl F i j k
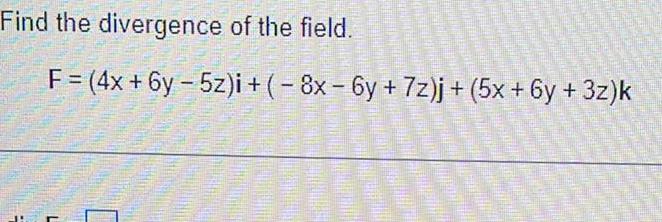
Calculus
Application of derivativesFind the divergence of the field F 4x 6y 5z i 8x 6y 7z j 5x 6y 3z k AMAN neuen Einfl Wirtu duben
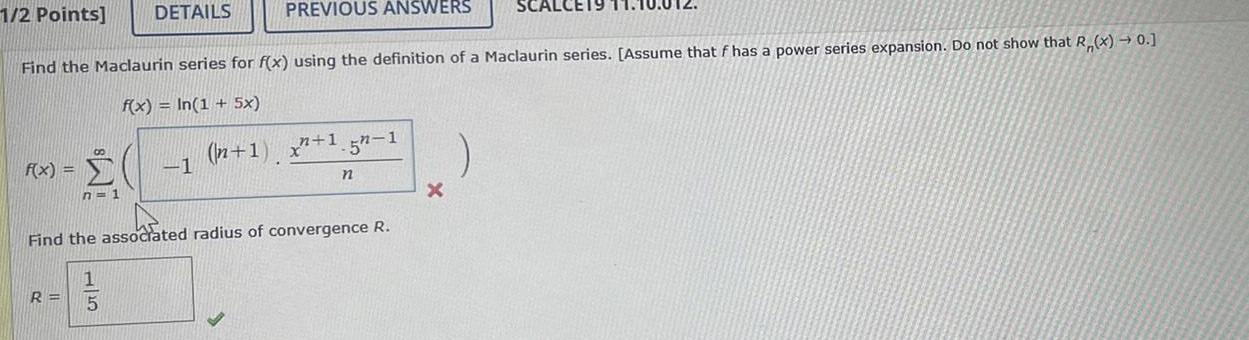
Calculus
Application of derivativesf x n 1 1 2 Points Find the Maclaurin series for f x using the definition of a Maclaurin series Assume that f has a power series expansion Do not show that R x 0 f x In 1 5x DETAILS R 15 PREVIOUS ANSWERS 1 Find the associated radius of convergence R n 1 x 1 5 1 n X SCALCE19
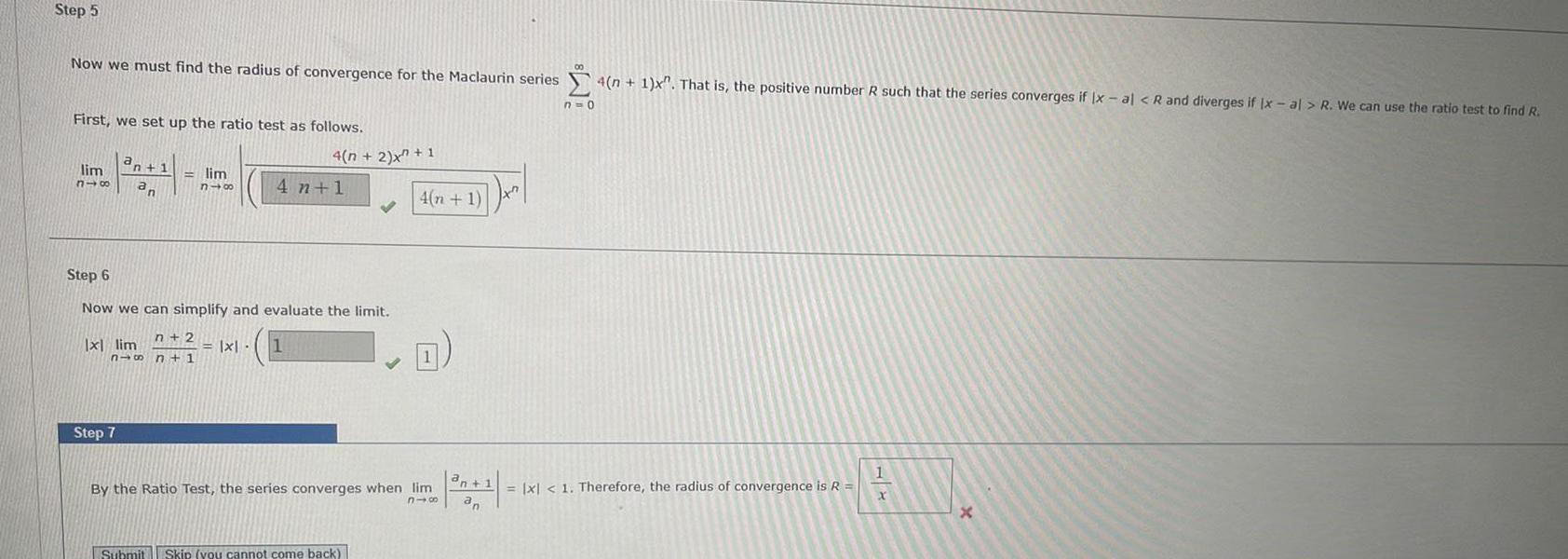
Calculus
Application of derivativesStep 5 Now we must find the radius of convergence for the Maclaurin series First we set up the ratio test as follows a lim n 1 318 an lim n48 n 2 816 n 1 x lim Step 7 Step 6 Now we can simplify and evaluate the limit 4 n 2 x 1 4 n 1 x 1 Submit Skip you cannot come back 4 n 1 x By the Ratio Test the series converges when lim 816 an 1 an 4 n 1 x That is the positive number R such that the series converges if x al R and diverges if Ix al R We can use the ratio test to find R n 0 x 1 Therefore the radius of convergence is R 1 X X
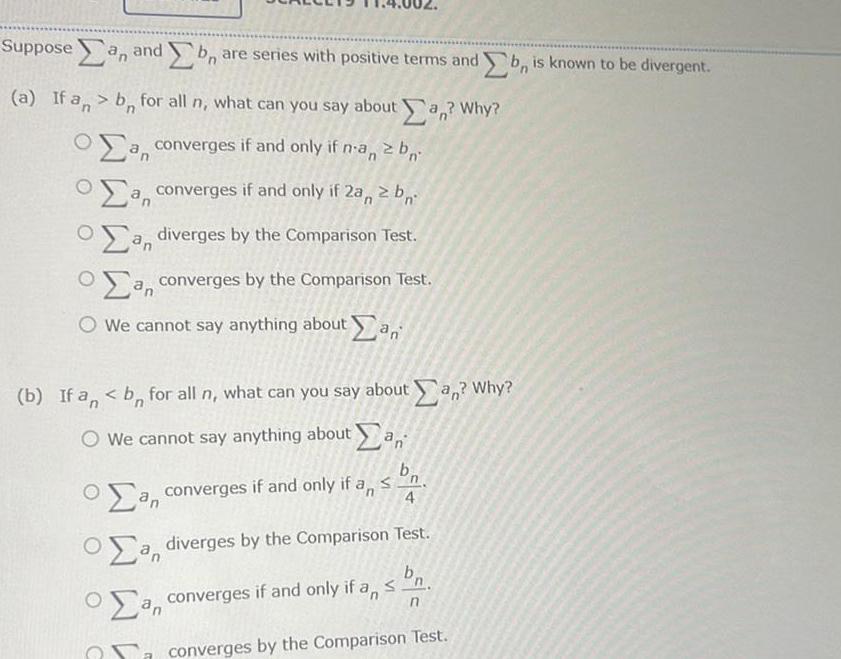
Calculus
Application of derivativesSuppose an and b are series with positive terms and b is known to be divergent a If an bn for all n what can you say about an Why a converges if and only if n an 2 b a converges if and only if 2a 2b a diverges by the Comparison Test a converges by the Comparison Test We cannot say anything about an b If an b for all n what can you say about an Why O We cannot say anything about an S a converges if and only if an 4 a diverges by the Comparison Test a converges if and only if an an n converges by the Comparison Test
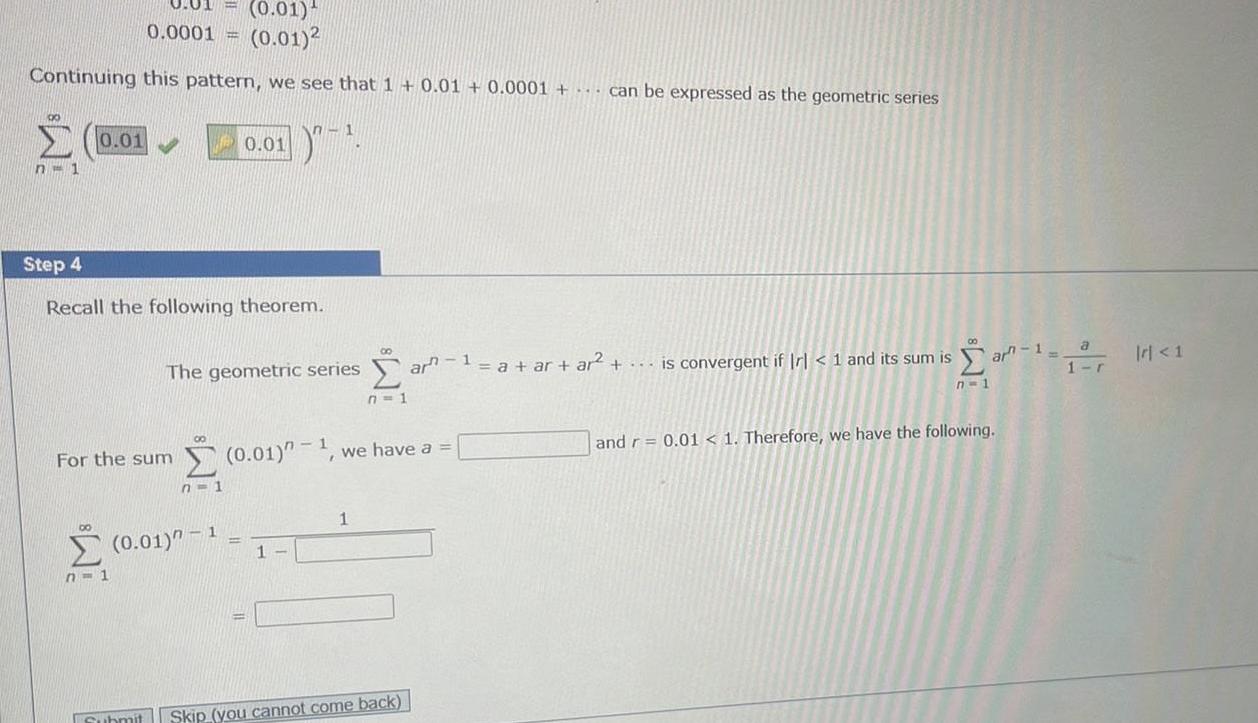
Calculus
Application of derivatives0 01 0 01 0 0001 0 01 2 Continuing this pattern we see that 1 0 01 0 0001 can be expressed as the geometric series 00 0 01 n 1 Step 4 Recall the following theorem For the sum n 1 00 0 01 The geometric series n 1 n 1 0 01 1 1 0 01 1 1 ar 1 a ar ar is convergent if r 1 and its sum is we have a 1 Submit Skip you cannot come back n 1 ar 1 a and r 0 01 1 Therefore we have the following 1 r r 1

Calculus
Application of derivativesSupposea and b bare series with positive terms and b is known to be convergent n a If a b for all n what can you say about a Why Oa diverges by the Comparison Test a converges if and only if a 2b a converges if and only if a 4b a converges by the Comparison Test an O O We cannot say anything about an b If an b for all n what can you say about an Why O We cannot say anything about an b a converges if and only if n sans br an 2 a converges by the Comparison Test a diverges by the Comparison Test bn converges if and only if n sans br 4 Ox an
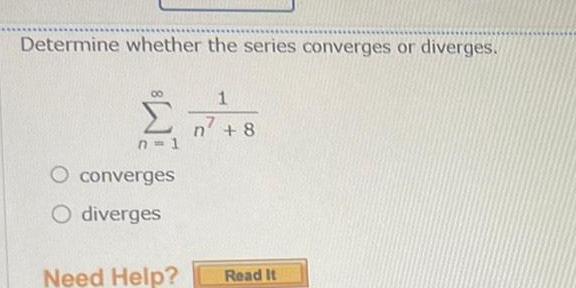
Calculus
Application of derivativesDetermine whether the series converges or diverges 1 n 8 n 8 n 1 converges O diverges Need Help Read It
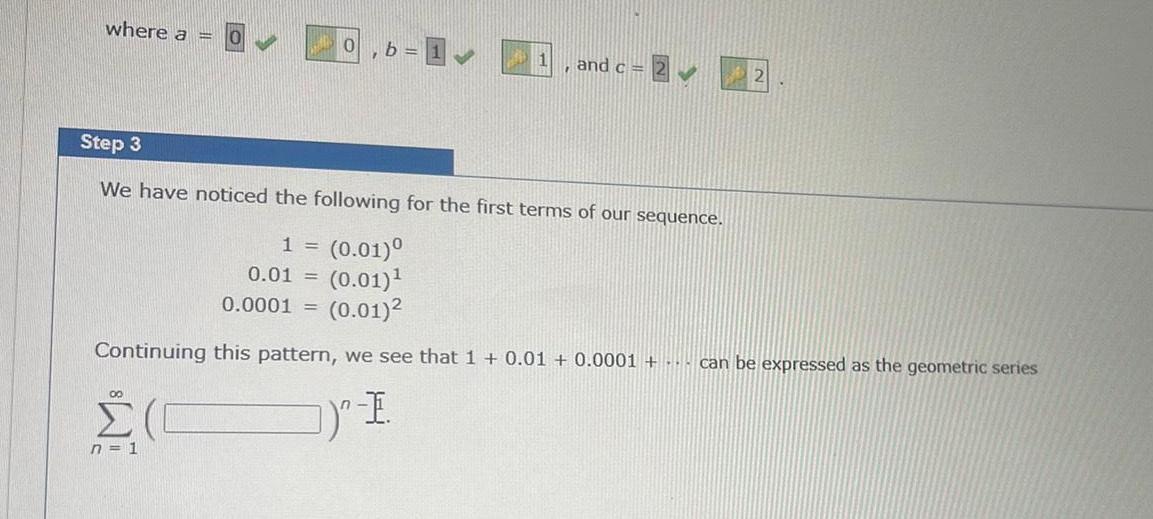
Calculus
Application of derivativeswhere a 0 00 n 1 b 1 1 and c 2 Step 3 We have noticed the following for the first terms of our sequence 1 0 01 0 01 0 01 0 0001 0 01 Continuing this pattern we see that 1 0 01 0 0001 can be expressed as the geometric series I
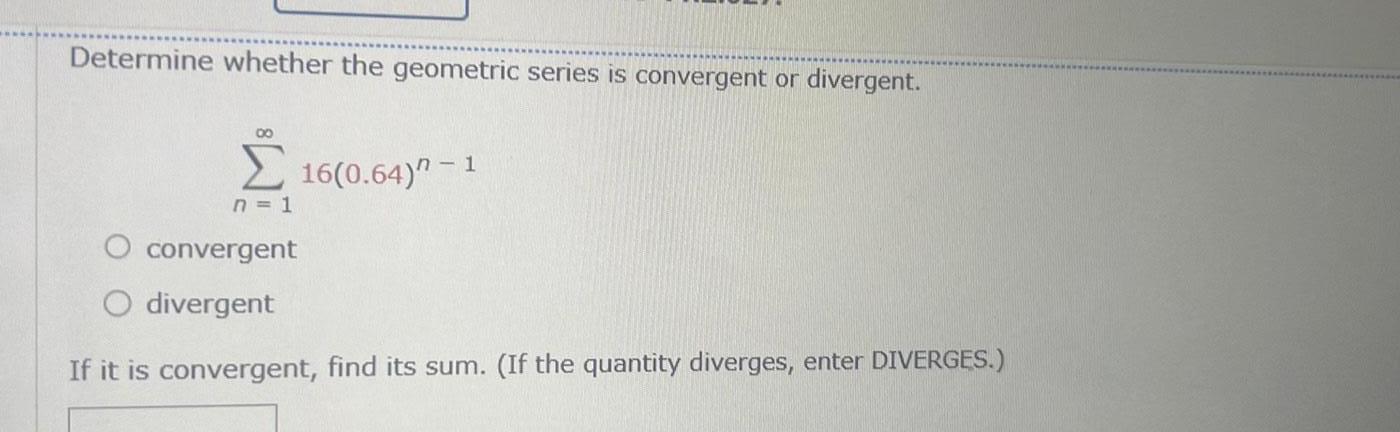
Calculus
Application of derivativesDetermine whether the geometric series is convergent or divergent 80 16 0 64 1 n 1 O convergent O divergent If it is convergent find its sum If the quantity diverges enter DIVERGES

Calculus
Application of derivativesFind the area of the region that lies inside the first curve and outside the second curve r 16 sin 8 r 8
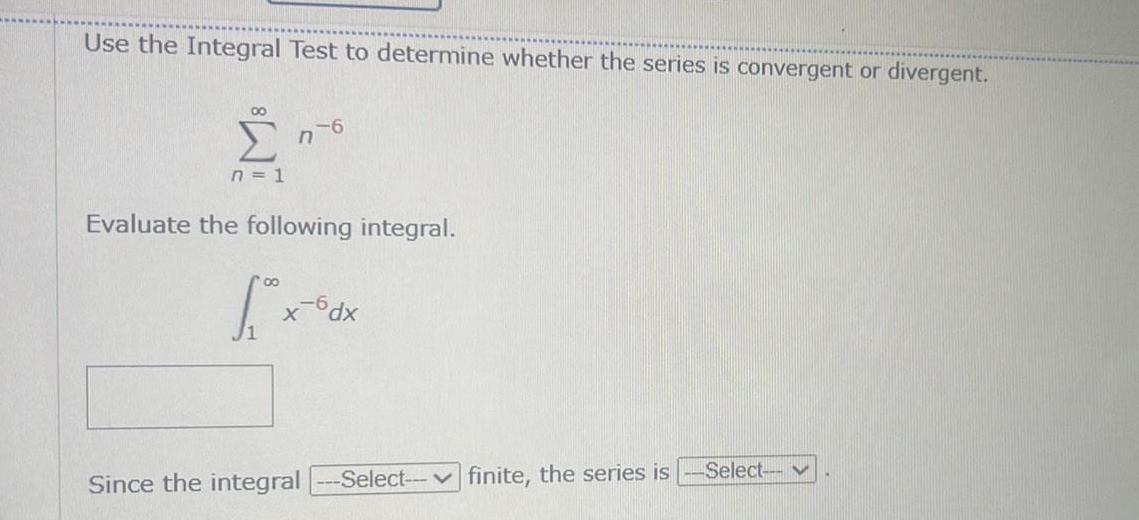
Calculus
Application of derivativesUse the Integral Test to determine whether the series is convergent or divergent 00 n 1 76 Evaluate the following integral X 6dx Since the integral Select finite the series is Select

Calculus
Application of derivativesAILS n 1 SCALCET9 11 2 019 Determine whether the series is convergent or divergent by expressing s as a telescoping sum If it is convergent find its sum If the quantity diverges enter DIVERGE 27 n n 3 M
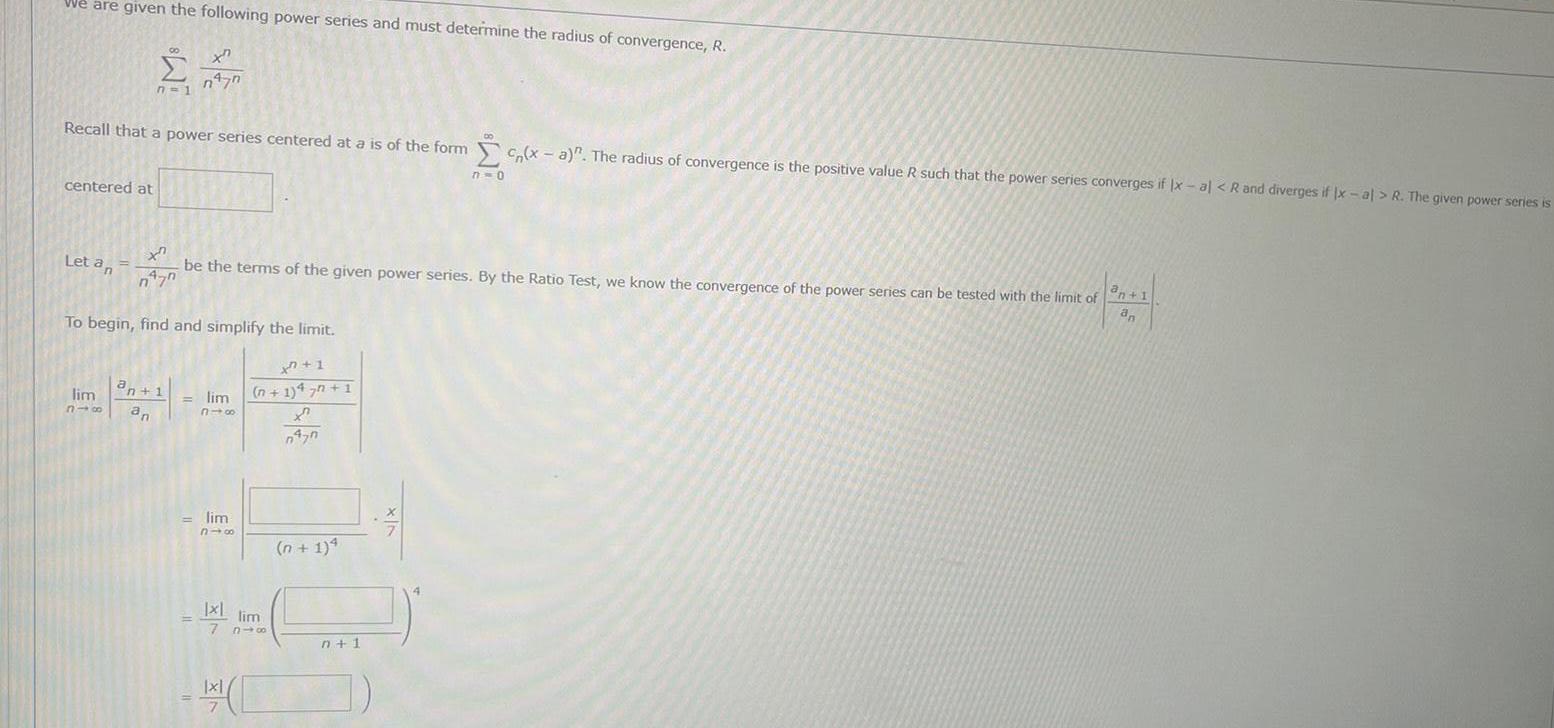
Calculus
Application of derivativesWe are given the following power series and must determine the radius of convergence R centered at Recall that a power series centered at a is of the form x a The radius of convergence is the positive value R such that the power series converges if x al R and diverges if Ix al R The given power series is n 1 Let an xn n 70 be the terms of the given power series By the Ratio Test we know the convergence of the power series can be tested with the limit of an 1 an To begin find and simplify the limit xn 1 n 1 47n 1 X 0470 n477 lim an 1 318 an lim 318 lim 310 Ixl lim le 7 816 x n 1 4 7 0 n 1

Calculus
Application of derivativesConsider the following series n 1 Evaluate the following limit where an R 7427 lim 818 I Find the radius of convergence R of the series an 1 an Find the interval I of convergence of the series Enter your answer using interval notation
Calculus
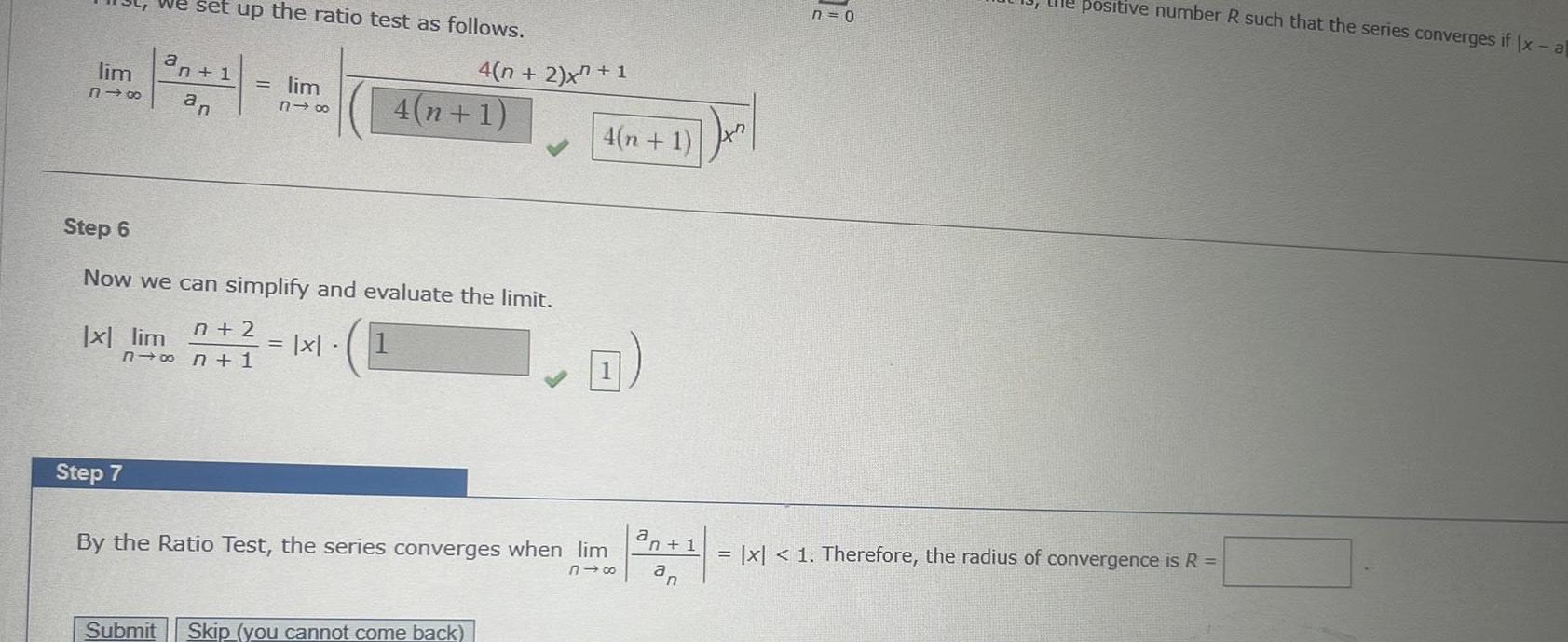
Application of derivativesWe set up the ratio test as follows an 1 318 an lim x lim Step 7 lim 818 Step 6 Now we can simplify and evaluate the limit n 2 n n 1 1 x 4 n 2 x 1 4 n 1 Submit Skip you cannot come back 4 n 1 By the Ratio Test the series converges when lim 818 a n 1 an Jx n 0 positive number R such that the series converges if Ix al x 1 Therefore the radius of convergence is R

Calculus
Application of derivativesSCALCET9 11 10 006 Use the definition of a Taylor series to find the first four nonzero terms of the series for f x centered at the given value of a Enter your answers as a comma separated list 4 1 x 4 3 4 31 f x x 2 4 a 2 x 2 2 4 x 2 3 MY NOTES


Calculus
Application of derivativesThe shaded region in the figure consists of all points whose distances from the center of the square are less than their distances from the edges of the square Find the area of the region Round your to three decimal places 64 5 y 5 5 5

Calculus
Application of derivativesla Assignment Status Click here for incorrect Answer ded answer is not correct and ecific feedback is available e hints and review the relevant material and stay on this question 3 4 5 6 7 S 9 10 11 Completed Completed Completed kicked over flat ground and the acceleration due to gravity on the planet is 5 18 m s The planet has no atmosphere Partial Partial Partial Partial How far horizontally does the ball travel in meters while it is in flight x 109 758 sin cos cotan asin atan acotan cosh 789 HOME tan acos ET 45 6 sinh 123 tanh cotanh C 0 Degrees O Radians NO BACKSPACE INL CLEAR END Submit Hint Frothick I give not 1 Grade Summary Deductions Potential 29 98 Submissions Attempts remaining 2 2 per attempt detailed view 1 296