Differentiation Questions and Answers

Calculus
Differentiation11. (20 points) Use Newton's method to find the zero of f(x)=x²-3 with zo = 2. (Perform
four iterations.)

Calculus
DifferentiationA lighthouse is located 720 feet from the nearest point P on a straight shoreline. The revolving beacon in the
lighthouse makes one revolution every 6 seconds. Find the rate at which a ray from the light moves along the
shore at a point 990 feet from P.
feet per minute

Calculus
DifferentiationDivide.
(12x³ + 14x²-22x-8) ÷ (6x² + x)
Your answer should give the quotient and the remainder.

Calculus
DifferentiationAt 4:00pm, ship A is 53 kilometers west of ship B. Ship A is sailing north at 41 kilometers per hour whereas ship
B is sailing south at 35 kilometers per hour. Determine the rate of change of the distance between the two
ships at 1:00am. Round the solution to the nearest ten-thousandth, if necessary.
kilometers per hour
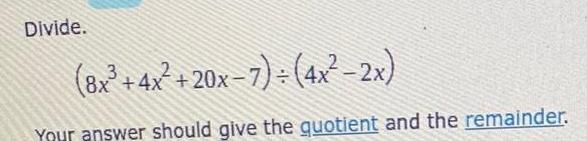
Calculus
DifferentiationDivide.
(8x³+4x²+20x-7)+(4x²-2x)
Your answer should give the quotient and the remainder.

Calculus
DifferentiationLet g(x) = log3(x+5) + 3
Determine the derivative of g-¹ at x = 4.
(g-¹)'(4) =
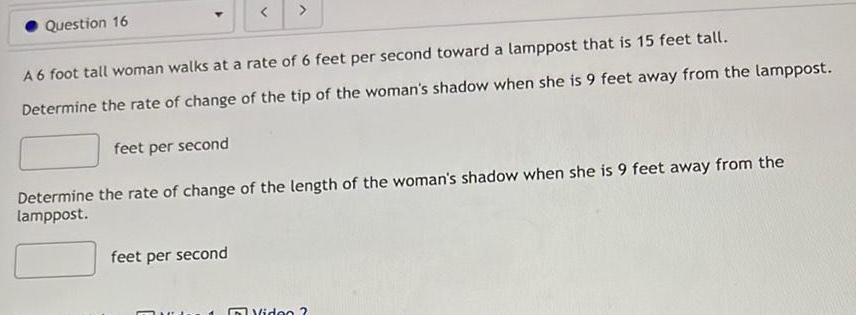
Calculus
DifferentiationQuestion 16
feet per second
<
A 6 foot tall woman walks at a rate of 6 feet per second toward a lamppost that is 15 feet tall.
Determine the rate of change of the tip of the woman's shadow when she is 9 feet away from the lamppost.
feet per second
Determine the rate of change of the length of the woman's shadow when she is 9 feet away from the
lamppost.
dra d
>
Video ?
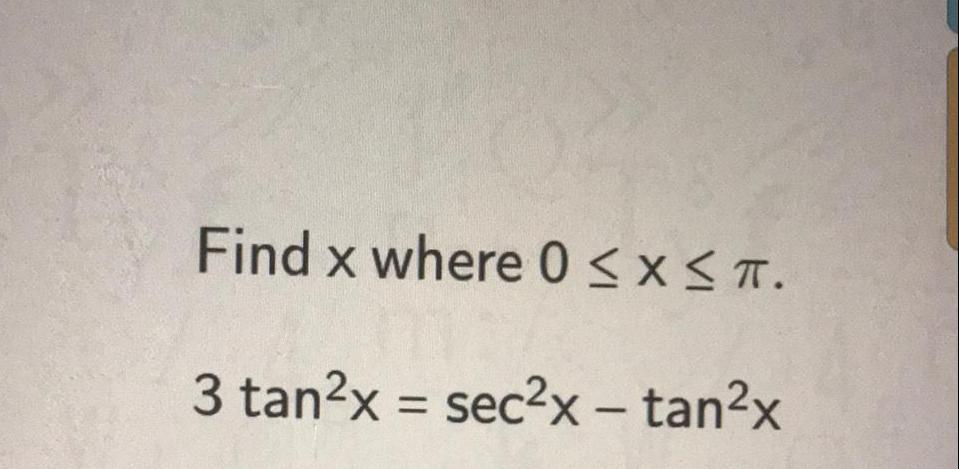
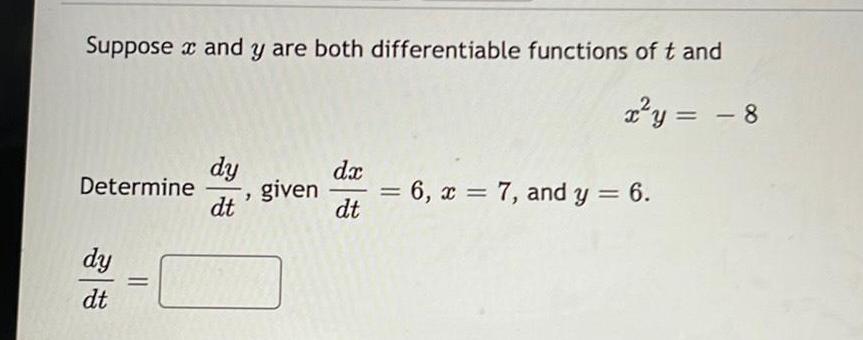
Calculus
DifferentiationSuppose and y are both differentiable functions of t and
x²y = − 8
Determine
dy
dt
=
dy
dt
"
dx
dt
given = 6, 7, and y = 6.
=

Calculus
DifferentiationSuppose and y are both differentiable functions of t and
y =- 3x² + 6x - 2
Determine dy / dt given dx/dt =2 and x=8
dy/dt=


Calculus
DifferentiationLet h(v) = arcsin ( - 5v³)
Determine the derivative of h.
h'(v) =
Determine the slope of h at v = 0.
h'(0) =

Calculus
DifferentiationLet f(y) = arctan
6
(5)
Determine the derivative of f.
Determine the slope of f at y = -7.
f'(-7)=


Calculus
DifferentiationLet g(v)
arccsc (e7v)
Determine the derivative of g.
=
g'(v) =
Determine the slope of g at v = 12.
g'(12) =
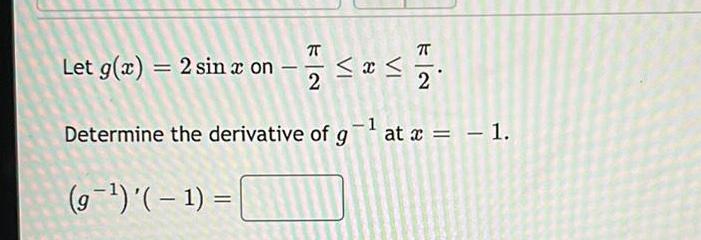
Calculus
DifferentiationLet g(x) = 2 sin x on
π
2
≤ x ≤
FIN
Determine the derivative of g¯¹ at x = − 1.
(g-¹) '(-1) =

Calculus
DifferentiationLet h(x) = x³ + 7x + 6
Determine the derivative of h-¹ at x = 14.
(n-¹) '(14) =

Calculus
DifferentiationLet g(z)= z^2 /3 +10 cos(z) +e^z +10 sin(z)
Determine the third derivative of g.
d^3 z/dz³=

Calculus
DifferentiationLet f(x) = (x+8)² +8, for x > - 8.
Determine the derivative of f-¹ at x = 12.
(f ¹)'(12) =

Calculus
DifferentiationDivide.
(12x² + 30x+12) + (2x+4)
Your answer should give the quotient and the remainder.

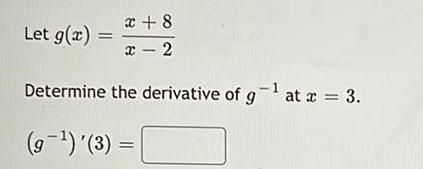
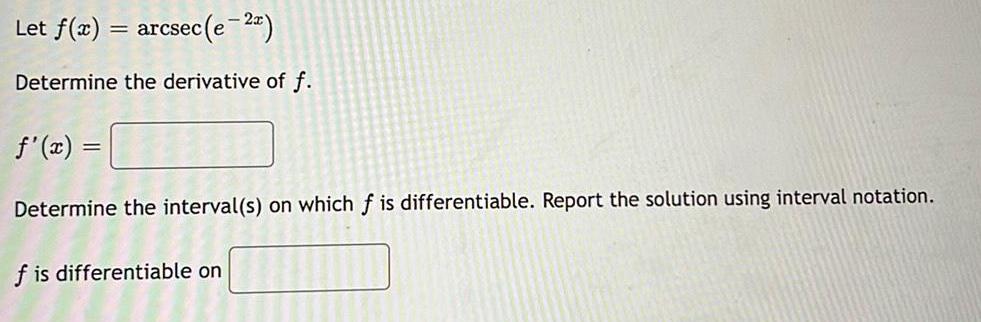
Calculus
DifferentiationLet f(x) = arcsec (e-2)
Determine the derivative of f.
f'(x) =
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on

Calculus
DifferentiationLet h(t) = arccos (9t7)
Determine the derivative of h.
h'(t) =
-63t6
V1-81t14
Determine the slope of h at t = 0.
h'(0) =
0

Calculus
DifferentiationLet g(y) = arctan(- 9y)
Determine the derivative of g.
g'(y) =
Determine the slope of g at y = -6.
g'(- 6) =

Calculus
DifferentiationLet f(x) = 7 3√x-7+2
Determine the derivative of f-¹ at x = - 12.
(f-¹) '(- 12) =

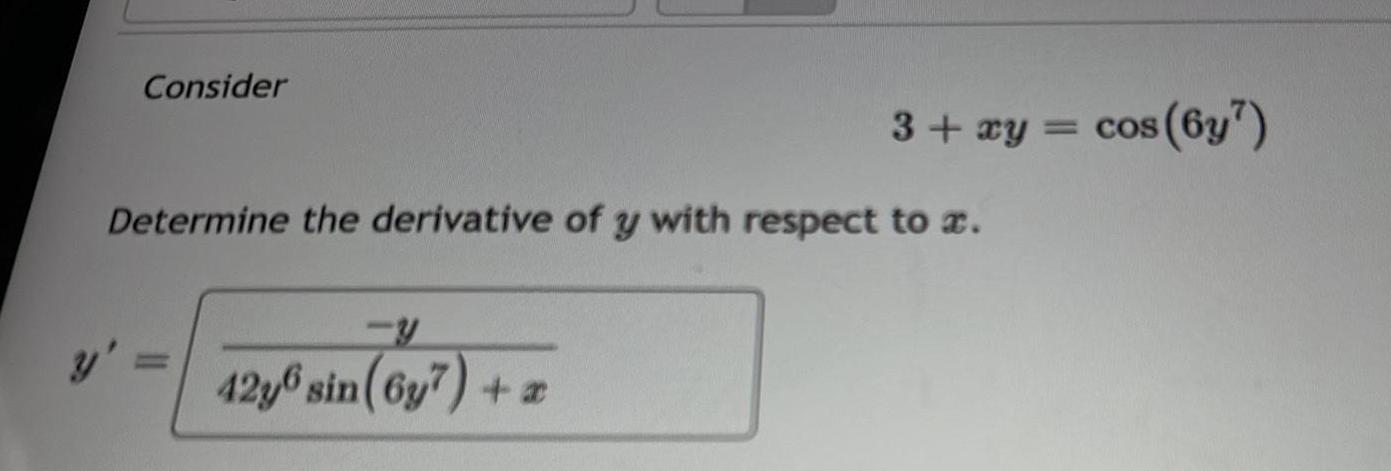
Calculus
DifferentiationConsider
Determine the derivative of y with respect to a.
y = 42y6 sin (6y7) +
3+ xy = cos
cos (6y7)

Calculus
Differentiationª(7)
4
Determine the derivative of f.
Let f(v) = - 7arctan (
f'(v) =
Determine the slope of f at v= - 2.
f'(-2) =
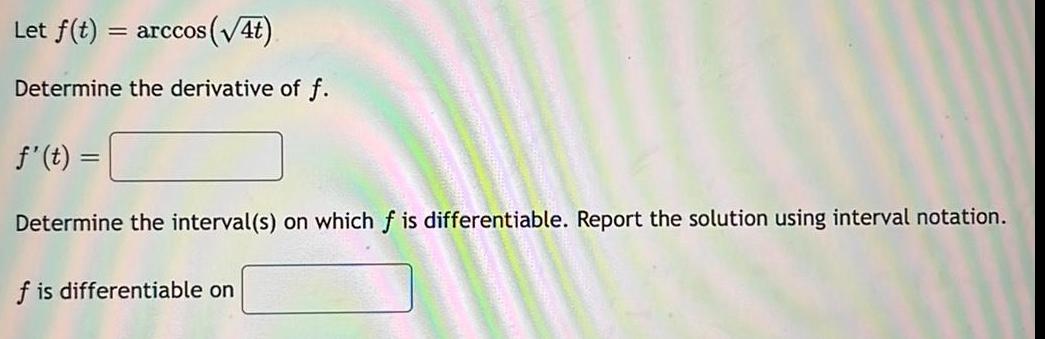
Calculus
DifferentiationLet f(t)= = arccos (√4t)
Determine the derivative of f.
f'(t) =
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on
![Cliff divers on an exotic island dive off cliffs that are 59 meters above the sea. The position of a diver
above the sea at time t is given by s(t) = -4.9t2 + 5t + 59, where t is measured in seconds and s is
measured in meters.
Determine the average rate of change of a diver over the time interval [1, 2].
Average Rate of Change =
Determine the velocity function and the diver's velocity at t = 1 seconds and t = 2 seconds.
I
v(t)
a(t)
=
Velocity of the diver at t = 1 seconds:
Velocity of the diver at t = 2 seconds:
=
Determine the accelerations function and the diver's acceleration at t = 1 seconds and t = 2 seconds.
Acceleration of the diver at t = 1 seconds:
Select an answer
Acceleration of the diver at t = 2 seconds:
Select an answer
Select an answer
Select an answer
Select an answer](https://media.kunduz.com/media/sug-question/raw/84142746-1660407240.4288776.jpeg?w=256)
Calculus
DifferentiationCliff divers on an exotic island dive off cliffs that are 59 meters above the sea. The position of a diver
above the sea at time t is given by s(t) = -4.9t2 + 5t + 59, where t is measured in seconds and s is
measured in meters.
Determine the average rate of change of a diver over the time interval [1, 2].
Average Rate of Change =
Determine the velocity function and the diver's velocity at t = 1 seconds and t = 2 seconds.
I
v(t)
a(t)
=
Velocity of the diver at t = 1 seconds:
Velocity of the diver at t = 2 seconds:
=
Determine the accelerations function and the diver's acceleration at t = 1 seconds and t = 2 seconds.
Acceleration of the diver at t = 1 seconds:
Select an answer
Acceleration of the diver at t = 2 seconds:
Select an answer
Select an answer
Select an answer
Select an answer
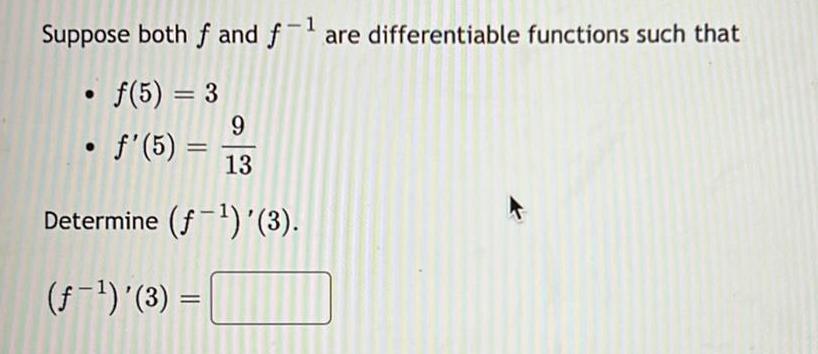
Calculus
DifferentiationSuppose both f and f-¹ are differentiable functions such that
• f(5) = 3
9
13
Determine (f¹) (3).
(ƒ-¹) '(3) =
• f'(5) =
=

Calculus
DifferentiationLet f(x) =
9
Determine the derivative of f.
f'(x) = -(9)(x)
3G
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on (-∞,0) u (0,00)
![Let h(u)
Determine
Du[h(u)]
4e" tan(u)
D [h(u)]](https://media.kunduz.com/media/sug-question/raw/84142658-1660407181.3662713.jpeg?w=256)
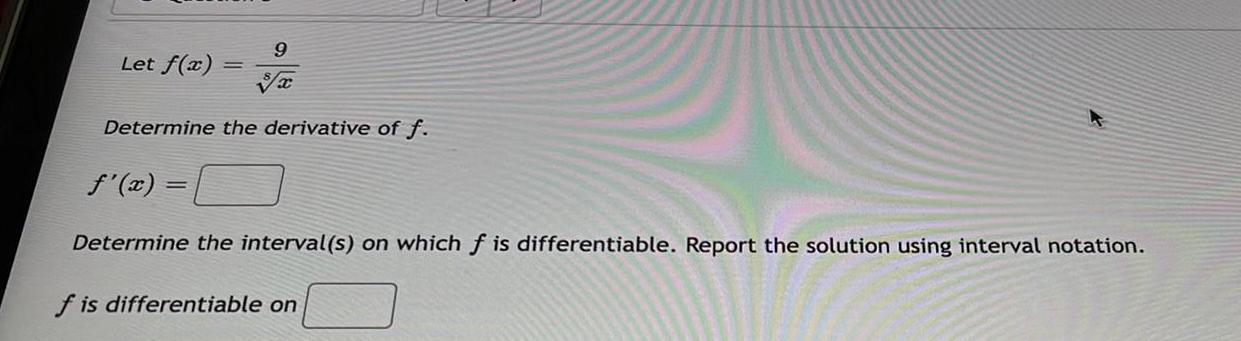
Calculus
DifferentiationLet f(x) =
9
Determine the derivative of f.
f'(x) =
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on

Calculus
DifferentiationLet h(x) = x³ + 9x - 3
Determine the derivative of h -¹ at x = 7.
(h-¹) '(7) =
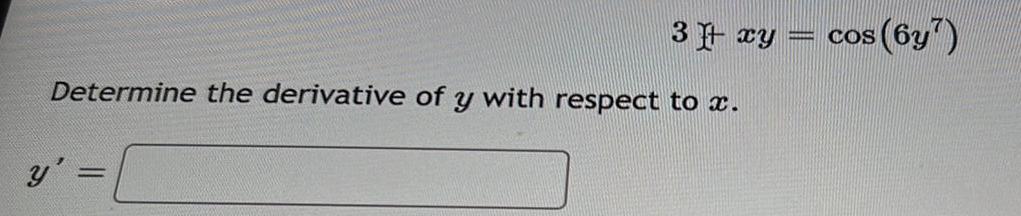
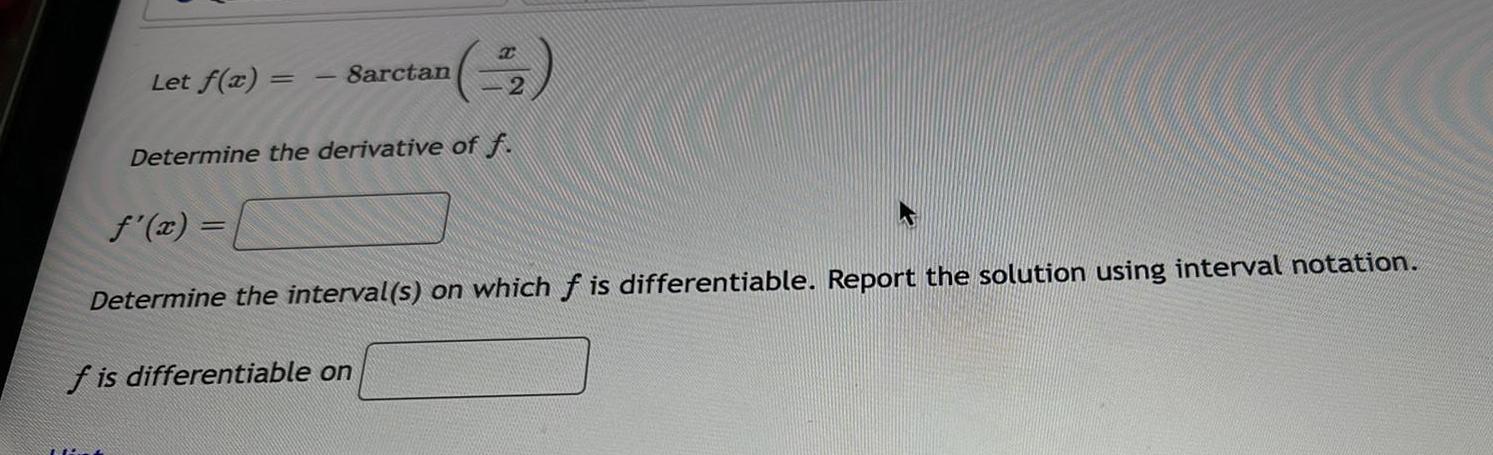
Calculus
DifferentiationLet f(x)
8arctan
Min
Determine the derivative of f.
f'(x) =
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on
x

Calculus
DifferentiationLet f(a)
P
9
Determine the derivative of f.
f'(x) =
Determine the interval(s) on which f is differentiable. Report the solution using interval notation.
f is differentiable on
![Let g(u) =- 10u/√u²-6
Use logarithmic differentiation to determine the derivative of g.
d/du[g(u)]=](https://media.kunduz.com/media/sug-question/raw/84142789-1660407058.9344077.jpeg?w=256)
Calculus
DifferentiationLet g(u) =- 10u/√u²-6
Use logarithmic differentiation to determine the derivative of g.
d/du[g(u)]=

Calculus
DifferentiationLet h(t) = arccos (9t)
Determine the derivative of h.
[
Determine the slope of h at t = 0.
h'(0) =
h'(t) =
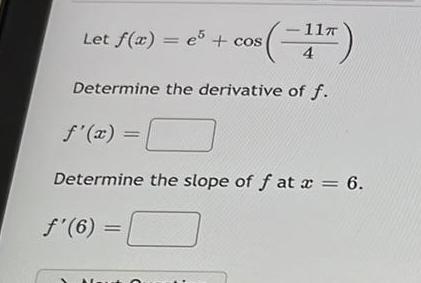
Calculus
DifferentiationLet f(x) = e5 + cos
s (−117)
4
Determine the derivative of f.
f'(x) =
Determine the slope of f at x = 6.
f'(6) =

Calculus
DifferentiationLet h(x) = x² - 15x + 4.
Use either of the limit definitions of the derivative to differentiate h.
h'(x)=
Determine the slope of h at x = 7.
h'(7) =
=

Calculus
DifferentiationAn object's velocity after t seconds is v(t) = 26 – 2t feet per second.
(a) How many seconds does it take for the object to come to a stop (velocity = 0)?
seconds
(b) How far does the car travel during that time?
feet
(c) How many seconds does it take the car to travel half the distance in part (b)?

Calculus
DifferentiationFind a function f such that f '(x) = 5x³ and the line 135x + y = 0 is tangent to the graph of f.
=
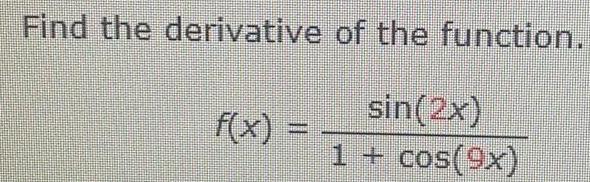

Calculus
DifferentiationUse Newton's method with the specified initial approximation x₁ to find x3, the third approximation to the solution of the given equation. (Round your answer to four decimal places.)
2-x²+1=0,
x₁-2
=
=
X

Calculus
DifferentiationConsider the function below.
f(x) = -3x² + 6x + 6
Exercise (a)
Find the critical numbers of f.
Step 1
Differentiate f(x)=-3x² + 6x + 6 with respect to x.
f'(x)=
=
Submit
Skip (you cannot come back)
Exercise (b)
Find the open intervals on which the function is increasing or decreasing.
Click here to begin!
Exercise (c)
Apply the First Derivative Test to identify the relative extrema.

Calculus
DifferentiationExplain why Newton's method doesn't work for finding the root of the equation
x³ 3x + 1 = 0
if the initial approximation is chosen to be x₁ = 1.
f(x) = x³ 3x + 1 = f'(x) =
-
X
. If x₁ = 1, then f'(x₁) =
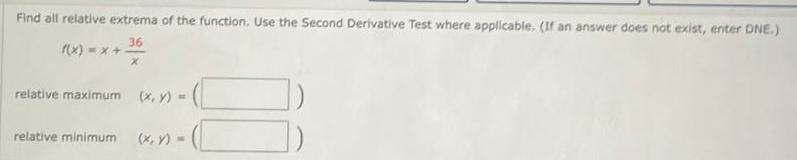
Calculus
DifferentiationFind all relative extrema of the function. Use the Second Derivative Test where applicable. (If an answer does not exist, enter DNE.)
36
X
f(x) = x +
relative maximum
relative minimum
(x, y) =
(x, y) =