Differentiation Questions and Answers

Calculus
DifferentiationLet f(x) = 8. Use logarithmic differentiation to determine the derivative.
f'(x) =
ƒ'(1) =
Question Help
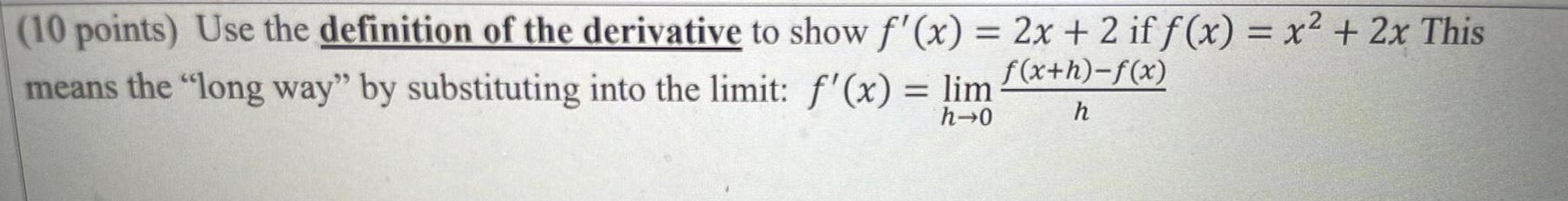
Calculus
Differentiation(10 points) Use the definition of the derivative to show f'(x) = 2x + 2 if f(x) = x² + 2x This
f(x+h)-f(x)
means the "long way" by substituting into the limit: f'(x) = lim
h→0
h

Calculus
DifferentiationConsider the following transformed function> y = 7 cos(x +45) - 2.
(i) Complete the following "old" original table of values for the parent function.
Yold
Xold
(ii) Write the transformation equations> xnew=? and ynew=?
(iii) Complete the "new" transformed table of values for the new sinusoidal function.
Xnew
Ynew
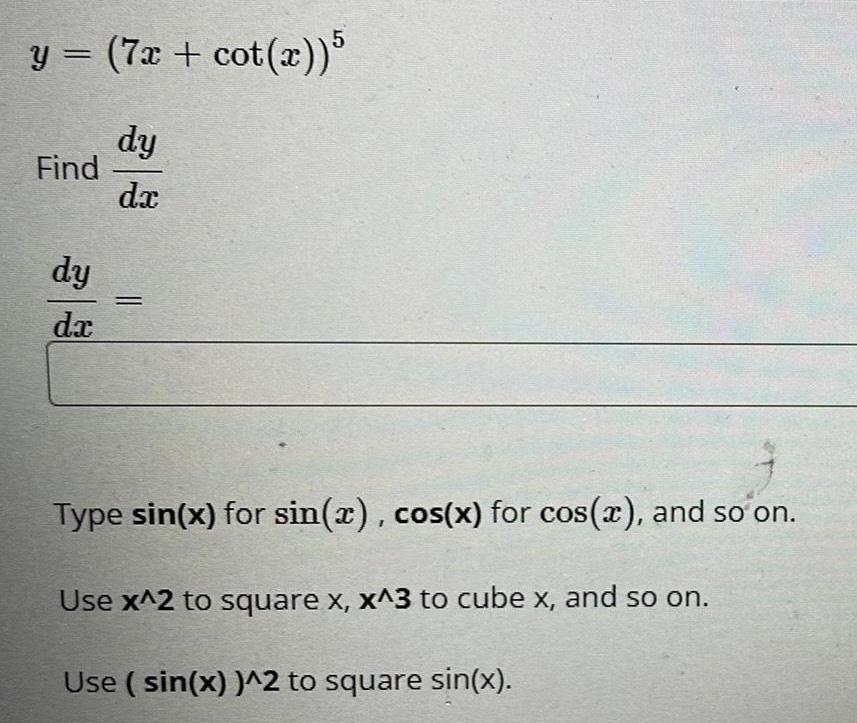
Calculus
Differentiationy = (7x + cot(x)) 5
dy
dx
Find
dy
da
Type sin(x) for sin(x), cos(x) for cos(x), and so on.
Use x^2 to square x, x^3 to cube x, and so on.
Use (sin(x))^2 to square sin(x).
![Consider the differential equation
=y-t.
dy
Is each of the following a solution to y - t?
Select true or false for each proposed solution.
y=t+2 [Select]
y=t+1 [Select]
y=t+1+2et [Select]](https://media.kunduz.com/media/sug-question/raw/83587660-1660319596.1489615.jpeg?w=256)
Calculus
DifferentiationConsider the differential equation
=y-t.
dy
Is each of the following a solution to y - t?
Select true or false for each proposed solution.
y=t+2 [Select]
y=t+1 [Select]
y=t+1+2et [Select]

Calculus
DifferentiationFind an equation of the tangent line to the graph of fat the given point.
f(x) = √√x, (9, 3)
y =
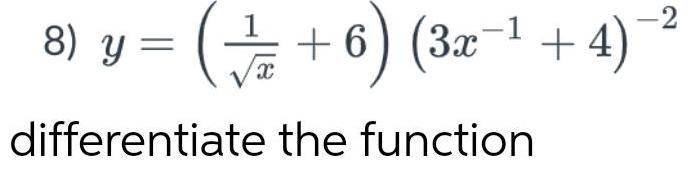
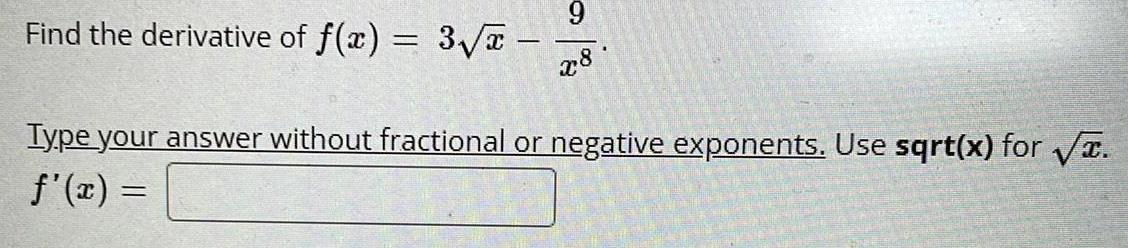
Calculus
DifferentiationFind the derivative of f(x) = 3√x -
9
a 10/2
x8.
Type your answer without fractional or negative exponents. Use sqrt(x) for √.
ƒ'(x) =

Calculus
DifferentiationSuppose that the position of a particle is given by s = f(t) = 2t³ + 6t+ 9.
(a) Find the velocity at time t.
v(t) =
(b) Find the velocity at time t = 3 seconds.
m
S
a(t) =
m
S
(c) Find the acceleration at time t.
m
82
(d) Find the acceleration at time t = 3 seconds.
m
8²
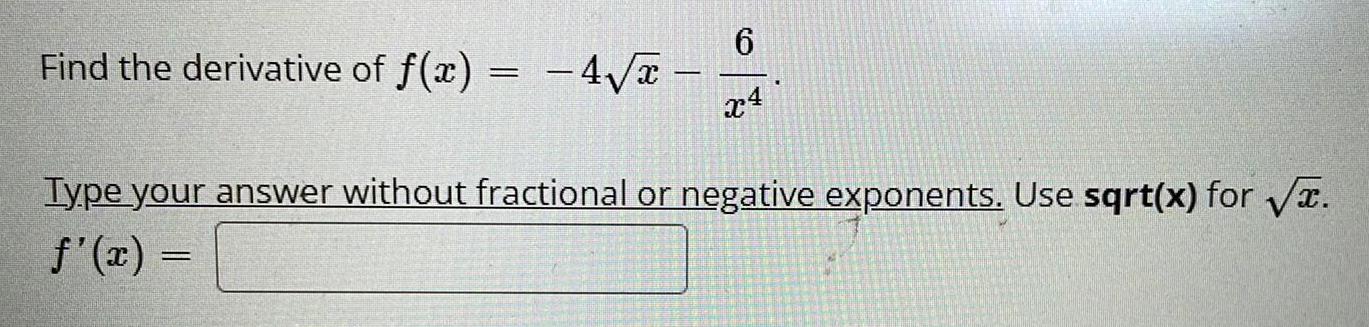
Calculus
DifferentiationFind the derivative of f(x)
=
=
- 4√x
6
x4
Type your answer without fractional or negative exponents. Use sqrt(x) for √.
f'(x) =
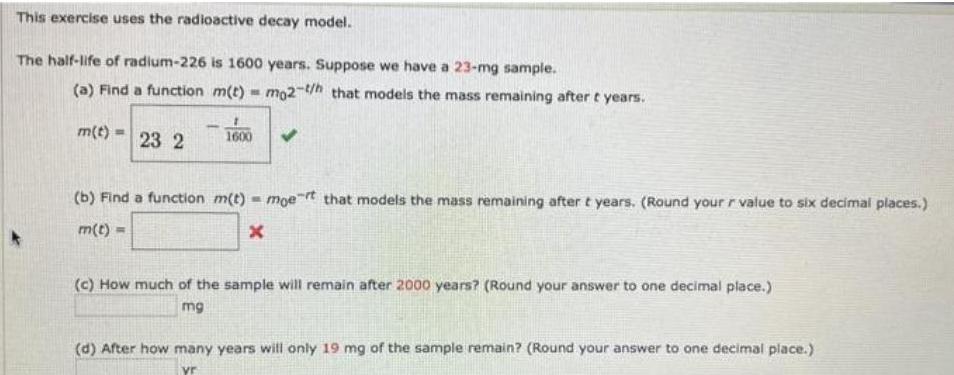
Calculus
DifferentiationThis exercise uses the radioactive decay model.
The half-life of radium-226 is 1600 years. Suppose we have a 23-mg sample.
(a) Find a function m(t)= mo2-/h that models the mass remaining after t years.
m(t)= 23 2
1
1600
(b) Find a function m(t) = moet that models the mass remaining after t years. (Round your r value to six decimal places.)
m(t) =
x
(c) How much of the sample will remain after 2000 years? (Round your answer to one decimal place.)
mg
(d) After how many years will only 19 mg of the sample remain? (Round your answer to one decimal place.)
vr

Calculus
DifferentiationUse the product rule to find the derivative of
(-3x¹0 + 5x³)(7e² - 7)
Use e^x for et. You do not need to expand out your answer.
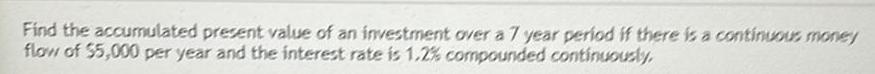
Calculus
DifferentiationFind the accumulated present value of an investment over a 7 year period if there is a continuous money
flow of $5,000 per year and the interest rate is 1.2% compounded continuously.

Calculus
DifferentiationIf f(x) = 3x² − 7x + 6, find ƒ'(1).
-
Use this to find the equation of the tangent line to the parabola y.= 3x² - 7x + 6 at the point
(1, 2). The equation of this tangent line can be written in the form y = mx + b
where m is:
and where b is:
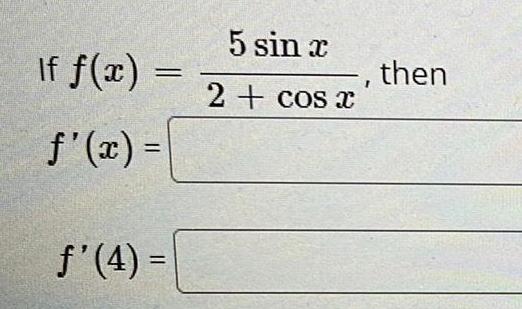

Calculus
DifferentiationLet f(x) = 2x + 14 - 3e. Then the equation of the tangent line to the graph of f(x) at the point
(0, 11) is given by y = mx + b for
m =
b=
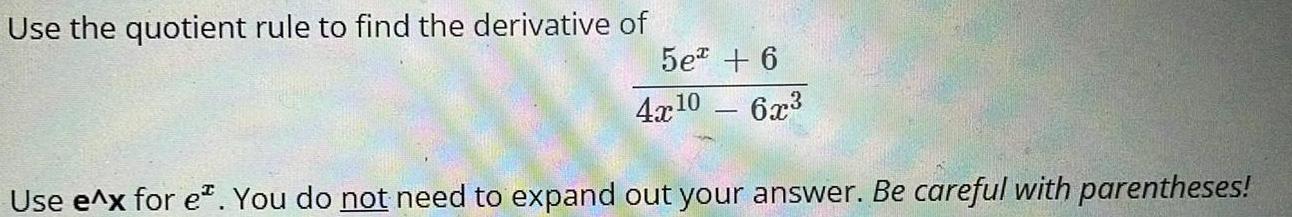
Calculus
DifferentiationUse the quotient rule to find the derivative of
5e + 6
4x¹0 - 6x³
Use e^x for e. You do not need to expand out your answer. Be careful with parentheses!

Calculus
DifferentiationFind the vertical asymptotes of the rational function y = 2-16
X
Ox= 0 and x = 1
Ox= 1 and x = -1
Ox=4 and x = -4
y = 4 and y = -4
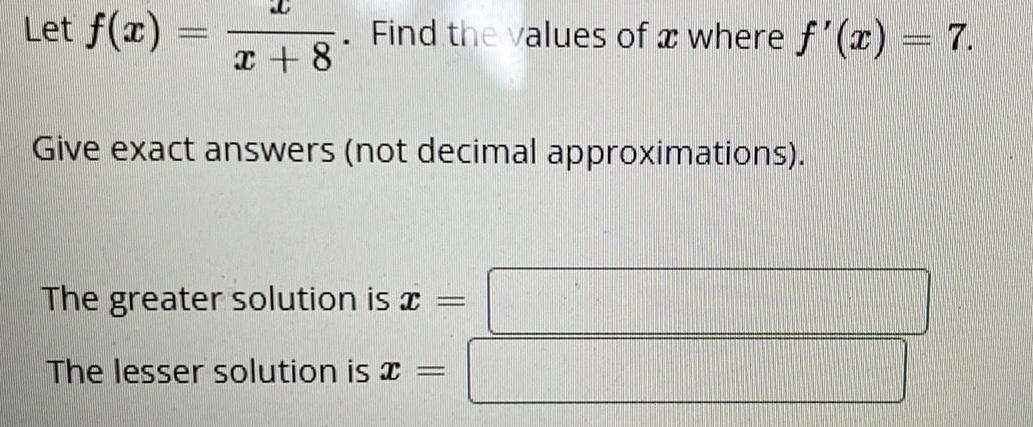
Calculus
DifferentiationLet f(x)
x + 8
.
Find the values of a where f'(x) = 7.
Give exact answers (not decimal approximations).
The greater solution is x =
The lesser solution is =
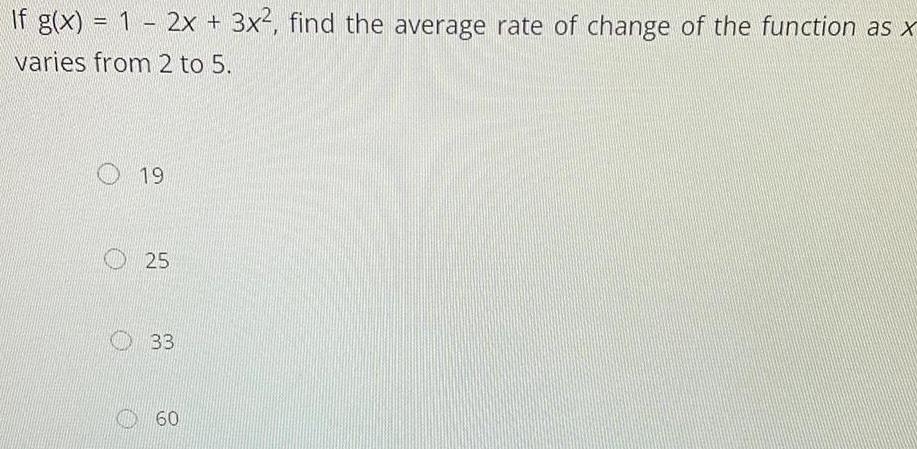
Calculus
DifferentiationIf g(x) = 1 - 2x + 3x2, find the average rate of change of the function as x
varies from 2 to 5.
19
25
33
60

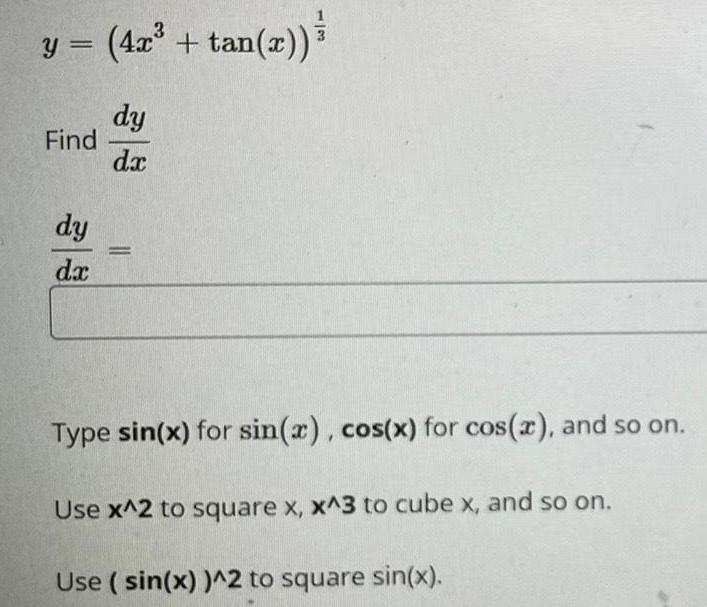
Calculus
Differentiationy = (4x³ + tan(x)) ³
dy
dx
Find
dy
dx
=
Type sin(x) for sin(x), cos(x) for cos(x), and so on.
Use x^2 to square x, x^3 to cube x, and so on.
Use (sin(x))^2 to square sin(x).
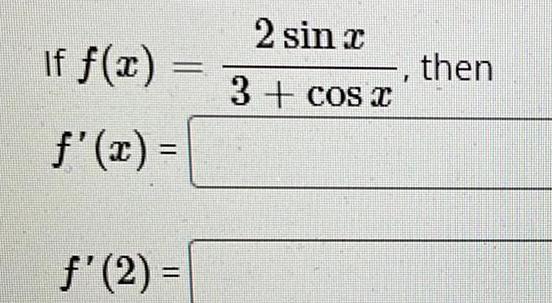
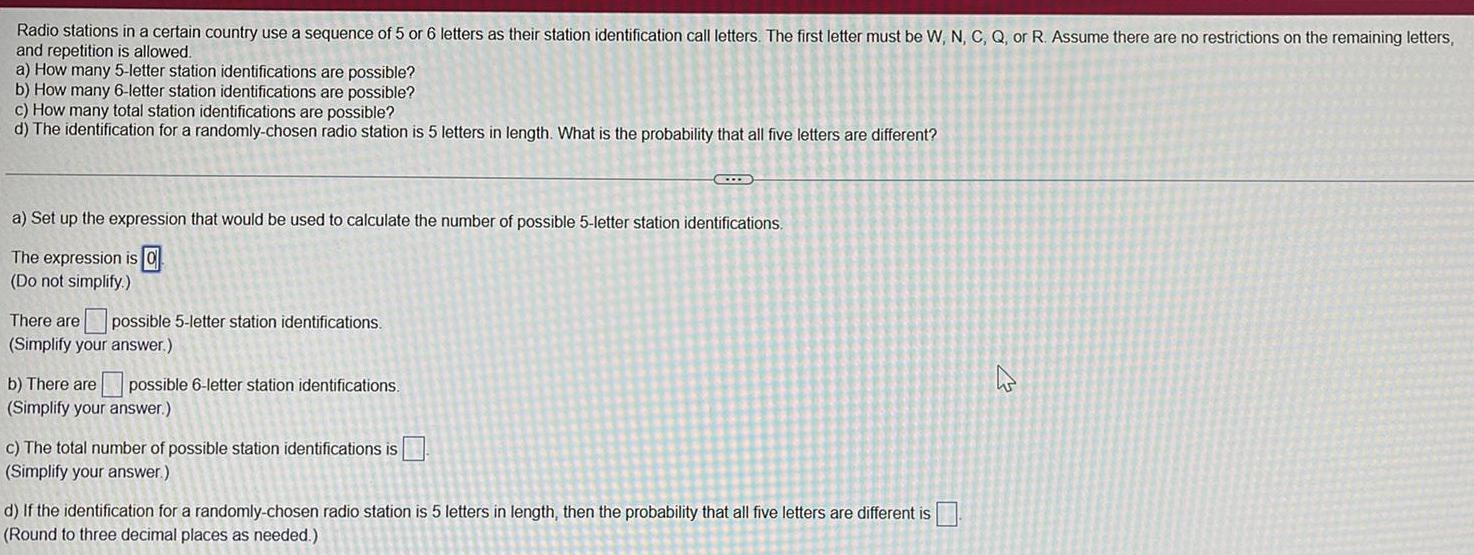
Calculus
DifferentiationRadio stations in a certain country use a sequence of 5 or 6 letters as their station identification call letters. The first letter must be W, N, C, Q, or R. Assume there are no restrictions on the remaining letters,
and repetition is allowed.
a) How many 5-letter station identifications are possible?
b) How many 6-letter station identifications are possible?
c) How many total station identifications are possible?
d) The identification for a randomly-chosen radio station is 5 letters in length. What is the probability that all five letters are different?
a) Set up the expression that would be used to calculate the number of possible 5-letter station identifications.
The expression is
(Do not simplify.)
There are possible 5-letter station identifications.
(Simplify your answer.)
b) There are possible 6-letter station identifications.
(Simplify your answer.)
C
c) The total number of possible station identifications is
(Simplify your answer.)
d) If the identification for a randomly-chosen radio station is 5 letters in length, then the probability that all five letters are different is
(Round to three decimal places as needed.)
4
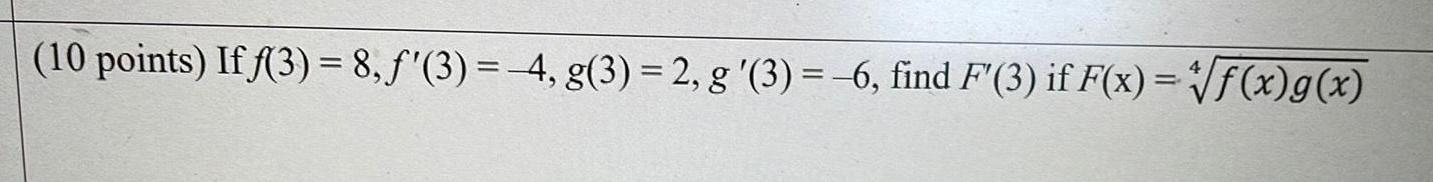
Calculus
Differentiation(10 points) If f(3) = 8, f'(3) = 4, g(3) = 2, g'(3)=-6, find F'(3) if F(x)=√f(x) g(x)

Calculus
DifferentiationLet f(x) =
4x + 14
if x < -2
√x+38 if x > - 2
if x = - 2
2
lim
H12
Select all statements below that you agree with.
Note: You may be checking more than one box. No partial credit.
Of(-2) is defined.
lim
HI12
f(x) exists.
f(x) = f(-2).
#
O The function is continuous at x = -2.
The function is not continuous at x = -2.

Calculus
DifferentiationUse the product rule to find the derivative of
(10x5 + 2x)(8 + 9)
Use e^x for e. You do not need to expand out your answer.
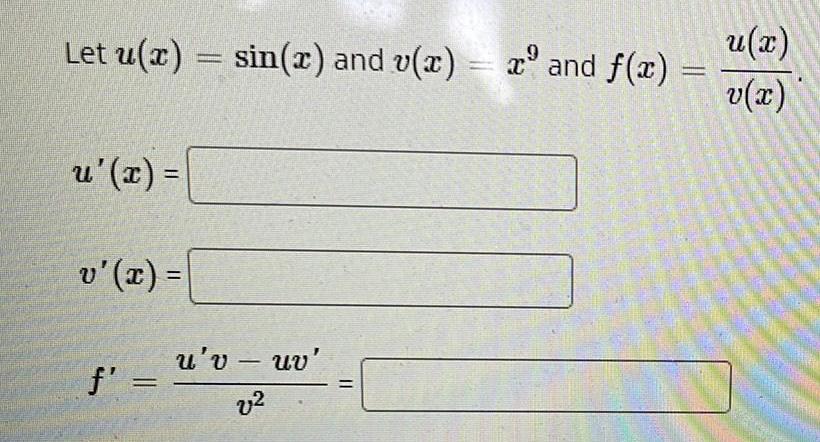
Calculus
DifferentiationLet u(x) = sin(x) and v(x) = x² and f(x)
u'(x) =
v'(x) =
f' =
u'v - uv'
v²
=
=
u(x)
v(x)
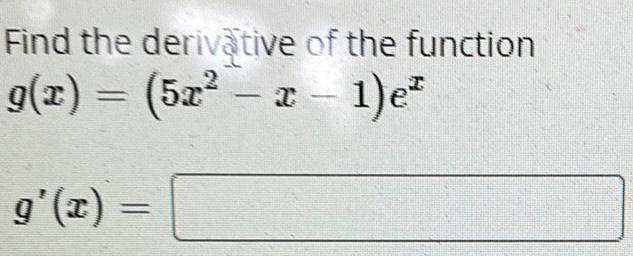
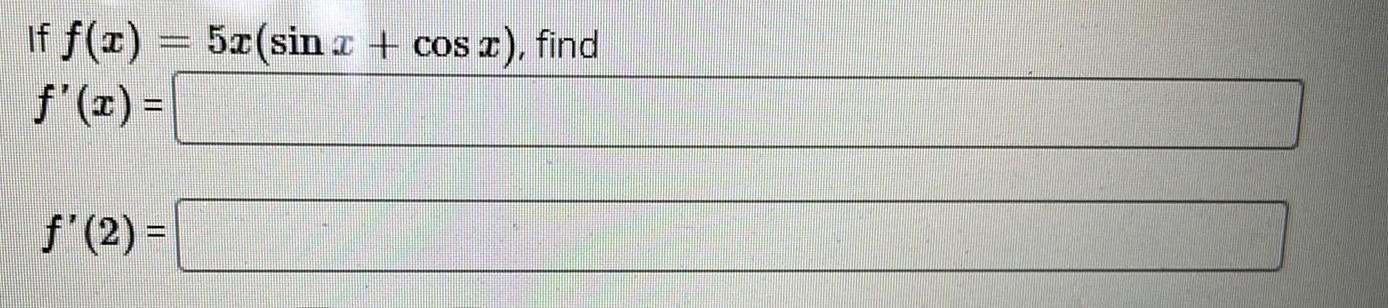
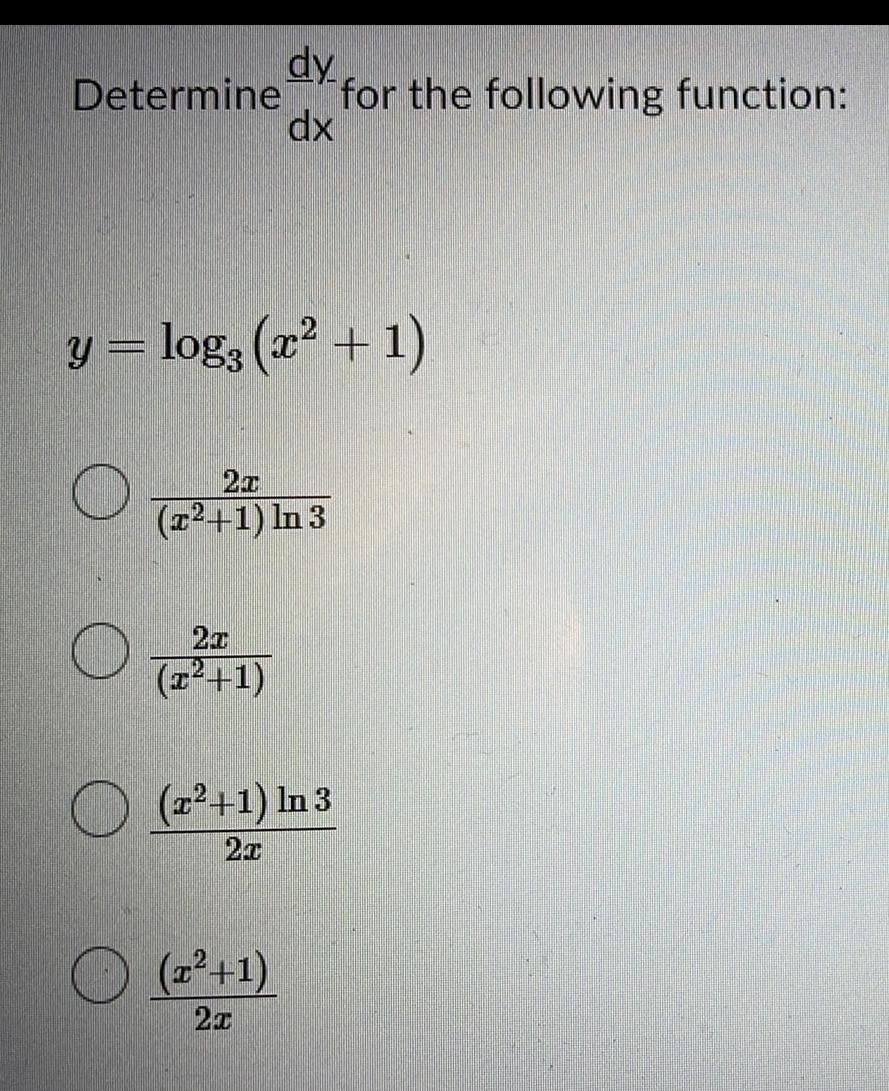
Calculus
DifferentiationDetermine
O
y = log; (x² + 1)
dy
dx
(T²+1) In 3
21
(T²+1)
(7²+1) In 3
20
(T²+1)
21
for the following function:
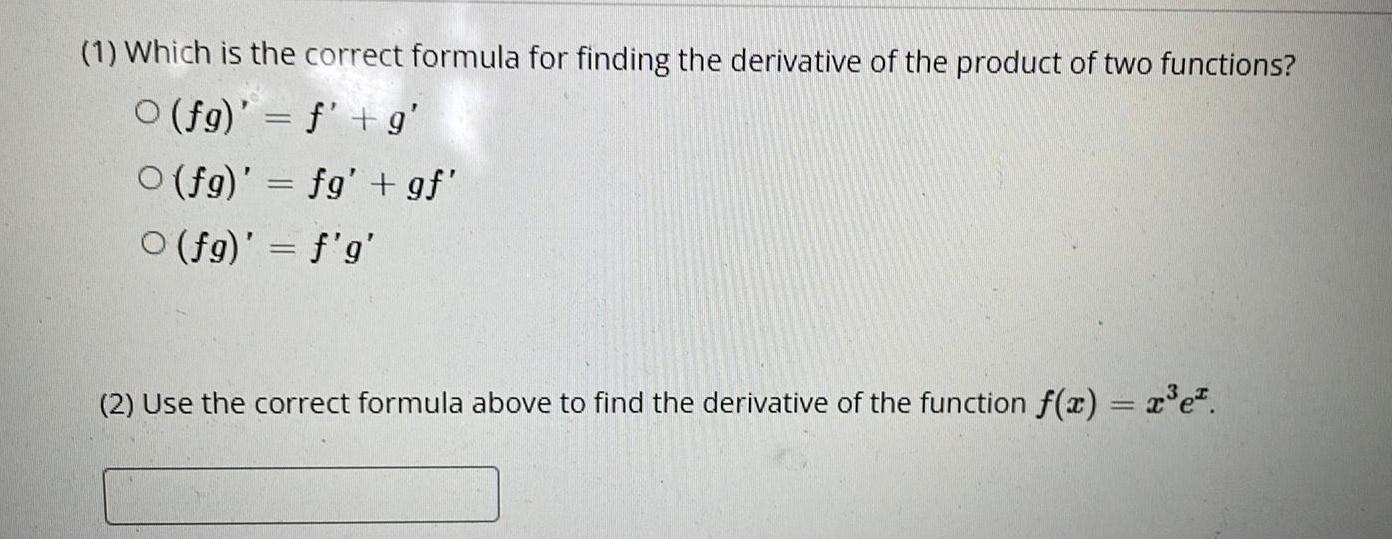
Calculus
Differentiation(1) Which is the correct formula for finding the derivative of the product of two functions?
(fg)' = f' + g'
O(fg)' = fg' + gf'
(fg)' = f'g'
(2) Use the correct formula above to find the derivative of the function f(x) = x³e².
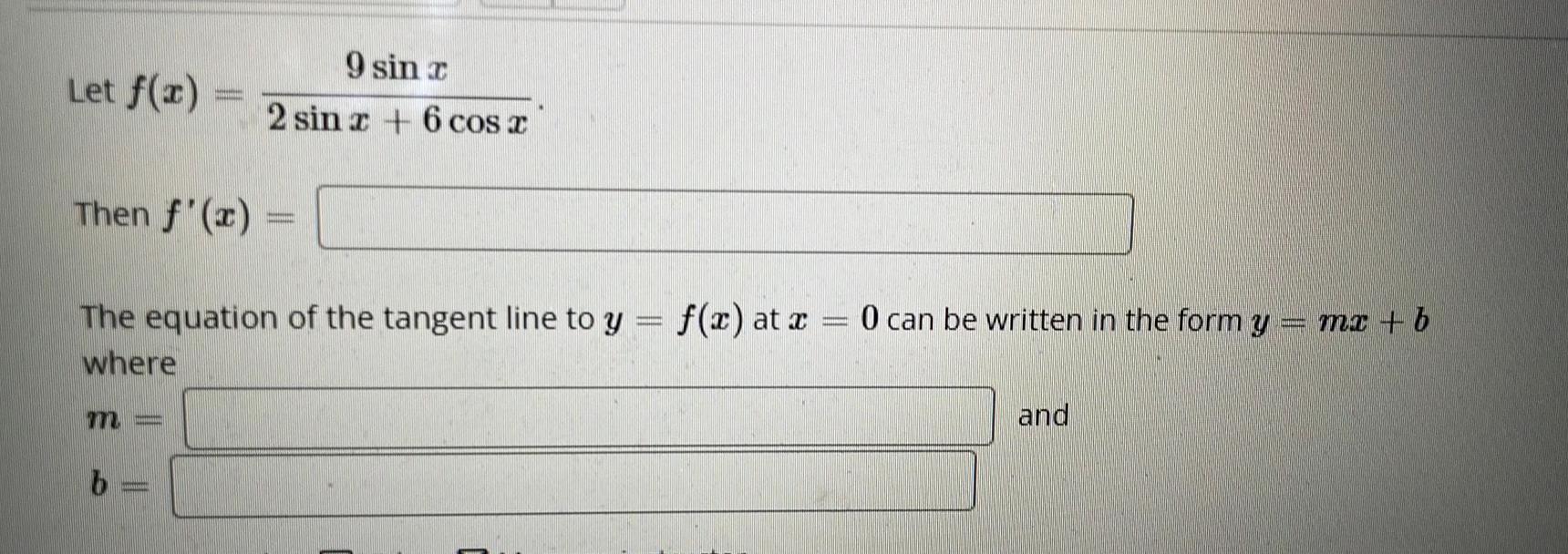
Calculus
DifferentiationLet f(x)
Ho
MINIMA
Then f'(x)
b-
|
9 sin r
2 sin x + 6 cos x
The equation of the tangent line to y = f(x) at x = 0 can be written in the form y = = mx + b
where
and
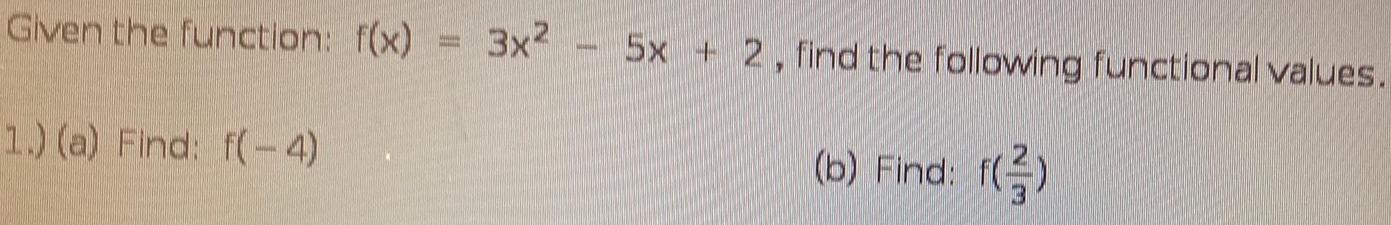
Calculus
DifferentiationGiven the function: f(x)
1.) (a) Find: f(-4)
11
-
3x²5x + 2, find the following functional values.
(b) Find: f(3)

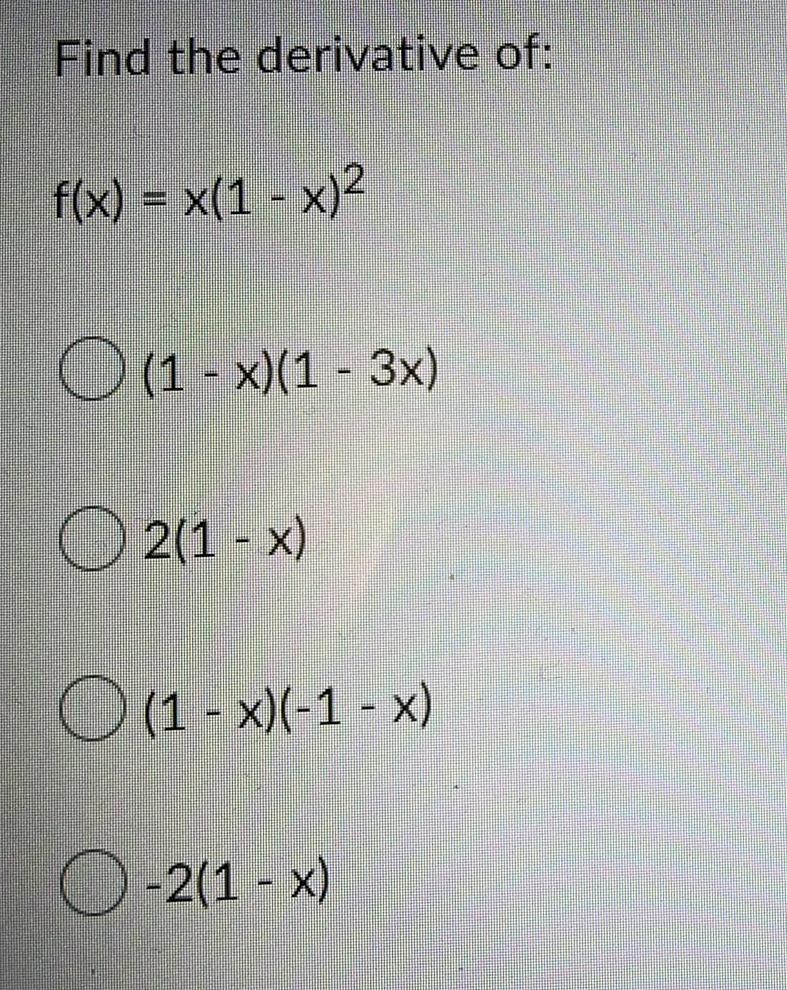
Calculus
DifferentiationFind the derivative of:
f(x) = x(1 - x)²
O (1 - x)(1 - 3x)
2(1-x)
O (1 - x)(-1 - x)
O-2 (1-x)

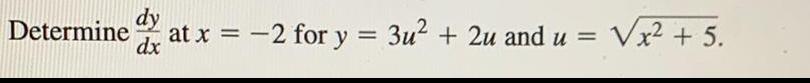

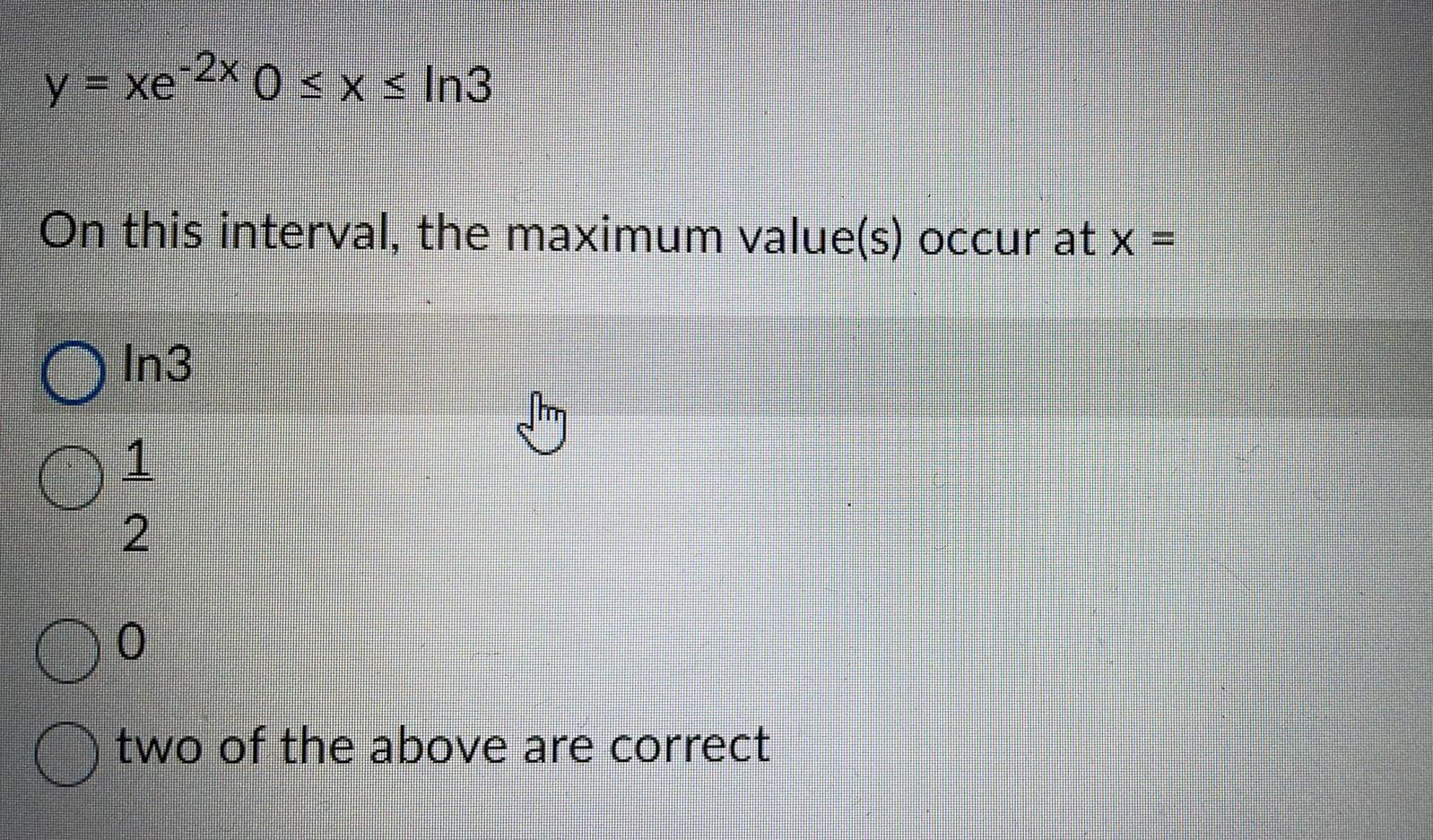
Calculus
Differentiationy = xe 2x 0 ≤ x ≤ In3
On this interval, the maximum value(s) occur at x =
In3
1
2
0
O two of the above are correct
Shy
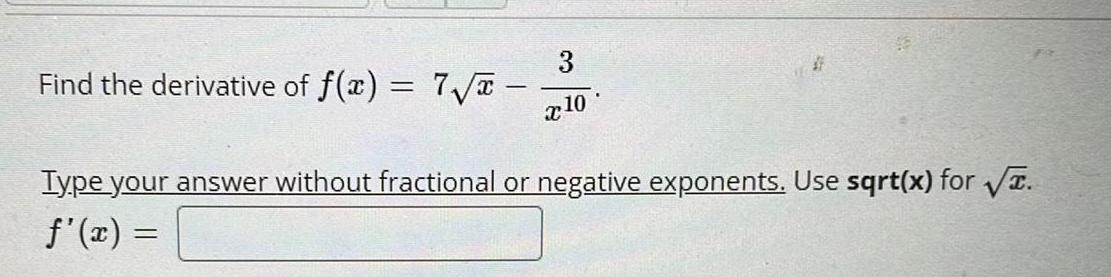
Calculus
DifferentiationFind the derivative of f(x) = 7√x
3
x10
#
Type your answer without fractional or negative exponents. Use sqrt(x) for √.
ƒ'(x) =



Calculus
DifferentiationIf f(x)= ex, which of the following lines is an asymptote to the graph of f?
Oy=x
Oy=0
Oy = -x
Oy=1
O x = 0
47
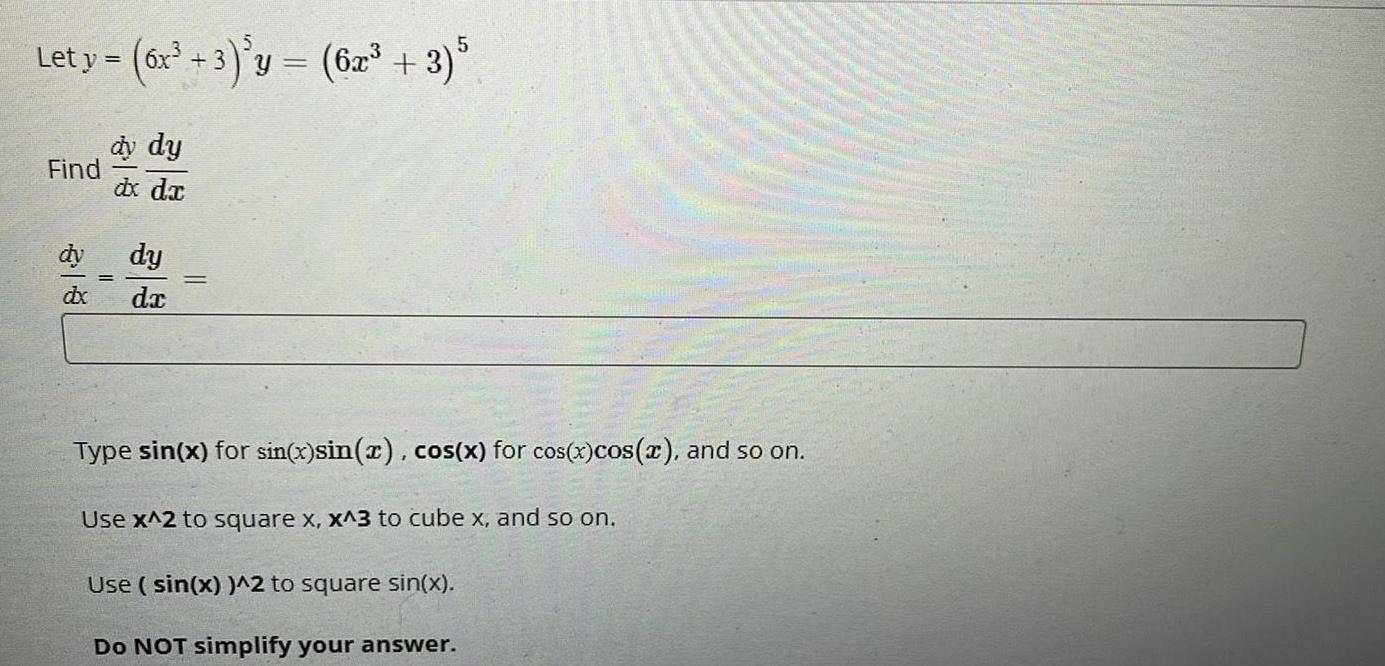
Calculus
Differentiationy = (6x³ + 3) ³y = (6x³ + 3) 5
Let y =
Find
dy
dx
dy dy
dx dx
dy
da
Type sin(x) for sin(x)sin(x), cos(x) for cos(x) cos(x), and so on.
Use x^2 to square x, x^3 to cube x, and so on.
Use (sin(x))^2 to square sin(x).
Do NOT simplify your answer.

Calculus
DifferentiationA cell culture contains 2 thousand cells, and is growing at a rate of r(t) = 6e0.00t thousand cells per hour.
Find the total cell count after 3 hours. Give your answer accurate to at least 2 decimal places.
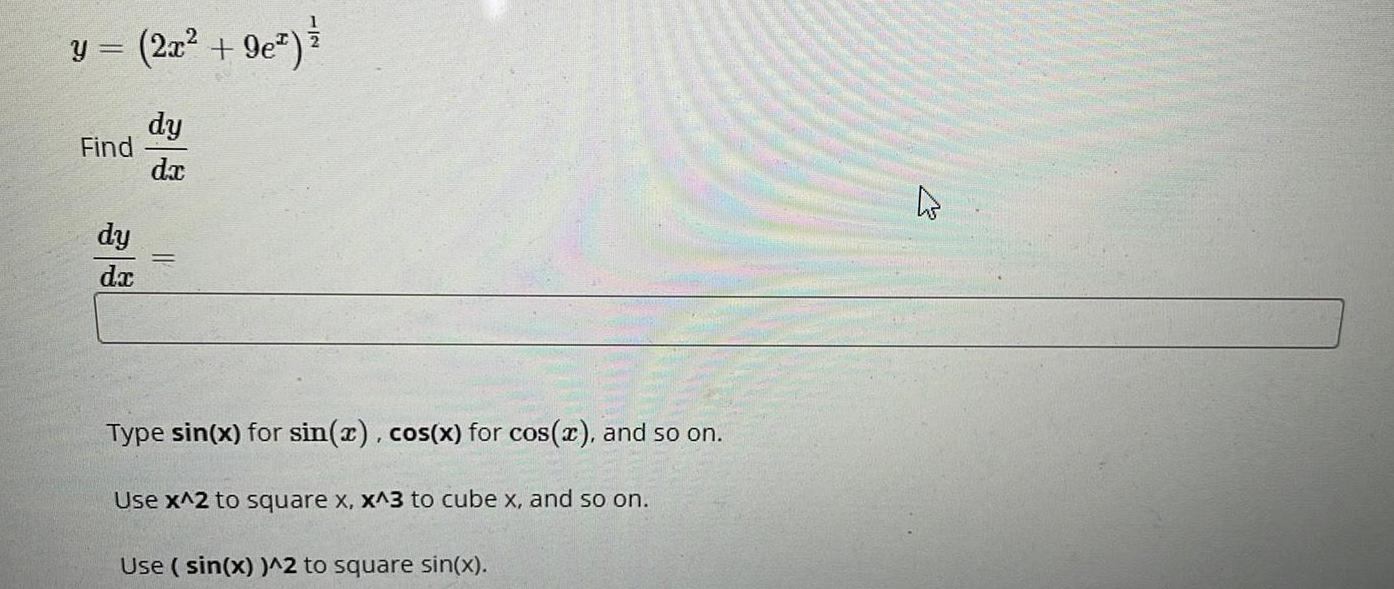
Calculus
Differentiationy =
Find
dy
dx
(2x² + 9e²) ²
dy
dx
Type sin(x) for sin(x), cos(x) for cos(x), and so on.
Use x^2 to square x, x^3 to cube x, and so on.
Use (sin(x))^2 to square sin(x).
A