Differentiation Questions and Answers
![ASK YOUR TEACHER
Determine whether the Mean Value theorem can be applied to f on the closed interval [a, b]. (Select all that apply.)
f(x) = 16x + 31, [-1,3]
Yes, the Mean Value Theorem can be applied.
No, because fis not continuous on the closed interval [a, b].
No, because fis not differentiable in the open interval (a, b).
None of the above.
If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such that f'(c) -
answers as a comma-separated list. If the Mean Value Theorem cannot be applied, enter NA.)
CH
PRACTICE ANO
f(b)-f(a)
b-a
(Enter your](https://media.kunduz.com/media/sug-question/raw/84128659-1660406734.0040545.jpeg?w=256)
Calculus
DifferentiationASK YOUR TEACHER
Determine whether the Mean Value theorem can be applied to f on the closed interval [a, b]. (Select all that apply.)
f(x) = 16x + 31, [-1,3]
Yes, the Mean Value Theorem can be applied.
No, because fis not continuous on the closed interval [a, b].
No, because fis not differentiable in the open interval (a, b).
None of the above.
If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such that f'(c) -
answers as a comma-separated list. If the Mean Value Theorem cannot be applied, enter NA.)
CH
PRACTICE ANO
f(b)-f(a)
b-a
(Enter your
Calculus
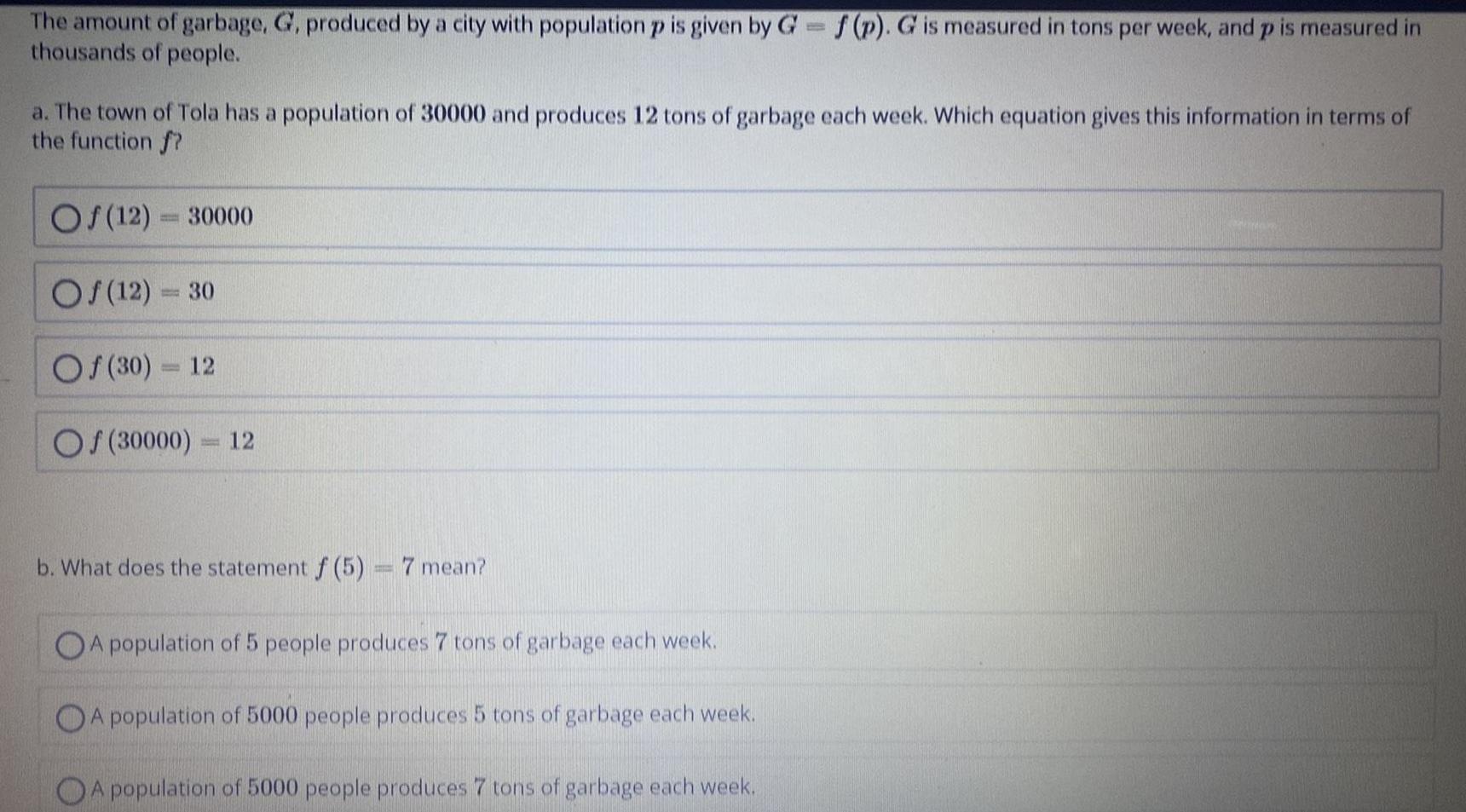
DifferentiationThe amount of garbage, G, produced by a city with population p is given by G = f(p). G is measured in tons per week, and p is measured in
thousands of people.
a. The town of Tola has a population of 30000 and produces 12 tons of garbage each week. Which equation gives this information in terms of
the function f?
Of(12)= 30000
Of (12)
Of (30) = 12
Of (30000) = 12
1
30
b. What does the statement f (5) = 7 mean?
A population of 5 people produces 7 tons of garbage each week.
A population of 5000 people produces 5 tons of garbage each week.
A population of 5000 people produces 7 tons of garbage each week.
![Find all values of 0 (in rad) that satisfy the equation over the interval [0, 2π].
sin(---)
sin(0) = sin
smaller value
larger value
8 =
0=
=
rad
rad](https://media.kunduz.com/media/sug-question/raw/84128309-1660406668.248196.jpeg?w=256)
Calculus
DifferentiationFind all values of 0 (in rad) that satisfy the equation over the interval [0, 2π].
sin(---)
sin(0) = sin
smaller value
larger value
8 =
0=
=
rad
rad
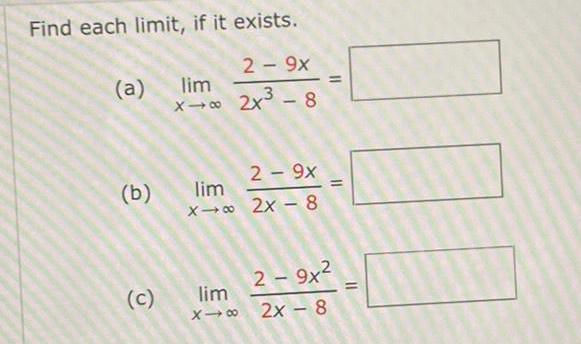
Calculus
DifferentiationFind each limit, if it exists.
2 - 9x
X-∞ 2x³-8
(a) lim
(b)
(c)
2 - 9x
lim
X- 2x - 8
=
11
2 - 9x²
lim
x18 2x - 8
11
Calculus
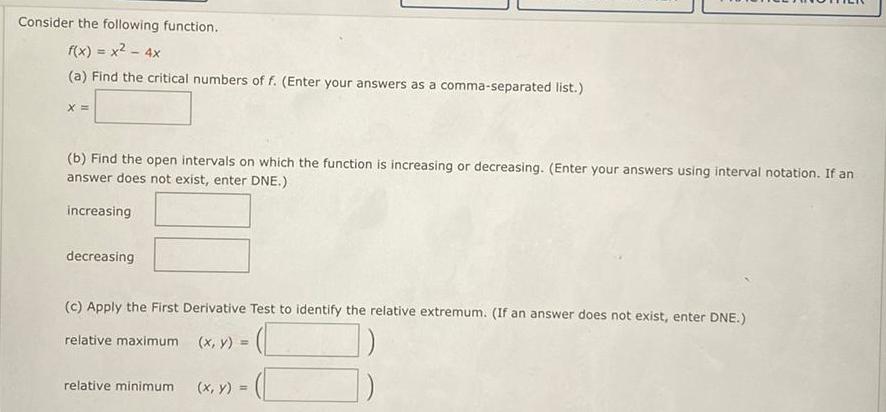
DifferentiationConsider the following function.
f(x) = x² - 4x
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
X=
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an
answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum
relative minimum (x, y) = =

Calculus
DifferentiationThis question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points
for the skipped part, and you will not be able to come back to the skipped part.
Tutorial Exercise
Identify the open intervals on which the function is increasing or decreasing.
g(x) = x² - 6x - 280
Step 1
To determine the intervals on which the function is increasing or decreasing, first find the critical numbers of the given
function.
Determine g'(x).
g(x) = x² - 6x - 280
g'(x)=2x-6
Step 2
To determine the critical numbers of g(x), set g'(x) equal to zero and solve for x.
g'(x) = 0
2(x-
2x-6=0
1)=0
2r-6
X =

Calculus
DifferentiationUse Newton's method with initial approximation x₁ = -1 to find x₂, the second approximation to the root of the equation x3 + x + 8 = 0. (Round your answer to four decimal place
X₂ =

Calculus
DifferentiationUse the Table of Integrals to evaluate the integral. (Use C for the constant of integration.)
" arctan(vx)
new window
√x
Calculus
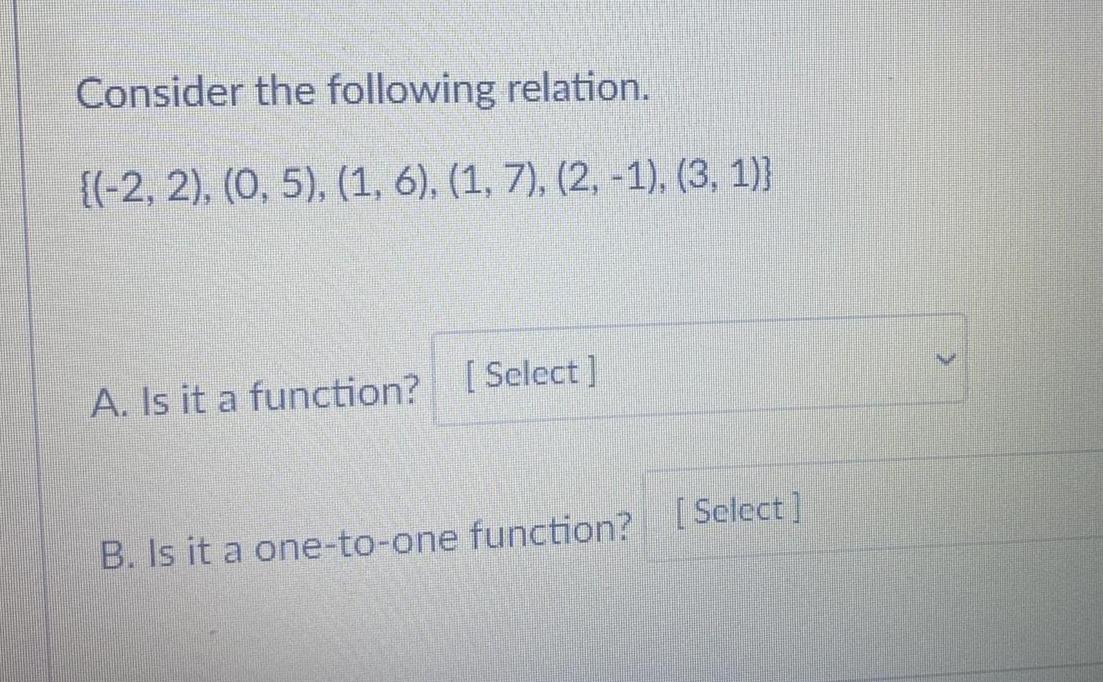
DifferentiationConsider the following relation.
{(-2, 2), (0, 5), (1, 6), (1, 7), (2, -1), (3, 1))
A. Is it a function?
B. Is it a one-to-one function?
![What is the amplitude of
y = cos x?
[?]](https://media.kunduz.com/media/sug-question/raw/84061044-1660326358.884958.jpeg?w=256)
![Let f be the function given by f(x)=x²-3x². What are all values of c that satisfy the conclusion
of the Mean Value Theorem of differential calculus on the closed interval [0,3]?
OA) 0 only
OB) 2 only
OC) 3 only
OD) 0 and 3
OE) 2 and 3](https://media.kunduz.com/media/sug-question/raw/84048051-1660326290.4685428.jpeg?w=256)
Calculus
DifferentiationLet f be the function given by f(x)=x²-3x². What are all values of c that satisfy the conclusion
of the Mean Value Theorem of differential calculus on the closed interval [0,3]?
OA) 0 only
OB) 2 only
OC) 3 only
OD) 0 and 3
OE) 2 and 3
![Let f be a function defined and continuous on the closed interval [a,b]. Iff has a relative
maximum at c and a<c<b, which of the following statements must be true?
I. f'(c) exists.
II. If f'(c) exists, then f'(c) = 0.
IH. If "(c) exists, then f"(c) ≤0.
OA) II only
B) III only
OC) I and II only
OD) I and III only
OE) II and III only](https://media.kunduz.com/media/sug-question/raw/84048139-1660326225.8961976.jpeg?w=256)
Calculus
DifferentiationLet f be a function defined and continuous on the closed interval [a,b]. Iff has a relative
maximum at c and a<c<b, which of the following statements must be true?
I. f'(c) exists.
II. If f'(c) exists, then f'(c) = 0.
IH. If "(c) exists, then f"(c) ≤0.
OA) II only
B) III only
OC) I and II only
OD) I and III only
OE) II and III only
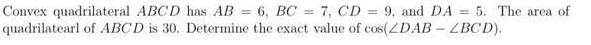
Calculus
DifferentiationConvex quadrilateral ABCD has AB = 6, BC = 7, CD = 9, and DA = 5. The area of
quadrilatearl of ABCD is 30. Determine the exact value of cos(ZDAB-ZBCD).


Calculus
DifferentiationUse a system of linear equations with two variables and two equations to solve. A moving company charges a flat rate of $80, and an
additional $5 for each box. A taxi service would charge $17 for each box. Write an equation to represent the cost, y dollars, of moving a
boxes with the taxi service.
Ret
Calculus
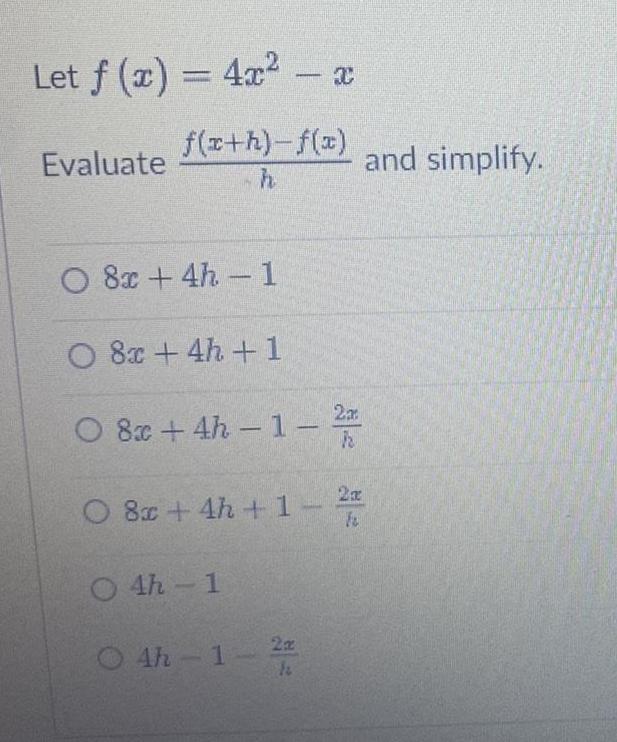
DifferentiationLet f (x) = 4x² - x
f(x+h)-f(x)
h
Evaluate
O 8x +4h-1
O 8x +4h+1
O 8x +4h-1-2
O 8x +4h+1
O4h-1
2x
04h-1-2/2
2x
and simplify.
![Let g(v) = v^14v
Use logarithmic differentiation to determine the derivative of g.
d/dv[g(v)]=
Determine the slope of g at v = 1.
g'(1) =](https://media.kunduz.com/media/sug-question/raw/83750550-1660323261.076566.jpeg?w=256)
Calculus
DifferentiationLet g(v) = v^14v
Use logarithmic differentiation to determine the derivative of g.
d/dv[g(v)]=
Determine the slope of g at v = 1.
g'(1) =
Calculus
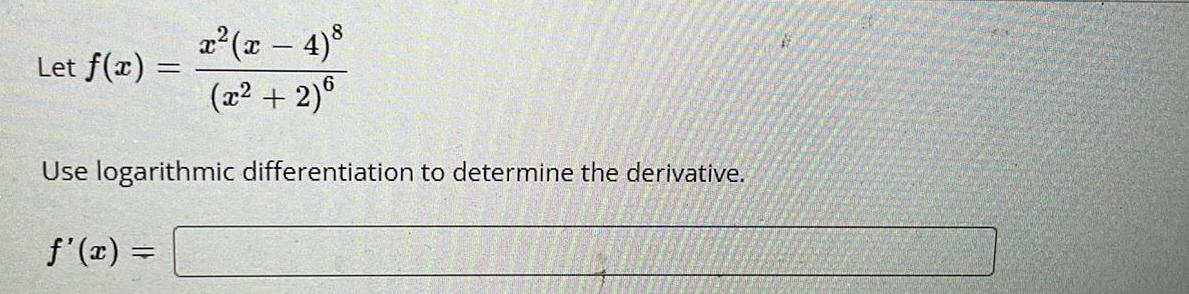
DifferentiationLet f(x)= x²(x − 4)^8/(x² + 2)^6
Use logarithmic differentiation to determine the derivative.
f'(x) =

Calculus
DifferentiationUse implicit differentiation to determine
dy
dx
dy
dx
given the equation a² + y² = − 3.
P

Calculus
DifferentiationA rocket is launched vertically upward with an initial velocity of 29 ft/sec. Its height h
in ft above the ground after t seconds can be represented by the following equation.
How many seconds will it take the rocket to hit the ground? Round to the nearest
hundredth.
h = - 16t² +29t+2
coconds
![(v + 3) (v + 7)
(v-7)(v-2)
Use logarithmic differentiation to determine the derivative of f.
Let f(v) =
dv
[f(v)]
=](https://media.kunduz.com/media/sug-question/raw/83748966-1660322374.328385.jpeg?w=256)
Calculus
Differentiation(v + 3) (v + 7)
(v-7)(v-2)
Use logarithmic differentiation to determine the derivative of f.
Let f(v) =
dv
[f(v)]
=
![Let g(y) = (y + 1)² (y + 3) (y — 9)³
Use logarithmic differentiation to determine the derivative of g.
Dy[g(y)]=](https://media.kunduz.com/media/sug-question/raw/83748934-1660322324.8952816.jpeg?w=256)
Calculus
DifferentiationLet g(y) = (y + 1)² (y + 3) (y — 9)³
Use logarithmic differentiation to determine the derivative of g.
Dy[g(y)]=
![9
u(u + 3) (u + 2)
Use logarithmic differentiation to determine the derivative of f.
d
du
Let f(u)
=
-[f(u)]
=](https://media.kunduz.com/media/sug-question/raw/83748941-1660322317.576676.jpeg?w=256)
Calculus
Differentiation9
u(u + 3) (u + 2)
Use logarithmic differentiation to determine the derivative of f.
d
du
Let f(u)
=
-[f(u)]
=

Calculus
DifferentiationConvert the
following equation
in
rectangular form to
polar form.
A. r sin 0 = 2
B. r cos 0 = 2
C. r = 2
x = 2
D. cos 0 = 2

Calculus
DifferentiationThe function f(x) =
is increasing on the open interval (
4x³ + 15x² + 435.12z - 6.05
It is decreasing on the open interval (-∞,
The function has a local maximum at
) and the open interval (
,00).
![Let h(w) = wln (15w)
Use logarithmic differentiation to determine the derivative of h.
Dw[h(w)]=
=](https://media.kunduz.com/media/sug-question/raw/83748925-1660322120.376579.jpeg?w=256)
Calculus
DifferentiationLet h(w) = wln (15w)
Use logarithmic differentiation to determine the derivative of h.
Dw[h(w)]=
=

Calculus
DifferentiationConsider the function f(z)-5-47², -5 ≤ ≤2
The absolute maximum value is
and this occurs at z =
The absolute minimum value is
and this occurs at x =

Calculus
DifferentiationSolve the rational equation and identify the solution set.
6
²-x-6
1
2-3-242
O a) {30}
20
Ob) {-2, 3}
000
d) {6}
Calculus
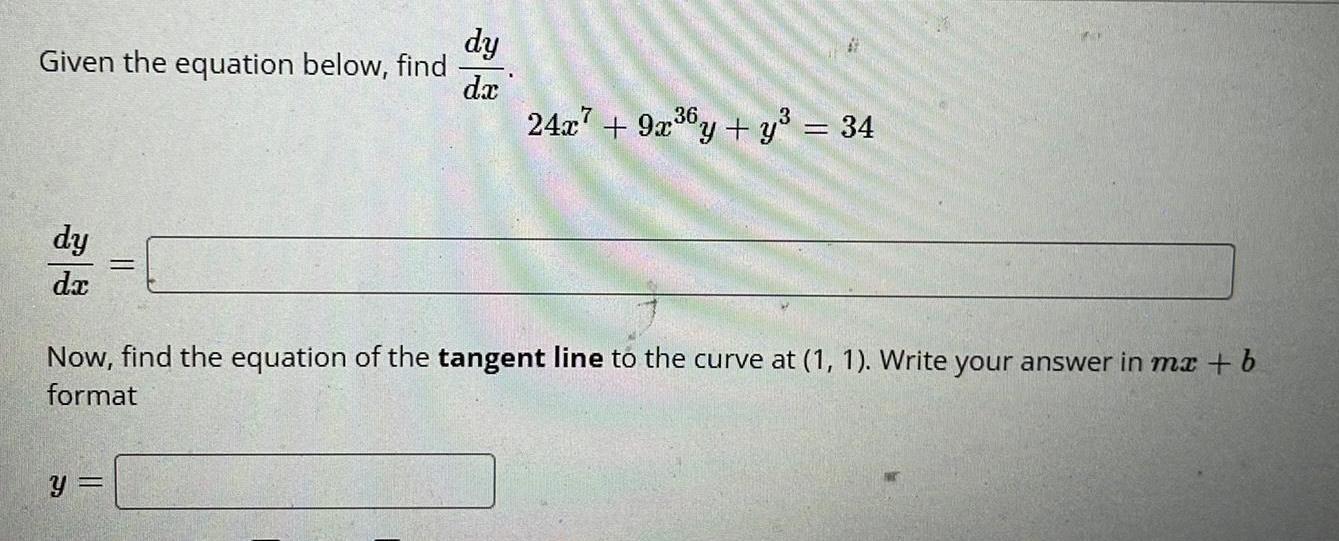
DifferentiationGiven the equation below, find
dy
dx
=
y =
dy
dx
24x7 + 9x³6y + y³ = 34
3
Now, find the equation of the tangent line to the curve at (1, 1). Write your answer in mx + b
format

Calculus
DifferentiationFind the critical numbers of the function f(x) =
using a graph.
I=
I=
I=
is a Select an answer V
is a Select an answer V
is a Select an answer
Question Help: Video Message instructor
125 75x+ 202³ + 2 and classify them
-
Calculus
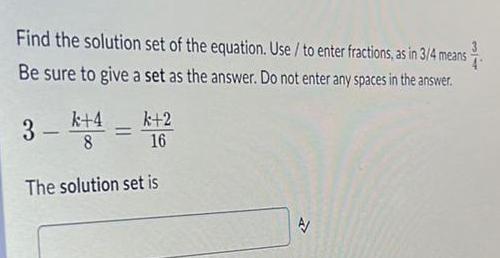
DifferentiationFind the solution set of the equation. Use / to enter fractions, as in 3/4 means $³/1.
Be sure to give a set as the answer. Do not enter any spaces in the answer.
k+4
k+2
16
The solution set is
N
![Let h(x) = (17x)
Use logarithmic differentiation to determine the derivative of h.
d
dx
- [h(x)] =
=
Determine the slope of h at x = 1.
h' (1) =
=](https://media.kunduz.com/media/sug-question/raw/83748908-1660321372.3713877.jpeg?w=256)
Calculus
DifferentiationLet h(x) = (17x)
Use logarithmic differentiation to determine the derivative of h.
d
dx
- [h(x)] =
=
Determine the slope of h at x = 1.
h' (1) =
=

![Let f(x) = xcot (22x)
Use logarithmic differentiation to determine the derivative of f.
d
dx
-[f(x)] =](https://media.kunduz.com/media/sug-question/raw/83748920-1660321264.7947042.jpeg?w=256)
Calculus
DifferentiationLet f(x) = xcot (22x)
Use logarithmic differentiation to determine the derivative of f.
d
dx
-[f(x)] =
![Let g(u) = 12"-2
Use logarithmic differentiation to determine the derivative of g.
Dulg(u)] =
Determine where g is differentiable.
g is differntiable on](https://media.kunduz.com/media/sug-question/raw/83748915-1660321226.1170845.jpeg?w=256)
Calculus
DifferentiationLet g(u) = 12"-2
Use logarithmic differentiation to determine the derivative of g.
Dulg(u)] =
Determine where g is differentiable.
g is differntiable on
![Let g(w) = 2ww-4
Use logarithmic differentiation to determine the derivative of g.
d
dw
-[g(w)] =
Determine where g is differentiable.
g is differntiable on](https://media.kunduz.com/media/sug-question/raw/83750556-1660321196.0728126.jpeg?w=256)
Calculus
DifferentiationLet g(w) = 2ww-4
Use logarithmic differentiation to determine the derivative of g.
d
dw
-[g(w)] =
Determine where g is differentiable.
g is differntiable on
![w (w - 7)8
(w8 - 4)8
Use logarithmic differentiation to determine the derivative of h.
Let h(w) =
Dw[h(w)] =](https://media.kunduz.com/media/sug-question/raw/83748948-1660321178.295003.jpeg?w=256)
Calculus
Differentiationw (w - 7)8
(w8 - 4)8
Use logarithmic differentiation to determine the derivative of h.
Let h(w) =
Dw[h(w)] =
![Let h(v) = 23v
Use logarithmic differentiation to determine the derivative of h.
d
- [h(v)]
dv
=
Determine the slope of h at v = 1.
h' (1) =
=](https://media.kunduz.com/media/sug-question/raw/83748900-1660321143.2870934.jpeg?w=256)
Calculus
DifferentiationLet h(v) = 23v
Use logarithmic differentiation to determine the derivative of h.
d
- [h(v)]
dv
=
Determine the slope of h at v = 1.
h' (1) =
=

Calculus
DifferentiationLet F(x) = f(1³) and G(x) = (f(x))³.
You also know that a = 9, f(a) = 3, f'(a) = 6, f'(a³) = 10
Then F'(a)
and G'(a) =
Question Help: Video Message instructor
=
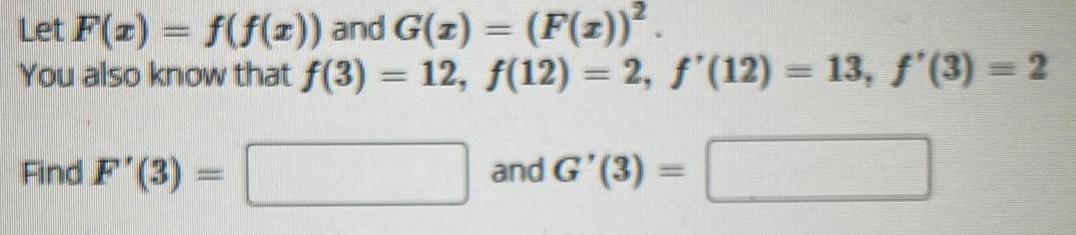
Calculus
DifferentiationLet F(x) = f(f(z)) and G(z) = (F(z))².
You also know that f(3) = 12, f(12) = 2, f'(12) = 13, f'(3) = 2
Find F'(3) -
and G'(3) =
![11v (v6 - 5)
√v + 10
Use logarithmic differentiation to determine the derivative of f.
Let f(v)
=
Dv[f(v)]
=](https://media.kunduz.com/media/sug-question/raw/83748963-1660320983.552929.jpeg?w=256)
Calculus
Differentiation11v (v6 - 5)
√v + 10
Use logarithmic differentiation to determine the derivative of f.
Let f(v)
=
Dv[f(v)]
=

Calculus
Differentiation19. Determine which line is perpendicular to the line 2x-3y + 17 = 0.
a. 7 = (1,2) + s(3,2), s e R
= $(3,2), SER
= (2,-3) +-8(3,-2), s & R
b.
7 = (1,7) + s(2,-3), s € R
C.
d.
![2
√z(z + 2)
Use logarithmic differentiation to determine the derivative of g.
Let g(z) =
=
Dz[g(z)]
=](https://media.kunduz.com/media/sug-question/raw/83748944-1660320722.7640562.jpeg?w=256)
Calculus
Differentiation2
√z(z + 2)
Use logarithmic differentiation to determine the derivative of g.
Let g(z) =
=
Dz[g(z)]
=
![Let h(z) = (z - 6)z-12+2
Use logarithmic differentiation to determine the derivative of h.
Dz[h(z)] =](https://media.kunduz.com/media/sug-question/raw/83748960-1660320718.2920363.jpeg?w=256)
Calculus
DifferentiationLet h(z) = (z - 6)z-12+2
Use logarithmic differentiation to determine the derivative of h.
Dz[h(z)] =
![Let f(w) = (w + 8) +9
Use logarithmic differentiation to determine the derivative of f.
d
dw
-[f(w)]
=
Determine where f is differentiable.
f is differntiable on](https://media.kunduz.com/media/sug-question/raw/83748911-1660320712.6334243.jpeg?w=256)
Calculus
DifferentiationLet f(w) = (w + 8) +9
Use logarithmic differentiation to determine the derivative of f.
d
dw
-[f(w)]
=
Determine where f is differentiable.
f is differntiable on

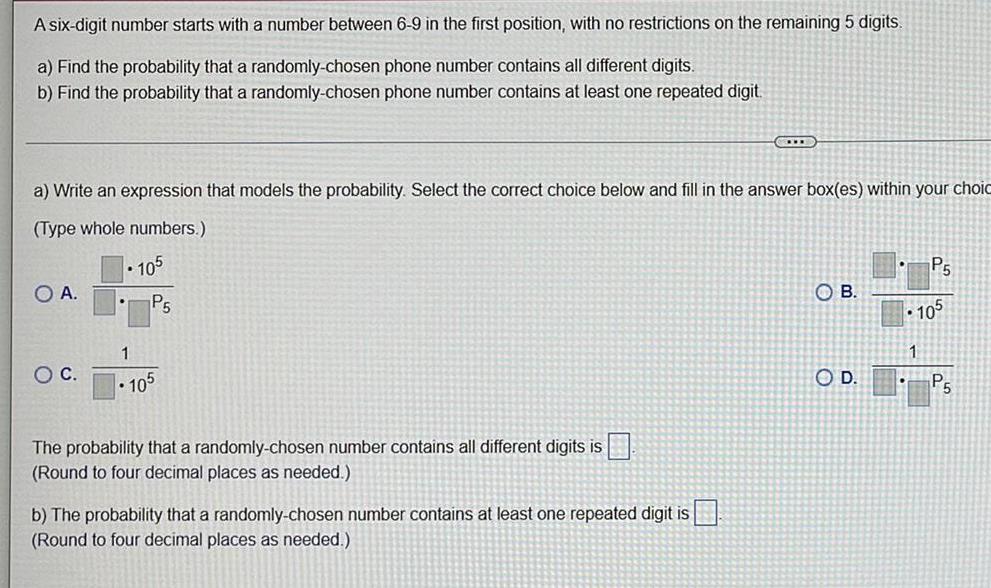
Calculus
DifferentiationA six-digit number starts with a number between 6-9 in the first position, with no restrictions on the remaining 5 digits.
a) Find the probability that a randomly-chosen phone number contains all different digits.
b) Find the probability that a randomly-chosen phone number contains at least one repeated digit.
a) Write an expression that models the probability. Select the correct choice below and fill in the answer box(es) within your choic
(Type whole numbers.)
O A.
O C.
•105
P5
1
• 105
The probability that a randomly-chosen number contains all different digits is.
(Round to four decimal places as needed.)
CELLE
b) The probability that a randomly-chosen number contains at least one repeated digit is
(Round to four decimal places as needed.)
OB.
O D.
.
P5
105
1
P5

Calculus
DifferentiationUse implicit differentiation to find given the equation sin(xy) = y².
dy
dx
dy
dx
=

Calculus
DifferentiationThe displacement (in meters) of a particle moving in a straight line is given by the equation of motion s=-
8
where t is measured in seconds. Find the velocity (in m/s) of the particle at times t = a, t= 1, t=2, and t = 3.
2'
t=a
t=1
t=2
t = 3
V =
V =
V =
V=
m/s
m/s
m/s
m/s