Differentiation Questions and Answers
![Continue to go with f[x] = Log[x] So that f'[x]=1/x
But this time come up with a small h so that f[x+h] - f[x]/h
calculates f'[x] to at least four accurate decimals for all the x 's with 0.25 ≤x≤2.5.](https://media.kunduz.com/media/sug-question/raw/82028039-1660068715.953645.jpeg?w=256)
Calculus
DifferentiationContinue to go with f[x] = Log[x] So that f'[x]=1/x
But this time come up with a small h so that f[x+h] - f[x]/h
calculates f'[x] to at least four accurate decimals for all the x 's with 0.25 ≤x≤2.5.
![Let ƒ(u) = log₈ (u⁶)
Determine Du[f(u)]
Du[f(u)]-______](https://media.kunduz.com/media/sug-question/raw/82027644-1660068379.705913.jpeg?w=256)
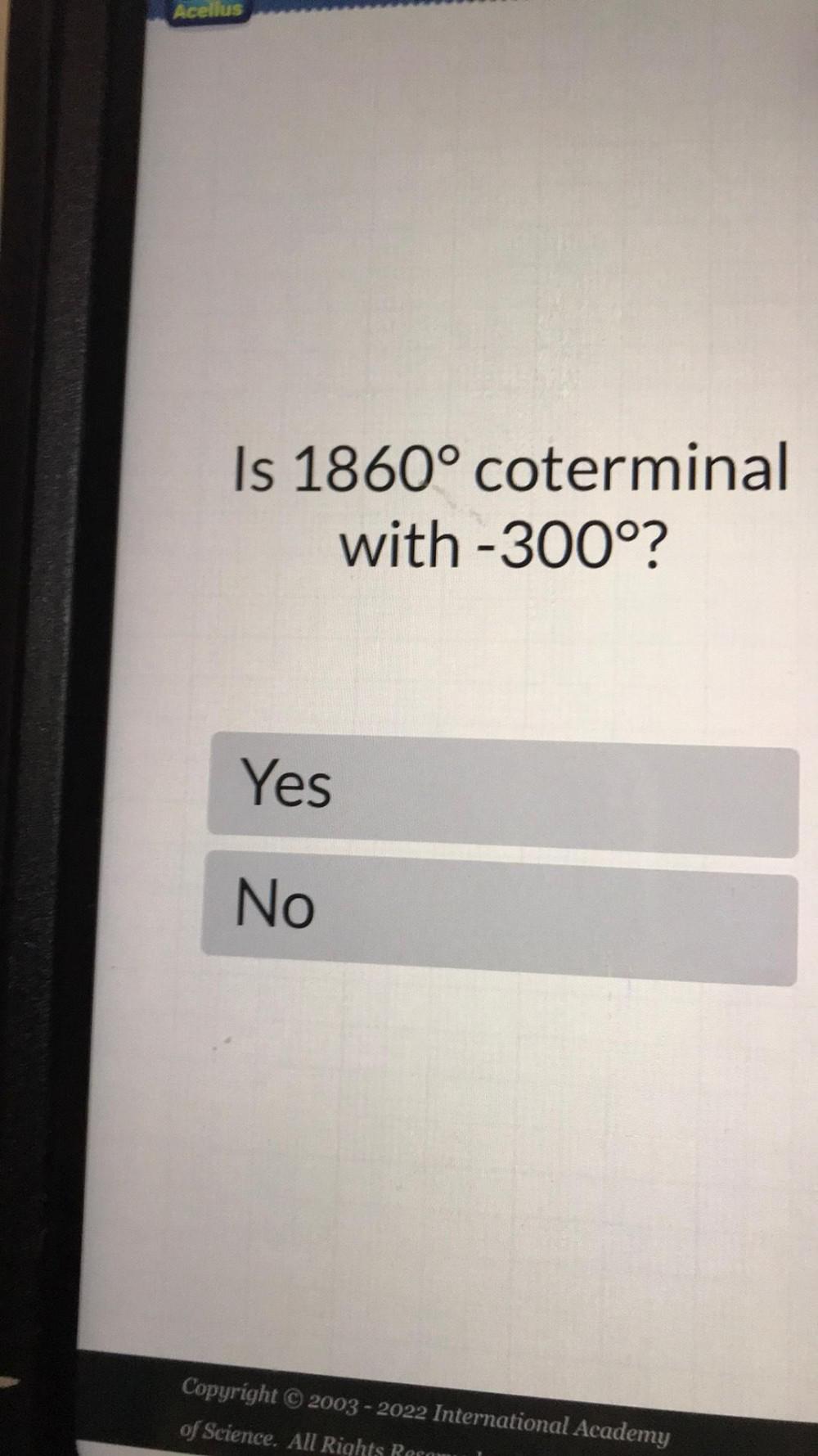

Calculus
DifferentiationFind the first three non-zero terms of the Taylor series about 0 for the func-tion
y(x)=√1+2x².sin(3x)
by multiplying the Taylor series for √1+ 2x² and the Taylor series for sin (3x).

Calculus
Differentiation. Walter drives 7 mph over the speed limit on a suburban street. In the time that Walter drives 4 miles, a car driving the posted speed limit could drive 3 1/3 miles. What is the speed limit and how fast is Walter driving?

Calculus
DifferentiationCreate a real-world situation involving bearing angles (pages 633-635), where the solution would
require the use of either the Law of Sines or the Law of Cosines. Include a description of the real-
world problem as well as what needs to be determined. (10pts)
Be sure to solve the problem before posting to make sure it's solvable. Don't include your analysis in
your post. Keep this work for later in the discussion and to respond to your classmates.

Calculus
DifferentiationState the domain and range for y = sin x, y = cos x, y = tan x. Why is it so important to restrict each of these domains to be one-to-one? State the restricted domain and the range for each of these functions. Beside each restriction sketch a drawing of the new function
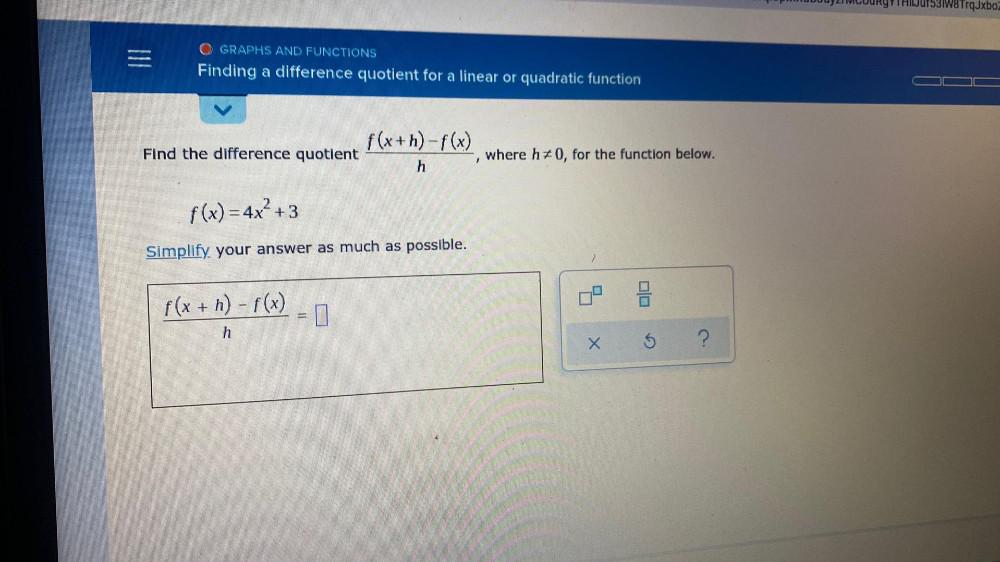
Calculus
DifferentiationFind the difference quotient f(x+h)-f(x)/h, where h ≠ 0, for the function below.
f(x) = 4x² +3 Simplify your answer as much as possible.
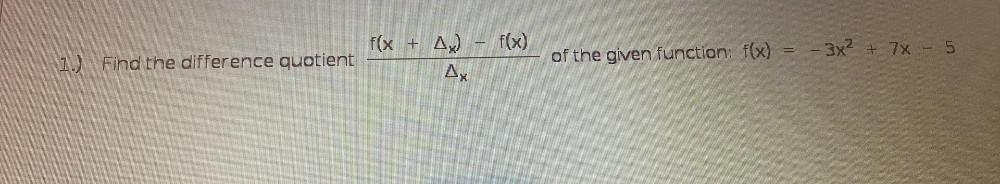
Calculus
DifferentiationFind the difference quotient f(x+△_x) - f(x)/△_x of the given function: f(x) = - 3x² + 7x-5

Calculus
DifferentiationIf you want to calculate your take-home pay you will need to determine the amount of taxes that will be taken out of your paycheck. To do this, you will:
a) Subtract your gross income by your net pay.
b) Multiply your net income by the number of taxes. Then subtract that amount to find your net pay.
c) Multiply your gross income by the percent of taxes. Then subtract that amount to find your net pay.

Calculus
DifferentiationSuppose the cost, in dollars, of manufacturing x items is approximated by the function C(x) = 0.2x²+5x+500, for 1≤x≤1000. If the cost of manufacturing one item can be represented by the function U(x)=c(x)/x determine how many items should be manufactured to minimize the unit cost.
a) 50
b) 1000
c) 13
d) 500

Calculus
DifferentiationObtain the derivative dy/dx.
y = 6x-¹-5x - 10
dy/dx=___
State the rules that you use. (Select all that apply.)
O power rule
O difference rule
O constant multiple rule
O sum rule
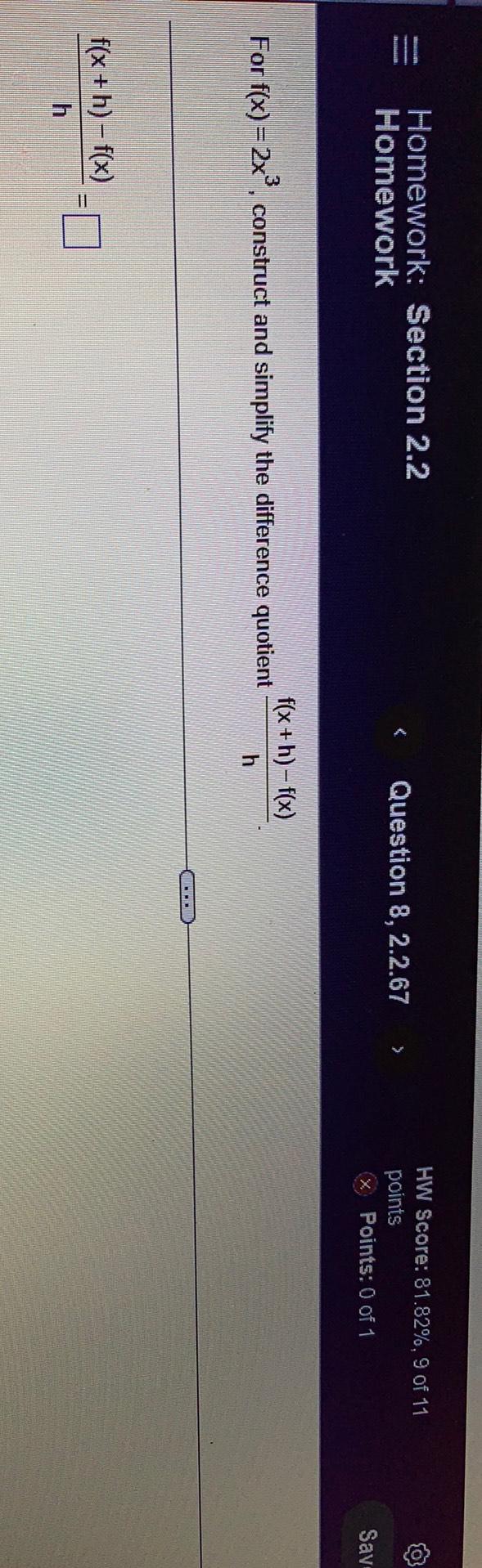
Calculus
DifferentiationFor f(x) = 2x³, construct and simplify the difference quotient f(x+h)-f(x)/h
f(x+h)-f(x)/h =

Calculus
DifferentiationSuppose f(x) = 4" and g(x) = -3x - 2. Find a simplified formula for the function:
k(x) = g(f(x)²)

Calculus
DifferentiationA hot brick is removed from a kiln at 225°C above room temperature. Over time, the brick cools off. After 2 hours have elapsed, the brick is 30° C above room temperature. Let t be the time in hours since the brick was removed from the kiln. Let y = H(t) be the difference between the brick's and the room's temperature at time t. Assume that H(t) is an exponential function.
How much time elapses before the brick's temperature is 10°C above room temperature? Round your answer to 2 places after the decimal.
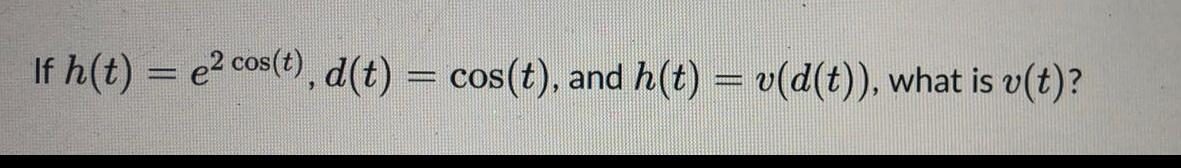

Calculus
DifferentiationLet f(a) = [² (7t³ - 9t4+t3+6t²) dt
x
Determine the fourth derivative of f.
d4f/dx4_______
Calculus
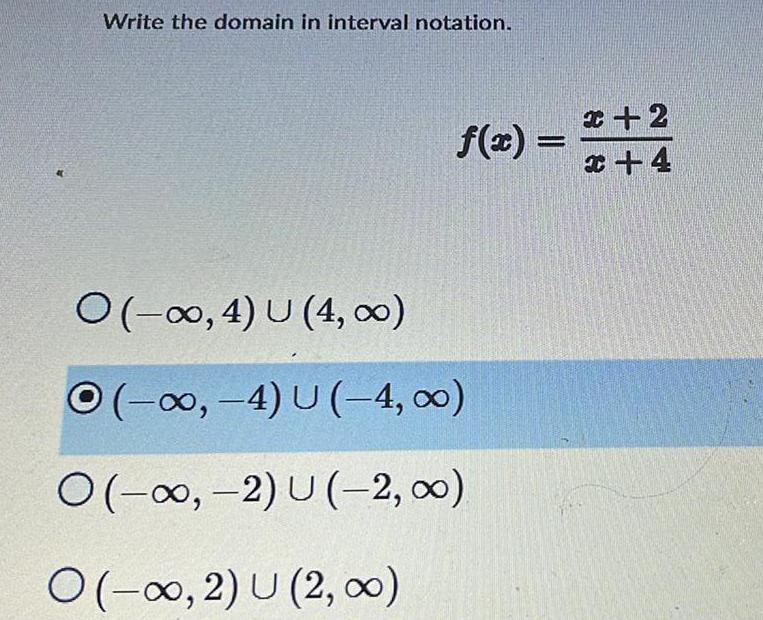
DifferentiationWrite the domain in interval notation.
f(x) =X+2/X+4
(-∞, 4) U (4,00)
(-∞, -4) U (-4,00)
(-∞, -2) U (-2, 0)
(-∞, 2) U (2, ∞)
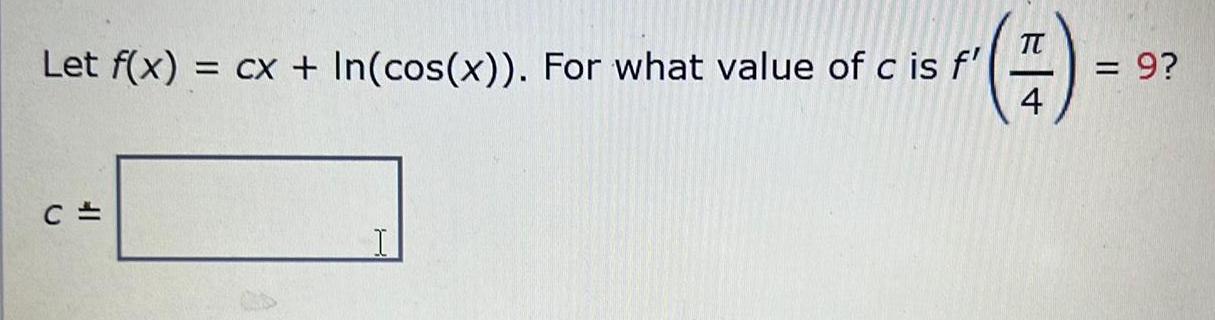

Calculus
DifferentiationFind the second-order partial derivatives of the function. Show that the mixed partial derivatives f and fx are equal.
f(x, y) = 3x√y + 3y√x
Calculus
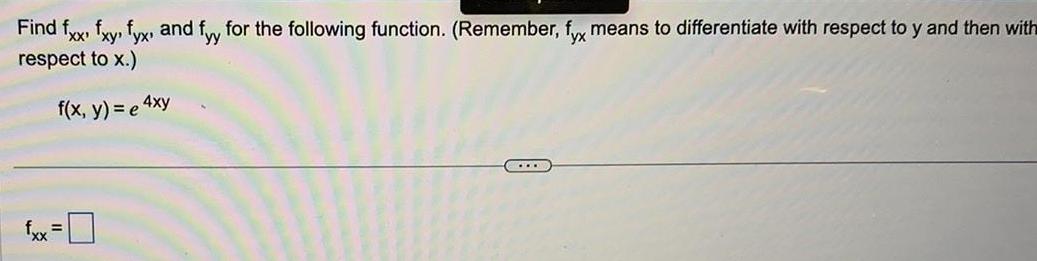
DifferentiationFind fxx fxy, fyx,fand yy for the following function. (Remember, fyx means to differentiate with respect to y and then with respect to x.)
f(x, y) = e^4xy
fxx =
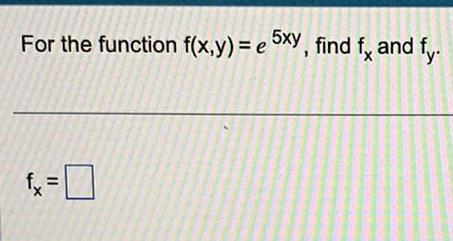


Calculus
DifferentiationFind dy/dx by implicit differentiation.
x² + 5x+9xy-²-4
dy/dx= 2x-5+9y/2y-9x
dy/dx= 2x+5+9y/2x-9y
dy/dx=x+5+9y/y-9x
dy/dx=2x+5+9y/2y-9x
dy/dx=2x+5-9y/2y-9x
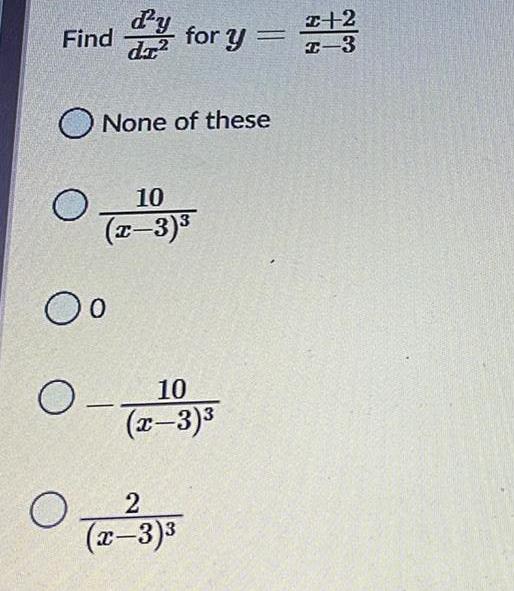

Calculus
DifferentiationFind the open interval(s) on which f(x) = -2x² + 12x+8 is increasing or decreasing.
increasing on (→∞,6); decreasing on (6,∞)
increasing on (-∞,16); decreasing on (16,∞)
increasing on (-∞, 32); decreasing on (32,∞)
increasing on (-∞, 24); decreasing on (24,∞)
increasing on (-∞,3); decreasing on (3,∞)

Calculus
DifferentiationDifferentiate: y = sec²x + tan² x
sec²x (sec²x + tan² x)
tan + sec4x
2(secx + tanx)
4sec²x tan x
sec4x + tan² x

Calculus
DifferentiationFind the derivative of the function f(x) = x5-9/x4
f'(x) = 1+36/x5
f'(x)- 1-36/x5
f'(x) = 1 + 4/x5
f'(x) = 1-9x5
f'(x) = 1 + 9/x5
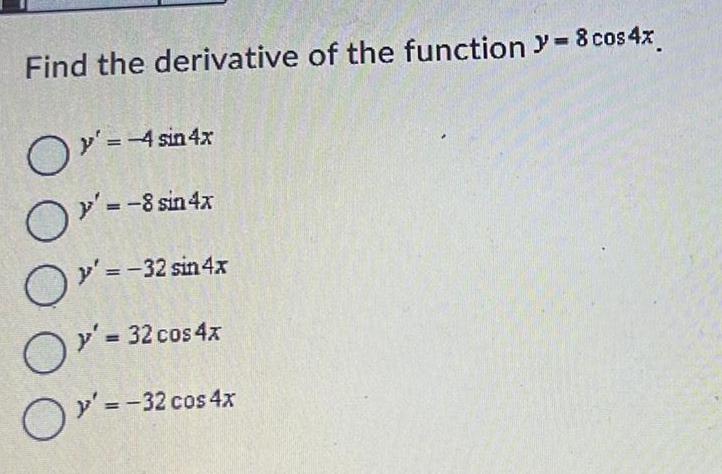
Calculus
DifferentiationFind the derivative of the function = 8 cos 4x
y' = -4 sin 4x
y' = -8 sin 4x
y' = −32 sin 4x
y² = 32 cos 4x
y' = -32 cos 4x

![For the function
y = ln x
on the interval [1, 5], find the number guaranteed by the Mean Value Theorem.
x = [?]](https://media.kunduz.com/media/sug-question/raw/84687675-1659176399.2460718.jpeg?w=256)
Calculus
DifferentiationFor the function
y = ln x
on the interval [1, 5], find the number guaranteed by the Mean Value Theorem.
x = [?]

Calculus
DifferentiationGiven g(x, y) = x² + 3xy + 2y²
I. Find the domain of the function.
II. Evaluate g(2, -1)
III. Find ALL second partial derivatives.

Calculus
DifferentiationFind dy/dx using partial derivatives, given that
x² - 2xy + y² = 4.
Hint: Use the Implicit Function Theorem which uses partial derivatives to find dy/dx
![Show all work and explain your reasoning to write a formula for a trigonometric function that has the following characteristics:
a) The domain is (-∞, ∞) and the range is [-2, 6].
b) The period is 2π/5
c) f(0) = 2](https://media.kunduz.com/media/sug-question/raw/84686816-1659176209.6518636.jpeg?w=256)
Calculus
DifferentiationShow all work and explain your reasoning to write a formula for a trigonometric function that has the following characteristics:
a) The domain is (-∞, ∞) and the range is [-2, 6].
b) The period is 2π/5
c) f(0) = 2
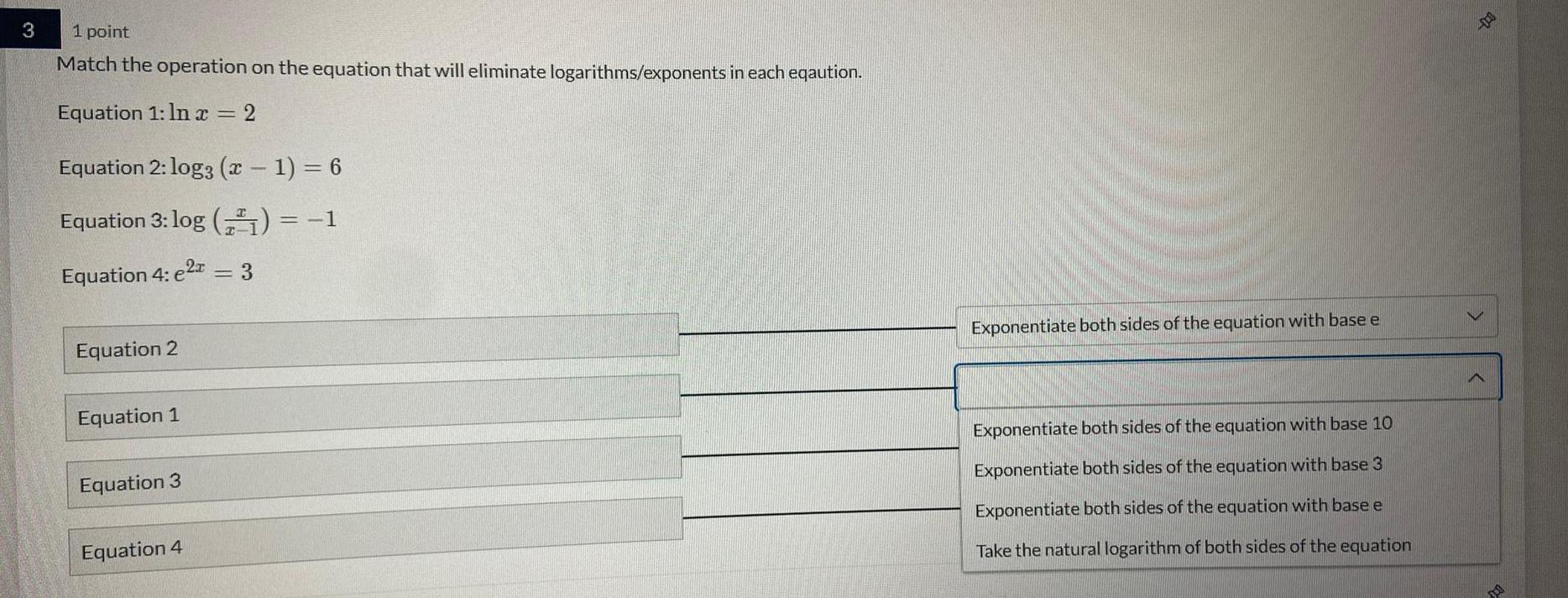
Calculus
DifferentiationMatch the operation on the equation that will eliminate logarithms/exponents in each eqaution.
Equation 1: In x = 2
Equation 2: log3 (x − 1) = 6
Equation 3: log (x x - 1) = -1
Equation 4: e2x = 3
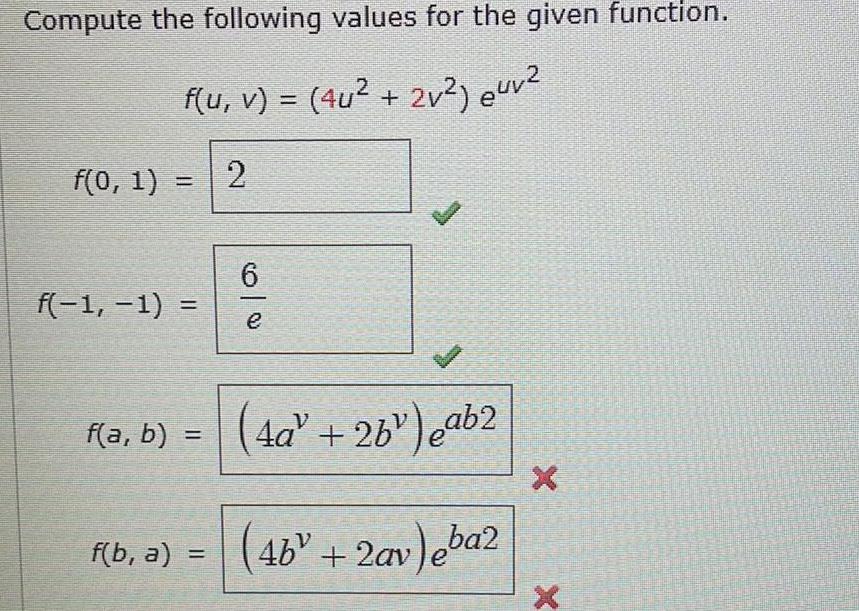
Calculus
DifferentiationCompute the following values for the given function.
f(u, v) = (4u² + 2v²) e^uv^2
f(0, 1) =
f(−1, − 1) =
f(a, b) =
f(b, a) =

Calculus
DifferentiationFind the second-order partial derivatives of the function. Show that the mixed partial derivatives fxy and fyx equal.
f(x, y) = x² + x²y² + y² + x + y

Calculus
DifferentiationGive the first five terms of the sequence.
a₁ = -34, an = (6 + an−1)(1/2)n
Give your answers as fractions; do not round.

Calculus
DifferentiationFor the given geometric sequence, find r and write an explicit formula for an.
a = {5, 40, 320, 2560,... }
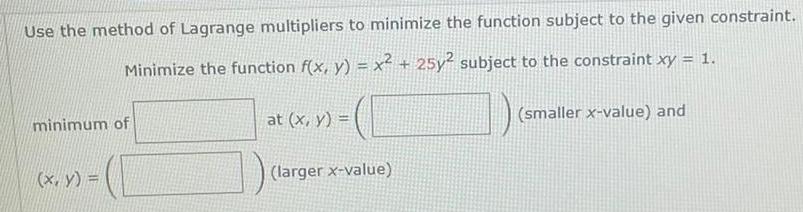
Calculus
DifferentiationUse the method of Lagrange multipliers to minimize the function subject to the given constraint.
Minimize the function f(x, y) = x² + 25y² subject to the constraint xy = 1.
minimum of at (x, y) = (smaller x-value) and (x, y) = (larger x-value)
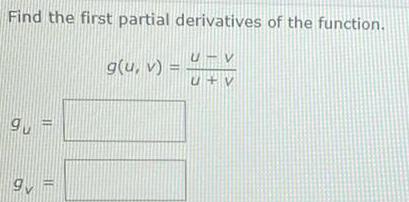
Calculus
DifferentiationFind the first partial derivatives of the function.
g(u, v) = u - v
u +v
gu =
gv =

Calculus
DifferentiationLuis goes out to lunch. The bill, before tax and tip, was $13.65. A sales tax of 8% was added on. Luis tipped 16% on the amount after the sales tax was added. How much was the sales tax? Round to the nearest cent.
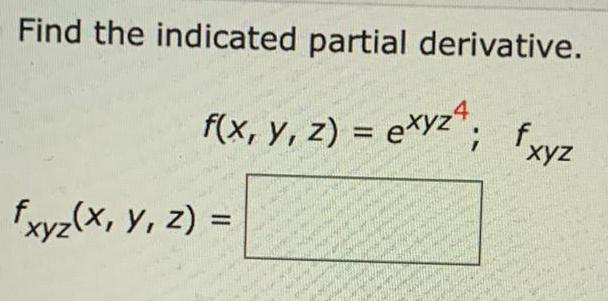
Calculus
DifferentiationFind the indicated partial derivative.
f(x, y, z) = exyz4; fxyz
fxyz(x, y, z) =




Calculus
DifferentiationSuppose h(t) = 3t+5 t and k(t) = 5 t - 3. Show that h(t) and k(t) are inverse functions using algebra.

Calculus
DifferentiationA cook needs 3 cups of vegetable stock for a soup recipe. How much is this in pints? Write your answer as a whole number or a mixed number in simplest form. Include the correct unit in your answer.

Calculus
DifferentiationPlease state the definition of the kth Taylor polynomial, p(x), for f(x) at x = a. Please also include the definition using summation notation.

Calculus
DifferentiationGiven f(x, y) = -5x5 - xy² + 5y^6, find
fxx(x, y) =
fxy(x, y) =
fyy (x, y) =
fyz(x, y) =