Differentiation Questions and Answers

Calculus
DifferentiationGiven the function p(x)={-5x-7 x<0
3x^2-2x-8 x≥0
Calculate the following values:
p(7)
p(4)
p(0)
p(-8)

Calculus
DifferentiationA common inhabitant of human intestines is the bacterium Escherichia coli, named after the German pediatrician Theodor Escherich, who identified it in 1885. A cell of this bacterium in a nutrient-broth medium divides into two cells every 20 minutes. The initial population of a culture is 50 cells.
(a) Find the relative growth rate.
k =
(b) Find an expression for the number of cells after t hours.
P(t) =
(c) Find the number of cells after 8 hours.
(d) Find the rate of growth after 8 hours. (Round your answer to the nearest integer.)
cells/h
(e) When will the population reach a million cells? (Round your answer to two decimal places.)

Calculus
DifferentiationSuppose f(x) = 2x²-3x. Find a simplified formula for the difference quotient
f(x+h)-f(x)/h
Calculus
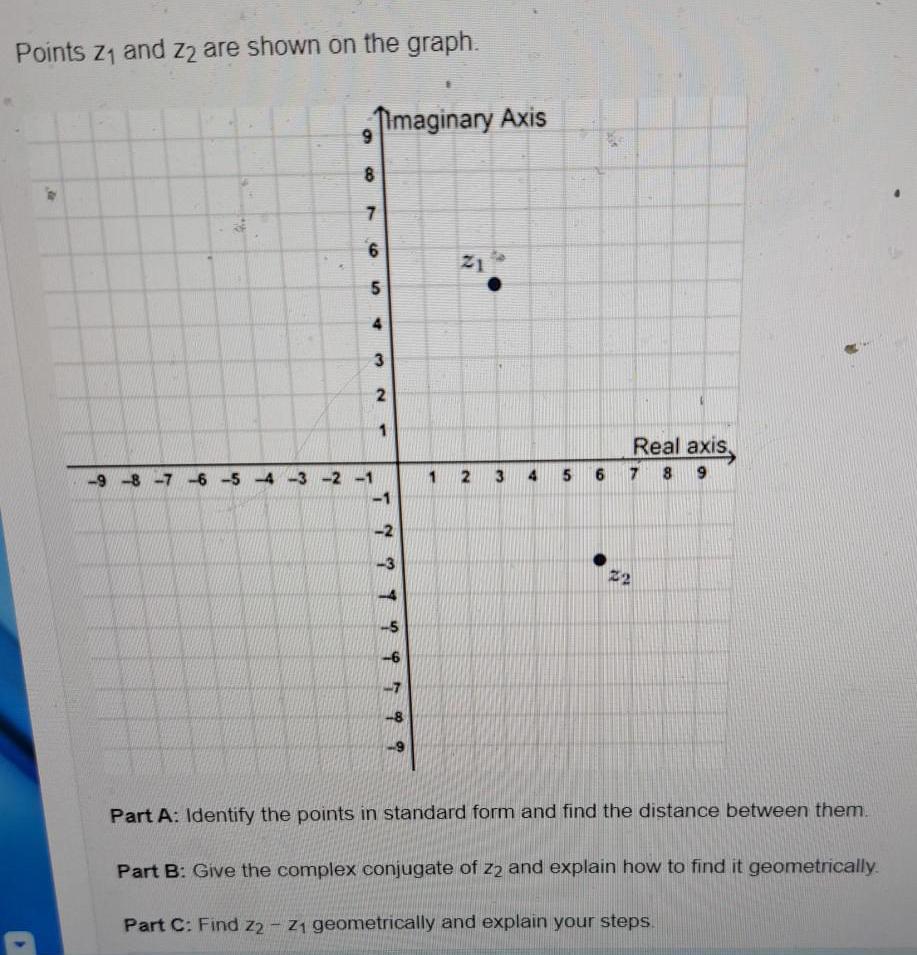
DifferentiationPoints z₁ and z2 are shown on the graph.
Part A: Identify the points in standard form and find the distance between them.
Part B: Give the complex conjugate of z2 and explain how to find it geometrically.
Part C: Find z2-z1 geometrically and explain your steps.
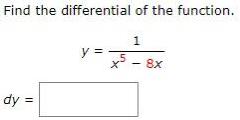

Calculus
DifferentiationYou invested $6000 between two accounts paying 2% and 9% annual interest, respectively. If the total interest earned for the year was $470, how much was invested at each rate?

Calculus
DifferentiationFind fx, fy, fx(2,-5), and fy(4,6) for the following equation.
f(x,y)=√(x² +y²)
fx=
(Type an exact answer, using radicals as needed.)
fy=
(Type an exact answer, using radicals as needed.)
fx(2,-5) =
(Type an exact answer, using radicals as needed.)
fy(4,6)=
(Type an exact answer, using radicals as needed.)

Calculus
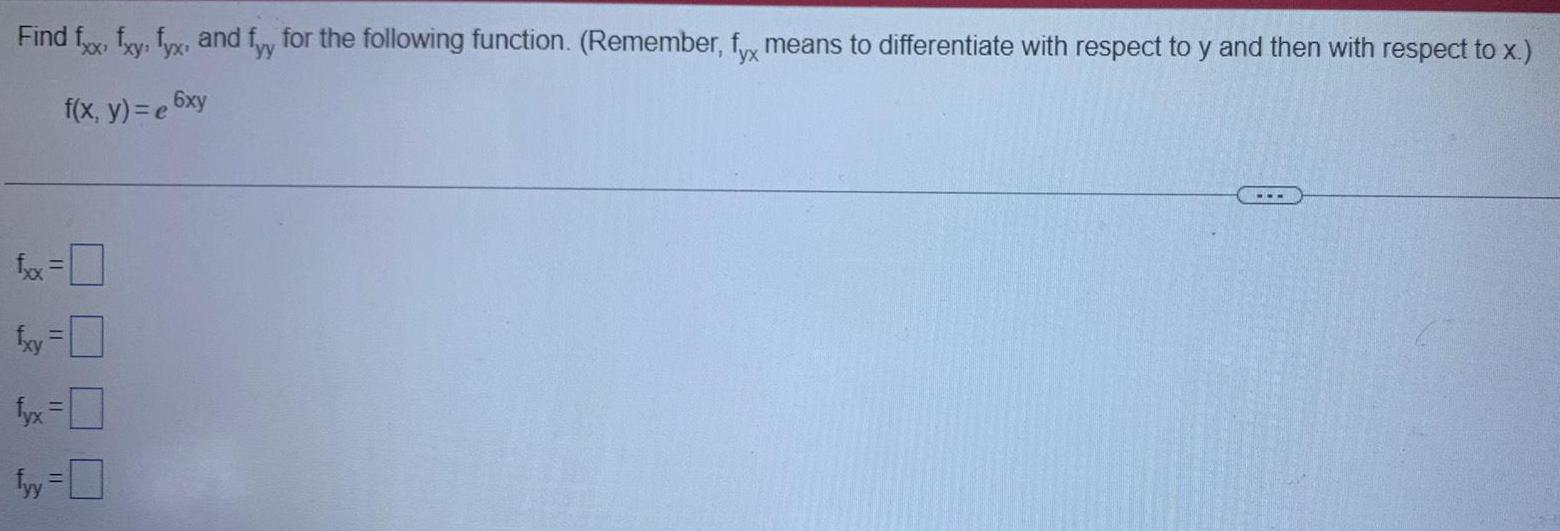
DifferentiationFind fxx, fxy, fyx, and fry for the following function. (Remember, fx means to differentiate with respect to y and then with respect to x.)
f(x, y) = e^6xy
fxx=
fxy =
fyx=
fyy=

Calculus
DifferentiationSolve the following system of equations using Gaussian elimination or Gauss-Jordan elimination.
8x - y + 2z = 11
2x + y - z = -3
- 6x + y + 2z = 2
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The solution is ()
(Type integers or simplified fractions.)
B. There are infinitely many solutions of the form (z)
(Type expressions using z as the variable.)
C. There is no solution.

Calculus
DifferentiationConsider the following.
7x² - y³ = 6
(a) Find y' by implicit differentiation.
y' =
(b) Solve the equation explicitly for y and differentiate to get y' in terms of x.
y' =
Calculus
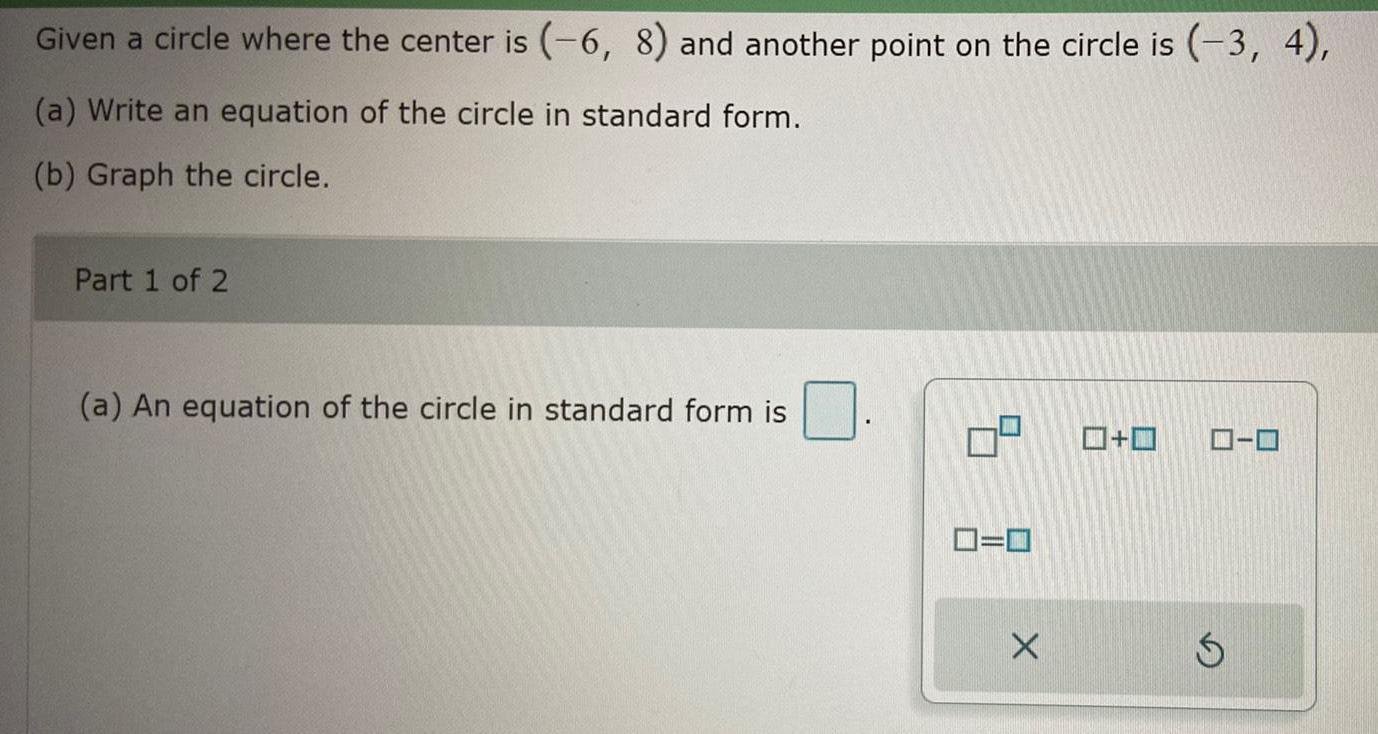
DifferentiationGiven a circle where the center is (-6, 8) and another point on the circle is (-3, 4),
(a) Write an equation of the circle in standard form.
(b) Graph the circle.
Part 1 of 2
(a) An equation of the circle in standard form is
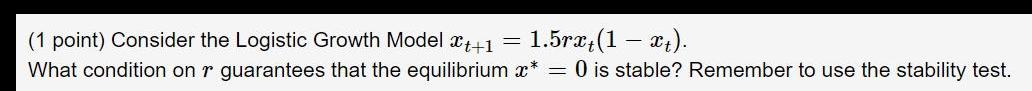
Calculus
DifferentiationConsider the Logistic Growth Model xt+1 = 1.5rxt(1 - xt).
What condition on r guarantees that the equilibrium x* = 0 is stable? Remember to use the stability test.

Calculus
DifferentiationLet f'''(x) = 8
Find the particular solution to the above differential equation that satisfies the following initial conditions.
f has a horizontal tangent line at (3, 7).
f' has a horizontal tangent line at x = 9.

Calculus
DifferentiationA canyon is 1966 meters deep at its deepest point. Suppose a rock is dropped from the rim of the canyon above this point. Determine the time required for the rock to hit the canyon floor. Round the solution to the nearest hundredth, if necessary.


Calculus
DifferentiationLet f''(z) =7/x^3
Find the particular solution to the above differential equation that satisfies the following initial conditions.
• f'(-3)=3
• f(-1) = -1
f(z) =
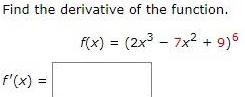
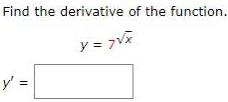
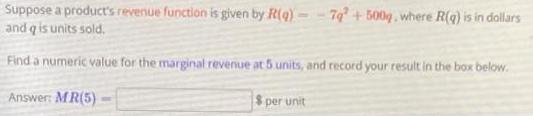
Calculus
DifferentiationSuppose a product's revenue function is given by R(q)=-7q+500g, where R(q) is in dollars
and q is units sold.
Find a numeric value for the marginal revenue at 5 units, and record your result in the box below.
Answer: MR(5).
per unit


Calculus
DifferentiationA graphing calculator is recommended.
Use Newton's method to find all solutions of the equation correct to eight decimal places. Start by looking at a graph to find initial approximations. (Enter your answers as a comma-separated list.)
-3x7 - 4x4 + 9x³ + 9 = 0
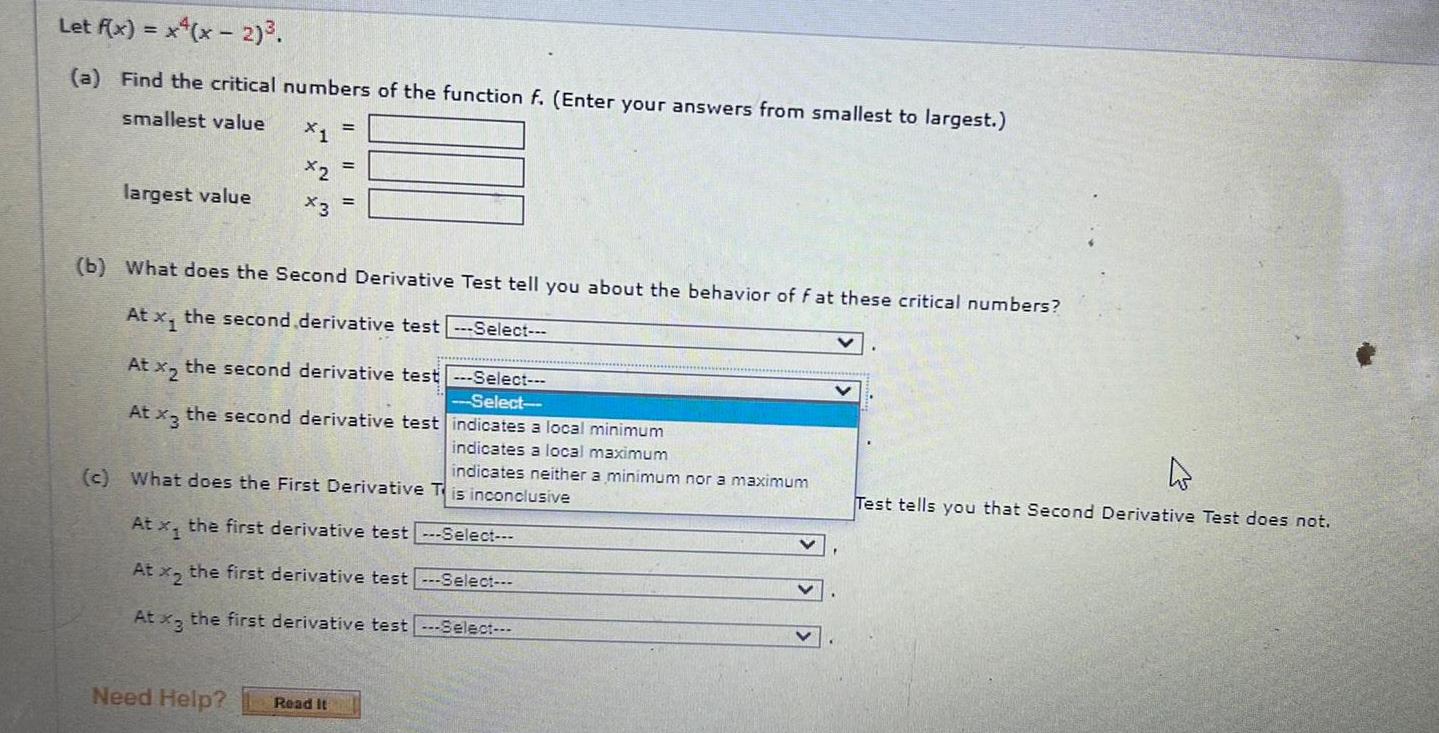
Calculus
DifferentiationLet f(x) = x4(x - 2)³.
(a) Find the critical numbers of the function f. (Enter your answers from smallest to largest.)
smallest value
largest value
(b) What does the Second Derivative Test tell you about the behavior of f at these critical numbers?
At x₁ the second derivative test
At x₂ the second derivative test
At x3 the second derivative test
(c) What does the First Derivative Test tells you that Second Derivative Test does not.
At x1 the first derivative test
At x₂ the first derivative test
At x3 the first derivative test
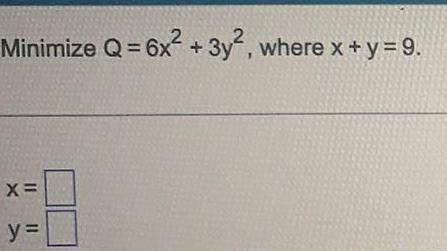

Calculus
DifferentiationFind a function that gives the vertical distance v between the line y = x + 42 and the parabola y = x2 for -6 ≤ x ≤ 7.
v(x) =
Find v'(x).
v'(x) =
What is the maximum vertical distance between the line y = x + 42 and the parabola y = x² for -6 ≤ x ≤ 7?

Calculus
DifferentiationFind the derivative of the function
F(x) = x4-7x³ + √x x²
in two ways: by using the Quotient Rule and by simplifying first. (Check that your answers are equivalent. Which method do you prefer?)
Quotient Rule F'(x) =
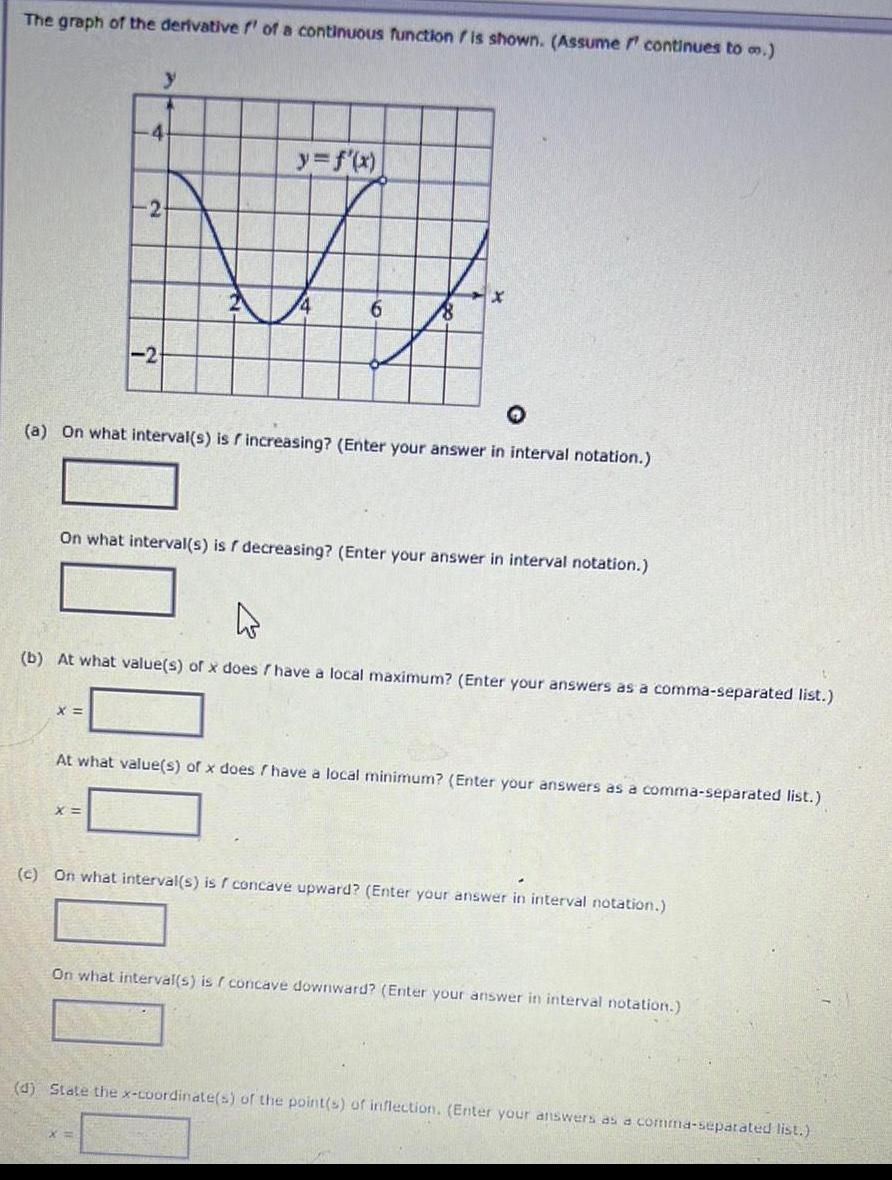
Calculus
DifferentiationThe graph of the derivative f' of a continuous function is shown. (Assume continues to m.)
(a) On what interval(s) is increasing? (Enter your answer in interval notation.)
On what interval(s) is / decreasing? (Enter your answer in interval notation.)
(b) At what value(s) of x does have a local maximum? (Enter your answers as a comma-separated list.)
At what value(s) of x does have a local minimum? (Enter your answers as a comma-separated list.)
(c) On what interval(s) is f concave upward? (Enter your answer in interval notation.)
On what interval(s) is / concave downward? (Enter your answer in interval notation.)
(d) State the x-coordinate(s) of the point(s) of inflection. (Enter your answers as a comma-separated list.)

Calculus
DifferentiationConsider the following function. (If an answer does not exist, enter DNE.)
h(x) = (x + 1)9 - 9x - 2
(a) Find the interval of increase. (Enter your answer using interval notation.)
Find the interval of decrease. (Enter your answer using interval notation.)
(b) Find the local minimum value(s). (Enter your answers as a comma-separated list.)
Find the local maximum value(s). (Enter your answers as a comma-separated list.)
(c) Find the inflection point.
(x, y).
Find the interval where the graph is concave upward. (Enter your answer using interval notation.)
Find the interval where the graph is concave downward. (Enter your answer using interval notation.)
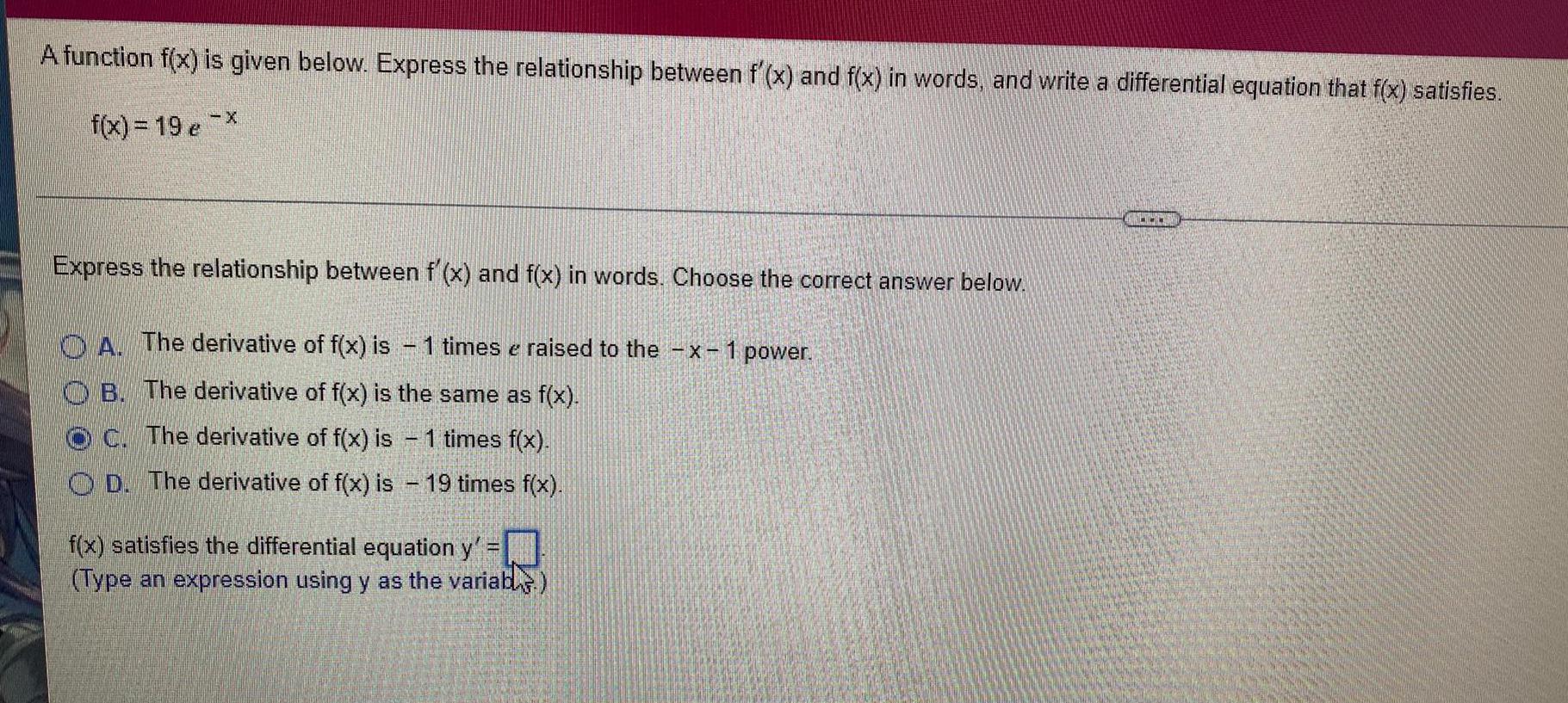
Calculus
DifferentiationA function f(x) is given below. Express the relationship between f'(x) and f(x) in words, and write a differential equation that f(x) satisfies.
f(x) = 19e-x
Express the relationship between f'(x) and f(x) in words. Choose the correct answer below.
A. The derivative of f(x) is - 1 times e raised to the -x-1 power.
B. The derivative of f(x) is the same as f(x).
C. The derivative of f(x) is - 1 times f(x).
D. The derivative of f(x) is - 19 times f(x).
f(x) satisfies the differential equation y' =
(Type an expression using y as the variab)

Calculus
DifferentiationFind the derivative of f with respect to x of f(x) = In x ^15
The derivative of f with respect to x of f(x) = In x^ 15
is
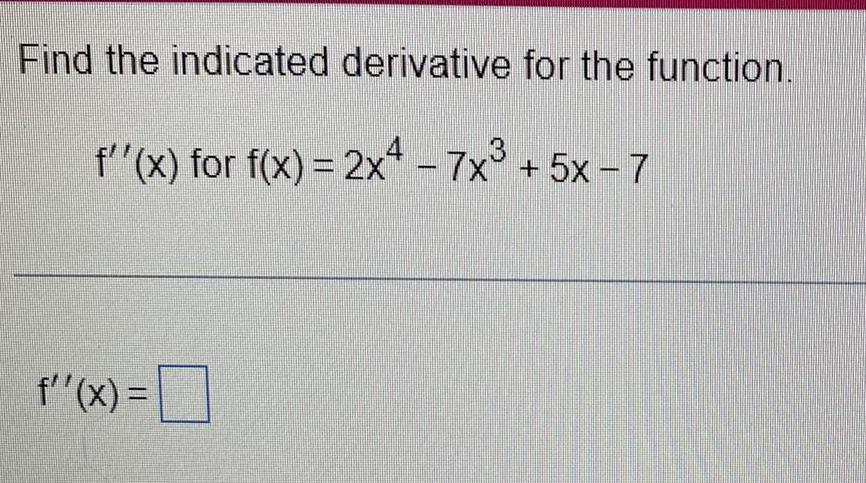
Calculus
DifferentiationFind the indicated derivative for the function.
f''(x) for f(x) = 2x^4 - 7x³ +5x-7
f''(x) =
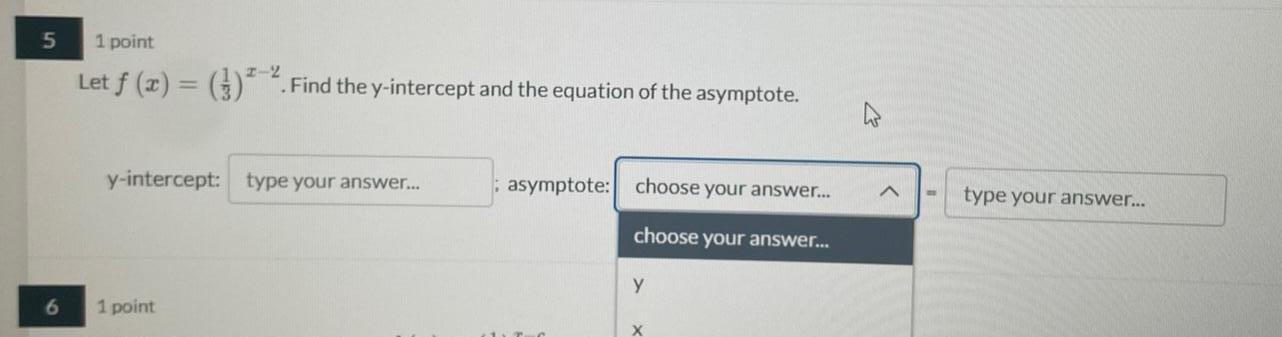
Calculus
DifferentiationLet f (x) = (1/3)^x-2 . Find the y-intercept and the equation of the asymptote.
y-intercept: type your answer...
asymptote: choose your answer...
.

Calculus
DifferentiationComplete the equation to illustrate the identity property of multiplication.
1(k+p) =

Calculus
DifferentiationUse only the associative property to rewrite the following algebraic expression.
10+(1+x)

Calculus
DifferentiationA parabola opening up or down has vertex (4, 5) and passes through (-14, -61/4). Write its equation in vertex form.
Simplify any fractions.
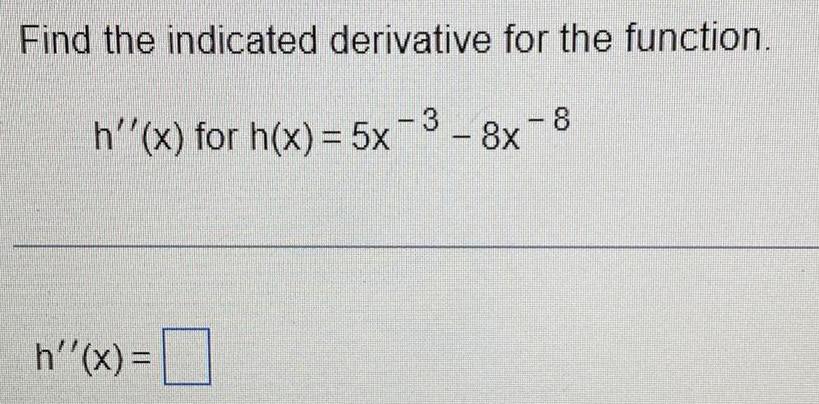
Calculus
DifferentiationFind the indicated derivative for the function.
h''(x) for h(x) = 5x-3 - 8x-8
h''(x) =

Calculus
DifferentiationFind the derivative and simplify.
d/dx 5x4 - x² +7x+8
What is d/dx 5x4 - x² +7x+8? Choose the correct answer below.
A. 5x4-x² +7x+8 (4x³ - 2x + 7) In 5
B. 5x4-x² +7x+8 (4x³ - 2x + 7) In (x4-x² + 7x+8)
C. ex4-x² +7x+8 (4x³-2x+7) In (5x4-x²+7x+8)
D. ex4-x2+7x+8 (4x³ - 2x + 7) In 5
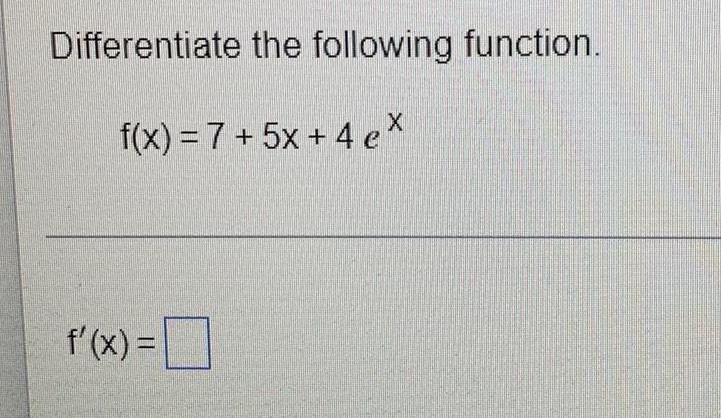
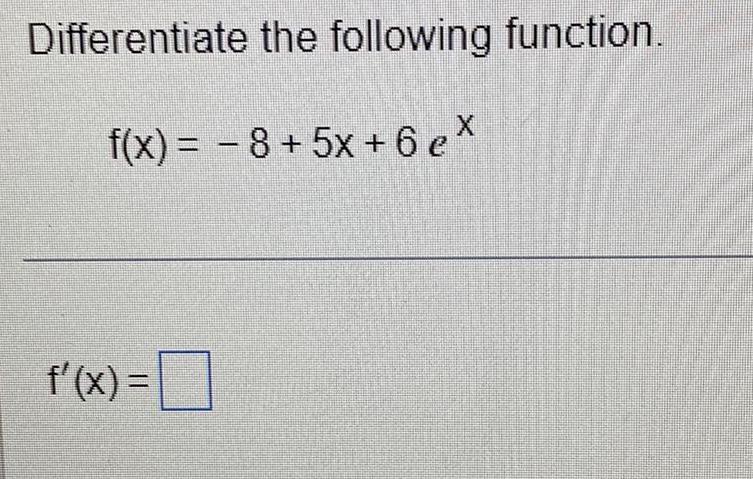
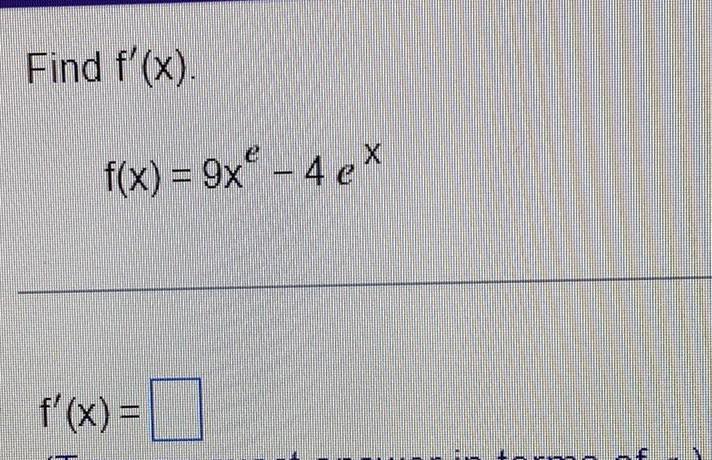

Calculus
DifferentiationFind the coordinates of a point on a circle with radius 5 corresponding to an angle of 145⁰
(x,y) = (,)
Round your answers to three decimal places.
If θ=1л4θ=1л4, then
sin(θ)sin(θ) =
cos(θ)cos(θ) =
Give exact values. No decimals allowed!

Calculus
DifferentiationTo measure the height of a building, a person stands away from the base and measures the angle of elevation to the top of the building to be 52. Moving 180 feet closer, the angle of elevation to the top of the building is 70°. How tall is the building? Building height= feet Note: Round your answers to 2 places after the decimal when applicable
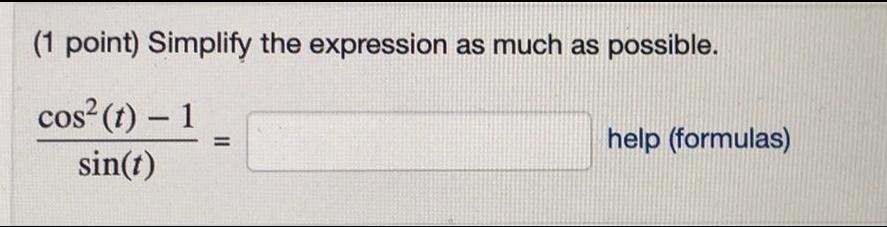

Calculus
DifferentiationA city has a population of 220,000 people. Suppose that each year the population grows by 3.75%. What will the population be after 9 years? Use the calculator provided and round your answer to the nearest whole number.
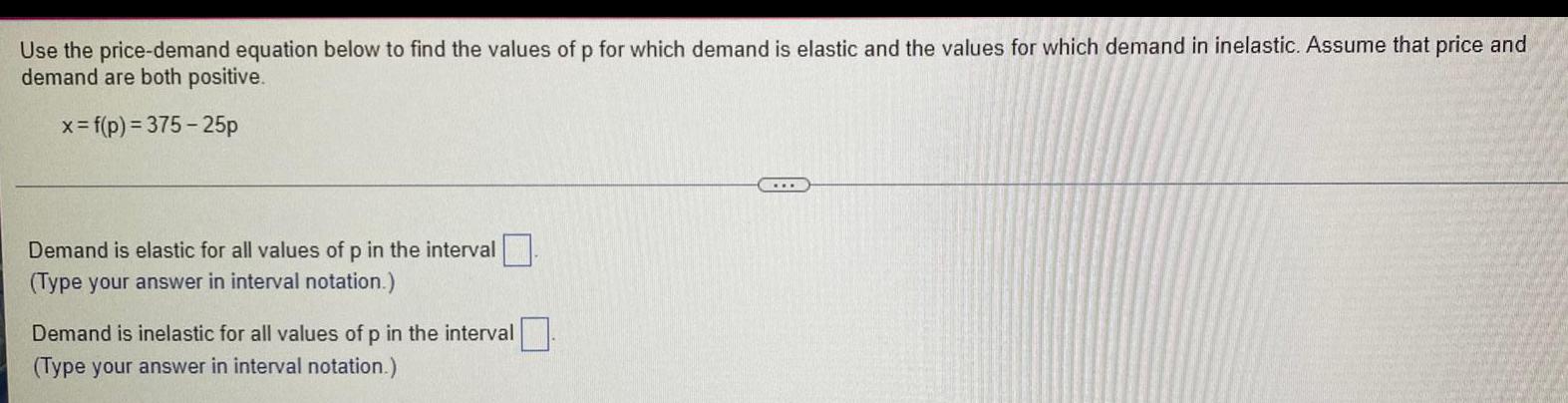
Calculus
DifferentiationUse the price-demand equation below to find the values of p for which demand is elastic and the values for which demand in inelastic. Assume that price and demand are both positive.
x = f(p) = 375-25p
Demand is elastic for all values of p in the interval
(Type your answer in interval notation.)
Demand is inelastic for all values of p in the interval
(Type your answer in interval notation.)

Calculus
DifferentiationIf f(3) = 3 and f'(x) ≥ 2 for 3 ≤ x ≤ 5, how small can f(5) possibly be?
f(5) ≥

Calculus
DifferentiationUse the price-demand equation x = f(p)=√√522-6p to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.
Demand is inelastic for all values of p in the interval
(Type your answer in interval notation. Type integers or decimals.)
Demand is elastic for all values of p in the interval
(Type your answer in interval notation. Type integers or decimals.)