Differentiation Questions and Answers
Calculus
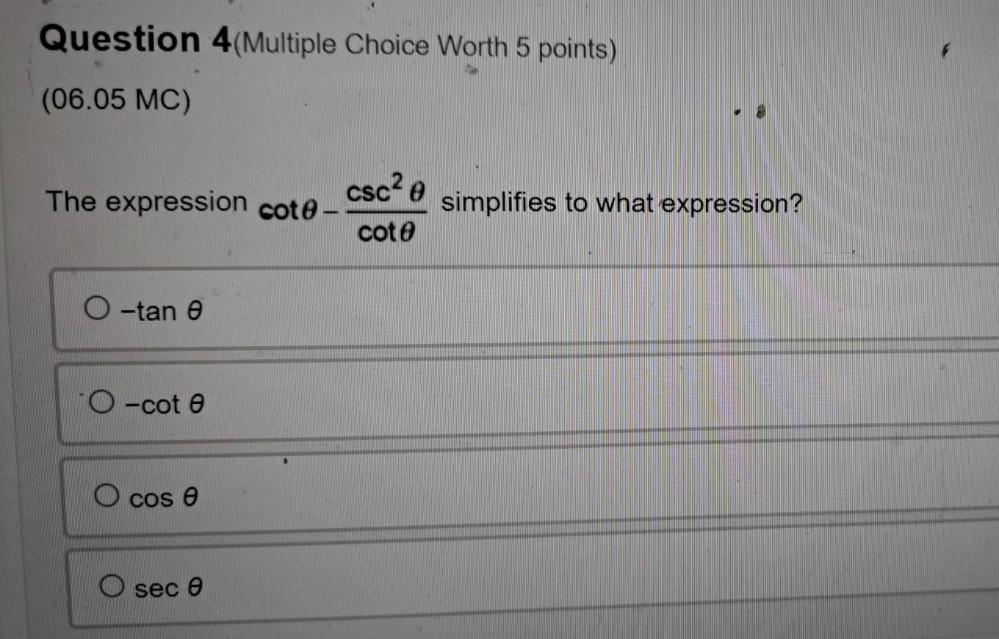
DifferentiationThe expression cotθ-csc² θ/cotθ simplifies to what expression?
-tanθ
-cotθ
cosθ
secθ
Calculus
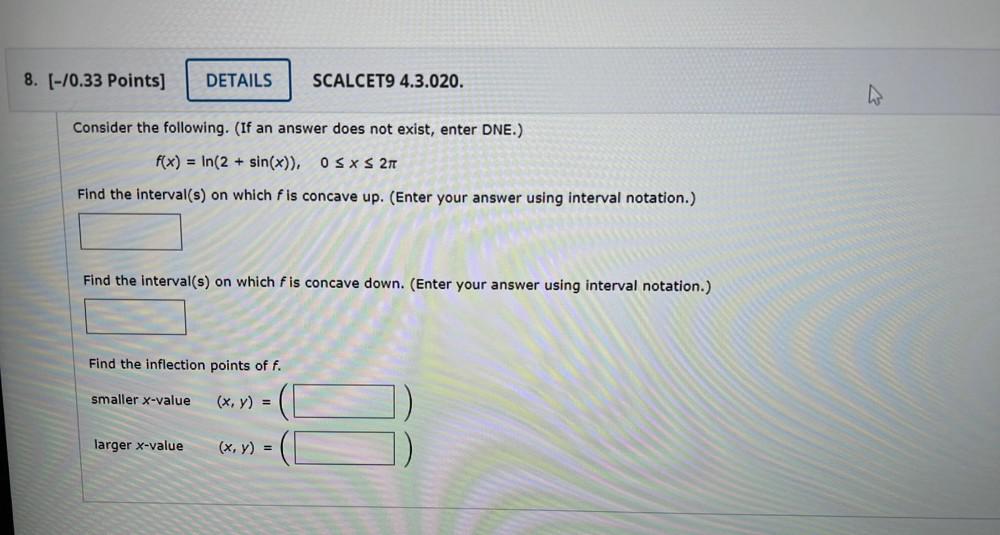
DifferentiationConsider the following. (If an answer does not exist, enter DNE.)
f(x) = ln(2+ sin(x)), 0≤x≤ 2π
Find the interval(s) on which f is concave up. (Enter your answer using interval notation.)
Find the interval(s) on which f is concave down. (Enter your answer using interval notation.)
Find the inflection points of f.
smaller x-value (x, y) =
larger x-value (x, y) =
Calculus
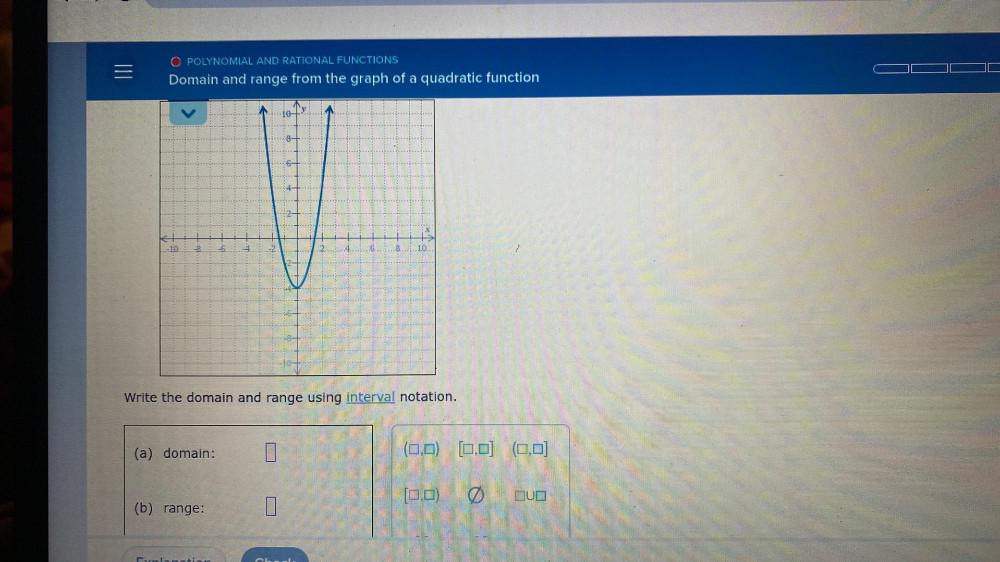
DifferentiationDomain and range from the graph of a quadratic function Write the domain and range using interval notation.
(a) domain:
(b) range:
Calculus
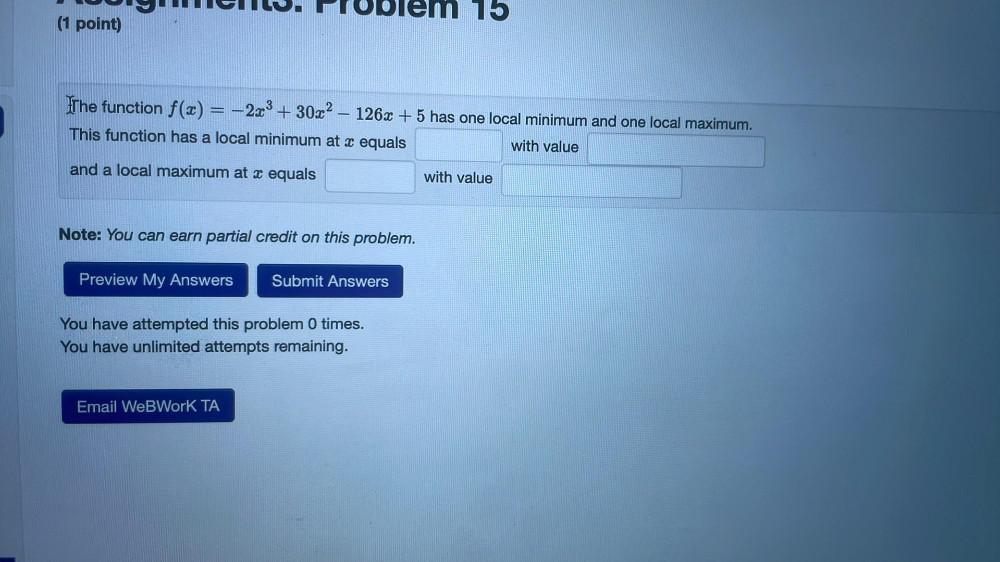
DifferentiationThe function f(x) = −2x³ + 30x² - 126x + 5 has one local minimum and one local maximum.
This function has a local minimum at x equals _______ with value ________ and a local maximum at x equals _________ with value _______________.
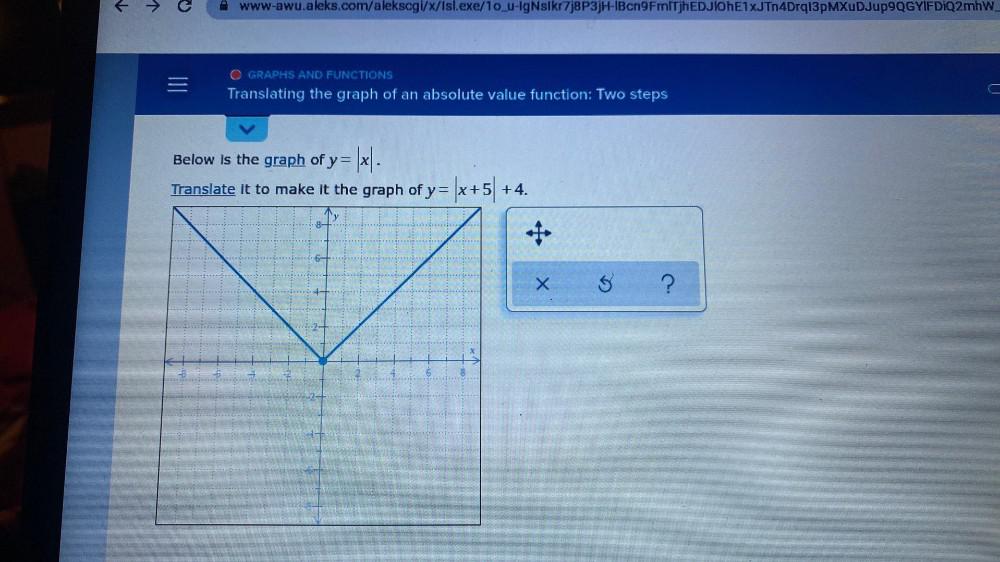
Calculus
DifferentiationLet f(x) = (2x − 1)(x² − 2). Find all the values of x for which f'(x) = 0.
Present your answer as a comma-separated list:


Calculus
DifferentiationFor the equation given below, evaluate y' at the point (1, -1).
y at (1, -1) =
eʸ+8-e‾¹= 6x²+2y²
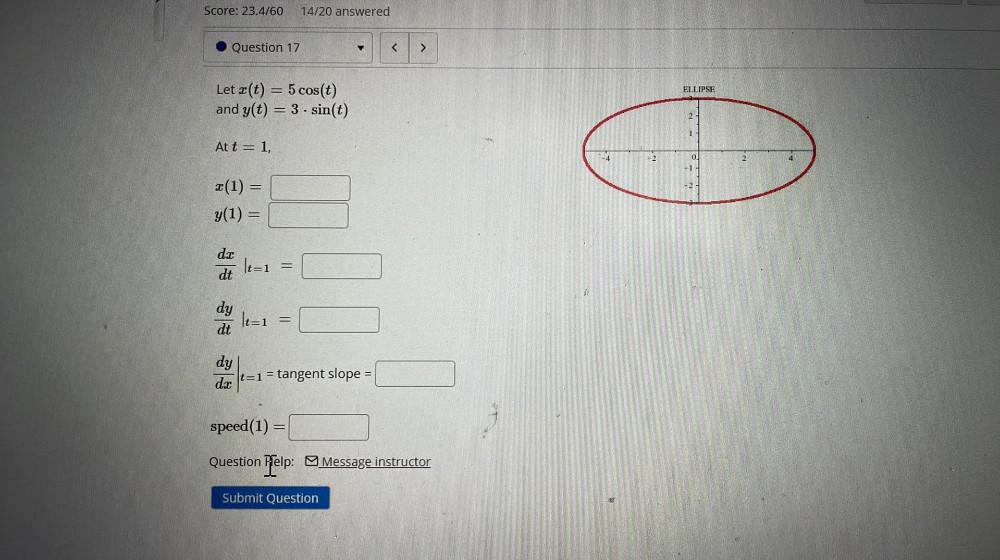
Calculus
DifferentiationLet x (t) = 5 cos(t)
and y(t) = 3 sin(t)
At t = 1,
x(1) =
y(1) =
dx/dt |t=1 =
dy/dt |t=1 =
dy/dx |t=1 = tangent slope =
speed (1) =
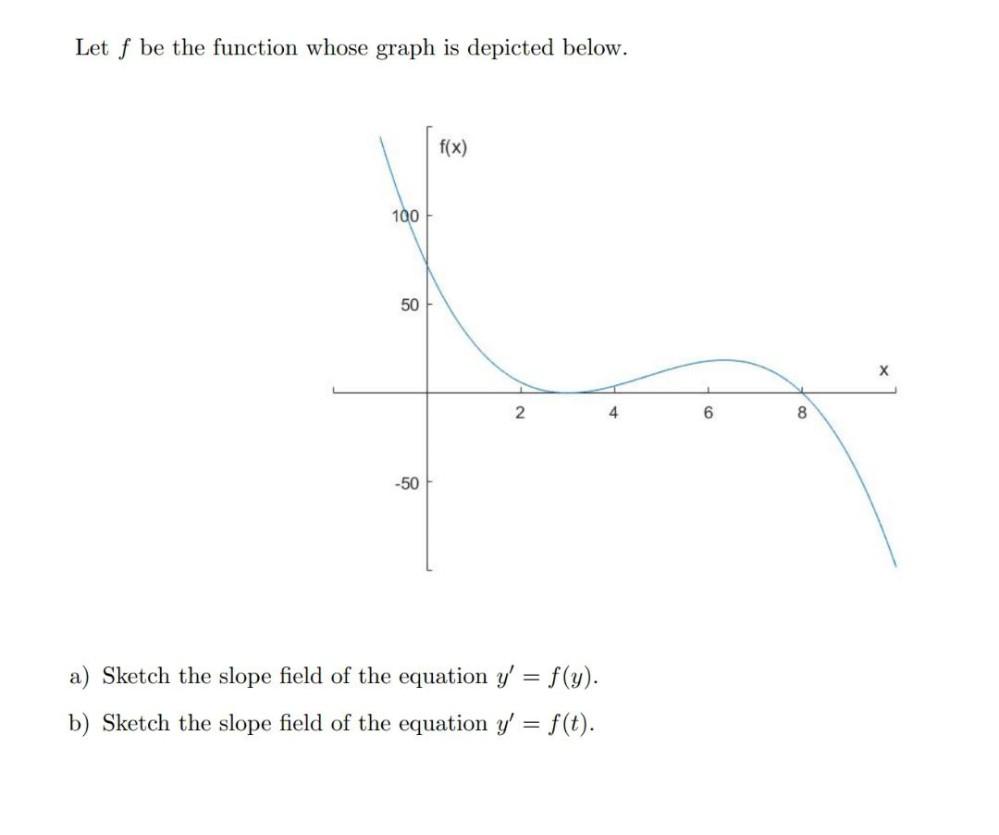
Calculus
DifferentiationLet f be the function whose graph is depicted below.
(a) Sketch the slope field of the equation y'= f(y).
(b) Sketch the slope field of the equation y'= f(t).

Calculus
DifferentiationDetermine the equation of the sinusoidal function in the form y = a sin(bx +c)+d. Show how you calculated each value using the given information:
Maximum = 13, Minimum = 5, Period = π, No horizontal shift

Calculus
DifferentiationThe height of a tidal wave approaching the face of the cliff on an island is represented by the equation h(t) = 7.5 cos(2πt/9.5) where h(t) is the height, in meters, of the wave above normal sea level t minutes after the wave strikes the cliff.
1. What is the maximum height of the wave relative to normal sea level?
2. What is the period of the function?
3. How high, to the nearest tenth of a metre, will the wave be, relative to normal sea level, one minute after striking the cliff?

Calculus
DifferentiationAt which values in the interval [0, 2π) will the functions f (x) = cos 2x + 1 and g(x) = sin x + 2 intersect?

Calculus
DifferentiationThe following table shows the rate of water flow (in L/min) through a dam.
t (min) 1 4 7 10 13 16 19
V'(t) (L/min) 1 10 5 6 8 3 8
Approximate the total volume of water that passed through the dam from t=1 to t=19 using Simpson's rule, with n=6.
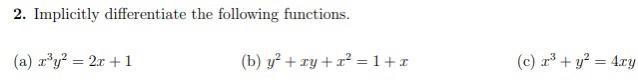
Calculus
Differentiation2. Implicitly differentiate the following functions.
(a) x³y² = 2x + 1
(b) y² + xy + x²=1+x
(c) x³ + y²= 4xy
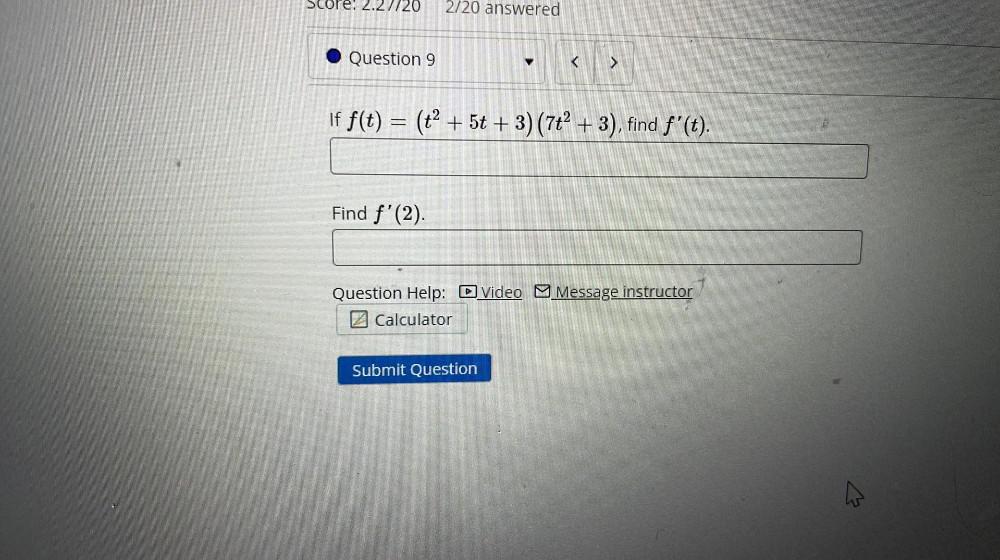
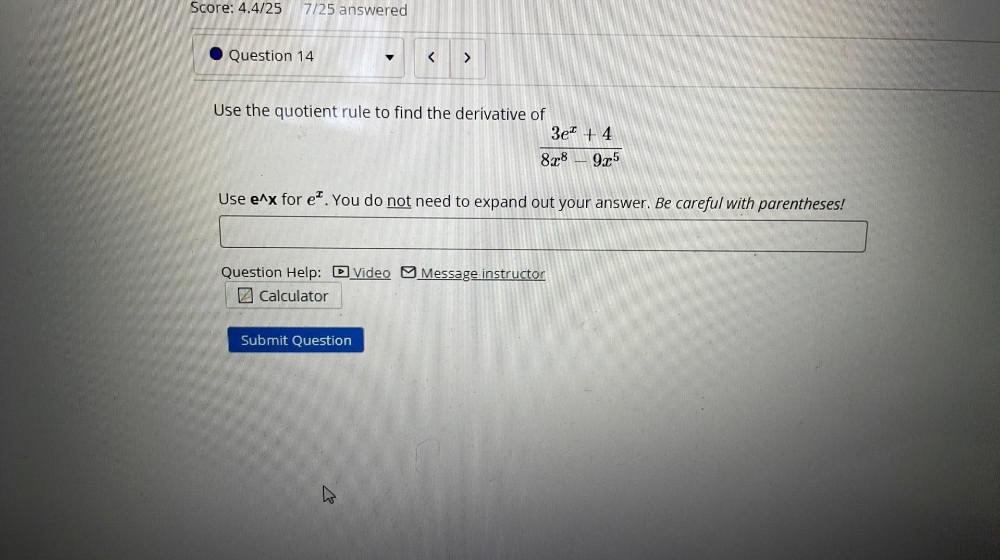
Calculus
DifferentiationUse the quotient rule to find the derivative of 3e^x +4 / 8x⁸ - 9x⁵
Use e^x for e^x. You do not need to expand out your answer. Be careful with parentheses!
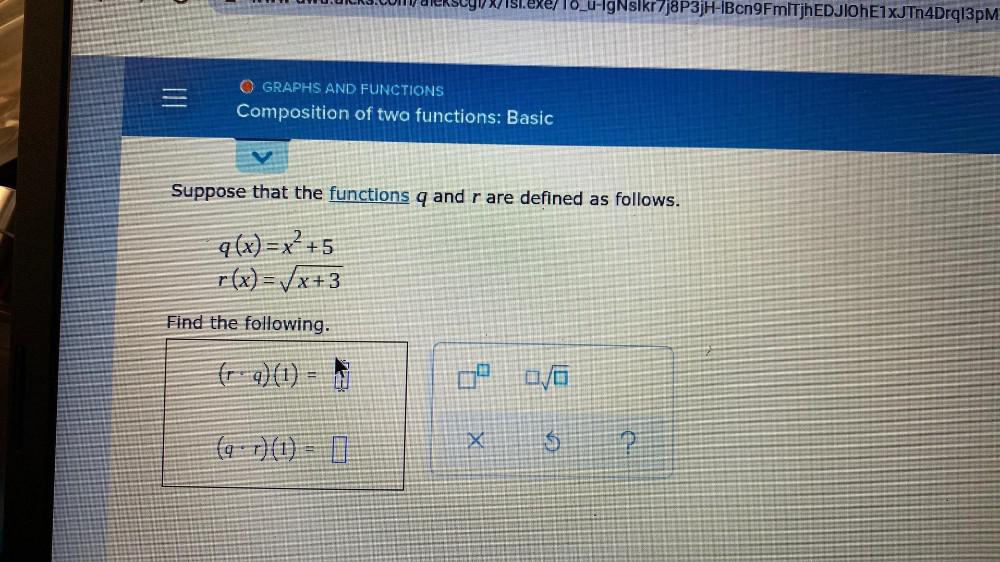
Calculus
DifferentiationSuppose that the functions q and r are defined as follows.
q (x) = x² +5
r(x)=√(x +3)
Find the following.
(r.q)(1) =
(q.r) (1) =
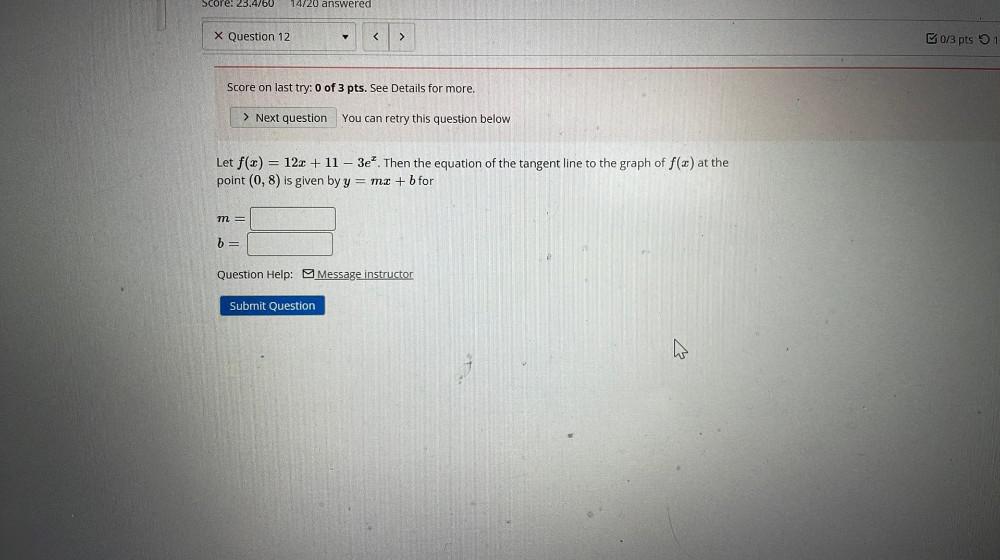
Calculus
DifferentiationLet f(x) = 12x + 11 - 3e^x. Then the equation of the tangent line to the graph of f(x) at the point (0,8) is given by y = mx + b for
m=
b =

Calculus
DifferentiationA ladder 10 m long is leaning against a wall. If the base of the ladder is sliding away from the wall at the rate of 1 m per second, at what instantaneous rate, d/dt, will the top of the ladder be moving when the base of the ladder is 6 m from the wall?
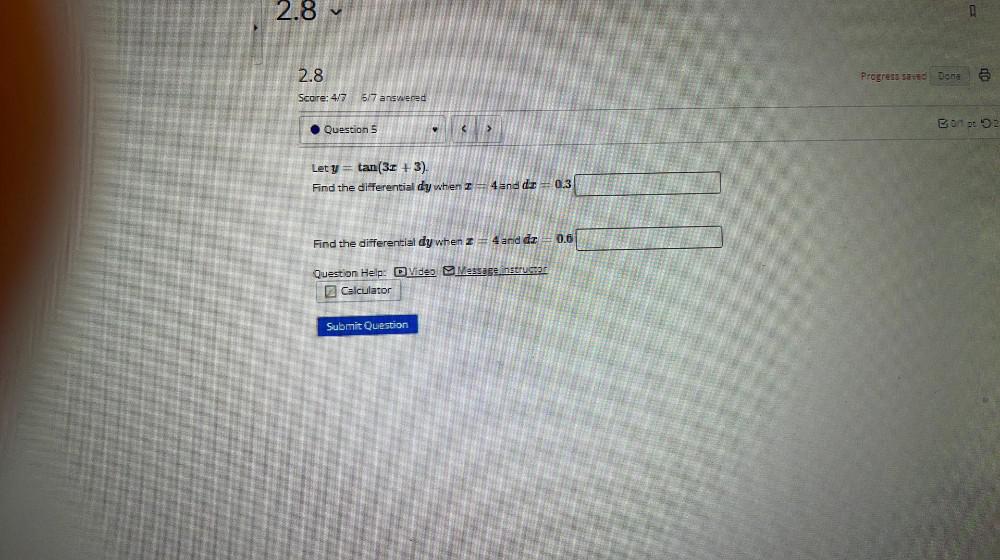
Calculus
DifferentiationLet y = tan (3x + 3).
Find the differential dy when x = 4 and dx = 0.3
Find the differential dy when x = 4 and drx = 0.6

Calculus
DifferentiationGiven f(x, y) = - 4x^6 - 5x²y^5 + 3y³, find
fz(x, y) =
fy(x,y) =
fxx (x, y) =
fzy (x, y) =
fyz(x, y) =
fyy(x, y) =
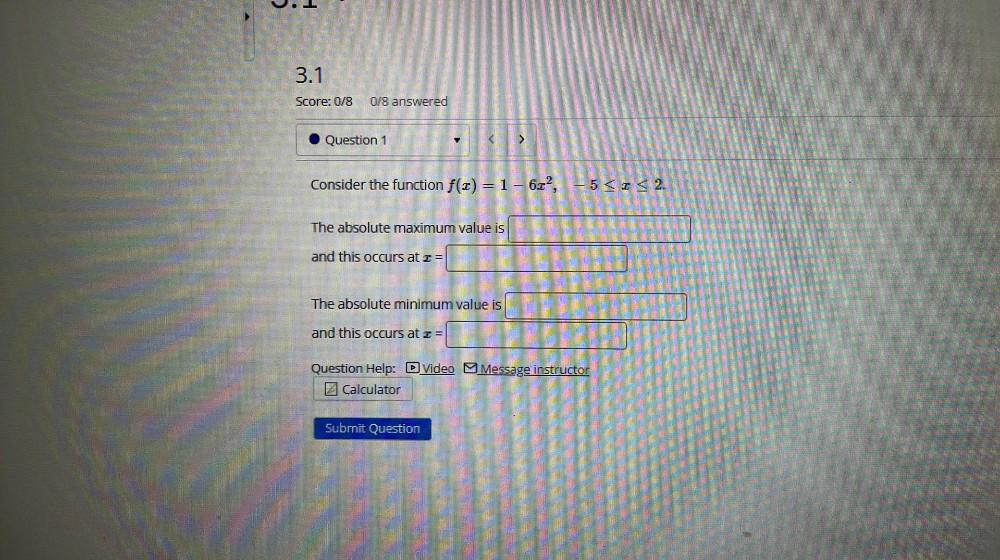
Calculus
DifferentiationConsider the function f(x) = 1 - 6x², -5 ≤ x ≤ 2.
The absolute maximum value is
and this occurs at x =
The absolute minimum value is
and this occurs at x =
![A spherical balloon is inflated so that its volume is increasing at the rate of 20 cubic cm per second. What is the instantaneous change in surface area, ds/dt, of the balloon increasing when the radius is 40 cm? [Use V=4/3 πr² and S = 4πr².]](https://media.kunduz.com/media/sug-question/raw/83677736-1658665355.4985685.jpeg?w=256)
Calculus
DifferentiationA spherical balloon is inflated so that its volume is increasing at the rate of 20 cubic cm per second. What is the instantaneous change in surface area, ds/dt, of the balloon increasing when the radius is 40 cm? [Use V=4/3 πr² and S = 4πr².]
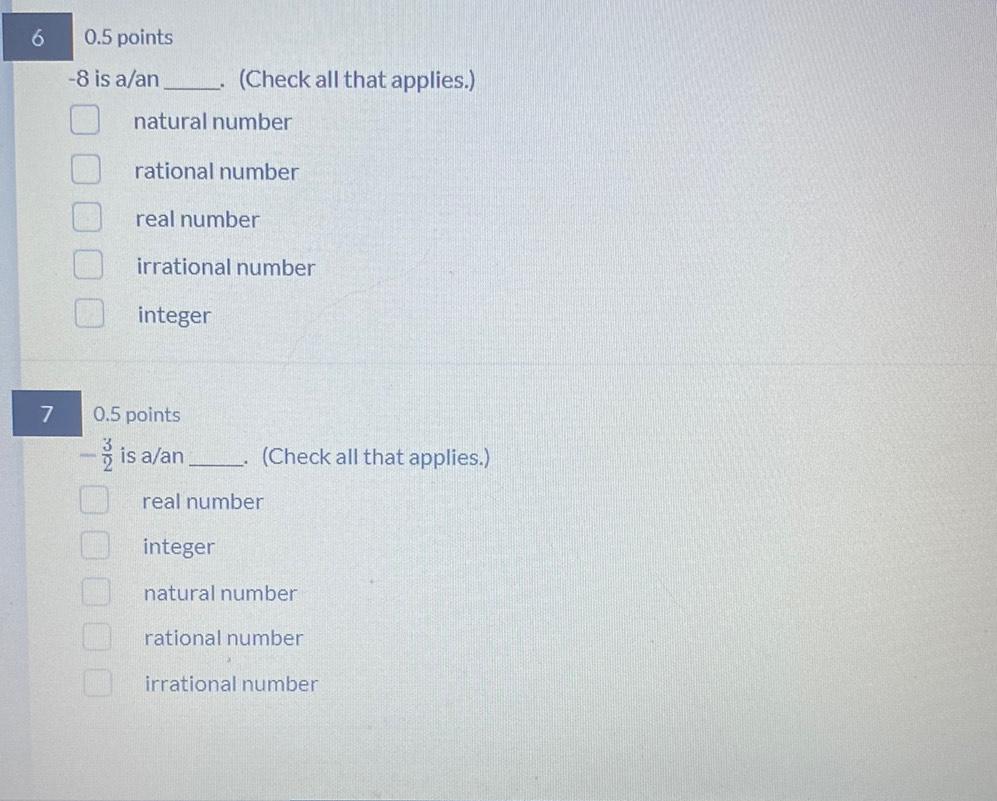
Calculus
Differentiation-8 is a/an. (Check all that applies.)
natural number
rational number
real number
irrational number
integer
is a/an.
-3/2 is a/an. (Check all that applies.)
real number
integer
natural number
rational number
irrational number
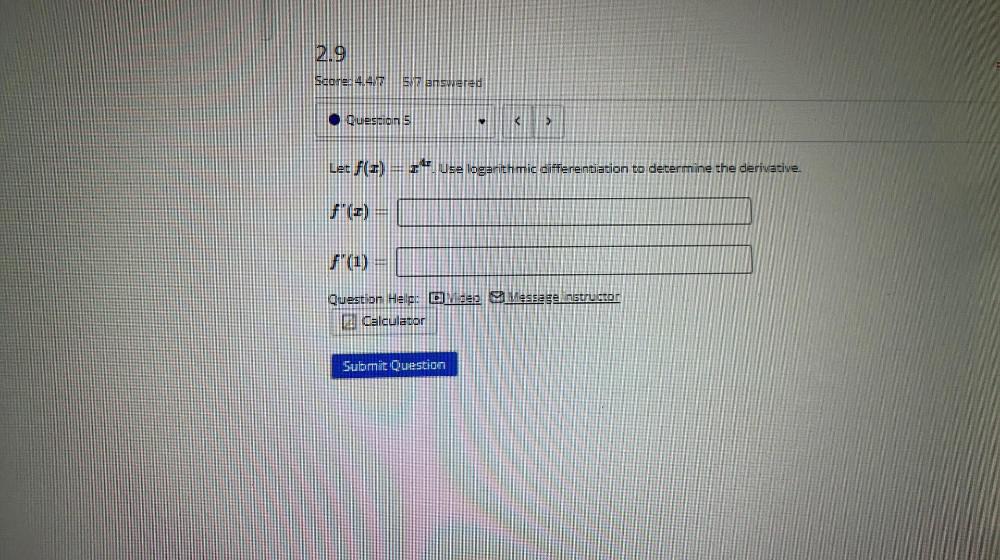
Calculus
DifferentiationLet f(x)= x^4x .Use logarithmic differentiation to determine the derivative.
ƒ'(x) =
ƒ'(1) =
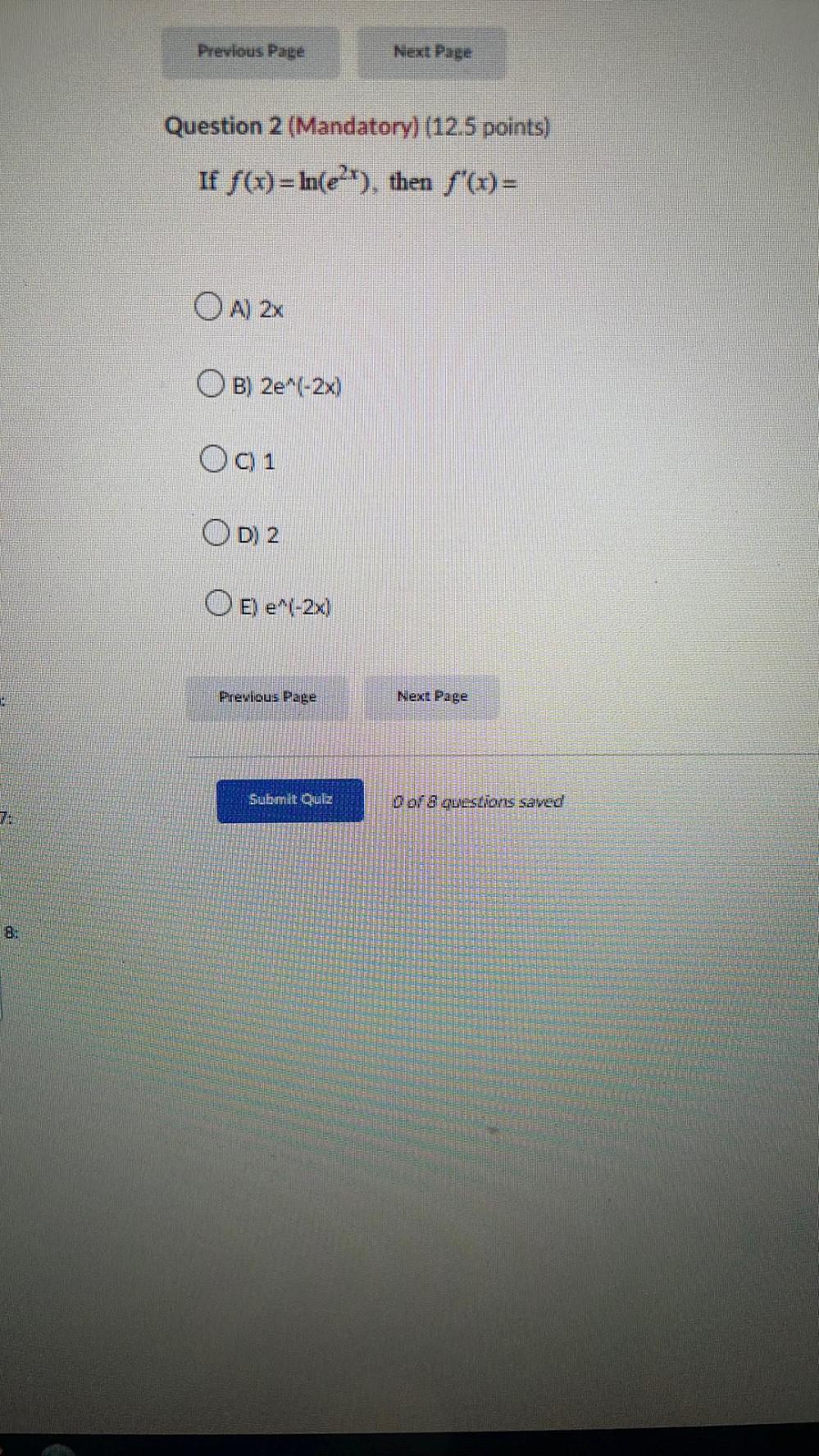
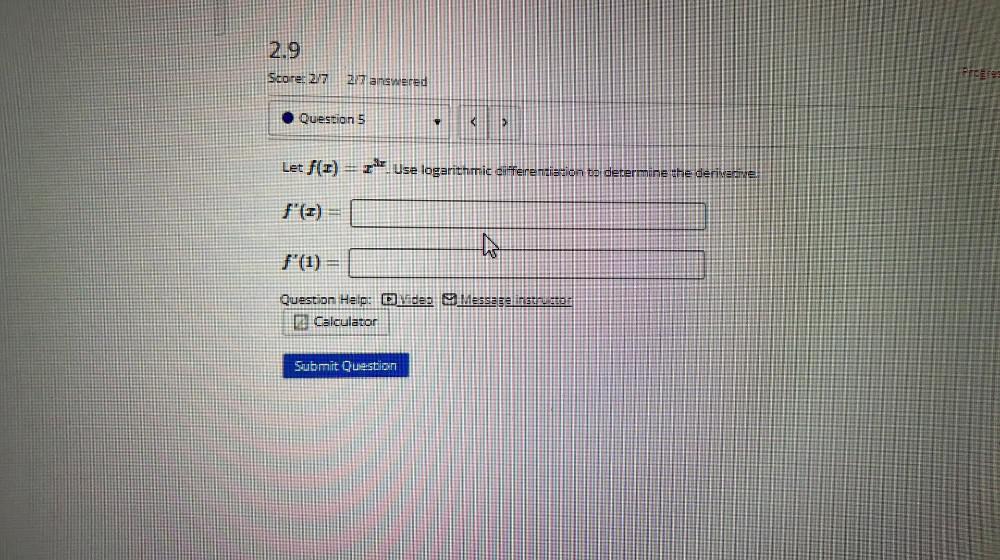
Calculus
DifferentiationLet f(x) = x^3x. Use logarithmic differentiation to determine the derivative.
f'(x)= ______
ƒ'(1)= ______
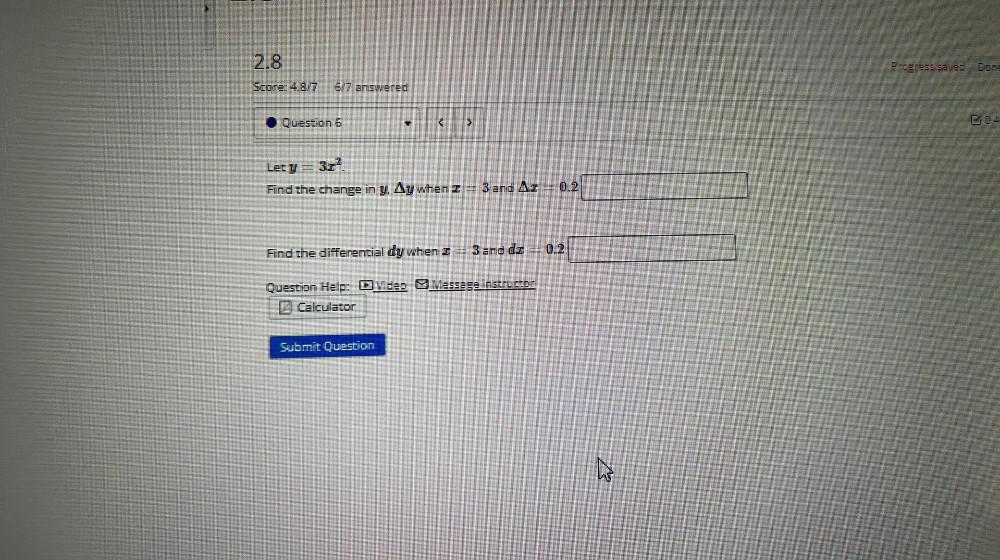
Calculus
DifferentiationLet y =3x²
Find the change in y. ∆y when x =3 and ∆x = 0.2 ______
Find the differential dy when x = 3 and dx= 0.2___
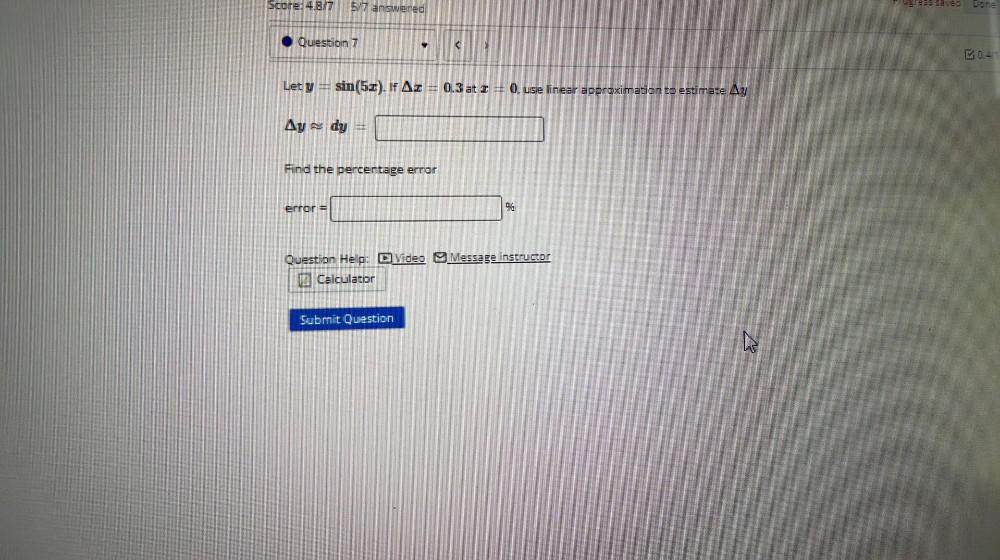
Calculus
DifferentiationLet y = sin(5x). If Δx = 0.3 at x = 0, use linear approximation to estimate Δy
Δy ≈ dy =
Find the percentage error
error = %
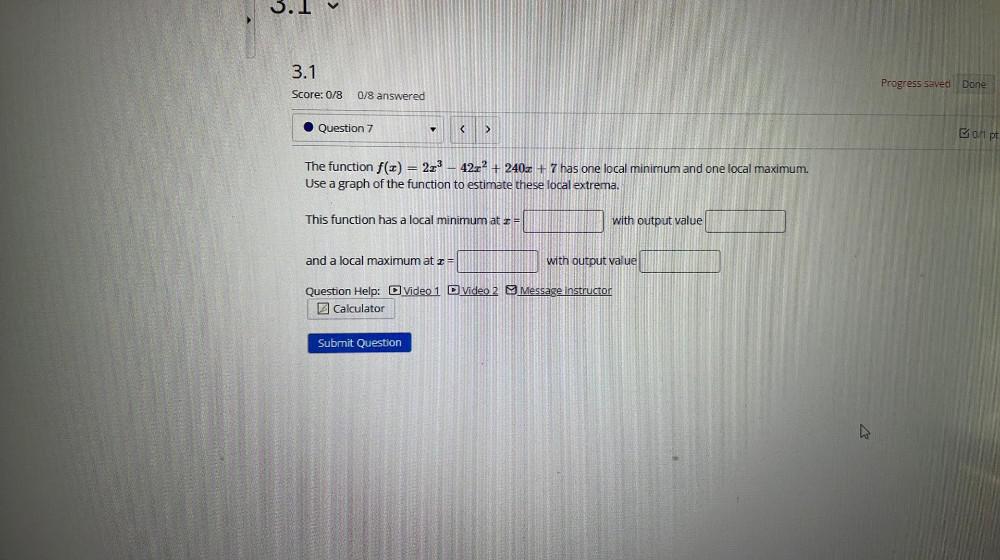
Calculus
DifferentiationThe function f(x) = 2x³ - 42x² + 240x + 7 has one local minimum and one local maximum.
Use a graph of the function to estimate these local extrema.
This function has a local minimum at x = with output value and a local maximum at x = with output value
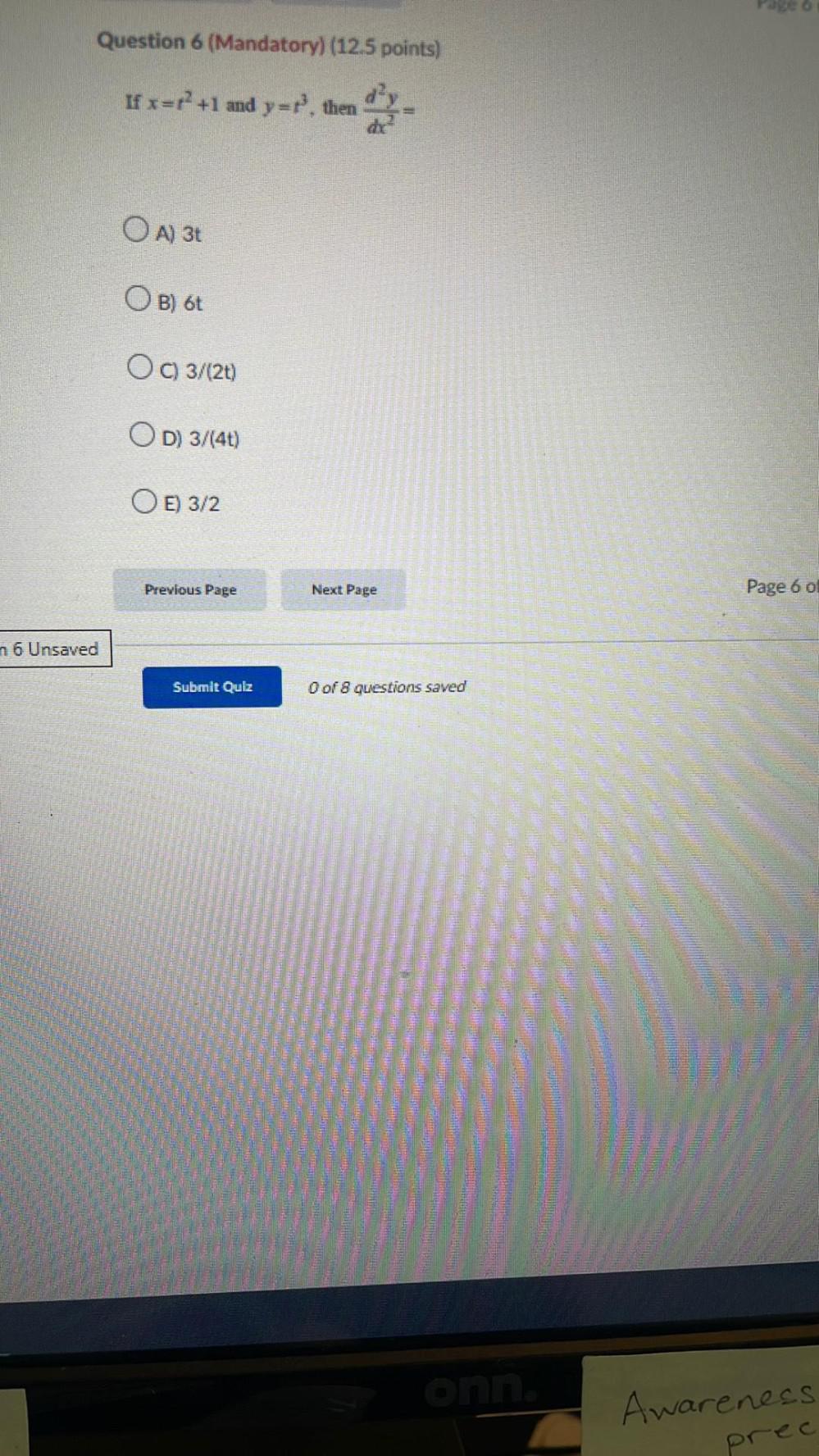
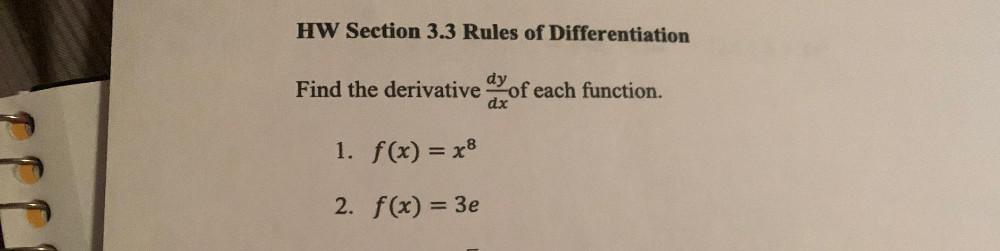
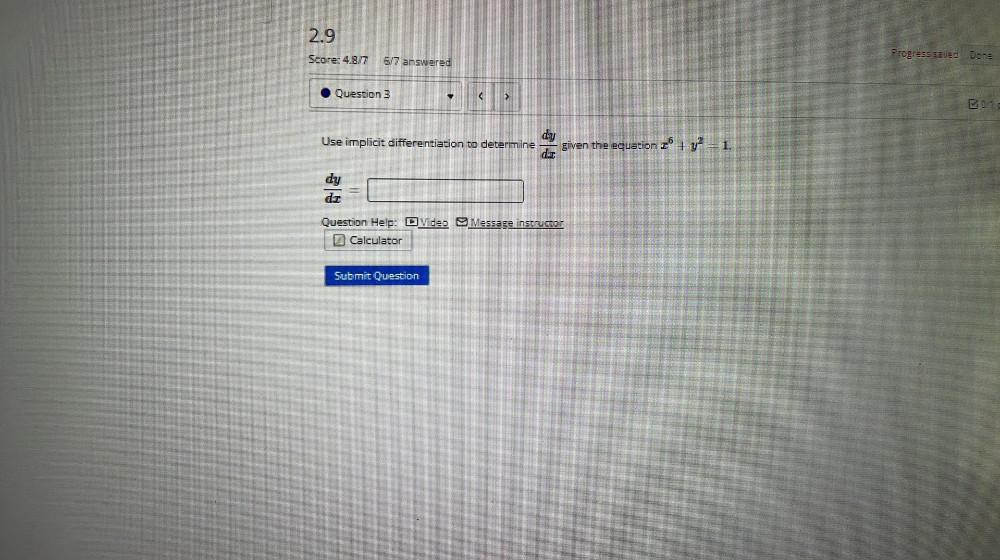
Calculus
DifferentiationUse implicit differentiation to determine dy/dx given the equation x^6+ y² = 1.
dy/dx =
![Perform the operation and simplify the result.
2/3 - 5/12
[Give your answer as a fraction.]
Solve for x : 2x/3 - 1 = 5
X = type your answer...](https://media.kunduz.com/media/sug-question/raw/83884778-1658664865.3428023.jpeg?w=256)
Calculus
DifferentiationPerform the operation and simplify the result.
2/3 - 5/12
[Give your answer as a fraction.]
Solve for x : 2x/3 - 1 = 5
X = type your answer...
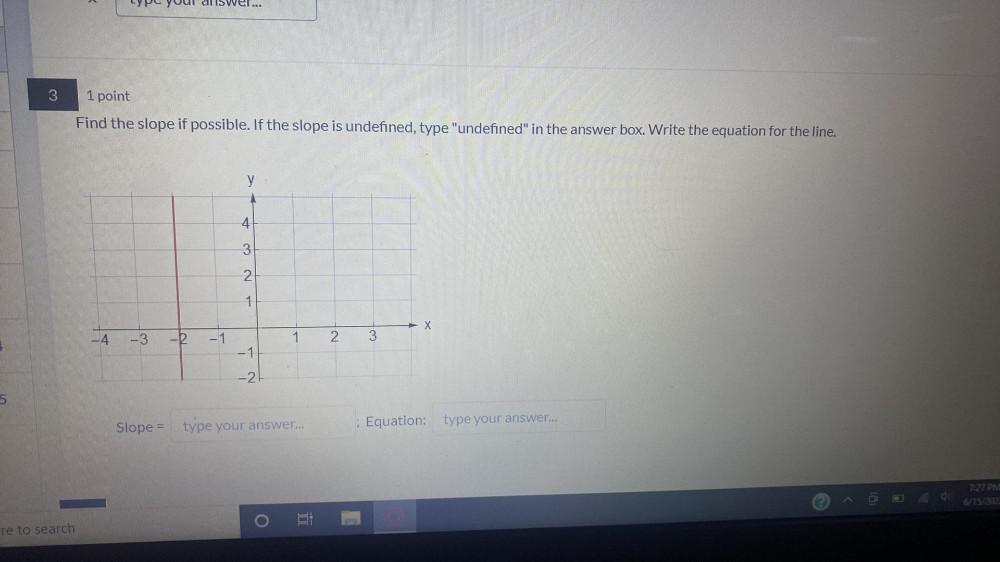
Calculus
DifferentiationFind the slope if possible. If the slope is undefined, type "undefined" in the answer box. Write the equation for the line.
Slope =
Equation:


Calculus
DifferentiationUse the quotient rule to get the derivative of f(x) = cot x and f(x) = sec x
Find the derivative of each function.
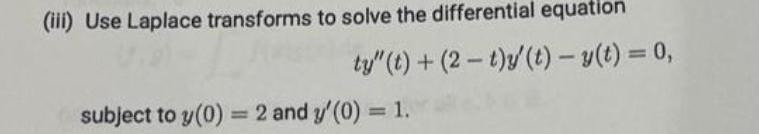
Calculus
DifferentiationUse Laplace transforms to solve the differential equation
ty"(t)+(2-t)y' (t)- y(t) = 0,
subject to y(0) = 2 and y'(0) = 1.
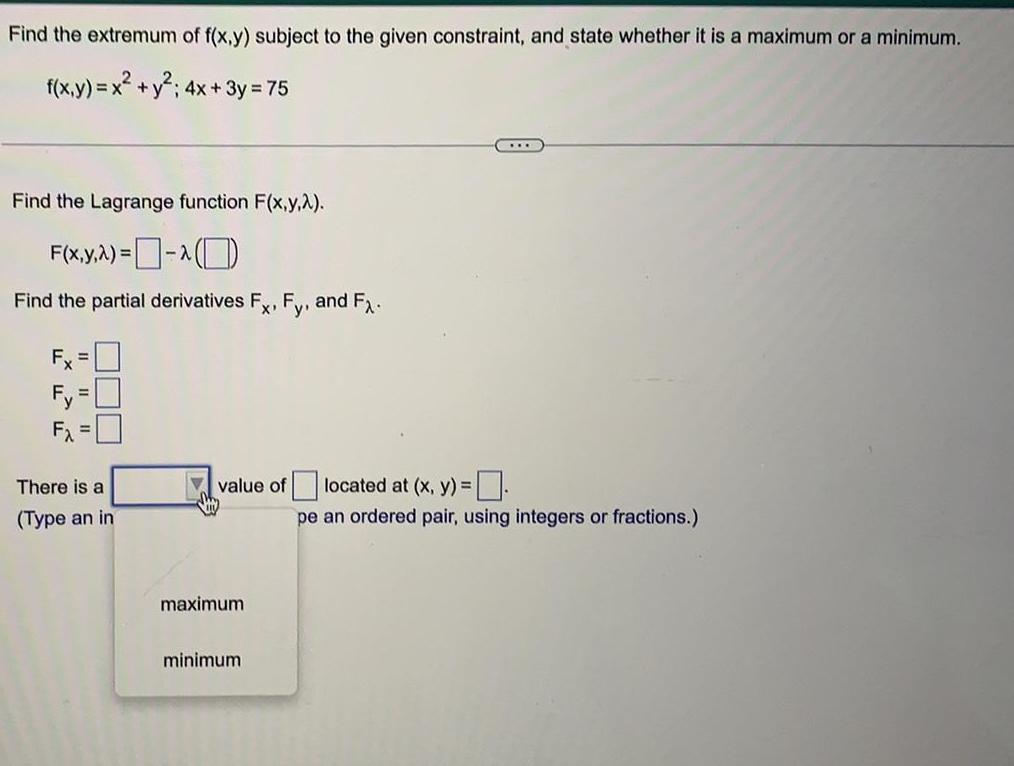
Calculus
DifferentiationFind the extremum of f(x,y) subject to the given constraint, and state whether it is a maximum or a minimum.
f(x,y) = x² + y²; 4x + 3y = 75
Find the Lagrange function F(x,y,λ).
F(x,y,λ)=
Find the partial derivatives Fx, Fy, and Fλ.
Fx=
Fy=
Fλ=
There is a maximum minimum value of located at (x, y) =
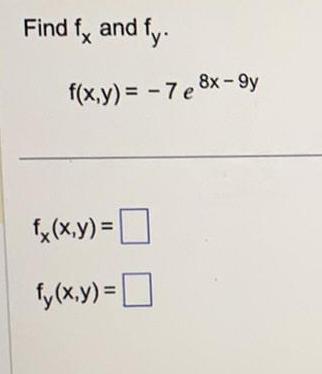

Calculus
DifferentiationSuppose 0≤θ≤π/2. Solve the equation: 5 tan (2θ) + 4 = 2(tan(2θ) + 5) for θ.
Give your answer rounded to 2 places after the decimal point.
![For the function y = sin x² on the interval [0,π/4], find the number guaranteed by the Mean Value Theorem. x = [?] Round to the nearest thousandth.](https://media.kunduz.com/media/sug-question/raw/84629511-1658663996.9219627.jpeg?w=256)
Calculus
DifferentiationFor the function y = sin x² on the interval [0,π/4], find the number guaranteed by the Mean Value Theorem. x = [?] Round to the nearest thousandth.


Calculus
DifferentiationThe produce manager at a market orders 40 lb of tomatoes, 50 lb of zucchini, and 30 lb of onions from a local farmer one week.
a) Write a 1x3 matrix A that represents the amount of each item ordered.
b) The following week, the produce manager increases his order by 10%. "Find a matrix B that represents this order.
c) Find A + B and tell what the entries represent.
a) Write the entries in the order in which they are given in the problem statement.
A=
b) Write the entries in the order in which they are given in the problem statement
B=
c) A+B=
What do the entries of A + B represent?
A. The entries represent the maximum weekly produce orders for the two weeks.
B. The entries represent the total produce orders for the two weeks.
C. The entries represent the change in produce orders between the two weeks.
D. The entries represent the projected produce orders for the third week

Calculus
DifferentiationA farmer wants to fence in a rectangular plot of land adjacent to the north wall of his barn. No fencing is needed along the barn, and the fencing along the west side of the plot is shared with a neighbor who will split the cost of that portion of the fence. If the fencing costs $10 per linear foot to install and the farmer is not willing to spend more than $4000, find the dimensions for the plot that would enclose the most area. (Enter the dimensions as a comma separated list.)
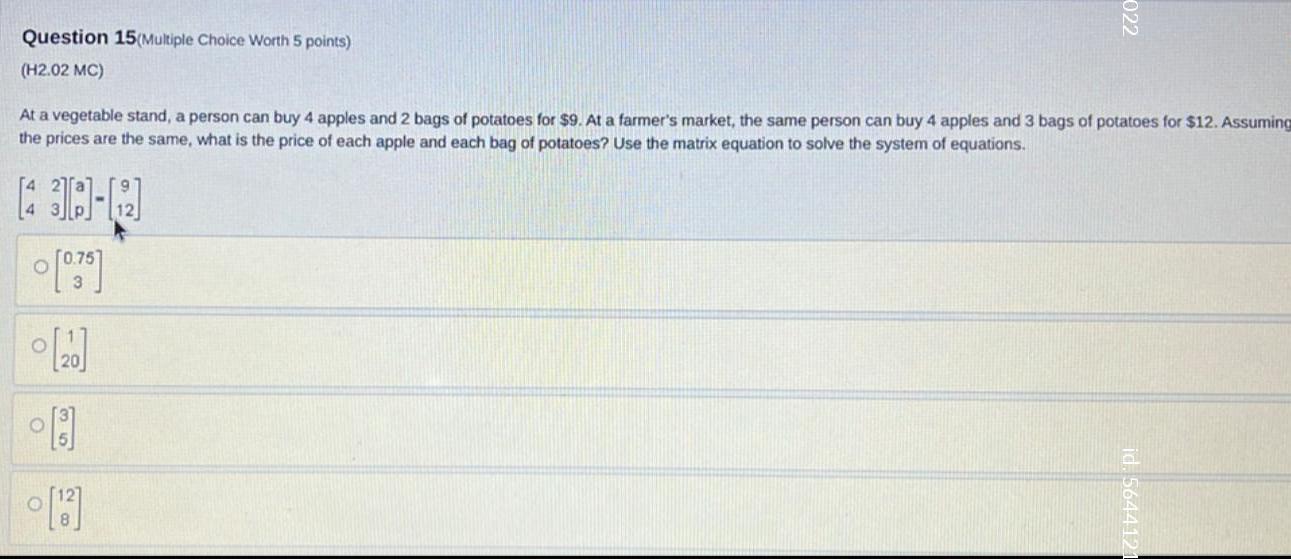
Calculus
DifferentiationAt a vegetable stand, a person can buy 4 apples and 2 bags of potatoes for $9. At a farmer's market, the same person can buy 4 apples and 3 bags of potatoes for $12. Assuming the prices are the same, what is the price of each apple and each bag of potatoes? Use the matrix equation to solve the system of equations.

Calculus
DifferentiationAir Purification During testing of a certain brand of air purifier, the amount of smoke remaining (as a percent of the original a function.
A(t) = -0.00006t^5 +0.00468t^4 -0.111t^3 +1.801t² - 17.63t + 102
Compute the following values.
A'(10) =
A"(10) =