Limits & Continuity Questions and Answers

Calculus
Limits & ContinuityThe function f(x) =x³ +8/x² has derivatives f(x) =x³ -16/x³ and f"(x)=48/x⁴
(a) Determine the x- and y-intercepts.
(b) Determine the equations of any asymptotes and classify the
behaviour at their endpoints.
(c) Determine the intervals of increase and decrease and classify any
local extrema.
(d) Determine the intervals of concavity and identify any points of
inflection.
(e) Complete the 2nd derivative test.
(f) Use this information to sketch the curve. Make sure all key features
are clearly presented.
Calculus
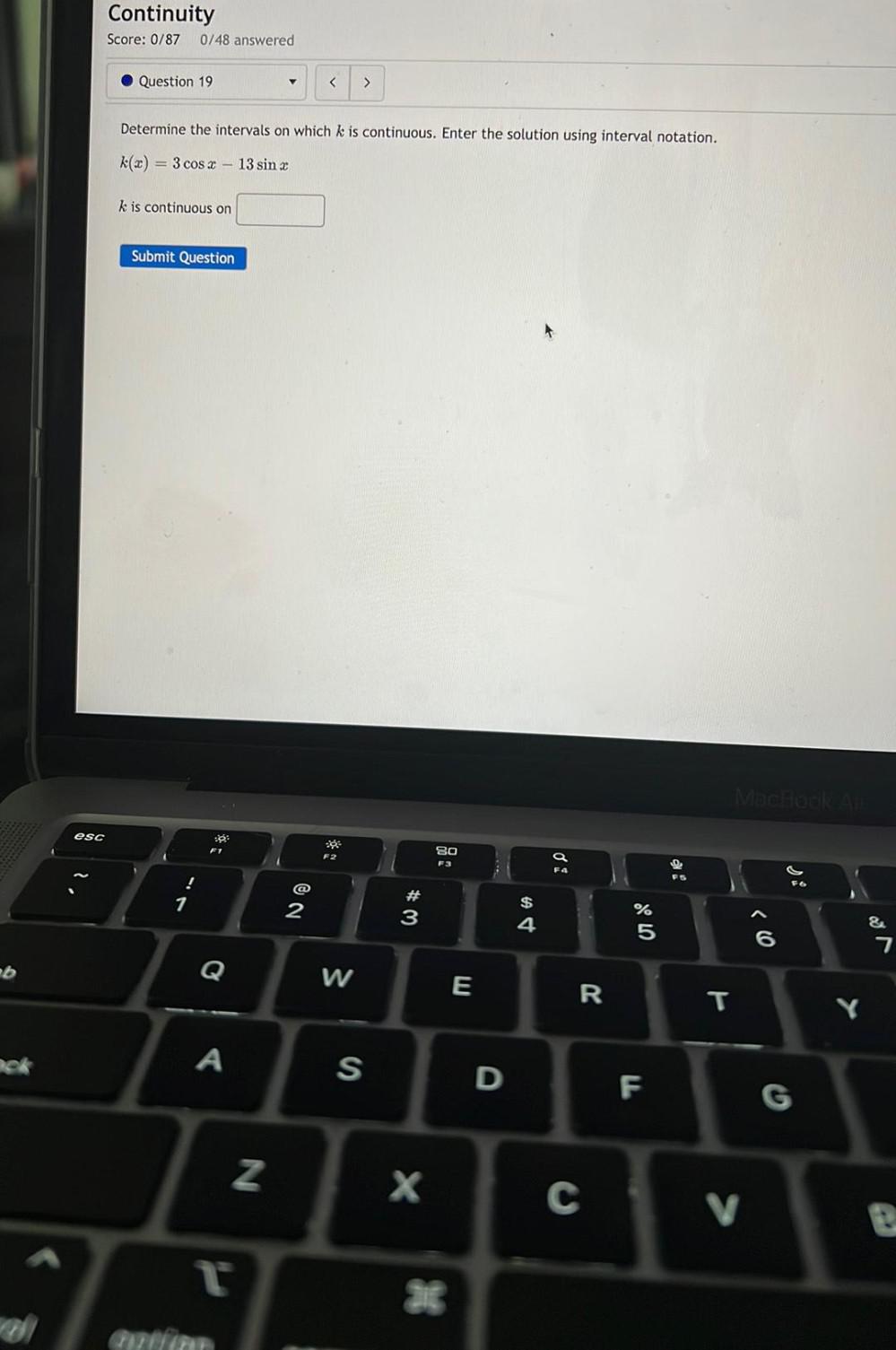
Limits & ContinuityDetermine the intervals on which k is continuous. Enter the solution using interval notation.
k(x) = 3 cos x – 13 sin x
k is continuous on ______
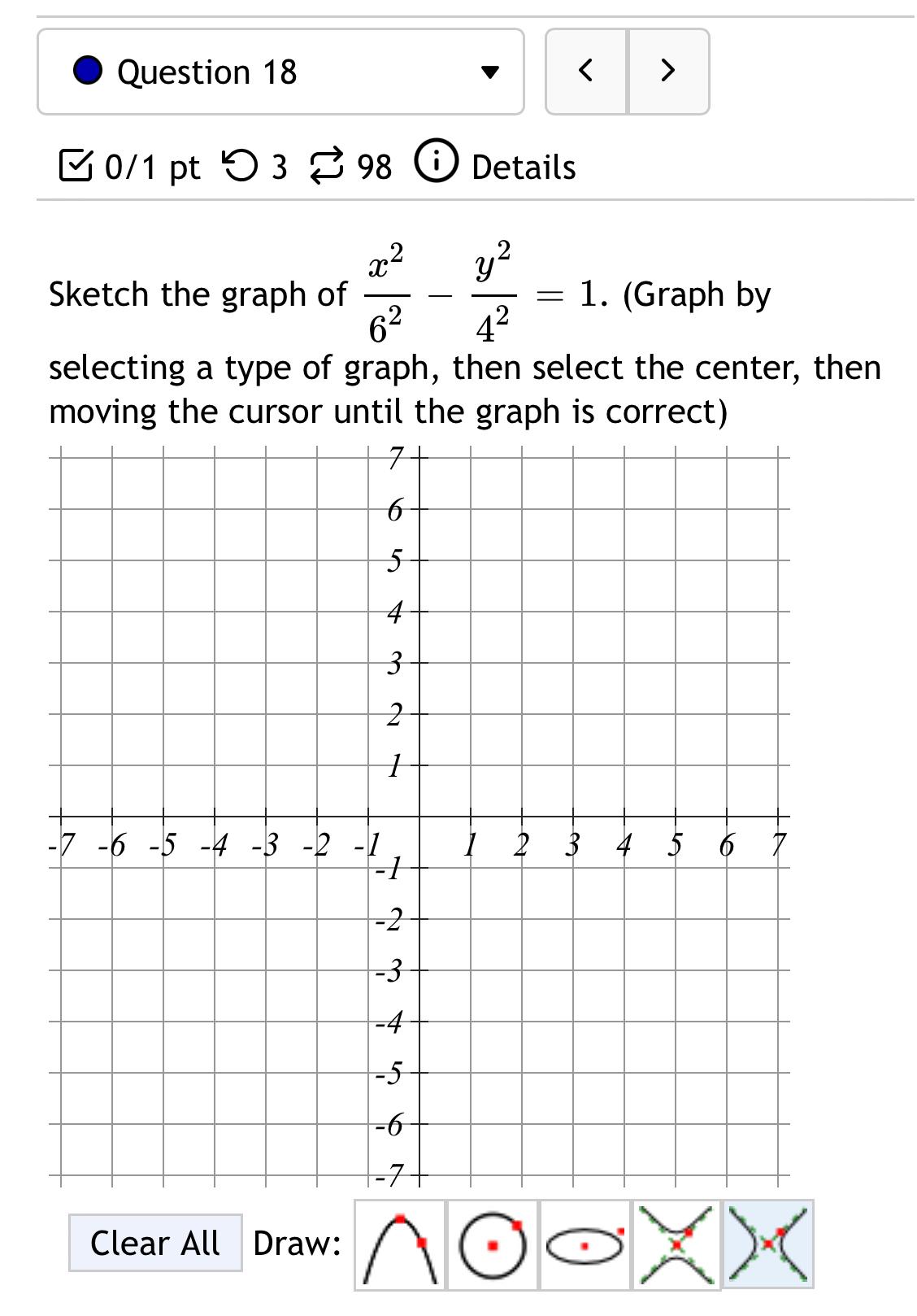
Calculus
Limits & ContinuitySketch the graph of x²/6² - y²/4² = 1 selecting a type of graph, then select the center, then moving the cursor until the graph is correct).

Calculus
Limits & ContinuityA seagull, flying above a lake, dives for a fish according to the function h(t)=0.25t^3 -4t^2 +15t, where h(t) represents the height above the water, in feet, at t seconds.
(A) Determine the velocity of the seagull when it exits the water.
(B) Determine the acceleration of the seagull at 9 seconds.

Calculus
Limits & ContinuityComplete the table shown to the right for the half-life of a certain radioactive substance.
Half-Life Decay Rate, k
18. 3 days
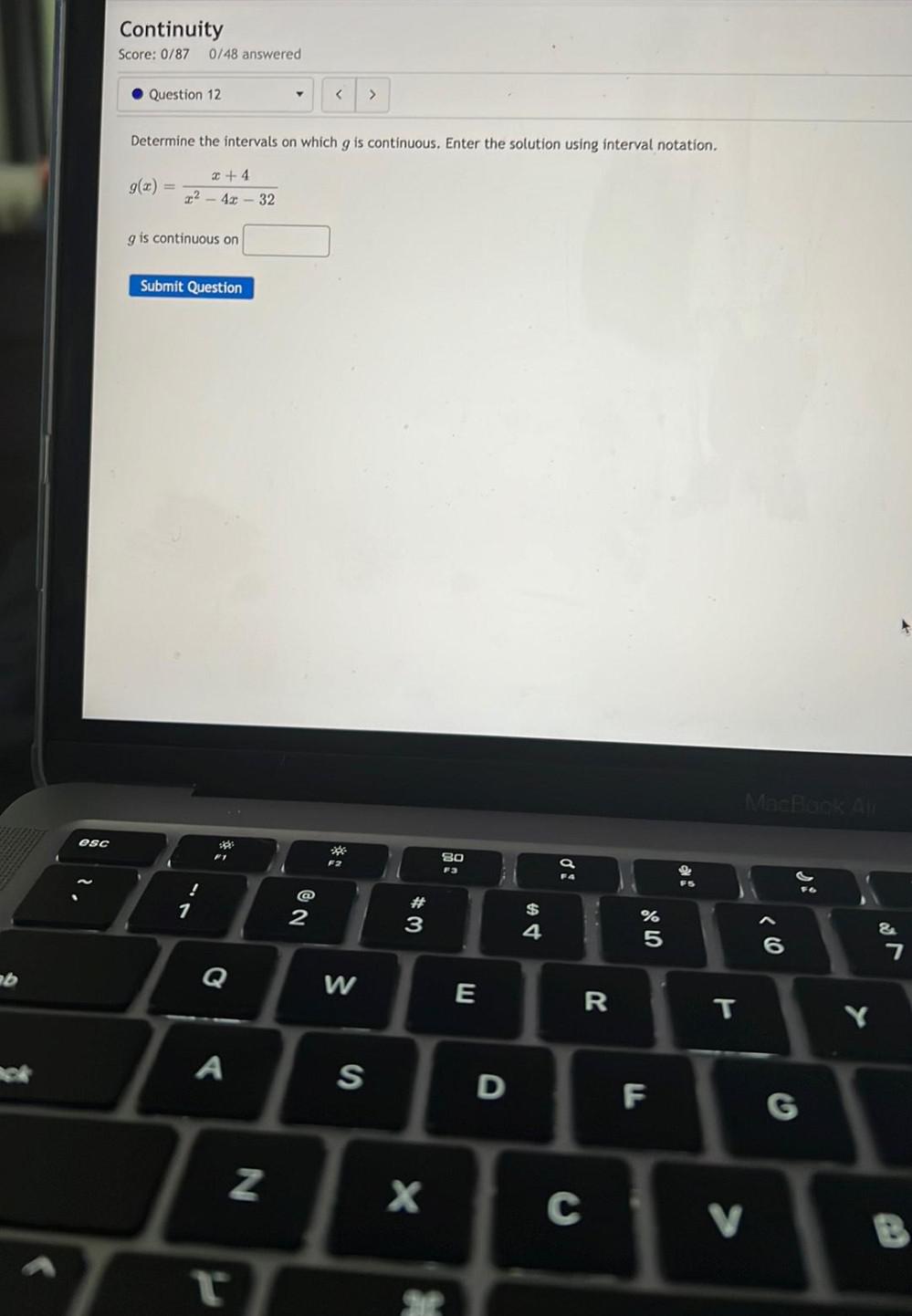
Calculus
Limits & ContinuityDetermine the intervals on which g is continuous. Enter the solution using interval notation.
g(x) =x +4/(x^2 - 4x - 32)
g is continuous on ______________
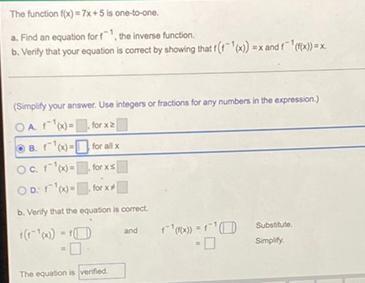
Calculus
Limits & ContinuityThe function f(x) = 7x +5 is one-to-one.
a. Find an equation for f⁻¹,the inverse function
b. Verity that your equation is correct by showing that f(f⁻¹(x)) =x and f⁻¹(f(x))=x.(Simplify your answer. Use integers or fractions for any numbers in the expression)
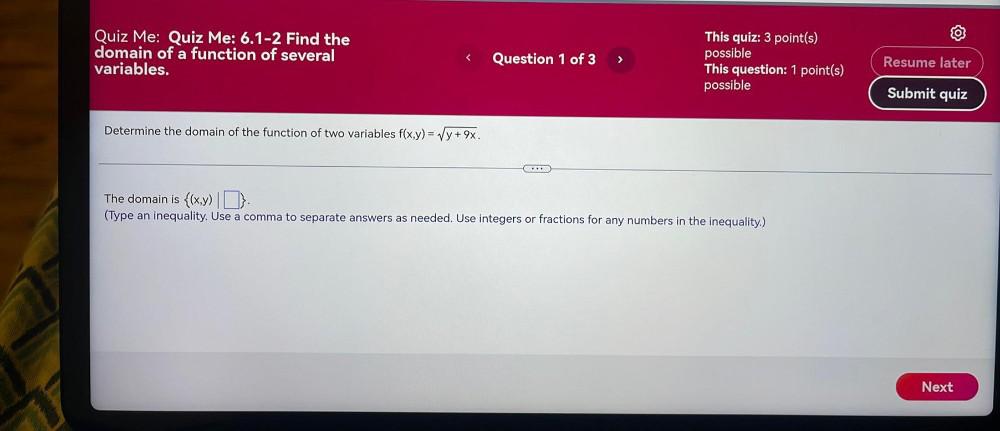
Calculus
Limits & ContinuityDetermine the domain of the function of two variables f(x, y)= √(y+9x).
The domain is {(x, y) | ___}.
(Type an inequality. Use a comma to separate answers as needed. Use integers or fractions for any numbers in the inequality.)
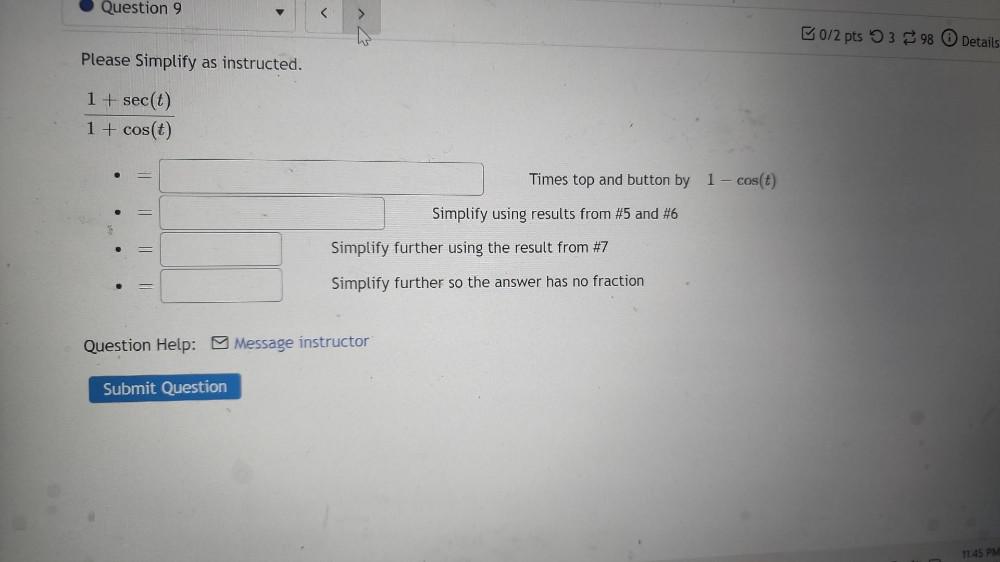
Calculus
Limits & ContinuityPlease Simplify as instructed.
1 + sec(t)/1 + cos(t)
Times top and button by 1 - cos(t)
Simplify using results from #5 and #6
Simplify further using the result from #7
Simplify further so the answer has no fraction
![R is the region bounded by the functions f(x) = 14 / (-1 + x) and g(x) = 2x – 14. Find the area of the region bounded by the functions on the interval [6, 8].
Enter an exact answer.
Provide your answer below:
A = ________units^2.](https://media.kunduz.com/media/sug-question/raw/78944824-1660220741.1907597.jpeg?w=256)
Calculus
Limits & ContinuityR is the region bounded by the functions f(x) = 14 / (-1 + x) and g(x) = 2x – 14. Find the area of the region bounded by the functions on the interval [6, 8].
Enter an exact answer.
Provide your answer below:
A = ________units^2.
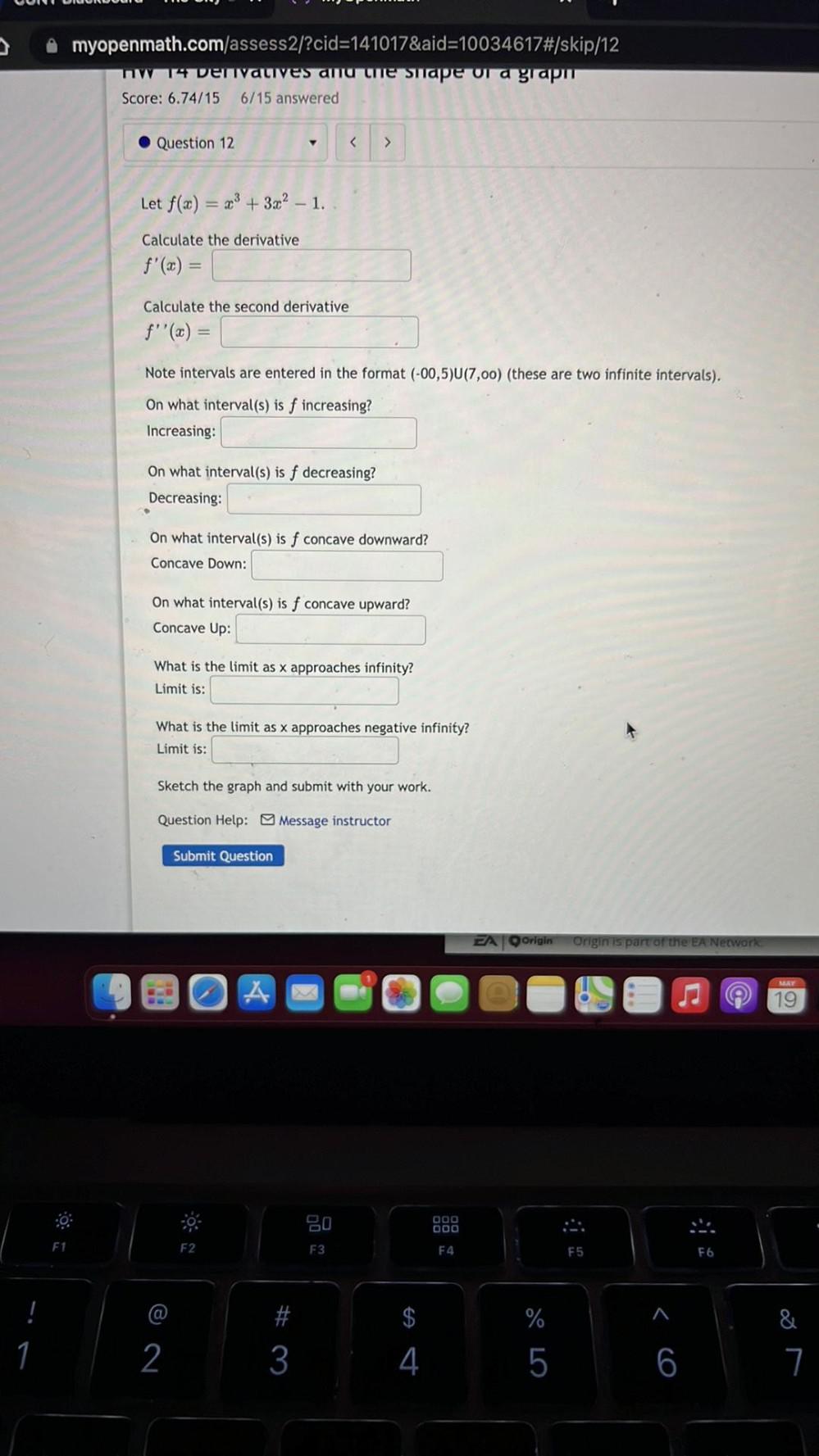
Calculus
Limits & ContinuityLet f(x) = x³+ 3x² – 1.
Calculate the derivative
f'(x) =________________
Calculate the second derivative
f''(x) =________________
Note intervals are entered in the format (-00,5)U(7,oo) (these are two infinite intervals).
On what interval(s) is f increasing?
Increasing:_________________
On what interval(s) is f decreasing?
Decreasing:____________________
On what interval(s) is f concave downward?
Concave Down:____________________
On what interval(s) is f concave upward?
Concave Up:____________
What is the limit as x approaches infinity?
Limit is:______________
What is the limit as x approaches negative infinity?
Limit is:-__________________-
Sketch the graph and submit with your work.
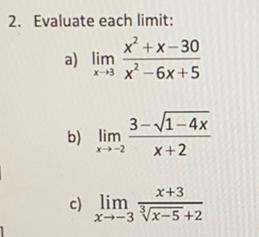
Calculus
Limits & ContinuityEvaluate each limit:
a) lim (x + x - 30) / (x - 6x + 5)
x-3
b) lim {3 - √(1-4x)} / (x + 2)
x->-2
c) lim (x +3) / ∛(x - 5) + 2
x->-3
Calculus
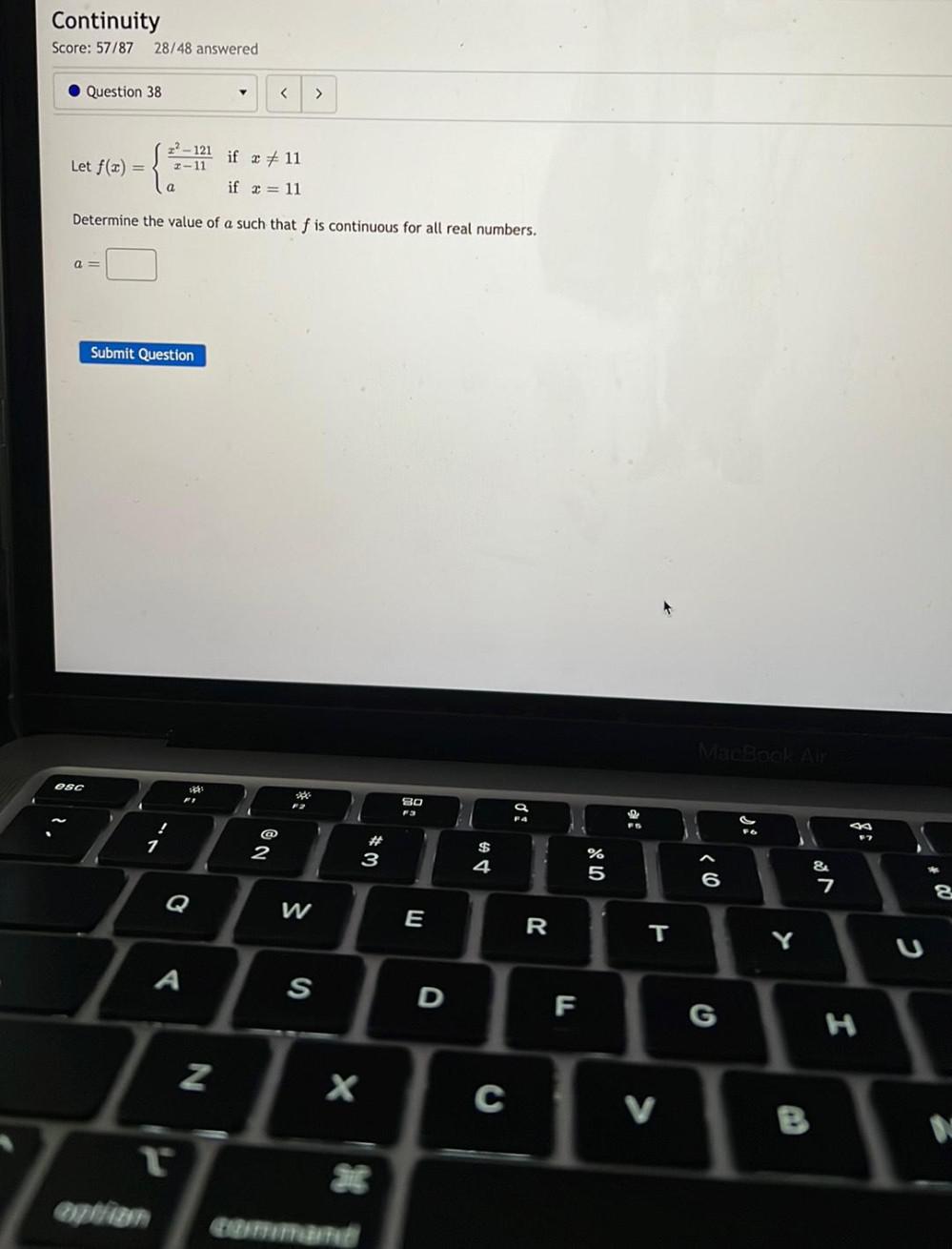
Limits & ContinuityLet f(x) = { (x² - 121) /(x - 11) if x ≠ 11
{ a if x = 11
Determine the value of a such that f is continuous for all real numbers.
a = ______
Calculus
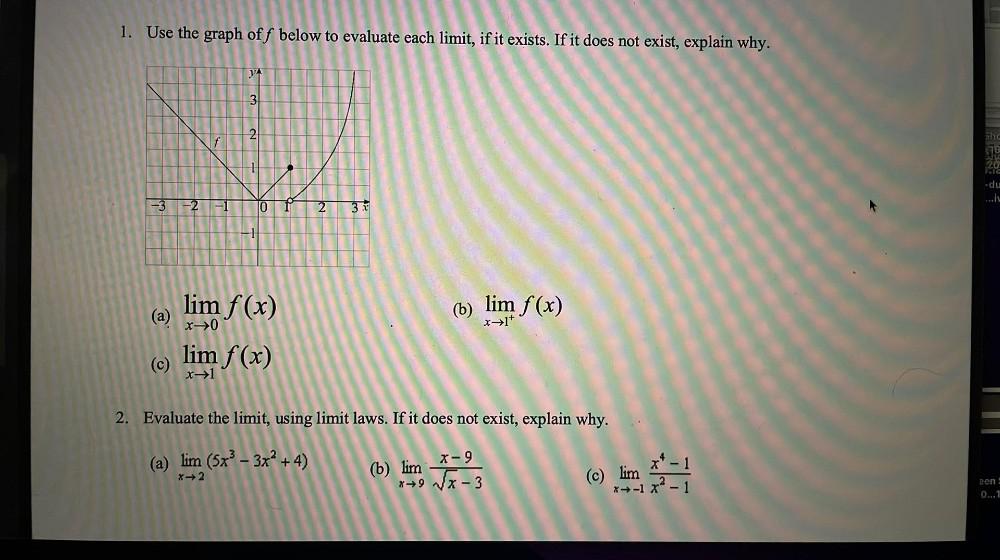
Limits & Continuity1) Use the graph off below to evaluate each limit, if it exists. If it does not exist, explain why.
a) lim f (x)
x->0
(b) lim f(x)
x->1+
(c) lim f(x)
x->1
2) Evaluate the limit, using limit laws. If it does not exist, explain why.
(a) lim (5x³ - 3x² + 4)
x->2
(b) lim x-9 / √(x-3)
x->9
(c) lim (x⁴ - 1) /(x² - 1)
x->1

Calculus
Limits & ContinuityUse the Limit Comparison Test to prove convergence or divergence of the infinite series.
Σ∞ n=2 n²/n⁴ - 1
Σ∞ n=2 1/n(n-1)
Σ∞ n=2 n/√n³+1
Σ∞ n=2 n³/√n⁷+2n²+1


Calculus
Limits & ContinuityQuestion 31
Convert the angle to decimal degrees and round to the nearest hundredth of a degree.
29°41'=__________
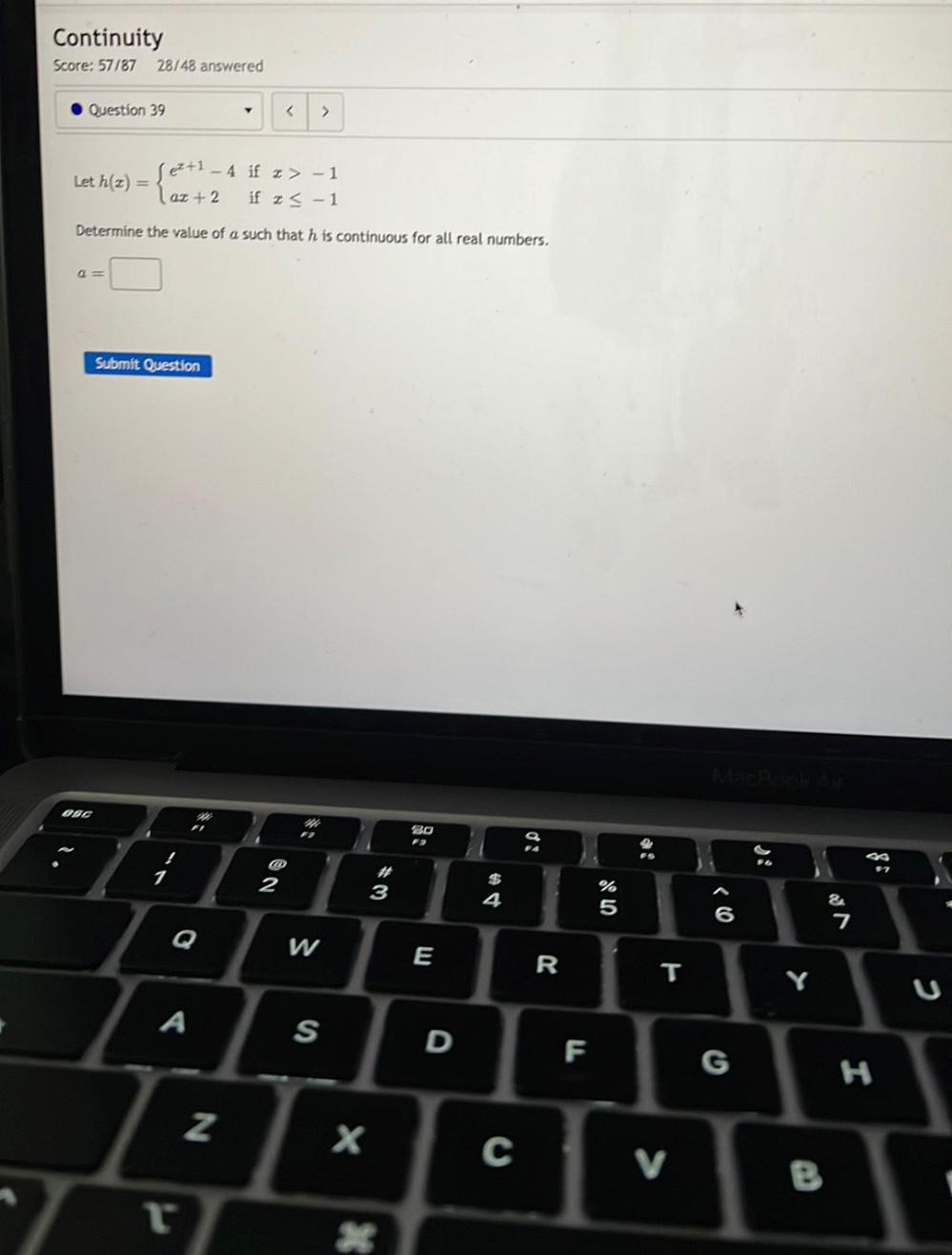
Calculus
Limits & ContinuityLet h(x) = { eˣ+¹ if x > -1
{ ax + 2 if x≤ -1
Determine the value of a such that his continuous for all real numbers.
a = ____
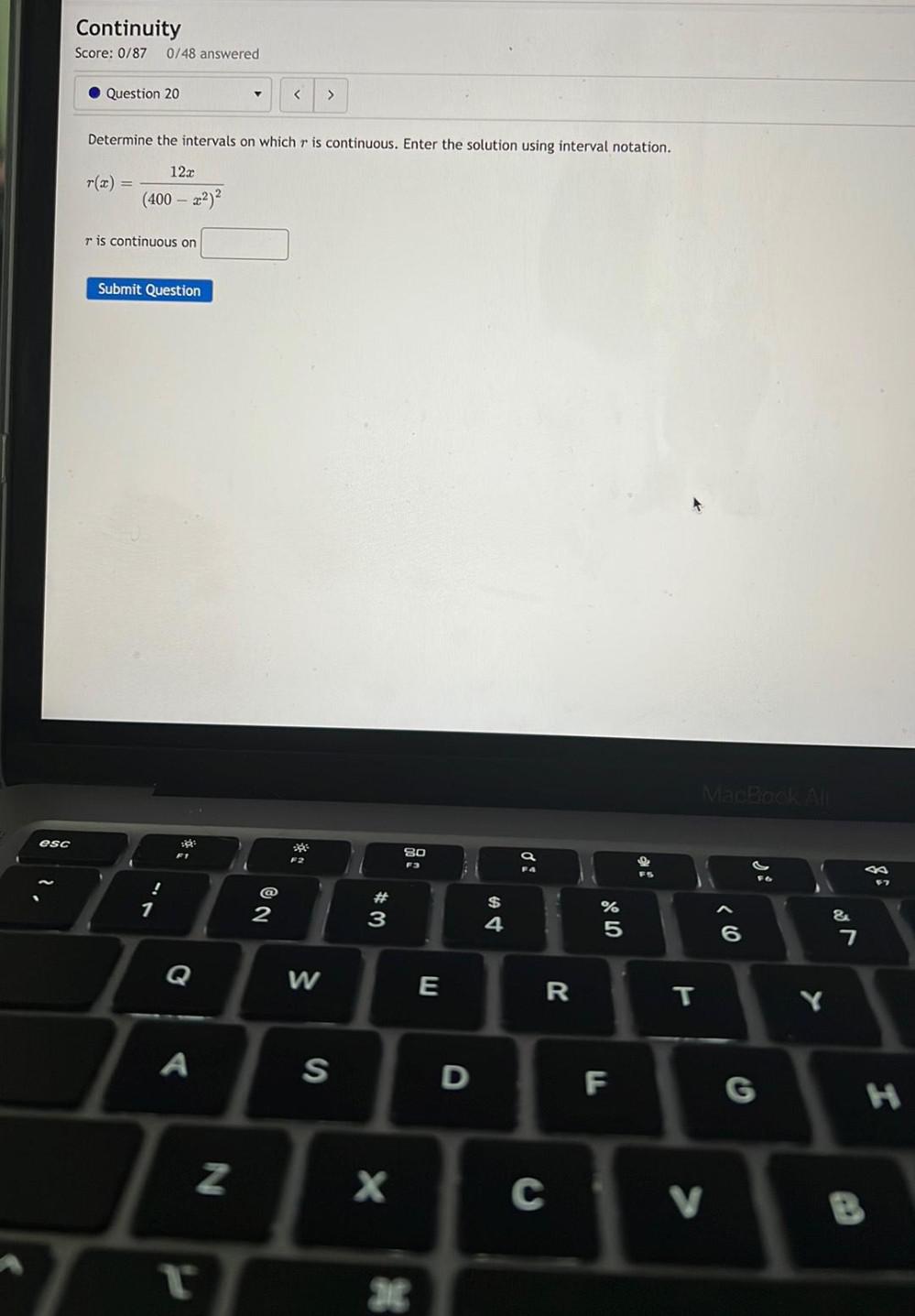
Calculus
Limits & ContinuityDetermine the intervals on which r is continuous. Enter the solution using interval notation.
r(x) =12x/ (400 – x^2)^2
r is continuous on ______________

Calculus
Limits & ContinuityA bag has seven balls labeled A, B, C, D, E, F, and G. One ball will be randomly picked, and its letter will be recorded as the outcome. Give the sample space describing all possible outcomes. Then give all of the outcomes for the event of choosing a vowel. If there is more than one element in the set, separate them with commas.
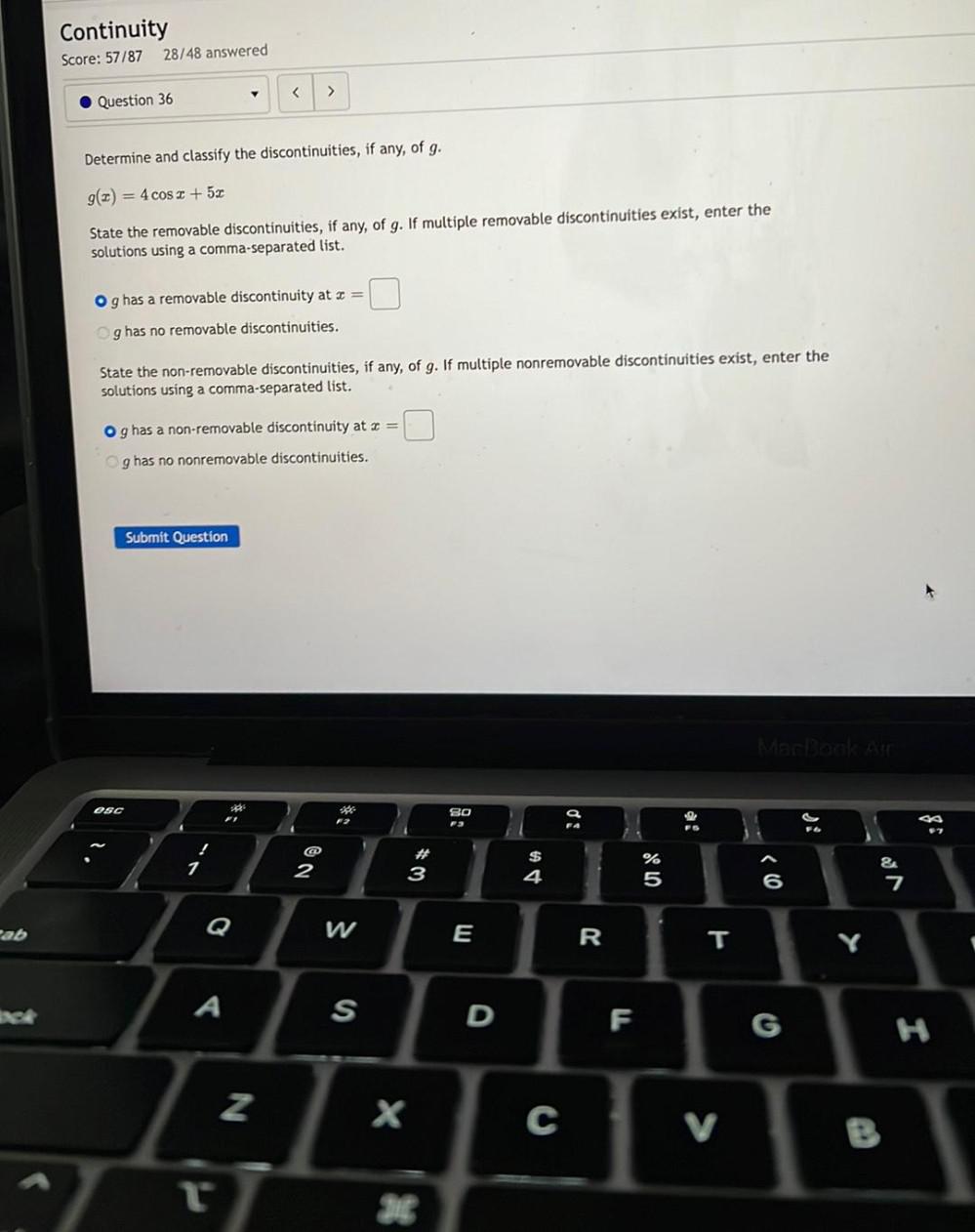
Calculus
Limits & ContinuityDetermine and classify the discontinuities, if any, of g.
g(x) = 4cosx + 5x .
State the removable discontinuities, if any, of g. If multiple removable discontinuities exist, enter the solutions using a comma-separated list.
(a) g has a removable discontinuity at x = __
g has no removable discontinuities.
State the non-removable discontinuities, if any, of g. If multiple non removable discontinuities exist, enter the
solutions using a comma-separated list.
(a) g has a non-removable discontinuity at x = __
g has no non removable discontinuities.
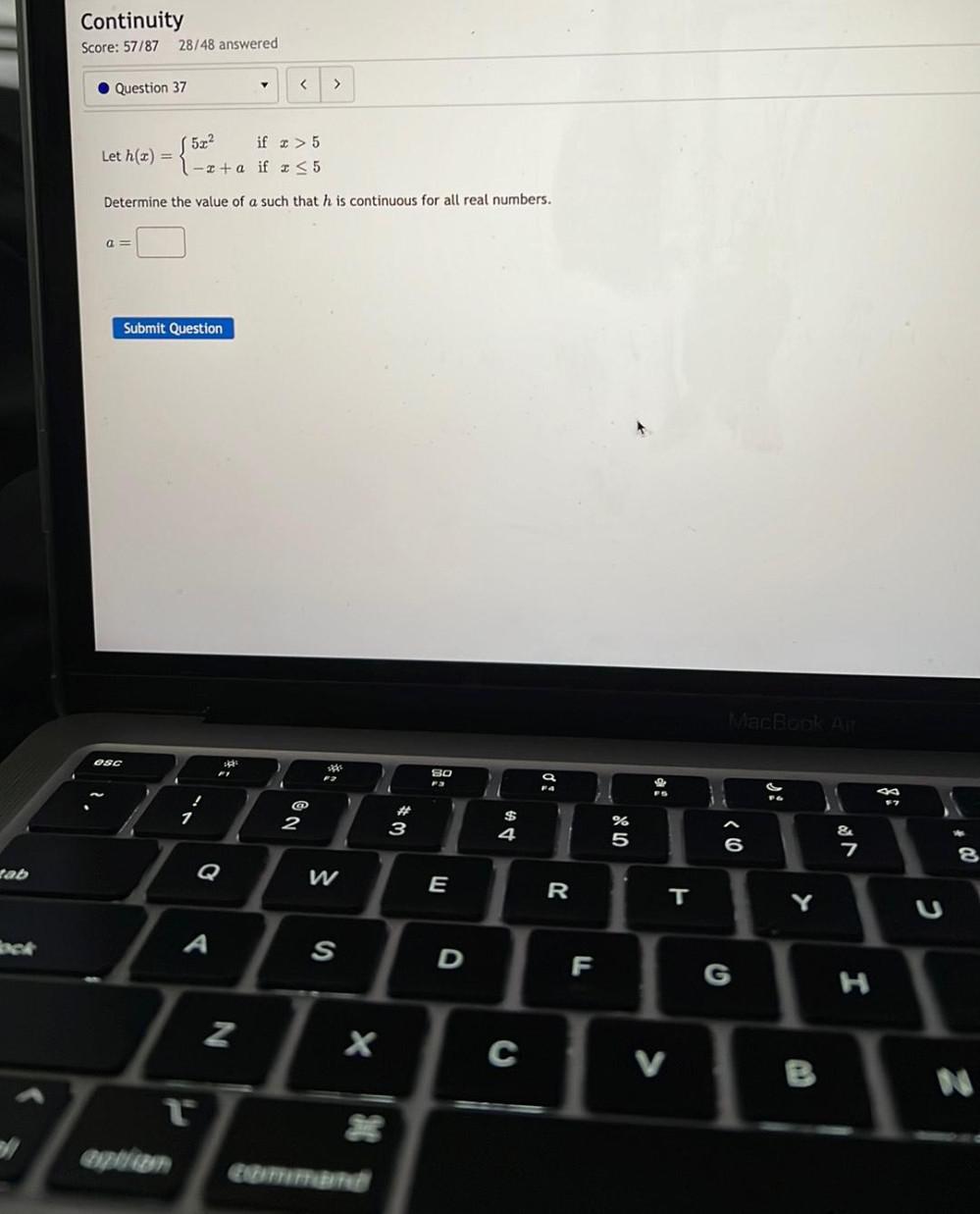
Calculus
Limits & ContinuityLet h(x) = { 5x² if x > 5
{ -x + a if ≤ 5
Determine the value of a such that h is continuous for all real numbers.
a = ____

Calculus
Limits & ContinuityWhen a skydiver free-falls from an airplane, her downward velocity in feet per second is given as v(t) = 240(1 – 0.85'), where t is the number of seconds since the jump.
a. First, find the limit of v(t) as t -> ∞. This is the terminal velocity of the jumper.

Calculus
Limits & ContinuityUse the Direct Comparison Test to determine whether the infinite series is convergent.
Σ∞ n=1 1/n2ⁿ
Σ∞ n=1 n³/n⁵+4n+1
Σ∞ n=1 1/n¹/³+2ⁿ
Σ∞ n=1 1/√n³+2n-1
Σ∞ n=1 4/m!+4ᵐ
Σ∞ n=1 √n/n-3
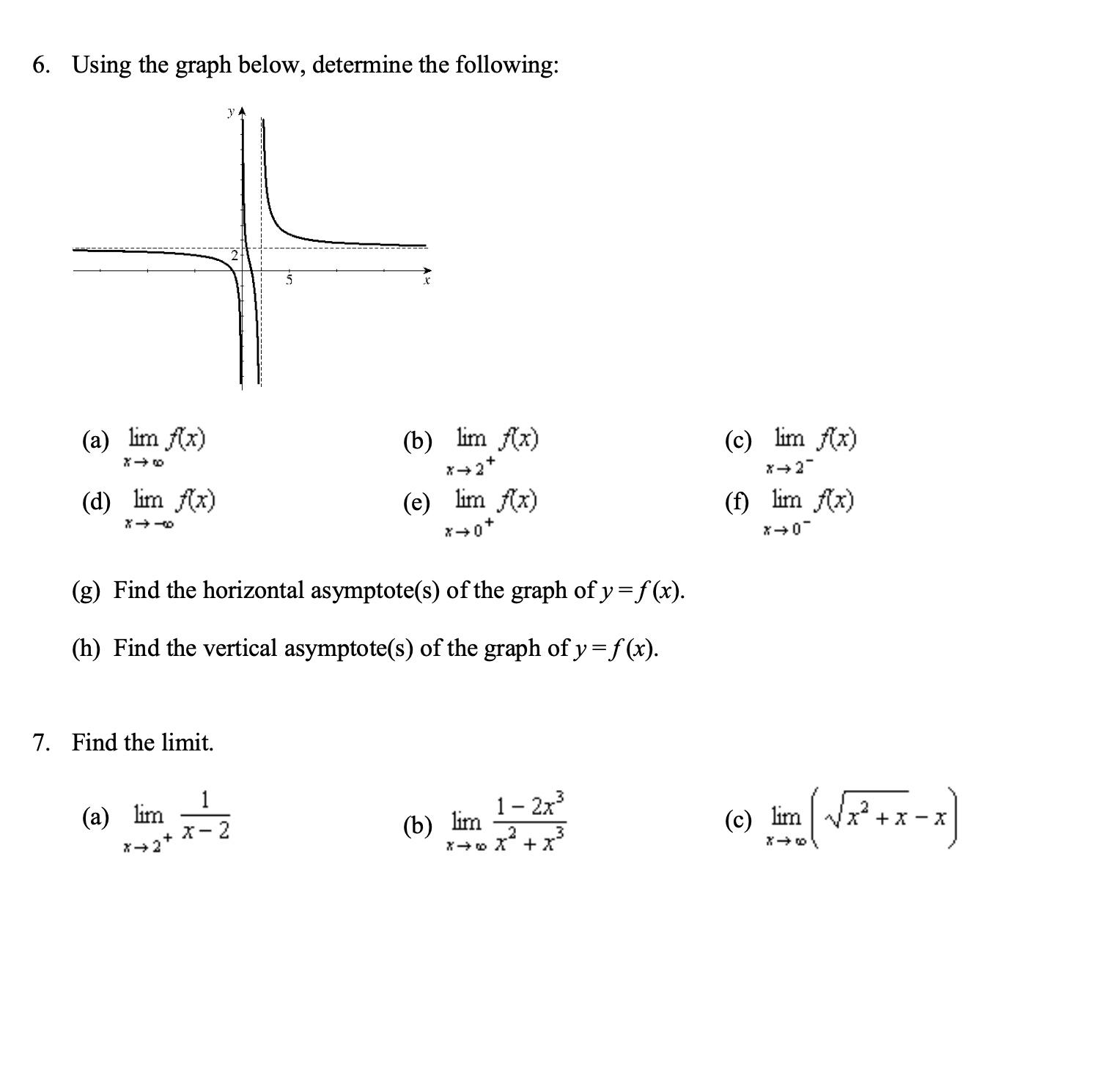
Calculus
Limits & ContinuityUsing the graph below, determine the following:
(a) lim f(x)
(c) lim f(x)
(b) lim f(x)
(e) lim (x)
(d) lim f(x)
(f) lim f(x)

Calculus
Limits & ContinuityIn Exercises, determine whether the series converges absolutely, conditionally, or not at all.
Σ∞ n=1 (-1)ⁿ‾¹/n¹/³
Σ∞ n=1 (-1)ⁿn⁴/n³+1
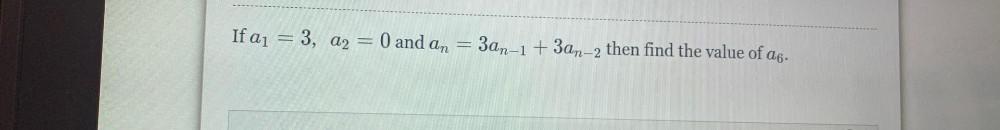

Calculus
Limits & ContinuityDoes the table represent a linear or exponential function? Find a formula
x 1 2 3 4
h(x) 70 49 34.3 24.01

Calculus
Limits & ContinuityUse the derivative formula f'(x)= lim h->0 f(x + h) – f(x)/h to find the derivative of
f(x) = √x
Find the derivative of
y = 4x² - 3x/sinx
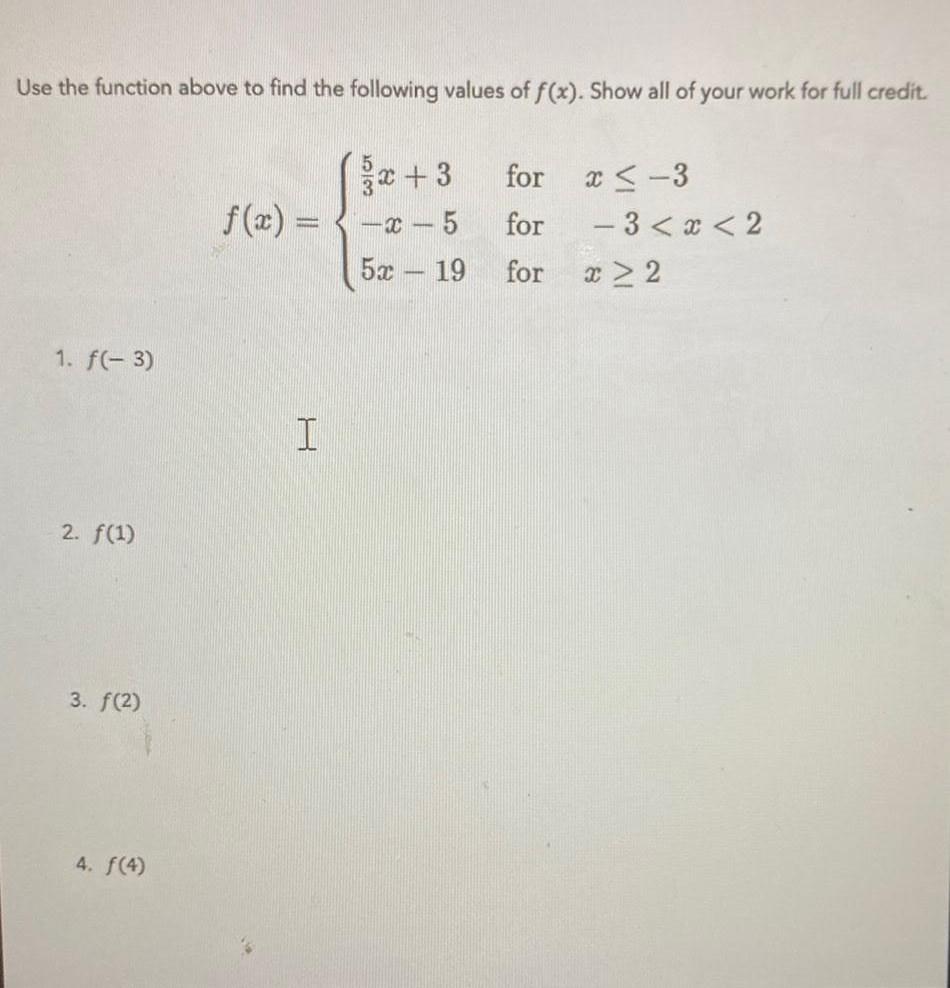
Calculus
Limits & ContinuityUse the function above to find the following values of f(x). Show all of your work for full credit.
f(x) = {5/3 x + 3 for x ≤ -3, {-x -5 for -3 < x <, {5x - 19 for x ≥ 2
a. f(-3)
b. f(1)
c. f(2)
d. f(4)
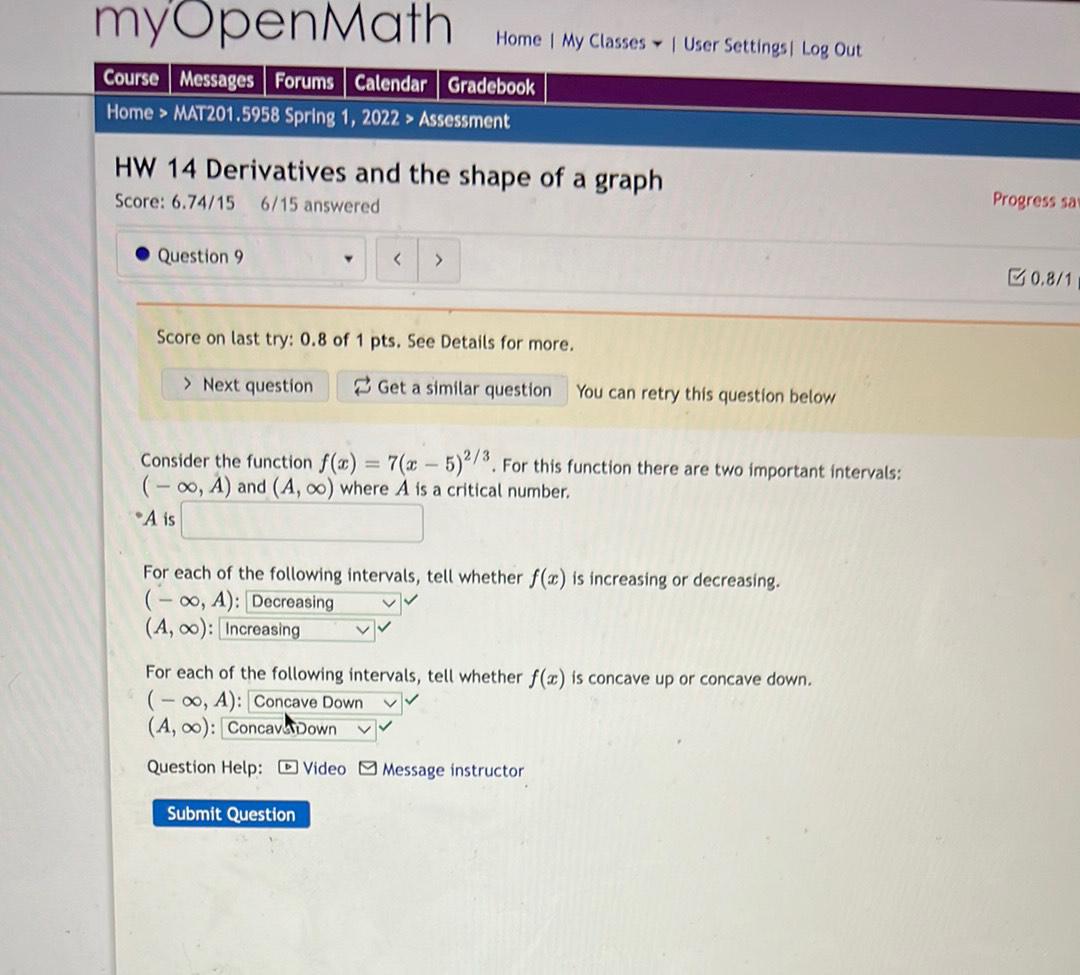
Calculus
Limits & ContinuityConsider the function f(c) = 7(x - 5)^(2/3). For this function there are two important intervals:
(- ∞, A) and (A, ∞) where A is a critical number.
A is _______________
For each of the following intervals, tell whether f(x) is increasing or decreasing.
(- ∞, A): ____________
(A, ∞): _____________
For each of the following intervals, tell whether f(x) is concave up or concave down.
(-∞, A): ____________
(A, ∞):_____________

Calculus
Limits & ContinuitySuppose sin 2x =-√ 2/2
Find all solutions 0≤x≤2π . Give exact values in radians,and type "pi" for π.
x=____________
(If there is more than one answer, enter the answers separated by
commas)
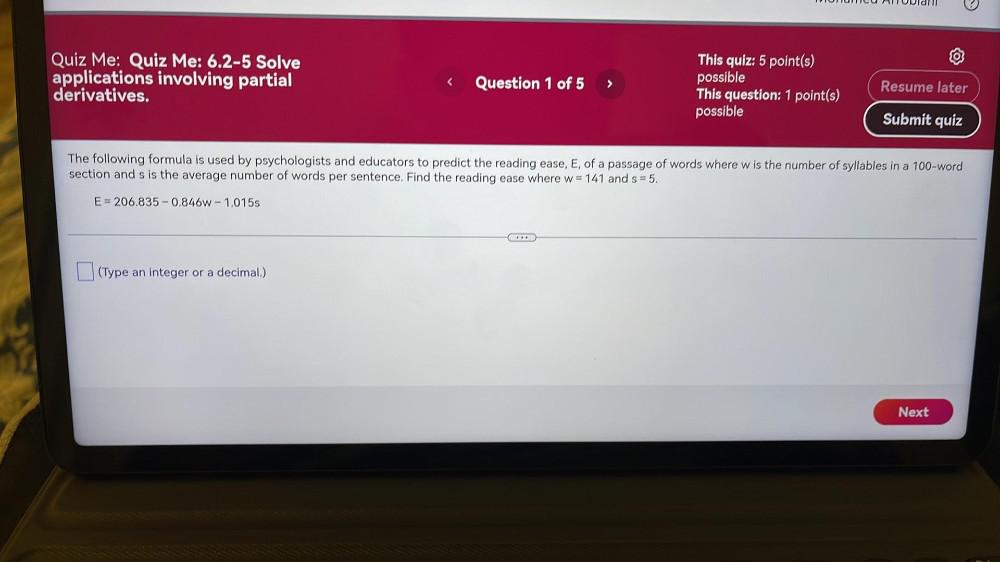
Calculus
Limits & ContinuityThe following formula is used by psychologists and educators to predict the reading ease, E, of a passage of words where w is the number of syllables in a 100-word
section and s is the average number of words per sentence. Find the reading ease where w= 141 and s=5.
E = 206.835 -0.846W - 1.015s
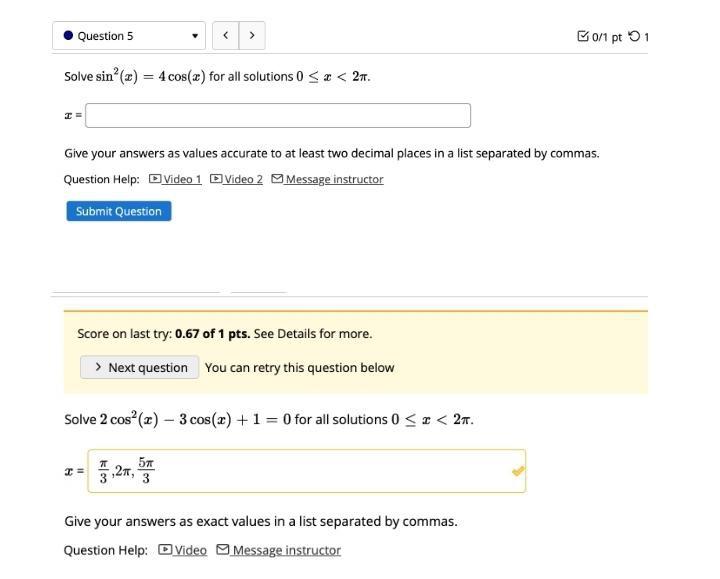
Calculus
Limits & ContinuitySolve sin^2(x) = 4 cos(x) for all solutions 0 ≤ x < 2π.
x =
Give your answers as values accurate to at least two decimal places in a list separated by commas.

Calculus
Limits & ContinuityLet F be the set of functions of the form f(x) = A sin(x) + B cos(2x), where A, B are some real constants. Show that there must exist exactly one function f in F so that for any f∈F
√∫(f(x)- arctan(x))²dx≤ √∫(f(x)- arctan(x))²dx
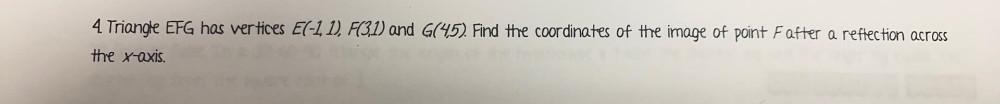
Calculus
Limits & ContinuityTriangle EFG has vertices El-11), F(3.1) and G(45) Find the coordinates of the image of point Fafter a reflection across the x-axis.
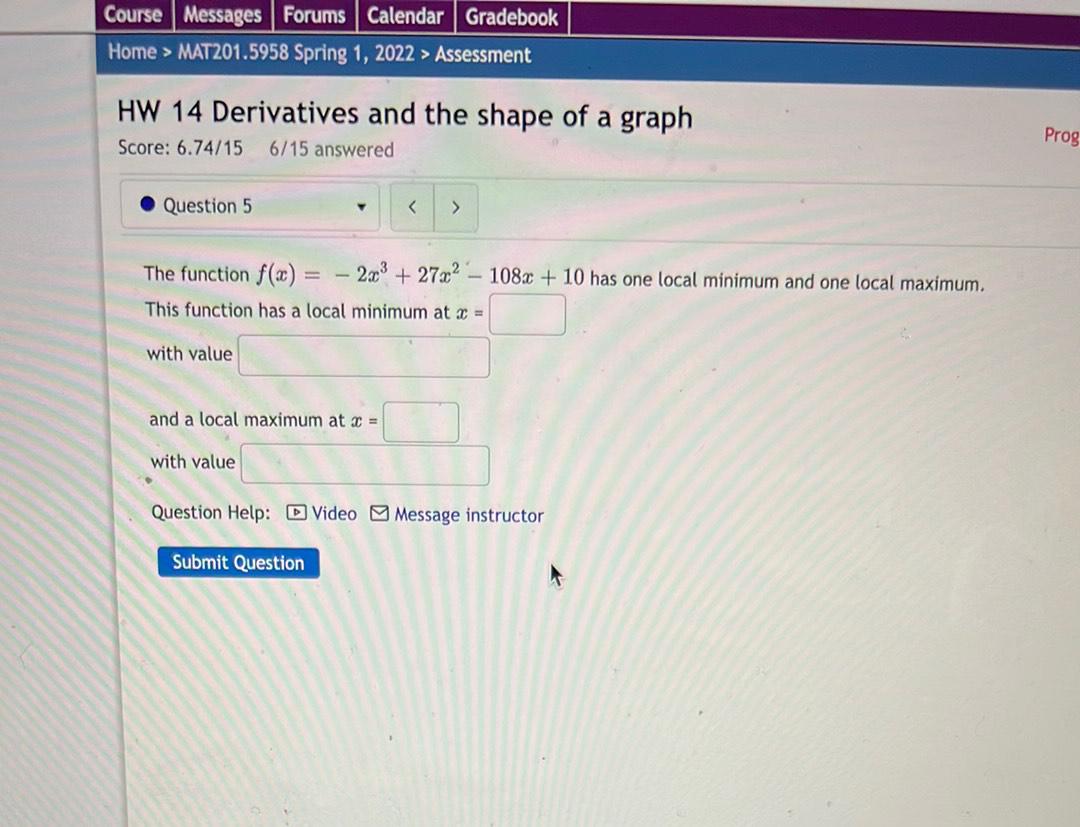
Calculus
Limits & ContinuityThe function f(x)=- 2x^3 +27x^2 - 108x + 10 has one local minimum and one local maximum.
This function has a local minimum at x =_______________
with value ___________
and a local maximum at x =___________
with value______________

Calculus
Limits & ContinuityJocelyn invested $56,000 in an account paying an interest rate of 7(3/8)% compounded continuously. Oliver invested $56,000 in an account paying an interest rate of 7(1/4)% compounded monthly. After 13 years, how much more money would Jocelyn have in her account than Oliver, to the nearest dollar?
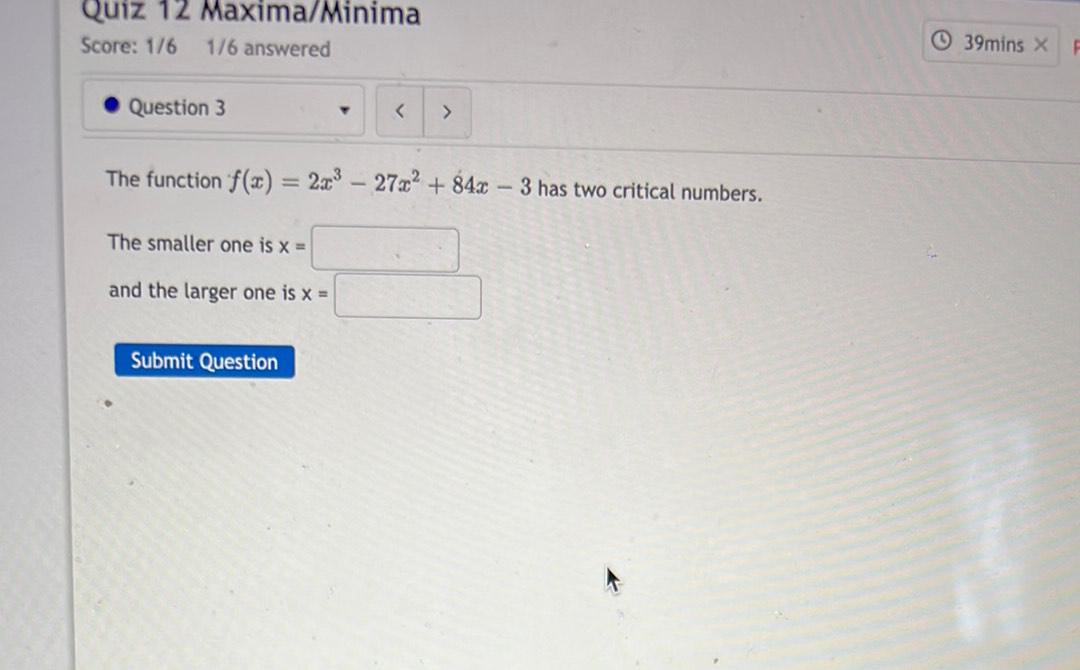
Calculus
Limits & ContinuityThe function f(x) = 2x^3 – 27x² + 84x – 3 has two critical numbers.
The smaller one is x =
and the larger one is x =
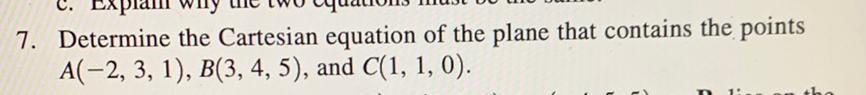
Calculus
Limits & ContinuityDetermine the Cartesian equation of the plane that contains the points A(-2, 3, 1), B(3,4,5), and C(1, 1, 0).
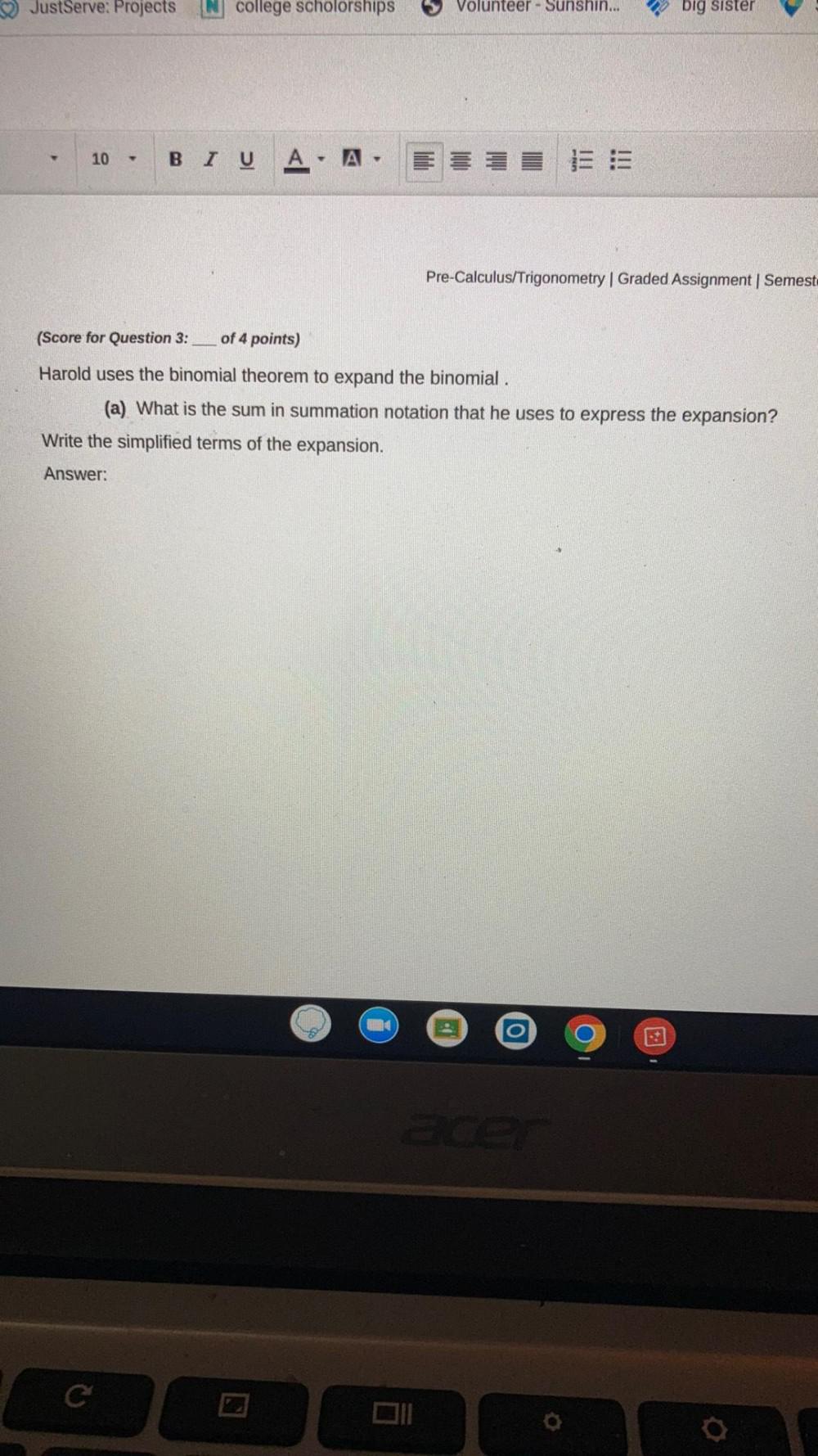
Calculus
Limits & ContinuityHarold uses the binomial theorem to expand the binomial.
(a) What is the sum in summation notation that he uses to express the expansion?
Write the simplified terms of the expansion.

Calculus
Limits & ContinuitySet up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
y = In(x), y = 0, x = 5; about the y-axis
dx
![Find the average value ha of the function h on the given interval.
ave
have
=
h(u):
12
In(u)
U
(3.78656)
[1, 7]](https://media.kunduz.com/media/sug-question/raw/84982997-1660218421.0174103.jpeg?w=256)
Calculus
Limits & ContinuityFind the average value ha of the function h on the given interval.
ave
have
=
h(u):
12
In(u)
U
(3.78656)
[1, 7]
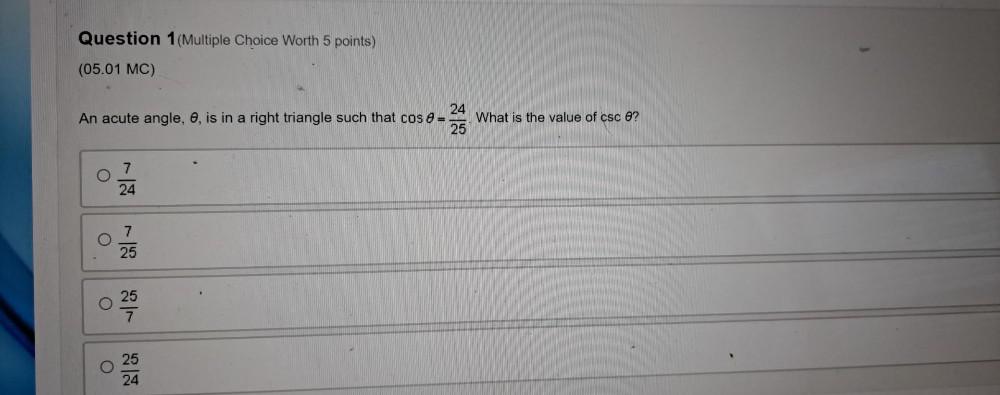
Calculus
Limits & ContinuityAn acute angle, o, is in a right triangle such that cosθ=24/25. What is the value of
csc θ?
(a)7/24
(b)7/25
(c)25/7
(d)25/24

Calculus
Limits & Continuitylim (cos²θ - sin²θ)/(cosθ - sinθ) =
θ->π/4
(A) - 1
(B) 0
(C) √2
(D) 1
(E)1/√2

Calculus
Limits & ContinuityUse the table below to find the limit, if it exists. If the limit does not exist type DNE. If you get infinity, you must type out the entire word, for negative infinity type-infinity. Bolded terms must be typed as you see them here or Schoology will count it wrong.
Use the table below of the rational function y = H(x) to find the indicated limits. For limits that do not exist, write D.N.E.
x H(x)
-1000 -0.998
-4.001 0.666
-4 undefined
-3.999 0.666
1.999 -4497
2 undefined
2.001 4504
1000 3.0002
A. limH(x)=
x->-4(from left)
B.limH(x)=
x->-4(from right)
C.limH(x)=
x->-∞
D.limH(x)=
x->-4
E.limH(x)=
x->2(from left)
F.limH(x)=
x->2+


Calculus
Limits & ContinuityIf a curve is defined by the parametric equations x(t) = 2t and y(t) = -4t² - 2 over the interval
- 2 ≤ t ≤ 2, which of the following gives the correct equation and domain of the path of the particle?
(A) y = -2x² - 1, -2 ≤ x ≤ 2
(B) y = -x² - 2, - 2 ≤ x ≤ 2
(C) y = -x² - 2, -4 ≤ x ≤ 4
(D) y = x² - 2, -2 ≤ x ≤ 2
(E) y = x² - 2, -4 ≤ x ≤ 4
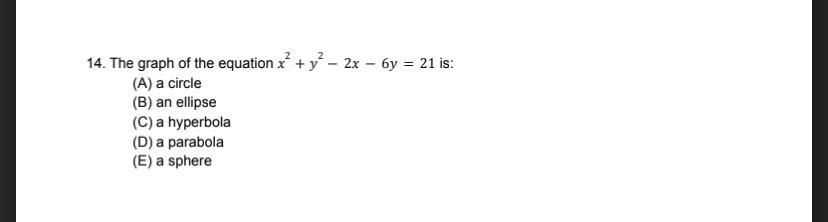
Calculus
Limits & ContinuityThe graph of the equation x² + y² - 2x - 6y = 21 is:
(A) a circle
(B) an ellipse
(C) a hyperbola
(D) a parabola
(E) a sphere