Limits & Continuity Questions and Answers
Calculus
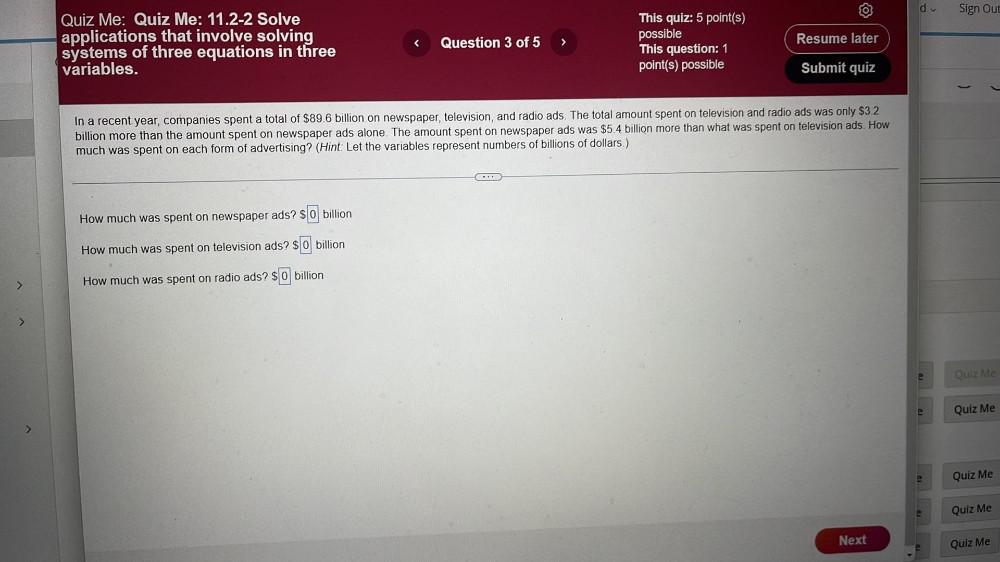
Limits & ContinuityIn a recent year, companies spent a total of $89.6 billion on newspaper, television, and radio ads. The total amount spent on television and radio ads was only $3.2 billion more than the amount spent on newspaper ads alone. The amount spent on newspaper ads was $5.4 billion more than what was spent on television ads. How much was spent on each form of advertising? (Hint: Let the variables represent numbers of billions of dollars.)
How much was spent on newspaper ads? $_____ billion
How much was spent on television ads? $_____ billion
How much was spent on radio ads? $______ billion
Calculus
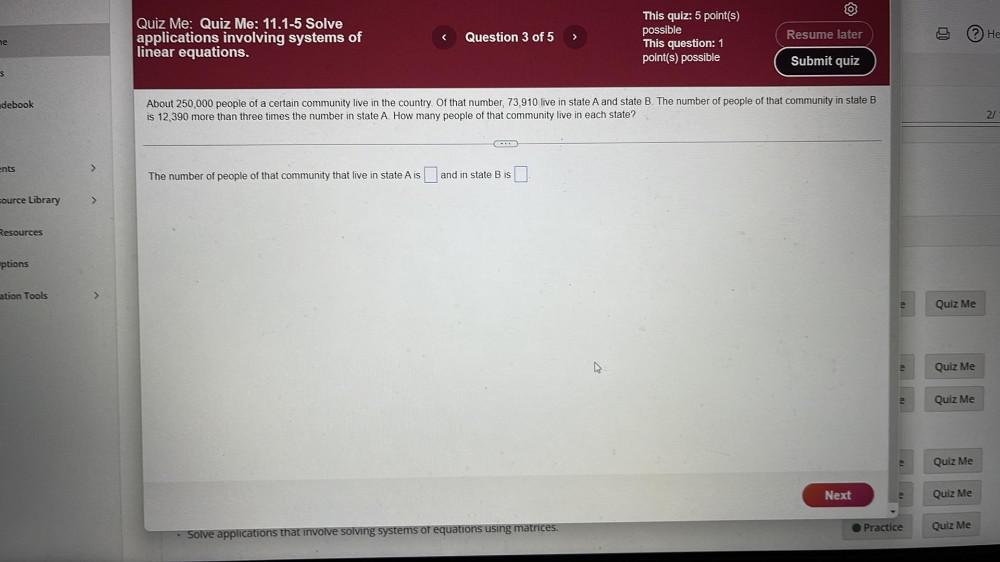
Limits & ContinuityAbout 250,000 people of a certain community live in the country. Of that number, 73,910 live in state A and state B. The number of people of that community in state B is 12,390 more than three times the number in state A. How many people of that community live in each state? The number of people of that community that live in state A is? and in state B is ?

Calculus
Limits & ContinuitySolve:
log_3 (9x + 17) - log_3(-5x - 15)
X =_____ (Enter DNE if no solution exists)

Calculus
Limits & ContinuityAt low altitudes the altitude of a parachutist and time in the air are linearly related. A jump at 2,500 feet lasts 100 seconds.
(A) Find a linear model relating altitude a (in feet) and time in the air t (in seconds).
(B) Find the rate of change of the parachutist in the air.
(C) Find the speed of the parachutist at landing.
(Type an equation using t as the variable.)
Calculus
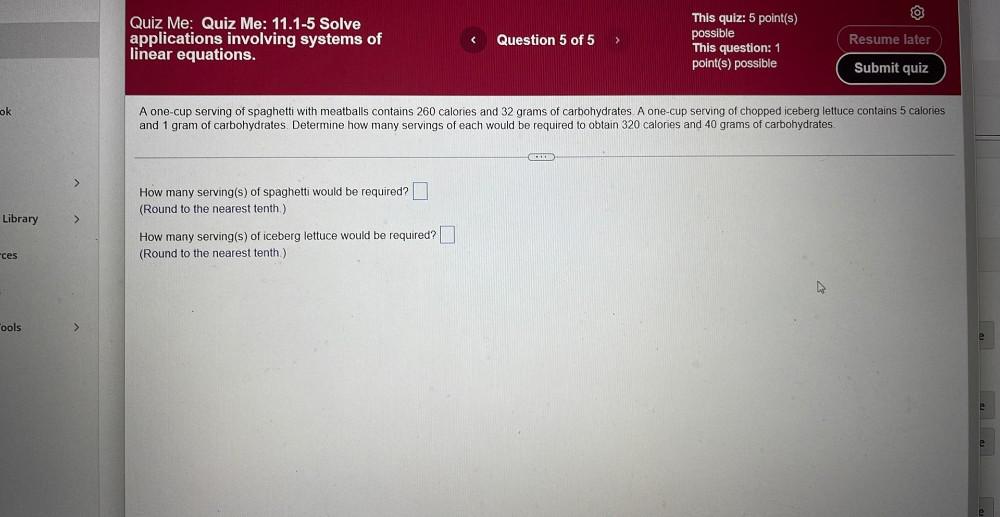
Limits & ContinuityA one-cup serving of spaghetti with meatballs contains 260 calories and 32 grams of carbohydrates. A one-cup serving of chopped iceberg lettuce contains 5 calories and 1 gram of carbohydrates. Determine how many servings of each would be required to obtain 320 calories and 40 grams of carbohydrates.
(a)How many serving(s) of spaghetti would be required?
(Round to the nearest tenth.)
(b)How many serving(s) of iceberg lettuce would be required?
(Round to the nearest tenth.)

Calculus
Limits & ContinuitySuppose - 2x² - 4x - 5 ≤ g(x) ≤ - 3 for all x-values near x = - 1, except possibly at x = − 1.
Use the Squeeze Theorem to determine the following limit. Enter DNE if the limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.
lim g(x ) = _________
x→ -1
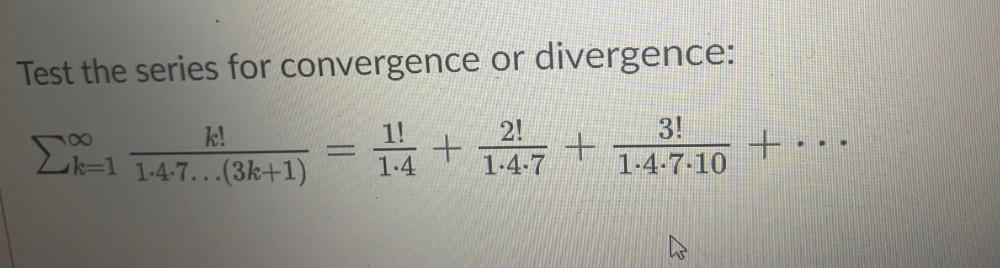
Calculus
Limits & ContinuityTest the series for convergence or divergence:
Σ∞ k=1 k!/1.4.7.........(3k+1) = 1!/1.4 + 2!/1.4.7 + 3!/1.4.7.10 + .................
![lim (√x + x²)
x->4
[A] 4 [B] 4.472 [C] 20 [D] 18
A
B
C
D](https://media.kunduz.com/media/sug-question/raw/79887718-1660163376.7871344.jpeg?w=256)
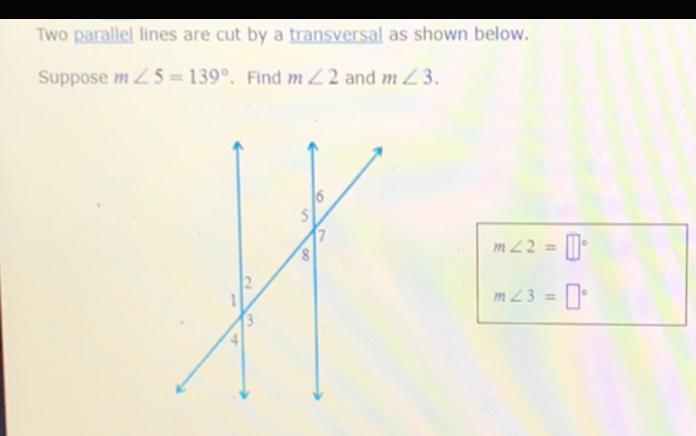
Calculus
Limits & ContinuityTwo parallel lines are cut by a transversal as shown below.
Suppose m ∠5=139°. Find m ∠2 and m ∠3.
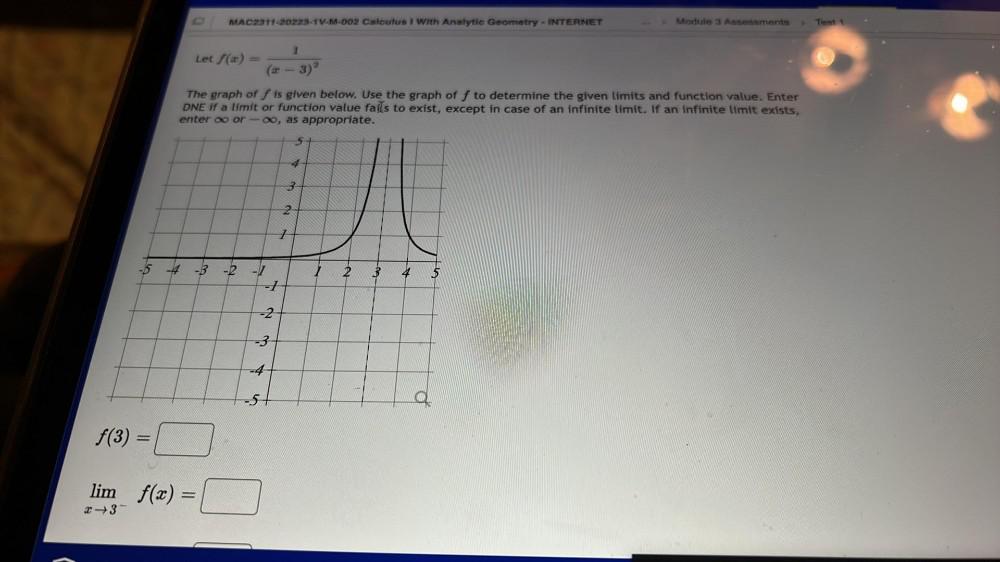
Calculus
Limits & ContinuityThe graph of f is given below. Use the graph of f to determine the given limits and function value. Enter DNE if a limit or function value fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or-oo, as appropriate.
Calculus
Limits & ContinuityUse analytic methods to evaluate the following limit. Enter DNE if the limit fails to exist, except in case of an infinite limit. If an infinite limit exists, enter ∞ or -∞, as appropriate.
limₓ→-₄ (x² - 5x - 36)/(x² + 10x + 24) = ____
![Solve the following integral, using remainders:
∫ [sin(z) + cos(z)]/e²(z² + 1)]dz
where C is the circumference |z| = 2, travel in positive direction.](https://media.kunduz.com/media/sug-question/raw/79938288-1660163039.8866262.jpeg?w=256)
Calculus
Limits & ContinuitySolve the following integral, using remainders:
∫ [sin(z) + cos(z)]/e²(z² + 1)]dz
where C is the circumference |z| = 2, travel in positive direction.
Calculus
Limits & ContinuityIf f is a polynomial function and x+2 is a factor of f, then f(-2)= ______
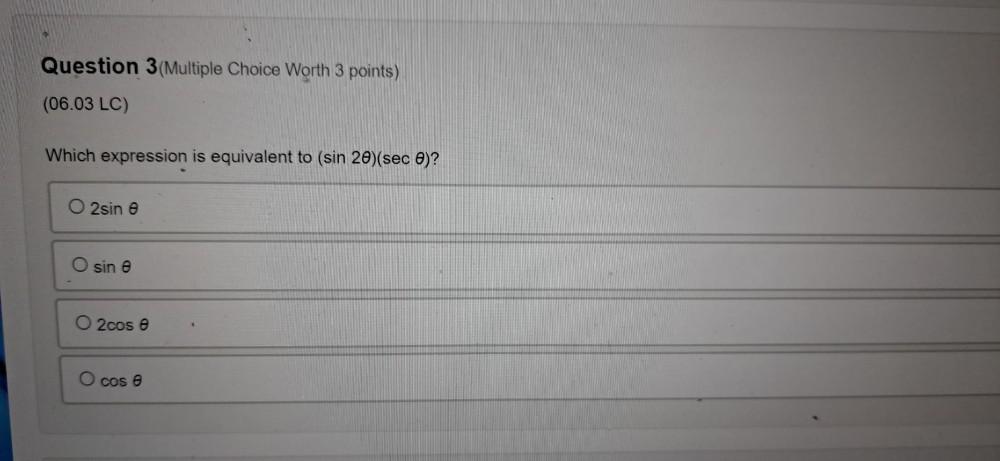
Calculus
Limits & ContinuityWhich expression is equivalent to (sin 2θ)(sec θ)?
2sin θ
sin θ
2cos θ
cos θ
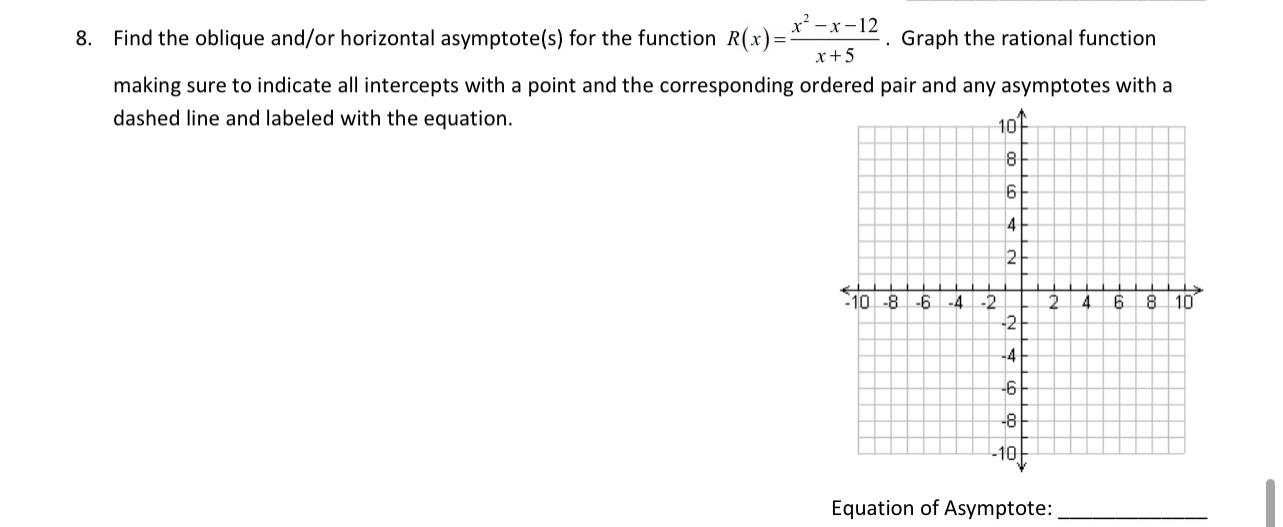
Calculus
Limits & ContinuityFind the oblique and/or horizontal asymptote(s) for the function R(x)=(x^2-x-12)/(x+5). Graph the rational function making sure to indicate all intercepts with a point and the corresponding ordered pair and any asymptotes with a dashed line and labeled with the equation.
Equation of Asymptote:___________

Calculus
Limits & ContinuityIn Exercises, determine convergence or divergence using any method covered in the text
so far.
Σ∞ n=1 2ⁿ+4ⁿ/7ⁿ
Σ∞ n=1 n³n¡

Calculus
Limits & ContinuityGiven the series
Σ(n!)³/(6n)!
find the ratio|an+1/an|=________
(Express numbers in exact form. Use symholic notation and fractions where needed.)
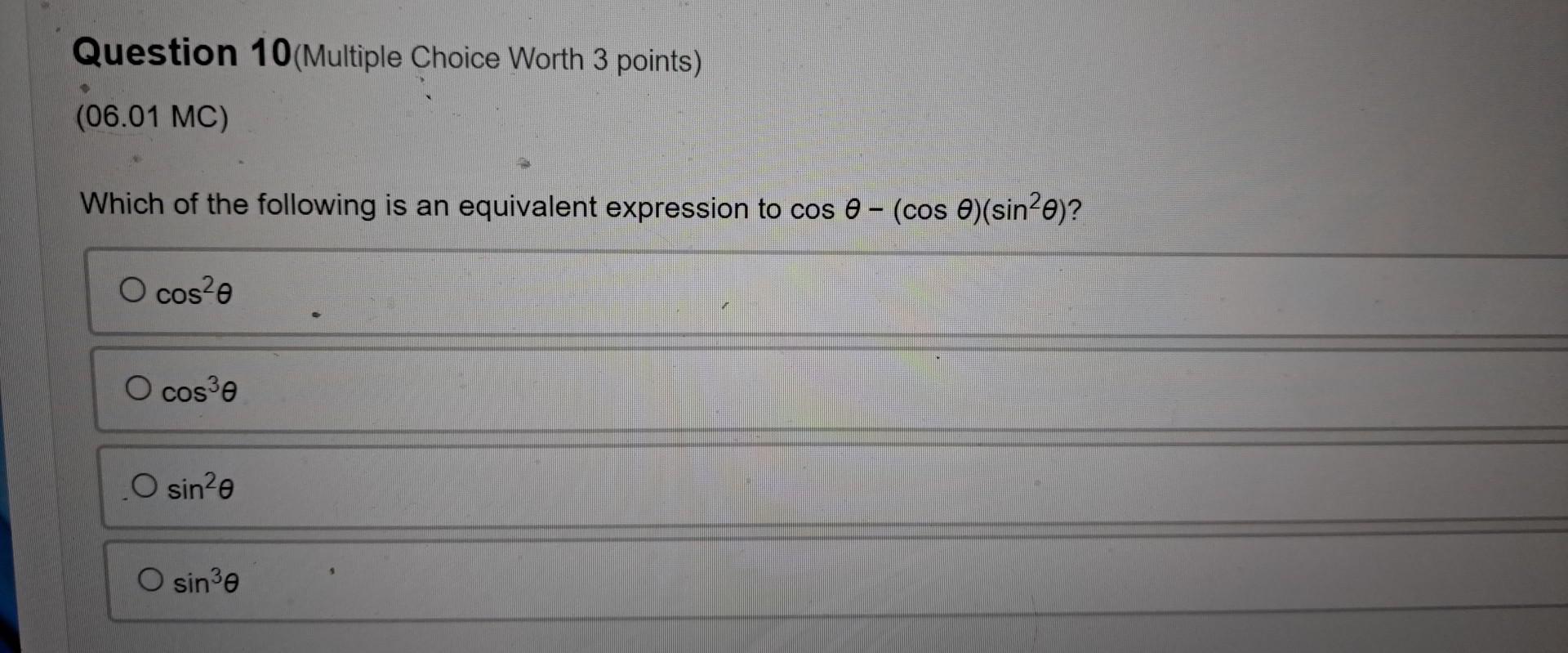
Calculus
Limits & ContinuityWhich of the following is an equivalent expression to cosθ - (cos θ (sin²θ)? cos²θ cos³θ sin²θ sin³θ
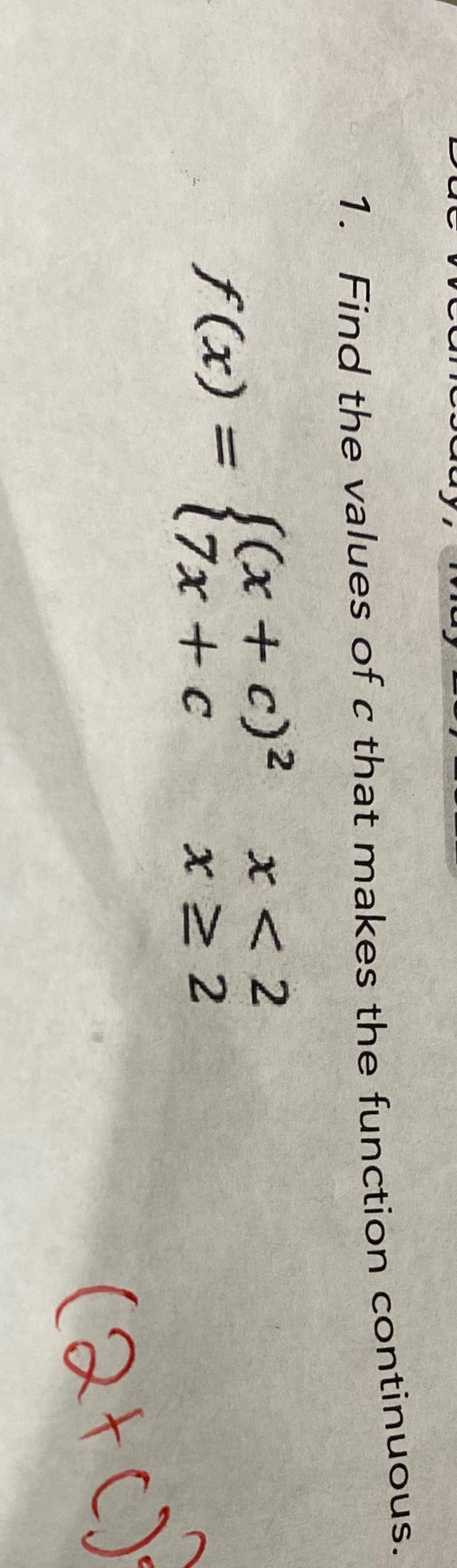
Calculus
Limits & ContinuityFind the values of c that makes the function continuous.
f(x) = (x + c)² x < 2
(7x + c) x ≥ 2

Calculus
Limits & ContinuityDetermine if the function is a polynomial. If it is, state the degree. If it is not, state why it is not a polynomial.
a. h(x)=3 - 1/x Polynomial? YES OR NO
Degree/Why Not:
b. G(p)=p²(p-1) Polynomial? YES OR NO
Degree/Why Not:

Calculus
Limits & ContinuityWhich numbers are equivalent to 25, 000 - 1.56 × 10³?
Select all correct numbers.
o 9,400
o 23,440
o 24, 844
o 9.4 × 10³
o 2.344 x 10^4
o 2.4844 x 10^4
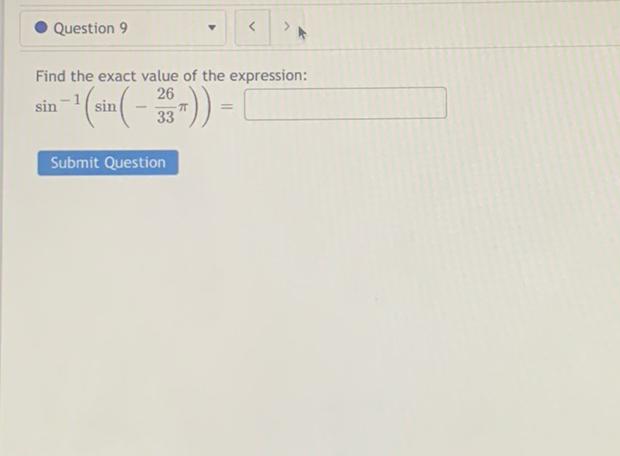
Calculus
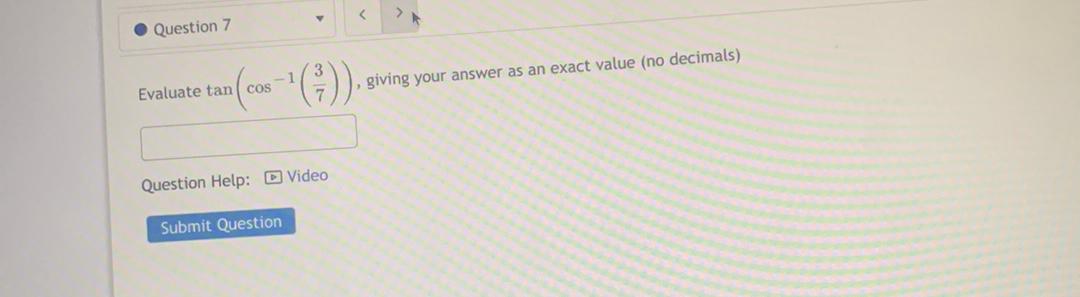
Limits & ContinuityEvaluate tan (cos-¹(3/7)), giving your answer as an exact value (no decimals)


Calculus
Limits & ContinuityLet f(x) = x²+2x-15/x²-9
g(x) = {f(x) x ≠ 3 find the value of a that makes g(x) continuous.
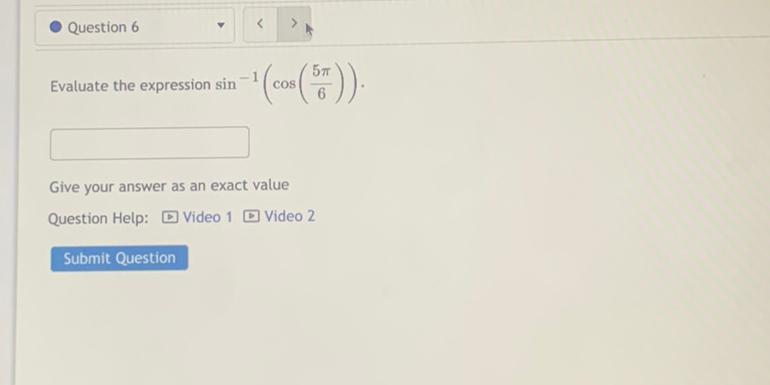
Calculus
Limits & ContinuityEvaluate the expression sin-¹(cos(5π/6))
Give your answer as an exact value

Calculus
Limits & ContinuityThe length of a rectangle is six centimeters more than the width. If the perimeter is 60cm, find the width and length.

Calculus
Limits & Continuity23. The height of a ball (h), in feet, after t seconds is modeled by the equation h = -16t² + 40t + 6.
What is the height of the ball after 2 seconds?
A) 22 feet B) 54 feet C) 150 feet D) 118 feet
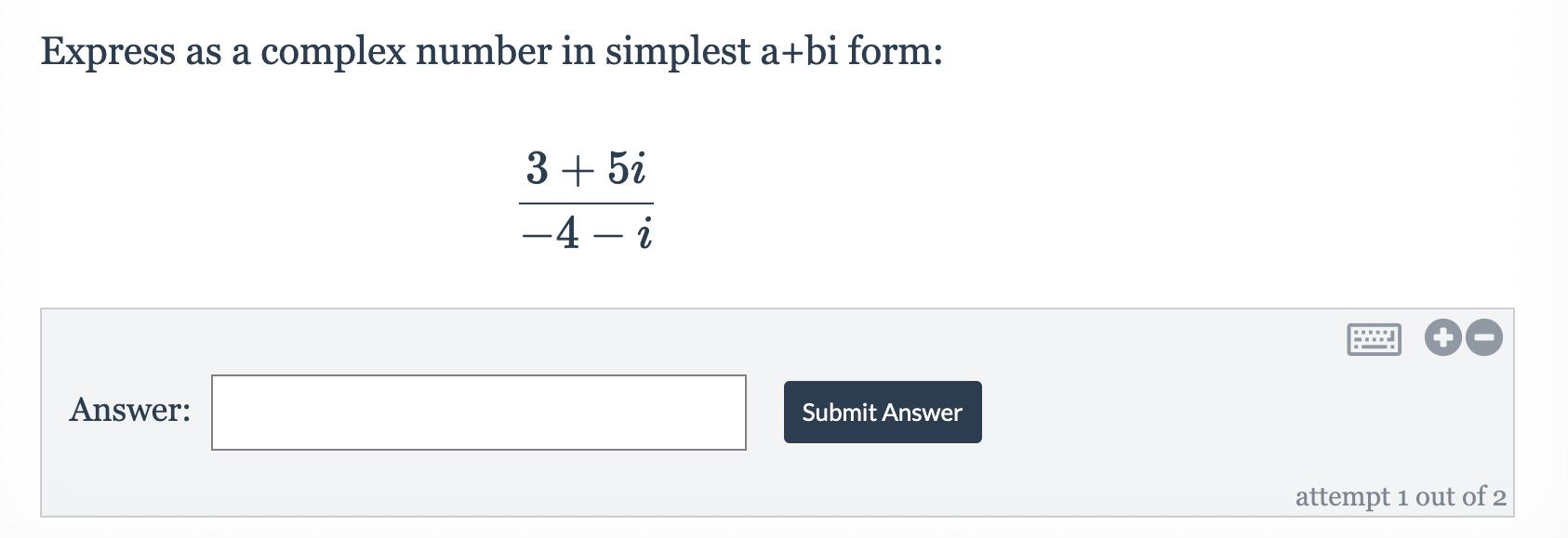


Calculus
Limits & ContinuitySolve the following system of equations.
3x+5y-52=21
-4x=5z+17
2x-5y+62--16
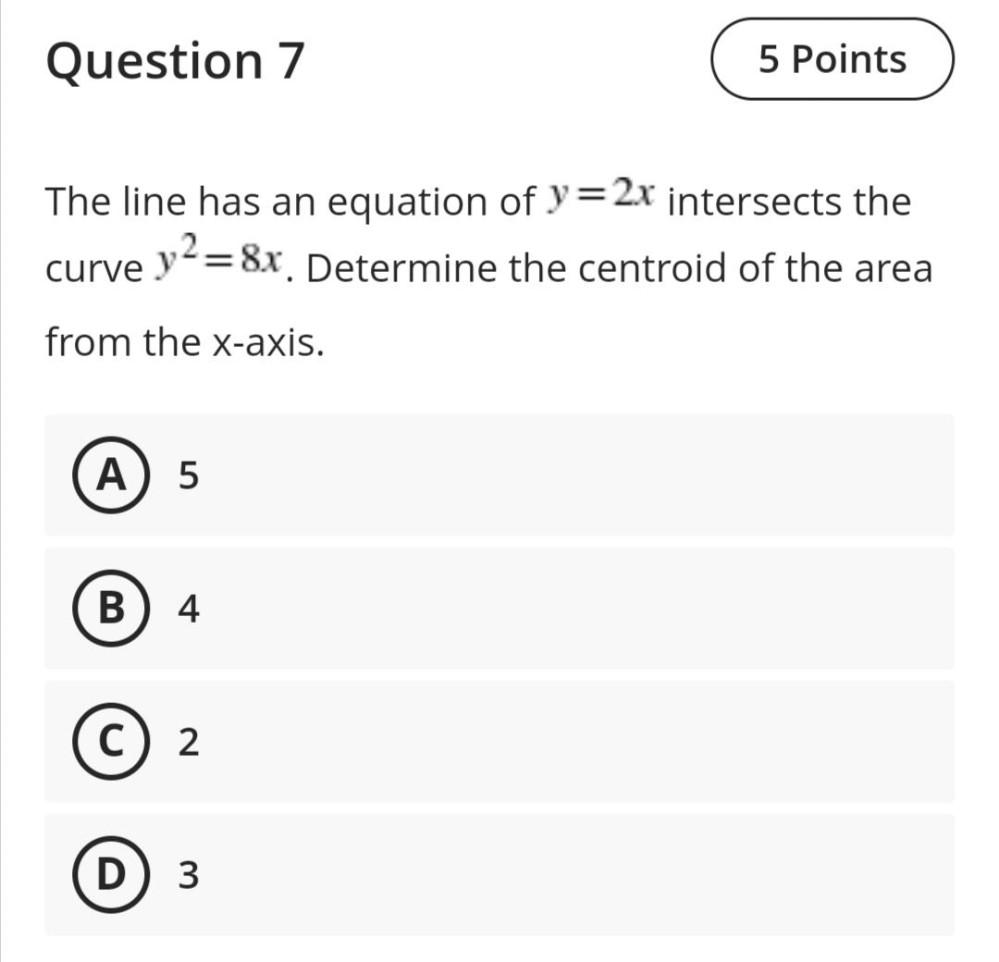
Calculus
Limits & ContinuityThe line has an equation of y = 2x intersects the curve y² = 8x.Determine the centroid of the area from the x-axis.
(A) 5
(B) 4
(C) 2
(D) 3

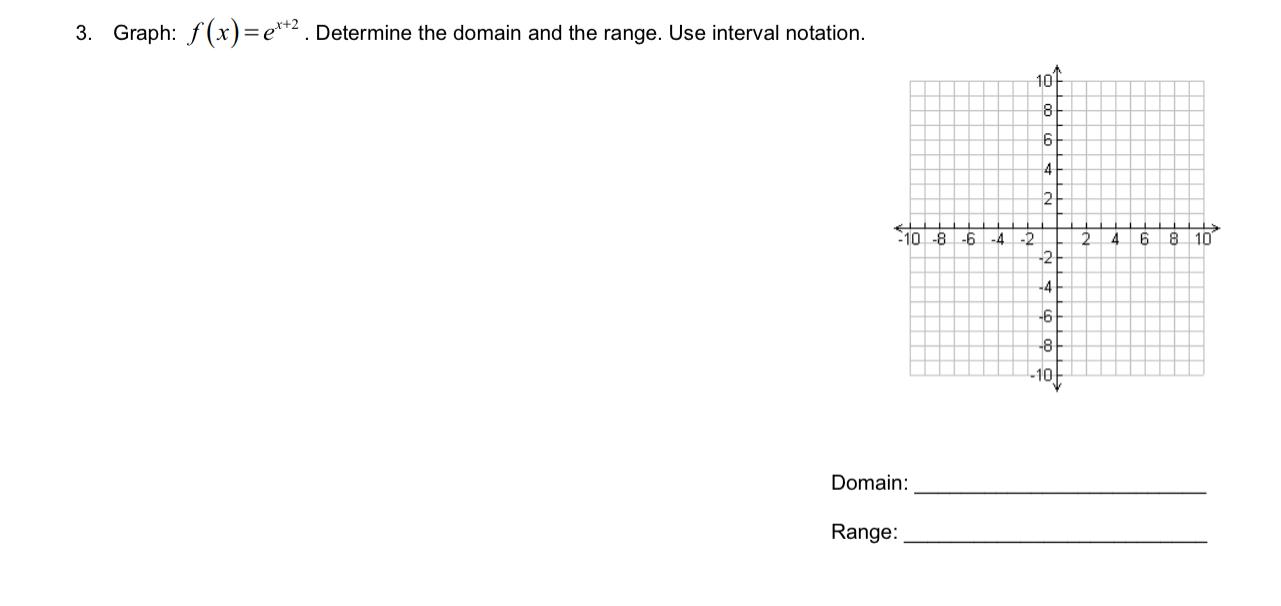
Calculus
Limits & Continuity3. Graph: f(x)=e^(x+2). Determine the domain and the range. Use interval notation.
Domain:_______
Range:_______
Calculus
Limits & ContinuityA science fair poster is a rectangle 36 inches long and 24 inches wide. What is the area of the poster in square feet? Be sure to include the correct unit in your answer._________

Calculus
Limits & ContinuityUse a calculator to evaluate the trigonometric function. Round your answer to four decimal places.
tan (33⁰) = ____

Calculus
Limits & Continuity6. Firing a piece of pottery in a kiln takes place at different temperatures for different amounts of time. The graph below shows the temperatures in a kiln while firing a piece of pottery after the kiln is preheated to 200°F. During which time interval did the temperature in the kiln show the greatest average rate of change?
a. 0 to 1 hour
b. 1 hour to 1.5 hours
C. 2.5 hours to 5 hours
d. 5 hours to 8 hours
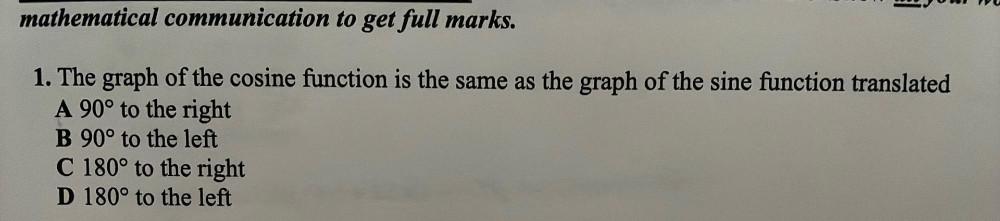
Calculus
Limits & ContinuityThe graph of the cosine function is the same as the graph of the sine function translated
A) 90° to the right
B) 90° to the left
C) 180° to the right
D) 180° to the left
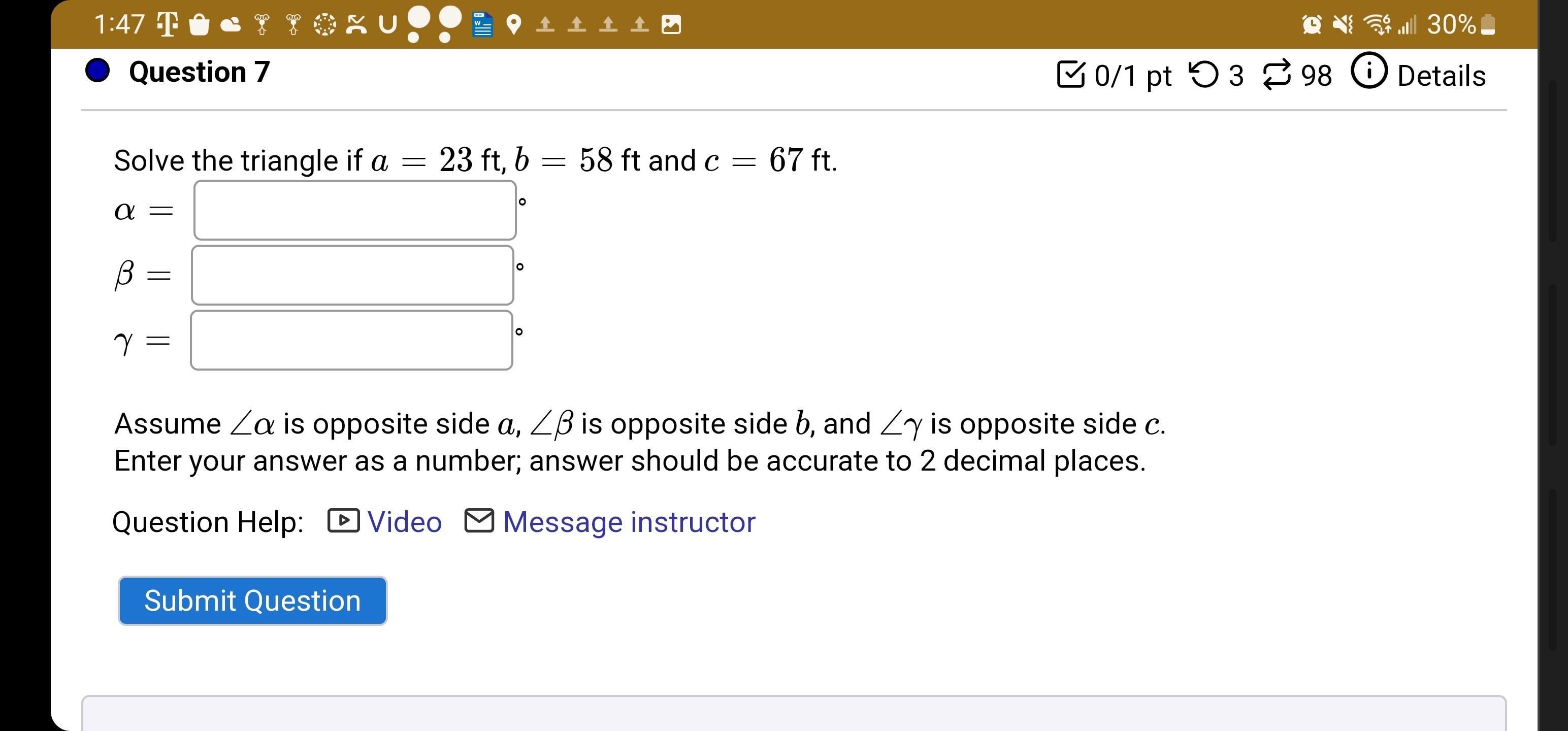
Calculus
Limits & ContinuitySolve the triangle if a = 23 ft, b = 58 ft and c = 67 ft.
α = _____________________°
β = _____________________°
γ = _____________________°
Assume ∠α is opposite side a, ∠β is opposite side b, and ∠γ is opposite side c.
Enter your answer as a number; answer should be accurate to 2 decimal places.
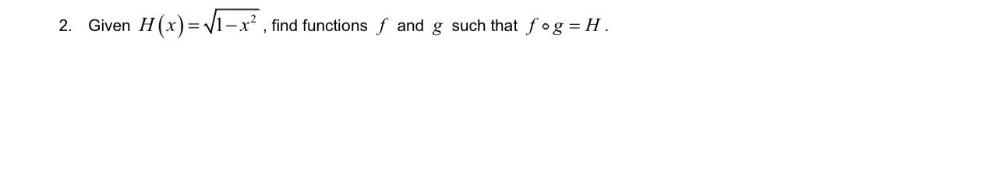
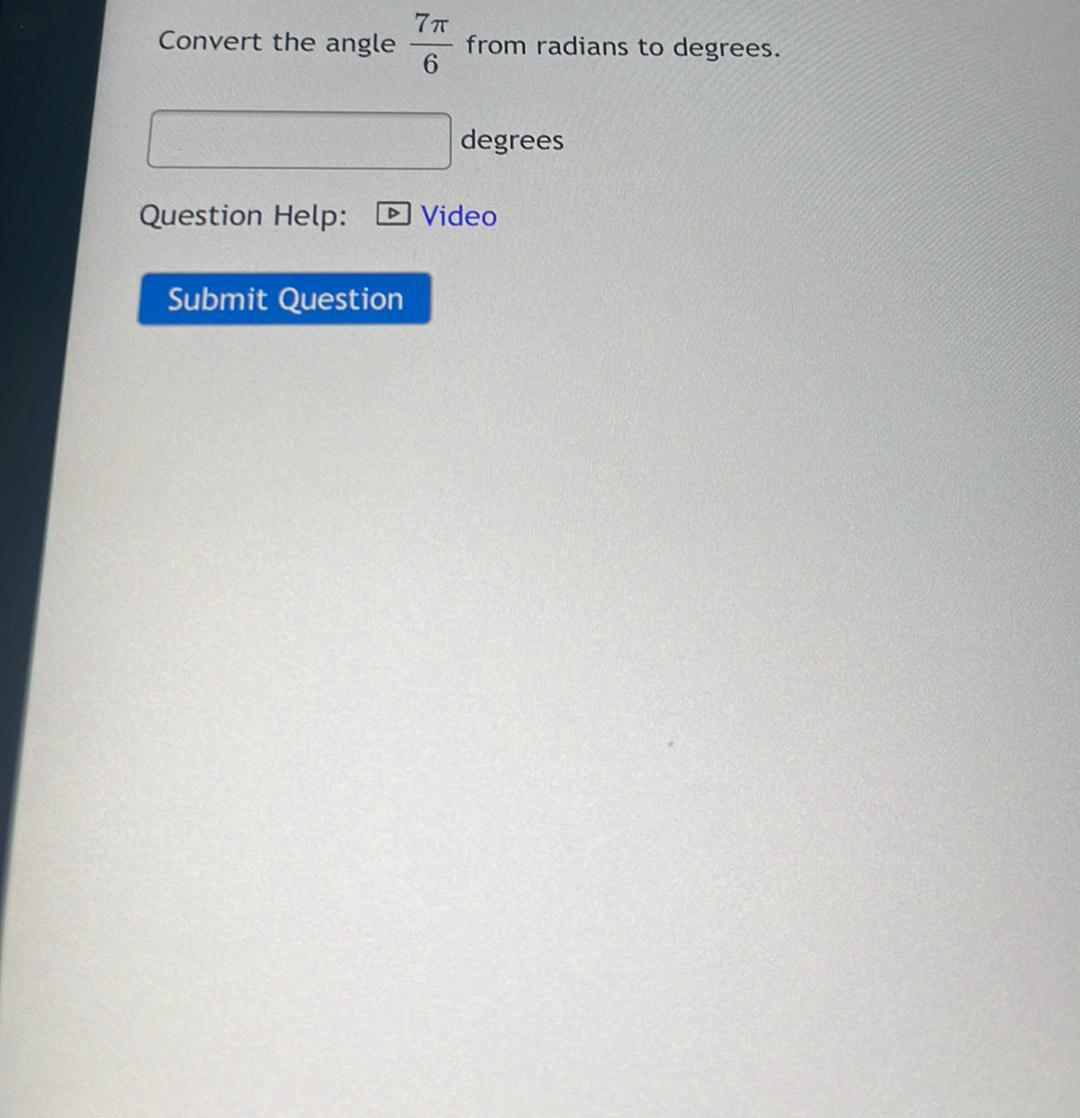

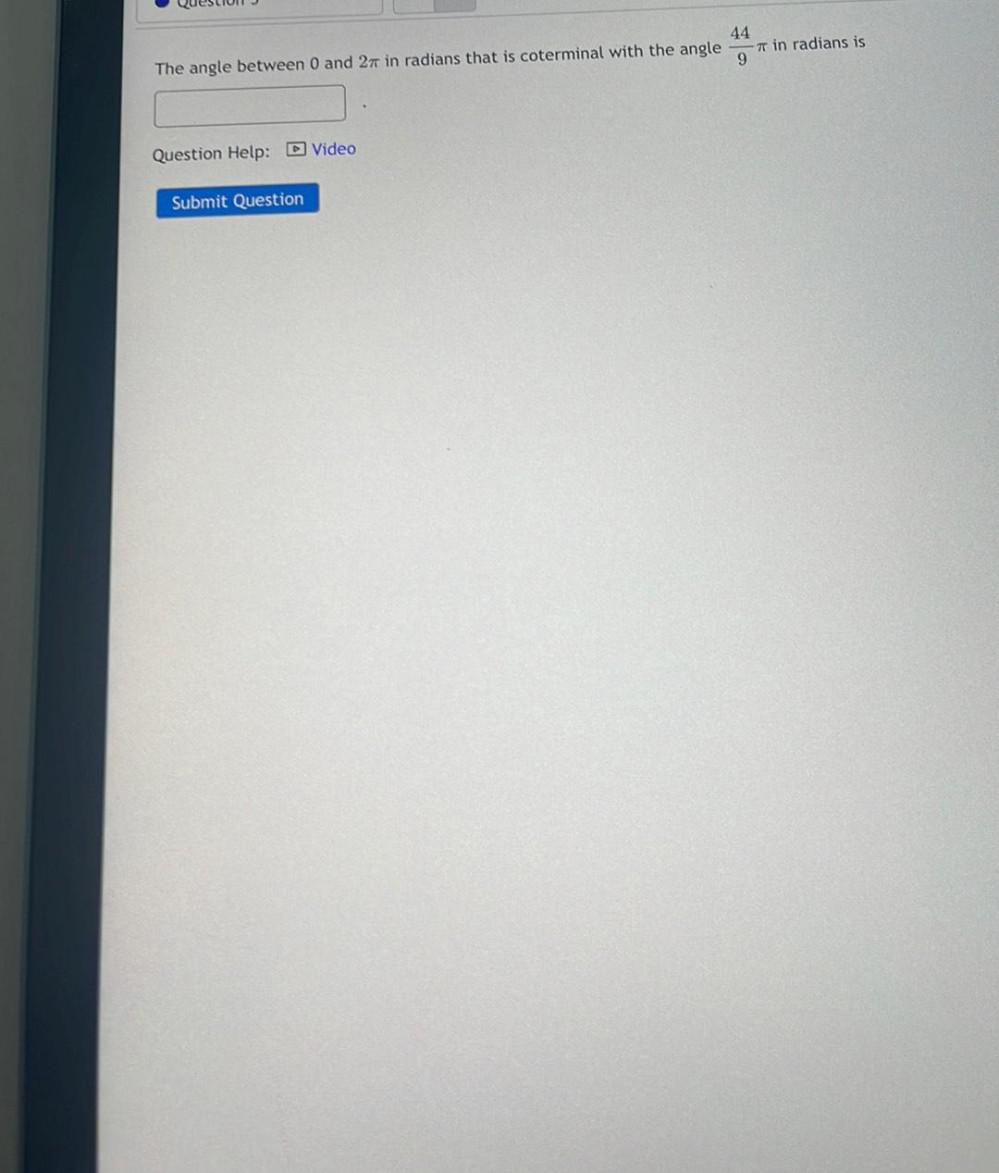
Calculus
Limits & ContinuityThe angle between 0 and 2π in radians that is coterminal with the angle 44π/9 in radian is;
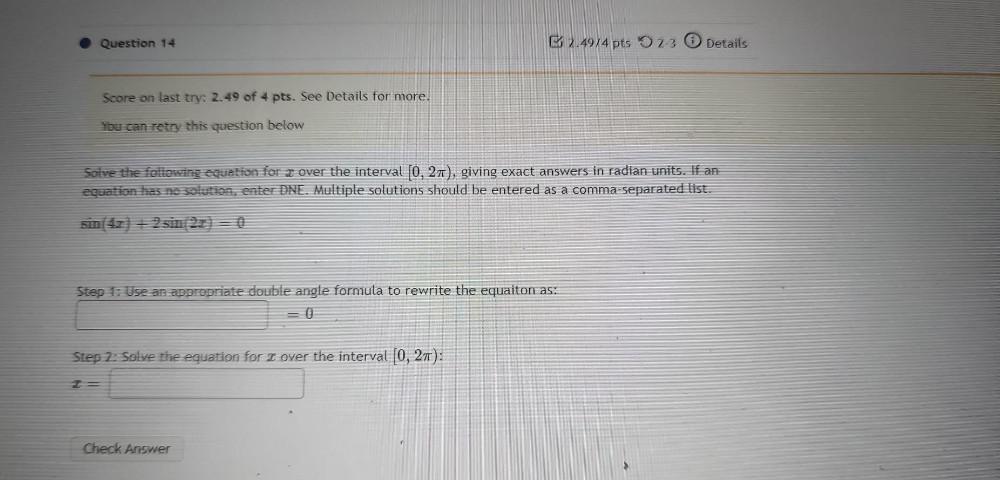
Calculus
Limits & ContinuitySolve the following equation for å over the interval [0, 2π), giving exact answers in radian units. If an equation has no solution, enter DNE. Multiple solutions should be entered as a comma-separated list.
sin(4x) + 2 sin(2x) = 0
1)Use an appropriate double angle formula to rewrite the equaiton 2)Solve the equation for æ over the interval [0, 2π):
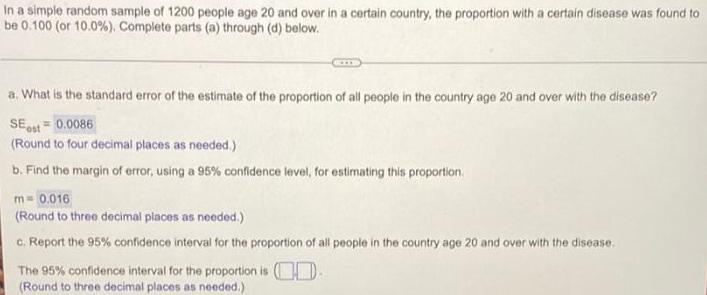
Calculus
Limits & ContinuityIn a simple random sample of 1200 people age 20 and over in a certain country, the proportion with a certain disease was found to
be 0.100 (or 10.0%). Complete parts (a) through (d) below.
a. What is the standard error of the estimate of the proportion of all people in the country age 20 and over with the disease?
SE est=0.0086
(Round to four decimal places as needed.)
b. Find the margin of error, using a 95% confidence level, for estimating this proportion.
m= 0.016
(Round to three decimal places as needed.)
c. Report the 95% confidence interval for the proportion of all people in the country age 20 and over with the disease.
The 95% confidence interval for the proportion is D.
(Round to three decimal places as needed.)
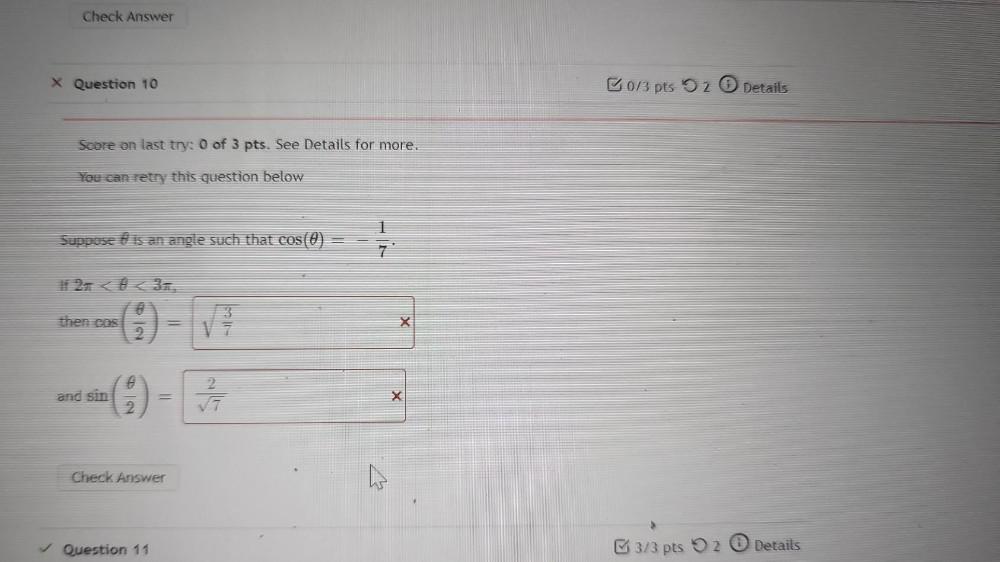
Calculus
Limits & ContinuitySuppose is an angle such that cos(θ)=-1/7
If 2π <θ< 3π
then cos(θ/2)=___
and sin(θ/2)=___
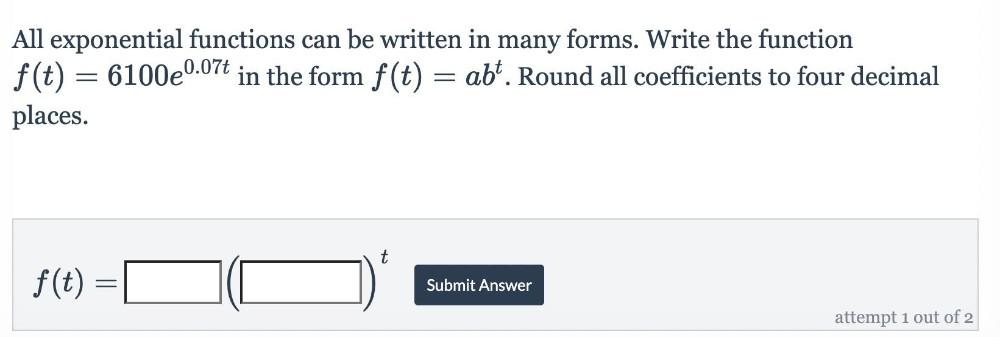
Calculus
Limits & ContinuityAll exponential functions can be written in many forms. Write the function
f(t) = 6100e⁰∙⁰⁷ᵗ in the form f(t) = abᵗ. Round all coefficients to four decimal
places.
f(t) = _____(_____)ᵗ


Calculus
Limits & ContinuityFor the function f(x) = 12 sin x + 30, the value off (30) is
A) 40
B) 30
C) 36
D) 12
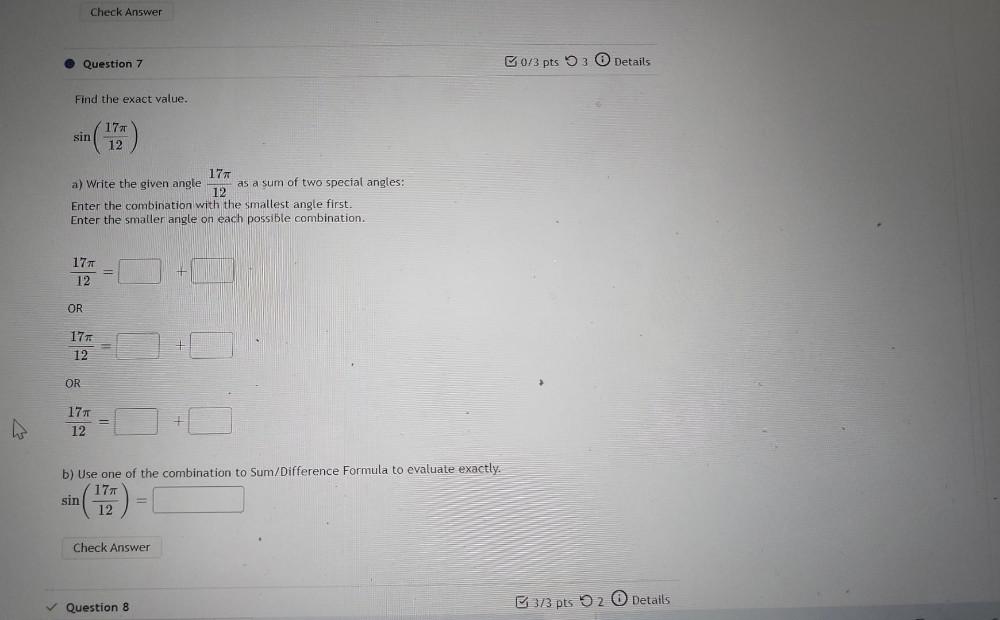
Calculus
Limits & ContinuityFind the exact value.
sin
(17π\12)
a) Write the given angle 17π\12 as a sum of two special angles Enter the combination with the smallest angle first. Enter the smaller angle on each possible combination.
17π\12 = _____+_____
OR
17π\12 = _____+_____
OR
17π\12 = _____+_____
b) Use one of the combination to Sum/Difference Formula to evaluate exactly.
Sin (17π\12)= __________