Limits & Continuity Questions and Answers

Calculus
Limits & ContinuityFind the following limits for the rational function f(x)=x+2/(4x² -16) and justify your answers. If the limit does not exist, state so and show or explain why it does not exist.
(a) lim f(x) =
x➡ -2
(b)lim f(x) =
x ➡2
(c)lim f(x) =
x➡∞
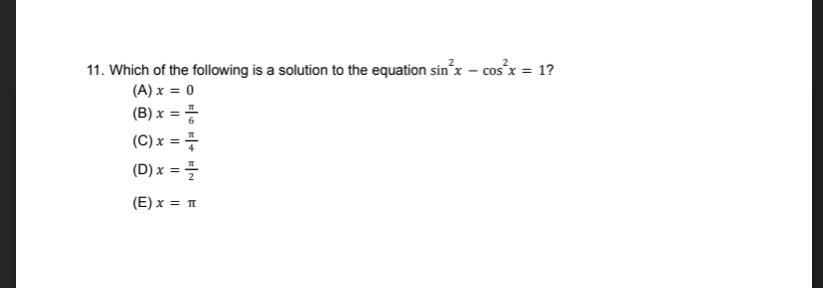
Calculus
Limits & ContinuityWhich of the following is a solution to the equation sin²x - cos²x = 1?
(A) x = 0
(B) x = π/6
(C) x = π/4
(D) x = π/2
(E) x = π

Calculus
Limits & ContinuityWhich of the following statements is NOT true about the curve defined by the parametric equations x(t) = 12 cos πt and y(t) = 12 sinπt?
(A) The curve is centered at the origin
(B) The path of the curve can be represented by the polar equation r = 12
(C) A particle following the path of the curve will be located at the point(0,12)at t=0
(D) A particle following the path of the curve will travel counterclockwise as t increases
(E) A particle following the path of the curve will be at the same point along the curve at t = 0 and t = 2
![If lim f(x) = 5 and lim g(x) = 3, then lim [g(x) = f(x)] =
(A)- 2
(B) 0
(C) 2
(D) 3
(E) 5](https://media.kunduz.com/media/sug-question/raw/79231887-1660206100.0605524.jpeg?w=256)
Calculus
Limits & ContinuityIf lim f(x) = 5 and lim g(x) = 3, then lim [g(x) = f(x)] =
(A)- 2
(B) 0
(C) 2
(D) 3
(E) 5
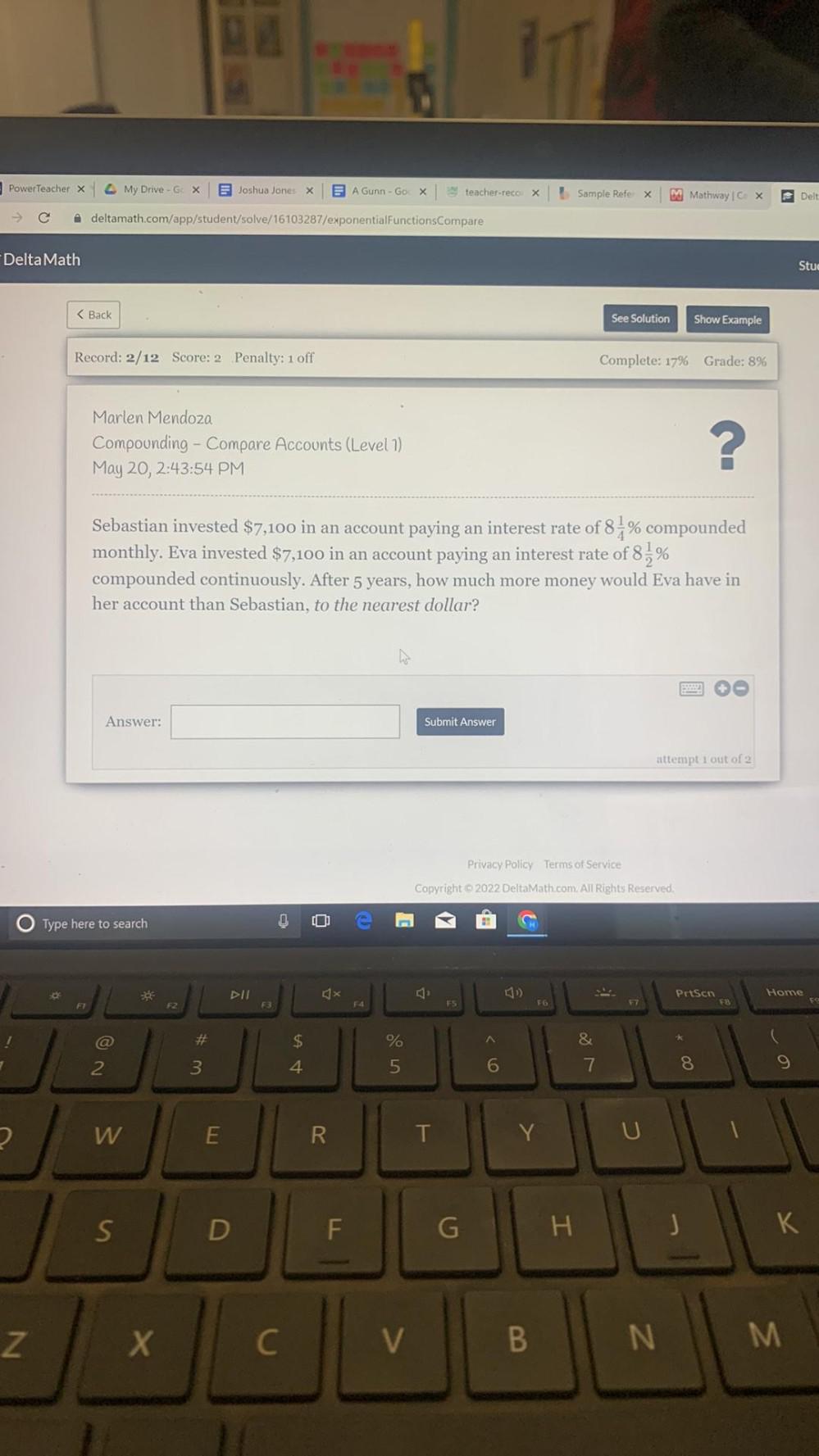
Calculus
Limits & ContinuitySebastian invested $7,100 in an account paying an interest rate of 81% compounded monthly. Eva invested $7,100 in an account paying an interest rate of 81% compounded continuously. After 5 years, how much more money would Eva have in her account than Sebastian, to the nearest dollar?

Calculus
Limits & ContinuityA petroleum company is making a cylindrical oil drum. The drum must hold 1.9 m³ of liquid. The drum must be taller than it is wide, but no more than 1.7 m tall. What are the dimensions of the drum that uses the least amount of material?
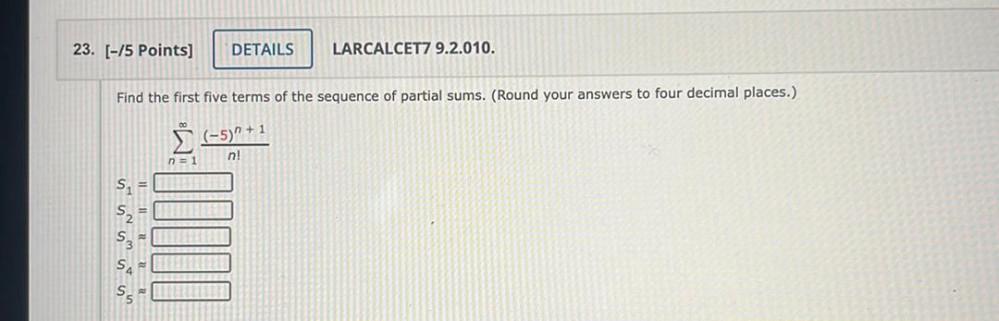
Calculus
Limits & ContinuityFind the first five terms of the sequence of partial sums. (Round your answers to four decimal places.)
∑ (-5)ⁿ+¹
s₁=
s₂=
s₃=
s₄=
s₅=
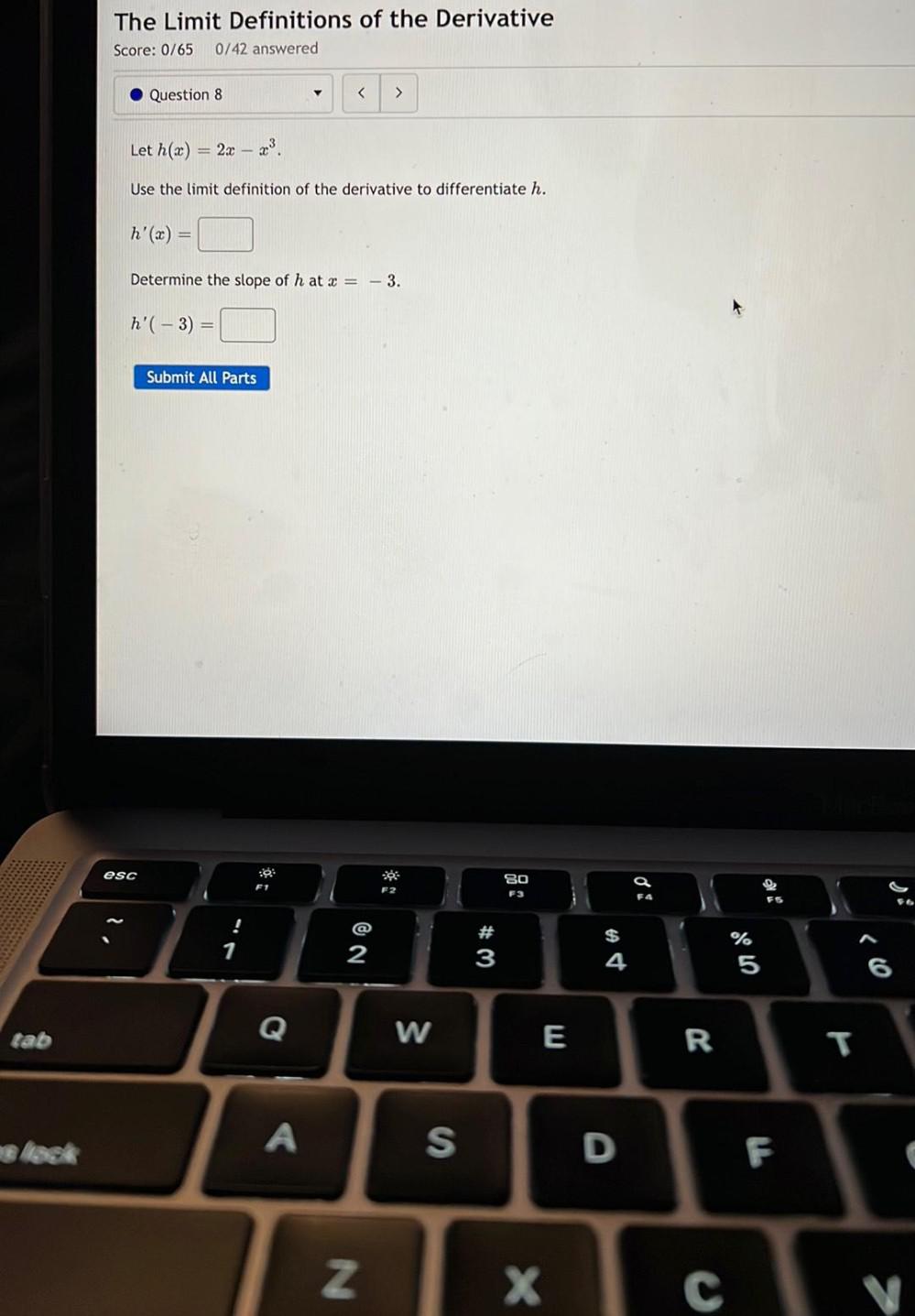
Calculus
Limits & ContinuityLet h(x) = 2x - x³.
Use the limit definition of the derivative to differentiate h.
h'(x) = ____________
Determine the slope of h at x = -3.
h'(-3) =
![The limit below represents f'(c) for some function f and real number c.
Iim [-1+(-2+Δx)^2+9]/Δx
Δx→0
a)Determine the function f. f(x) =
b)Determine the value of c. C=](https://media.kunduz.com/media/sug-question/raw/79379886-1660205739.656572.jpeg?w=256)
Calculus
Limits & ContinuityThe limit below represents f'(c) for some function f and real number c.
Iim [-1+(-2+Δx)^2+9]/Δx
Δx→0
a)Determine the function f. f(x) =
b)Determine the value of c. C=
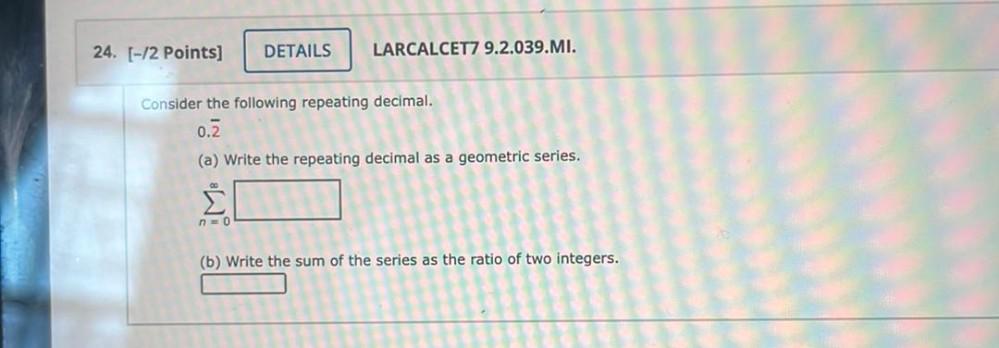
Calculus
Limits & ContinuityConsider the following repeating decimal.
(a) Write the repeating decimal as a geometric series. n=0
(b) Write the sum of the series as the ratio of two integers.
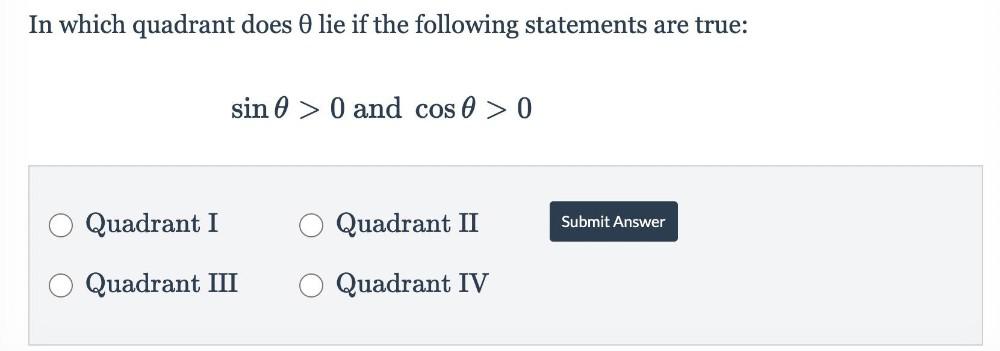
Calculus
Limits & ContinuityIn which quadrant does θ lie if the following statements are true:
sin θ > θ and cos θ > θ
A)Quadrant I
B) Quadrant II
C) Quadrant III
D) Quadrant IV

Calculus
Limits & ContinuityEvaluate the following limits. Justify each step. If the limit does not exist, explain why.
a) lim 2ln|x + 2| − ln(x^4 + 4x³ + 4x²)
b) lim sin(5x) csc (7x)
c) lim(16x^3-2x^2+1)^(1/2)/(1+x^6)^(1/4)
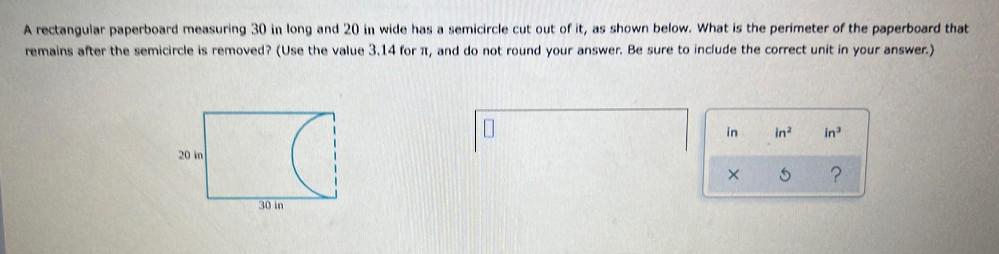
Calculus
Limits & ContinuityA rectangular paperboard measuring 30 in long and 20 in wide has a semicircle cut out of it, as shown below. What is the perimeter of the paperboard that remains after the semicircle is removed?
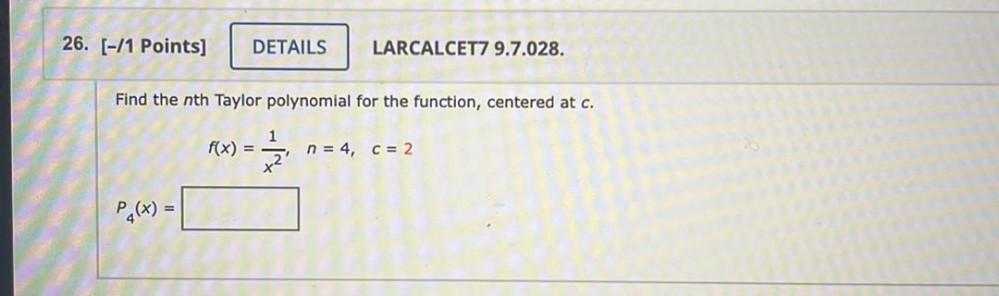
Calculus
Limits & ContinuityFind the nth Taylor polynomial for the function, centered at c.
f(x) =1/x² n = 4, c = 2
P₄(x) =

Calculus
Limits & ContinuityMartha Stewart is designing a box for her cat to sleep in. It has 4 sides and a bottom but no top. The plush material for the square bottom of the box costs $18/ft² and the material for the sides costs $12/ft². She needs a box with a volume of 18 ft^ 2. Find the dimensions of the box that minimize the cost.
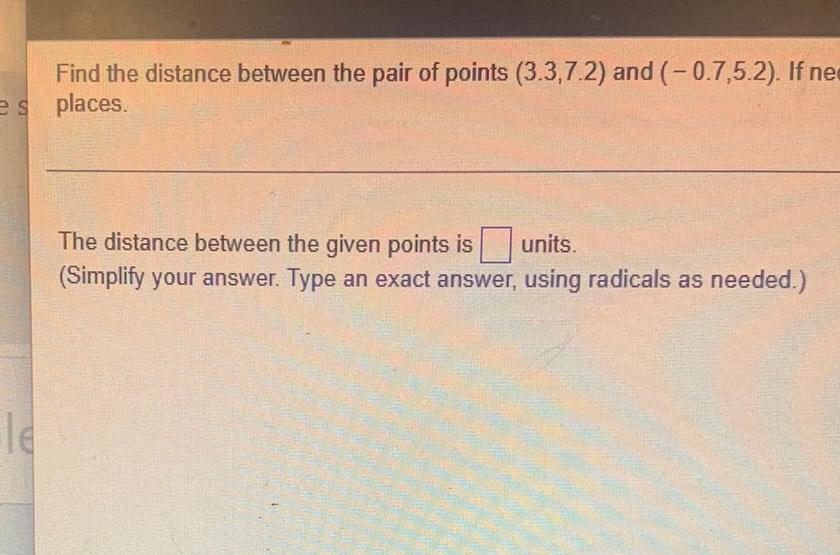
Calculus
Limits & ContinuityFind the distance between the pair of points (3.3,7.2) and (-0.7,5.2). If numbers
places.
The distance between the given points is ________ units.
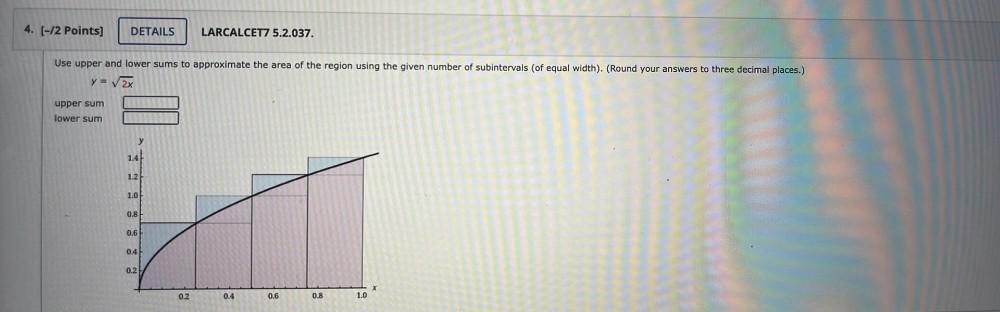
Calculus
Limits & ContinuityUse upper and lower sums to approximate the area of the region using the given number of subintervals (of equal width). (Round your answers to three decimal places.)
y = √2x
upper sum _______
lower sum________
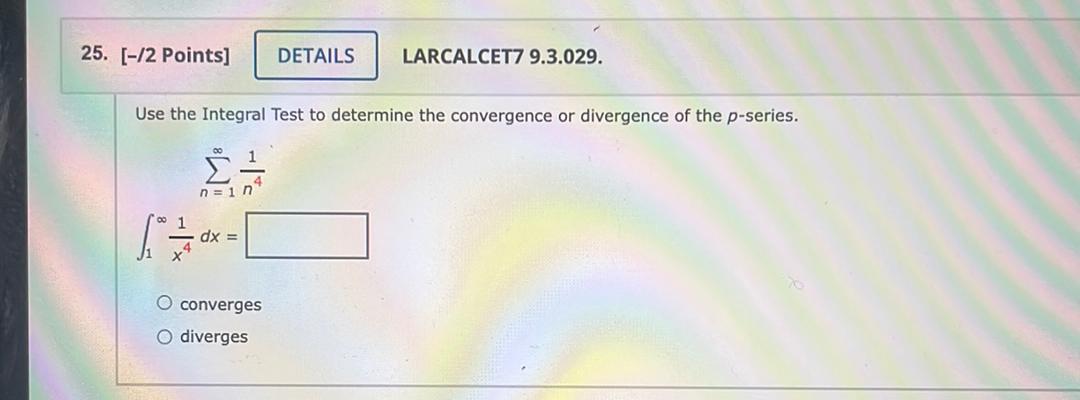
Calculus
Limits & ContinuityUse the Integral Test to determine the convergence or divergence of the p-series.
∑ 1/n⁴
∫₁1/n⁴
(a) converges
(b) diverges

Calculus
Limits & ContinuityDetermine if the following series are convergent or divergent. Justify your steps and state which test you are using. When necessary, make sure you check the hypotheses of the test that are satisfied before you apply it.
(a)Σ (-1)^n*(1/n^n)
(b)Σ 6^n/(5^n+8)
(c)Σn^3/(2n^4+3n+2)
(d)Σn!/(n+2)!
(e)Σcos(πn+5)/3^n
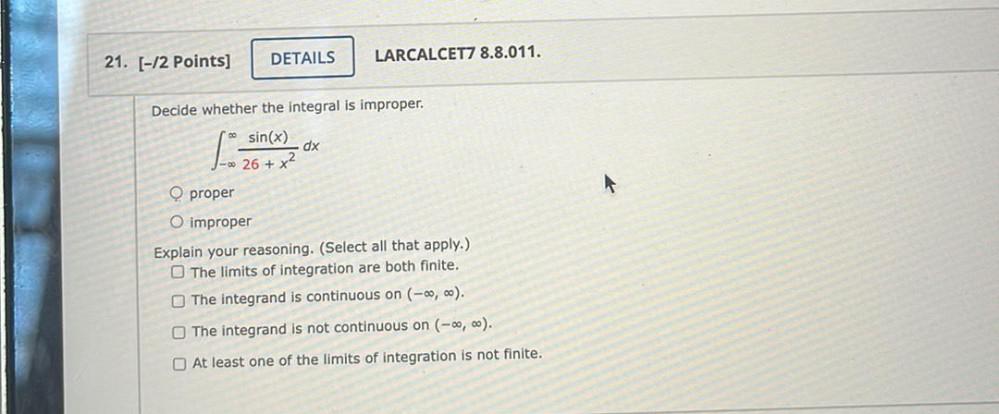
Calculus
Limits & ContinuityDecide whether the integral is improper.
∫ sin(x)/26+x² dx
(a)proper
(b)improper
Explain your reasoning. (Select all that apply.)
(a)The limits of integration are both finite.
(b)The integrand is continuous on (-∞, ∞).
(c)The integrand is not continuous on (-∞, ∞).
(d)At least one of the limits of integration is not finite.
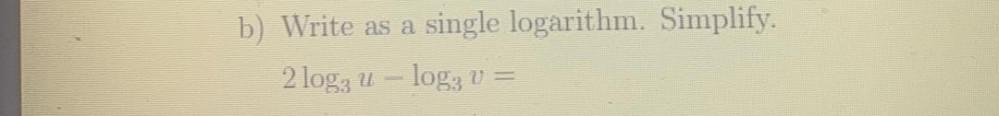
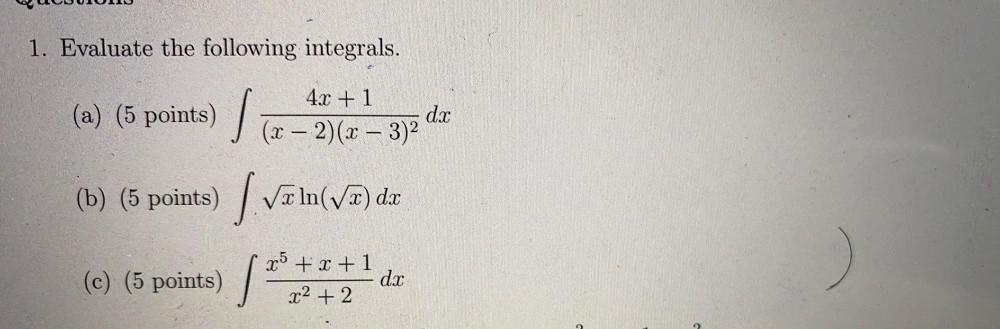
Calculus
Limits & ContinuityEvaluate the following integrals.
(a) ∫(4x + 1)/(x-2)(x - 3)² dx
(b) (√x)ln(√x) dx
(c)(x⁵ + x + 1)/(x² + 2)dx

Calculus
Limits & ContinuityDuring the design phase of one of its model spacecraft, Spacez launches the Atlas 31415 rocket vertically. A camera is positioned 5000 ft from the launch pad. When the rocket is 12,000 feet above the launch pad, its velocity is 800 ft/sec. Find the necessary rate of change of the camera's angle as a function of time so that it stays focused on the rocket.

Calculus
Limits & ContinuityFor the series problems, show ALL conditions required for the specified test for convergence or divergence.
The Limit Comparison Test Σ₁ ∞ 2/4n+1

Calculus
Limits & ContinuityJackson invested $590 in an account paying an interest rate of 61% compounded monthly. Ellie invested $590 in an account paying an interest rate of 61% compounded continuously. After 19 years, how much more money would Ellie have in her account than Jackson, to the nearest dollar?
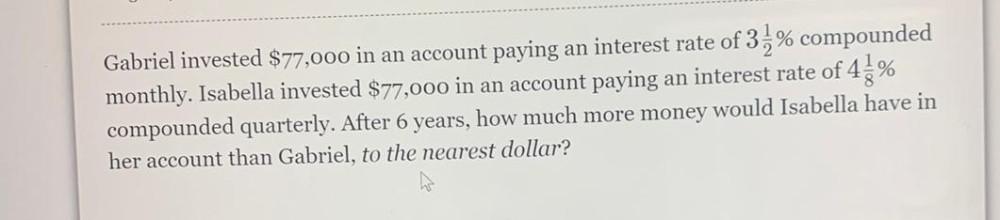
Calculus
Limits & ContinuityGabriel invested $77,000 in an account paying an interest rate of 3 1/2% compounded monthly. Isabella invested $77,000 in an account paying an interest rate of 41/8% compounded quarterly. After 6 years, how much more money would Isabella have in her account than Gabriel, to the nearest dollar?
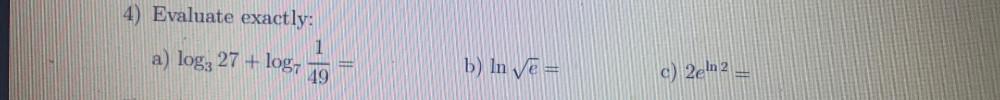
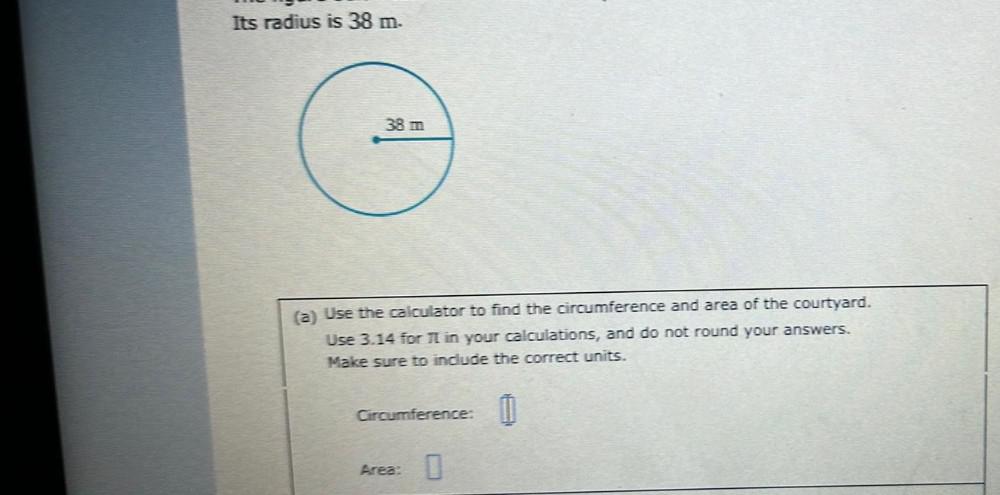
Calculus
Limits & ContinuityIts radius is 38 m. Find the circumference and area of the courtyard.
Circumference:_________
Area:________________
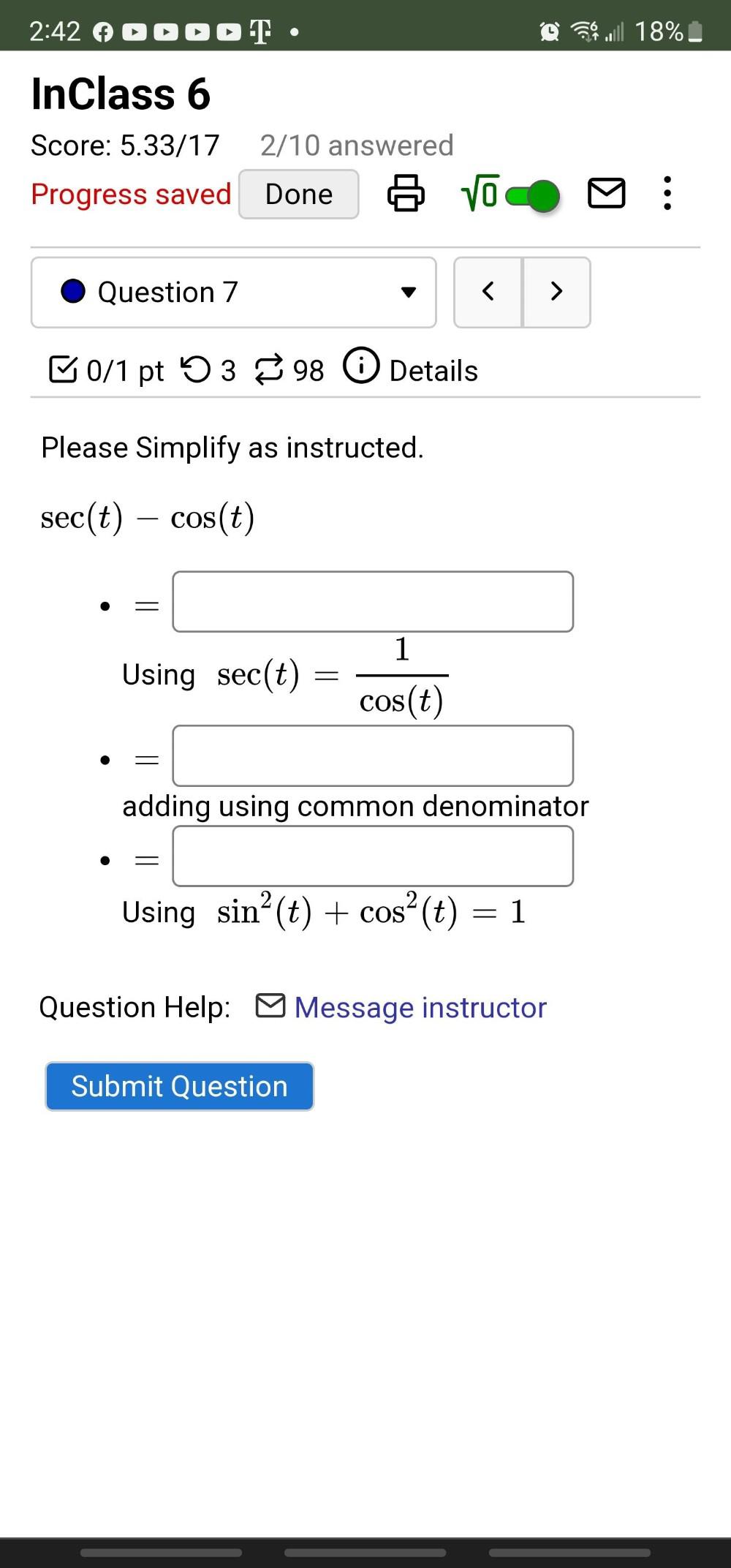
Calculus
Limits & ContinuitySimplify as instructed.
(1) sec(t) — cos(t)= _________
Using sec(t) = 1 / cos(t)
(2) = _________
adding using common denominator
(3) = ____________
Using sin²(t) + cos² (t) = 1
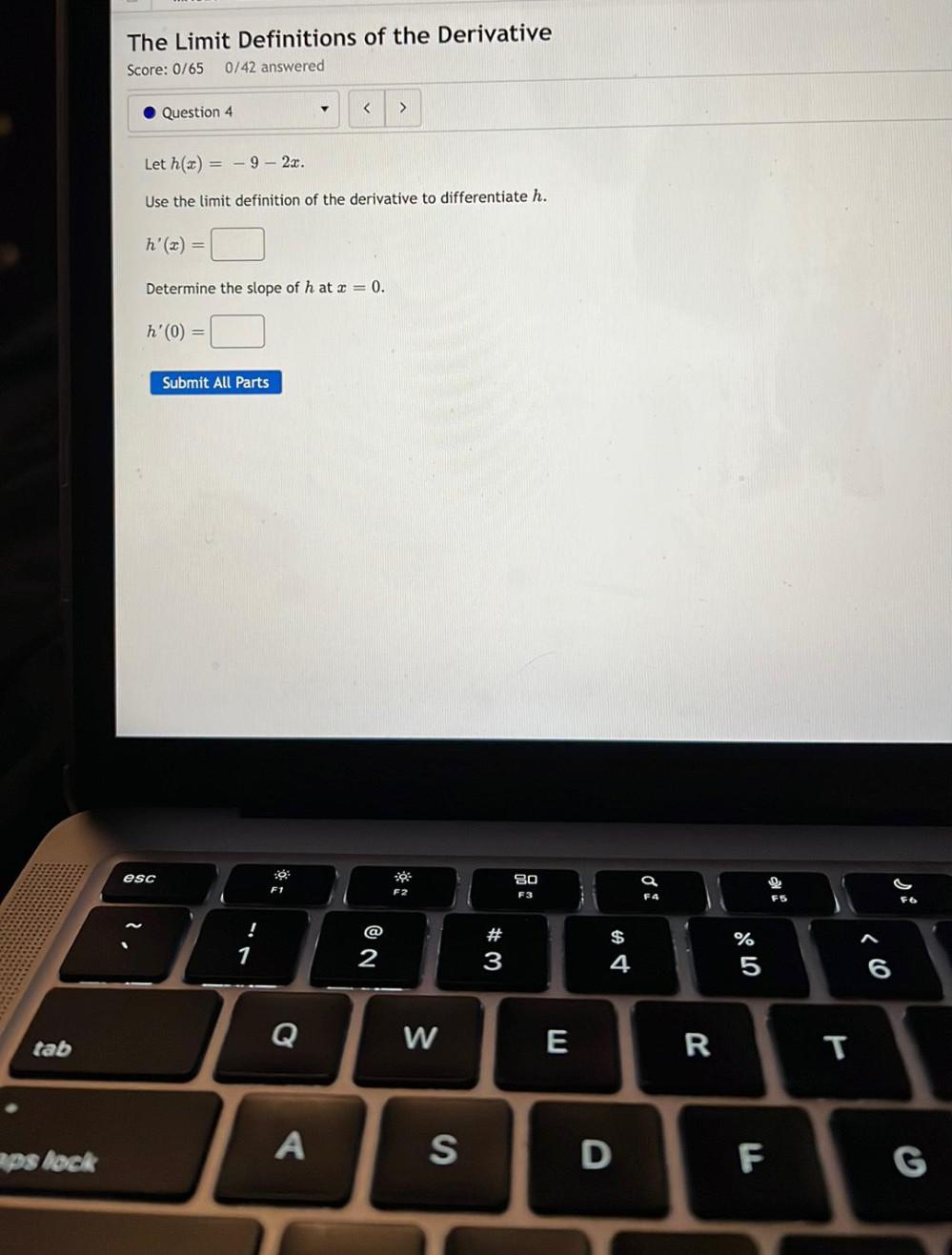
Calculus
Limits & ContinuityLet h(x) = -9 - 2x.
Use the limit definition of the derivative to differentiate h.
h'(x) = _ ______________
Determine the slope of h at x = 0.
h'(0) =_______________
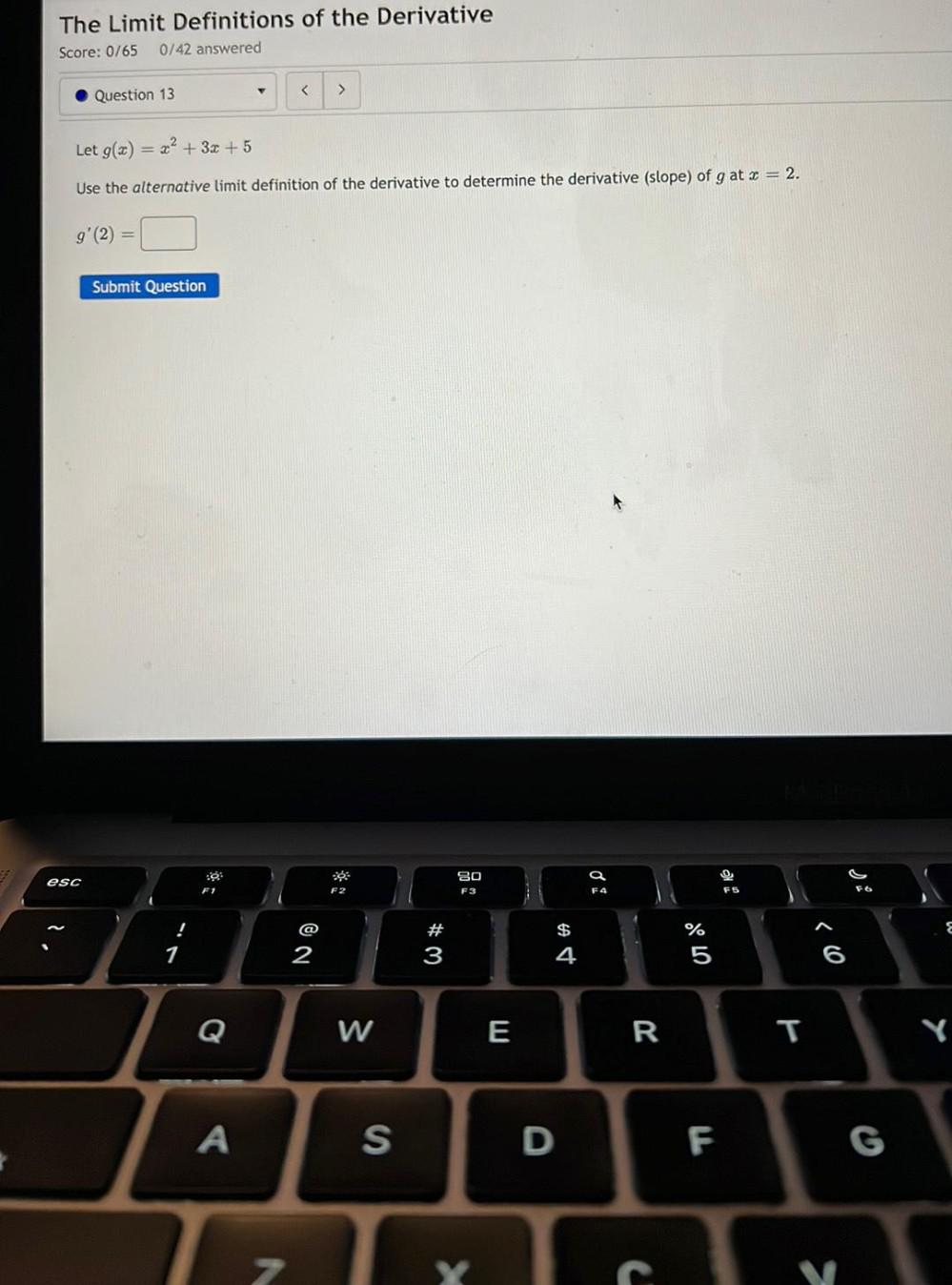
Calculus
Limits & ContinuityLet g(x) = x² + 3x +5
Use the alternative limit definition of the derivative to determine the derivative (slope) of g at x = 2.
g'(2) = _____________
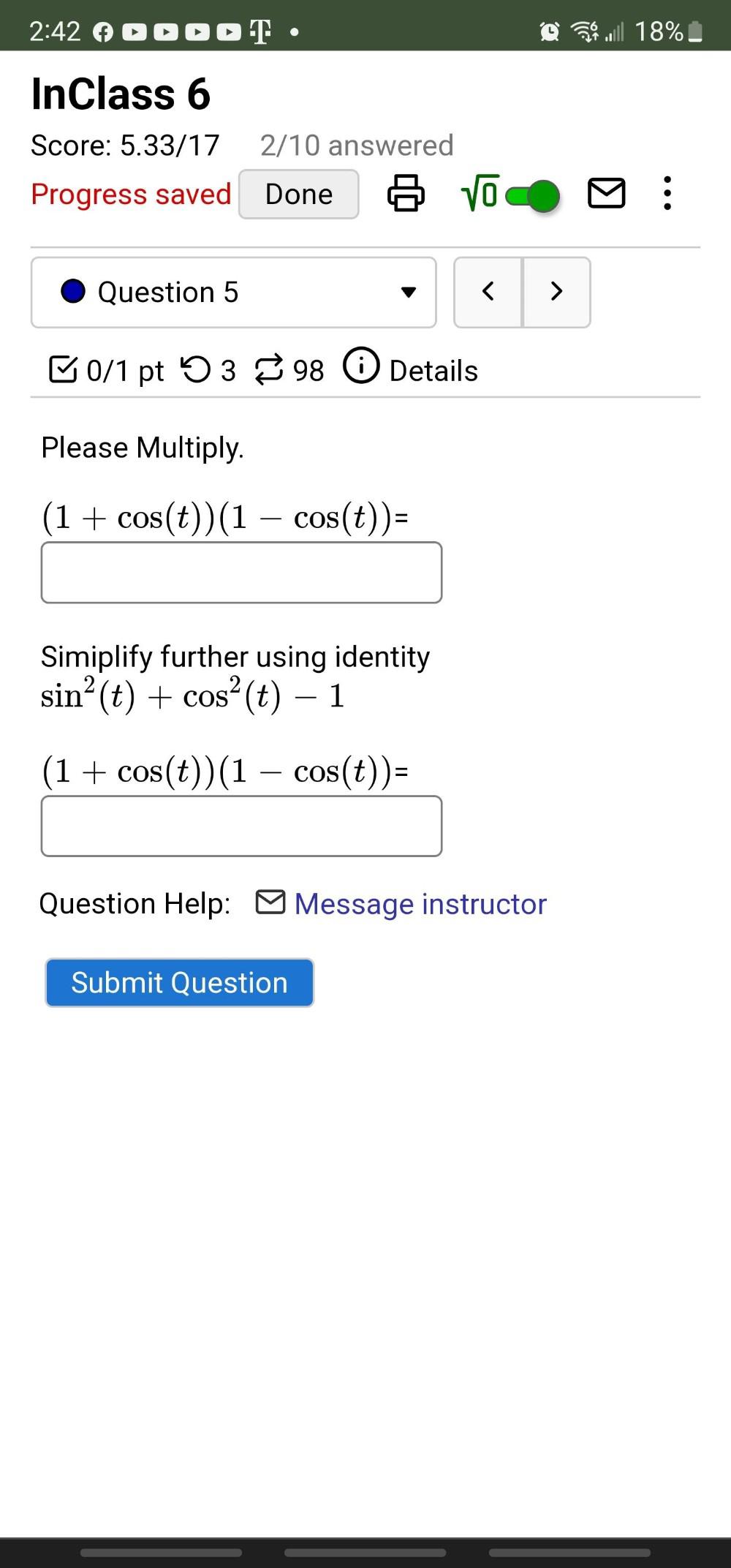
Calculus
Limits & Continuity(1) Multiply. (1 + cos(t))(1 − cos(t))= __________________
(2) Simplify further using identity
sin² (t) + cos² (t) - 1
(1 + cos(t)) (1 - cos(t))= ___________
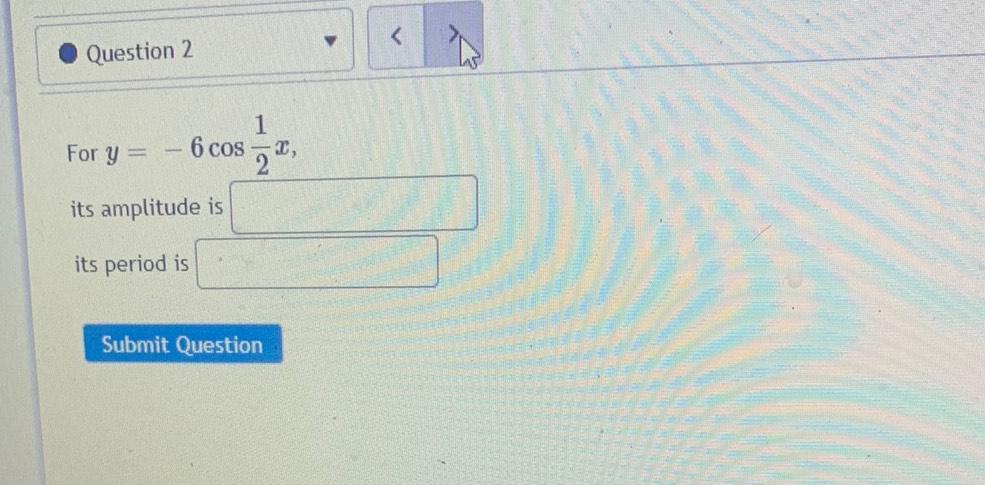
Calculus
Limits & ContinuityFor y = 6 cos(1/2)x
(1) it's amplitude is __________
(2) it's period is _________
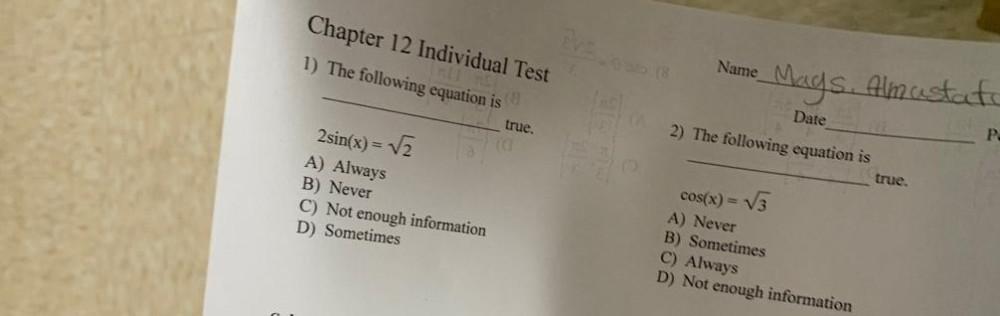
Calculus
Limits & ContinuityThe following equation is_______ true.
2sin(x)=√₂
(A) Always
(B) Never
(C) Not enough information
(D) Sometimes
The following equation is_______ true
cos(x) = √3
(A) Never
(B) Sometimes
(C) Always
(D) Not enough information

Calculus
Limits & ContinuityLet f(x) = {√x+1 if x<3
{5- -x if x ≥ 3.
Determine the one-sided limits as x approaches 3, and determine the limit as x approaches 3.

Calculus
Limits & ContinuityGiven x = t² + 2t - 1 and y = t² + 4t + 4, what is the equation of the tangent line at t = 1.

Calculus
Limits & ContinuityDetermine whether each of the following geometric series converges or diverges. If it converges, find
its sum.
(a)∑^∞n=1 36ⁿ/2²ⁿ+¹
(b) ∑^∞n=3 4ⁿ3-²ⁿ-²
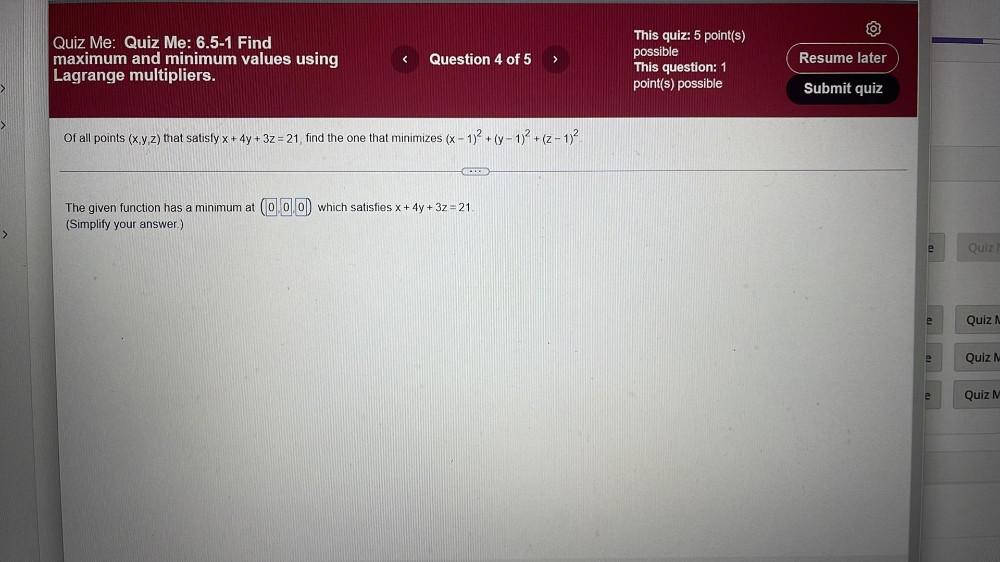
Calculus
Limits & ContinuityOf all points (x ,y ,z) that satisfy x + 4y + 3z=21, find the one that minimizes (x − 1)² + (y − 1)² + (z − 1)².The given function has a minimum at (0,0,0) which satisfies x + 4y + 3z = 21.
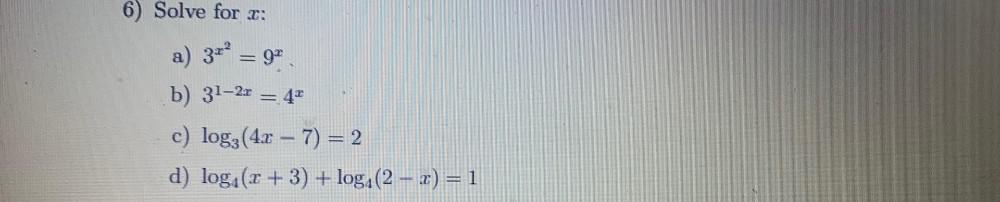
Calculus
Limits & ContinuitySolve for x:
a) 3ˣ² = 9ˣ
b) 3¹-²ˣ = 4ˣ
c) log₃ (4x - 7) = 2
d) log₄(x + 3) + log₄(2-x) = 1
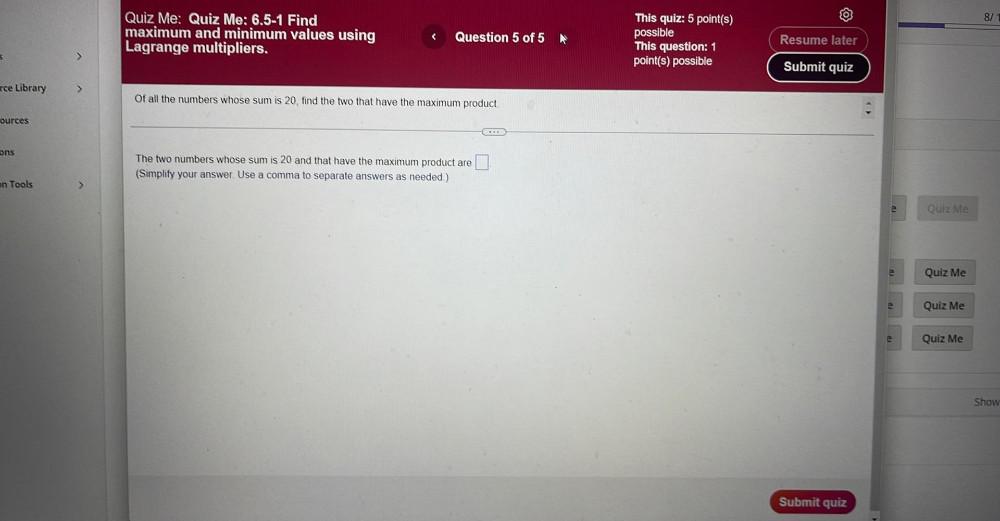
Calculus
Limits & ContinuityOf all the numbers whose sum is 20, find the two that have the maximum product.
The two numbers whose sum is 20 and that have the maximum product are....
Simplify your answer. Use a comma to separate answers as needed.
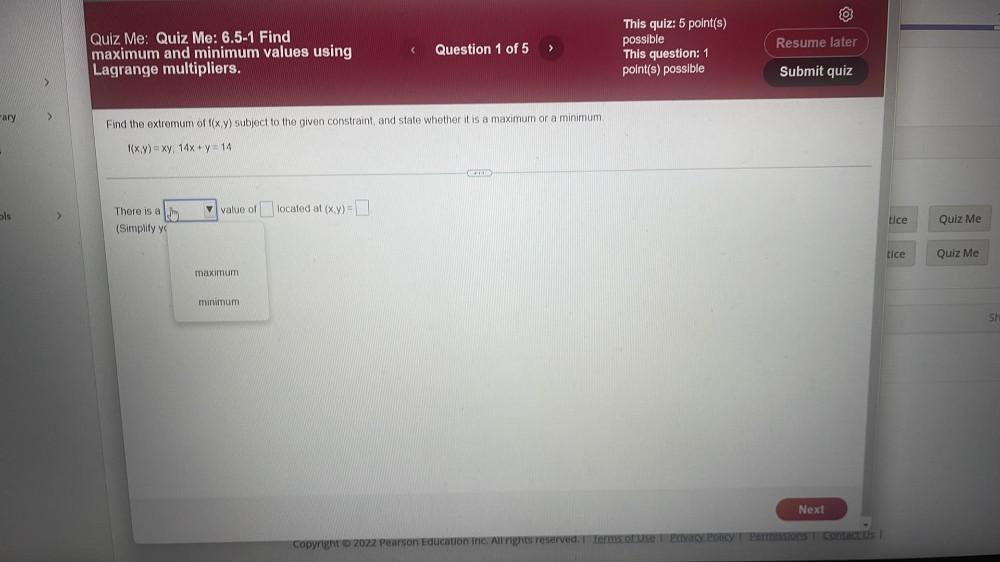
Calculus
Limits & ContinuityFind the extremum of f(x,y) subject to the given constraint, and state whether it is a maximum or a minimum.
f(x,y) = xy; 14x + y = 14
There is a ________ value of ________ located at (x ,y)=
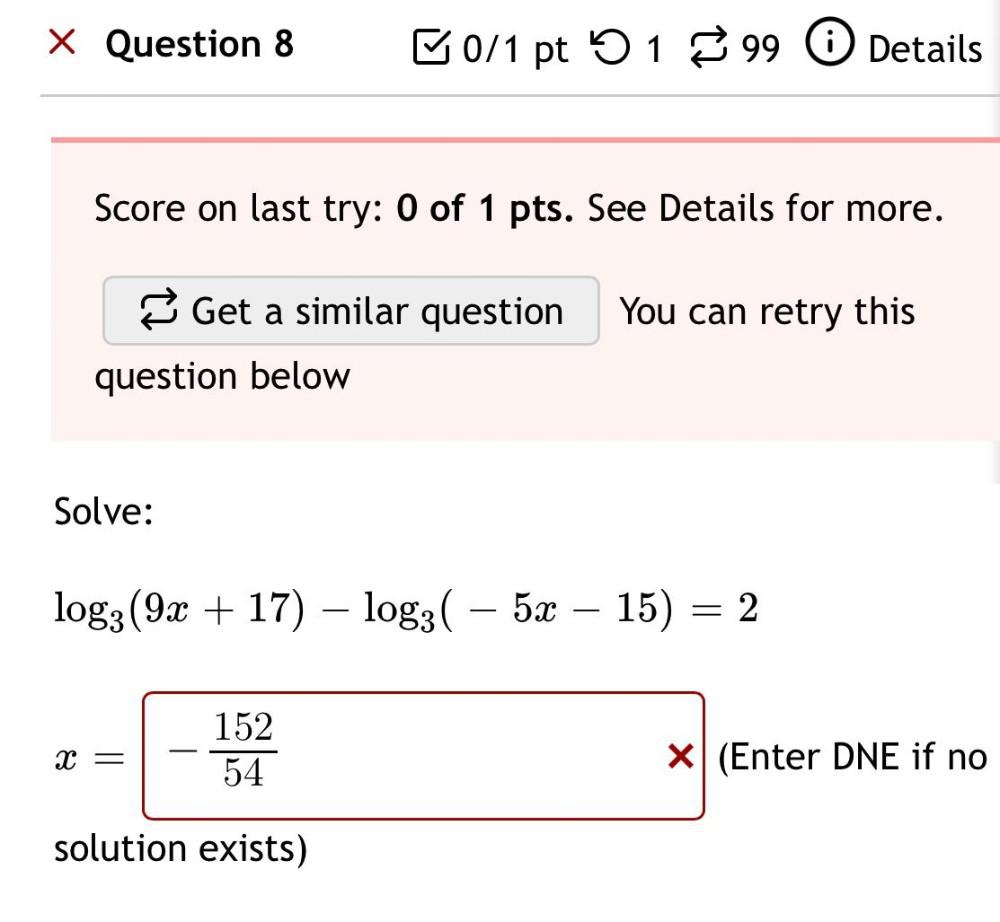
Calculus
Limits & ContinuityQuestion 8
Solve: log_3(9x + 17) – log_3( – 5x - 15)=2
x=_____ (Enter DNE if no solution exists)
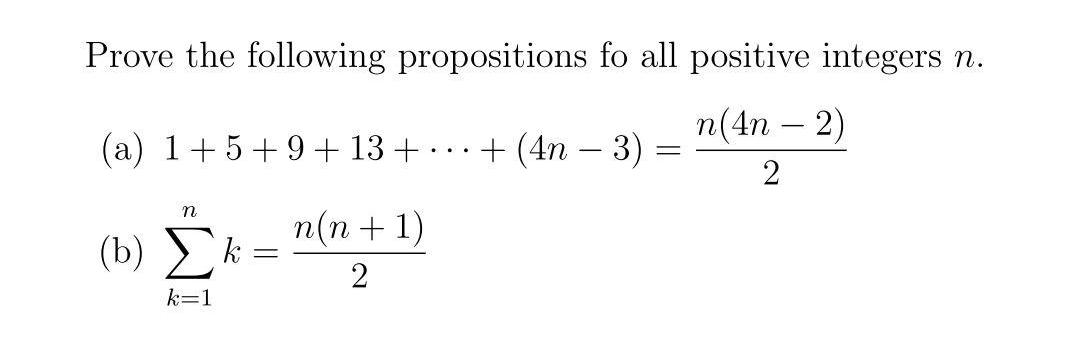
Calculus
Limits & ContinuityProve the following propositions for all positive integers n.
(a) 1+5+9+ 13 +...(4n - 3)=n(4n-2)/2
(b)Σk(k=1,n)=n(n+1)/2

Calculus
Limits & Continuity(05.01, 5.05, 5.07 MC)
Let θ = - (8π/3)
Part A: What is a coterminal angle of θ such that 0 ≤ θ ≤ 2π?
Part B: What are the exact values of all six trigonometric functions evaluated at θ?

Calculus
Limits & ContinuityThis problem has two parts.
Part 1: Given that y = 4 sin(α), with α € (0,π/2), express each of the following as a function of y.
cos(α)
cos(α) cot(α) =
tan(α)² =
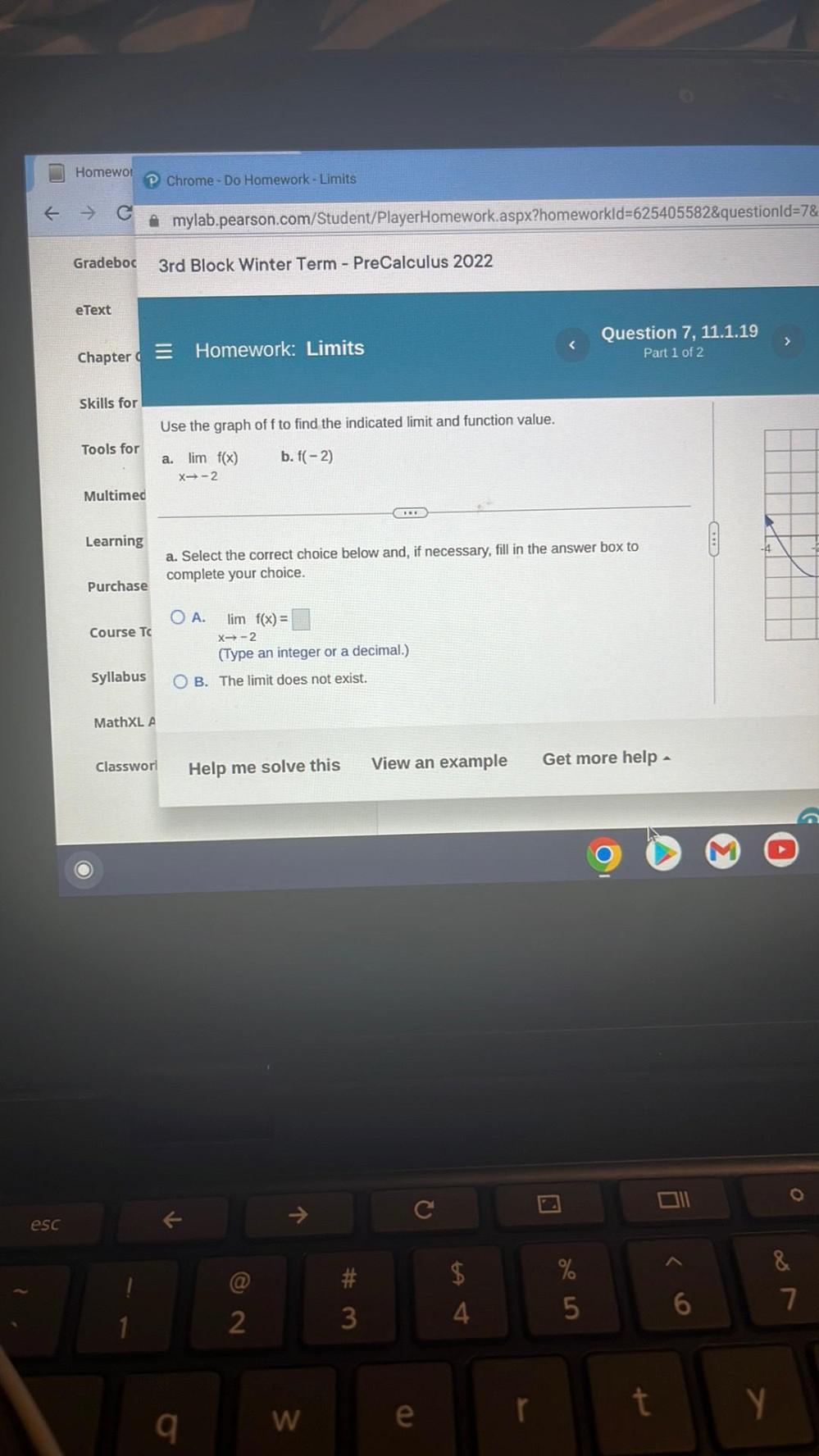
Calculus
Limits & ContinuityUse the graph of f to find the indicated limit and function value.
a. lim f(x) b. f(-2)
a. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A.lim f(x) =
x->-2
(Type an integer or a decimal.)
B. The limit does not exist.

Calculus
Limits & ContinuitySolve:
(4x - 21)/ (x - 6) ≤ 3
x ∈ ___________ (Enter your answer in INTERVAL notation, using U to indicate a union of intervals; or enter DNE if no solution exists)
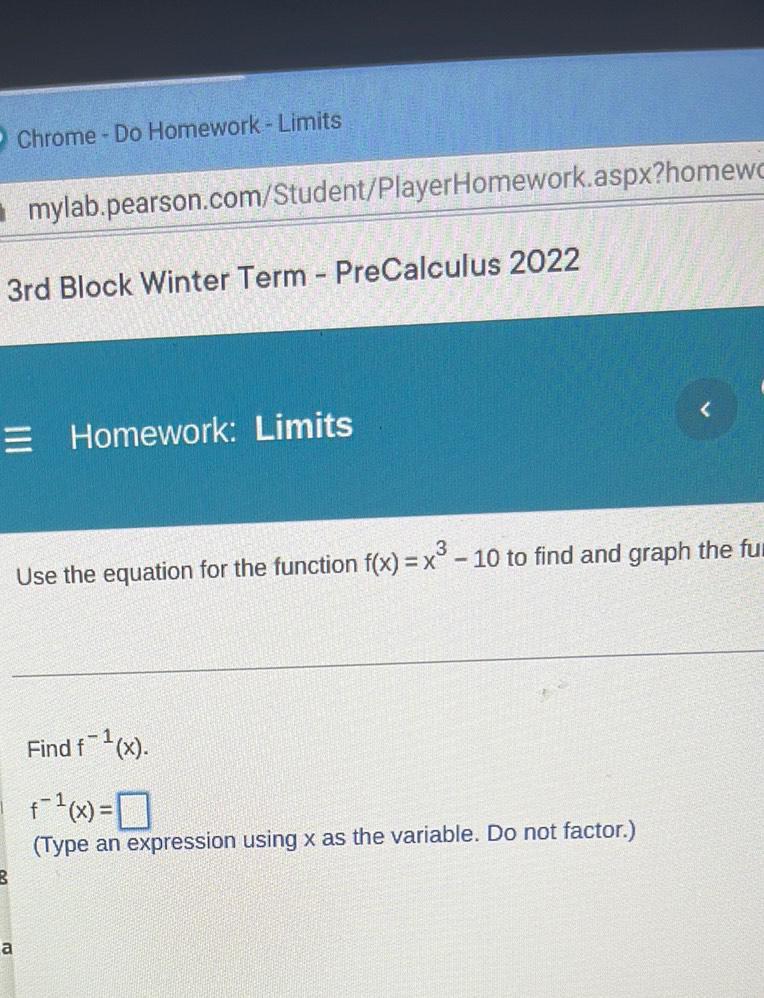
Calculus
Limits & ContinuityUse the equation for the function f(x) = x³ - 10 to find and graph the further
Find f¯¹(x).
f-¹(x) =_____
Calculus
Limits & ContinuityOrange juice, a raisin bagel, and a cup of coffee from Billy's Breakfast Bar cost a total of $3.00. Billy posts a notice announcing that, effective the following week, the price of orange juice will increase 50% and the price of bagels will increase 20%. After the increase, the same purchase will cost a total of $3.75, and the orange juice will cost twice as much as coffee. Find the price of each item before the increase.
(A) What was the cost of a glass of orange juice before the increase?
(B) What was the cost of a raisin bagel before the increase?
(C) What was the cost of a cup of coffee before the increase?