Limits & Continuity Questions and Answers

Calculus
Limits & ContinuityA good rule of thumb is to save 10 percent of what you earn, and have at least three months' worth of living expenses saved up in case of an emergency.
True
False
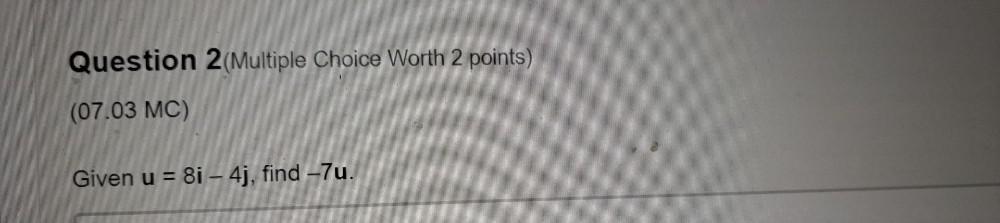

Calculus
Limits & ContinuityCreate a function of form f(x) = A sin(Bx - C) + D, where the values of A, B, C, and D are not equal to 1. Sketch an accurate graph of this function, showing at least 5 key points. Identify the important characteristics: period, amplitude, phase shift, midline, and y-intercept.

Calculus
Limits & ContinuityCreate a real-world situation where you would need to calculate an arc length or area of a sector. Be
creative! For example, you could calculate the distance between two cities on Earth or find the area
of lawn watered by a circular sprinkler.
Don't include your analysis in your post. Keep this work for later in the discussion and to respond to
your classmates.
Calculus
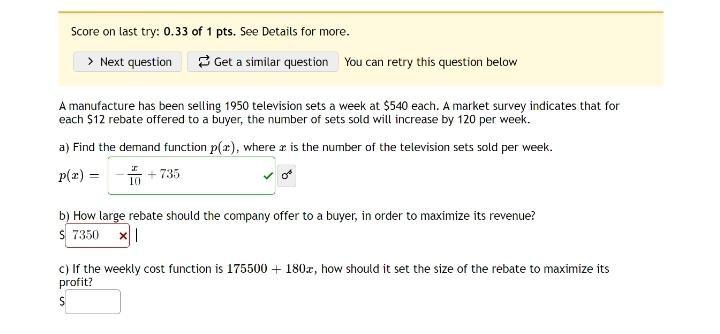
Limits & ContinuityA manufacture has been selling 1950 television sets a week at $540 each. A market survey indicates that for each $12 rebate offered to a buyer, the number of sets sold will increase by 120 per week.
a) Find the demand function p(x), where is the number of the television sets sold per week.
p(x) = ?
b) How large rebate should the company offer to a buyer, in order to maximize its revenue?
$ ____
c) If the weekly cost function is 175500 + 180x, how should it set the size of the rebate to maximize its profit?
$ ___

Calculus
Limits & ContinuityEnter your response into the blank field using one word only.
_________income is the total amount of what you earned.
Calculus
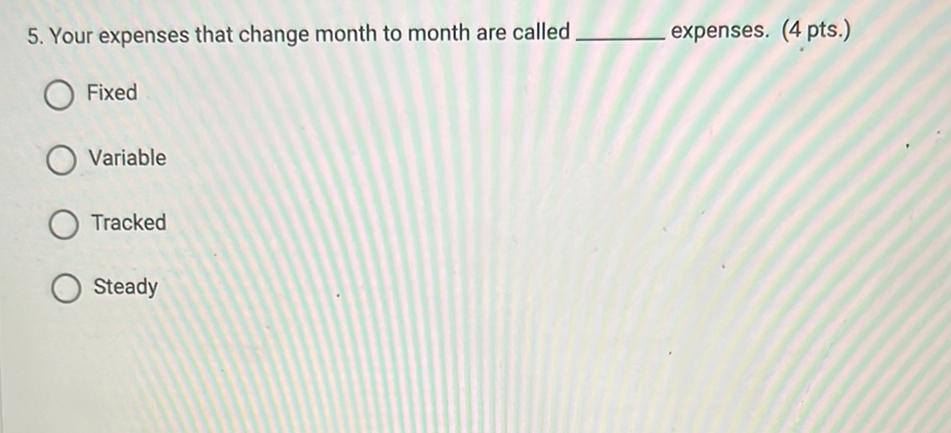
Limits & ContinuityYour expenses that change month to month are called ______ expenses.
(A) Fixed
(B) Variable
(C) Tracked
(D) Steady

Calculus
Limits & ContinuityGiven g(x) = -9.2f(-0.1x - 9) - 0.3 and f(1) = 4 Fill in the blanks: Round answers to 2 decimal places as needed g(___) = ______
Calculus
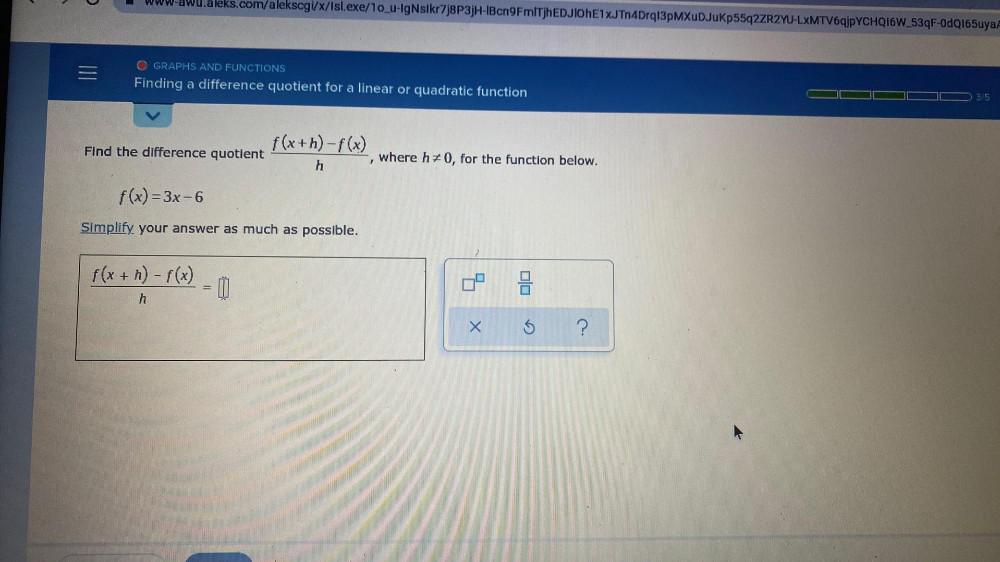
Limits & ContinuityFinding a difference quotient f(x+h)-f(x)/h, where h ≠ 0, for the function below. f(x)=3x-6 Simplify your answer as much as possible. f(x +h)-f(x)/h=

Calculus
Limits & ContinuityBeth starts her day at the state fair with $20.00. She buys roasted corn for $2.25 and a water bottle for $2.00. Then she buys 10 ride tickets that cost $0.75 each. How much money does she have left? Select the correct expression. A. 20 (10.0.75) = $12.50 B. 20-2.25 +2-10 0.75= $12.25 C. 20 (2.25 +2+10 0.75) = $8.25 D. 2.25 +2+10 0.75= $11.75

Calculus
Limits & ContinuityFor y²-(x-6)²/12=1,
(a) Identify the center.
(b) Identify the vertices.
(c) Identify the foci.
(d) Write equations for the asymptotes.
(e) Graph the hyperbola.
Give exact answers. Express numbers in simplest form using integers, fractions, or radicals.
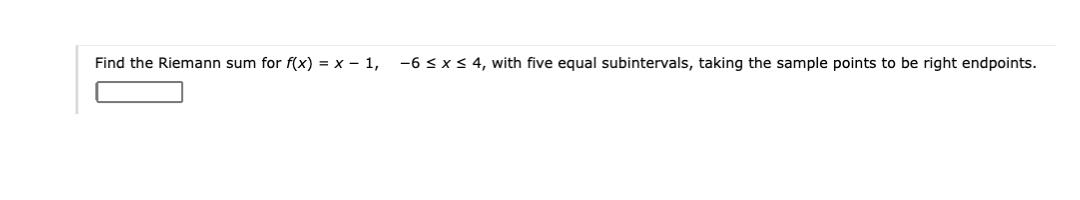
Calculus
Limits & ContinuityFind the Riemann sum for f(x) = x - 1, -6 ≤ x ≤ 4, with five equal sub intervals, taking the sample points to be right endpoints.
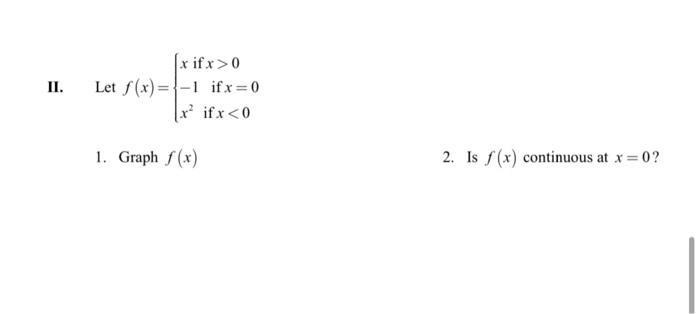
Calculus
Limits & ContinuityLet f(x) = { x if x > 0
-1 if x=0
x² if x < 0
(a) Graph f(x)
(b) Is f(x ) is continuous at x = 0 ?
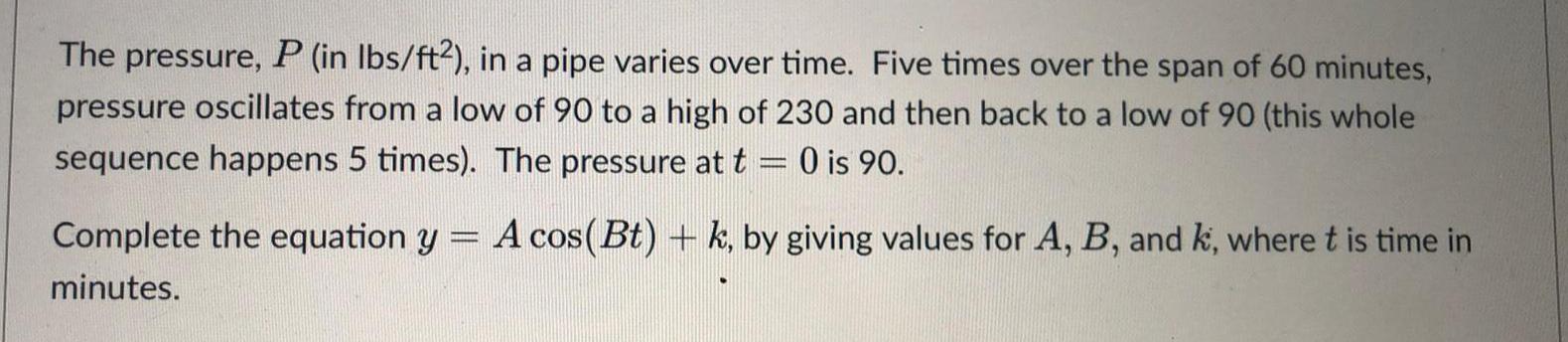
Calculus
Limits & ContinuityThe pressure, P (in lbs/ft2), in a pipe varies over time. Five times over the span of 60 minutes, pressure oscillates from a low of 90 to a high of 230 and then back to a low of 90 (this whole sequence happens 5 times). The pressure at t = 0 is 90. Complete the equation y = A cos(Bt) + k, by giving values for A, B, and k, where t is time in minutes.

Calculus
Limits & ContinuitySuppose s(t) -13t²-14t+100 (3t+6)(3t-9) What is the long run behavior of s(t) as t→ co?

Calculus
Limits & ContinuityTo estimate the width of an archaeological mound, archaeologists place two stakes on opposite ends of the widest point. They set a third stake 82 feet from one stake and 97 feet from the other stake. The angle formed is 125°. Find the width of the mound.

Calculus
Limits & ContinuityA triangular sail for a sailboat has sides of length 6'2", 7'3", and 10'7". What is the sail area? Round to the nearest tenth of a square foot.
The area of the sail is approximately ft^2.
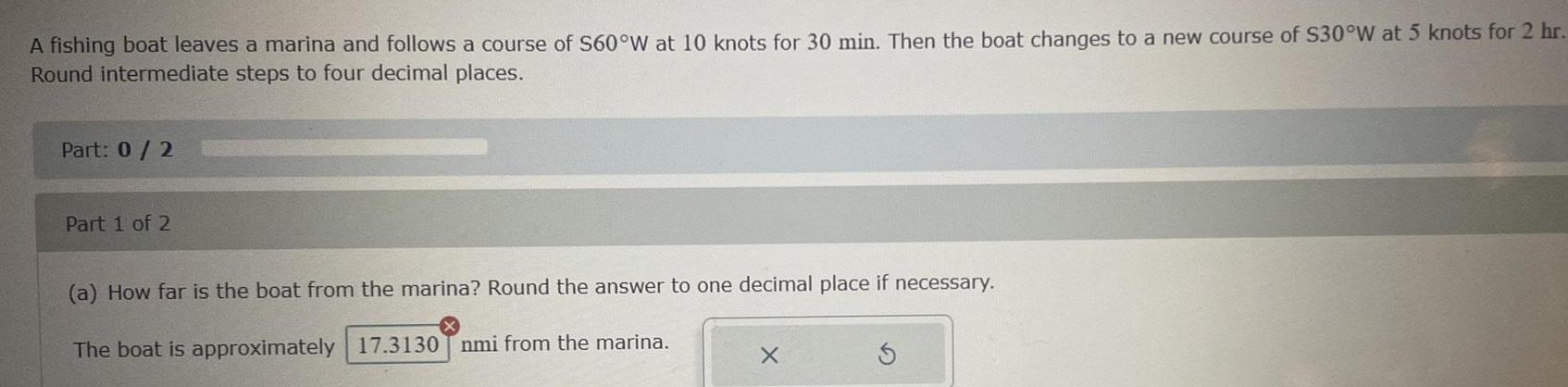
Calculus
Limits & ContinuityA fishing boat leaves a marina and follows a course of S60°W at 10 knots for 30 min. Then the boat changes to a new course of $30°W at 5 knots for 2 hr. Round intermediate steps to four decimal places.
How far is the boat from the marina? Round the answer to one decimal place if necessary. The boat is approximately 17.3130 nmi from the marina.

Calculus
Limits & Continuityf(t)Suppose f(t) =
-15t² +41t+34/(-5t+9) (t+2) What is the long run behavior of as too?
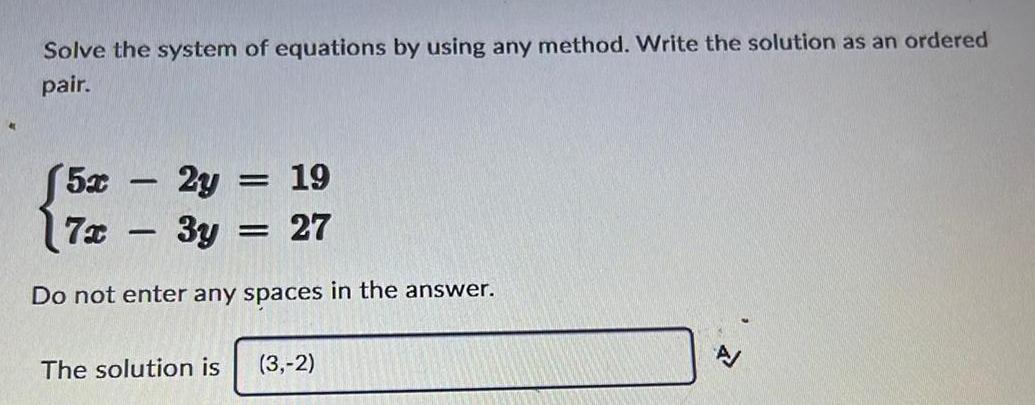
Calculus
Limits & ContinuitySolve the system of equations by using any method. Write the solution as an ordered
pair.
(5x-2y = 19
7x- 3y = 27
Do not enter any spaces in the answer.
The solution is (3,-2)A/
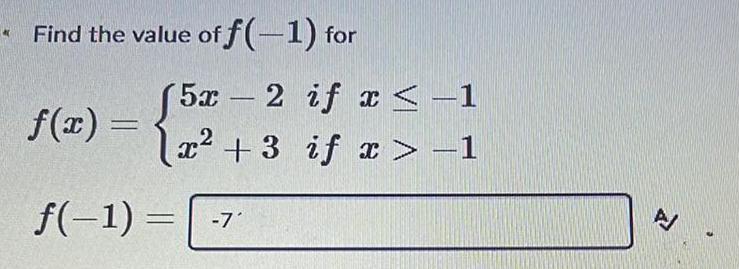
Calculus
Limits & ContinuityFind the value of f(-1) for
f(x) =
(5x-2 if x < -1
,2
x² +3 if x>-1
f(-1) = -7'
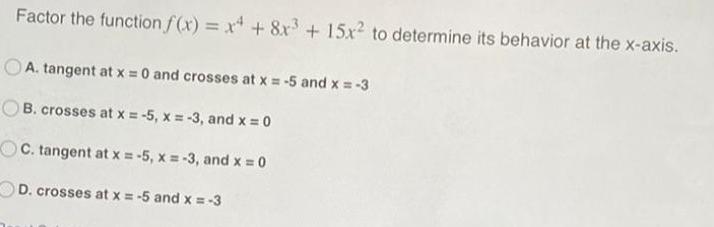
Calculus
Limits & ContinuityFactor the function f(x) = x4 + 8x³ + 15x² to determine its behavior at the x-axis.
A. tangent at x = 0 and crosses at x = -5 and x = -3
B. crosses at x = -5, x = -3, and x = 0
C. tangent at x = -5, x = -3, and x = 0
D. crosses at x = -5 and x = -3

Calculus
Limits & ContinuityDetermine the convergence or divergence of the sequence {a}. an=3n²+ n-1/5n² +n + 1 converges diverges If the sequence converges, find its limit. (If an answer does not exist, enter DNE.)

Calculus
Limits & ContinuityFind the nth Taylor polynomial of the function at the indicated number.
f(x) = x^5 at x = -1, n = 3
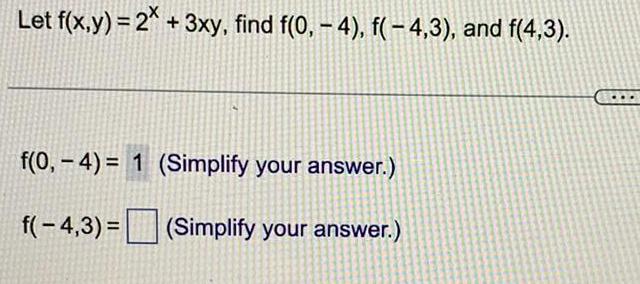
Calculus
Limits & ContinuityLet f(x,y)=2^x + 3xy, find f(0, – 4), f(− 4,3), and f(4,3).
f(0,-4)= (Simplify your answer.)
f(-4,3)= (Simplify your answer.)
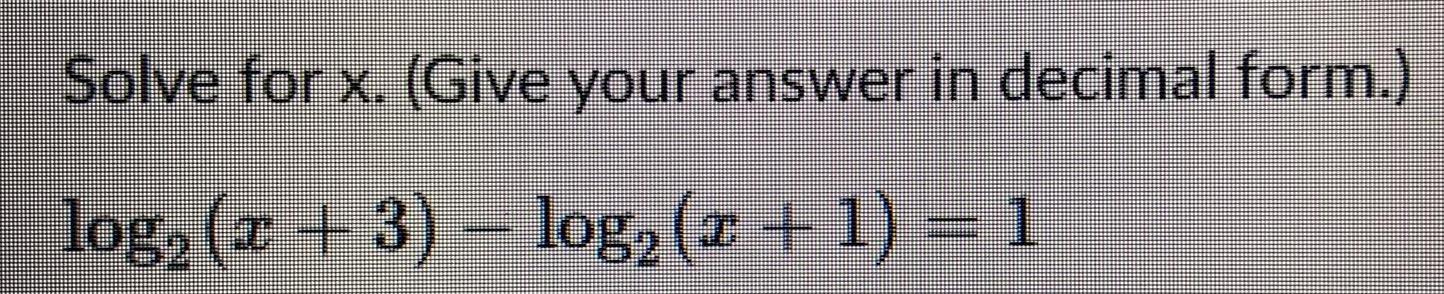
Calculus
Limits & ContinuitySolve for x. (Give your answer in decimal form.)
log₂ (x + 3) - log₂ (x + 1) = 1

Calculus
Limits & ContinuityIn a study a researcher measured a plant to be 8 centimeters tall. If the plant continues to grow 2 centimeters every week, after how many weeks will the plant reach the height
of 24 centimeters?
The plant will reach the height of 24 centimeters after ______ weeks.
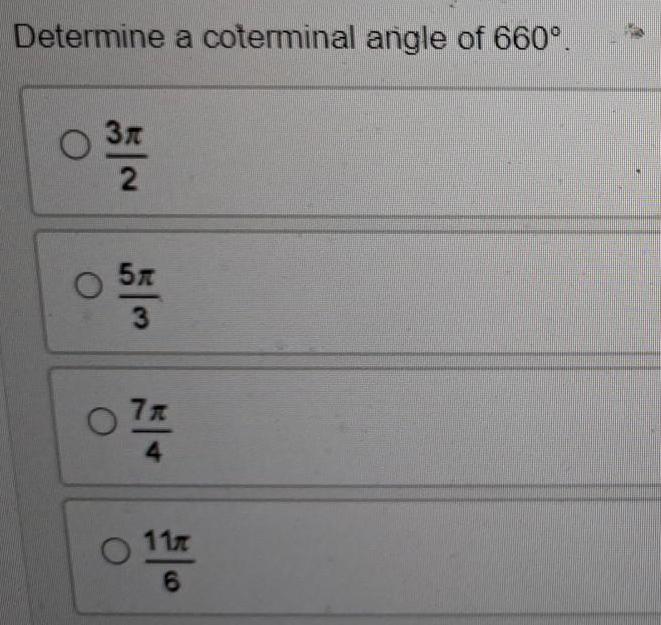

Calculus
Limits & ContinuityFind the area of the surface.
The part of the surface 2y + 4z - x² = 5 that lies above the triangle with vertices (0, 0), (2, 0), and (2, 4)

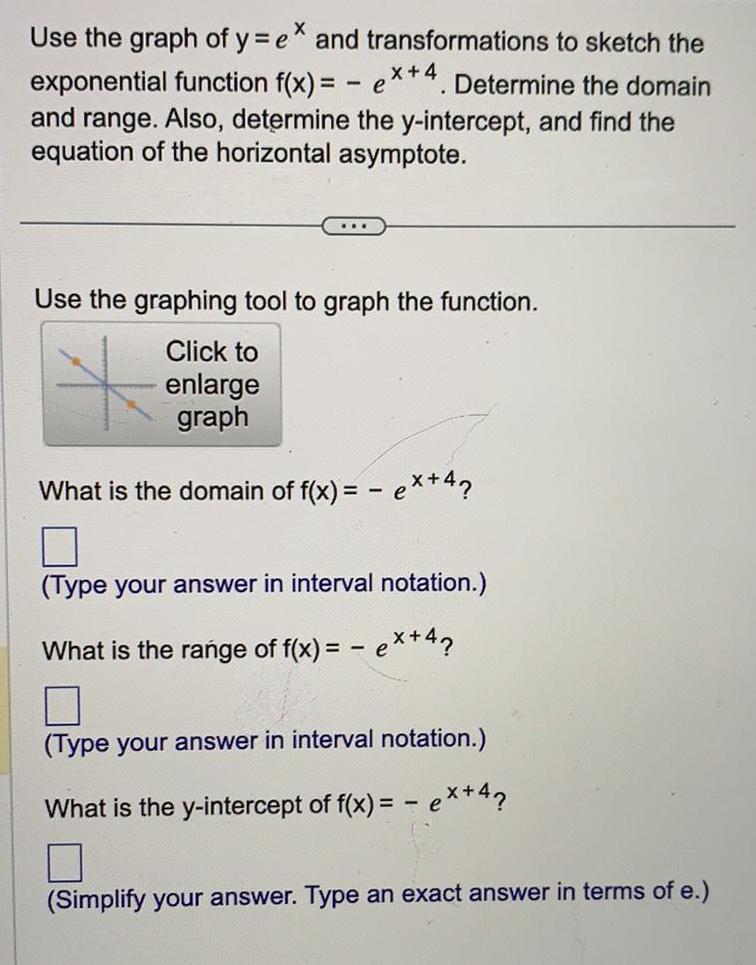
Calculus
Limits & ContinuityUse the graph of y=e* and transformations to sketch the exponential function f(x)= - ex+4. Determine the domain and range. Also, determine the y-intercept, and find the equation of the horizontal asymptote.
Use the graphing tool to graph the function.
What is the domain of f(x) = - ex+4?
(Type your answer in interval notation.)
What is the range of f(x) = - ex+4?
(Type your answer in interval notation.)
What is the y-intercept of f(x) =
(Simplify your answer. Type an exact answer in terms of e.)

Calculus
Limits & ContinuityA storm is approaching and causing the depth of the water in the bay to fluctuate. The depth D(t), in meters, can be described by the function D(t)= 6sin(π/5)t+10 such that t represents the time in minutes. Which of the following graphs represents the depth of the water in the bay?

Calculus
Limits & ContinuityThe number of hours of sunlight in a particular location S(t) can be modeled by the function S(t)=12+2cos(2π/183)t where t is the number of days after January 1st. (That is, t=0 means January 1st.)
After how many days will there be 12 hours of sunlight for the first time during the year?

Calculus
Limits & ContinuityBased on the graph of the trigonometric functions f (θ) = 4sinθ + 3 and g(θ) = cos 2θ, at what value(s) on the interval [0, 2π) does f(θ) = g (θ)?
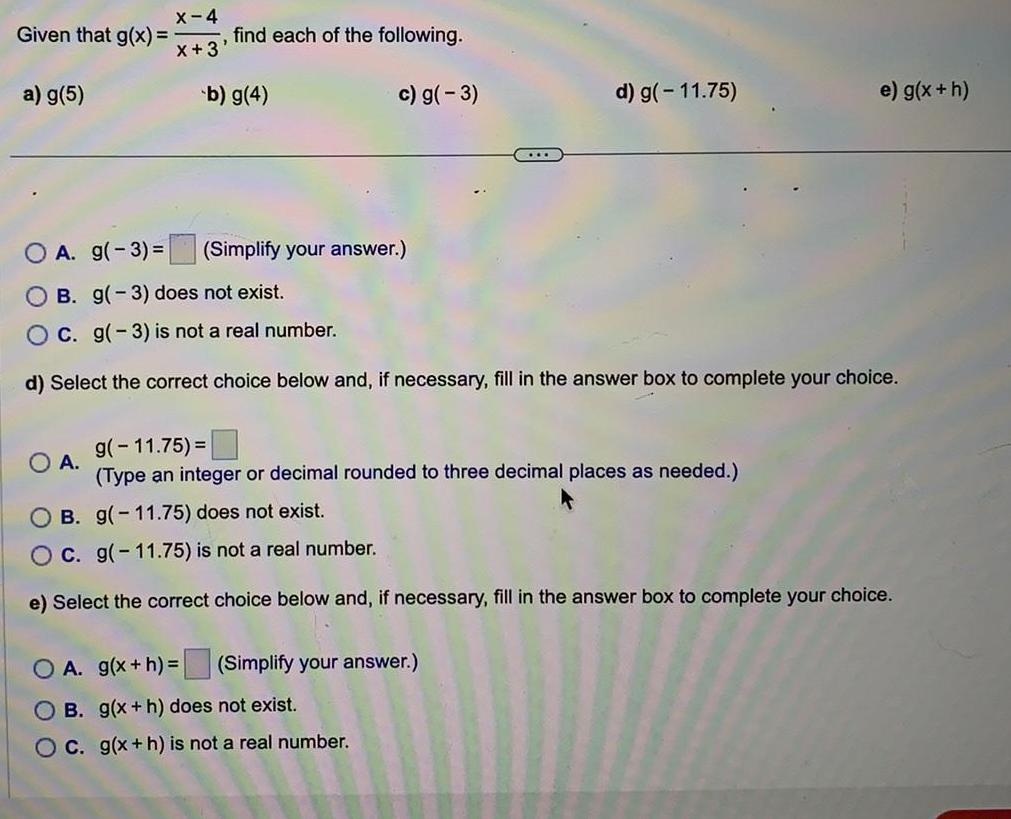
Calculus
Limits & ContinuityGiven that g(x) = x-4/x+3, find each of the following.
a) g(5) b) g(4) c) g(-3) d) g( - 11.75) e) g(x+h)
A. g(-3)= (Simplify your answer.)
B. g(-3) does not exist.
C. g(-3) is not a real number.
d) Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
(Type an integer or decimal rounded to three decimal places as needed.)
A. g(-11,75)=
B. g(-11.75) does not exist.
C. g(-11.75) is not a real number.
e) Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. g(x + h) = (Simplify your answer.)
B. g(x+h) does not exist.
C. g(x+h) is not a real number.
Calculus
Limits & ContinuityFind the intercepts and then use them to graph the equation.
2x + 4y = 8
Use the graphing tool to graph the line. Use the intercepts when drawing the line. If only one intercept exists, use it and another point to draw the line.

Calculus
Limits & ContinuityThere is an angle such that cos(θ)= 4/7 and 3π/2 ≤ θ ≤ 2π. Find the values of the other five trigonometric functions of θ. (There is no equation option, so do the best you can. For example, you may write 19/ -√53 as 19/(- square root(53)).)
a) sin(θ)
b) tan(θ) =
c) csc(θ) =
d) sec(θ) =
e) cot (θ)=

Calculus
Limits & ContinuitySuppose that 4 - x² ≤ f(x) ≤ cos(x) + 3. Find lim f(x)
x->0
Show all your work and reasoning on your paper and enter only the final numerical answer in D2L.
Calculus
Limits & ContinuityIf m<A = 56°, m<B = 60°, and c = 8, what is the measure of side length b?


Calculus
Limits & ContinuityUse polar coordinates to find the volume of the solid inside the sphere x² + y² + z² = 16 and outside the cylinder x² + y² = 4.

Calculus
Limits & ContinuityFind the monthly house payments necessary to amortize a 9.6% loan of $293,700 over 25 years.

Calculus
Limits & ContinuityThere is a building that is known to be 200 feet tall. I walk a certain distance away and find that the angle of elevation to the top of the building is 60°. How far from the building am I?

Calculus
Limits & ContinuityHow many numbers are there between 100 and 1000 in which the sum of digits is equal to 3 ?
(a) 6
(b) 8
(c) 9
(d) 12
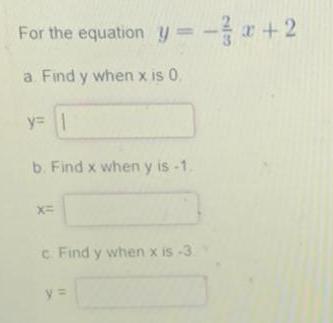
Calculus
Limits & ContinuityFor the equation y=-2 3x + 2
a. Find y when x is 0.
y=
b. Find x when y is -1.
x=
c. Find y when x is -3.
y =

Calculus
Limits & ContinuityA polynomial P is given. Find all zeros of P, real and Complex. Factor P completely.
P(x) = x² + 4x²
P(x) = x³ - 2x² + 2x
P(x) = x² + 2x² + 1

Calculus
Limits & ContinuityLet S be a circle with centre O and radius 2. A and B be two points on the circle. ∠AOB=x, tangents at A and B intersect at D and OA and BD intersect at C. Then which of the following must be correct?
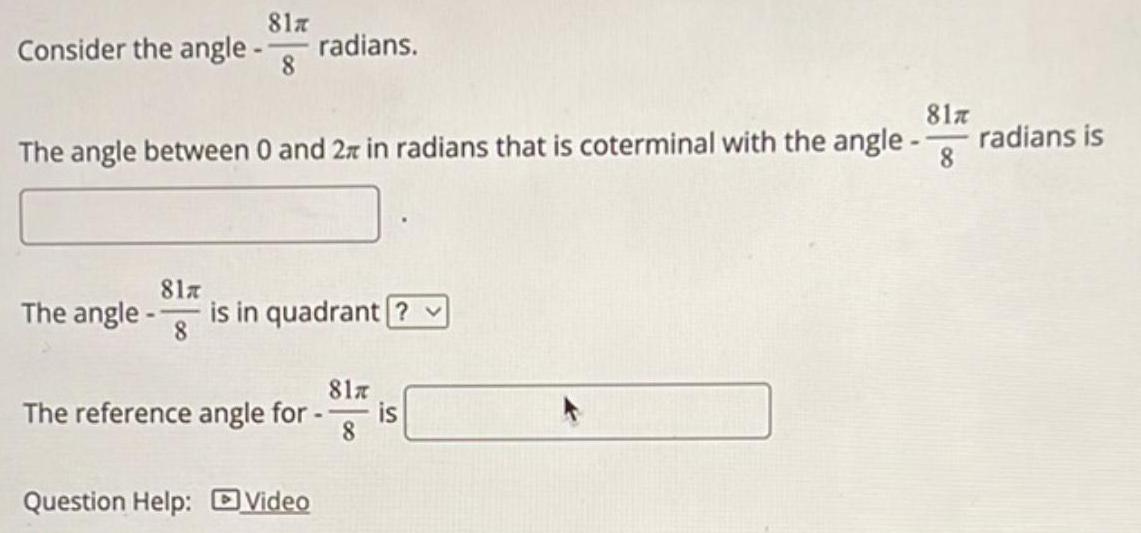
Calculus
Limits & ContinuityConsider the angle -81π 8 radians.
The angle between 0 and 2 in radians that is coterminal with the angle -81π 8 radians is
The angle -81π 8 is in quadrant
The reference angle for -81π 8
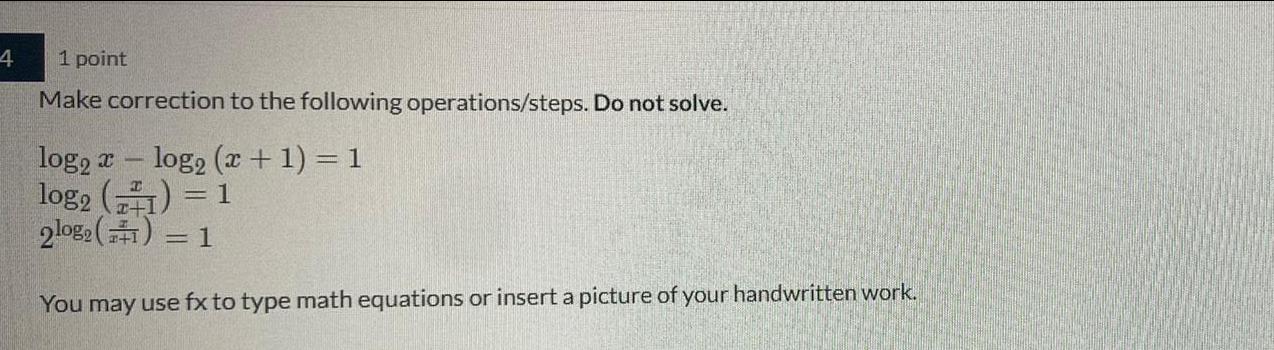
Calculus
Limits & ContinuityMake correction to the following operations/steps. Do not solve.
log₂ x - log₂ (x + 1) = 1
log2 (x x+1) = 1
2log₂ (x x+1) = 1
You may use fx to type math equations or insert a picture of your handwritten work.

Calculus
Limits & ContinuityFrank is putting 12 colored light bulbs into a string of lights. There are 6 blue light bulbs, 2 red light bulbs, and 4 pink light bulbs. How many distinct orders of
light bulbs are there if two light bulbs of the same color are considered identical (not distinct)?
0