Matrices & Determinants Questions and Answers
![Find the matrix A if (Aᵀ – 2I)-¹ = 3 1
2 2
(a) A = 0 -2 (b) A = 5/2 -1/2 (c) A = 1/4[ 1 -2
-1 1 -1/4 11/4 -1 5]
(d) A = 1 -2 (e) A = -3/2 -1/2
-1 5 -1/4 -5/4](https://media.kunduz.com/media/sug-question/raw/78775408-1660048118.3626888.jpeg?w=256)
Algebra
Matrices & DeterminantsFind the matrix A if (Aᵀ – 2I)-¹ = 3 1
2 2
(a) A = 0 -2 (b) A = 5/2 -1/2 (c) A = 1/4[ 1 -2
-1 1 -1/4 11/4 -1 5]
(d) A = 1 -2 (e) A = -3/2 -1/2
-1 5 -1/4 -5/4
Algebra
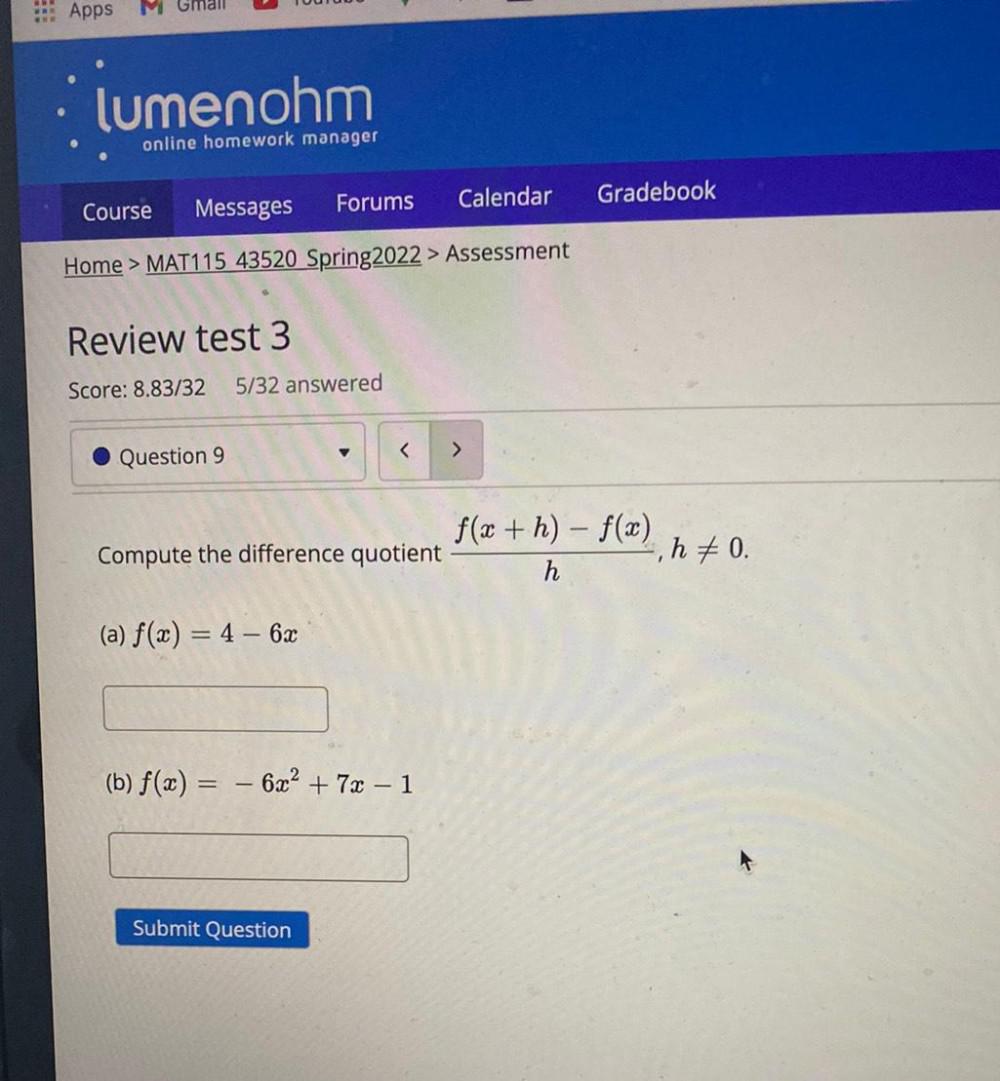
Matrices & DeterminantsCompute the difference quotient f(x + h) – f(t)/ h, h≠0.
(a) f(x) = 4 - 6x
(b) f(x) = - 6x² + 72 - 1

Algebra
Matrices & Determinants(1) If the equation Ax = b has two different solutions then it has infinitely many solutions
(A) True
(B) False
(2) The line
{ (1 2 ) + ( -2 -4 ) t : t∈ R } is a subspace of R² .
(A) Yes
(B) No
(3) Each row of Ax = b corresponds to a linear equation.
(A) Yes
(B) No
Algebra
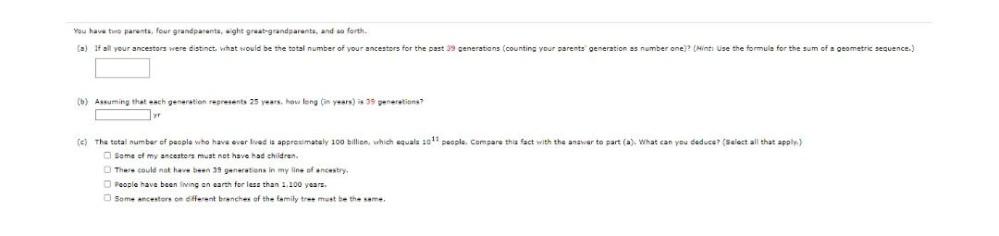
Matrices & DeterminantsYou have two parents, four grandparents, eight great-grandparents, and so forth.
(a) If all your ancestors were distinct, what would be the total number of your ancestors for the past 39 generations (counting your parents generation as number one)? (Hint: Use the formula for the sum of a geometric sequence.)
(b) Assuming that each generation represents 25 years, how long (in years) is 39 generations?
(c) The total number of people who have ever lived is approximately 100 billion, which equals 1011 people. Compare this fact with the answer to part (a). What can you deduce? (Select all that apply.)
Some of my ancestors must not have had children.
There could not have been 39 generations in my line of ancestry
People have been living on earth for less than 1, 100 years.
Some ancestors on different branches of the family tree must be the same

Algebra
Matrices & DeterminantsFind the eigenvalues and the corresponding eigenspaces for each of the following matrices:

Algebra
Matrices & DeterminantsFind a singular value decomposition of the matrix of A
Where, A = 1 0 0
6 -2 0
7 -4 2
![Which scenario could be represented by the following matrix? [10 20 40]
1. The star player had 10 rebounds and 20 points in the game where the final score was 40 points.
2. None of these choices are correct.
3. A book store sold 40 paperbacks and 20 hardbacks on the 10th of the month
4 A music store averages sales of 15 CDs, 40 DVDs per day, and an average of 80 customers per day
5 Two stores are competing for sales. One store sold 10 perfumes and 20 soaps, the other sold 20 perfumes and 40 soaps.](https://media.kunduz.com/media/sug-question/raw/78934344-1660038180.651945.jpeg?w=256)
Algebra
Matrices & DeterminantsWhich scenario could be represented by the following matrix? [10 20 40]
1. The star player had 10 rebounds and 20 points in the game where the final score was 40 points.
2. None of these choices are correct.
3. A book store sold 40 paperbacks and 20 hardbacks on the 10th of the month
4 A music store averages sales of 15 CDs, 40 DVDs per day, and an average of 80 customers per day
5 Two stores are competing for sales. One store sold 10 perfumes and 20 soaps, the other sold 20 perfumes and 40 soaps.

Algebra
Matrices & DeterminantsThe navy bean soup recipe requires 120 g of bacon. If the EP unit cost of the bacon is $3.15 per kg, what is the total cost of the ingredient? Round to the nearest cent.
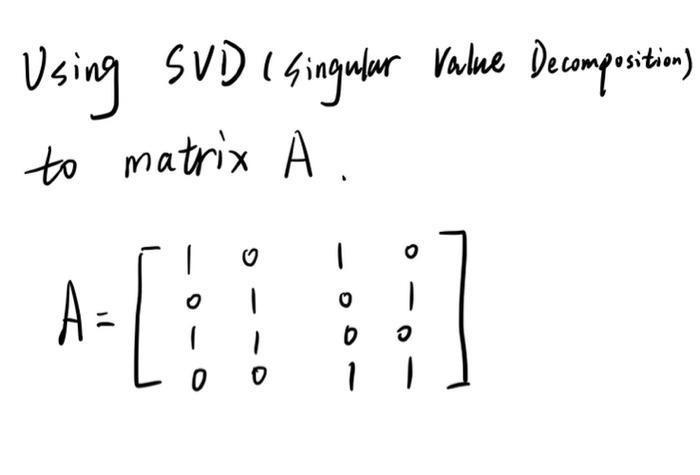
Algebra
Matrices & DeterminantsUsing SVD ( singular Value Decomposition)
to matrix A.
A= 1 0 1 0
0 1 0 1
1 1 0 0
0 0 1 1

Algebra
Matrices & DeterminantsThe dimensions of a triangular lot are 192 feet by 102 feet by 163 feet. If the price of such land is $3 per square foot, how much does the lot cost?

Algebra
Matrices & DeterminantsList the eigenvalues of A. The transformation X-Ax is the composition of a rotation and a scaling. Give the angle of the rotation, where - π<p≤ π, and give the scale factor r.

Algebra
Matrices & DeterminantsSolve the first order homogeneous differential equation
dy/dx = x²-2xy/y² + x²
Algebra
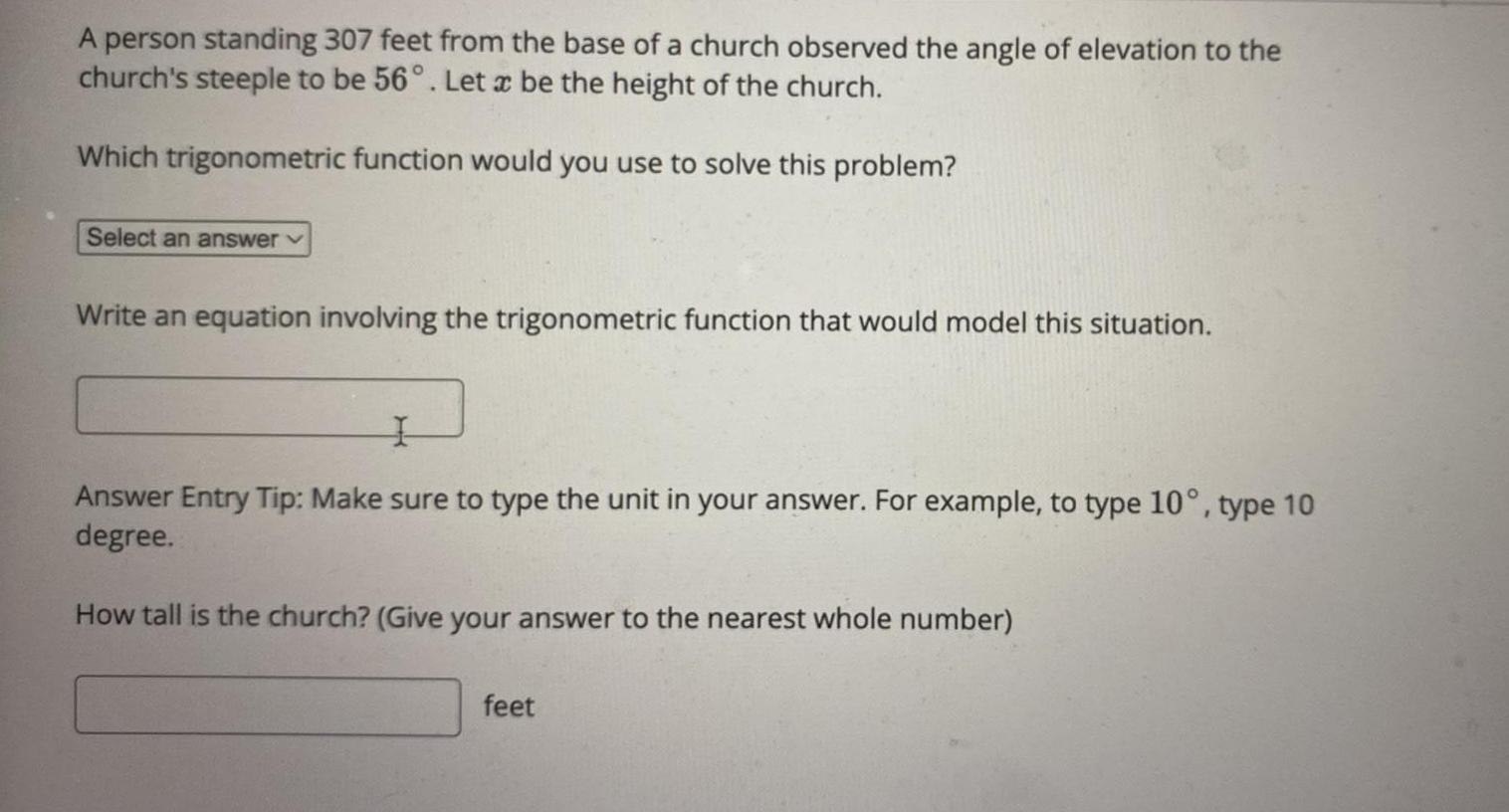
Matrices & DeterminantsA person standing 307 feet from the base of a church observed the angle of elevation to the
church's steeple to be 56°. Let a be the height of the church.
Which trigonometric function would you use to solve this problem?
Write an equation involving the trigonometric function that would model this situation.
Answer Entry Tip: Make sure to type the unit in your answer. For example, to type 10°, type 10
degree.
How tall is the church? (Give your answer to the nearest whole number)
feet
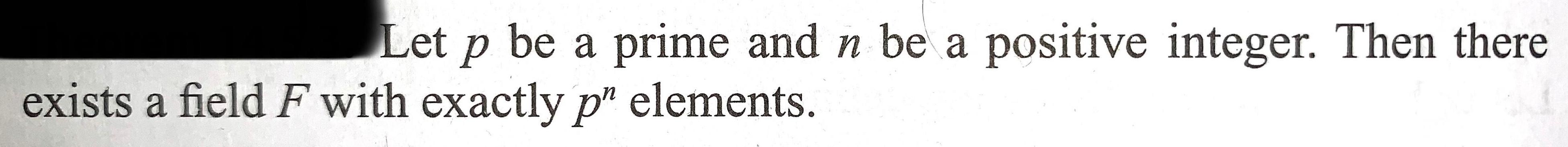
Algebra
Matrices & DeterminantsLet p be a prime and n be a positive integer. Then there exists a field F with exactly p" elements.
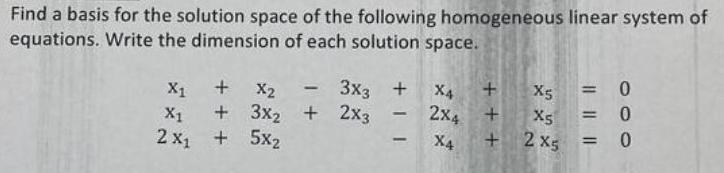
Algebra
Matrices & DeterminantsFind a basis for the solution space of the following homogeneous linear system of equations. Write the dimension of each solution space.
x1 + x2 - 3x3 + x4 + x5 = 0
x1 + 3x2 + 2x3 - 2x4 + x5 = 0
2x1+ 5x2 - x4 + 2x5 = 0
![Define T:R² → R² by T(x) = Ax, where A = 4 -5
-3 6 . Find a basis B for R² with the
property that [T]B is diagonal.](https://media.kunduz.com/media/sug-question/raw/79079335-1659986542.750511.jpeg?w=256)
Algebra
Matrices & DeterminantsDefine T:R² → R² by T(x) = Ax, where A = 4 -5
-3 6 . Find a basis B for R² with the
property that [T]B is diagonal.
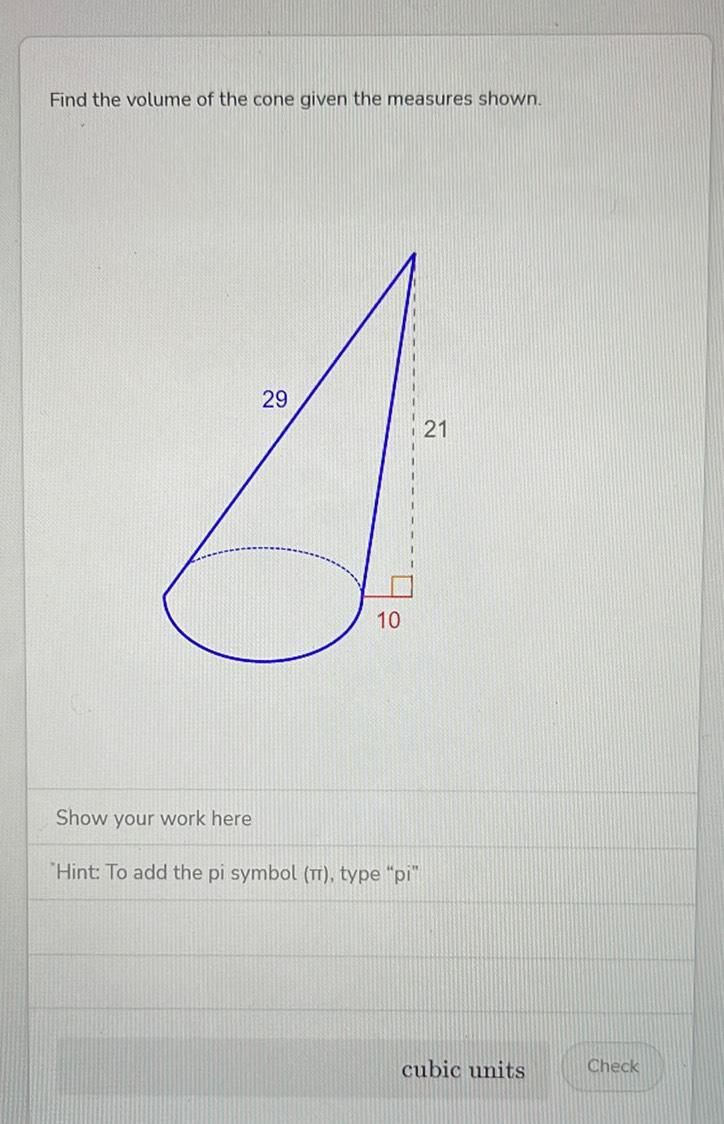
Algebra
Matrices & DeterminantsFind the volume of the cone given the measures shown.
"Hint: To add the pi symbol
"pi

Algebra
Matrices & DeterminantsFind (a) the orthogonal projection of b onto Col A and (b) a least-squares solution of Ax=b.
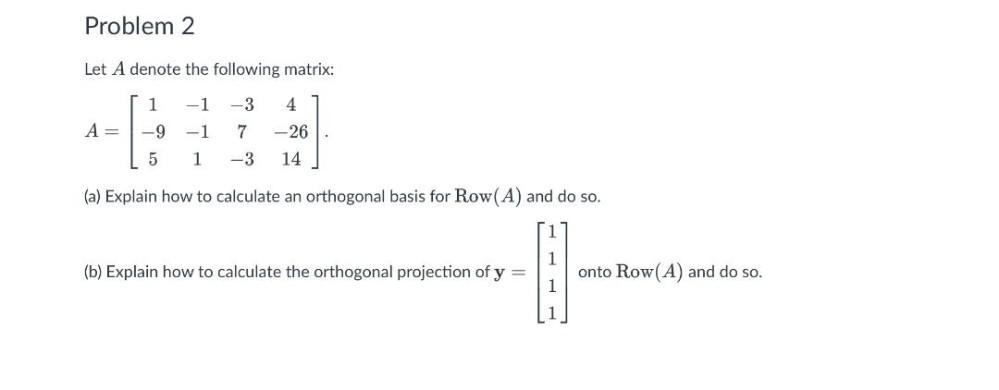
Algebra
Matrices & DeterminantsLet A denote the following matrix:
A= 1 -1 -3 4
-9 -1 7 -26
5 1 -3 14
(a) Explain how to calculate an orthogonal basis for Row(A) and do so.
(b) Explain how to calculate the orthogonal projection of y = 1 1 1 1 onto Row(A) and do so.
![Suppose A is the matrix for T: R³ - R³ relative to the standard basis. Find the diagonal matrix A' for T relative to the basis B.
[0 2 0
1 -1 0
0 1 1]
B' = {(-1, 1, 0), (2, 1, 0), (0, 0, 1)}
A=
A'=](https://media.kunduz.com/media/sug-question/raw/79075757-1659975992.5522573.jpeg?w=256)
Algebra
Matrices & DeterminantsSuppose A is the matrix for T: R³ - R³ relative to the standard basis. Find the diagonal matrix A' for T relative to the basis B.
[0 2 0
1 -1 0
0 1 1]
B' = {(-1, 1, 0), (2, 1, 0), (0, 0, 1)}
A=
A'=
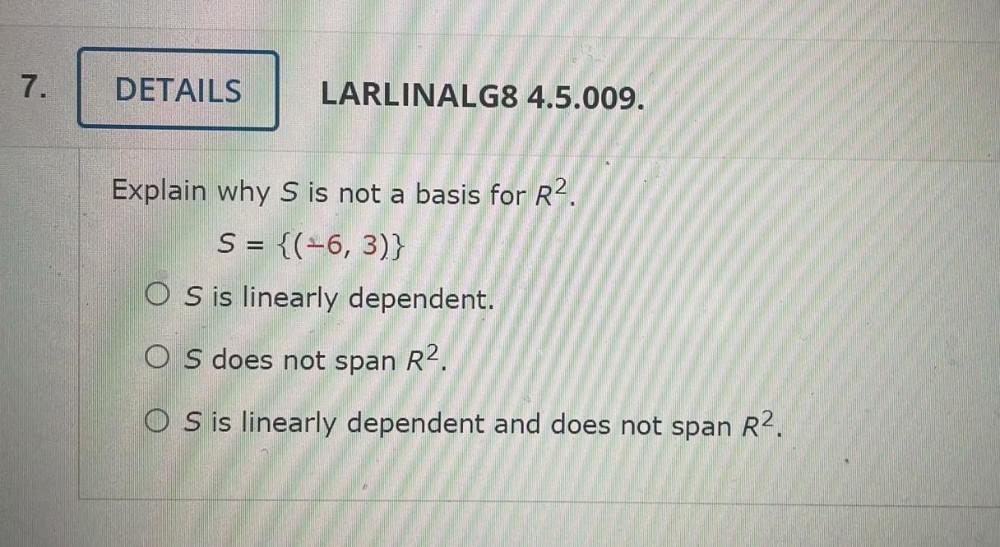
Algebra
Matrices & DeterminantsExplain why S is not a basis for R². S = {(-6,3)}
1. S is linearly dependent.
2. S does not span R².
3. S is linearly dependent and does not span R².

Algebra
Matrices & DeterminantsFor the matrix M = 3 -1 -2
0 5 4
0 3 9
(a) List the eigenvalues in increasing order, including any that are repeated
(b) Enter a basis for the eigenspace that corresponds to the highest eigenvalue.
(c) Enter a basis for the eigenspace that corresponds to the lowest eigenvalue.
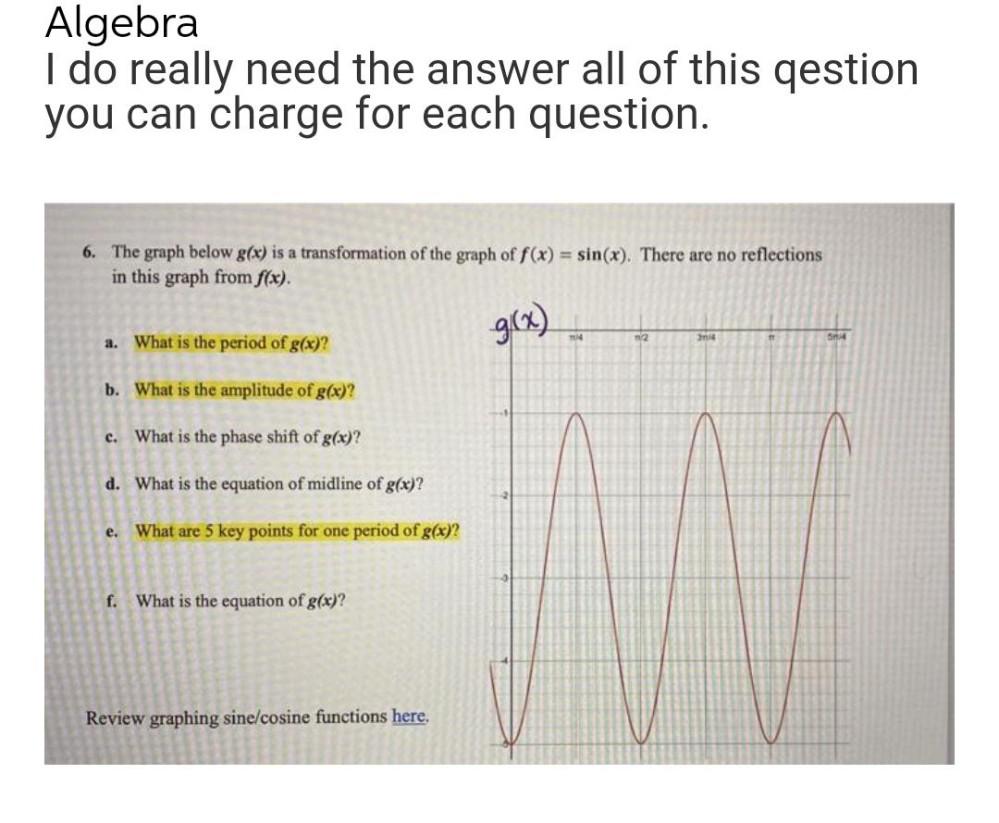
Algebra
Matrices & DeterminantsThe graph below g(x) is a transformation of the graph of f(x) = sin(x). There are no reflections in this graph from f(x).
a. What is the period of g(x)?
b. What is the amplitude of g(x)?
c. What is the phase shift of g(x)?
d. What is the equation of midline of g(x)?
e. What are 5 key points for one period of g(x)?
f. What is the equation of g(x)?
![Suppose
A =
2001
0 3 0
0 0 1
1 -10
2 0 2
0
Which of the followings are the eigenvectors of A?
(a)
HUBE
-{1:00
- {E}] 0 [0]
»{AA)
-{
(b)
(c)
(d)
Please check ALL the answers you think are correct.
Suppose A is not diagonalizable.
If the characteristic equation of Ais:
-1 +212 - W=0.
then dim Nul(A) = 1
dim Nul(A - 13) = 2](https://media.kunduz.com/media/sug-question/raw/79084763-1659974341.4604833.jpeg?w=256)
Algebra
Matrices & DeterminantsSuppose
A =
2001
0 3 0
0 0 1
1 -10
2 0 2
0
Which of the followings are the eigenvectors of A?
(a)
HUBE
-{1:00
- {E}] 0 [0]
»{AA)
-{
(b)
(c)
(d)
Please check ALL the answers you think are correct.
Suppose A is not diagonalizable.
If the characteristic equation of Ais:
-1 +212 - W=0.
then dim Nul(A) = 1
dim Nul(A - 13) = 2
![Find the general solution of the given system using the eigenvalue method.
3] Z(0)
' (t) =
5
-2](https://media.kunduz.com/media/sug-question/raw/84928474-1659974014.0624387.jpeg?w=256)
Algebra
Matrices & DeterminantsFind the general solution of the given system using the eigenvalue method.
3] Z(0)
' (t) =
5
-2
![P-1.34 Consider the matrix A of size n x n and the vector z ER",
-1 ...
(11)-0)
A =
00
a. Compute Ax, ||Ax||2, and ||||2.
b. Show that || A||2 ≥ √n.
c. Give a lower bound for ₂ (A).
=
1/2
1/4
1/8]
1/2-1](https://media.kunduz.com/media/sug-question/raw/84917355-1659974001.651212.jpeg?w=256)
Algebra
Matrices & DeterminantsP-1.34 Consider the matrix A of size n x n and the vector z ER",
-1 ...
(11)-0)
A =
00
a. Compute Ax, ||Ax||2, and ||||2.
b. Show that || A||2 ≥ √n.
c. Give a lower bound for ₂ (A).
=
1/2
1/4
1/8]
1/2-1

Algebra
Matrices & DeterminantsQuestion 2. Determine whether S is a basis for the indicated vector space.
S = {(1, 5, 3), (0, 1, 2), (0, 0, 6)) for R³
a.
b. S = {(0, 3,-2), (4, 0, 3), (-8, 15, -16)} for R³
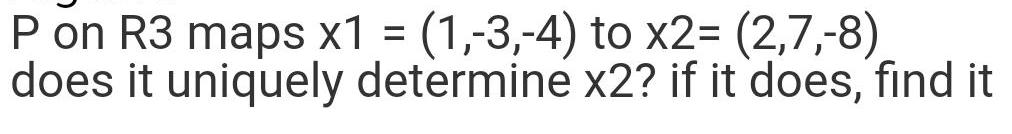
Algebra
Matrices & DeterminantsP on R3 maps x1 = (1,-3,-4) to x2=(2,7,-8) does it uniquely determine x2? if it does, find it
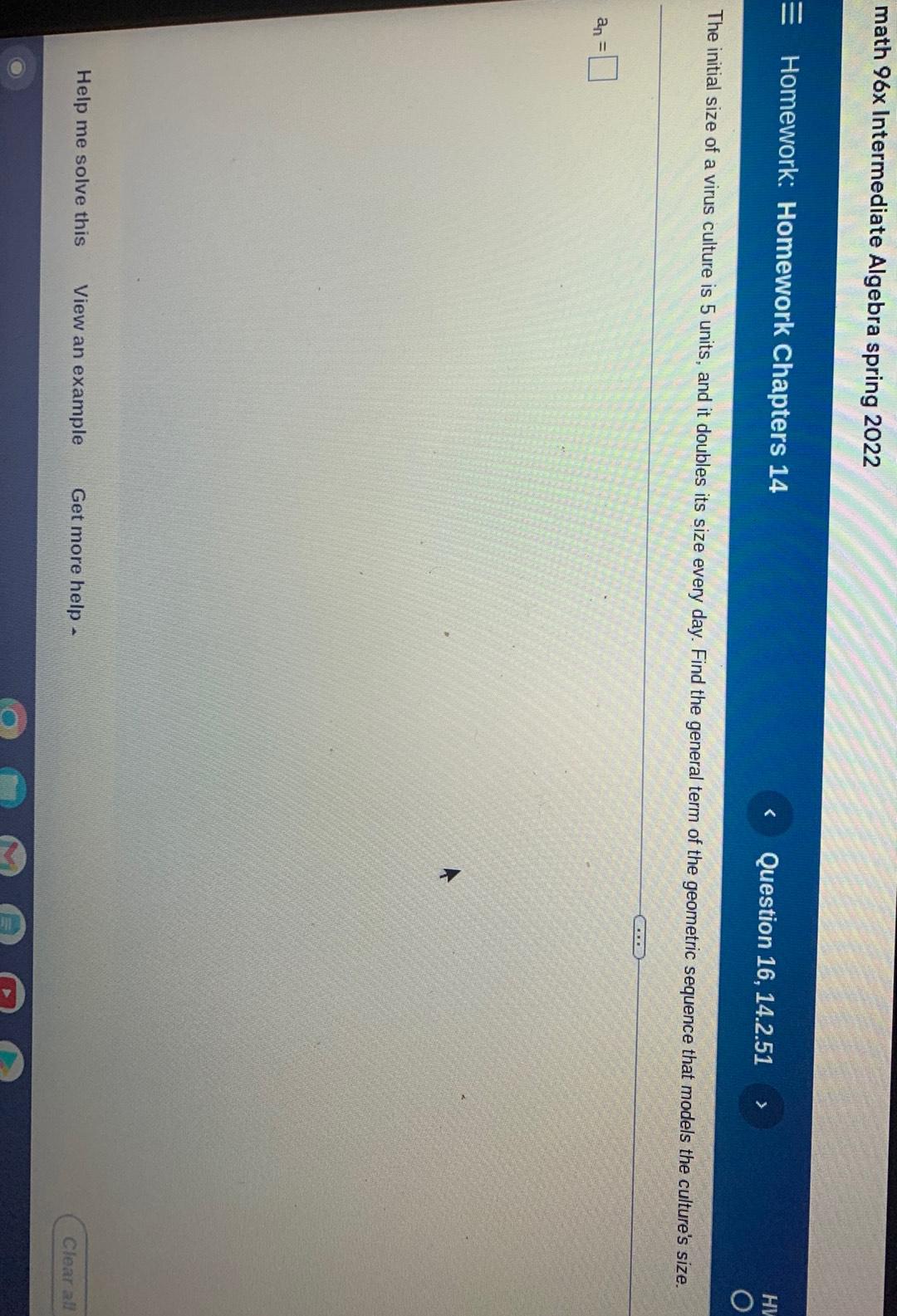
Algebra
Matrices & DeterminantsThe initial size of a virus culture is 5 units, and it doubles its size every day. Find the general term of the geometric sequence that models the culture's size.
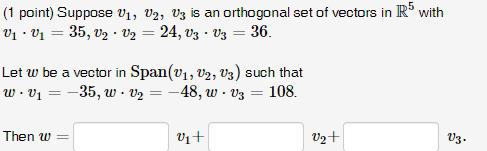
Algebra
Matrices & DeterminantsSuppose V₁, V2, V3 is an orthogonal set of vectors in R5 with
V₁ = 35, V₂ V₂ = 24, V3 V3 = 36.
Let w be a vector in Span(V₁, V₂, V3) such that
w. v₁ = -35, w V₂ = -48
![The position of two particles on the x-axis are x₁ = sin t and x₂ = sin(t+ π/3) where t denotes the time.
(a) At what time(s) in the interval t = [0, 27] do the particles meet?
(b) What is the farthest distance between the two particles?
(c) When in the interval t ∈[0, 2 π] is the distance between the particles changing at the fastest rate?](https://media.kunduz.com/media/sug-question/raw/79236733-1659893327.4292068.jpeg?w=256)
Algebra
Matrices & DeterminantsThe position of two particles on the x-axis are x₁ = sin t and x₂ = sin(t+ π/3) where t denotes the time.
(a) At what time(s) in the interval t = [0, 27] do the particles meet?
(b) What is the farthest distance between the two particles?
(c) When in the interval t ∈[0, 2 π] is the distance between the particles changing at the fastest rate?
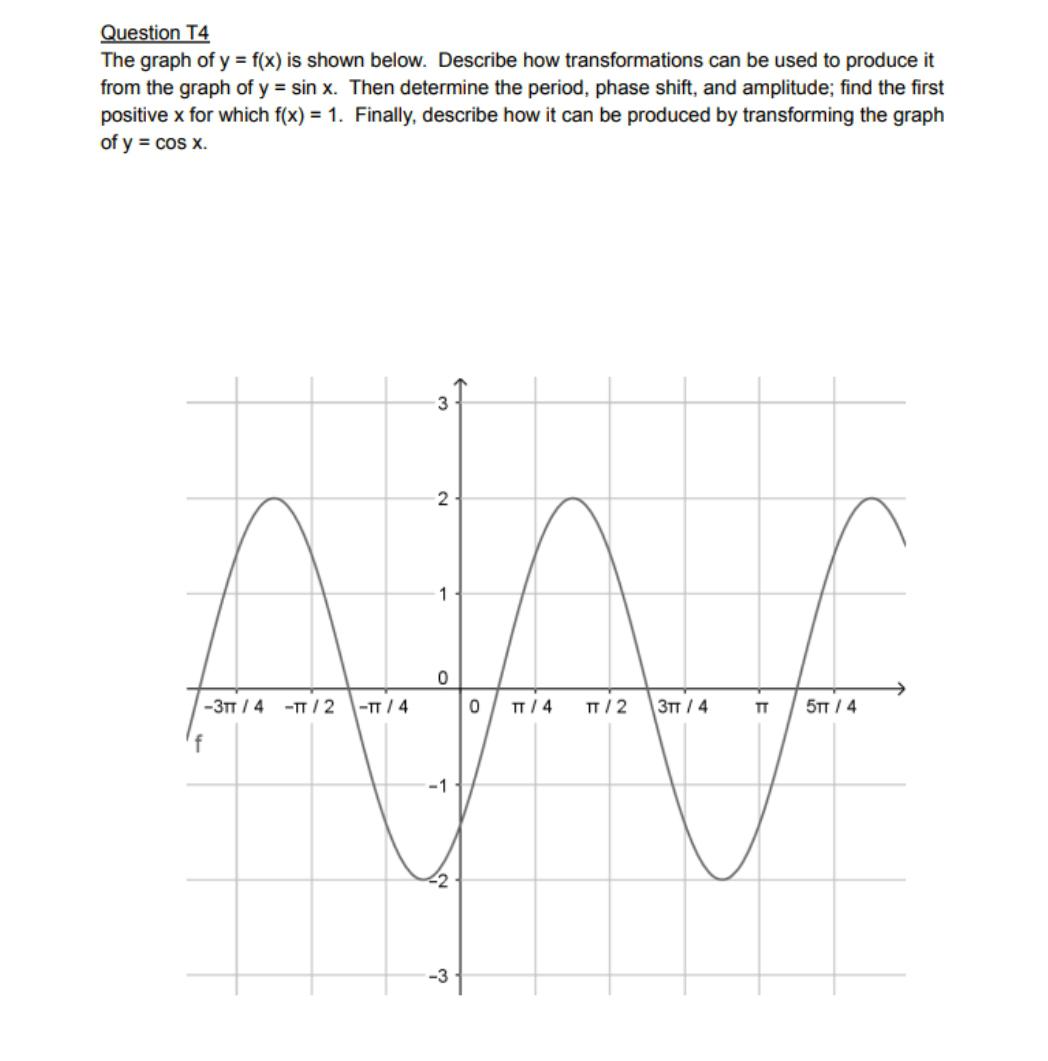
Algebra
Matrices & DeterminantsThe graph of y = f(x) is shown below. Describe how transformations can be used to produce it from the graph of y= sin x. Then determine the period, phase shift, and amplitude; find the first positive x for which f(x) = 1. Finally, describe how it can be produced by transforming the graph of y = cos x.

Algebra
Matrices & DeterminantsThe system of linear equations { x + 9y + 7z = -3
y + 2z = 2
z = 4
(A) has infinitely many solutions
(B) has exactly 2 solutions
(C) has exactly 1 solution
(D) has 0 solutions
Algebra
Matrices & DeterminantsAn initial population of 4,500 undergoes a growth of 4% each month. What will the population be in 5 years?
A. 47,338
B. 15,300
C.5,475
D.36,023
Algebra
Matrices & DeterminantsThe number of kilograms of water in a human body varies directly as the mass of the body. A 93-kg person contains 62 kg of water. How many kilograms of water are in an kg of water are in an 81-kg person.

Algebra
Matrices & DeterminantsFind the coordinate vector of p relative to the basis S = {P₁, P₂, P₃} for P₂
p = 15 - 21x + 6x²; P₁= 3, P₂= 3x, P₃ = 2x².
(P)s=
![Find the inverse of the matrix. [7 4] [9 2]
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
(A) [ 7 4 ] -¹
(B) The matrix is not invertible.](https://media.kunduz.com/media/sug-question/raw/79375740-1659891095.778315.jpeg?w=256)
Algebra
Matrices & DeterminantsFind the inverse of the matrix. [7 4] [9 2]
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
(A) [ 7 4 ] -¹
(B) The matrix is not invertible.

Algebra
Matrices & DeterminantsFor the following matrix A, find a basis of its null space Null(A), and determine its dimension. Explain why vectors you find satisfy conditions for a basis.
1 -2 -1 -1 -1
2 -4 -1 -2 0
4 -8 -4 -3 -6
1 -2 -2 0 -5
![Find the matrix that is similar to matrix A.
A=[-1-3] [1 3]](https://media.kunduz.com/media/sug-question/raw/79380121-1659890613.4481149.jpeg?w=256)

Algebra
Matrices & DeterminantsProve that if two distinct hyperplanes in R^4 intersect, then they intersect in a plane.
Algebra
Matrices & DeterminantsDecide and justify whether the following real quadratic form is positive definite
f(x, y, z) = x² + 2xy + 2xz+ 2y² + 5z²

Algebra
Matrices & DeterminantsThe 2 x 2 elementary matrix E can be obtained from the identity matrix using the row operation r₁ ← r₁ + 2r2. Find EA if A = 4 -5
Algebra
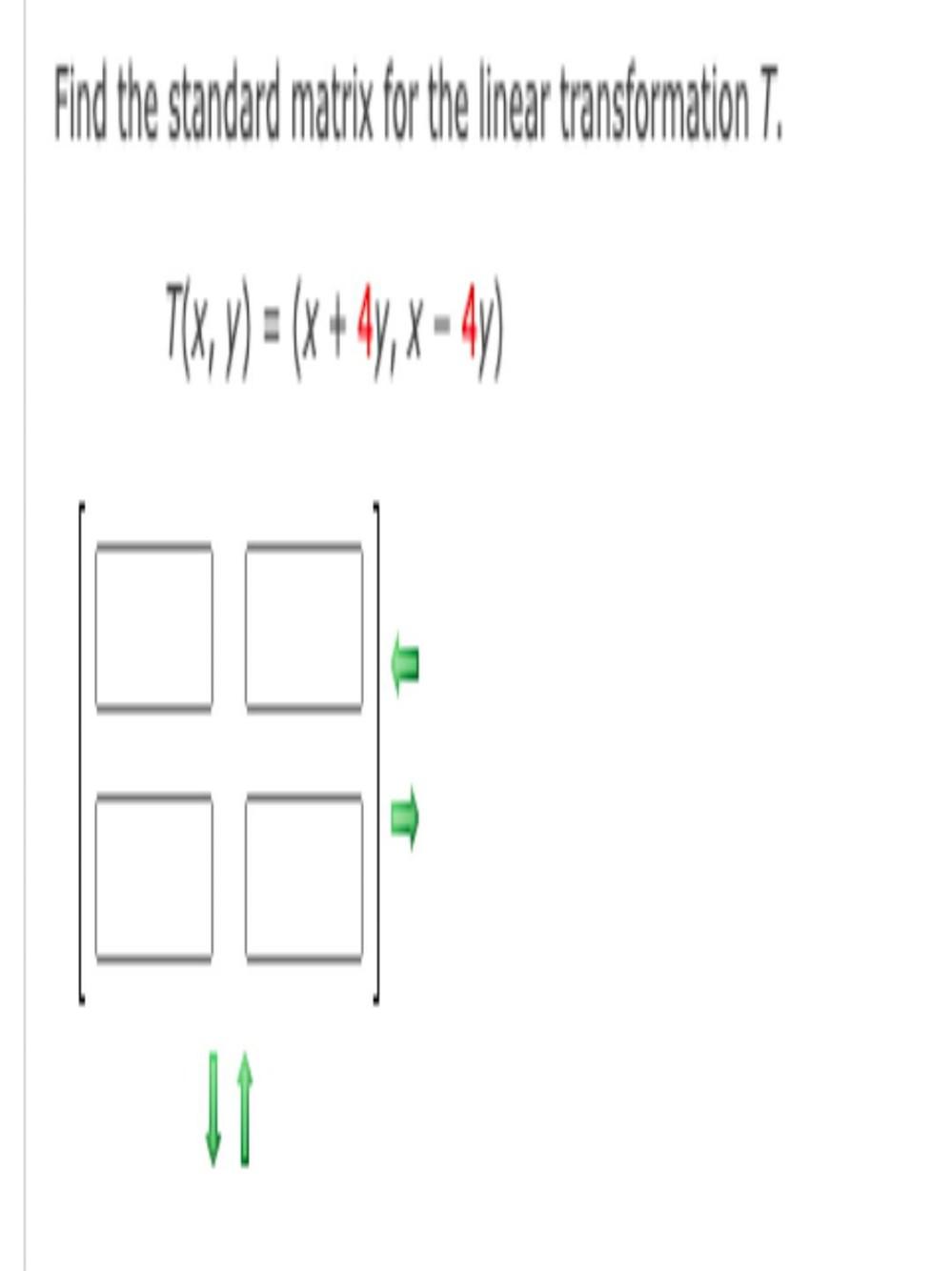
Matrices & DeterminantsFind the standard matrix for the linear transformation T,
T(X, Y) = (X + 4Y, X = 4Y)
Algebra
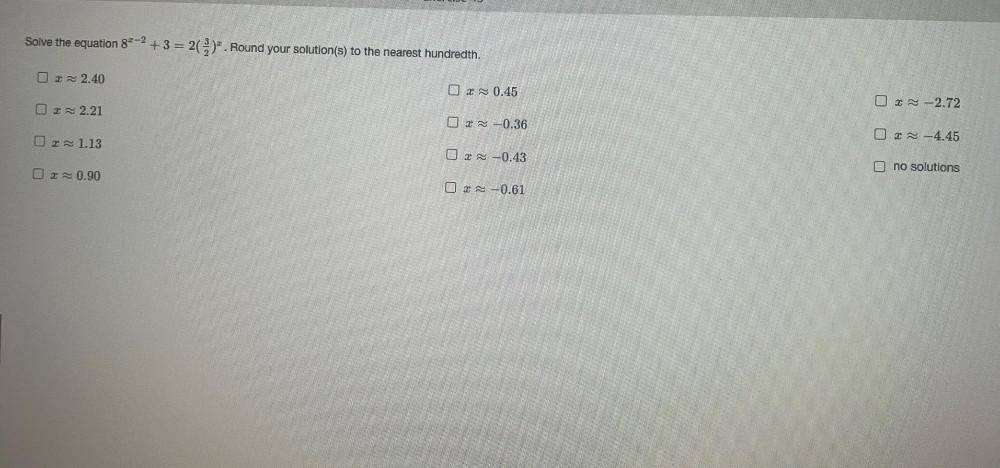
Matrices & DeterminantsSolve the equation 8x-² +3 = 2(³/ ²)x . Round your solution(s) to the nearest hundredth.
(a)x≈2.40 (b)≈ 0.45 (c)≈ 2.21 (d)≈ 1.13 (e)≈ 0.90
(f)x≈-0.36 (g)x≈-0.43 (h)x≈-0.61 (I)x≈-2.72
(j)x≈-4.45 (k)no solutions

Algebra
Matrices & DeterminantsSuppose U, V and W are finite-dimensional vector spaces and S∈ L(V, W) and T∈L(U, V). Prove that dim(range(ST)) ≤ min{dim(range(S)), dim(range(T))}.

Algebra
Matrices & DeterminantsSolve the system of linear equations. (Enter your answers as a comma-
separated list. If there is no solution, enter NO SOLUTION. If the system has an infinite number of solutions, set w = t and solve for x, y, and z in terms of t.)
x + y +z+w = 6
2x+ 3y-w= 4
-3x+ 4y + z+2w = -4
x+ 2y -z+2w=4
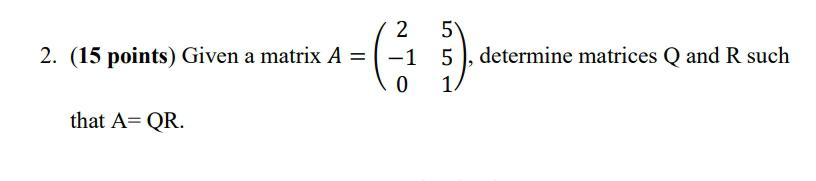
Algebra
Matrices & DeterminantsGiven a matrix
2 5
A = -1 5
0 1
determine matirces Q and R such that A = QR
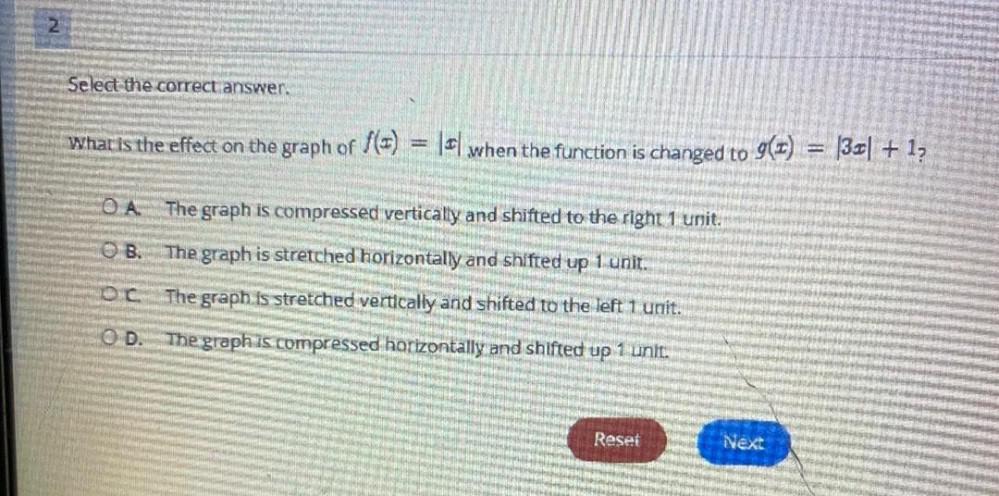
Algebra
Matrices & DeterminantsWhat is the effect on the graph of f(x) = |x| when the function is changed to 9(1) = |3x| + 1,
A The graph is compressed vertically and shifted to the right 1 unit.
B The graph is stretched horizontally and shifted up 1 unit.
B.C The graph is stretched vertically and shifted to the left 1 unit.
D. The graph is compressed horizontally and shifted up 1 unit.

Algebra
Matrices & DeterminantsSolve the matrix equation for X:
-1 0 1 1 3 0
X 1 1 0 = -9 1 12
3 1 -1