Matrices & Determinants Questions and Answers
![If f(x) = 3x + 2 and g(x)= 1/3(x-1) what is the value of f[g(4)]?
A 5
B.-3
C= 50/3
D.-4](https://media.kunduz.com/media/sug-question/raw/79710890-1659885514.836004.jpeg?w=256)
Algebra
Matrices & DeterminantsIf f(x) = 3x + 2 and g(x)= 1/3(x-1) what is the value of f[g(4)]?
A 5
B.-3
C= 50/3
D.-4
![All solutions [x, y, z] of the linear equation 9x- 25y + 24z = -20 geometrically represent a plane P in R³. Find a normal vector n to P and the position vectors p, q, r of three distinct points in P:](https://media.kunduz.com/media/sug-question/raw/79887857-1659885483.3755796.jpeg?w=256)
Algebra
Matrices & DeterminantsAll solutions [x, y, z] of the linear equation 9x- 25y + 24z = -20 geometrically represent a plane P in R³. Find a normal vector n to P and the position vectors p, q, r of three distinct points in P:
Algebra
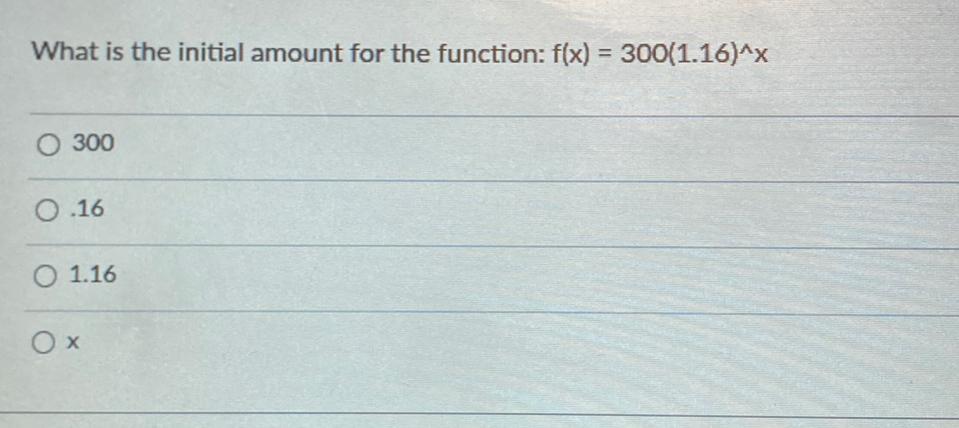
Matrices & DeterminantsWhat is the initial amount for the function: f(x) = 300(1.16)^x
(A) 300
(B) 16
(C) 1.16
(D) x
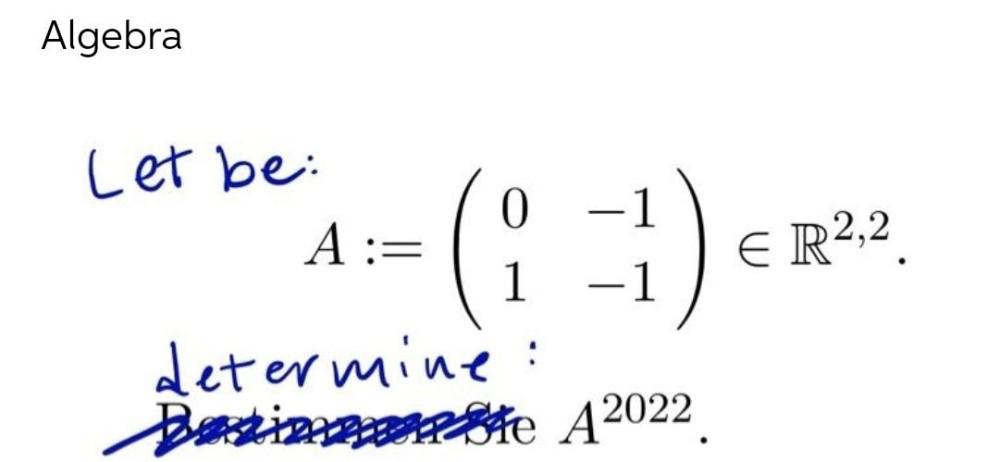
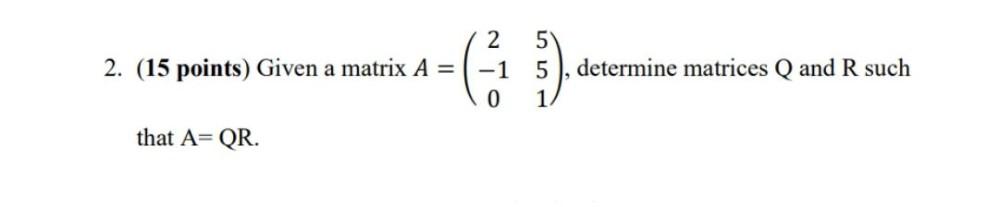
Algebra
Matrices & DeterminantsGiven a matrix A = ( 2 5, -1 5, 0 1) determine matrices Q and R such that A= QR.

Algebra
Matrices & DeterminantsLet be the vector from initial point P₁ = (-2,15) to terminal point P₂ = (7,8). Write v in terms of i and j .
Algebra
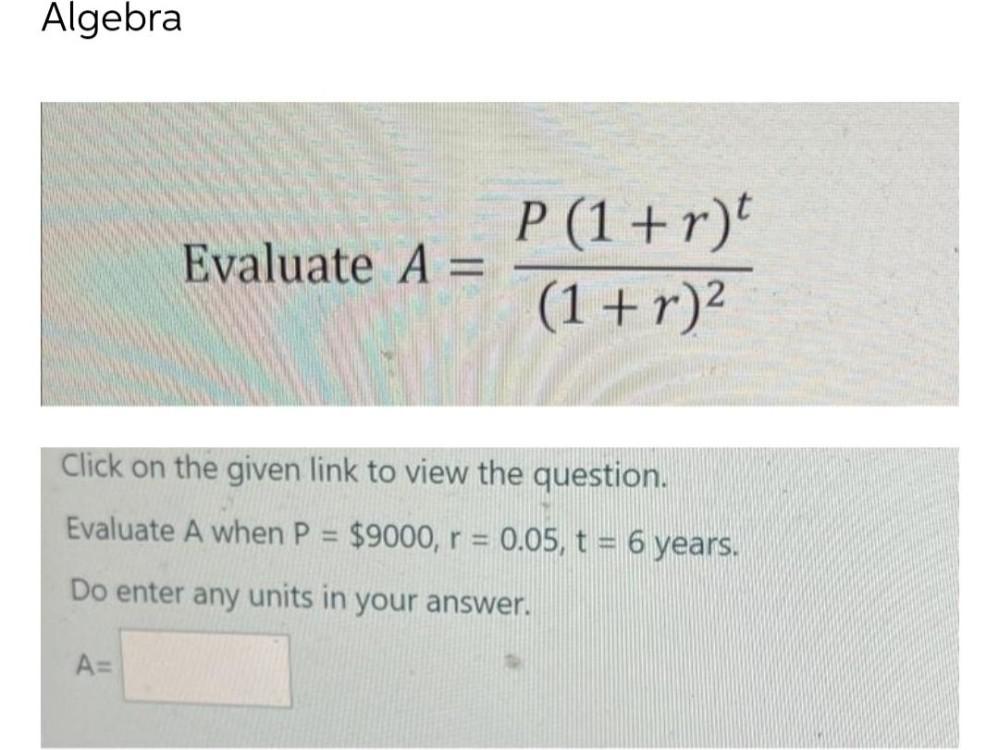
Matrices & DeterminantsEvaluate A = {P(1 + r)^t} / {(1 + r)^2}
Click on the given link to view the question.
Evaluate A when P = $9000, r = 0.05, t = 6 years.
Do enter any units in your answer.
A=
![Find the transition matrix from B' to B
Find [x]B , when provided with [x]B
B = {(1, 1, 1), (1, -1, 1), (0, 0, 1)},
B' = {(2, 2, 0), (0, 1, 1), (1, 0, 1)),
[X]B = 2
3
1](https://media.kunduz.com/media/sug-question/raw/79886143-1659883946.7473264.jpeg?w=256)
Algebra
Matrices & DeterminantsFind the transition matrix from B' to B
Find [x]B , when provided with [x]B
B = {(1, 1, 1), (1, -1, 1), (0, 0, 1)},
B' = {(2, 2, 0), (0, 1, 1), (1, 0, 1)),
[X]B = 2
3
1
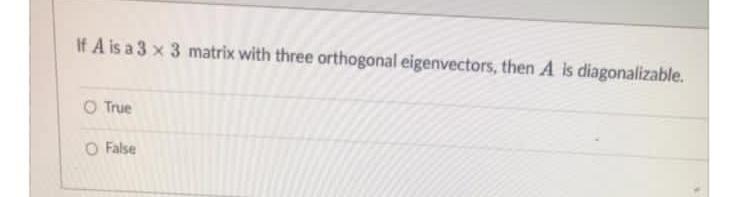
Algebra
Matrices & DeterminantsIf A is a 3 x 3 matrix with three orthogonal eigenvectors, then A is diagonalizable.
True
False

Algebra
Matrices & DeterminantsSolve the system of equations. If the system has an infinite number of solutions, express them in terms of the parameter z.
9x + 8y - 42z = 6
4x + 7y - 29z = 13
x + 2y - 8z = 4
x =
y =
z =
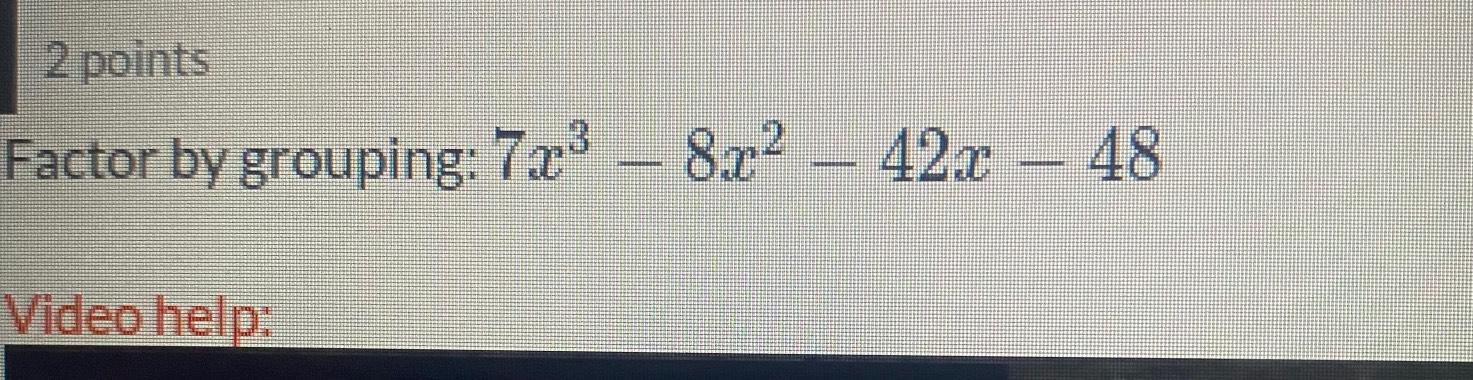
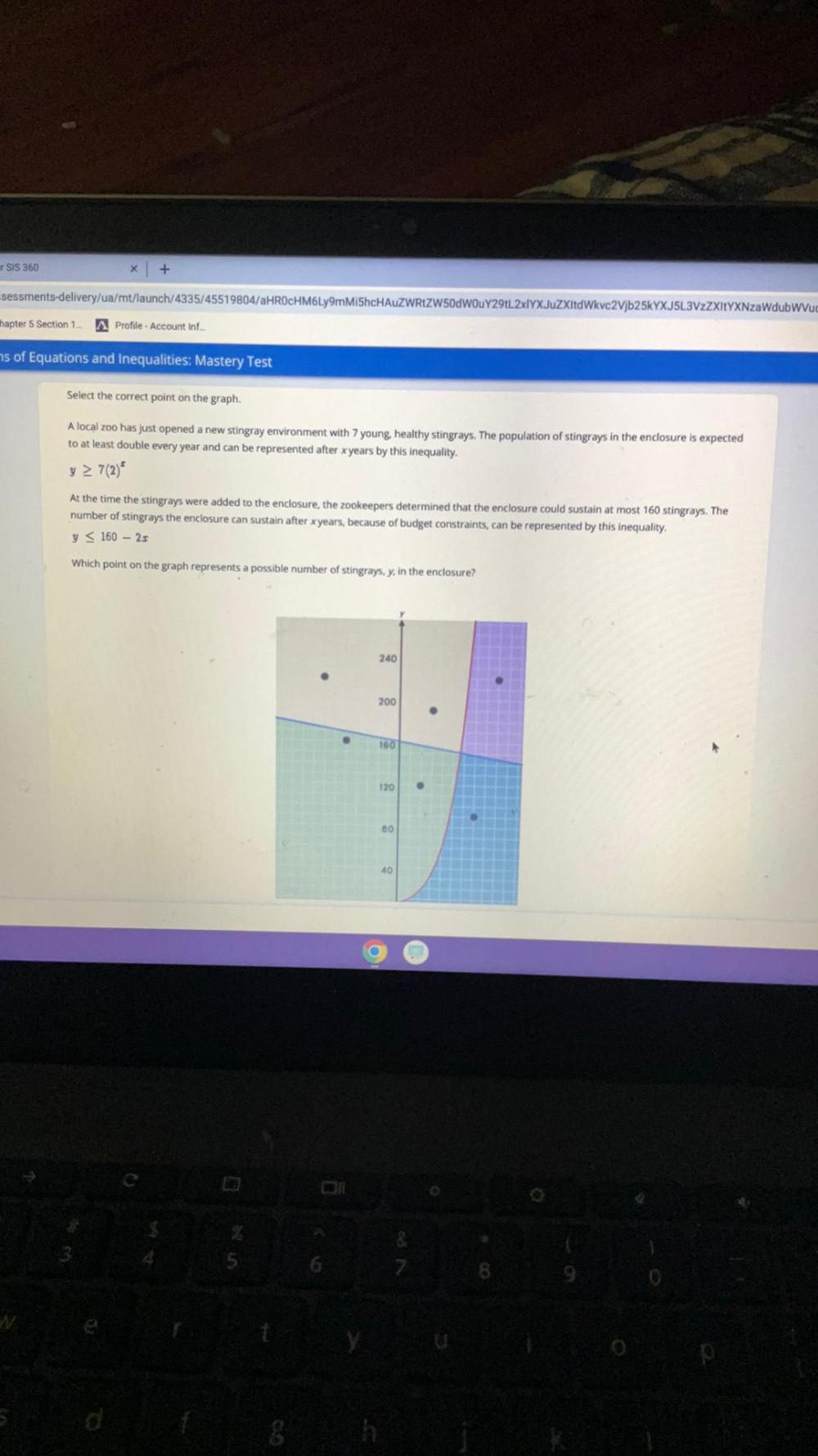
Algebra
Matrices & DeterminantsA local zoo has just opened a new stingray environment with 7 young, healthy stingrays. The population of stingrays in the enclosure is expected to at least double every year and can be represented after x years by this inequality.
y ≥ 7(2)ˣ
At the time the stingrays were added to the enclosure, the zookeepers determined that the enclosure could sustain at most 160 stingrays. The number of stingrays the enclosure can sustain after x years, because of budget constraints, can be represented by this inequality.
y≤ 160-2x Which point on the graph represents a possible number of stingrays, y, in the enclosure?

Algebra
Matrices & DeterminantsKevin, Kim, and Lyu are walking on a 2D surface embedded in a flat three-dimensional Euclidean space as
z = r cos Φ y = rsinΦ, z=2/3r^3/2
Show that the induced metric on the two-dimensional surface is
![All solutions [x, y, z] of the linear equation
9x - 25y + 24z = -20
geometrically represent a plane P in R³.
Find a normal vector n to P and the position vectors p, q, r of three distinct points in P:](https://media.kunduz.com/media/sug-question/raw/79887868-1659883053.1537097.jpeg?w=256)
Algebra
Matrices & DeterminantsAll solutions [x, y, z] of the linear equation
9x - 25y + 24z = -20
geometrically represent a plane P in R³.
Find a normal vector n to P and the position vectors p, q, r of three distinct points in P:

Algebra
Matrices & DeterminantsThe Routh Criterion Stability
S(S^2+8S+a)+4(S+8)=0
solution ...control systems
![Let W be the set of all vectors [x y x+y] with x and y real. Find a basis of W¹.](https://media.kunduz.com/media/sug-question/raw/79963200-1659876585.2768807.jpeg?w=256)
Algebra
Matrices & DeterminantsLet W be the set of all vectors [x y x+y] with x and y real. Find a basis of W¹.

Algebra
Matrices & DeterminantsThe rate of change of the number of coyotes in a population is directly proportional to N(t), where t is the time in years.
a.) Set up a differential equation and find the general solution containing C and k.
b.) Find the particular solution to the above differential equation given the coyote population increases from 300 to 500 in two years.

Algebra
Matrices & DeterminantsLet R be a ring. On which of the following sets is matrix multiplication a well-defined operation? Select all correct answers.
1. The set of all matrices of all sizes with entries in R
2. The set of all 2x2 matrices with entries in R
3. The set of all 2x3 matrices with entries in R
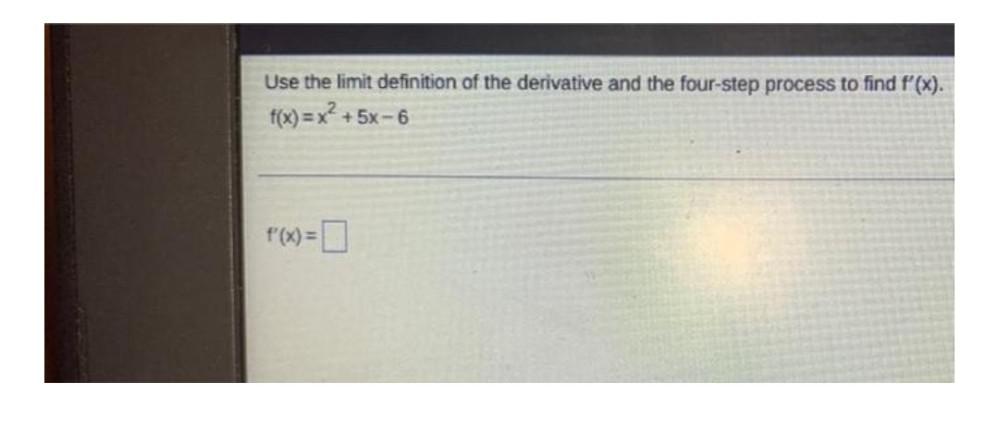
Algebra
Matrices & DeterminantsUse the limit definition of the derivative and the four-step process to find f'(x). f(x)=x²+ 5x-6
f'(x)=

Algebra
Matrices & DeterminantsSolve the system of linear equations algebraically. Show/explain all steps in an organized manner.
x+y+z=1
-2x+y+z= -2
3x + 6y + 6z = 5

Algebra
Matrices & DeterminantsGiven that W is the subspace of R^4 spanned by the vectors
(1,0,-1,2), (-1,2,1,1), (1,5,0,1) find a basis for the orthogonal complement of W
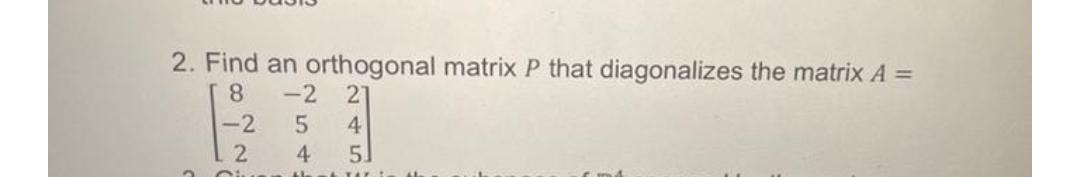
Algebra
Matrices & DeterminantsFind an orthogonal matrix P that diagonalizes the matrix
A = 8 -2 2
-2 5 4
2 4 5

Algebra
Matrices & DeterminantsA polyhedron is a figure whose surfaces are
b. A net is a pattern that can be folded to form a figure.
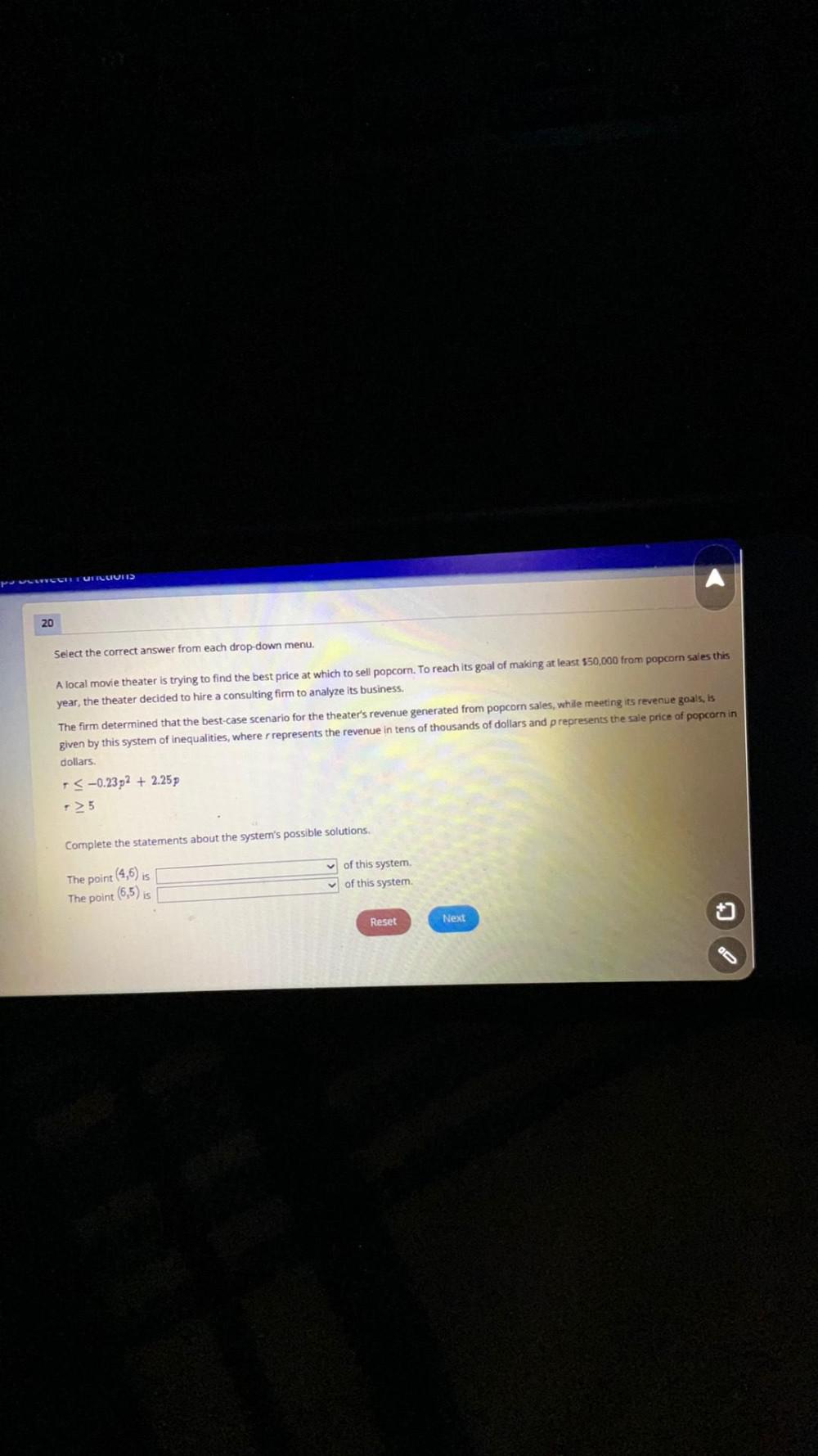
Algebra
Matrices & DeterminantsA local movie theater is trying to find the best price at which to sell popcorn. To reach its goal of making at least $50,000 from popcorn sales this year, the theater decided to hire a consulting firm to analyze its business. The firm determined that the best-case scenario for the theater's revenue generated from popcorn sales, while meeting its revenue goals, is given by this system of inequalities, where r represents the revenue in tens of thousands of dollars and p represents the sale price of popcorn in dollars.
r≤-0.23² +2.25 p
r⋝5
Complete the statements about the system's possible solutions.
The point (4,6) is_____ of this system.
The point (6,5) is_____ of this system.
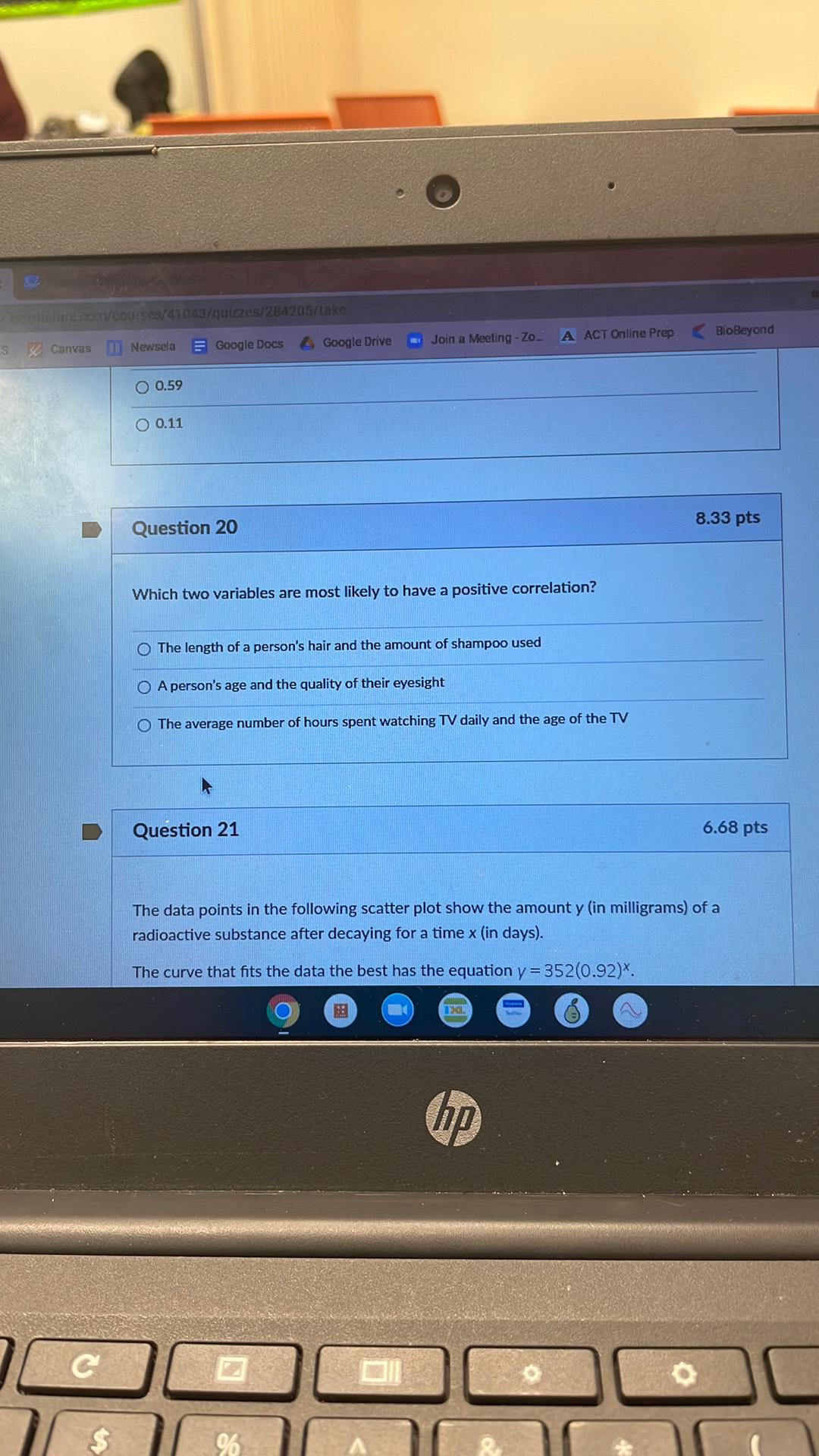
Algebra
Matrices & DeterminantsWhich two variables are most likely to have a positive correlation?
a)The length of a person's hair and the amount of shampoo used
b)A person's age and the quality of their eyesight
c)The average number of hours spent watching TV daily and the age of the TV

Algebra
Matrices & DeterminantsAssume that T and S are matrix of the same size. Prove or Disprove that (T+ S)² is a symmetric, skew- symmetric or neither.

Algebra
Matrices & DeterminantsSolve the following system of linear equations using the LU factorization method.
x₁ + x₂ + 3x4 = 7
2x₁ + x₂-x3+ x4 = 5
3x₁-x₂-x₂ + 2x4 = 8
-x₁ + 2x₂ + 3x₂ - x4 = -6

Algebra
Matrices & DeterminantsMartin made a net of a rectangular prism with a square cardboard of side 16 cm as shown in the figure. He then cut and folded the cardboard to make the prism.
(a) What was the total surface area of the prism?
(b) What was the volume of the prism?

Algebra
Matrices & DeterminantsProblem 4. For each of the following conditions, either draw a simple graph with the required conditions,
or show that no such graph can exist.
(a) 6 vertices, 4 edges.
(b) 5 vertices with degrees 1, 2, 2, 3, 4.
(c) 6 vertices with degrees 1, 1, 2, 3, 4, 4.
(d) 6 vertices with degrees 1, 1, 3, 4, 4, 5.

Algebra
Matrices & DeterminantsX = 8.
Goes through the origin.
Has a normal vector parallel to the xy-plane.
Goes through the point (0, 8, 0).
Has a normal vector whose dot products withi,j,k are all positive.
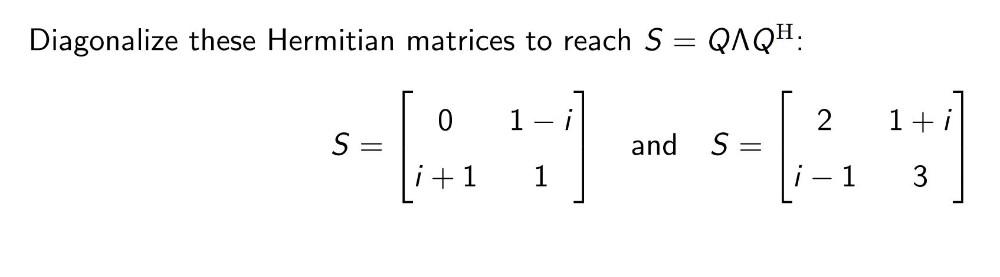
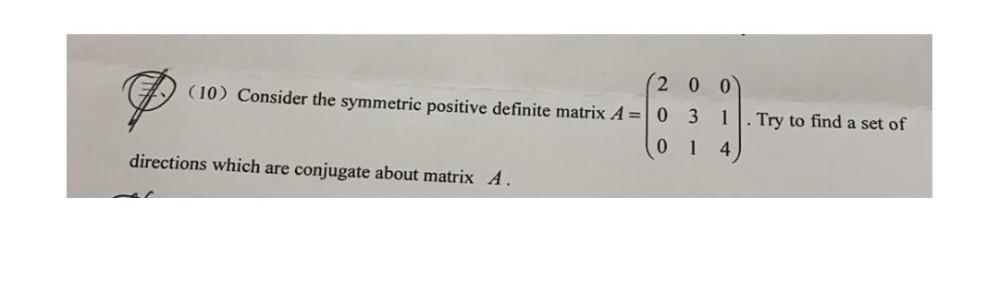
Algebra
Matrices & DeterminantsConsider the symmetric positive definite matrix A =
Try to find a set of directions which are conjugate about matrix A.
Algebra
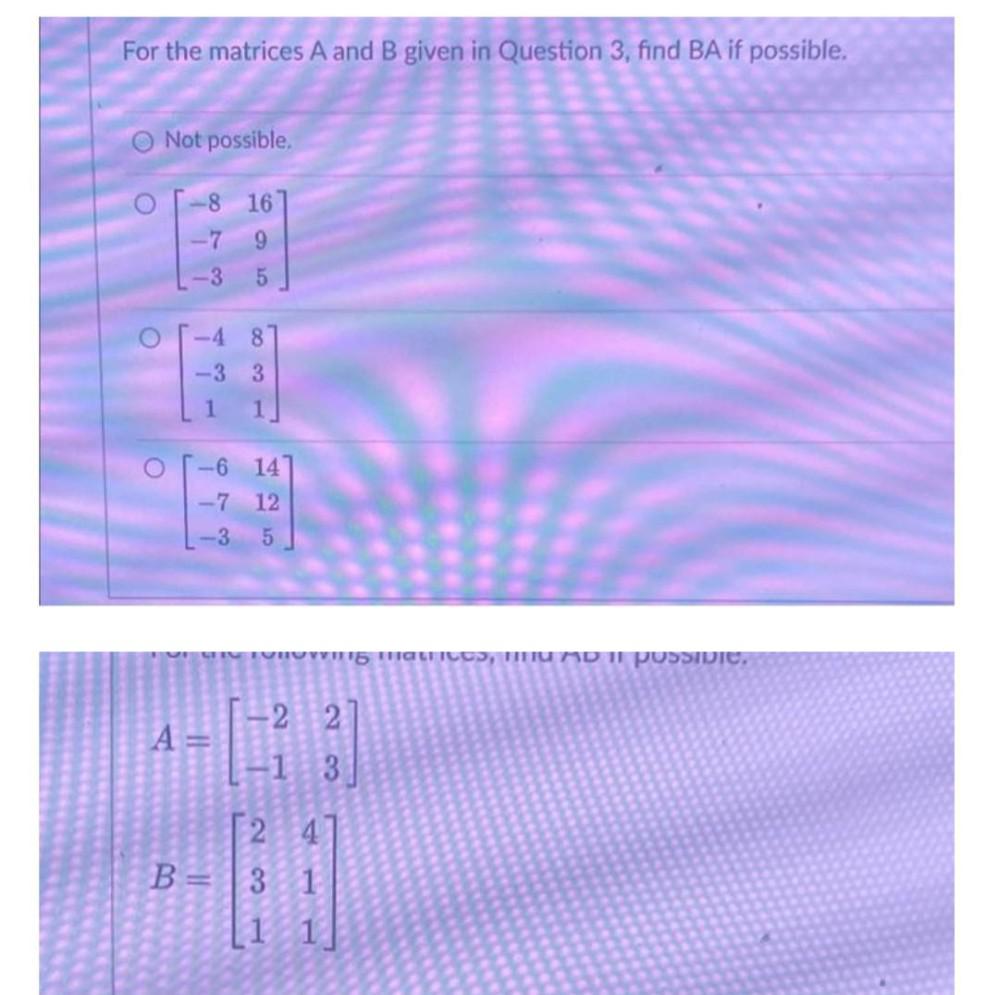
Matrices & DeterminantsFor the matrices A and B given in Question 3, find BA if possible.
a) Not possible.
b) -8 16
-7 9
-3 5
c) -4 8
-3 3
1 1
A=-2 2
-1 3
B= 2 4
3 1
Algebra
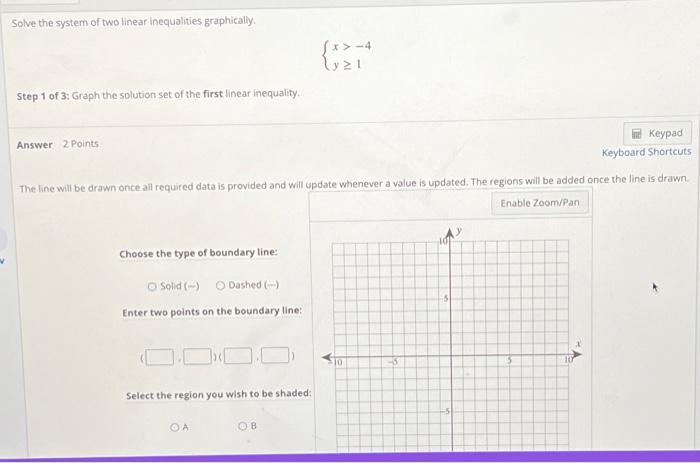
Matrices & DeterminantsSolve the system of two linear inequalities graphically.
{ x > -4
{ y ≥ 1

Algebra
Matrices & DeterminantsGive a geometric description of Span (v₁ , V₂) for the vectors
(A) Span (v₁, v₂) cannot be determined with the given information.
(B) Span (v₁ , v₂) is the plane in R³ that contains V₁, V₂, and 0.
(C) Span (v₁ , v₂) is the set of points on the line through v, and 0.
(D) Span (v₁ , v₂) is R³.
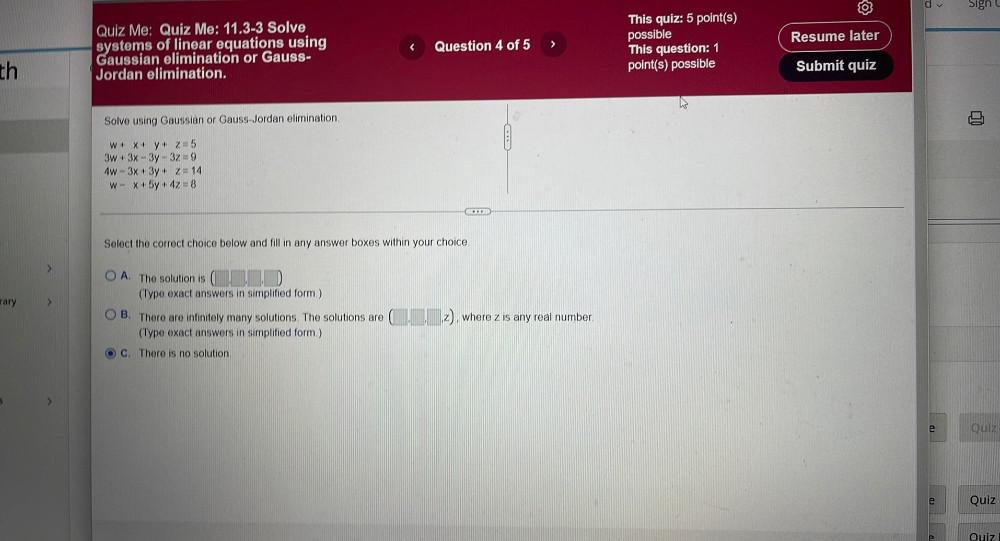
Algebra
Matrices & DeterminantsSolve using Gaussian or Gauss-Jordan elimination.
W+ x + y + z = 5
3w+ 3x-3y 3z=9
4w 3x + 3y + Z=14
W-x + 5y + 4z = 8
(A). The solution is
(B). There are infinitely many solutions. The solutions are where z is any real number.
(C). There is no solution.
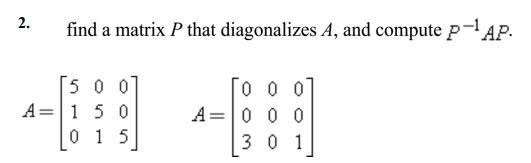

Algebra
Matrices & DeterminantsConsider the matrix A = 3
(a) Compute the adjoint matrix adj(A).
(b) Compute the determinant det(A) and find the inverse matrix A-¹,
Consider the matrix B= 2 1
(a) Use the cofactor exapansion to evaluate the determinant det(B) with using the second column.
(b) Use the cofactor exapansion to evaluate the determinant det(B) with using the third row.
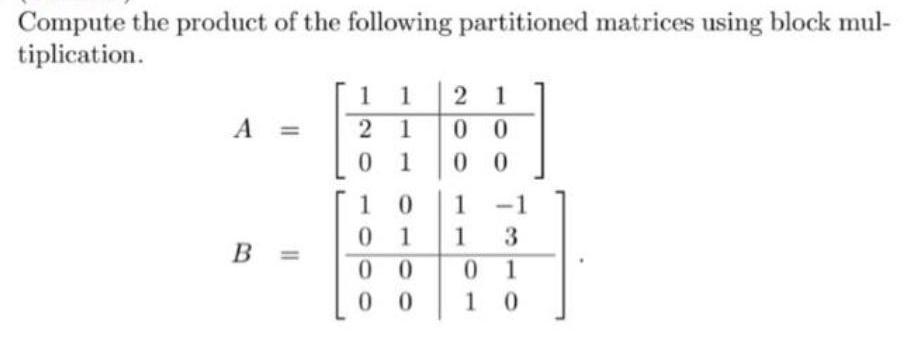
Algebra
Matrices & DeterminantsCompute the product of the following partitioned matrices using block multiplication.
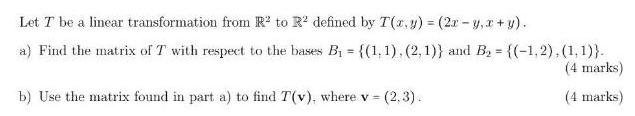
Algebra
Matrices & DeterminantsLet T be a linear transformation from R² to R² defined by T(x,y) = (2x -y, x + y).
a) Find the matrix of T with respect to the bases B₁ = {(1.1). (2,1)} and B₂ = {(-1,2), (1,1)).
b) Use the matrix found in part a) to find T(v), where v = (2.3).
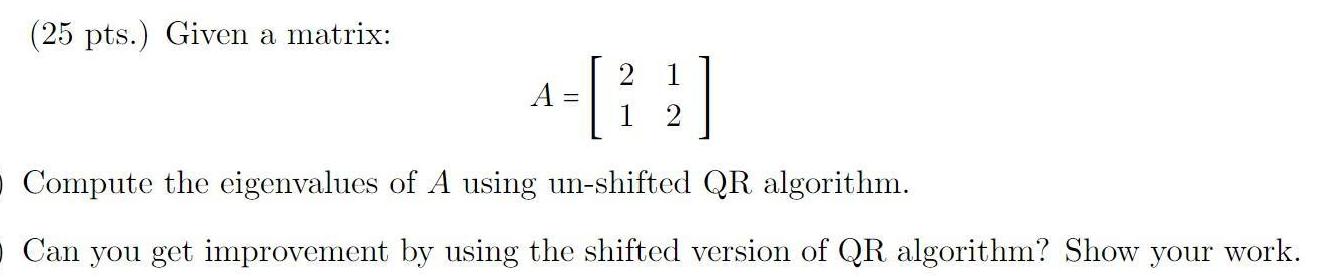
Algebra
Matrices & DeterminantsCompute the eigenvalues of A using un-shifted QR algorithm.
Can you get improvement by using the shifted version of QR algorithm? Show your work.
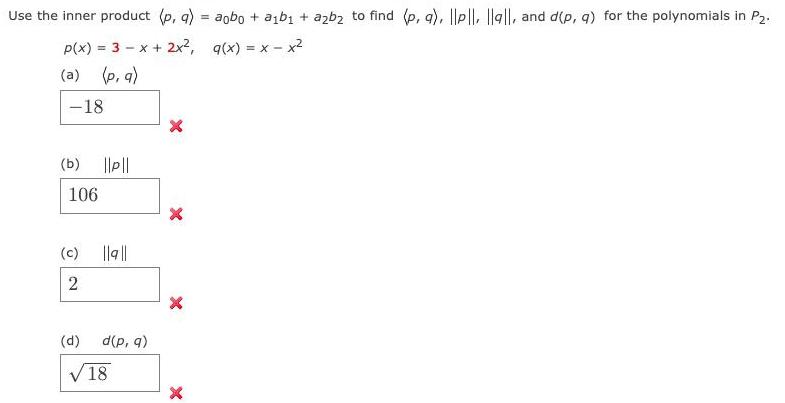
Algebra
Matrices & DeterminantsUse the inner product (p, q) = aobo + a₁b₁ + a2b₂ to find (p, q), ||pl|, |la||, and d(p, q) for the polynomials in P2.
p(x) = = 3- x + 2x², g(x) = x - x²

Algebra
Matrices & DeterminantsDefine the linear transformation T by T(x) = Ax. Find ker(7), nullity(7), range(7), and rank(7).
![Let A = {a₁a2 a3} and B = {b₁ b2b3} be bases for a vector space V, and
suppose a₁ = 3b₁-b₂, a2 = -b₁ + b₂ + b3, a3 = b₂ - 4b3-
a. Find the change-of-coordinates matrix from A to B.
b. Find [x]g for x =2a₁ + a₂ + a3.](https://media.kunduz.com/media/sug-question/raw/84897773-1659860288.348371.jpeg?w=256)
Algebra
Matrices & DeterminantsLet A = {a₁a2 a3} and B = {b₁ b2b3} be bases for a vector space V, and
suppose a₁ = 3b₁-b₂, a2 = -b₁ + b₂ + b3, a3 = b₂ - 4b3-
a. Find the change-of-coordinates matrix from A to B.
b. Find [x]g for x =2a₁ + a₂ + a3.

Algebra
Matrices & DeterminantsProve that if the matrix A has orthogonal columns, then Az = b has a unique least squares solution, and find this unique solution.

Algebra
Matrices & DeterminantsChange each degree measure to radian measure in terms of π
1) 135°
2) 300°
3) 210°

Algebra
Matrices & DeterminantsFind the first & second derivatives of the following functions:
a) f(x) = Q^(⅓)
b) f(x)=(Y⁴-1)/Y⁴
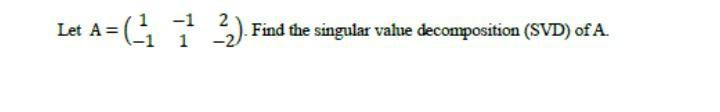
Algebra
Matrices & DeterminantsLet A=(¹₋₁ ⁻¹ ₁ ²₋₂). Find the singular value decomposition (SVD) of A

Algebra
Matrices & DeterminantsA store is having a sale on almonds and jelly beans. For 5 pounds of almonds and 3 pounds of jelly beans, the total cost is $23. For 2 pounds of aimonds and 12 pounds of jelly beans, the total cost is $47. Find the cost for each pound of almonds and each pound of jelly beans.
a)Cost for each pound of almonds: ___
b)Cost for each pound of yelly beans: