Application of derivatives Questions and Answers
Calculus
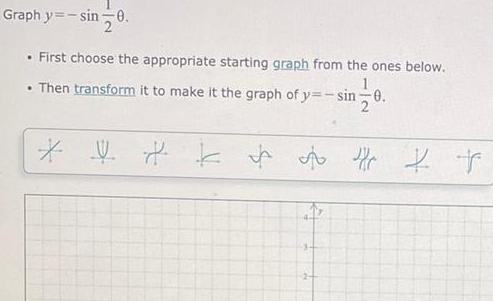
Application of derivativesGraph y sin 0 First choose the appropriate starting graph from the ones below Then transform it to make it the graph of y sin 0 2 z k f fr

Calculus
Application of derivativesg Find the equation of the major axis h Find the equation of the minor axis i Plot the foci and the center j Draw the major and minor axes k Graph the ellipse 5 points 1 Label the vertices covertices foci center major and minor axes 1 point 54
Calculus
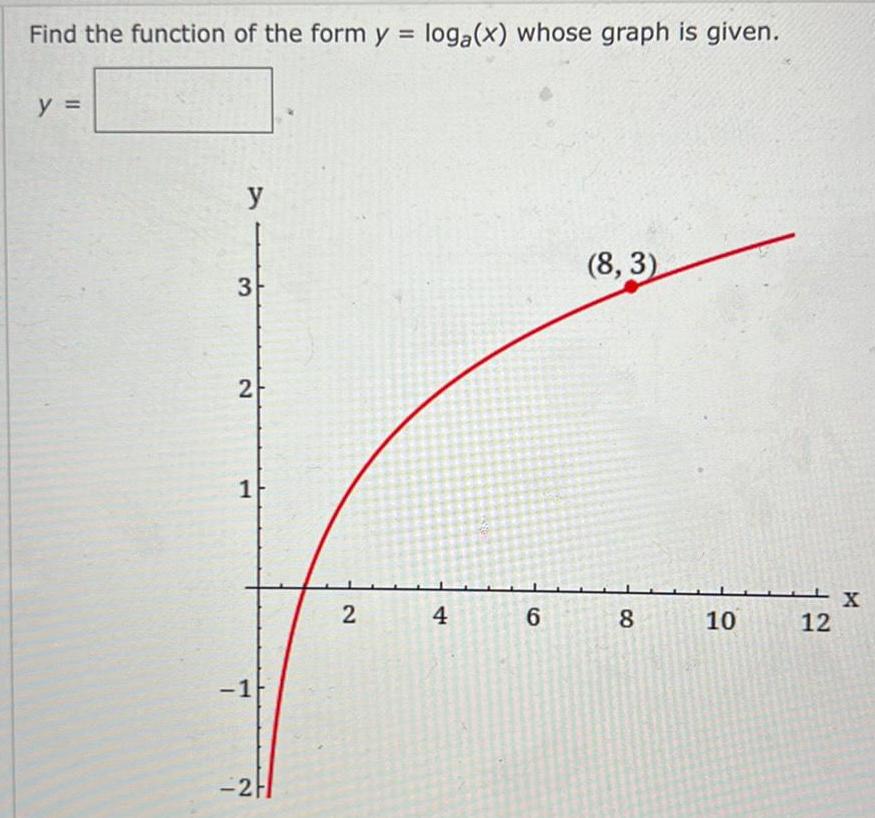
Application of derivativesFind the function of the form y loga x whose graph is given y y 3 2 1 1 2H 2 4 6 8 3 Co 8 10 12 X

Calculus
Application of derivativesJason is going to invest 1 900 and leave it in an account for 6 years Assuming the interest is compounded continuously what interest rate to the nearest hundredth of a percent would be required in order for Jason to end up with 2 400 Question 22 4 Points Dec 10 6 58 32 PM L

Calculus
Application of derivativesFind the indefinite integral by making a change of variables Use C for the constant of integration x x 6 dx
Calculus
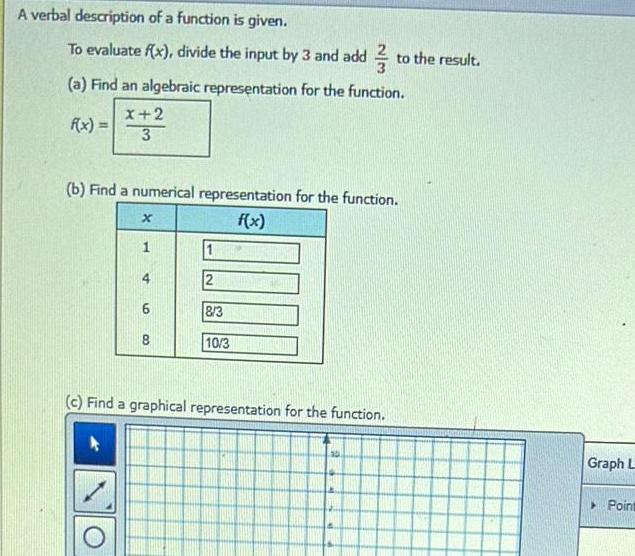
Application of derivativesA verbal description of a function is given To evaluate f x divide the input by 3 and add to the result a Find an algebraic representation for the function f x x 2 3 b Find a numerical representation for the function f x x 1 4 6 8 2 8 3 10 3 c Find a graphical representation for the function Graph L Point
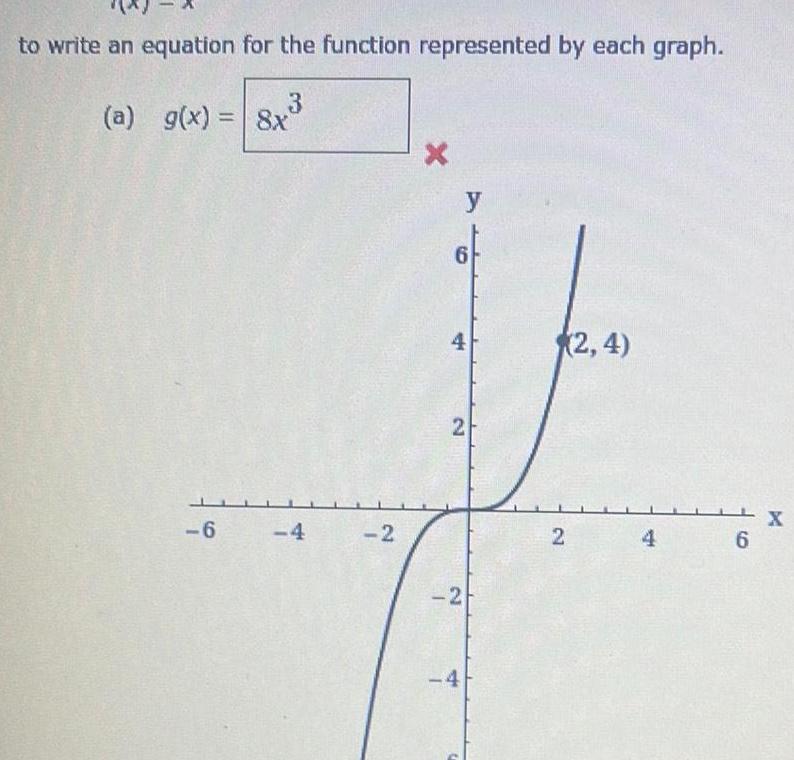
Calculus
Application of derivativesto write an equation for the function represented by each graph 3 a g x 8x 6 4 2 X y 6 2 2 4 2 4 2 4 6 X

Calculus
Application of derivativesf A rectangular flower garden with an area of 30 m is surrounded by a grass border 1 m wide on two sides and 2 m wide on the other two sides What dimensions of the garden minimize the combined area of the garden and border 15 by 1

Calculus
Application of derivativesFind the vertex of the parabola defined by the equation x Vertex y y 40 335
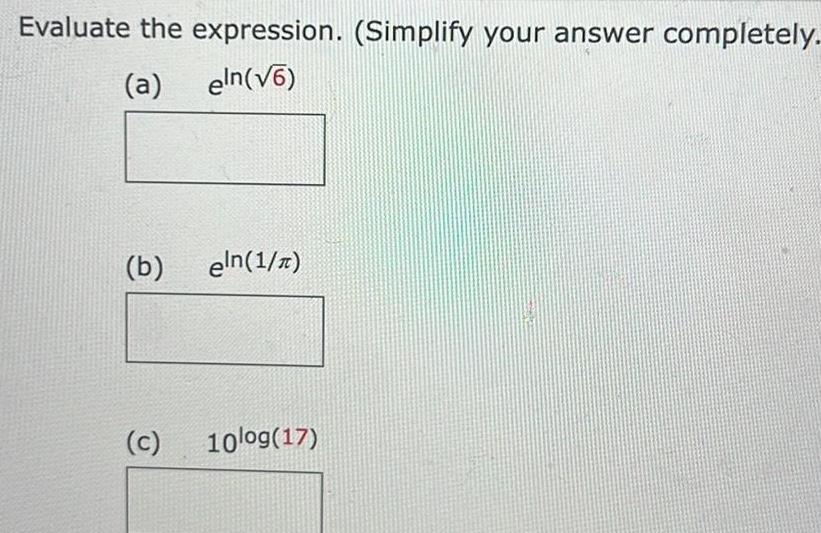
Calculus
Application of derivativesEvaluate the expression Simplify your answer completely a eln 6 b eln 1 c 10log 17

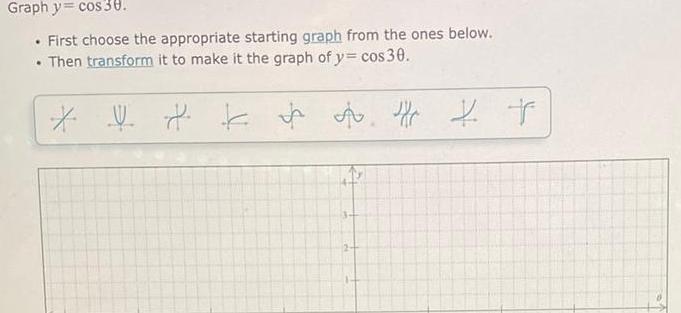
Calculus
Application of derivativesGraph y cos 30 First choose the appropriate starting graph from the ones below Then transform it to make it the graph of y cos 30 k Ar x y z
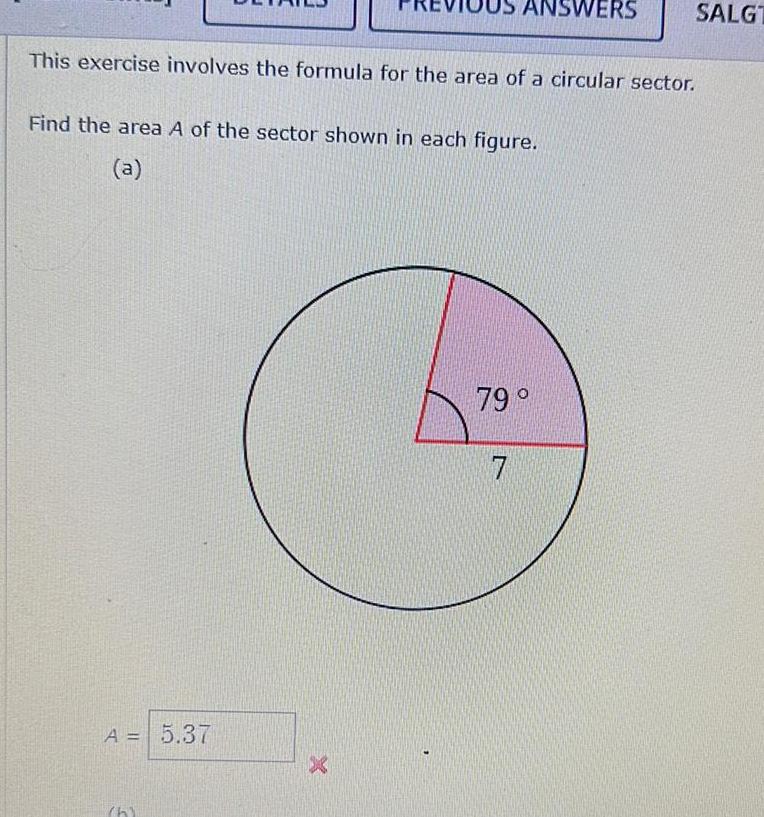
Calculus
Application of derivativesFind the area A of the sector shown in each figure a This exercise involves the formula for the area of a circular sector A 5 37 h X 79 NSWERS 7 SALG
Calculus
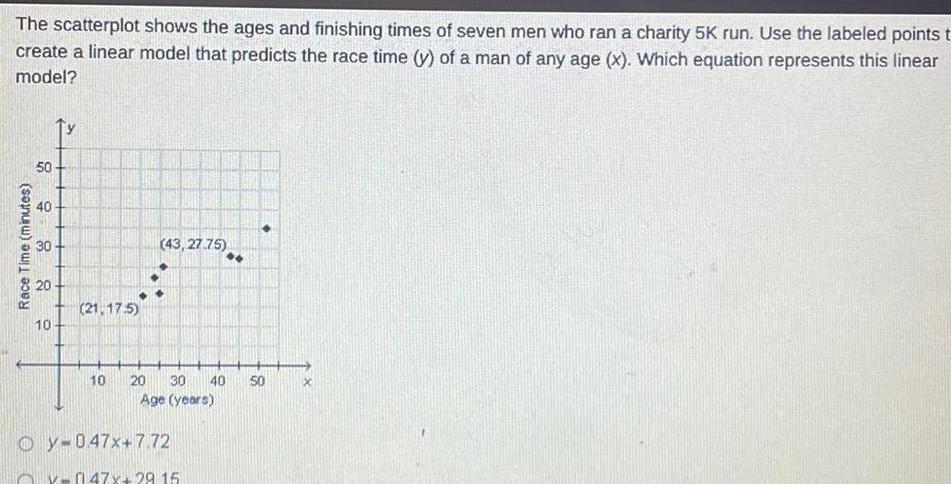
Application of derivativesThe scatterplot shows the ages and finishing times of seven men who ran a charity 5K run Use the labeled points t create a linear model that predicts the race time y of a man of any age x Which equation represents this linear model Race Time minutes 50 40 30 20 10 21 175 43 27 75 Oy 047x 7 72 10 20 30 40 50 Age years v 047x 29 15 X
Calculus
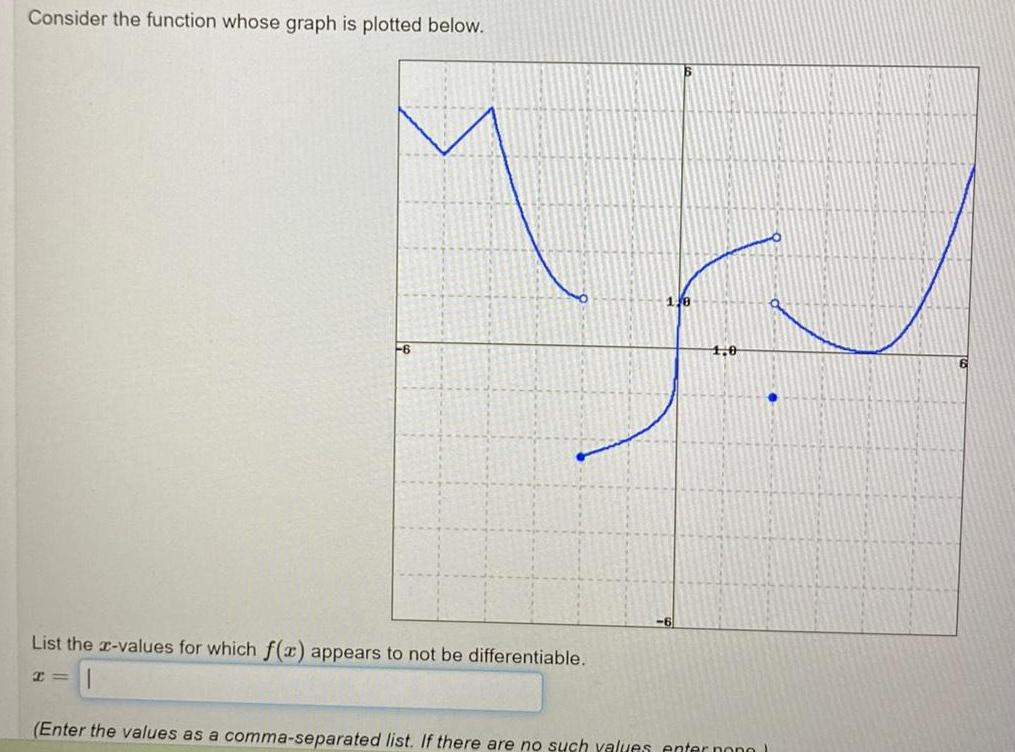
Application of derivativesConsider the function whose graph is plotted below 6 List the x values for which f x appears to not be differentiable P 1 0 Enter the values as a comma separated list If there are no such values enter pon

Calculus
Application of derivativesFind an equation of the tangent line to the curve y 9 sin x sin x at the point 0 0 Result y Check your result by plotting the graph of the curve and the tangent line together

Calculus
Application of derivativesThe height y in feet of a football x seconds after it is thrown is modeled by the equation y 16x2 24x 1 Wha information does the zero of the equation 6 16x 24x 1 represent O the height of the ball after 6 seconds Owhen the ball is 6 ft above the ground the initial upward velocity of the ball Othe horizontal distance traveled by the ball when it is 6 ft above the ground
Calculus
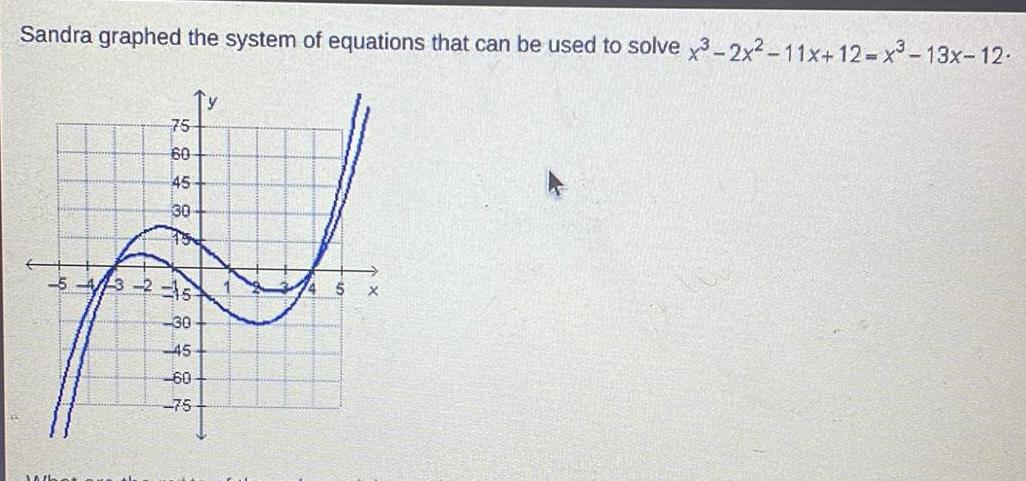
Application of derivativesSandra graphed the system of equations that can be used to solve x3 2x 11x 12 x 13x 12 75 60 45 3 30 15 Ty 5 4 3 2 15 1 a g h t 30 45 75 374 5 X

Calculus
Application of derivativesThe function that represents the average cost per person including transportation to a museum is y statement is true about the graph of the function O The horizontal asymptote y 0 means the cost approaches zero as the number of people increases O The horizontal asymptote y 8 means the average cost approaches 8 as the number of people increases O The vertical asymptote x 0 means the cost approaches zero as the number of people increases The vertical asymptote x 8 means the cost approaches zero as the number of people increases 25 8x X Which
Calculus
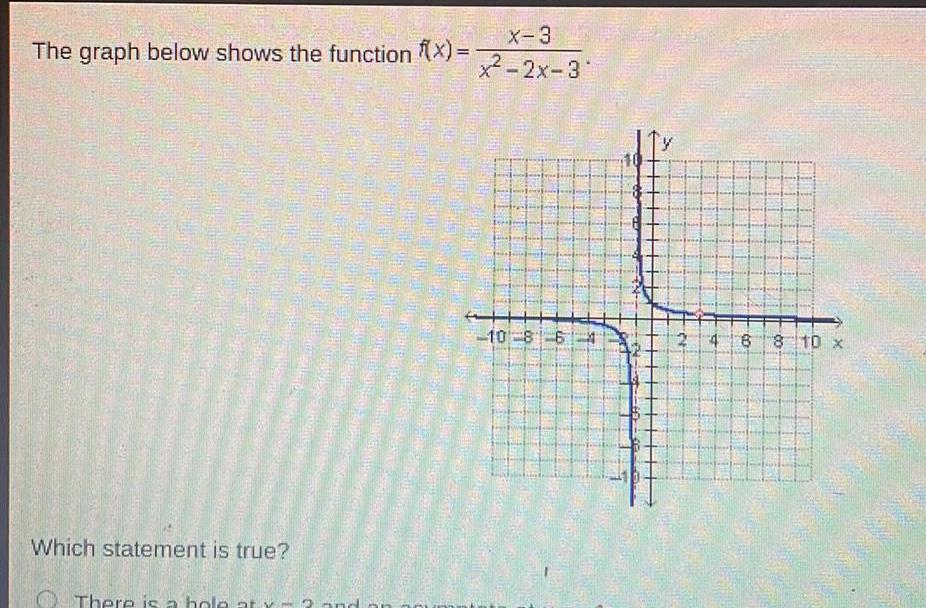
Application of derivativesThe graph below shows the function f x Which statement is true There is a hole a Land an X 3 x 2x 31 10 8 6 2 4 6 8 10 x

Calculus
Application of derivativesWhich of the following graphs could be the graph of the function f x x 8
Calculus
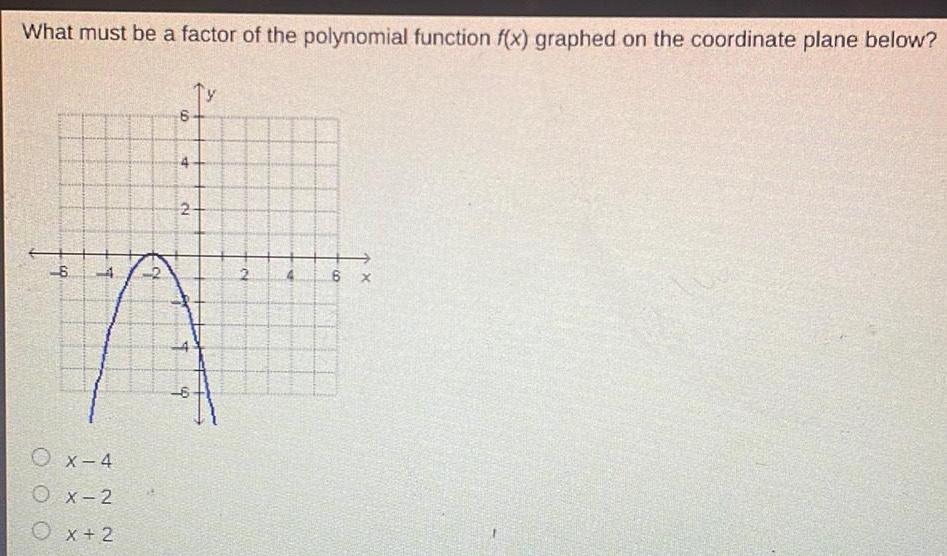
Application of derivativesWhat must be a factor of the polynomial function f x graphed on the coordinate plane below TY 6 4 2 Ox 4 OX 2 Ox 2 S A4 2 6 2 6 X

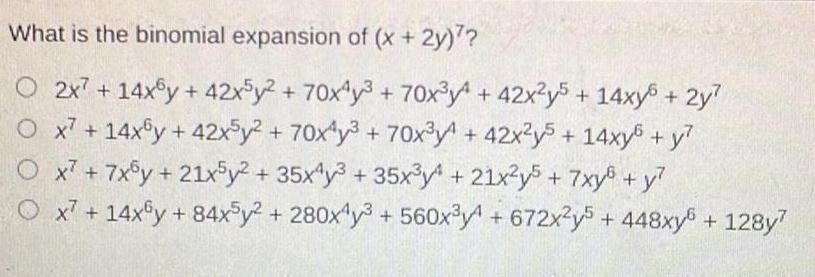
Calculus
Application of derivativesWhat is the binomial expansion of x 2y O 2x7 14xy 42x5y 70x4y 70x y 42x2y5 14xy 2y Ox7 14xy 42x5y 70x y3 70x y 42x2y5 14xy y Ox7 7x6y 21x5y2 35x4y 35x y 21x y5 7xy y Ox7 14xy 84x5y 280x4y3 560x y4 672x2y5 448xy 128y7

Calculus
Application of derivativesWhich aranh can be used to find the real solution sy to 2 v 2 2 122
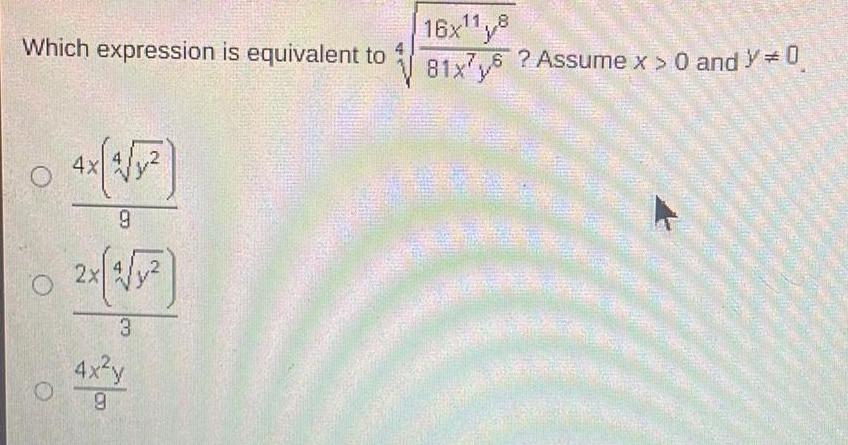
Calculus
Application of derivativesWhich expression is equivalent to O O 4x 3 y 9 2 1 1 3 4x y 9 16x11 8 7 6 Assume x 0 and Y 0 81x76

Calculus
Application of derivativesDecimal answers MUST be correct to THREE decimal places Question 4 4 ln 2x 3 11 1 pts
Calculus
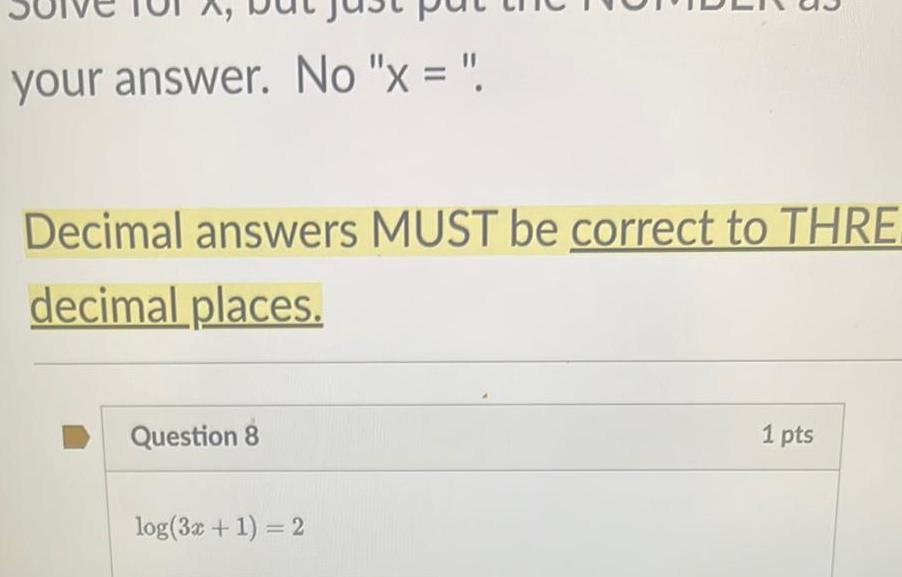
Application of derivativesyour answer No x Decimal answers MUST be correct to THRE decimal places Question 8 log 3x 1 2 1 pts

Calculus
Application of derivativesDuring flu season, the number of people that contract the flu virus at any time increases at a rate proportional to the number of people that contract the flu virus at that time. There were 700 people that contracted the virus when flu season began, and 1,051 contracted it seven days later. How many people contracted the virus 14 days after it first began? Round to the nearest person.
1,151
1,578
1,751
2,369


Calculus
Application of derivativesA tank of water in the shape of an inverted cone (i.e. circular base on top) is leaking water a constant rage of 1 ft3/min. The base radius of the tank is 5 ft and the height of the tank is 14 ft.
(a) At what rate is the depth of the water in the tank changing when the depth of the water is 6 ft?
(b) At what rate is the radius of the top of the water in the tank changing when the depth of the water is 6 ft?

Calculus
Application of derivativesConsider the set of all rectangles that lie in the first quadrant, have one edge along the posi- tive x-axis, one corner at the origin, and the diagonally opposite corner on the curve y = e. Find the dimensions of the rectangle in the set that has the largest area (remember to justify you have a max).
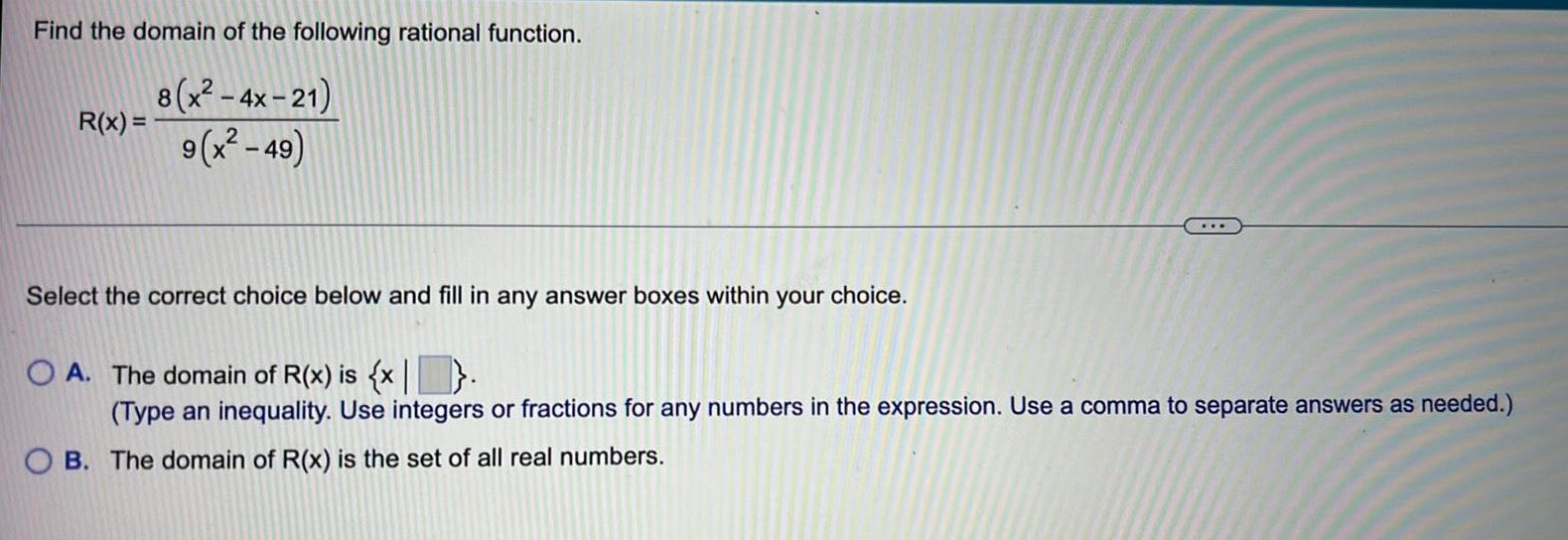
Calculus
Application of derivativesFind the domain of the following rational function. R(x) =8(x²-4x-21)/9(x²-49) Select the correct choice below and fill in any answer boxes within your choice. A. The domain of R(x) is {x}. (Type an inequality. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.) B. The domain of R(x) the set of all real numbers.
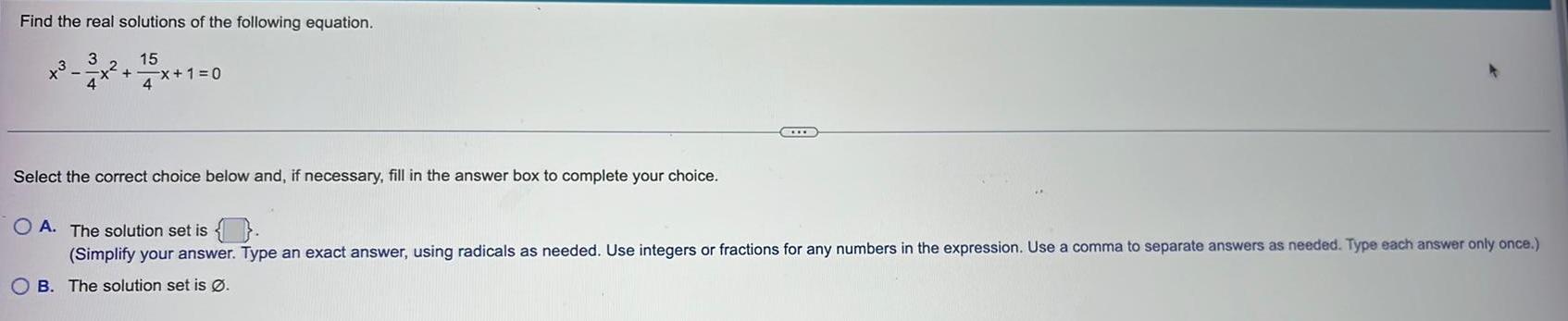
Calculus
Application of derivativesFind the real solutions of the following equation.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is.
B. The solution set is Ø.
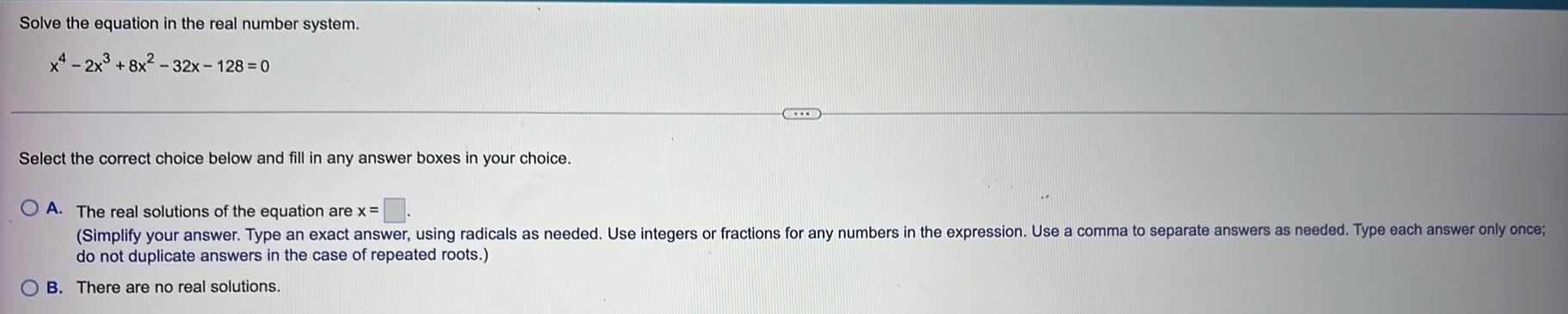
Calculus
Application of derivativesSolve the equation in the real number system.
x4-2x3 +8x²-32x-128=0
Select the correct choice below and fill in any answer boxes in your choice.
A. The real solutions of the equation are x =
B. There are no real solutions.
![Let f(x, y) 6x² 2x³ - 3y² + 6ay. This function has critical points at (0, 0) and (3, 3). Determine if these points are a local
maximum, local minimum, or a saddle point.
(0, 0) is a [Select]
(3, 3) is a [Select]](https://media.kunduz.com/media/sug-question/raw/78109531-1660422115.0866847.jpeg?w=256)
Calculus
Application of derivativesLet f(x, y) 6x² 2x³ - 3y² + 6ay. This function has critical points at (0, 0) and (3, 3). Determine if these points are a local
maximum, local minimum, or a saddle point.
(0, 0) is a [Select]
(3, 3) is a [Select]
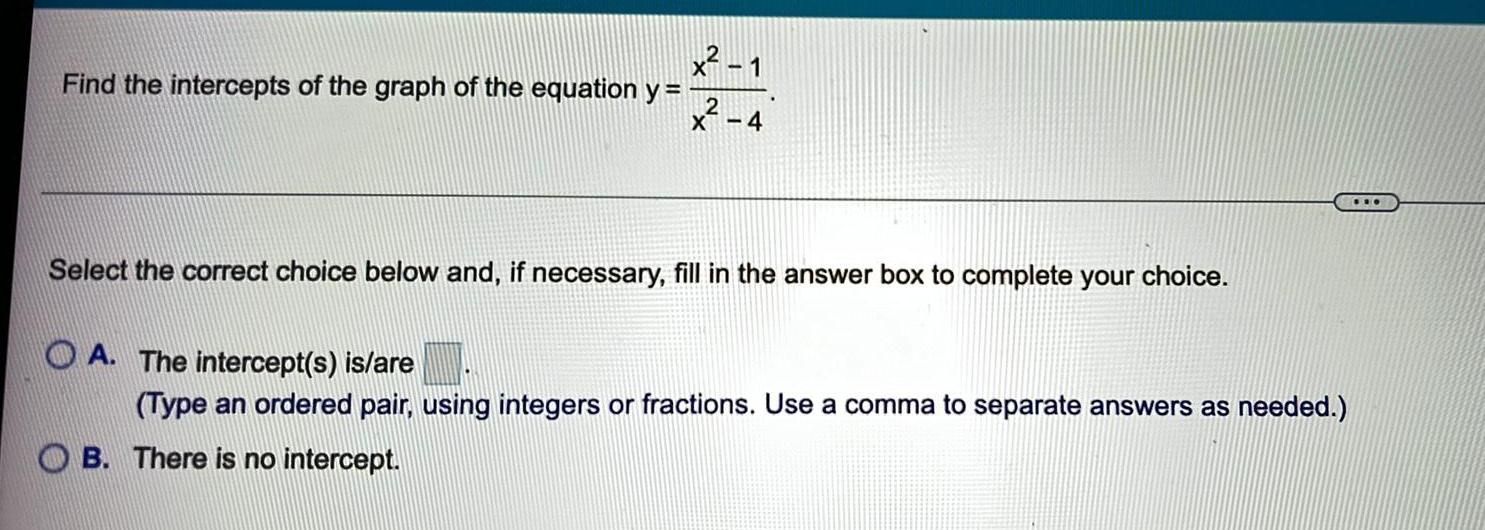
Calculus
Application of derivativesFind the intercepts of the graph of the equation y = x²-1/x²-4
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The intercept(s) is/are
(Type an ordered pair, using integers or fractions. Use a comma to separate answers as needed.)
B. There is no intercept.

Calculus
Application of derivativesAll but one of the functions is differentiable for all real values of x. Which function is
not differentiable for at least one real value of x?
f(x)=x² +1
g(x) = 1/x² +1
h(x) = |x|
j(x) = x³ - 3x

Calculus
Application of derivativesa. Determine the coordinates of the point on the graph of f(x)=-x²+3x+1 where the
tangent line is perpendicular to the line y=x+2.
b. Write the equation of the tangent line at this point. Write your answer in the form
y=mx+b.

Calculus
Application of derivativesIn this question, you should determine the asymptotes and
Use calculus and algebraic methods to do a complete analysis (i.e., intercepts, critical points, intervals of
increase and decrease, points of inflection, intervals of concavity, local maximum or minimum points) for
each of the following functions and then sketch the graph of the function. You can use graphing software
(such as GeoGebra) to verify your analysis and graph. Keep in mind that your analysis is the most
important aspect of this question, not the graph.
-2
(x+3)²
Calculus
Application of derivativesAndrea plots
(-5,-2)
on the polar plane.
How does she proceed?
Drag a phrase to each box to correctly complete the statements.
Andrea first determines which line the angle of rotation places the point on. This line tells Andrea that the point must lie on the
if ris positive or
if ris negative.
The radius of 5 tells Andrea that the point lies on the fifth circle of the polar plane. The value of r is negative. Therefore, the point

Calculus
Application of derivativesProblem 6. (10 points) (Related Rates) Suppose you have an ice cream cone with radius 4
cm and height 12 cm with some melted boysenberry ice cream in it. The ice cream leaks out
the bottom of the cone at a rate of 8 cm³/min. At what rate is the height of the ice cream
changing when the height of the ice cream is 2 cm? (Hint: The volume of a cone is given by
V = r²h)
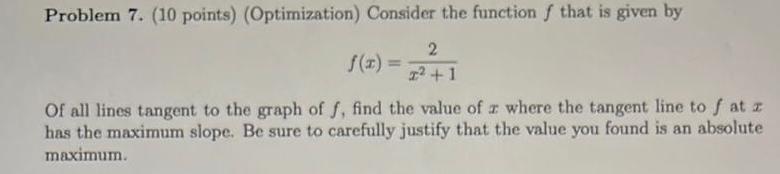
Calculus
Application of derivativesProblem 7. (10 points) (Optimization) Consider the function f that is given by
2/x2+1
Of all lines tangent to the graph of f, find the value of a where the tangent line to fat z
has the maximum slope. Be sure to carefully justify that the value you found is an absolute
maximum.

Calculus
Application of derivativesAssume that the rate of evaporation for water is proportional to the initial amount of water in a bowl. Jill places 1 cup and 8 ounces of water outside and notices that there is cup of water 6 hours later. After how many hours, t, will there be less than 1 oz left?
Let W (1) be the amount of water in the cup, and let t be measured in hours. Round your answer to the nearest hour.
Ot=14
O t = 13
Ot=12
O t = 11

Calculus
Application of derivatives2. In this question, you should determine the asymptotes and Use calculus and algebraic methods to do a complete analysis (i.e., intercepts, critical points, intervals of increase and decrease, points of inflection, intervals of concavity, local maximum or minimum points) for each of the following functions and then sketch the graph of the function. You can use graphing software (such as GeoGebra) to verify your analysis and graph. Keep in mind that your analysis is the most important aspect of this question, not the graph. g(x) = -2/ (x+3)²

Calculus
Application of derivativesConsider the curve e^xy + 3x² + y² = 65.
a. Find the equation of the tangent line at the point (0,8).
b. There are two points on the curve with x-coordinate 0.1. Use part a. to estimate one
possible y-coordinate of the point (0.1, y).

Calculus
Application of derivativesLet S = {r: r is a positive number such that ork/k! converges absolutely for || <r
}. Which of the following statement is true?
(a) S is empty.
(b) S is nonempty and r ≤ 1 for all r € S.
(c) S is nonempty and if for some r € S, a function f is defined as
f(x) = Σ
k=0
k!
for x = (-r, r), then f'(x) > f(x) for x = (0,r).
(d) S = (0, ∞0).
(c) None of the above statements is true.

Calculus
Application of derivativesA lighthouse is located 215 feet from the nearest point P on a straight shoreline. The revolving beacon in the
lighthouse makes one revolution every 6 seconds. Find the rate at which a ray from the light moves along the
shore at a point 475 feet from P.
feet per minute

Calculus
Application of derivativesA highway and a railway cross at and angle of 22 degrees. A passenger train is approaching the intersection at
74 miles per hour while a car is approaching the intersection at 80 miles per hour. Determine the rate of
change of the distance between the passenger train and the car when the passenger train and the car are 5
and 1 miles away from the intersection, respectively. Round the solution to the nearest ten-thousandth, if
necessary.
miles per hour
car
passenger train