Application of derivatives Questions and Answers

Calculus
Application of derivativesA 5 foot tall man jogs at a rate of 23 feet per second toward a lamppost that is 19 feet tall.
Determine the rate of change of the tip of the man's shadow when he is 21 feet away from the lamppost.
feet per second
Determine the rate of change of the length of the man's shadow when he is 21 feet away from the lamppost.
feet per second
![Solve for x where T ≤ x ≤ 2π
sin²x - cos²x
cos²x
[?]T
= 0
=
π](https://media.kunduz.com/media/sug-question/raw/84149330-1660408250.1287181.jpeg?w=256)
![Perform the following operation,
and write the answer in scientific
notation with the correct number
of significant figures.
0.00851.3= [?] x 10](https://media.kunduz.com/media/sug-question/raw/84149346-1660408103.6444652.jpeg?w=256)
Calculus
Application of derivativesPerform the following operation,
and write the answer in scientific
notation with the correct number
of significant figures.
0.00851.3= [?] x 10
![Solve for x by factoring where
0≤x≤T.
tan²x - tan x = 0
0, [2] T
7
Enter the next smallest value.](https://media.kunduz.com/media/sug-question/raw/84148940-1660408095.996162.jpeg?w=256)
Calculus
Application of derivativesSolve for x by factoring where
0≤x≤T.
tan²x - tan x = 0
0, [2] T
7
Enter the next smallest value.

Calculus
Application of derivativesCorn is falling off a conveyor belt onto a conical pile at the rate of 10 cubic feet per minute. The diameter of
the base of the pile is 4 times the height. Determine the rate at which the height of the pile is changing when
the height is 31 feet.
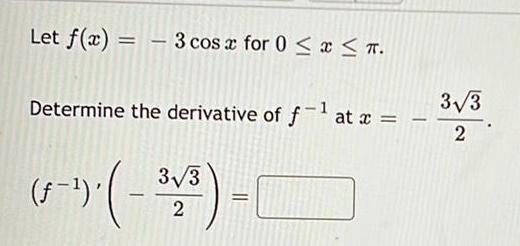
Calculus
Application of derivativesLet f(x) = - 3 cos x for 0 ≤ x ≤ π.
Determine the derivative of f-¹ at x =
(1-¹)-(-3√³) - (
2
3√3
2

Calculus
Application of derivativesPerform the mathematical operation and round the answer to the appropriate number of significant figures. 24.32 x 0.010 = [?

Calculus
Application of derivativesThe radius of a sphere is increasing at a rate of 2 centimeters per hour. Determine the rate of change of the
sphere's surface area when the radius is 25 centimeters.
square centimeters per hour

Calculus
Application of derivativesThe radius of a circle is increasing at a rate of 10 inches per minute. Determine the rate of change of the
circle's area when the radius is 41 inches.
square inches per minute

Calculus
Application of derivativesA 6 foot tall woman walks at a rate of 6 feer per second toward a lamppost that is 15 feet tall.
Determine the rate of change of the tip of the woman's shadow when she is 9 feet away from the lamppost.
feet per second
Determine the rate of change of the length of the woman's shadow when she is 9 feet away from the
lamppost.
feet per second

Calculus
Application of derivativesThe radius of a sphere is increasing at a rate of 3 centimeters per hour. Determine the rate of change of the
sphere's volume when the radius is 16 centimeters.
cubic centimeters per hour

Calculus
Application of derivativesLet h(x) = - 2x³ - 3
Determine the derivative of h-¹ at x = – 5.
(h-¹) '(-5) =

Calculus
Application of derivativesThe point P(3, -3) lies on the curve y =
(a) If Q is the point x,
(i) 2.9
MpQ
(ii) 2.99
MpQ =
E
(iii) 2.999
mpQ
(iv) 2.9999
MPQ
(v) 3.1
MPQ
(vi) 3.01
MPQ
=
(vii), 3.001
MPQ
=
3
(x₁__²_-).
(viii) 3.0001
m =
PQ
3
2-x
find the slope of the secant line PQ (correct to six decimal places) for the following values of x.
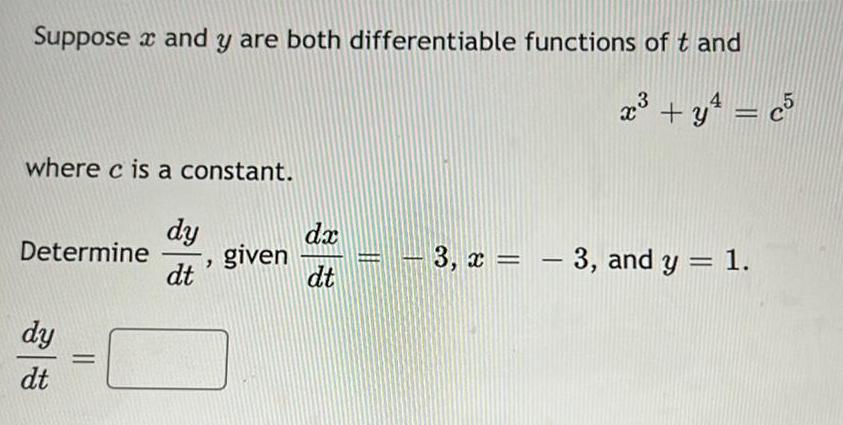
Calculus
Application of derivativesSuppose x and y are both differentiable functions of t and
x³ + y² = c5
where c is a constant.
Determine
dy
dt
=
dy
dt
"
given
dx
dt
23
3, x=-3, and y = 1.

Calculus
Application of derivativesAir traffic control detects two airplanes at the same altitude converging on a single point as they fly at right
angles to each other. One plane is 152 miles away from the point, flying at 420 miles per hour. The other plane
is 714 miles away from the point, traveling at 445 miles per hour. At what rate is the distance between the
two planes changing?
miles per hour

Calculus
Application of derivativesLet g(w) = arctan( - 6w)
Determine the derivative of g.
g'(w) =
=
Determine the slope of g at w = 9.
g'(9) =

Calculus
Application of derivativesSuppose both f and f-1 are differentiable functions such that
.
• f(7) = 8
• f'(7) =
7
9
Determine the equation of the tangent line of f¹ at x = 8. Report the solution using slope-intercept form.
-
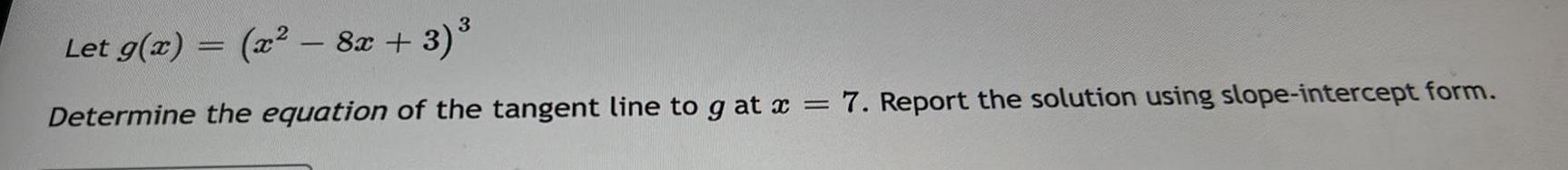
Calculus
Application of derivativesLet g(x) = (x² - 8x +
+3)³
Determine the equation of the tangent line to g at x = 7. Report the solution using slope-intercept form.
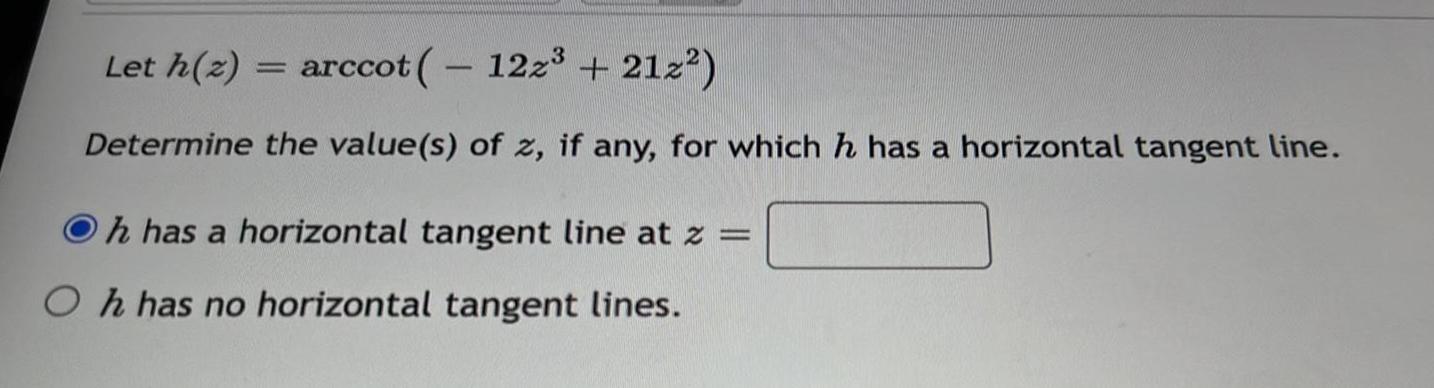
Calculus
Application of derivativesLet h(z)
arccot ( 122³ +212²)
-
Determine the value(s) of z, if any, for which h has a horizontal tangent line.
Oh has a horizontal tangent line at z =
Oh has no horizontal tangent lines.

Calculus
Application of derivativesLet f(x) =
Determine the derivative of f.
f'(x) =
Determine the slope of fat x = 3.
f'(3) =
=
-
3 cot(8x)

Calculus
Application of derivativesFor the given function, (a) find the slope of the tangent line to the graph at the given point;
(b) find the equation of the tangent line.
9
h(x) = -atx=7
X
(a) The slope of the tangent line at x = 7 is.

Calculus
Application of derivativesSuppose the line y = 5x - 9 is tangent to the curve y = f(x) when x = 3. If Newton's method is used to locate a root of the equation f(x) = 0 and the initial approximation is x₁ = 3, find the second approximation x2
x2 =
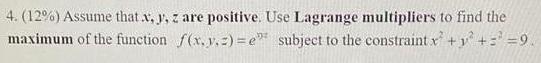
Calculus
Application of derivativesAssume that .x, y, z are positive. Use Lagrange multipliers to find the maximum of the function f(x.y.z)= e^xyz subject to the constraint x² + y² + = 9.
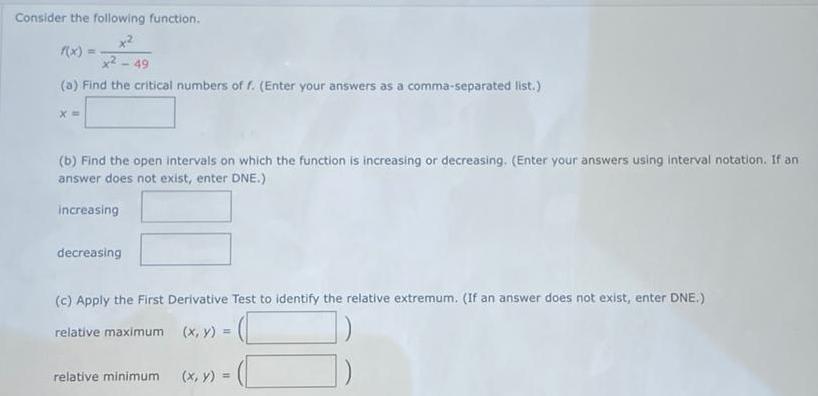
Calculus
Application of derivativesConsider the following function.
f(x) =
x2-49
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
X =
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an
answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum (x, y) =
relative minimum
(x, y) =
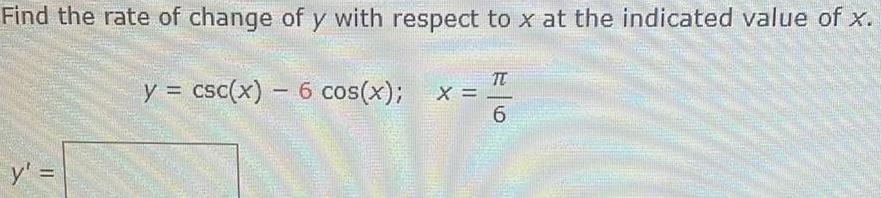
Calculus
Application of derivativesFind the rate of change of y with respect to x at the indicated value of x.
y csc(x) - 6 cos(x); x=π/6
y'=
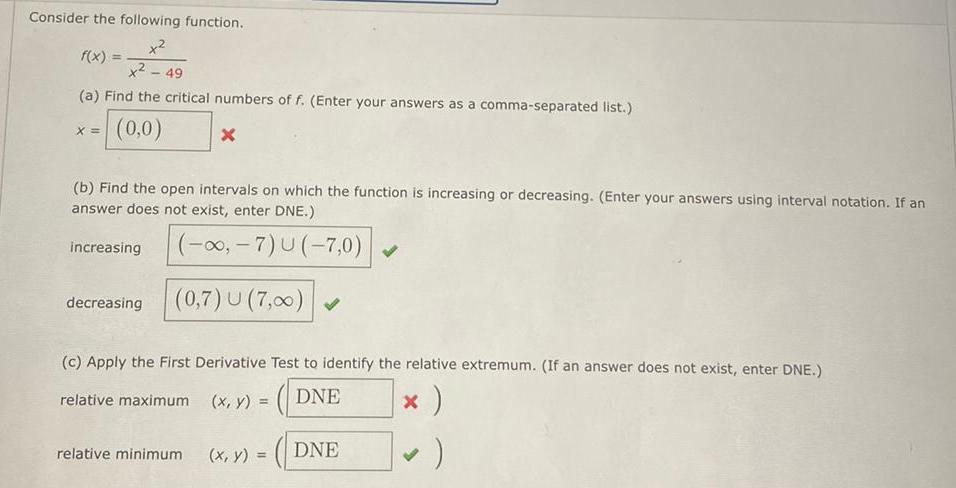
Calculus
Application of derivativesConsider the following function.
x2
x² - 49
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
x = (0,0)
=
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an
answer does not exist, enter DNE.)
(-∞, -7) U(-7,0)
(0,7) U (7,00)
increasing
decreasing
X
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum (x, y) =
(DNE
* )
relative minimum
(x, y) =
DNE
)

Calculus
Application of derivativesConsider the function on the interval (0, 2).
f(x) = sin(x) cos(x) + 2
(a) Find the open interval(s) on which the function is increasing or decreasing. (Enter your answers using interval notation.)
increasing
decreasing
(b) Apply the First Derivative Test to identify all relative extrema.
relative maxima
(x, y) =
(smaller x-value)
relative minima
(x, y) =
(x, y) =
(x, y) = (
(larger x-value)
(smaller x-value)
(larger x-value)
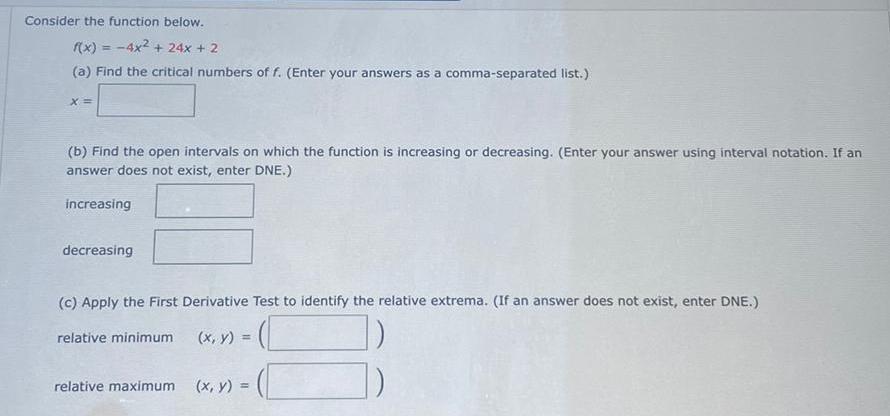
Calculus
Application of derivativesConsider the function below.
f(x) = -4x² + 24x + 2
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
X =
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answer using interval notation. If an
answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extrema. (If an answer does not exist, enter DNE.)
relative minimum
-C
relative maximum
(x, y) =
(x, y) =

Calculus
Application of derivativesConsider the following function.
f(x) = 5x +
1
x
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an
answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum (x, y) =
relative minimum
(x, y) =

Calculus
Application of derivativesConsider the following function.
f(x) = (5x)(x + 1)²
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
X =
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an answer
does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum (x, y) =
relative minimum
(x, y) =

Calculus
Application of derivativesNo, because p cannot be negative
P = 84
Yes, because each value of a corresponds to exactly one value of p
OYes, because the relation defines p in terms of s
O No, because some values of p correspond to more than one value of s
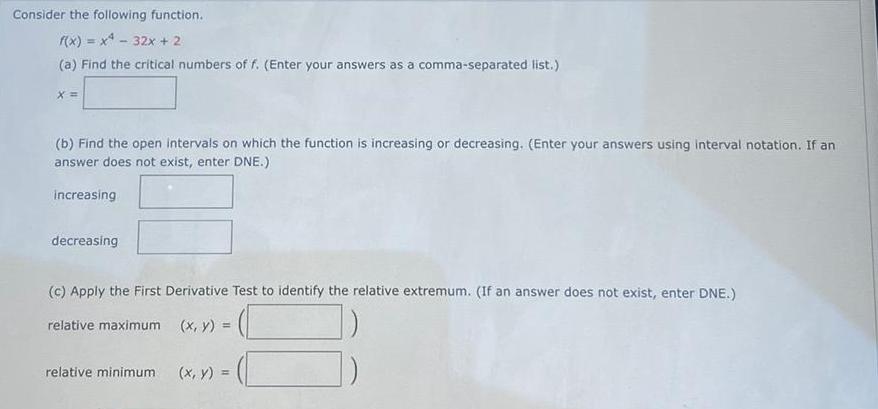
Calculus
Application of derivativesConsider the following function.
f(x) = x² - 32x + 2
(a) Find the critical numbers of f. (Enter your answers as a comma-separated list.)
X =
(b) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation. If an
answer does not exist, enter DNE.)
increasing
decreasing
(c) Apply the First Derivative Test to identify the relative extremum. (If an answer does not exist, enter DNE.)
relative maximum (x, y) =
relative minimum
(x, y) =

Calculus
Application of derivativesConsider the function on the interval (0, 2).
f(x) = sin x + cos x
(a) Find the open intervals on which the function is increasing or decreasing. (Enter your answers using interval notation.)
increasing
decreasing
(b) Apply the First Derivative Test to identify the relative extrema.
relative maximum (x, y) =
relative minimum.
(x, y) =
![Simplify.
sin x sec x - sin x csc x
[?]x - [ ]](https://media.kunduz.com/media/sug-question/raw/84112396-1660404439.0040977.jpeg?w=256)

Calculus
Application of derivativesIf the rate of change of T is proportional to (30+ T), where T > -30. If T(0) = 4, and
T(2) = 6, find T(5).

Calculus
Application of derivativesConsider the measurements shown. The most precise value is highlighted for each measurement. 9.3478 m + 2.73 m =
What place value must the answer be reported to?
1. ones place
2. tenths place
3. hundredths place 4. thousandths place

Calculus
Application of derivativesFind an equation for a positive sine function having an amplitude of 1/4, a period of 4π, and a horizontal shift of 4π to the right.
y = __/__ sin ( ___/___ x - π)
![Find the average value gave of the function g on the given interval.
g(t) = 2/(1 + t2')[0, 7]](https://media.kunduz.com/media/sug-question/raw/85021805-1660373230.7692695.jpeg?w=256)
Calculus
Application of derivativesFind the average value gave of the function g on the given interval.
g(t) = 2/(1 + t2')[0, 7]


Calculus
Application of derivativesAn open-top rectangular box is being constructed to hold a volume of 350 in³. The base of the box is made
from a material costing 6 cents/in². The front of the box must be decorated, and will cost 9 cents/in². The
remainder of the sides will cost 3 cents/in².
Find the dimensions that will minimize the cost of constructing this box.
Front width:
Depth:
Height:
in.
in.
in.

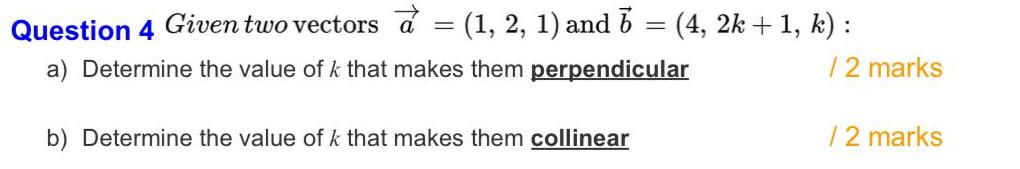
Calculus
Application of derivativesQuestion 4 Given two vectors a = (1, 2, 1) and 6 = (4, 2k + 1, k) :
a) Determine the value of k that makes them perpendicular
b) Determine the value of k that makes them collinear
/ 2 marks
/2 marks
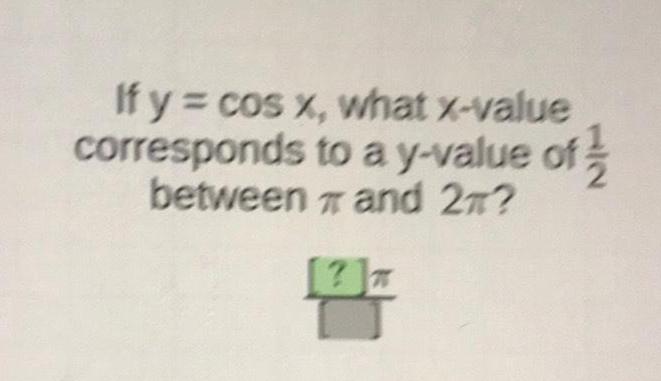
Calculus
Application of derivativescorresponds
between
If y = cos x, what x-value
to a y-value of
and 2π?
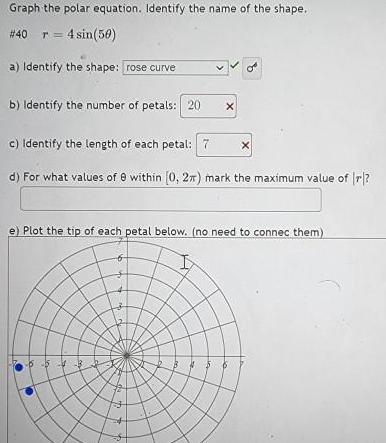
Calculus
Application of derivativesGraph the polar equation. Identify the name of the shape.
# 40 r 4 sin(50)
a) Identify the shape: rose curve
b) Identify the number of petals: 20 X
c) Identify the length of each petal: 7
d) For what values of 0 within [0, 2x) mark the maximum value of r?
e) Plot the tip of each petal below. (no need to connec them).
5 5 4
my
3
3 4 5

Calculus
Application of derivativesThe volume of a cone of radius r and height h is given by V-rªh.
tr²h. If the radius and the height
V=-
€½⁄³ centimeter per second, at what rate, in cubic centimeters per
second, is the volume increasing when the height is 9 centimeters and the radius is 6 centimeters?
both increase at a constant rate of
OA) 0.5*pi
OB) 10*pi
OC) 24*pi
D) 54*pi
E) 108*pi
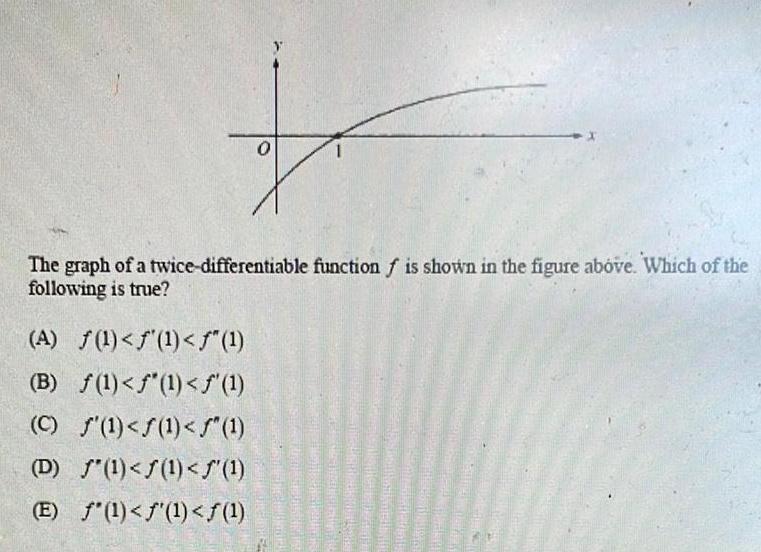
Calculus
Application of derivativesThe graph of a twice-differentiable function f is shown in the figure above. Which of the
following is true?
(A) f(1)<f'(1)<ƒ" (1)
(B) f(1)<f'(1)<f'(1)
(C) f'(1)<f(1)<ƒ^(1)
(D) f'(1)<f(1)<f'(1)
(E) f'(1)<f'(1)<ƒ(1)

Calculus
Application of derivativesWhich sound device does the
author use in the underlined
words from the poem?
In sunshine and in shadow,
Had journeyed long,
Singing a song,
In search of Eldorado.
A. repetition (repeated words)
B. end rhyme (repeated rhyme at end of
the line)
Help Resources
C. onomatopoeia (words that imitate
sounds)
D. alliteration (repeated beginning sounds)
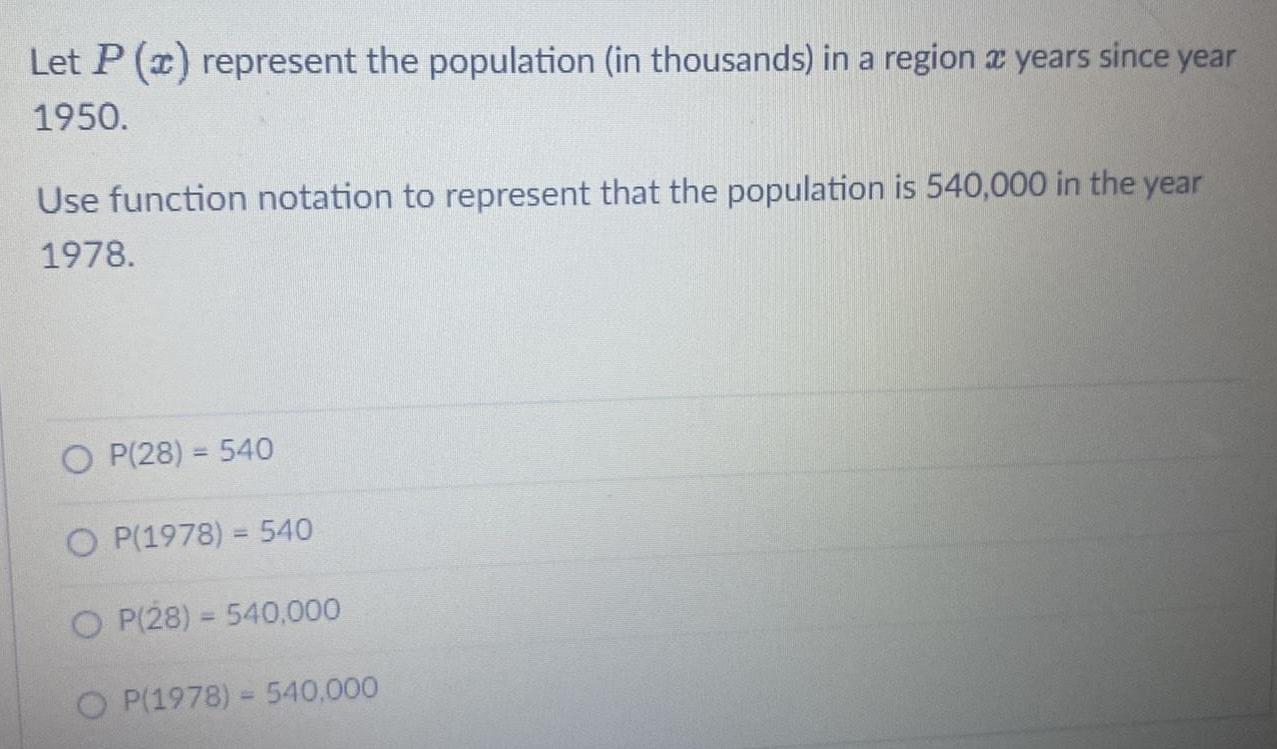
Calculus
Application of derivativesLet P (x) represent the population (in thousands) in a region a years since year
1950.
Use function notation to represent that the population is 540,000 in the year
1978.
OP(28) = 540
O P(1978) = 540
OP(28) = 540,000
O P(1978) = 540,000

Calculus
Application of derivatives65. A man starts walking from home and walks 3 miles at 20° north of west, then 5 miles at 10° west of south,
then 4 miles at 15° north of east. If he walked straight home, how far would he have to the walk, and in what
direction?
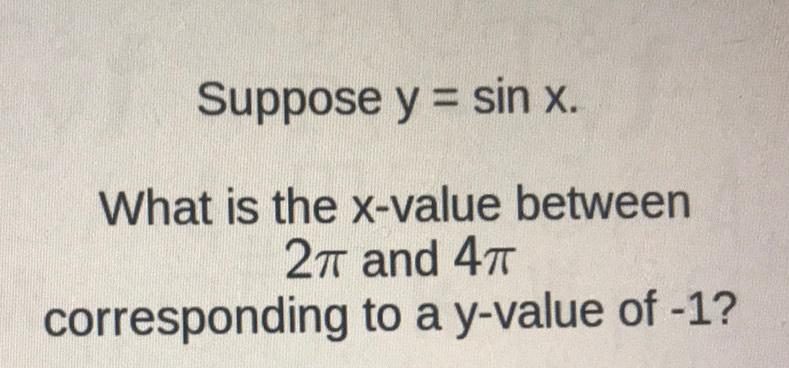
Calculus
Application of derivativesSuppose y sin x.
What is the x-value between
2π and 47
corresponding to a y-value of -1?