Application of derivatives Questions and Answers
![|
Convert the given polar
coordinates into rectangular
coordinates.
(-2, π) = ([?], [])
Enter](https://media.kunduz.com/media/sug-question/raw/84003292-1660325473.2738109.jpeg?w=256)
Calculus
Application of derivatives|
Convert the given polar
coordinates into rectangular
coordinates.
(-2, π) = ([?], [])
Enter
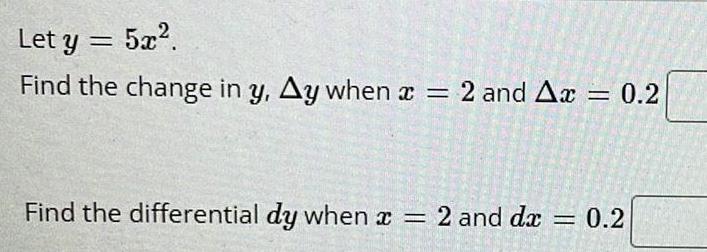
Calculus
Application of derivativesLet y = 5x².
Find the change in y, Δy when x = 2 and Δx = 0.2
Find the differential dy when x = 2 and dx=0.2
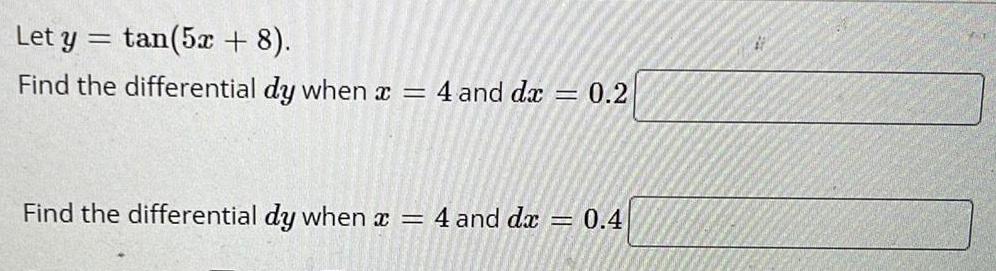
Calculus
Application of derivativesLet y = tan(5x + 8).
Find the differential dy when x = 4 and dx = 0.2
Find the differential dy when x = 4 and dx = 0.4
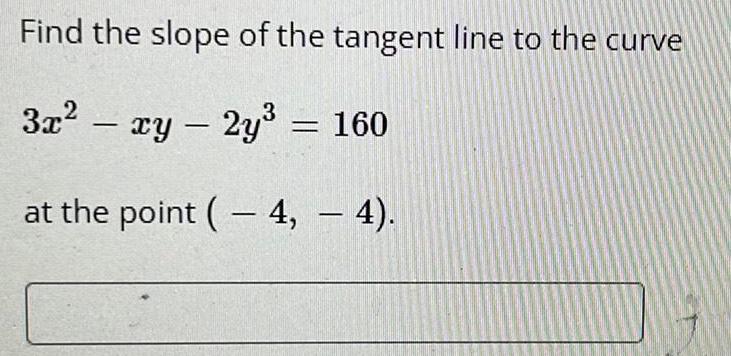
Calculus
Application of derivativesFind the slope of the tangent line to the curve
3x² – xy – 2y³ = 160
at the point ( – 4, — 4).
-

Calculus
Application of derivativesThe function f(x) = 6x +9-¹ has one local minimum and one local maximum.
This function has a local maximum at x =_____
with value______
and a local minimum at x=____
with value________
Calculus
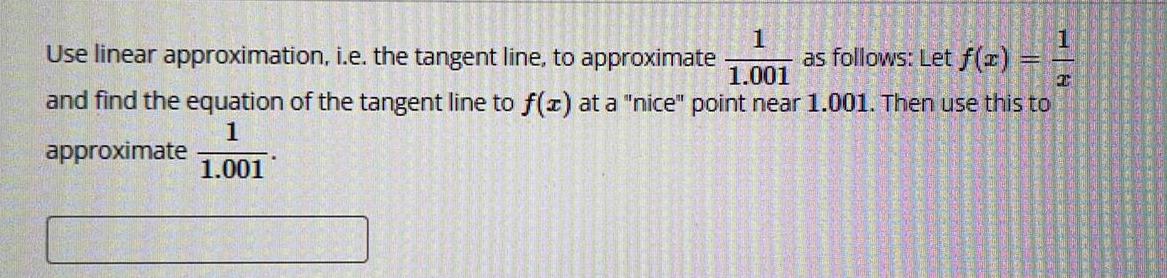
Application of derivatives1
as follows: Let f(x)
1.001
C
Use linear approximation, i.e. the tangent line, to approximate
and find the equation of the tangent line to f(x) at a "nice" point near 1.001. Then use this to
1
approximate
1.001
1
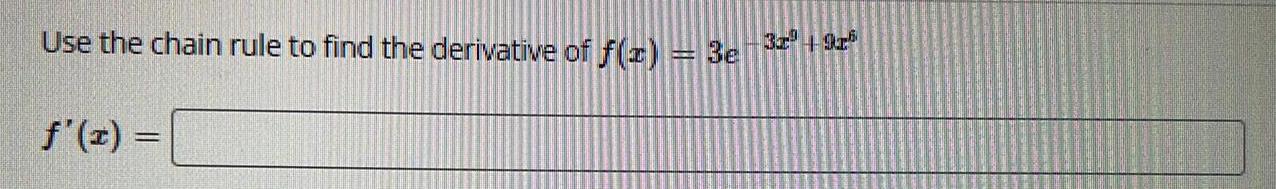
Calculus
Application of derivativesUse the chain rule to find the derivative of f(x) = 3e
f'(x) =
4-975
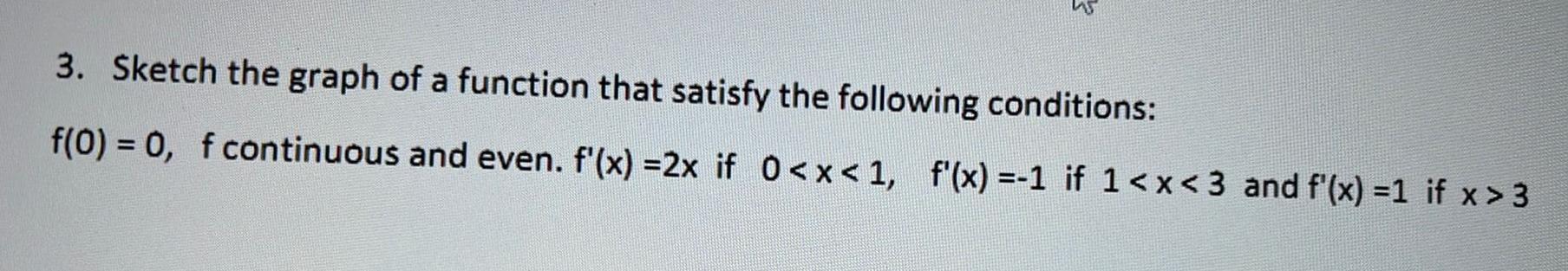
Calculus
Application of derivatives3
3. Sketch the graph of a function that satisfy the following conditions:
f(0) = 0, f continuous and even. f'(x)=2x if 0<x< 1, f'(x) =-1 if 1<x<3 and f'(x) =1 if x > 3

Calculus
Application of derivativesThe circumference of a sphere was measured to be 84 cm with a possible error of 0.5 cm. Use
linear approximation to estimate the maximum error in the calculated surface area.
Estimate the relative error in the calculated surface area.
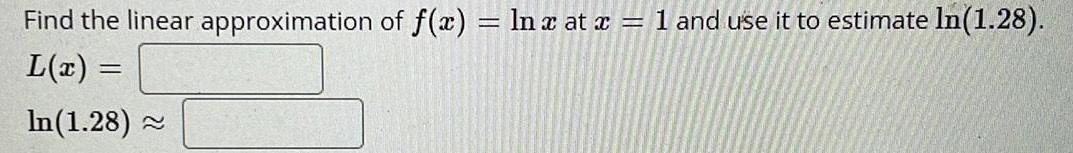
Calculus
Application of derivativesFind the linear approximation of f(x) = ln x at x = 1 and use it to estimate In(1.28).
L(x) =
In(1.28) ~
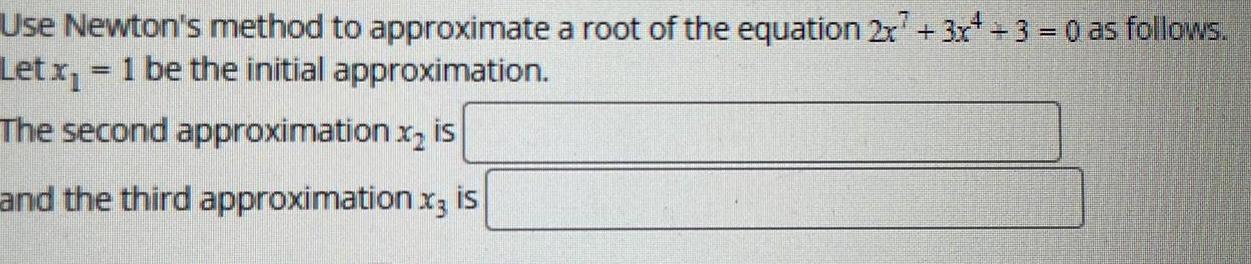
Calculus
Application of derivativesUse Newton's method to approximate a root of the equation 2x + 3x + 3 = 0 as follows.
Let x₁ = 1 be the initial approximation.
The second approximation x₂ is
and the third approximation x3 is

Calculus
Application of derivativesA rotating light is located 12 feet from a wall. The light completes one rotation every 3 seconds. Find
the rate at which the light projected onto the wall is moving along the wall when the light's angle is
25 degrees from perpendicular to the wall.
light
wall
K

Calculus
Application of derivativesA street light is at the top of a 16 ft tall pole. A woman 6 ft tall walks away from the pole with a speed
of 6 ft/sec along a straight path. How fast is the tip of her shadow moving when she is 45 ft from the
base of the pole?
ft
sec

Calculus
Application of derivativesA room contains 8 people, each of a different age. The people leave the room in random order, one at a time. What is the probability that they leave the room in ascending order of their ages (youngest to
oldest)?
The probability that they leave the room in ascending order of their ages is
(Round to six decimal places as needed.)
SECCI
![5. Suppose f is continuous on [0, 4], f(0) = 1, and 2 Sf'(x) ≤ 5 for all x in (0, 4). Show
that 9≤ f(4) ≤21. (Justify your work).](https://media.kunduz.com/media/sug-question/raw/83731123-1660320408.597694.jpeg?w=256)
Calculus
Application of derivatives5. Suppose f is continuous on [0, 4], f(0) = 1, and 2 Sf'(x) ≤ 5 for all x in (0, 4). Show
that 9≤ f(4) ≤21. (Justify your work).

Calculus
Application of derivativesA 9-digit phone number cannot start with 0 or 1. Assume that there are no restrictions on the remaining 8 numbers. How many telephone numbers are possible in which all 9 digits are different?
The possible number of 9-digit telephone numbers where all the digits are different is.

Calculus
Application of derivativesGiven that
f (x) =
2(3-x)²(x+4)
(x-1)³
Solve the following inequality f(x) ≥ 0
Include the following information:
The boundary points and the multiplicity of each
The intervals
. The sign(positive or negative) of the rational expression in each
interval
The solution set in interval notation
. The sketch of the graph of f(x)
●
![f(x)=-3x²+2x
g(x) = 2x+3
Find f-g and fg. Then, give their domains using interval notation.
(f - g)(x) = []
Domain of f - g :
(f*g)(x) =
Domain of fig](https://media.kunduz.com/media/sug-question/raw/83589157-1660320248.3325214.jpeg?w=256)
Calculus
Application of derivativesf(x)=-3x²+2x
g(x) = 2x+3
Find f-g and fg. Then, give their domains using interval notation.
(f - g)(x) = []
Domain of f - g :
(f*g)(x) =
Domain of fig

Calculus
Application of derivativesFind an equation of the tangent line to the graph of y = g(x) at x = 2 if g(2) = -4 and g'(2) = 3. (Enter your answer as an equation in terms of y and x.)

Calculus
Application of derivativesFind the magnitude and the direction of the
resultant vector.
(-6, -2) w
A. 8.06, 60.26°
B. 19.42, 34.51°
C. 8.06, 29.74°
D. 19.42, 55.50⁰
(10, 9)

Calculus
Application of derivativesGravel is being dumped from a conveyor belt at a rate of 50 cubic feet per minute. It forms a pile in
the shape of a right circular cone whose base diameter and height are always equal. How fast is the
height of the pile increasing when the pile is 11 feet high?
Recall that the volume of a right circular cone with height h and radius of the base r is given by
1
V =
πr²h
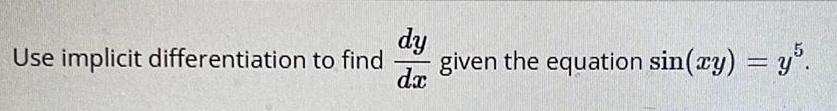
Calculus
Application of derivativesdy
Use implicit differentiation to find given the equation sin(xy) = y5.
dx

Calculus
Application of derivativesThe cost of a trip is $3.15 plus $0.95 for every kilometre that you ride on a bus.
Which of the following expressions gives the cost of a trip of & kilometres?
OC(k)= ($3.15+ $0.95)k
OC(k)=$3.15+ $0.95
OC(k)= $3.15+ $0.95k
OC(k) $3.15k + $0.95

Calculus
Application of derivativesIf the tangent line to y = f(x) at (4, 2) passes through the point (0, 1), find f(4) and f'(4).
(4) =
f'(4) =
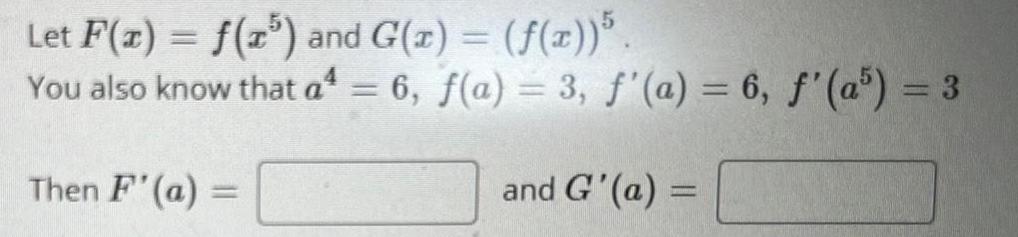
Calculus
Application of derivativesLet F(x) = f(x³) and G(x) = (f(x))³ .
You also know that a¹ = 6, f(a) = 3, f'(a) = 6, f'(a) = 3
and G'(a) =
Then F'(a) =

Calculus
Application of derivatives(10 points) A ladder 10 m long is leaning against a wall. If the base of the ladder is sliding away from
the wall at the rate of 1 m per second, at what instantaneous rate, d will the top of the ladder be moving
dt'
when the base of the ladder is 6 m from the wall?
![(10 points) A spherical balloon is inflated so that its volume is increasing at the rate of 20 cubic cm per
second. What is the instantaneous change in surface area, ds of the balloon increasing when the radius is
dt
40 cm? [Use V
4
==
3
r³ and S= 4².]](https://media.kunduz.com/media/sug-question/raw/83592816-1660319514.564862.jpeg?w=256)
Calculus
Application of derivatives(10 points) A spherical balloon is inflated so that its volume is increasing at the rate of 20 cubic cm per
second. What is the instantaneous change in surface area, ds of the balloon increasing when the radius is
dt
40 cm? [Use V
4
==
3
r³ and S= 4².]

Calculus
Application of derivativesAn oil spill is pouring oil onto a sea in the shape of a circle. The slick is growing at a
rate of 150 m2/s.
How fast is the radius changing when the radius is 25 m?
T m/s
O ² m/s
3 m/s
3π m/s

Calculus
Application of derivativesFor the real-valued functions g(x)=x²-5. and h(x)=√x-2, find the composition g h and specify its domain using interval notation.
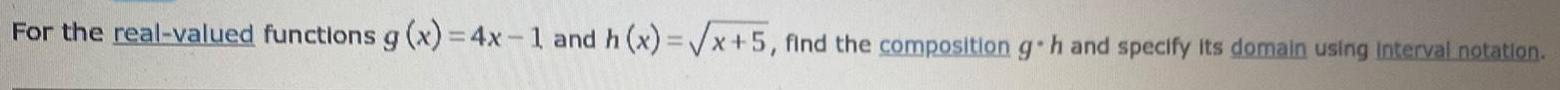
Calculus
Application of derivativesFor the real-valued functions g(x) = 4x-1 and h(x)=√x+5, find the composition g h and specify its domain using interval notation.

Calculus
Application of derivativesA company manufactures 2 models of MP3 players. Let x represent the number (in millions) of the first
model made, and let y represent the number (in millions) of the second model made.
The company's revenue can be modeled by the equation
R(z,y) = 140z + 170y - 2z² - 4y² - ry
Find the marginal revenue equations
R₂(z,y) =
Ry(x, y) =
0 and
We can achieve maximum revenue when both partial derivatives are equal to zero. Set Rz
Ry = 0 and solve as a system of equations to the find the production levels that will maximize revenue.
Revenue will be maximized when:
X=
y=
=

Calculus
Application of derivativesThe point A(3, 9) lies on the curve
y=x²
40
If B is the point (x, x^2), find the slope of the secant line AB for the following values
of x. Use all decimal places in your response.
If x= 3.1, the slope of AB is:
A/
If x= 3.01, the slope of AB is:
A
If x= 2.9, the slope of AB is:
A/
If x= 2.99, the slope of AB is:
A/
Based on the above results, guess the slope of the tangent line to the curve at A(3,
9):
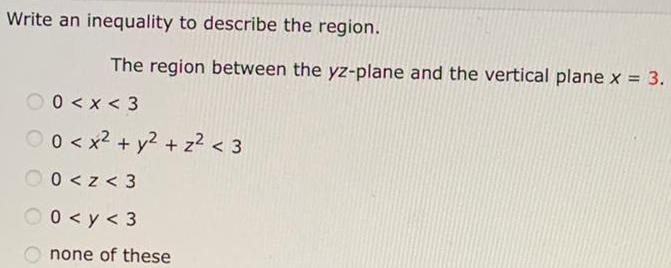
Calculus
Application of derivativesWrite an inequality to describe the region.
The region between the yz-plane and the vertical plane x = 3.
00<x<3
0 < x² + y² + z² < 3
0<z <3
0<y<3
none of these

Calculus
Application of derivativesIf Á = 2 +33 + 12kland B-3+43-6
are the two vectors, find the resultant vector.
O 5+7+6
O 5² 73 +6
O 573 6
→>
Osi+73-6

Calculus
Application of derivativesFor the real-valued functions g(x)=x² +1. and h(x)=x-5, find the composition g h and specify Its domain using interval notation.
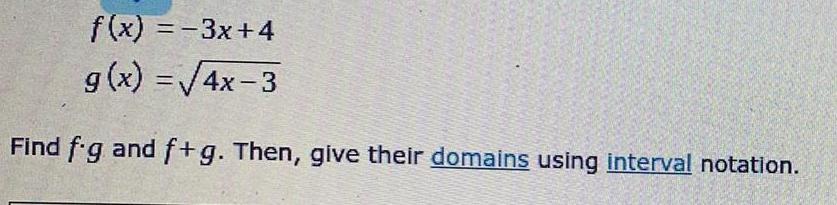
Calculus
Application of derivativesf(x) = -3x+4
g(x)=√4x-3
Find f.g and f+g. Then, give their domains using interval notation.

Calculus
Application of derivativesFind an equation of the sphere that passes through the point (1, 6, 3) and has center (3, 5, -5).

Calculus
Application of derivativesFind the scalar and vector projections of b onto a.
a = (6, 7, -6) b = (3,-1, 1)
scalar projection of b onto a
vector projection of b onto a
![In a composite function, If f[g(x)] = x=g[f(x)] then
Of(x) and g(x) must be same functions
Of(x) and g(x) is not a function
Of(x) and g(x) are inverses
Of(x) and g(x) must be different functions](https://media.kunduz.com/media/sug-question/raw/83532794-1660315615.9683812.jpeg?w=256)
Calculus
Application of derivativesIn a composite function, If f[g(x)] = x=g[f(x)] then
Of(x) and g(x) must be same functions
Of(x) and g(x) is not a function
Of(x) and g(x) are inverses
Of(x) and g(x) must be different functions

Calculus
Application of derivativesChoose the best description of the normal line.
a line parallel to a given line or curve
a line with a zero slope
C
C
a line with an undefined slope
C
a line perpendicular to a given line or curve
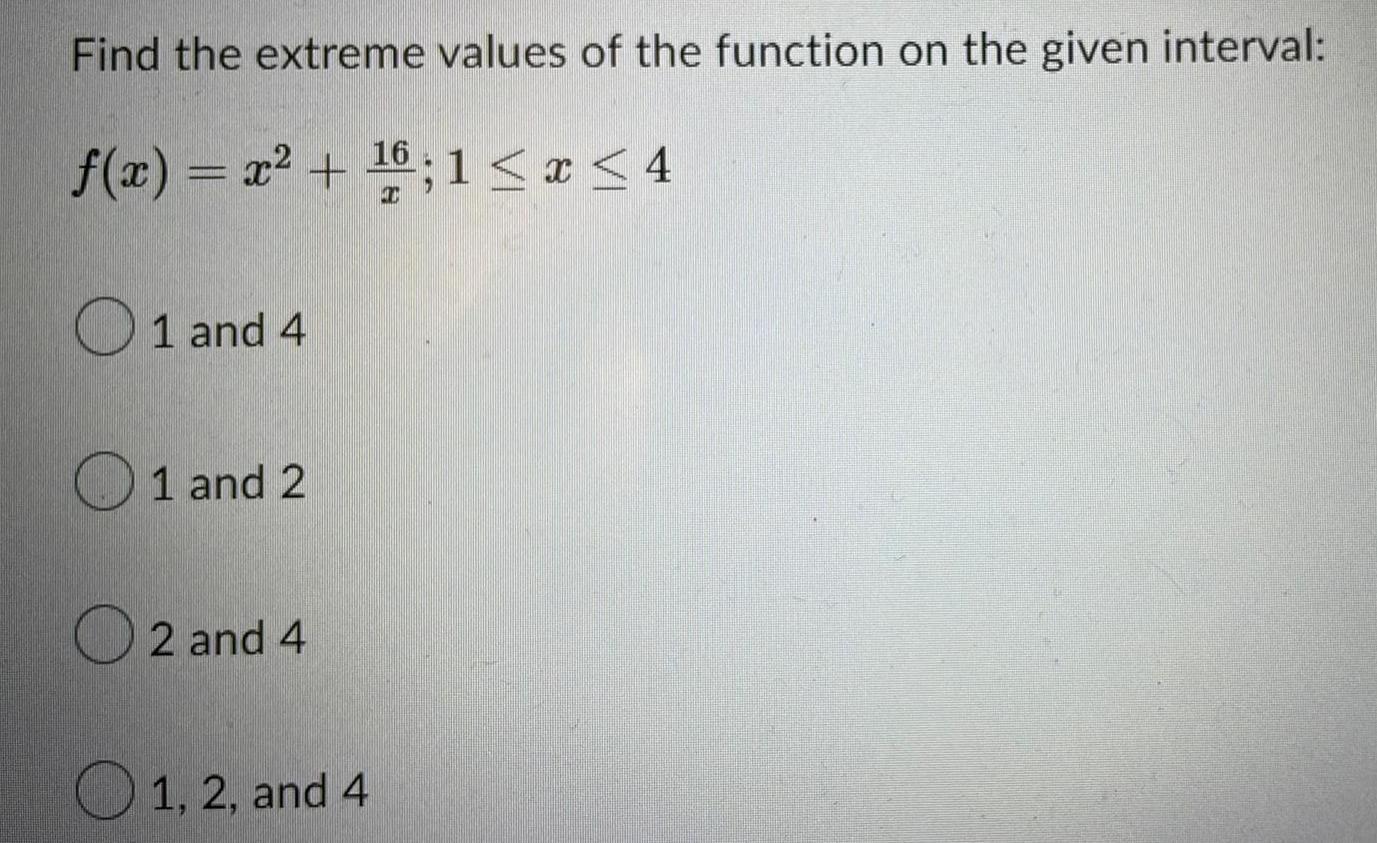
Calculus
Application of derivativesFind the extreme values of the function on the given interval:
16
f(x) = x² + ¹6; 1 ≤ x ≤4
1 and 4
1 and 2
2 and 4
1, 2, and 4
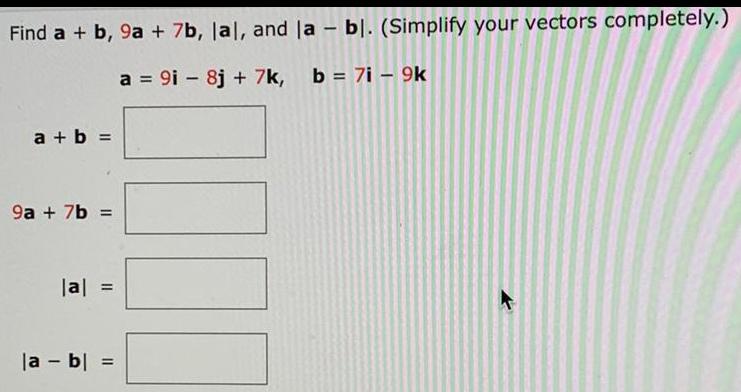
Calculus
Application of derivativesFind a + b, 9a + 7b, lal, and la - bl. (Simplify your vectors completely.)
a = 9i - 8j + 7k, b = 7i - 9k
a + b
11
9a + 7b =
|a| =
la - bl =

Calculus
Application of derivativesThe conjugate of a complex number a + bi is 25+ 3i. What is a + bi?
- 25 + 3i
O25-3i
O-25-3i
25+ 3i

Calculus
Application of derivativesWhich of the following statements is the most correct statement regarding the
critical points of the following function.
3
y = ax³ + bx² + cx+d
there can be any number of critical points
there are no critical points
there will be a minimum of 2 critical points
there will be a maximum of 2 critical points

Calculus
Application of derivativesDescribe the surface in R3 represented by the equation x + y = 4,
This is the set {(x, 4-x, z)|x ER, ze Ry which is a horizontal plane that intersects the xy-plane in the line y = 4 - x, z = 0.
This is the set {(x, 4-x, z)|x ER, ZER) which is a vertical plane that intersects the xy-plane in the line y = 4 - x, z = 0.
This is the set {(x, 4-x, z)|x ER, ZER3 which is a vertical plane that intersects the xz-plane in the line y = 4 - x, z = 0.
This is the set {(x, 4-x, z)|x ER, ZERY which is a horizontal plane that intersects the xz-plane in the line y = 4 - x, z = 0.
This is the set {(x, y, 4 - x - y) lx ER, YER) which is a vertical plane that intersects the xy-plane in the line y = 4 - x, z = 0.
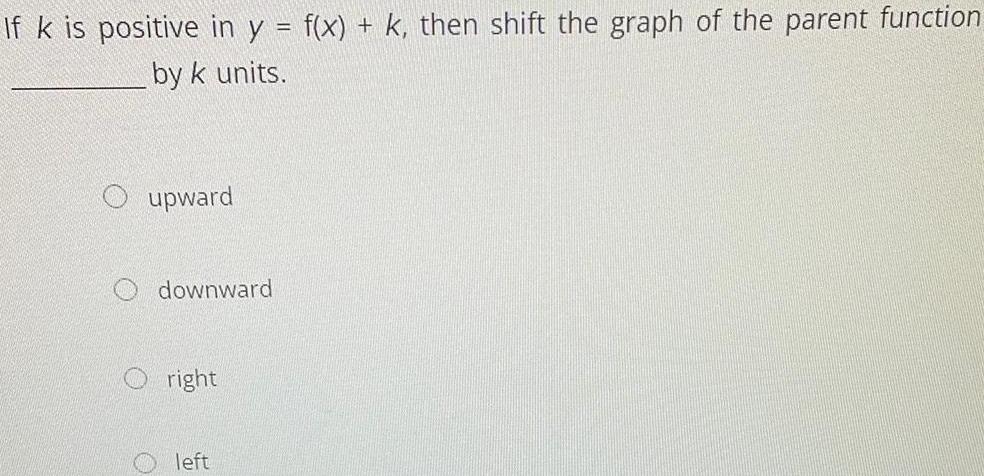
Calculus
Application of derivativesIf k is positive in y = f(x) + k, then shift the graph of the parent function
by k units.
upward
downward
right
left

Calculus
Application of derivativesFind the slope of the tangent to the curve
y = 1+ln z
at the point (1, 1).
0 F
N
O
1
O o
1

Calculus
Application of derivativesLet f(x)
10x+12
point (0,5) is given by y
m =
b
-
7e". Then the equation of the tangent line to the graph of f(x) at the
= mx + b for

Calculus
Application of derivatives-
Determine the slope of the tangent to the graph of y = (x² + 3x − 2)(7 - 3x)
at (1,8).

Calculus
Application of derivativesDetermine the equation of the tangent to y = (3x-2 - 2x³)5 at (1, 1).