Application of derivatives Questions and Answers

Calculus
Application of derivativesFind the coordinates of the ordered pair where the minimum value occurs
for the equation Q = 9x + 2y + 12, given these constraints:
x ≥-1
-2x+y 20
2x + y ≤ 4
O (1,-6)
O (-1,6)
O (-1,-2)
O (1,2)
Calculus
Application of derivativesMY NOTES PRACTICE A
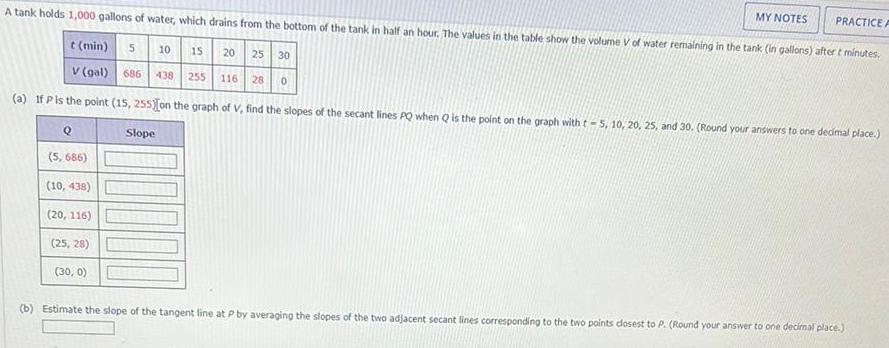
A tank holds 1,000 gallons of water, which drains from the bottom of the tank in half an hour. The values in the table show the volume V of water remaining in the tank (in gallons) after t minutes.
t (min) 5
686 438 255 116
V (gal)
(a) If P is the point (15, 255) on the graph of V, find the slopes of the secant lines PQ when Q is the point on the graph with t-5, 10, 20, 25, and 30. (Round your answers to one decimal place.)
Slope
Q
(5, 686)
(10, 438)
(20, 116)
(25, 28)
(30, 0)
10
15 20
25 30
28
(b) Estimate the slope of the tangent line at P by averaging the slopes of the two adjacent secant lines corresponding to the two points closest to P. (Round your answer to one decimal place.)

Calculus
Application of derivativesDetermine the equation of the tangent line to the curve
z
y = Ing
I
at x = 1:
Oy=-x+1
Oy=-x-1
Oy=x-1
Oy=x+1

Calculus
Application of derivativesy = log₂ (log₂x)
The slope of the tangent line to the given curve at its x-intercept is:
1
2(In 2)²
01
2x (log 2)
0

Calculus
Application of derivativesA local company rents a moving truck for $750 plus $0.60 per mile driven over 1000 mi. What is the maximum number of miles the truck can be driven so that the rental cost is at most $1200?

Calculus
Application of derivativesA game is played using a four-sided wooden top, with one of four letters on each face, A, B, C, or D. Players compete for a pot of tokens. A player spins the top and
takes one of the following actions, depending on which letter faces up.
If A faces up, the player neither adds nor subtracts tokens from the pot.
If B faces up, the player wins the entire pot of tokens.
• If C faces up, the player wins half of the tokens in the pot, rounding up if the number is odd.
• If D faces up, the player adds a token to the pot.
Assume that each face of the top is equally likely to face upward and that the pot holds 27 tokens. Let the random variable X be the amount of tokens won by a
player. Thus, the range of X is {-1,0,14,27). Let the probability mass function be f(x) = P(X=x) and the cumulative probability function be F(x)=P(X ≤x). Find f(0) and
F(0).
First, find the probability mass function f(x).
f(x) =
=
(Type an ordered pair. Use a comma to separate answers as needed.)
Now find f(0).
f(0) = (Simplify your answer.)
Find the cumulative probability function F(x)= P(X ≤x). Choose the correct answer below.
A.
B.
OC.
0.25 -1<x<0
F(x)= 0.5 0<x<14
0.75 14<x<27
BEKI
0 x < -1
F(x)= 1-1≤x≤27
0 27<x
0
x < -1
0.25 -1<x<0
F(x)= 0.5 0<x< 14
0.75 14≤x<27
1
27 ≤x
O D.
F(x)=
x < -1
0.251sx<0
0
0.75 0<x<27
1
27 ≤x

Calculus
Application of derivativesFind tanx and secx if sin a = -and cotx <0 without using a calculator. Show one line of work and then state the two exact
answers.

Calculus
Application of derivativesDescribe the intervals on which the functionf (x) = ln | x| is continuous. Are they
removable? Graph the function.
![Find constants a and b so that the minimum for the parabola f(x) = x² + ax + bis at the point (2, 11). [Hint: Begin by finding the
critical point in terms of a.]
a = i
b =
IM
Im](https://media.kunduz.com/media/sug-question/raw/82677261-1660231799.3531315.jpeg?w=256)
Calculus
Application of derivativesFind constants a and b so that the minimum for the parabola f(x) = x² + ax + bis at the point (2, 11). [Hint: Begin by finding the
critical point in terms of a.]
a = i
b =
IM
Im

Calculus
Application of derivativesThe population of rabbits (in thousands) in a forest at time t months is modeled by
the equation
R(t) = 50t2 et + 8 where t≥ 0
Determine the final number of rabbits in the forest by evaluating the limit at t
approaches infinity:
8
the population continues to increase as t increases
8000
50

Calculus
Application of derivativesy = xe-2x, 0 ≤ x ≤ In(3)
On this interval, the minimum value(s) occur at x =
0
In(3)
1
2
two of these are correct
Calculus
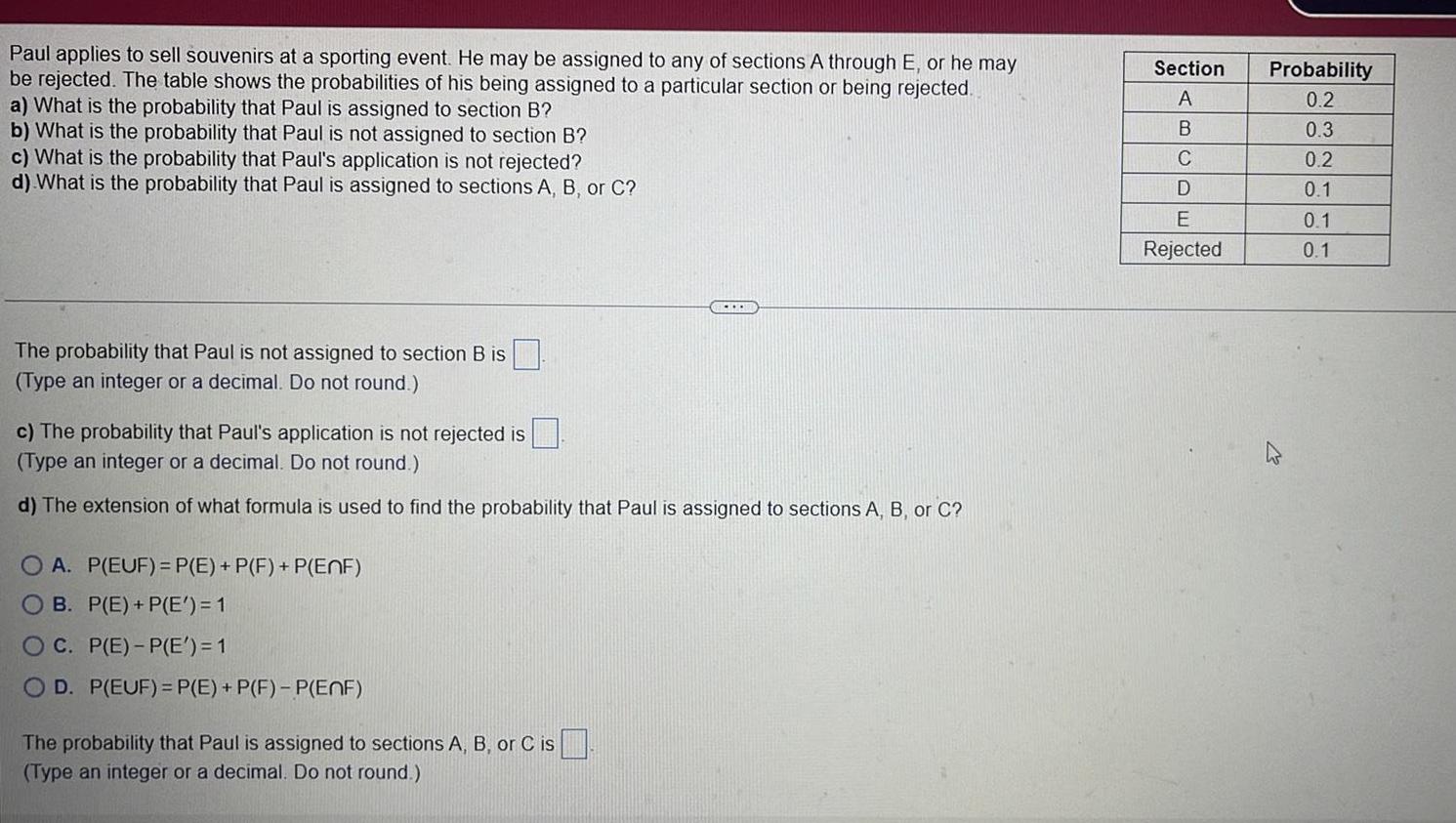
Application of derivativesPaul applies to sell souvenirs at a sporting event. He may be assigned to any of sections A through E, or he may
be rejected. The table shows the probabilities of his being assigned to a particular section or being rejected.
a) What is the probability that Paul is assigned to section B?
b) What is the probability that Paul is not assigned to section B?
c) What is the probability that Paul's application is not rejected?
d) What is the probability that Paul is assigned to sections A, B, or C?
The probability that Paul is not assigned to section B is
(Type an integer or a decimal. Do not round.)
c) The probability that Paul's application is not rejected is
(Type an integer or a decimal. Do not round.)
d) The extension of what formula is used to find the probability that Paul is assigned to sections A, B, or C?
OA. P(EUF) = P(E) + P(F) + P(EnF)
B. P(E) + P(E')= 1
OC. P(E)-P(E') = 1
OD. P(EUF) = P(E) + P(F)- P(ENF)
The probability that Paul is assigned to sections A, B, or C is
(Type an integer or a decimal. Do not round.)
Section
ABCD
E
Rejected
Probability
0.2
0.3
0.2
0.1
0.1
0.1

Calculus
Application of derivativesSuppose that f(x) = x³ + x² - 64x-64 and g(x)=x²-8. Find the zeros of (f o g)(x).
The zero(s) of (f o g)(x) is/are .
(Simplify your answer. Type an exact answer, using radicals as needed. Use a comma to separate answers as needed.)
Calculus
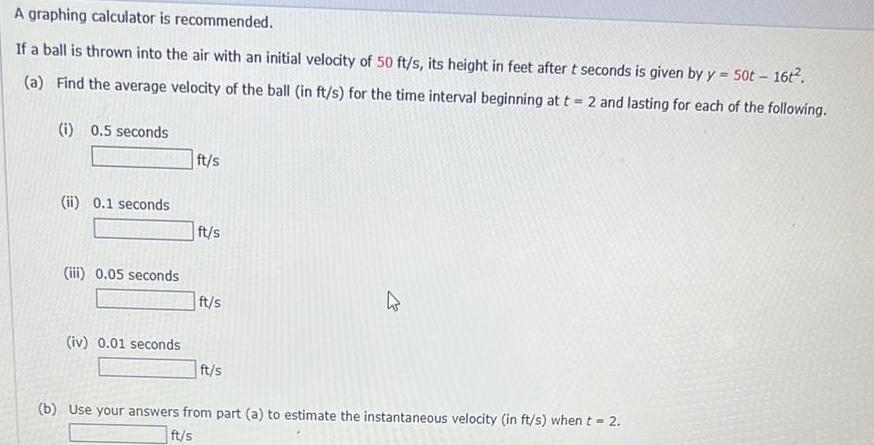
Application of derivativesA graphing calculator is recommended.
If a ball is thrown into the air with an initial velocity of 50 ft/s, its height in feet after t seconds is given by y
50t - 16t².
(a) Find the average velocity of the ball (in ft/s) for the time interval beginning at t = 2 and lasting for each of the following.
(i) 0.5 seconds
(ii) 0.1 seconds
(iii) 0.05 seconds
(iv) 0.01 seconds
ft/s
ft/s
ft/s
ft/s
4
(b) Use your answers from part (a) to estimate the instantaneous velocity (in ft/s) when t = 2.
ft/s

Calculus
Application of derivativesSuppose f''(x) = − 30x - 10, ƒ'(1) = − 16, and ƒ(1) = − 11.
Then f(x) =
Add Work
Check Answer
Calculus
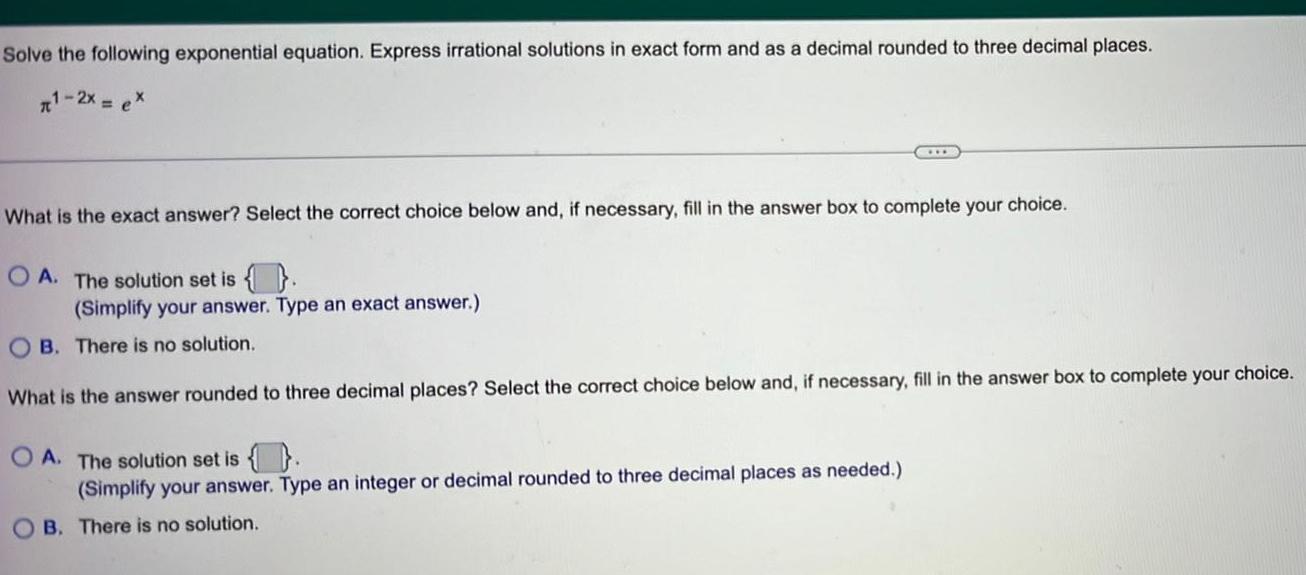
Application of derivativesSolve the following exponential equation. Express irrational solutions in exact form and as a decimal rounded to three decimal places.
¹-2x = ex
What is the exact answer? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. The solution set is {}.
(Simplify your answer. Type an exact answer.)
OB. There is no solution.
What is the answer rounded to three decimal places? Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
OA. The solution set is {}.
(Simplify your answer. Type an integer or decimal rounded to three decimal places as needed.)
OB. There is no solution.

Calculus
Application of derivativesFor the following exercises, convert the given Cartesian coordinates to polar coordinates with
r> 0, ≤0 2T. Remember to consider the quadrant in which the given point is located.
11. (4,2)
12. (-4, 6)
13. (3,-5)
14. (-10, -13)
15. (8,8)

Calculus
Application of derivativesConsider the Taylor series for cos z:
What is a series for
O
MIN
O
01/14-
1
NIN
NIN
+
+
6! 8!
I
4! 6!
6!
cos z − 1 + x²,
6! 8!
+
+
8!
1
IT
8!
21
4!
6!
8!
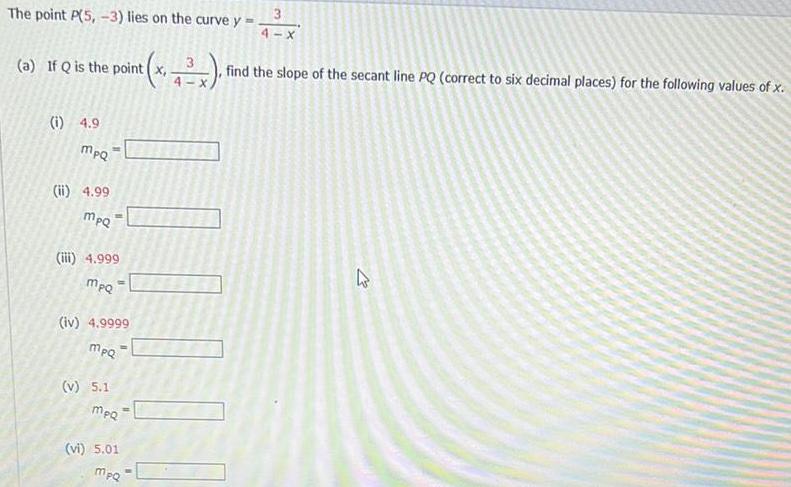
Calculus
Application of derivativesThe point P(5,-3) lies on the curve y
T
(a) If Q is the point
(1) 4.9
MpQ
11
(ii) 4.99
MpQ
(iii) 4.999
MpQ
(iv) 4.9999
MpQ
(v) 5.1
MPQ
#
(vi) 5.01
MpQ
nt (x, 43x), fi
4-X
"
3
4-X
find the slope of the secant line PQ (correct to six decimal places) for the following values of x.
27

Calculus
Application of derivativesA shopping center includes a grocery store and a drug store. One afternoon, a total of 200 people visited the shopping center, and 126 shopped at the grocery store,
82 shopped at the drug store, and 33 shopped at both businesses.
a) How many people shopped at the grocery store or the drug store?
b) How many people shopped at neither the grocery store nor the drug store?
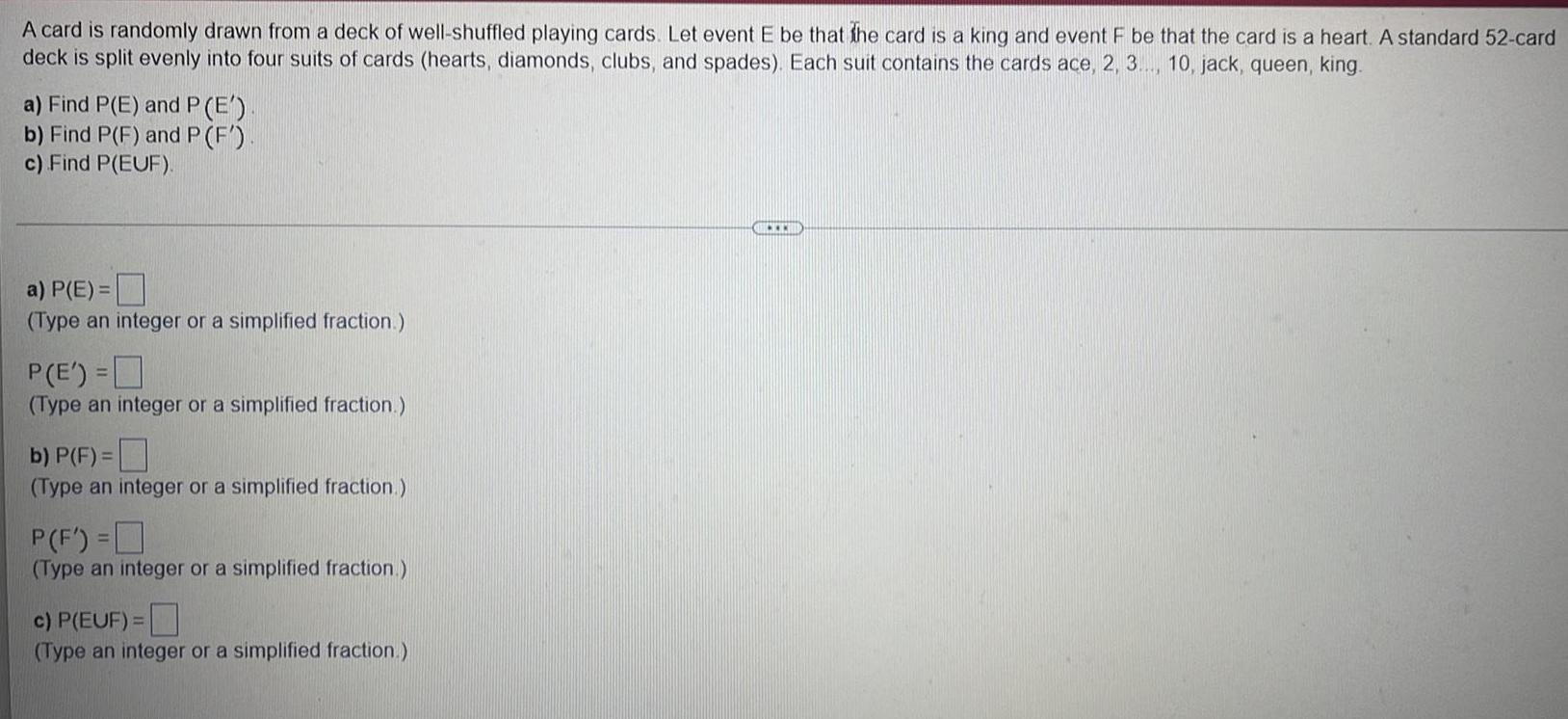
Calculus
Application of derivativesA card is randomly drawn from a deck of well-shuffled playing cards. Let event E be that the card is a king and event F be that the card is a heart. A standard 52-card
deck is split evenly into four suits of cards (hearts, diamonds, clubs, and spades). Each suit contains the cards ace, 2, 3..., 10, jack, queen, king.
a) Find P(E) and P (E').
b) Find P(F) and P (F')
c) Find P(EUF).
a) P(E)=
(Type an integer or a simplified fraction.)
P(E') =
(Type an integer or a simplified fraction.)
b) P(F) =
(Type an integer or a simplified fraction.)
P(F') =
(Type an integer or a simplified fraction.)
c) P(EUF) =
(Type an integer or a simplified fraction.)

Calculus
Application of derivativesYour expenses that stay the same every month, like a car payment are called.
O Steady
O Fixed
O Variable
Tracked
expenses.

Calculus
Application of derivativesSimplify cos(t)csc(t)
to a single trig function or constant with no fractions.
![Graded Assignment
Semester B Exam, Part 2
Answer the questions. When you have finished, submit this test to your teacher by the due date for full credit.
Total score! of 42 points
Seconst
(Beere for Question 1: of 12 points)
1. Graph the function /(x) = -see
Answer:
-21-38-
10
4
3
2
-3
4
-5
(4) +
+3 on the interval [-2n, 6n].
51
# 3 2 5 3 7 4
2
2
2
9 5 11 6
2
2](https://media.kunduz.com/media/sug-question/raw/81652919-1660230666.605537.jpeg?w=256)
Calculus
Application of derivativesGraded Assignment
Semester B Exam, Part 2
Answer the questions. When you have finished, submit this test to your teacher by the due date for full credit.
Total score! of 42 points
Seconst
(Beere for Question 1: of 12 points)
1. Graph the function /(x) = -see
Answer:
-21-38-
10
4
3
2
-3
4
-5
(4) +
+3 on the interval [-2n, 6n].
51
# 3 2 5 3 7 4
2
2
2
9 5 11 6
2
2
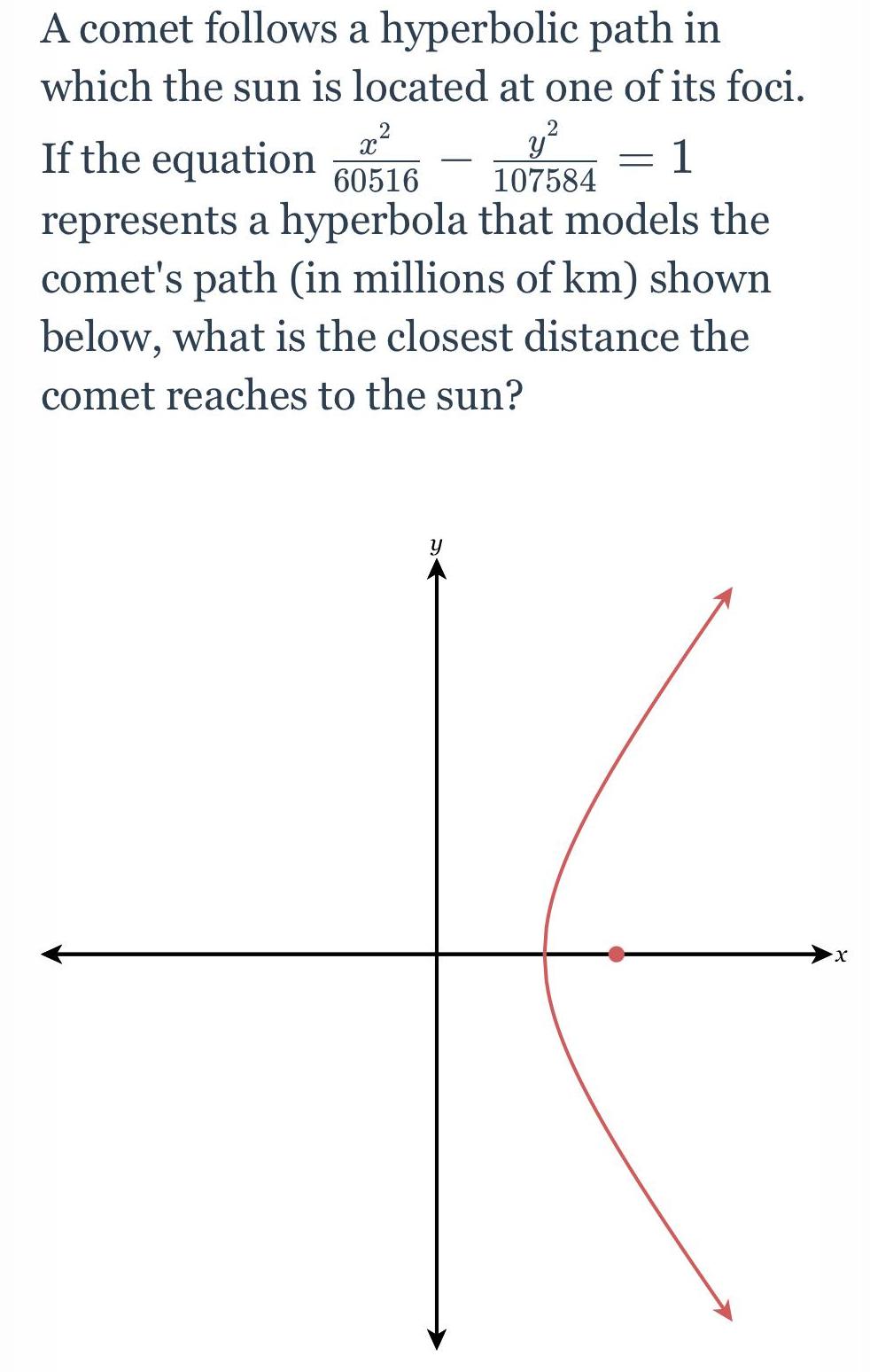
Calculus
Application of derivativesA comet follows a hyperbolic path in
which the sun is located at one of its foci.
1
2
If the equation
22
60516
y²
107584
represents a hyperbola that models the
comet's path (in millions of km) shown
below, what is the closest distance the
comet reaches to the sun?
-
X

Calculus
Application of derivatives13. The volumes of two similar figures are 512 mm³ and 3375 mm³. If the surface area of the
smaller figure is 128 mm2, what is the surface area of the larger figure?
450 mm²
68 mm²
240 mm²
844 mm²

Calculus
Application of derivativesConsider the discrete model
Xn+1 = x² +1.
Find the 2-cycle and determine its stability.

Calculus
Application of derivativesIn Exercises 3-18, find the Maclaurin series and find the interval on which the
expansion is valid.
3.
f(x)=
4.
=
X
1-x³
5. f(x) = cos 3x
6. f(x) = sin(2x)
1
1 + 10x
f(x) =

Calculus
Application of derivativesIn Exercises 1-16, calculate the Taylor polynomials T2 and T3 centered at x = a
for the given function and value of a.
1. f(x) = sin x, a = 0
2.
f(x) = sin x, a =
πT
2
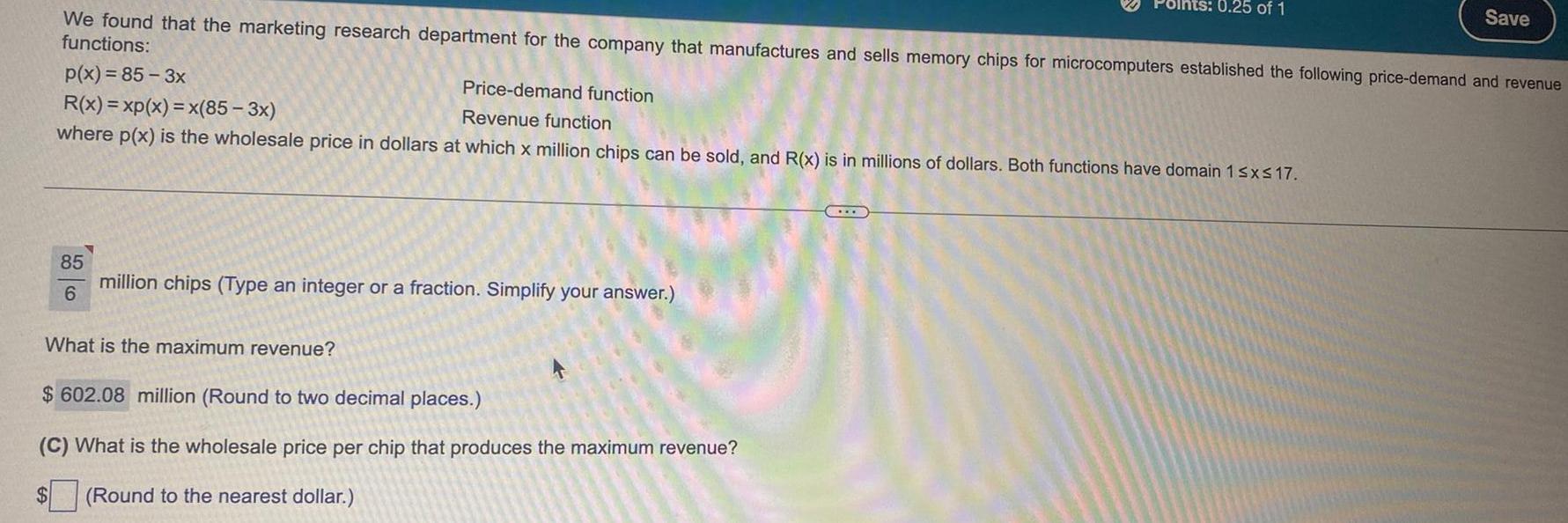
Calculus
Application of derivatives$
85
6
We found that the marketing research department for the company that manufactures and sells memory chips for microcomputers established the following price-demand and revenue
functions:
p(x) = 85-3x
Price-demand function
Revenue function
R(x)=xp(x) = x(85-3x)
where p(x) is the wholesale price in dollars at which x million chips can be sold, and R(x) is in millions of dollars. Both functions have domain 1 ≤x≤17.
million chips (Type an integer or a fraction. Simplify your answer.)
What is the maximum revenue?
$ 602.08 million (Round to two decimal places.)
(C) What is the wholesale price per chip that produces the maximum revenue?
(Round to the nearest dollar.)
0.25 of 1
Save

Calculus
Application of derivativesSolve each of the following systems using elementary operations:
b. 1 2x + 5y = 19
3x + 4y = 11
2
a. 2x - y = 11
2 x + 5y = 11
c.
1
(2)
-x + 2y = 10
3x + 5y = 3
![Consider the following vectors:
[]
[o]
Which of the following statements are true? (select all correct answers)
Vector x lies in the plane spanned by v and w.
u
Vector w lies in the plane spanned by u and v.
Vector x lies in the plane spanned by u and v.
Vectors u, v and w span a plane.
Vector w is not a linear combination of u and v.
=
W
H
(³0
[o]](https://media.kunduz.com/media/sug-question/raw/80253069-1660230153.9368887.jpeg?w=256)
Calculus
Application of derivativesConsider the following vectors:
[]
[o]
Which of the following statements are true? (select all correct answers)
Vector x lies in the plane spanned by v and w.
u
Vector w lies in the plane spanned by u and v.
Vector x lies in the plane spanned by u and v.
Vectors u, v and w span a plane.
Vector w is not a linear combination of u and v.
=
W
H
(³0
[o]
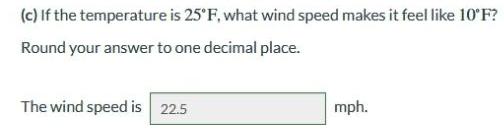
Calculus
Application of derivatives(c) If the temperature is 25°F, what wind speed makes it feel like 10°F?
Round your answer to one decimal place.
The wind speed is 22.5
mph.

Calculus
Application of derivativesSolve the heat conduction problem: δu/δt = k δ²u/δx² using NUMERICAL METHOD.
Subject to the boundary condition u(0,t) = 0, u(2,t) = 3t + 2 and initial condition u(x,0) = x²/2. Given that, △x = 0.25, △t = 0.1, k = 0.1 and t ranges from 0 to 1.
![Find the rate of change of f(x) = x² + 2x - 3 on the interval [1, a].](https://media.kunduz.com/media/sug-question/raw/78264751-1660230035.6702306.jpeg?w=256)
Calculus
Application of derivativesFind the rate of change of f(x) = x² + 2x - 3 on the interval [1, a].

Calculus
Application of derivativesThe rth term of a progression is R, the sth term is S, and the tth term is T.
(a) Show that, if the sequence is arithmetic, R(s - t) + S(t - r) +T(r - s) = 0.
(b) Show that, if the sequence is geometric, (s - t) log R+ (t-r) log S+ (r - s) log T = 0.
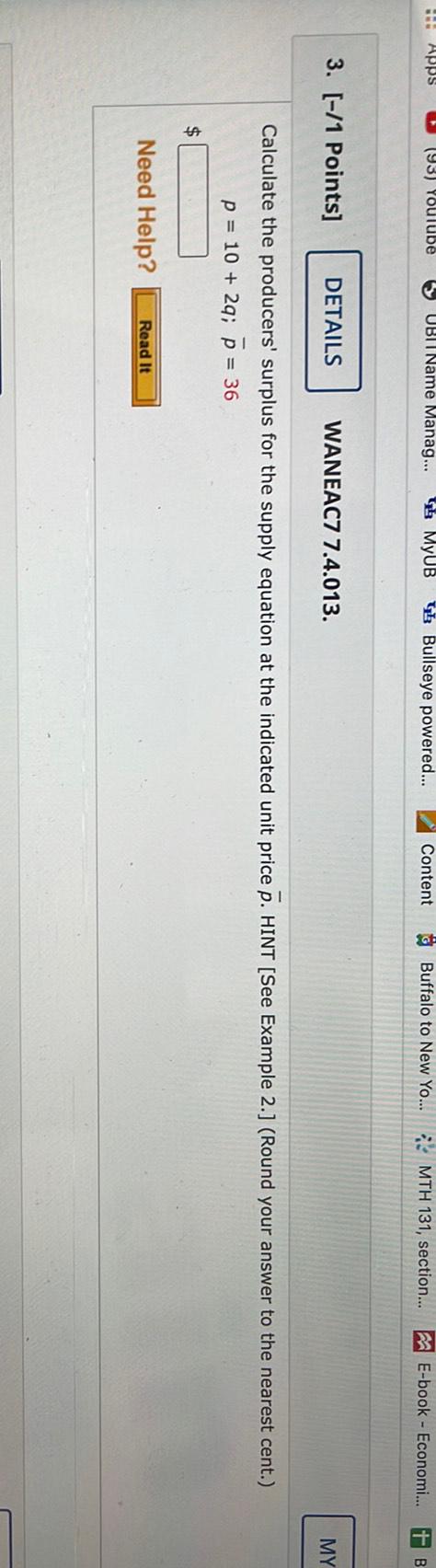
Calculus
Application of derivativesCalculate the producers' surplus for the supply equation at the indicated unit price p. (Round your answer to the nearest cent.)
p = 10 + 2q; D = 36
$ ________
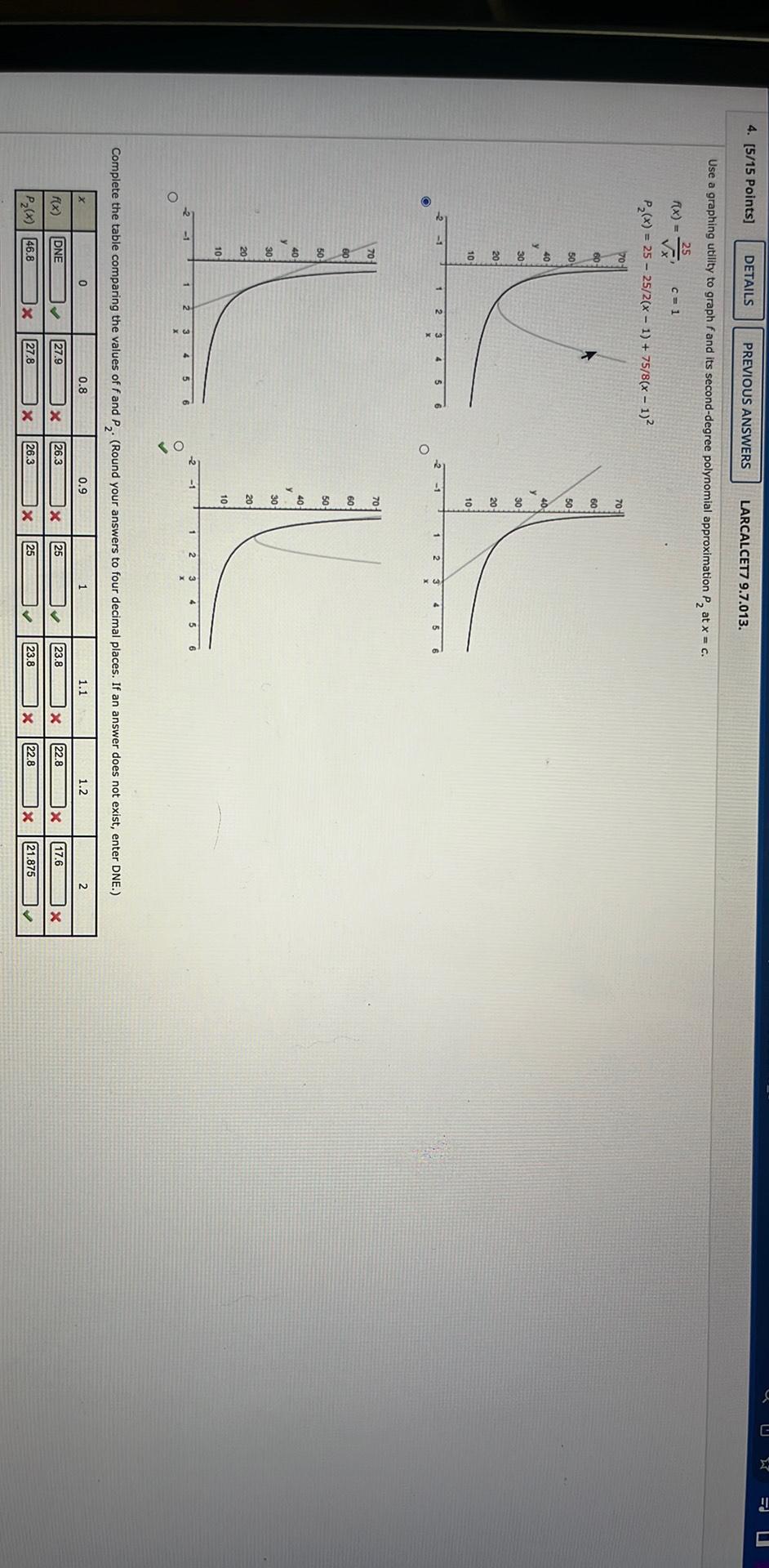
Calculus
Application of derivativesUse a graphing utility to graph fand its second-degree polynomial approximation P₂ at x = c.
f(x) = 25/√x, c = 1
P₂(x) = 25 - 25/2(x - 1) + 75/8(x - 1)²
Complete the table comparing the values of f and P2 (Round your answers to four decimal places. If an answer does not exist, enter DNE.)
x 0 0.8 0.9 1 1.1 1.2 2
f(x)
P₂(x)
Calculus
Application of derivativesIn your own words, define the following.
a. Rate of change
b. Average Rate of Change
How do you find the average rate of change?
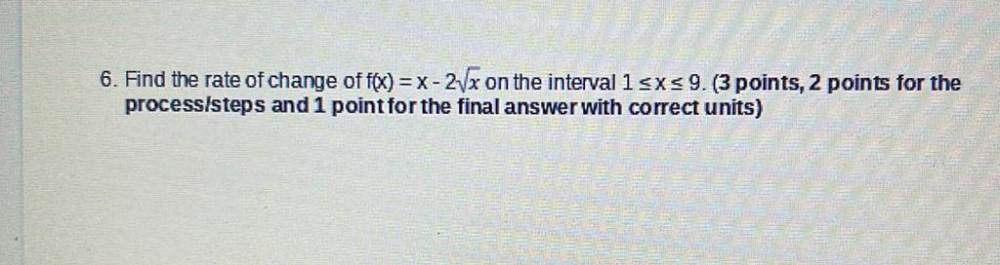
Calculus
Application of derivativesFind the rate of change of f(x) = x - 2√x on the interval 1 ≤ x ≤ 9.
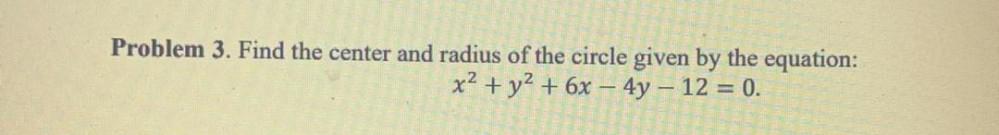
Calculus
Application of derivativesFind the center and radius of the circle given by the equation:
x^2 + y^2 + 6x – 4y - 12 = 0.
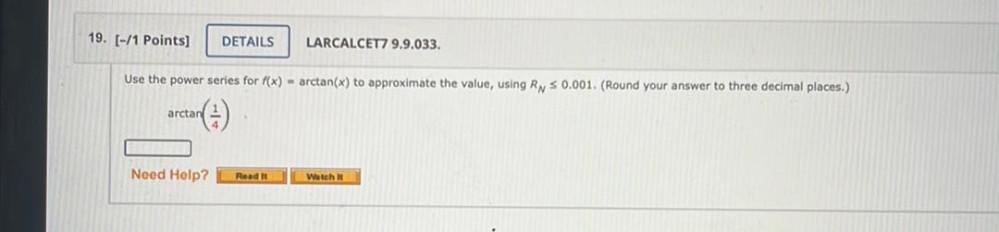
Calculus
Application of derivativesUse the power series for f(x) = arctan(x) to approximate the value, using RN ≤ 0.001. (Round your answer to three decimal places.) arctan(1/4).
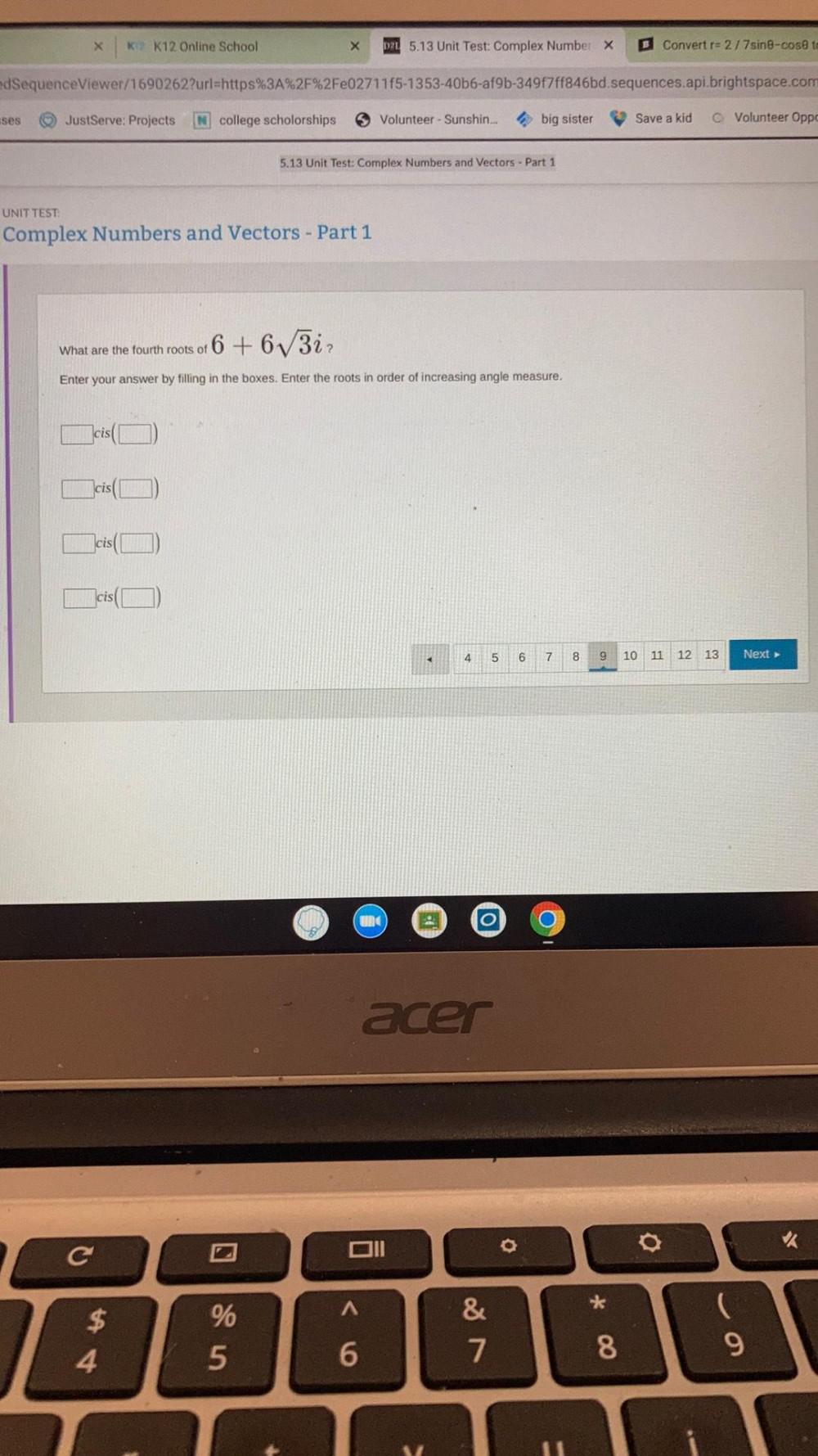
Calculus
Application of derivativesWhat are the fourth roots of 6 + 6√3i ?
Enter your answer by filling in the boxes. Enter the roots in order of increasing angle measure.
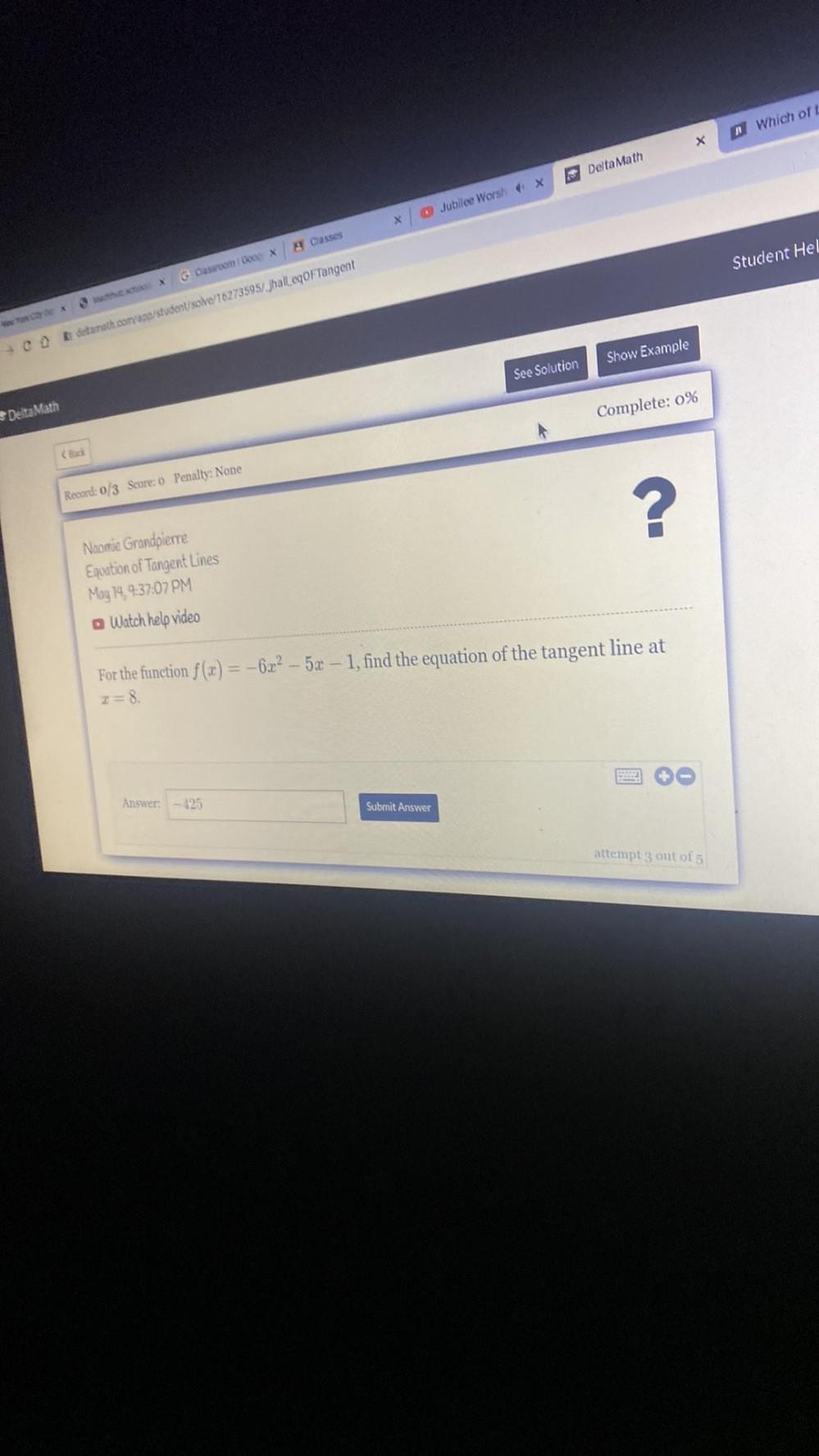
Calculus
Application of derivativesFor the function f(x) = -6x² - 5x - 1, find the equation of the tangent line at x=8.

Calculus
Application of derivativesCalculate the consumers' surplus at the indicated unit price p for the demand equation. (Round your answer to the nearest cent.)
q = 130 - 2p; p = 19
$ _________

Calculus
Application of derivativesUse a linear approximation (or differentials) to estimate the given number. (Round your answer to five decimal places.)
3√126
![Find the rate of change of f(x) = x^2 - on the interval 1 ≤ x ≤ 2.
Find the rate of change of f(x) = x^2 + 4x + 2 on the interval [0, a].](https://media.kunduz.com/media/sug-question/raw/78669257-1660229064.5028112.jpeg?w=256)
Calculus
Application of derivativesFind the rate of change of f(x) = x^2 - on the interval 1 ≤ x ≤ 2.
Find the rate of change of f(x) = x^2 + 4x + 2 on the interval [0, a].

Calculus
Application of derivativesA particle moves along a hyperbola xy 12. As it reaches the point (6,2), the y-coordinate is decreasing at a rate of 4 cm/s. How fast is the x-coordinate of the point changing at that instant?
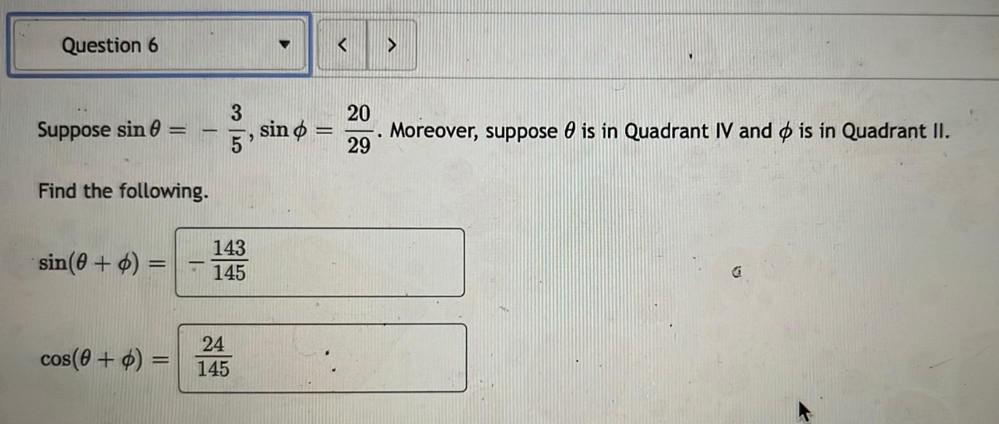
Calculus
Application of derivativesSuppose sinθ= 3/5, sinφ= 20/29. Moreover, suppose θ is quadrant IV and φ is in quadrant II.
Find the following.
sin( θ+ φ) =143/145
cos(θ+ φ)= 24/145

Calculus
Application of derivativesThe rate of water flow R(!) can be approximated by Q(t) = 1/79(768 + 23t - t²)
Use Q(t) to approximate the average rate of water flow during the 24-hour time period. Indicate units of measure.