Application of derivatives Questions and Answers
Calculus
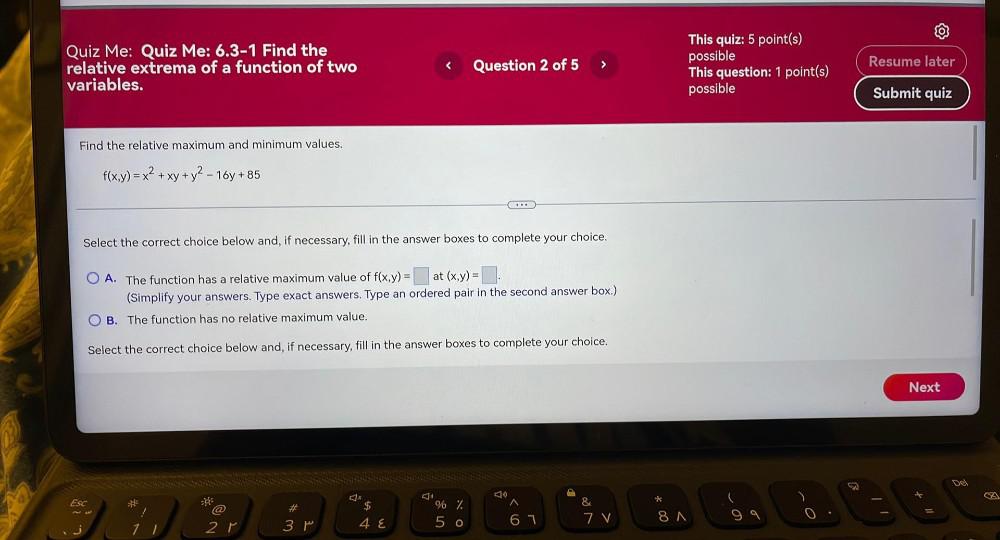
Application of derivativesFind the relative maximum and minimum values.
f(x , y) = x² + xy + y² - 16y + 85
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
(A)The function has a relative maximum value of f(x ,y) = __________ at (x ,y) = ____________
(B). The function has no relative maximum value.
Calculus
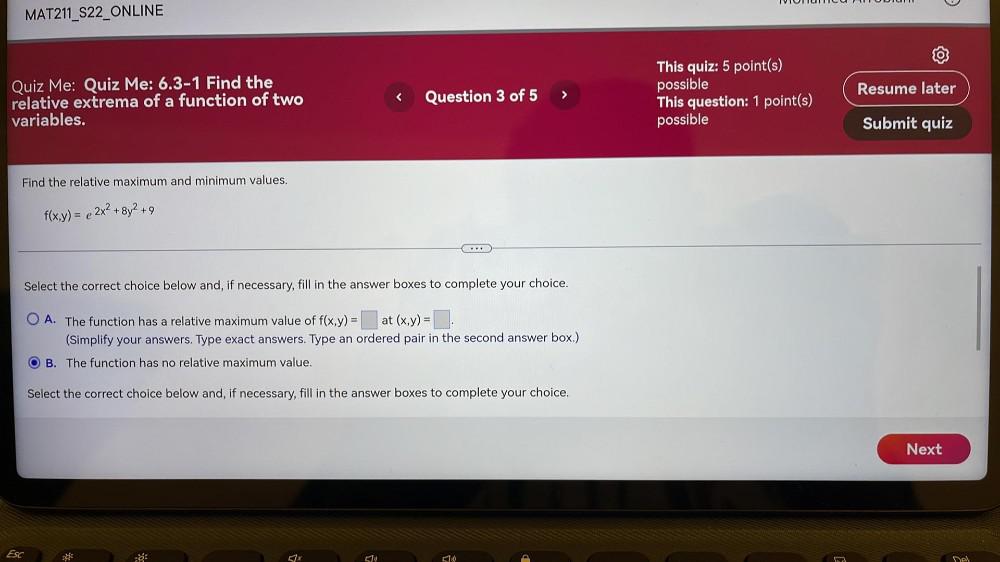
Application of derivativesIFind the relative maximum and minimum values.
f(x,y) = e²ˣ² + 8y² + 9
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y) = at (x,y) = .
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
Calculus
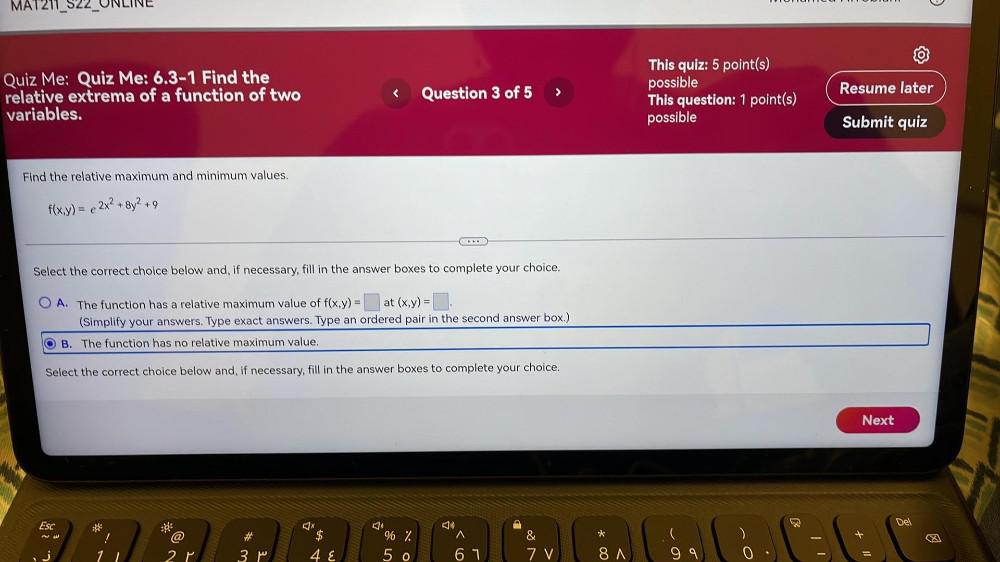
Application of derivativesFind the relative maximum and minimum values.
f(x, y) = e ^2x² + 8y²+ 9
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
(A). The function has a relative maximum value of f(x, y) = at (x ,y) =
(B). The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to
complete your choice.
![A 1000 L tank is draining such that the volume V of water remaining in the tank after t minutes is V = 1000[1 - t/60]² Find the rate at which the water is flowing out of the tank after 10 min.](https://media.kunduz.com/media/sug-question/raw/79243721-1660206447.58739.jpeg?w=256)
Calculus
Application of derivativesA 1000 L tank is draining such that the volume V of water remaining in the tank after t minutes is V = 1000[1 - t/60]² Find the rate at which the water is flowing out of the tank after 10 min.
Calculus
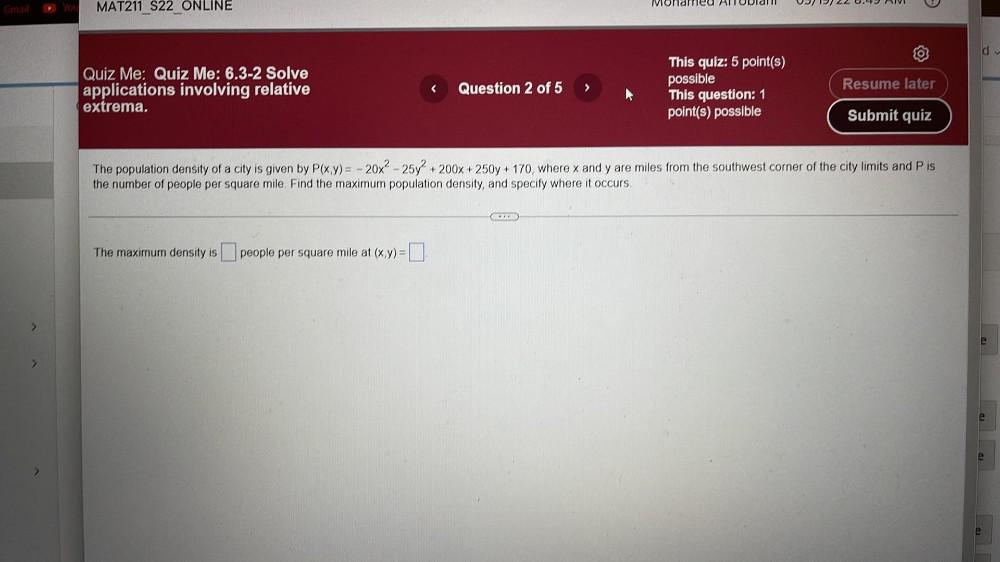
Application of derivativesThe population density of a city is given by P(x, y) = - 20x² - 25y² + 200x + 250y + 170, where x and y are miles from the southwest corner of the city limits and P is the number of people per square mile Find the maximum population density, and specify where it occurs.
The maximum density is___ people per square mile at (x ,y)=___
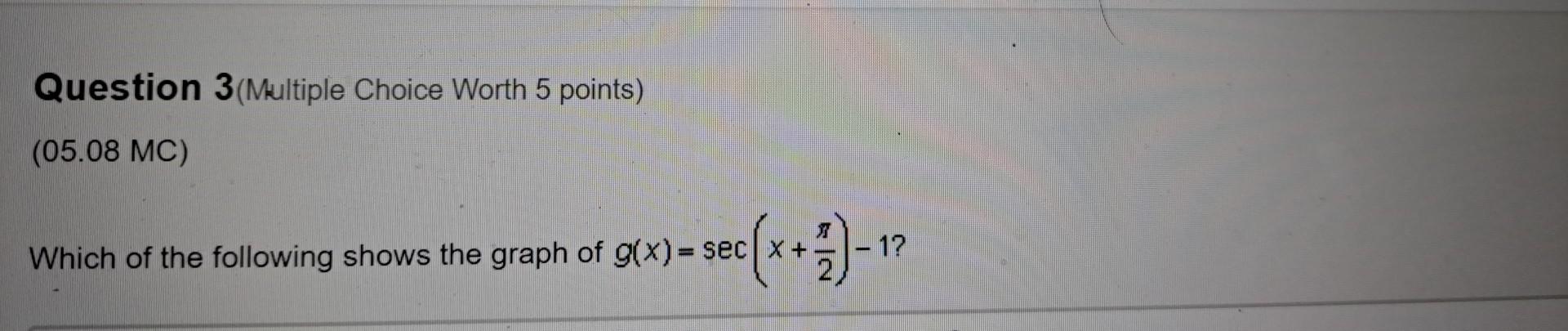
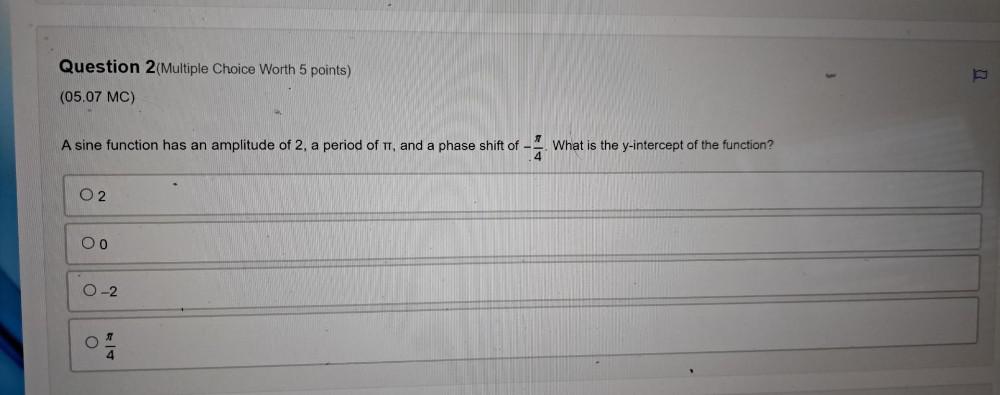
Calculus
Application of derivativesA sine function has an amplitude of 2, a period of π, and a phase shift of -π/4.
What is the y-intercept of the function?
(a)2
(b)0
(c)-2
(d)π/4

Calculus
Application of derivativesA closed rectangular box is to be made with a volume of 0.9 m³. In addition,
1. the box must have a square base;
2. the area of the base must not exceed 1.8 m²;
3. the height of the box must not exceed 0.75 m.
Determine the dimensions of the box that would generate:
a. a minimal surface area;
b. a maximal surface area.

Calculus
Application of derivativesIf cos α = sin β, which of the following could be true of α and β?
I. α + β = 90°
II. α and β lie in different quadrants
III. α = β
(A) I only
(B) II only
(C) III only
(D) I and III only
(E) I, II, and III

Calculus
Application of derivativesThe amount of daylight a particular location on Earth receives on a given day of the year can be modelled by a
sinusoidal function. The amount of daylight that Windsor, Ontario will experience in 2007 can be modelled by the
function D(t) = 12.18+ 3.1 sin(0.017t-1.376), where t is the number of days since the start of the year.
a. On January 1, how many hours of daylight does Windsor receive?
b. What would the slope of this curve represent?
c. The summer solstice is the day on which the maximum amount of daylight will occur. On what day of the year
would this occur?
d. Verify this fact using the derivative.
e. What is the maximum amount of daylight Windsor receives?
f. What is the least amount of daylight Windsor receives?
![Let g(x) = 7 sin x on [0, 2π].
Determine the value(s) of x, if any, for which g has a horizontal tangent line.
A. g has a horizontal tangent line at x = ______
B. g has no horizontal tangent lines.](https://media.kunduz.com/media/sug-question/raw/79379884-1660205976.7706738.jpeg?w=256)
Calculus
Application of derivativesLet g(x) = 7 sin x on [0, 2π].
Determine the value(s) of x, if any, for which g has a horizontal tangent line.
A. g has a horizontal tangent line at x = ______
B. g has no horizontal tangent lines.

Calculus
Application of derivativesQuestion 1
(domain & range: 1, intercepts - 2 marks, asymptotes - 1, intervals of
increase/decrease - 2, min/max - 2, points of inflection - 2, sketch 2)
y = x³ - 16x (Note: State ALL intercepts)
Question 2
(domain & range: 1, intercepts - 2 marks, asymptotes - 1, intervals of
increase/decrease - 2, min/max - 2, points of inflection - 2, sketch - 2)
y = (x^2 - 4)/(x^2 - 1)
(Note: State ALL intercepts, all horizontal & vertical asymptotes, )
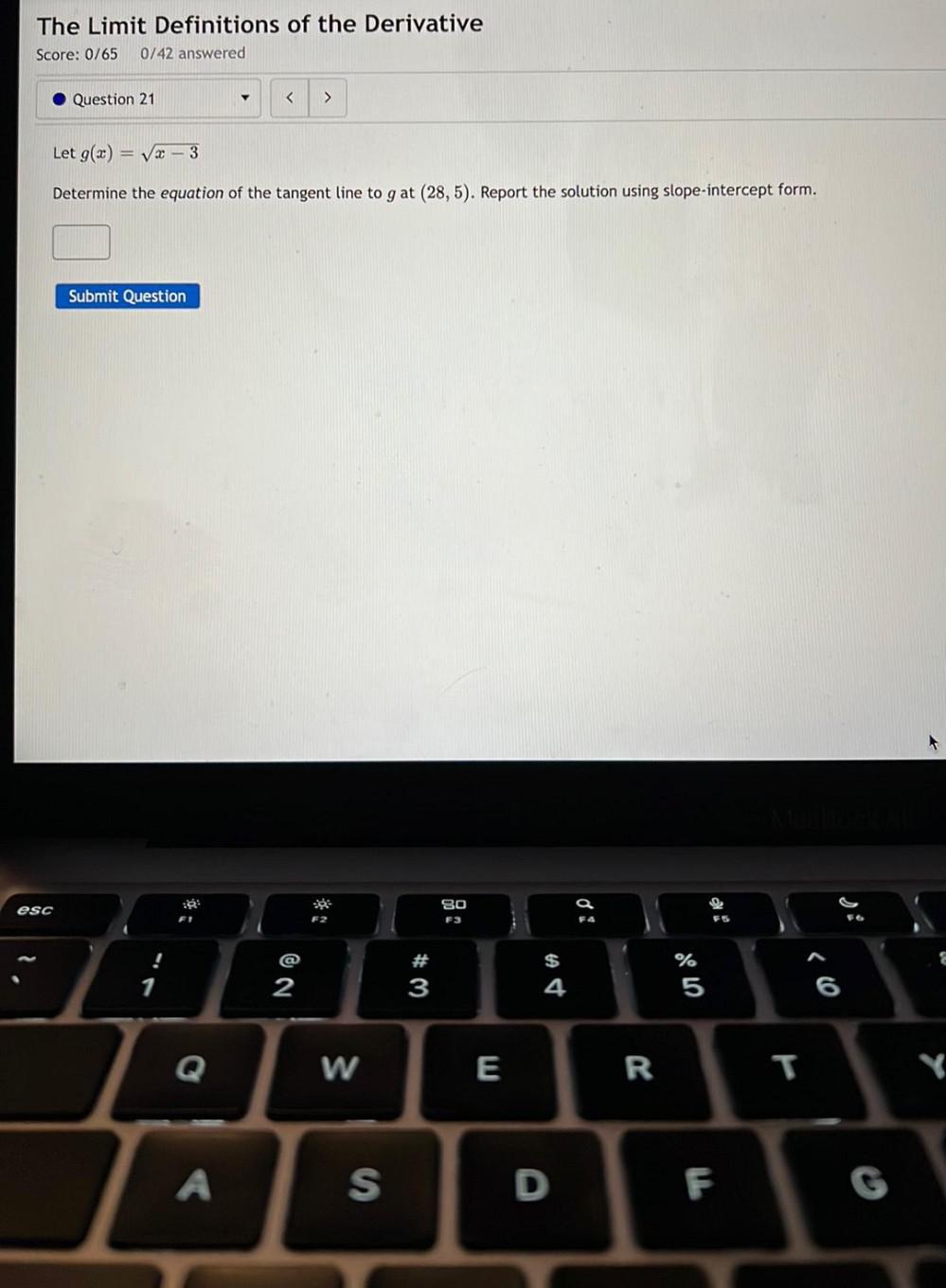
Calculus
Application of derivativesLet g(x)=(x-3)^(1/2)
Determine the equation of the tangent line to g at (28, 5). Report the solution using slope-intercept form_____
![Let d(t) = 30t² feet continue to be the distance function with respect to time (in seconds) of the car. We are going to compute the average velocity of d over the following smaller and smaller intervals: [3, 3+h]. where h = 1, 0.1, 0.01, and 0.001.
a. Write an expression for the average velocity from t = 3 to 3+h.
b. Use the simplified expression in part (a) to calculate the
AROC where h = 1, 0.1, 0.01 and 0.001.](https://media.kunduz.com/media/sug-question/raw/79295072-1660205720.4499648.jpeg?w=256)
Calculus
Application of derivativesLet d(t) = 30t² feet continue to be the distance function with respect to time (in seconds) of the car. We are going to compute the average velocity of d over the following smaller and smaller intervals: [3, 3+h]. where h = 1, 0.1, 0.01, and 0.001.
a. Write an expression for the average velocity from t = 3 to 3+h.
b. Use the simplified expression in part (a) to calculate the
AROC where h = 1, 0.1, 0.01 and 0.001.

Calculus
Application of derivativesProve it;
(secsec x-1)/ (secsec x+1) + (coscos x-1)/ (coscos x+1) = 23

Calculus
Application of derivativesThe formula t= 1/c in (A/A-N) is called the learning curve, since the formula relates time t passed, in weeks, to a measure N of learning achieved, to al earning style. A boy is learning to type. If he wants to type at a rate of 46 words per minute (N is 46) and his expected maximum rate is 69 words per minute (A is 69), find how many weeks it should . Assume that c is 0.07.
It takes approximately ________weeks for the boy to achieve his goal.

Calculus
Application of derivativesFind two linearly independent solutions of 2x²y" - x y' + (5x+1)y=0, x >0 of the form
y₁ = x^r1(1+ a₁ x + a₂ x² + a₃ x³ + ...).
y₂= x^r2(1+b₁x + b₂x² + b₃x³ + ...)
where r₁ > 2.
Enter
r₁ =
a₁ =
a₂ =
a₃=
r₂=
b₁ =
b₂ =
b₃=
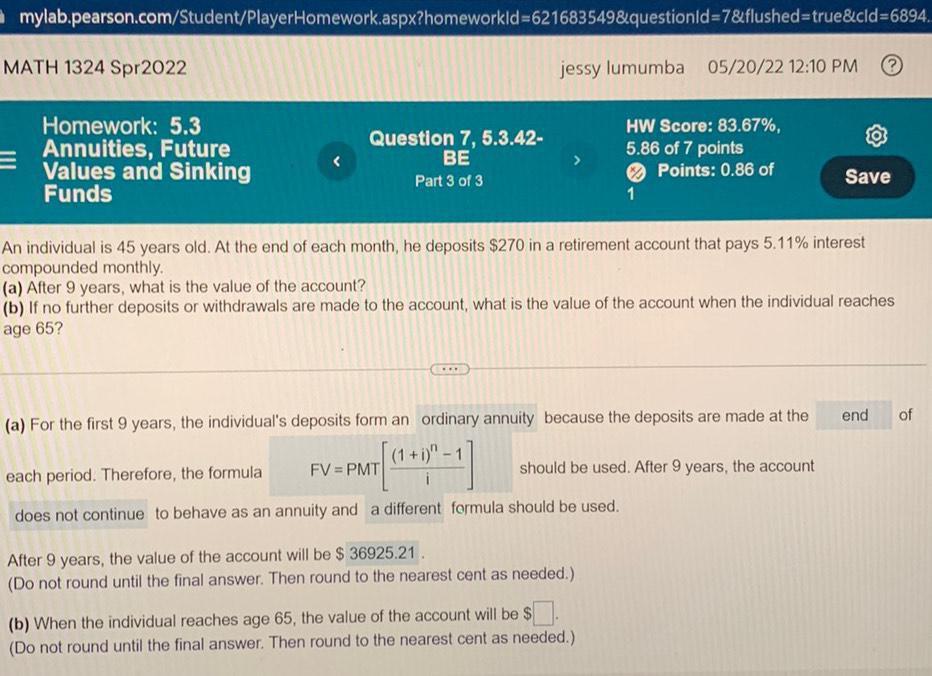
Calculus
Application of derivativesAn individual is 45 years old. At the end of each month, he deposits $270 in a retirement account that pays 5.11% interest
compounded monthly.
(a) After 9 years, what is the value of the account?
(b) If no further deposits or withdrawals are made to the account, what is the value of the account when the individual reaches
age 65?
(a) For the first 9 years, the individual's deposits form an ordinary annuity because the deposits are made at the
end
of
(1+i)" -
FV = PMT
20-11
should be used. After 9 years, the account
i
each period. Therefore, the formula
does not continue to behave as an annuity and a different formula should be used.
After 9 years, the value of the account will be $ 36925.21.
(Do not round until the final answer. Then round to the nearest cent as needed.)
(b) When the individual reaches age 65, the value of the account will be $.
(Do not round until the final answer. Then round to the nearest cent as needed.)
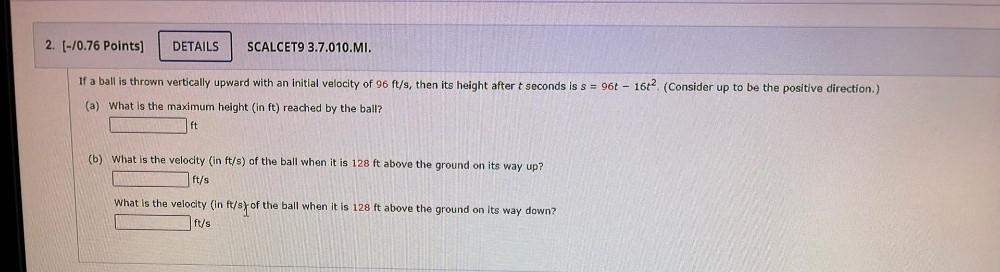
Calculus
Application of derivativesIf a ball is thrown vertically upward with an initial velocity of 96 ft/s, then its height after t seconds is s = 96t -16t²(consider up to the positive direction)
(a) What is the maximum height (in ft) reached by the ball?
(b) What is the velocity (in ft/s) of the ball when it is 128 ft above the ground on its way up?
What is the velocity (in ft/st of the ball when it is 128 ft above the ground on its way down?

Calculus
Application of derivativesa. For the plane with equation π : 2x - y + 5z = 0, determine
i. the coordinates of three points on this plane
ii. the equation of the line where this plane intersects the xy-plane

Calculus
Application of derivativesDetermine the equation of the tangent line to the curve f(x) = √(6x +4) at x = 2. Write your equation in standard form.

Calculus
Application of derivativesCharlotte invested $33,000 in an account paying an interest rate of 7(3/4)%
compounded continuously. Alyssa invested $33,000 in an account paying an interest rate of 7(1/4)% compounded daily. After 19 years, how much more money would Charlotte have in her account than Alyssa, to the nearest dollar?
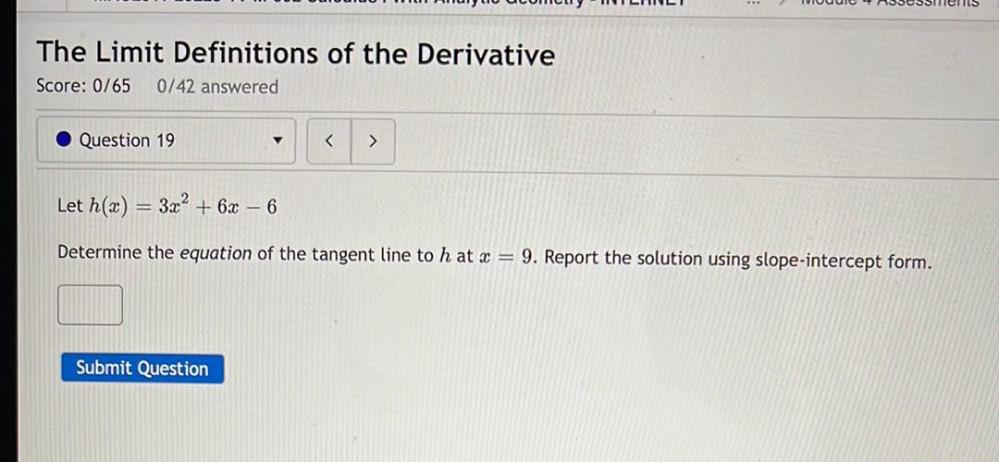
Calculus
Application of derivativesLet h(x) = 3x² + 6x - 6
Determine the equation of the tangent line to h at x = 9. Report the solution using slope-intercept form.
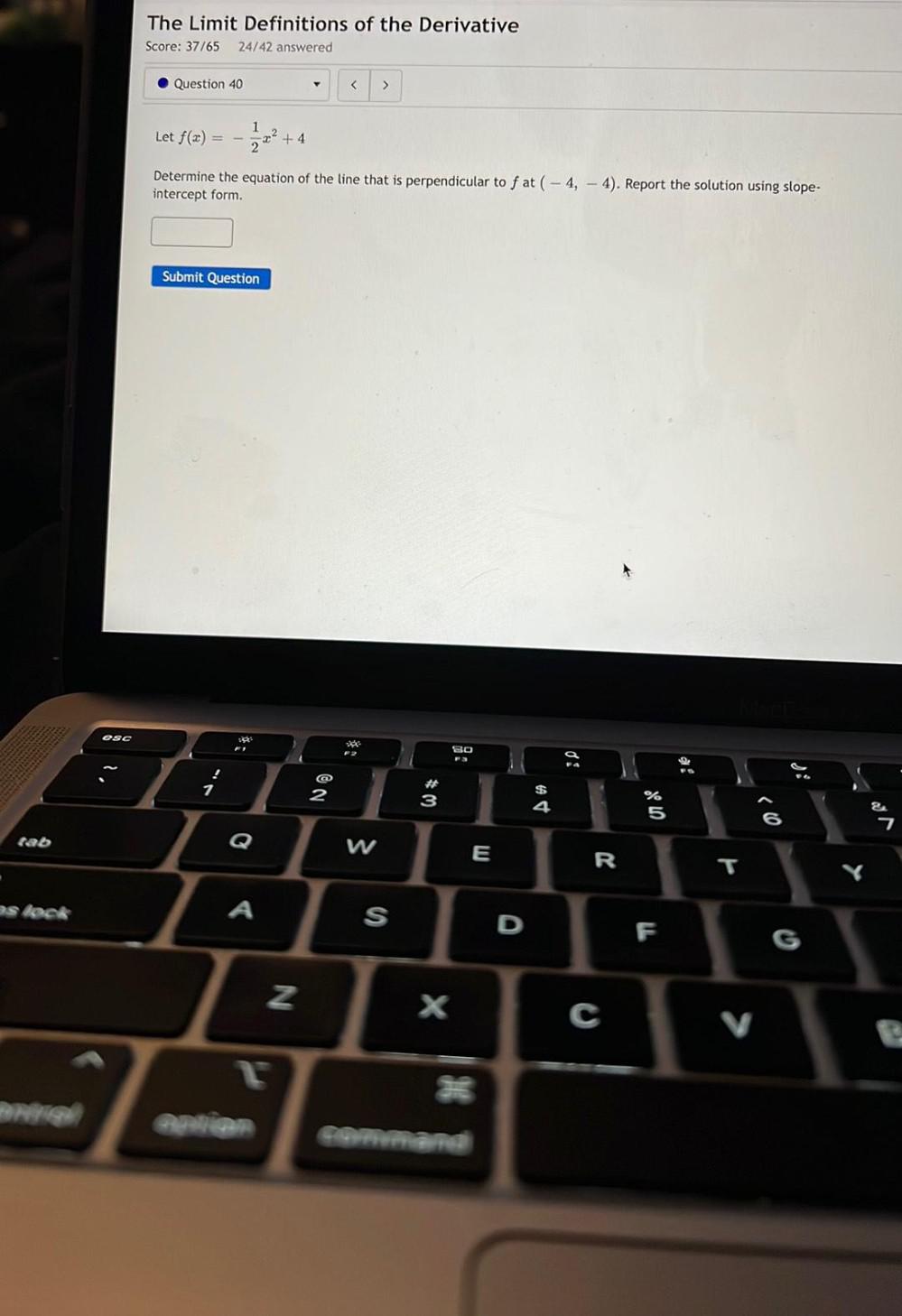
Calculus
Application of derivativesLet f(x) = -(1/2)x² + 4
Determine the equation of the line that is perpendicular to f at (-4, -4 ) .Report the solution using slope-intercept form .
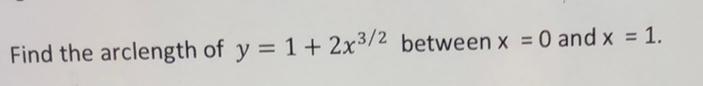

Calculus
Application of derivativesBella invested $7,400 in an account paying an interest rate of 5(3/8)% compounded continuously. Lily invested $7,400 in an account paying an interest rate of 5(3/4)% compounded quarterly. After 17 years, how much more money would Lily have in her account than Bella, to the nearest dollar?
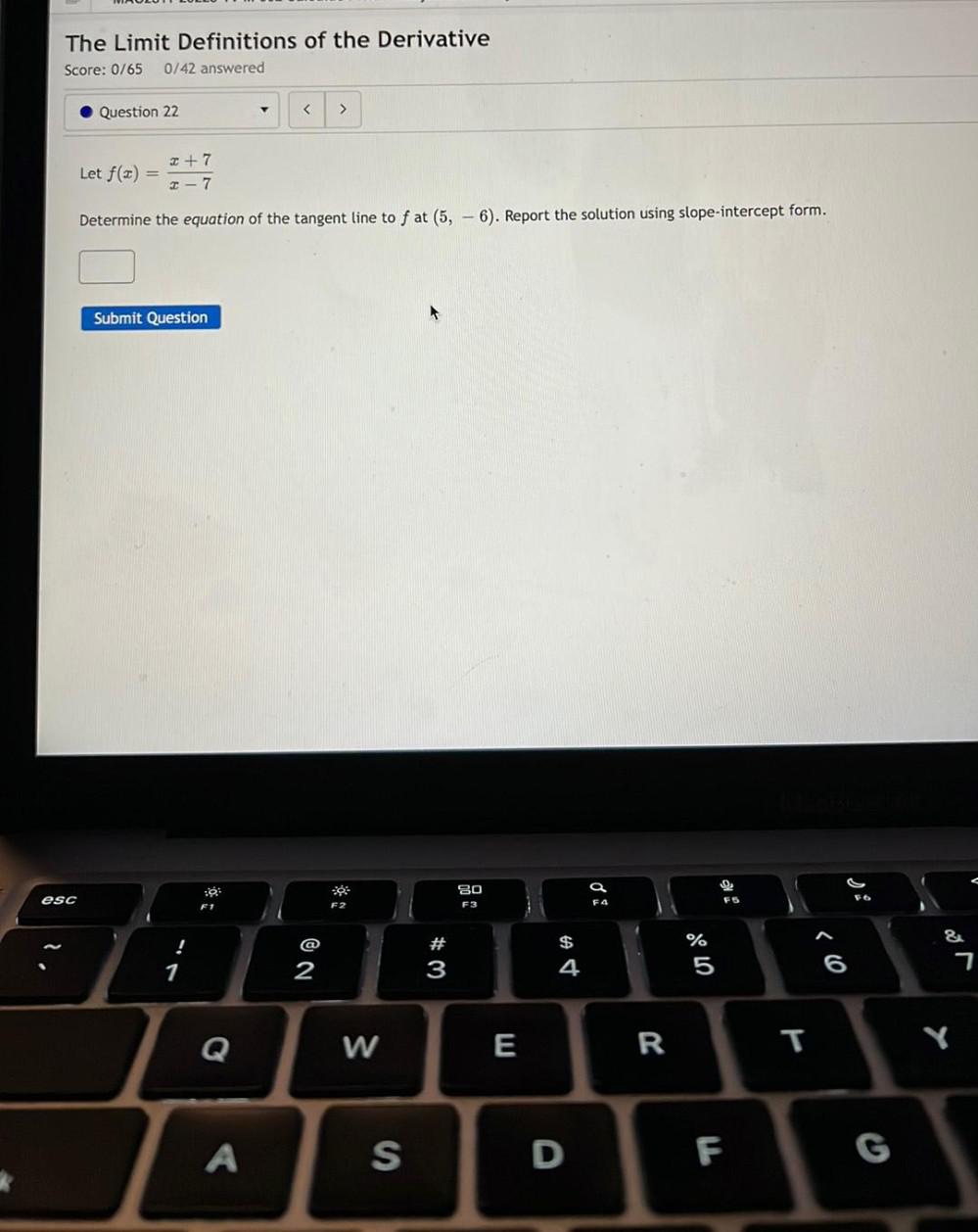
Calculus
Application of derivativesLet f(x) = (x+7) / (x-7)
Determine the equation of the tangent line to f at (5, 6). Report the solution using slope-intercept form.

Calculus
Application of derivativesNevaeh invested $80,000 in an account paying an interest rate of 5 1/8% compounded continuously. Aaliyah invested $80,000 in an account paying an interest rate of 5 3/8% compounded monthly. After 13 years, how much more money would Aaliyah have in her account than Nevaeh, to the nearest dollar?
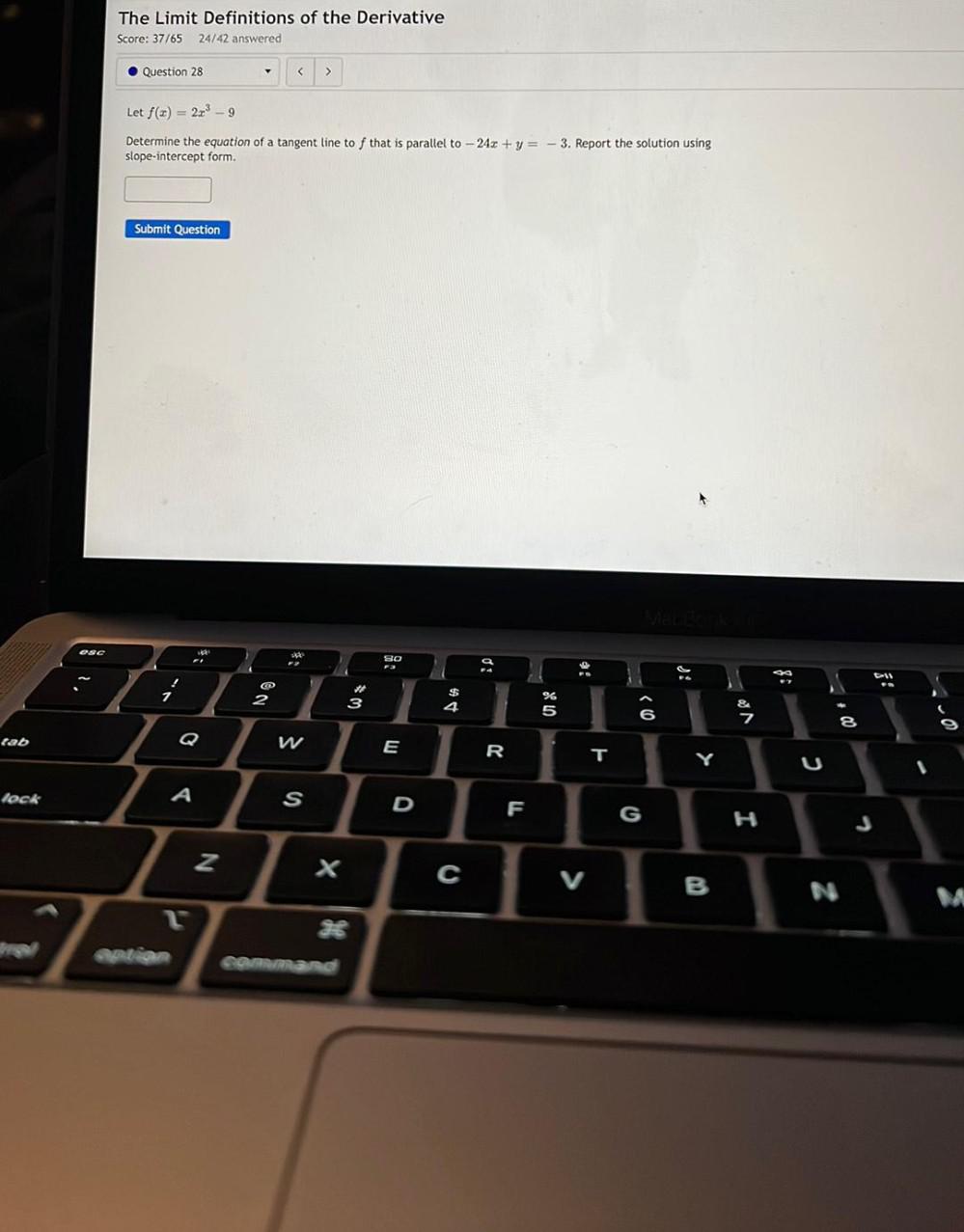
Calculus
Application of derivativesLet f(x) = 2x³-9
Determine the equation of a tangent line to f that is parallel to
-24x + y = -3 . Report the solution using slope - intercept form.
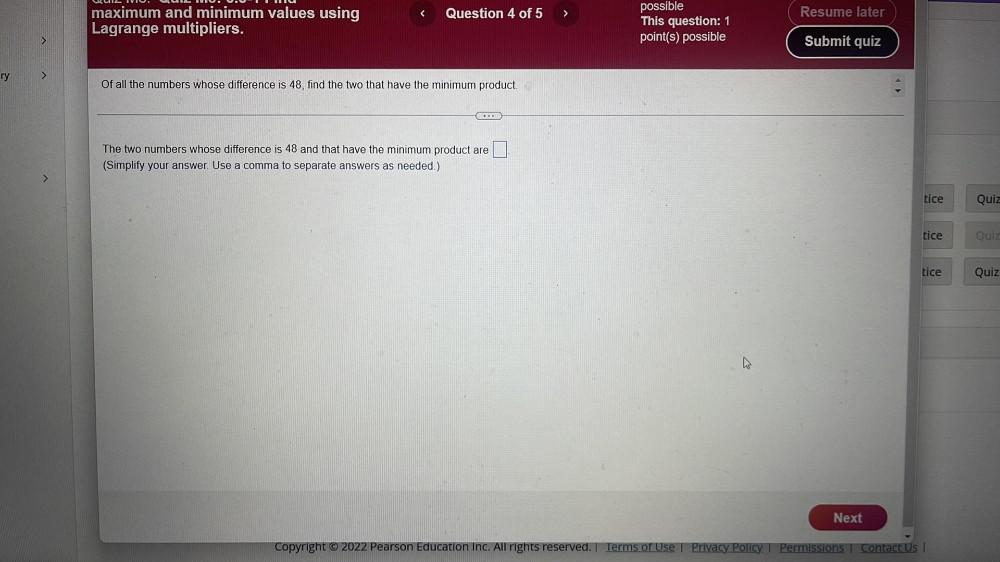
Calculus
Application of derivativesOf all the numbers whose difference is 48, find the two that have the minimum product.
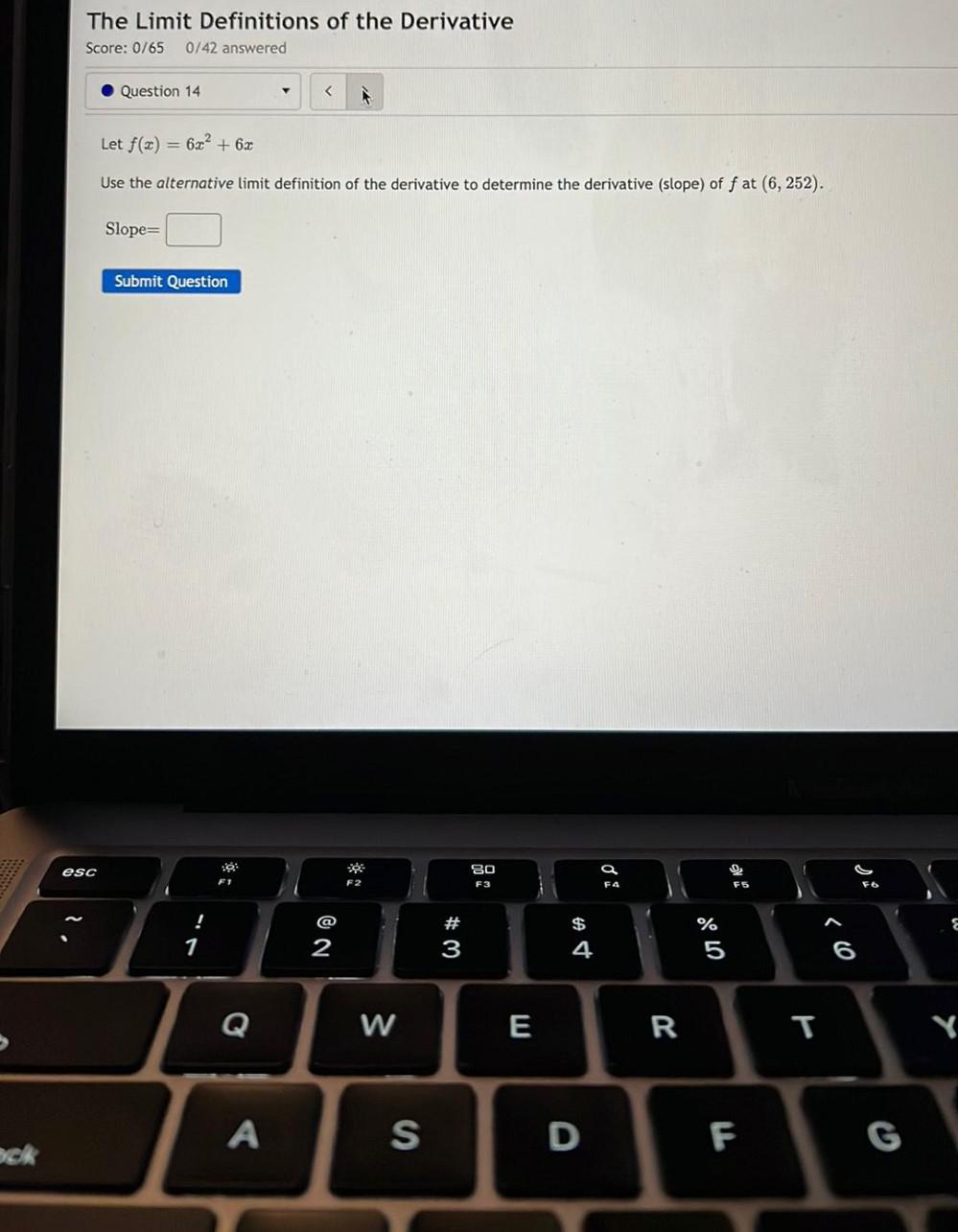
Calculus
Application of derivativesLet f(x) = 6x² + 6x
Use the alternative limit definition of the derivative to determine the derivative (slope) of f at (6, 252).
Slope=_________

Calculus
Application of derivativesThe number N of bacteria present in a culture at time t, in hours, obeys the law of exponential growth N(t) = 1000e⁰.⁰¹ᵗ
a) What is the number of bacteria at t = 0) hours?
b) When will the number of bacteria double? Give the exact solution in the simplest form. Do not evaluate.

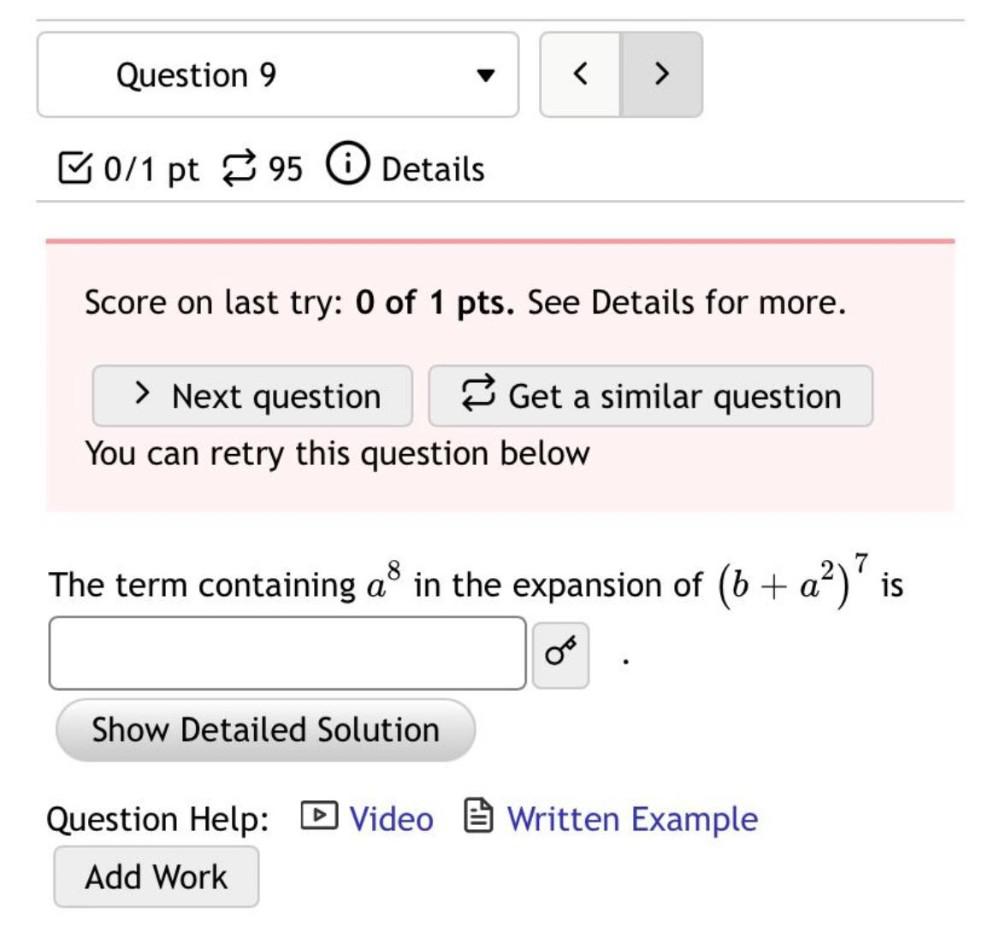
Calculus
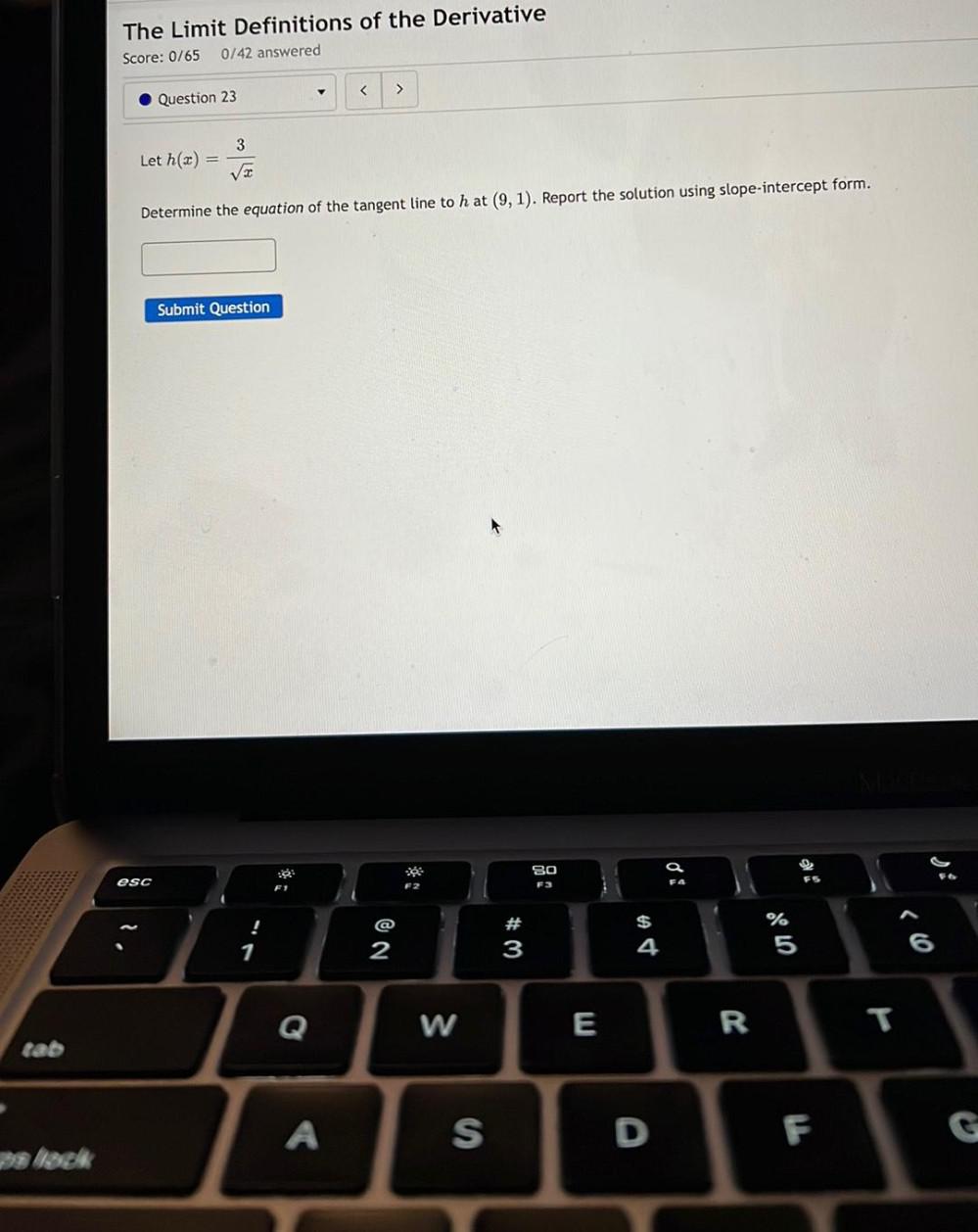
Application of derivativeslet h(x) = 3/√x
Determine the equation of the tangent line to h at (9, 1). Report the solution using slope-intercept form.
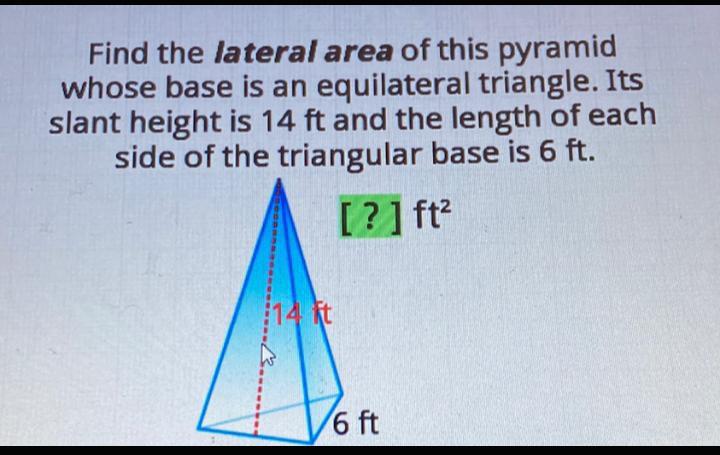
Calculus
Application of derivativesFind the lateral area of this pyramid whose base is an equilateral triangle. Its slant height is 14 ft and the length of each side of the triangular base is 6 ft.
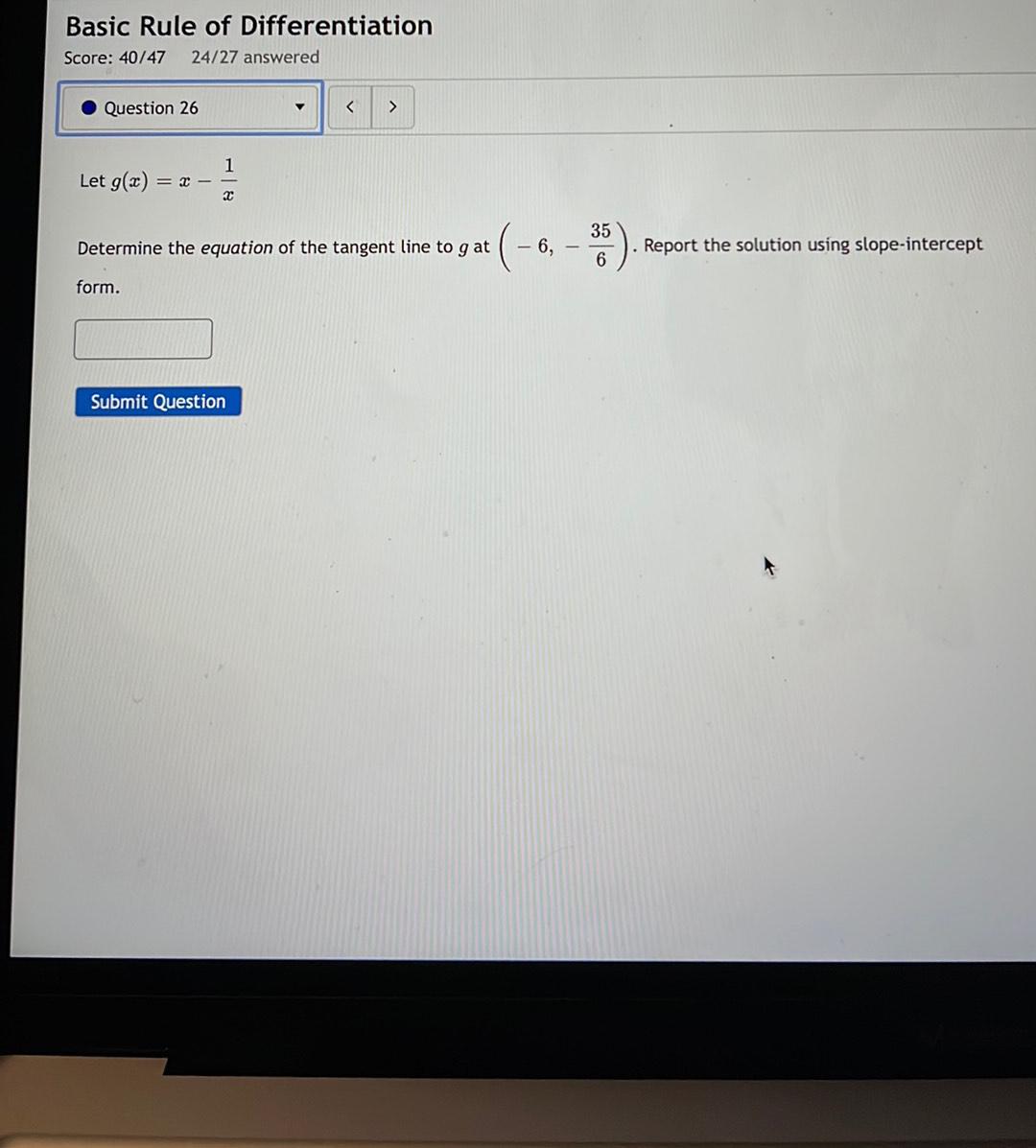
Calculus
Application of derivativesLet g(x)=x-(1/x).Determine the equation of the tangent line to g at (-6, - 35/6)
Report the solution using slope-intercept form.
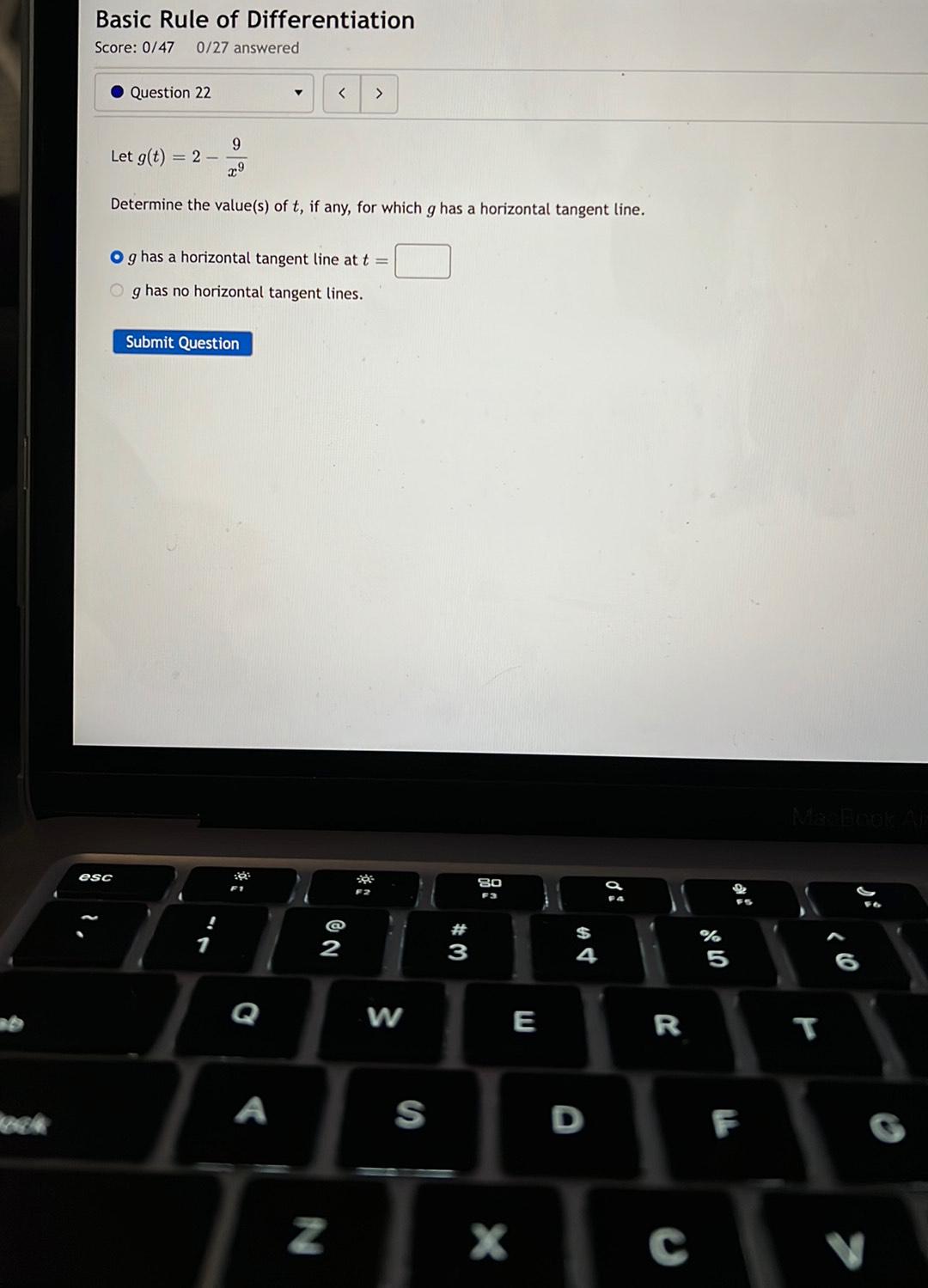
Calculus
Application of derivativeslet g(t)=2-9/x^9
Determine the value(s) of t, if any, for which g has a horizontal tangent line.
a)g has a horizontal tangent line at t =
b)g has no horizontal tangent lines.
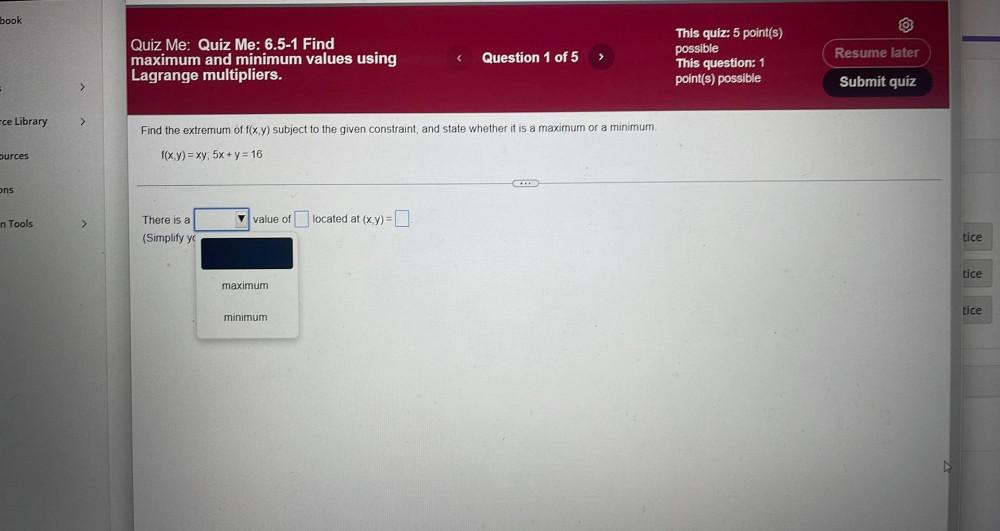
Calculus
Application of derivativesFind the extremum of f(x ,y) subject to the given constraint, and state whether it is a maximum or a minimum.
f(x, y)=x y; 5x+y=16
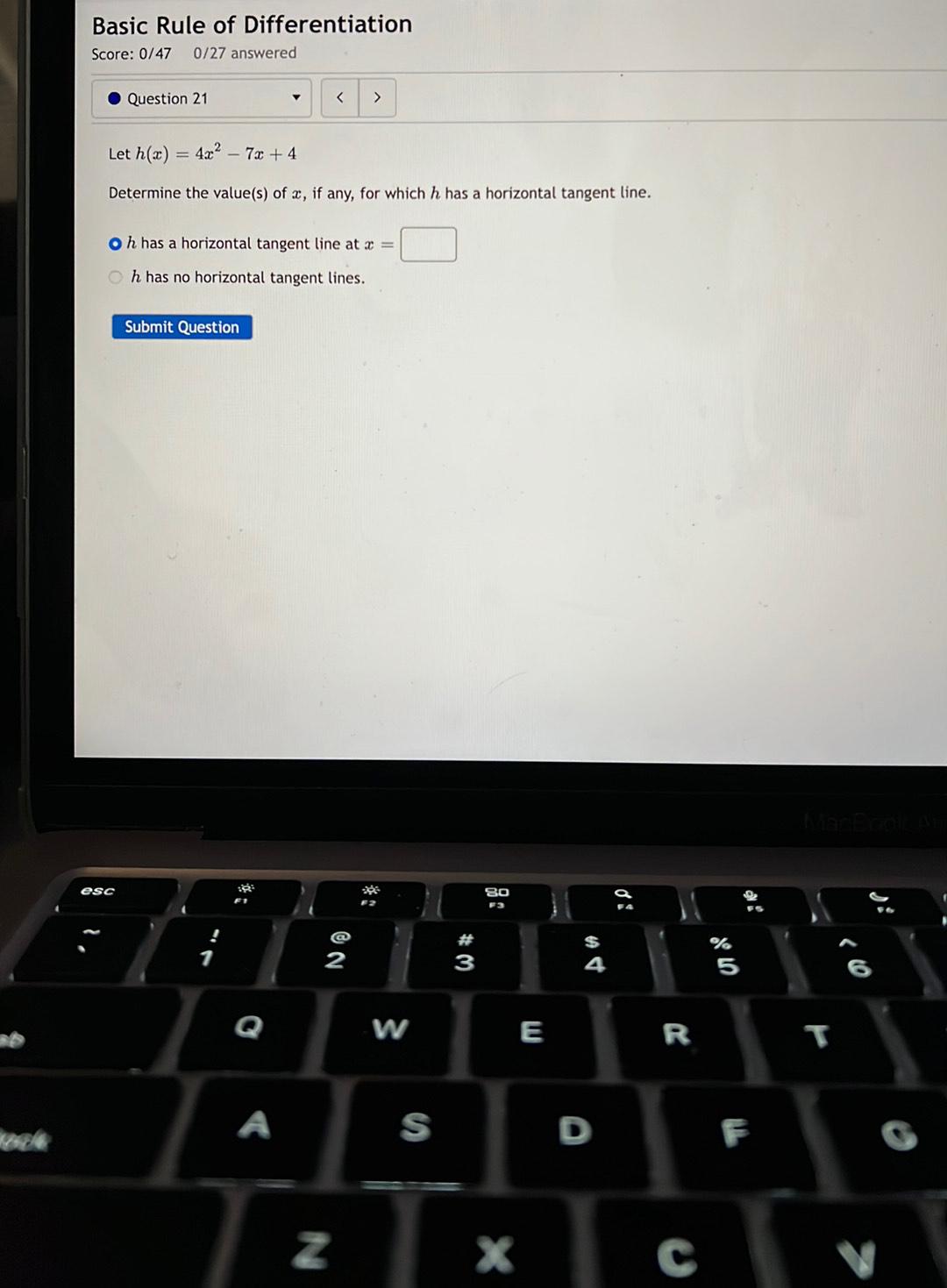
Calculus
Application of derivativesLet h(x) = 4x² - 7x +4
Determine the value(s) of x, if any, for which h has a horizontal tangent line.
a)h has a horizontal tangent line at x =
b)h has no horizontal tangent lines.

Calculus
Application of derivativesA disease spreads through a population. The number of cases t days after the start of the epidemic is shown below.
Days after start (t) 56 64
Number infected (N(t) thousand) 6 12
Assume the disease spreads at an exponential rate.
How many cases will there be on day 77?_______thousand (Round your answer to the nearest thousand)
On approximately what day will the number infected equal ninety thousand?________(Round your answer to the nearest whole number)
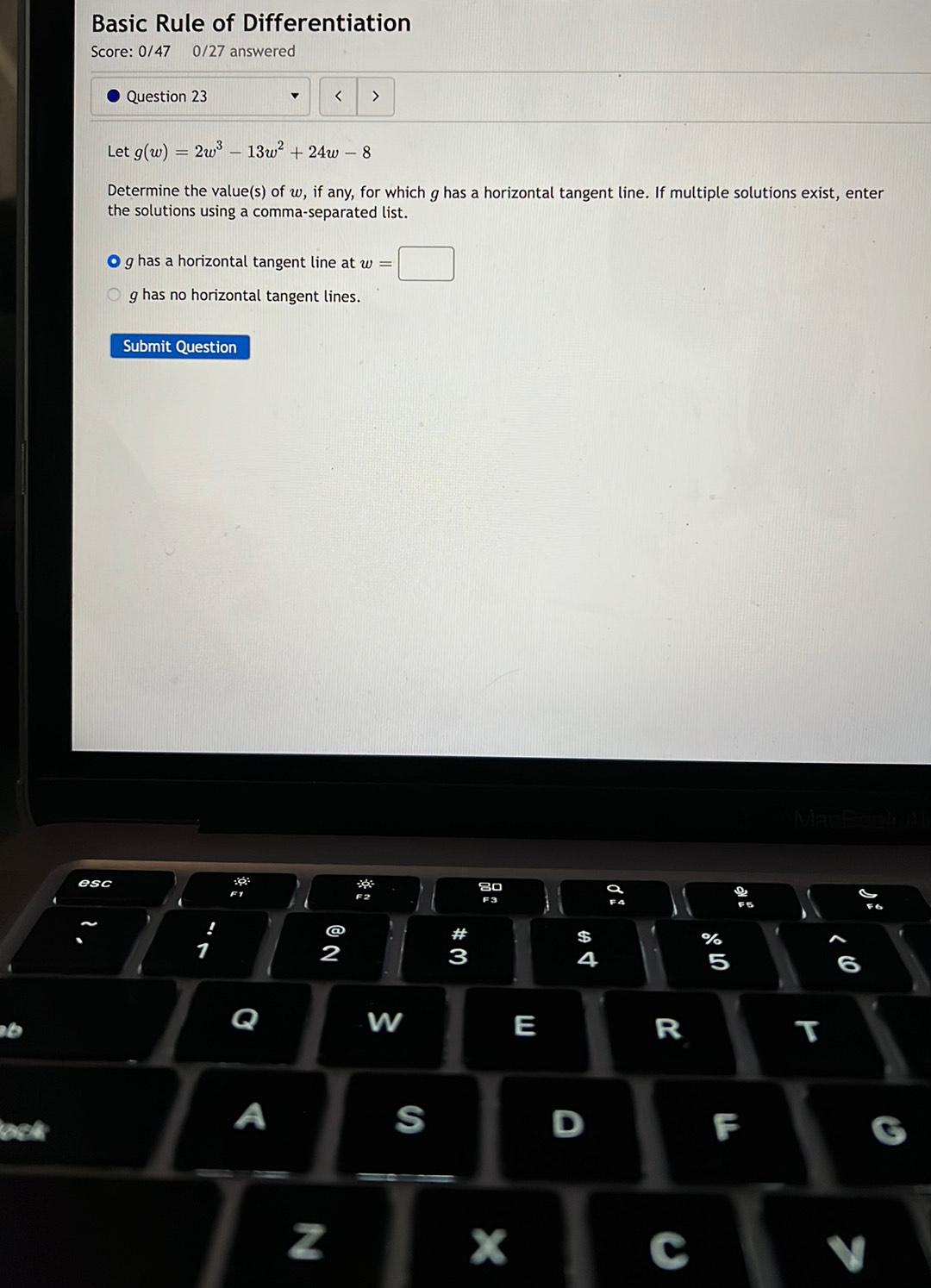
Calculus
Application of derivativesLet g(w) = 2w³ - 13w² + 24w - 8
Determine the value(s) of w, if any, for which g has a horizontal tangent line. If multiple solutions exist, enter the solutions using a comma-separated list.
(A) g has a horizontal tangent line at w = _______
(B) g has no horizontal tangent lines.
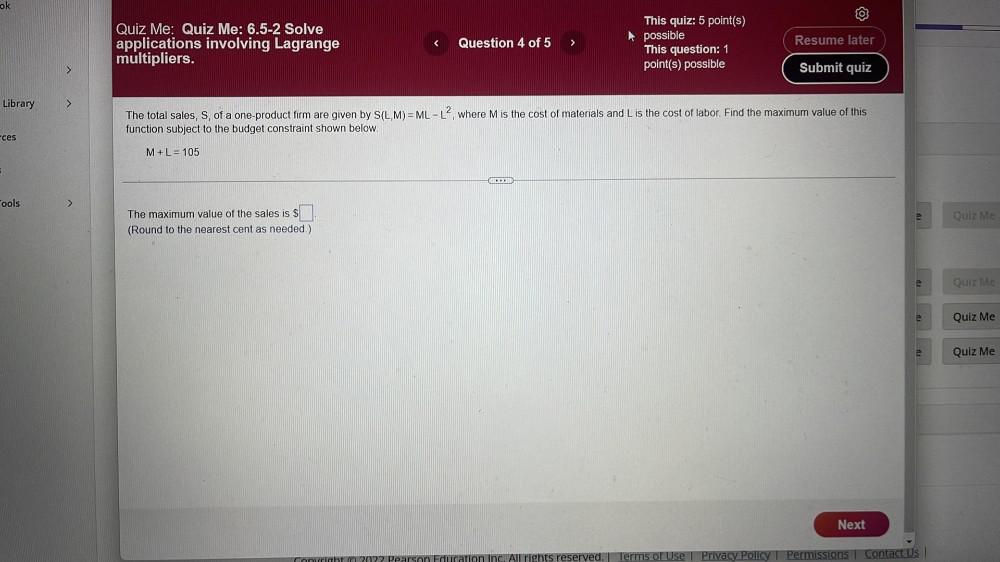
Calculus
Application of derivativesThe total sales, S, of a one-product firm are given by S(L,M) = ML - L², where M is the cost of materials and L is the cost of labor. Find the maximum value of this
function subject to the budget constraint shown below.
M + L = 105
The maximum value of the sales is $____.
(Round to the nearest cent as needed.)

Calculus
Application of derivativesIndicate local maxima and minima, inflections points and asymptotic behavior, and all of the calculus work necessary to find the information, of the following function, :
sketch the graph of f(x)= x/√(x²-9).
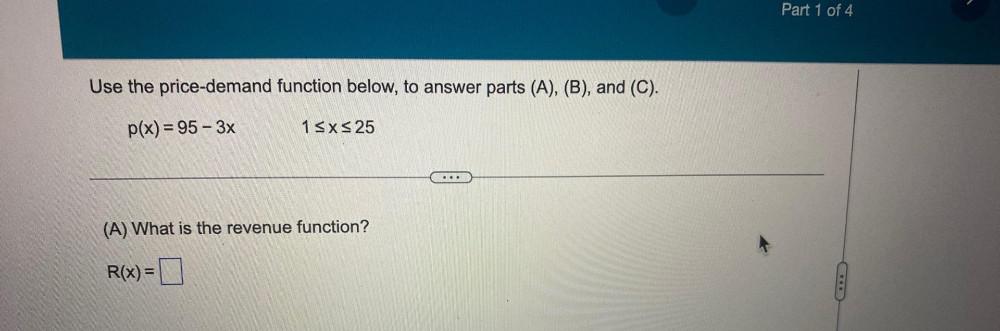
Calculus
Application of derivativesUse the price-demand function below, to answer parts (A), (B), and (C).
p(x)=95-3x 1 ≤x≤25
(A) What is the revenue function?
R(x) =__________
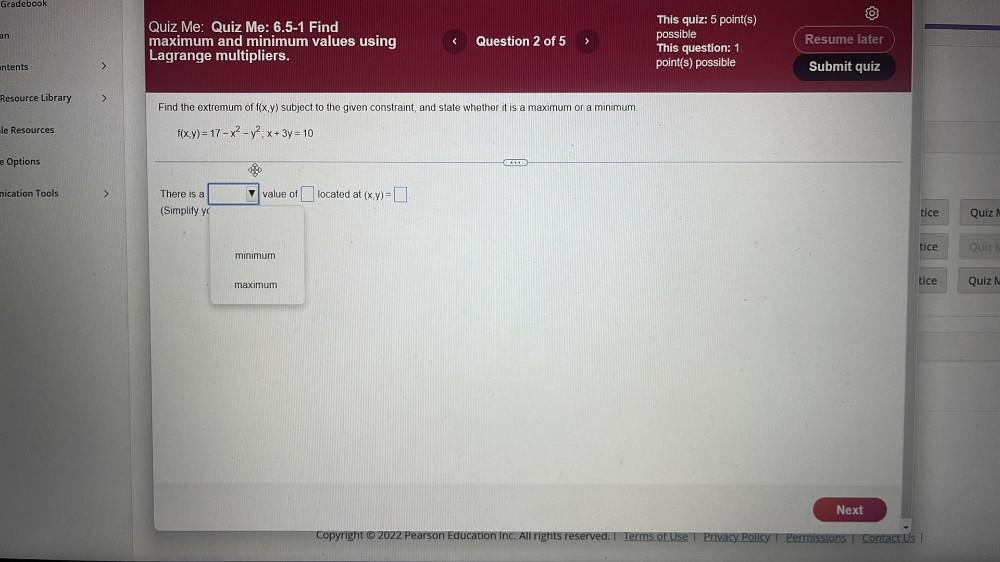
Calculus
Application of derivativesFind the extremum of f(x, y) subject to the given constraint, and state whether it is a maximum or a minimum. f(x, y) = 17-x² - y²; x + 3y = 10.There is ___value of_____ located at (x ,y)=________
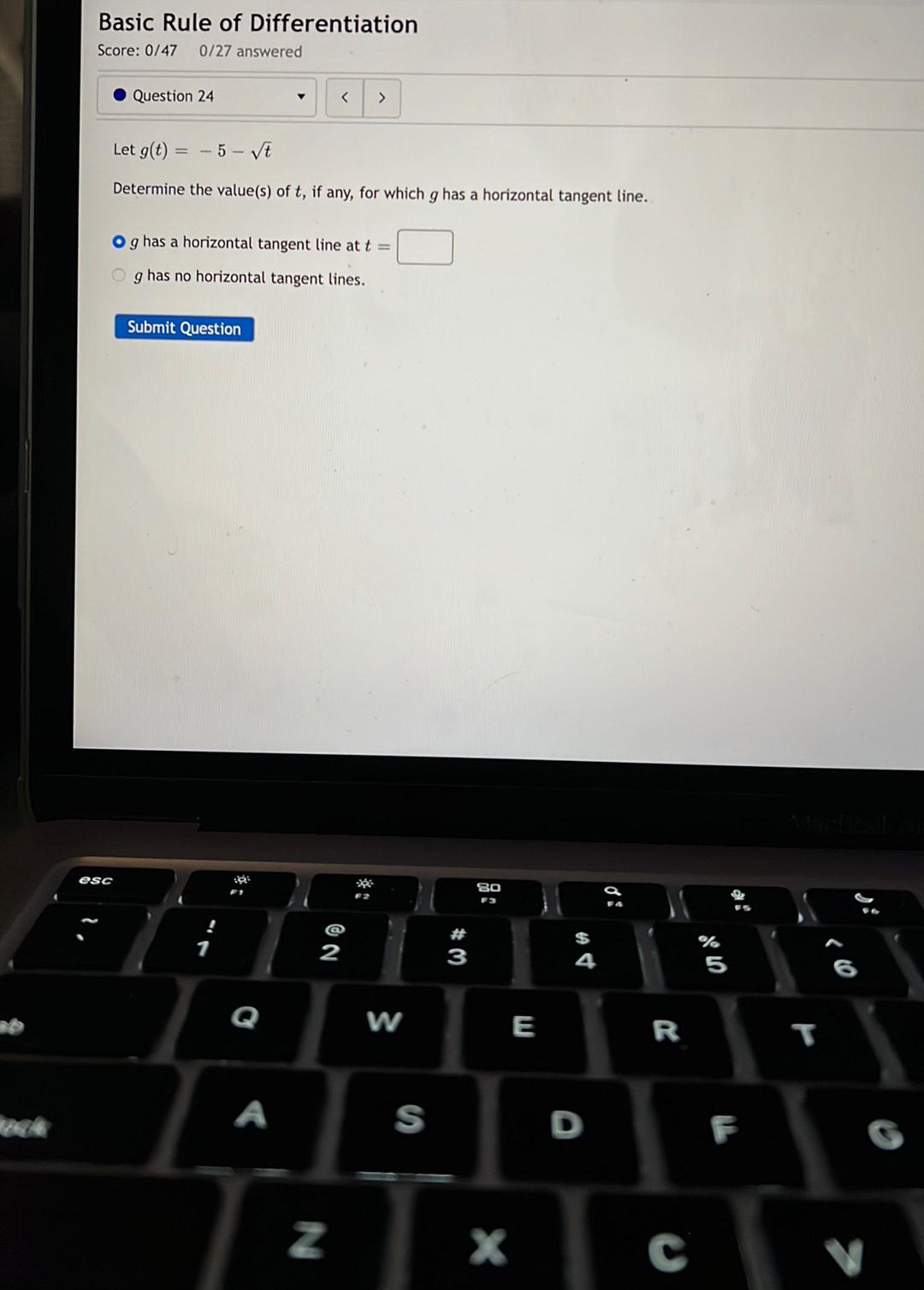
Calculus
Application of derivativesLet g(t) = -5-t^1/2
Determine the value(s) of t, if any, for which g has a horizontal tangent line..
a)g has a horizontal tangent line at t =
b)g has no horizontal tangent lines.
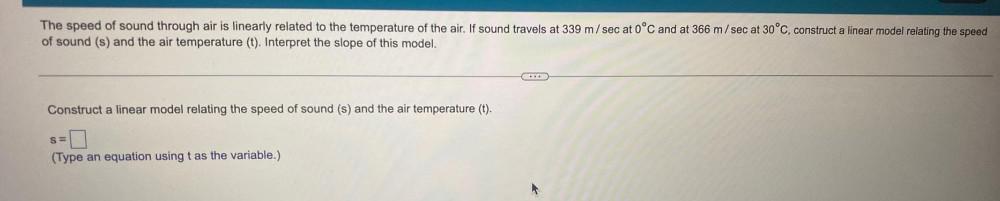
Calculus
Application of derivativesThe speed of sound through air is linearly related to the temperature of the air. If sound travels at 339 m/sec at 0°C and at 366 m/sec at 30°C, construct a linear model relating the speed of sound (s) and the air temperature (t). Interpret the slope of this model.
Construct a linear model relating the speed of sound (s) and the air temperature (t).
s=________________
(Type an equation using t as the variable.)

Calculus
Application of derivativesOn a May 22, 2022, Tauri visits Boston and sees a flock of birds. The angle of elevation to the flock of birds is 14°. If the flock of birds is directly above a point 16 meters away, what is the height of the flock of birds?
The height of the flock of birds is_______meters. (Round your answer to three decimal places)
The actual distance to the flock of birds is_______ meters. (Round your answer to three decimal places)
Part 2: Enter here (using math notation or by attaching in an image) an explanation of your answers.
Show or upload your work below.
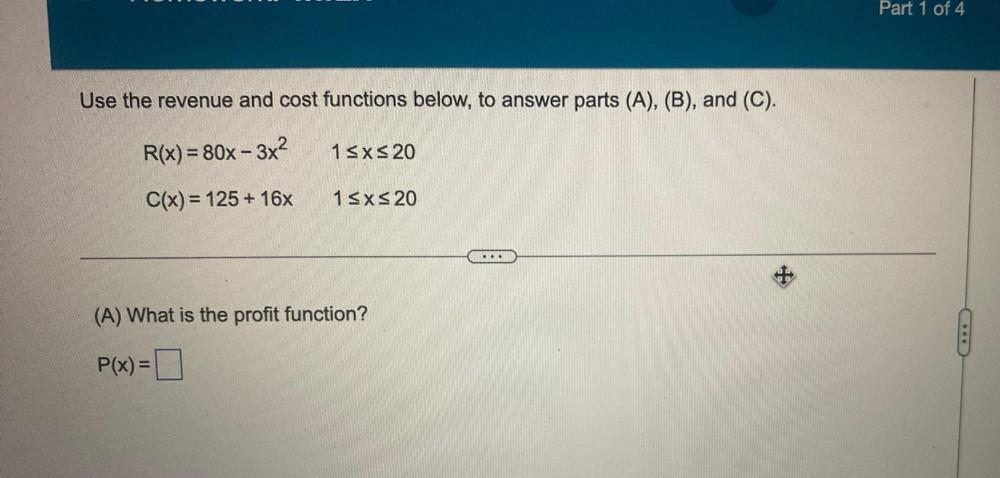
Calculus
Application of derivativesUse the revenue and cost functions below, to answer parts (A), (B), and (C).
R(x) = 80x - 3x² 1 ≤x≤20
C(x) = 125 + 16x 1≤x≤ 20
(A) What is the profit function?
P(x) =________