Application of derivatives Questions and Answers


Calculus
Application of derivativesA particle moves along the x-axis with acceleration given by a(t)=sin(t).
(a) ∫a(t) dt
(b) Find the velocity function for the particle if v(O)=3.
(c) Find the position function for the particle if x(0)=3.

Calculus
Application of derivativesIf c = -0.477, simplify the expression cos(cos-'(c)). If undefined, enter Ø. Provide your answer below:

Calculus
Application of derivativesA three-sided fence is to be built next to a straight section of the Aterno-Pescara river, which forms the fourth side of a rectangular region, as shown in the diagram. The enclosed area is to equal 1800 m² and the fence running parallel to the river must be set back at least 20 m from the river. Determine the minimum perimeter of such an enclosure and the dimensions of the corresponding enclosure.

Calculus
Application of derivativesWhat is the average value of f(x), between x = 1 and x = 5 for f(x) = 4ˣ + 1?

Calculus
Application of derivativesDetermine the equation of the tangent line to the curve, y =e^4x/x^3 at x = 1. Use exact values.

Calculus
Application of derivativesConsider the function f(x) = 1 – 3x², -5≤x≤ 2.
The absolute maximum value is and this occurs at I =
The absolute minimum value is and this occurs at I=

Calculus
Application of derivativesR is the region bounded by the functions f(x) = 9/(-1+x) and g(x) = x – 9. Find the area of the region bounded by the functions on the interval [8, 10).
Enter an exact answer.
Provide your answer below:
A = ____________units^2.

Calculus
Application of derivativesDetermine the intervals on which h is continuous. Enter the solution using interval notation.
h(x) = /11 - 2
h is continuous on _____

Calculus
Application of derivativesFor the function z= -4x³ - 2y² - xy, find ∂z/∂x , ∂z/∂y , ∂z(5,1)/∂x , and ∂z(5,1)/∂y
![If we apply Rolle's Theorem to the function f(x) = 2x² - 8x - 1 on the interval [0, 4], how many values of c exist such that f'(c) = 0?
____________
What is the value of c?
______________
If we try to apply Rolle's Thorem to the function f(«) = 2x^2 - 8x - 1 on the interval [ – 3,11], which
of the following conditions is not met?
a)continuty on [ - 3,11]
b)f(a)≠ f(b)
c)differentiability on [-3, 11]](https://media.kunduz.com/media/sug-question/raw/79081030-1660221190.6697245.jpeg?w=256)
Calculus
Application of derivativesIf we apply Rolle's Theorem to the function f(x) = 2x² - 8x - 1 on the interval [0, 4], how many values of c exist such that f'(c) = 0?
____________
What is the value of c?
______________
If we try to apply Rolle's Thorem to the function f(«) = 2x^2 - 8x - 1 on the interval [ – 3,11], which
of the following conditions is not met?
a)continuty on [ - 3,11]
b)f(a)≠ f(b)
c)differentiability on [-3, 11]

Calculus
Application of derivativesMohamed has a spherical balloon that has a diameter of 10 centimeters. Toby has a spherical balloon that holds 3 times as much air as Mohamed's balloon. What is the diameter of Toby's balloon?

Calculus
Application of derivativesThe function f(x)=7x + 5 is one-to-one.
a. Find an equation for f^-1, the inverse function
b. Verify that your equation is correct by showing that f(f^-1(x)) = x and f^-1(f'(x))= x

Calculus
Application of derivativesA ball is thrown directly upward. Its height (in feet) after t seconds is given by
y = 80t - 16t^2, for t ≥ 0.
19) ________What is the maximum height in feet attained by the ball?
A. 5
C. 7
B. 6
D. None of these
20) ______At what time in seconds does the maximum height occur?
A. 0.5
C. 2.5
B. 1.5
D. None of these

Calculus
Application of derivativesWrite the ratios for sin A and cos A.
A right angle triangle in which h = 26, p = 10 and b = 24.

Calculus
Application of derivativesThe slope of the line through the distinct points (x1, yı) and (x2. y2) can be interpreted as the rate of change in_______with respect to______.

Calculus
Application of derivativesOil spilling from a ruptured tanker spreads in a circle on the surface of the ocean. The radius of the spill increases at a rate of 9 m/min. How fast is the area of the spill increasing when the radius is 8 m?

Calculus
Application of derivativesA sports company has the following production function for a certain product, where p is the number of units produced with x units of labor and y units of capital.
Complete parts (a) through (d) below.
p(x,y) = 2200 4/5 y 1/5
(a) Find the number of units produced with 30 units of labor and 1424 units of capital.
(Round to the nearest whole number.)
(b) Find the marginal productivities.
![Consider the function defined by f(x) = Ax⁴ – 1Bx³ + 1Cx².
a) Determine the end behaviour and the intercepts? [K, 2]
b) Find the critical points and the points of inflection. [A, 3]
c) Determine the interval of increasing/decreasing and the concavity.
d) Sketch the graph. [K, 2]](https://media.kunduz.com/media/sug-question/raw/79048760-1660220321.2102458.jpeg?w=256)
Calculus
Application of derivativesConsider the function defined by f(x) = Ax⁴ – 1Bx³ + 1Cx².
a) Determine the end behaviour and the intercepts? [K, 2]
b) Find the critical points and the points of inflection. [A, 3]
c) Determine the interval of increasing/decreasing and the concavity.
d) Sketch the graph. [K, 2]

Calculus
Application of derivativesConsider the function f(x) = x^(2)e^(5x)For this function there are three important open intervals: ( - ∞, A), (A, B), and (B,∞) where A and
B are the critical numbers.
Find A______________ and B_____________
For each of the following intervals, tell whether f(x) is increasing or decreasing.
(- ∞,A): ___________
(A, B): ____________
(B,∞):____________

Calculus
Application of derivativesConsider the function f(x) = x²e^(20x)
f(x) has two inflection points at x = C and x = D with C<D
where C is ______________
and D is _______________
Finally for each of the following intervals, tell whether f(x) is concave up or concave down.
a) (-∞, C):___________
b) (C, D): ___________
c) (D, ∞):___________
![Find all solutions of the equation 2 sin x + √3 = 0.The answer is A + B kπ and C + D k π where k is any integer, 0 < A< C < 2π.
A=[?],B=[?],C=[?],D=[?]](https://media.kunduz.com/media/sug-question/raw/79082192-1660219921.6907978.jpeg?w=256)
Calculus
Application of derivativesFind all solutions of the equation 2 sin x + √3 = 0.The answer is A + B kπ and C + D k π where k is any integer, 0 < A< C < 2π.
A=[?],B=[?],C=[?],D=[?]

Calculus
Application of derivativesGiven △ABC with ∠B= 78°,m∠C = 52°, and a = 16 inches, what is the length of b?
O 31.343 inches
O 16.459 inches
O 19.861 inches
O 20.430 inches

Calculus
Application of derivativesDetermine the value(s) of x where the slope of the tangent line is horizontal. Use exact values.
f(x) = 2x√(3x - 4x²)

Calculus
Application of derivativesConsider the function f(x) = 2x^3 + 6x^2 - 144x + 7,-6≤x≤5.
This function has an absolute minimum value equal to _______
and an absolute maximum value equal to ___________
![Given function g(x)= 8x^3 - 108x^2 + 480x, find the first derivative, g'(x)____________
Notice that g'(x) = 0 when x = 4, that is, g'(4) = 0.
Now, we want to know whether there is a local minimum or local maximum at = 4, so we will use the second derivative test.
Find the second derivative, g''(x).
g''(x)_______________
Evaluate g''(4)
g''(4)=_________________
Based on the sign of this number, does this mean the graph of g(x) is concave up or concave down at= 4?
[Answer either up or down -- watch your spelling!!]
At x= 4 the graph of g(x) is concave_____________
Based on the concavity of g(x) at x = 4, does this mean that there is a local minimum or local maximum at x= 4?
[Answer either minimum or maximum -- watch your spelling!!)
At = 4 there is a local____________](https://media.kunduz.com/media/sug-question/raw/79080931-1660219789.6159475.jpeg?w=256)
Calculus
Application of derivativesGiven function g(x)= 8x^3 - 108x^2 + 480x, find the first derivative, g'(x)____________
Notice that g'(x) = 0 when x = 4, that is, g'(4) = 0.
Now, we want to know whether there is a local minimum or local maximum at = 4, so we will use the second derivative test.
Find the second derivative, g''(x).
g''(x)_______________
Evaluate g''(4)
g''(4)=_________________
Based on the sign of this number, does this mean the graph of g(x) is concave up or concave down at= 4?
[Answer either up or down -- watch your spelling!!]
At x= 4 the graph of g(x) is concave_____________
Based on the concavity of g(x) at x = 4, does this mean that there is a local minimum or local maximum at x= 4?
[Answer either minimum or maximum -- watch your spelling!!)
At = 4 there is a local____________
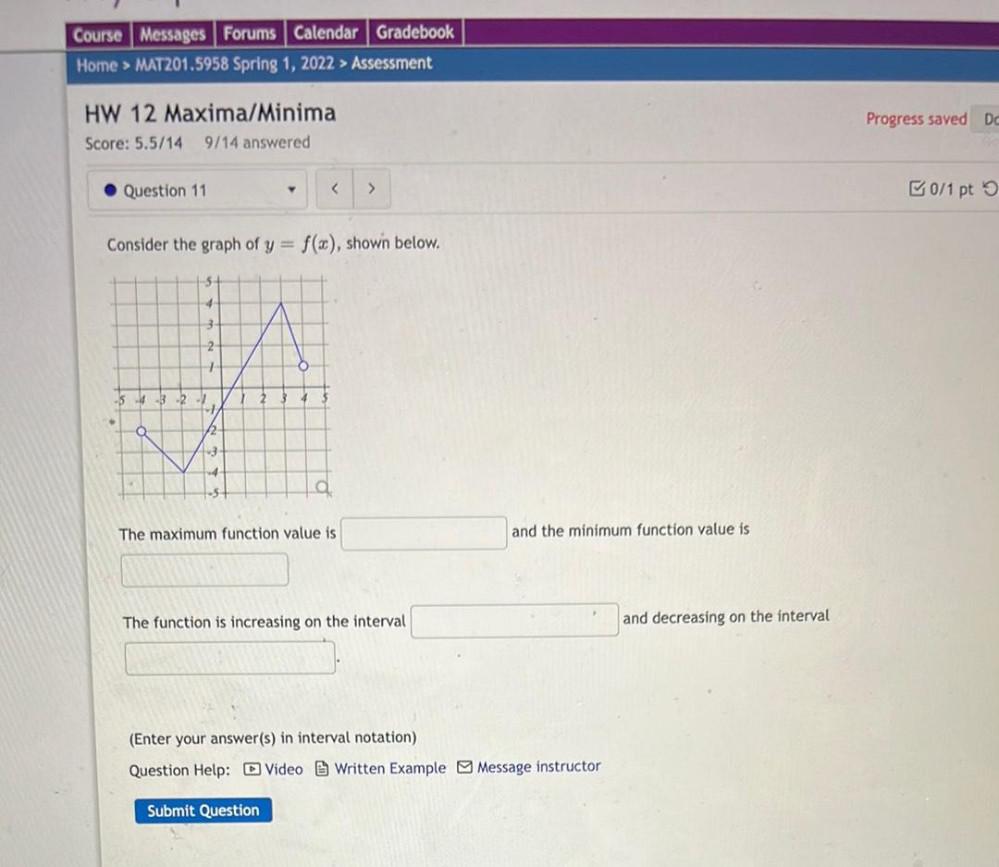
Calculus
Application of derivativesConsider the graph of y = f(x), shown below.
The maximum function value is___________
and the minimum function value is__________
The function is increasing on the interval__________
and decreasing on the interval____________
(Enter your answer(s) in interval notation)


Calculus
Application of derivativesConsider the function f(x) = x⁴ - 50x² +11, –4 ≤ x ≤ 11. The absolute maximum of f(a) (on the given interval) is at and the absolute maximum of f(x) (on the given interval) is at x = ___________
and the absolute minimum of f(x) (on the given interval) is ___________

Calculus
Application of derivativesQuestion 6
Suppose sinθ=3/5 , sinΦ =8/17. Moreover, suppose θ is in Quadrant II and Φ is in Quadrant I.
Find the following.
sin(θ+ Φ)=_________
cos(θ+Φ) =_________
![Given f(x) = 2|x – 7| +6
Give a closed interval in the form [a,b] that the mean value theorem would:
NOT APPLY
WOULD APPLY](https://media.kunduz.com/media/sug-question/raw/79081103-1660219581.0026588.jpeg?w=256)
Calculus
Application of derivativesGiven f(x) = 2|x – 7| +6
Give a closed interval in the form [a,b] that the mean value theorem would:
NOT APPLY
WOULD APPLY

Calculus
Application of derivativesFind the point on the tine y = 10x +1 closest to the point (4,3).
(a) The function giving the distance between the point and the line is s =
(b) The point on the line y = 10x + 1 closest to (4,3) is ________


Calculus
Application of derivativesLet f(x) = x^3 + 3x^2 – 1.
Calculate the derivative
f'(x) = 3x^2 + 63
Calculate the second derivative
f''(x) = 6x + 6
Note intervals are entered in the format (-00,5)U(7,00) (these are two infinite intervals).
On what interval(s) is f increasing?
Increasing:
On what interval(s) is f decreasing?
Decreasing:
On what interval(s) is f concave downward?
Concave Down:
On what interval(s) is f concave upward?
Concave Up:
What is the limit as x approaches infinity?
Limit is:
What is the limit as x approaches negative infinity?
Limit is:
Sketch the graph and submit with your work.

Calculus
Application of derivativesThe function f(x)=9x + 2/x has one local minimum and one local maximum.
This function has a local maximum at x=_______________
with value___________
and a local minimum at x =_____________
with value________________

Calculus
Application of derivativesFind the point on the tine - + 5y + 5 = 0 which is closest to the point (-2,-3).
![Consider the function f(3) = 2x + 7x^-1 . For this function there are four important intervals:
(-∞, A], [A, B),(B,C], and [C,∞) where A, and C are the critical numbers and the function is not defined at B.
Find A ____________
and B ___________
and C __________
For each of the following open intervals, tell whether f(x) is increasing or decreasing.
(-∞, A): __________
(A, B): __________
(B,C): __________
(C,∞): ___________
Note that this function has no inflection points, but we can still consider its concavity. For each of the following intervals, tell whether f(x) is concave up or concave down.
(-∞, B): ____________
(B,∞): ____________](https://media.kunduz.com/media/sug-question/raw/79082124-1660219516.9062896.jpeg?w=256)
Calculus
Application of derivativesConsider the function f(3) = 2x + 7x^-1 . For this function there are four important intervals:
(-∞, A], [A, B),(B,C], and [C,∞) where A, and C are the critical numbers and the function is not defined at B.
Find A ____________
and B ___________
and C __________
For each of the following open intervals, tell whether f(x) is increasing or decreasing.
(-∞, A): __________
(A, B): __________
(B,C): __________
(C,∞): ___________
Note that this function has no inflection points, but we can still consider its concavity. For each of the following intervals, tell whether f(x) is concave up or concave down.
(-∞, B): ____________
(B,∞): ____________

Calculus
Application of derivatives(1 + sec(t))(1 - cos(t))=
Simplify further using identity sec(t)=1/cos(t)
(1 + sec(t))(1 – cos(t))=

Calculus
Application of derivativesA stone is dropped into a calm lake causing a series of circular ripples. The radius of the outer one increases at 0.2 m/s. How rapidly is the disturbed area changing at the end of 3 s?
![Find the value of c on the interval (a, b)
such that f'(c) =f(b)-f(a)/b - a
f(x) = – 2x³– 3x² + 180x +1 on interval [-8, -1]
average rate of change
C =
(enter answers rounded to the nearest tenth)
(If there is more than one answer, enter your answers separated by a comma)](https://media.kunduz.com/media/sug-question/raw/79081134-1660219445.2079062.jpeg?w=256)
Calculus
Application of derivativesFind the value of c on the interval (a, b)
such that f'(c) =f(b)-f(a)/b - a
f(x) = – 2x³– 3x² + 180x +1 on interval [-8, -1]
average rate of change
C =
(enter answers rounded to the nearest tenth)
(If there is more than one answer, enter your answers separated by a comma)

Calculus
Application of derivativesA large totem pole in the state of Washington is 100 feet tall. At a particular time of day, the totem pole casts a 249- foot-long shadow. Find the measure of ZA to the nearest degree
![Given the function g(x) = 4x³ – 24x² + 36x, find the first derivative, g'(c).
Notice that g'(x) = 0 when I = 3, that is, g'(3) = 0.
Now, we want to know whether there is a local minimum or local maximum at I = 3, so we will use the
second derivative test.
Find the second derivative, g''(x).
g''(x)
Evaluate g''(3)
g''(3) Based on the sign of this number, does this mean the graph of g() is concave up or concave down at = 3?
[Answer either up or down -- watch your spelling!!]
At = 3 the graph of g() is concave Based on the concavity of g(x) at I = 3, does this mean that there is a local minimum or local maximum
at I = 3?](https://media.kunduz.com/media/sug-question/raw/79141983-1660219417.7725933.jpeg?w=256)
Calculus
Application of derivativesGiven the function g(x) = 4x³ – 24x² + 36x, find the first derivative, g'(c).
Notice that g'(x) = 0 when I = 3, that is, g'(3) = 0.
Now, we want to know whether there is a local minimum or local maximum at I = 3, so we will use the
second derivative test.
Find the second derivative, g''(x).
g''(x)
Evaluate g''(3)
g''(3) Based on the sign of this number, does this mean the graph of g() is concave up or concave down at = 3?
[Answer either up or down -- watch your spelling!!]
At = 3 the graph of g() is concave Based on the concavity of g(x) at I = 3, does this mean that there is a local minimum or local maximum
at I = 3?

Calculus
Application of derivativesConsider the function w() = - 12x⁵ + 30x⁴ - 2. Differentiate w and use the derivative to determine each of the following.
All intervals on which w is increasing. If there are more than one intervals, separate them by a comma. Use open intervals and exact values.
w increases on:
All intervals on which w is decreasing. If there are more than one intervals, separate them by a comma. Use open intervals and exact values.
w decreases on:
The value(s) of 2 at which w has a relative maximum. If there are more than one solutions, separate them by a comma. Use exact values.
w has relative maximum(s) at x =
The value(s) of zat which w has a relative minimum. If there are more than one solutions, separate them by a comma. Use exact values. w has relative minimum(s) at x=0

Calculus
Application of derivativesConsider the function f(x) = 3x^2 - 2x + 8, 0 ≤ x ≤ 8.
The absolute maximum of f(x) (on the given interval) is at x =
and the absolute minimum of f(x) (on the given interval) is at x =

Calculus
Application of derivativesWhen a certain object is placed in an oven at 540°C, its temperature T(t) rises according to the equation T(t) = 540(1- e^-0.1t), where t is the elapsed time (in minutes). What is the temperature after 10 minutes and how quickly is it rising at this time?
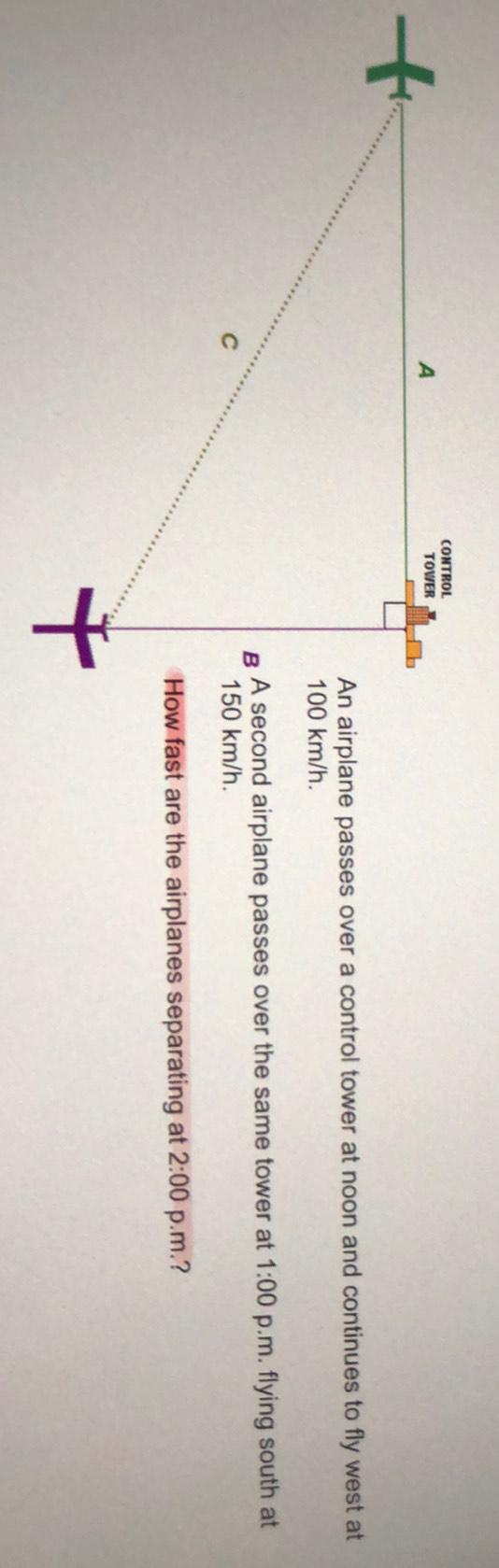
Calculus
Application of derivativesAn airplane passes over a control tower at noon and continues to fly west at 100 km/h.
A second airplane passes over the same tower at 1:00 p.m. flying south at 150 km/h.
How fast are the airplanes separating at 2:00 p.m.?

Calculus
Application of derivativesConsider the function r(a) = 36x⁵. + 270x⁴ + 480x³ +20. Differentiater and use the derivative to determine each of the following.
All intervals on which r is increasing. If there are more than one intervals, separate them by a comma. Use open intervals and exact values.
T increases on:
All intervals on which r is decreasing. If there are more than one intervals, separate them by a comma. Use open intervals and exact values. r decreases on:
The value(s) of x at which r has a relative maximum. If there are more than one solutions, separate them
by a comma. Use exact values. r has relative maximum(s) at x =
The value(s) of at which r has a relative minimum. If there are more than one solutions, separate them by a comma. Use exact values. r has relative minimum(s) at x =

Calculus
Application of derivativesSolve for x Rand to the nearest tenth if necessary
A right angle triangle with ∠35°, h = 16 and p = x.

Calculus
Application of derivativesWhat are the coordinates of the image of the point (-4, 9) after a 90° rotation followed by a translation 3 units to the left?

Calculus
Application of derivativesConsider the function f(x) = x⁴-50x² +11
The absolute maximum of /(w) (on the given interval) is at
and the absolute maximum of /(m) (on the given interval) is
The absolute minimum of $(w) (on the given interval) is at
and the absolute minimum of $(w) (on the given interval) is