Application of derivatives Questions and Answers
Calculus
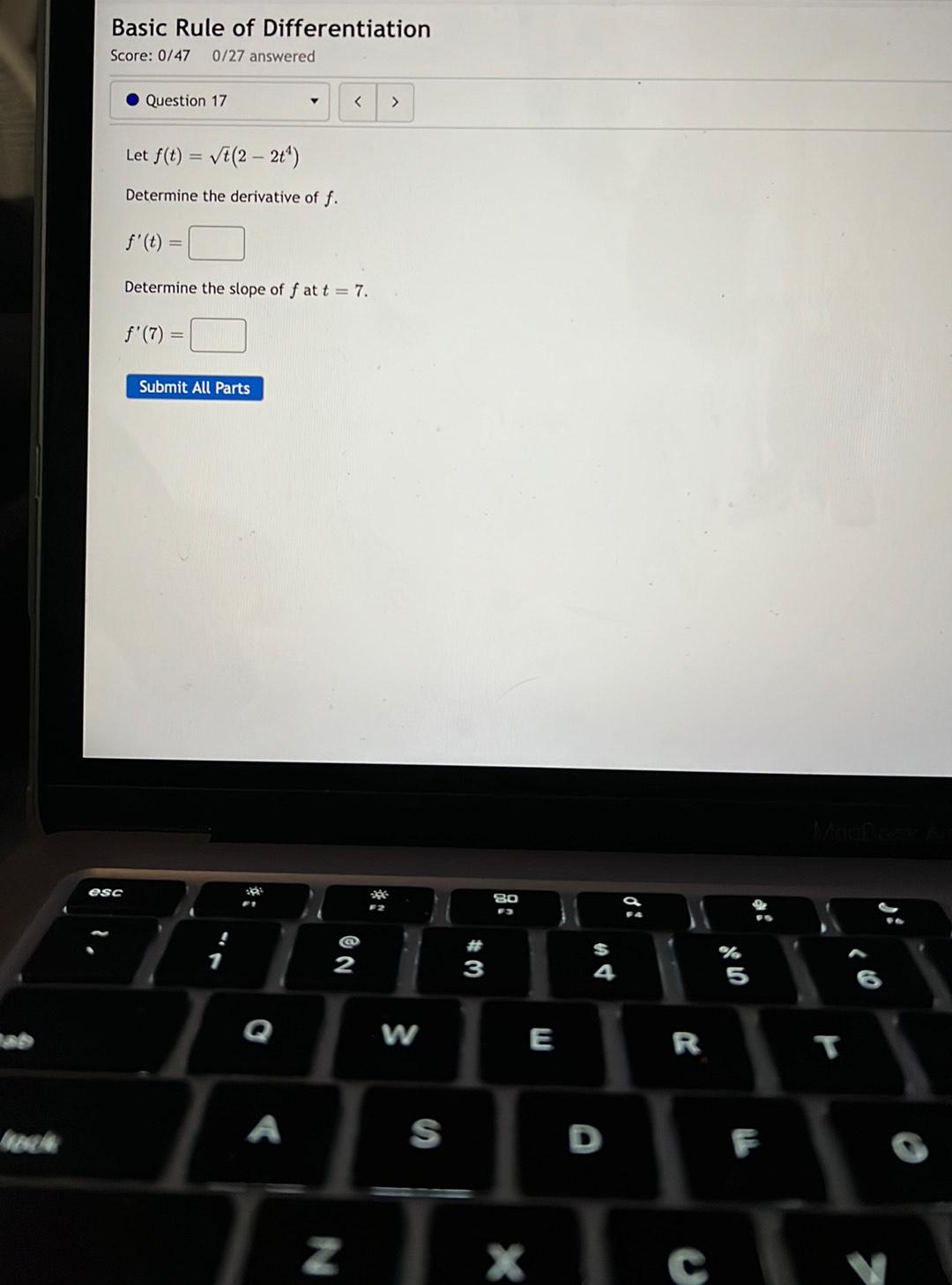
Application of derivativesLet f(t) = √t (2-2t⁴)
Determine the derivative of f.
f'(t) = ______
Determine the slope of f at t = 7.
f'(7) = ______
Calculus
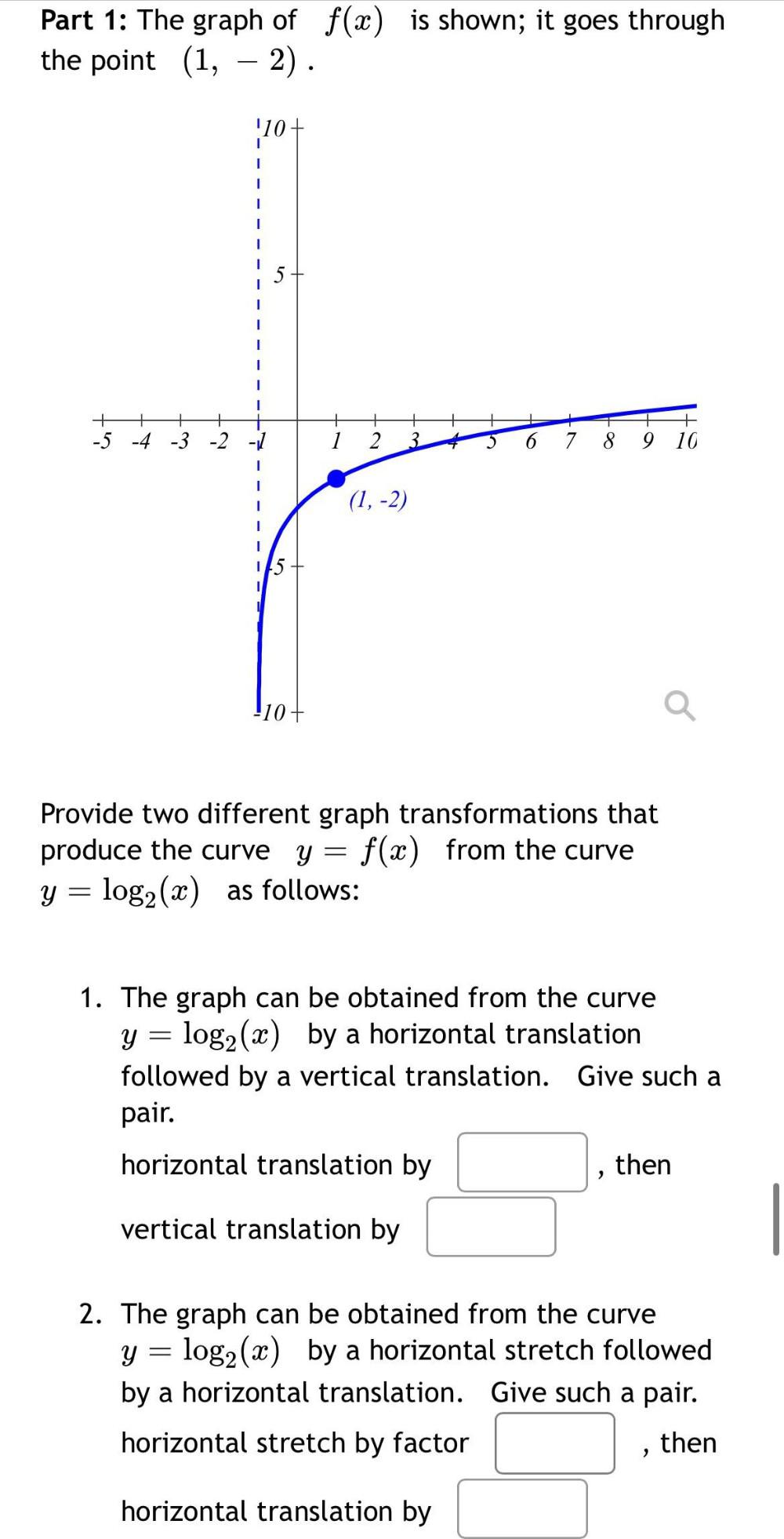
Application of derivativesPart 1: The graph of f(x) is shown; it goes through the point (1, -2).
Provide two different graph transformations that produce the curve y=f(x) from the curve y = log₂ (x) as follows:
1. The graph can be obtained from the curve y = log₂ (x) by a horizontal translation followed by a vertical translation. Give such a pair.
horizontal translation by_________then vertical translation by________
2. The graph can be obtained from the curve y = log₂ (x) by a horizontal stretch followed by a horizontal translation. Give such a pair.
horizontal stretch by factor________ then horizontal translation by_______

Calculus
Application of derivativesSuppose the field has a length of 6,000 feet. Sally buys fencing to enclose it, but has bought 4 feet too much. Rather than throwing away the extral fencing, Sally enclose a slightly larger field by enlarging each side of the field by the same amount, so the fencing encloses the field and a border:
What is the largest animal that could be at point X and be entirely within the border region, touching neither the fence nor the field?
(a)an ant
(b) a mouse
(c)a cat
(d)a cow
(d)an elephant
Give the average rate of change of the
perimeter, if the length increases from 6,000 feet to
7,000 feet:_________

Calculus
Application of derivativesThree airport runways intersect to form a triangle, ABC. The length of AB is 3.1 km, AC is 2.6 km, and BC is 2.4 km. A company is hired to cut the grass that grows in triangle ABC, but they need to know the area. Find the size, in degrees, of angle BÂC.

Calculus
Application of derivativesA drone operator is on a road running north and south, and using a drone to observe a herd of elk 3000 yards east and 1100 yards north of the operator's position. If the drone flies so that the distance from the herd is equal to the distance to the road, describe the path of the drone, then determine how far will it be from the drone operator when it crosses an east-west line through the operator's position. The path of the drone has the shape of a
a)ellipse
b)parabola
c)hyperbola
d)point
e)straight line
When the drone crosses the east-west line through the operator's position, it will be ____________yards from the operator (enter your answer rounded to the nearest whole number; if there is more than one answer, enter both, separated by commas)
Calculus
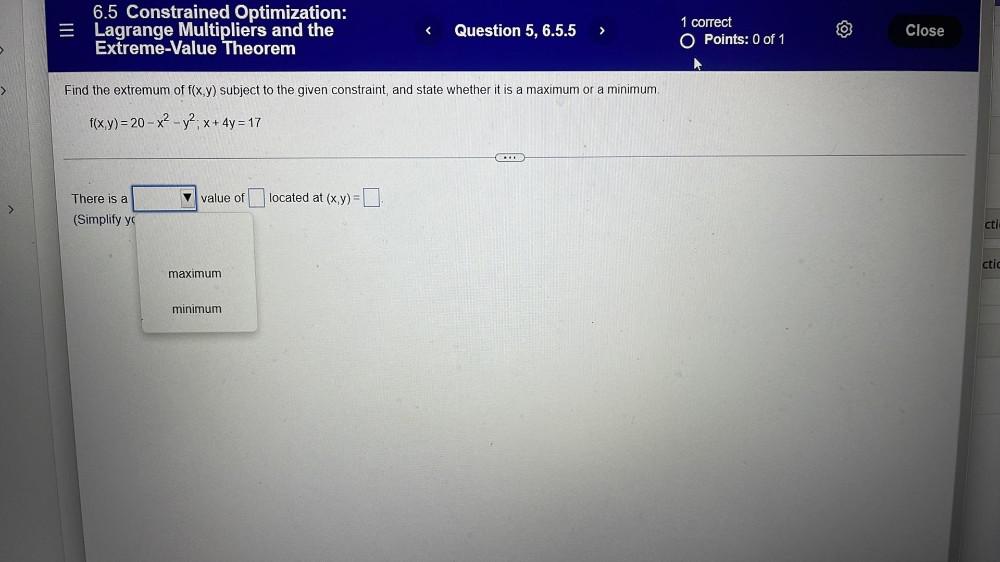
Application of derivatives1).Find the extremum of f(x,y) subject to the given constraint, and state whether it is a maximum or a minimum.
f(x,y)=20-x² - y²; x+4y=17
There is a ____ value of ____ located at (x,y) = ___
![Test the series for convergence or divergence:
Σ(7n+1)/(e^(n/5)-7) [n=1,∞]](https://media.kunduz.com/media/sug-question/raw/79814333-1660164041.0180895.jpeg?w=256)
Calculus
Application of derivativesTest the series for convergence or divergence:
Σ(7n+1)/(e^(n/5)-7) [n=1,∞]

Calculus
Application of derivativesExplain why the function is differentiable at the given point. Then find the linearization L(x, y) of the function at that point
f(x, y) = y + sin(x/y), (0, 3)

Calculus
Application of derivativesDavid invested $220 in an account paying an interest rate of 1.7% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest ten dollars, would be in the account after 10 years?
Calculus
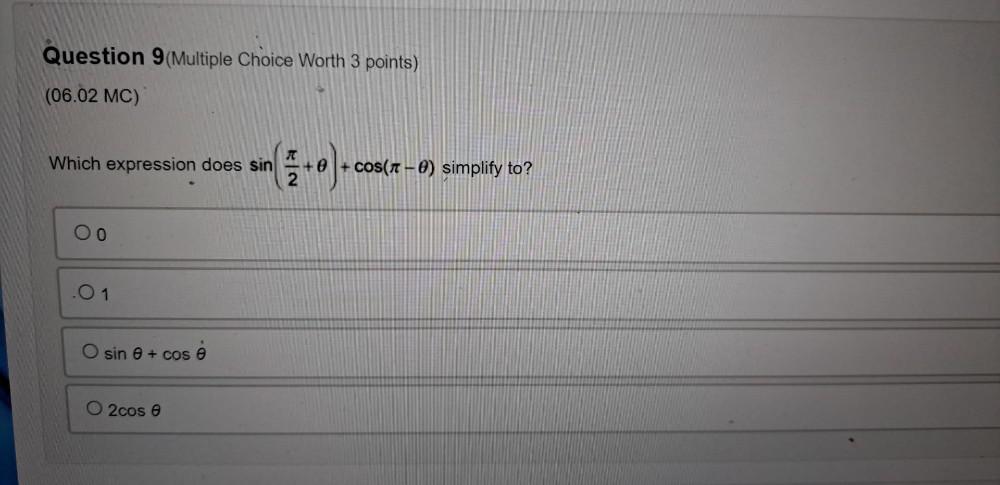
Application of derivativesWhich expression does sin(π/2+θ)+cos(π-θ)simplify to?
(a)0
(b)1
(c)sinθ+cosθ
(d)2cosθ

Calculus
Application of derivativesSketch a direction field for the differential equation y' = - x/y from -4 to 4. Then use it to sketch the initial conditions y(0) = 2 and y(0) = -1
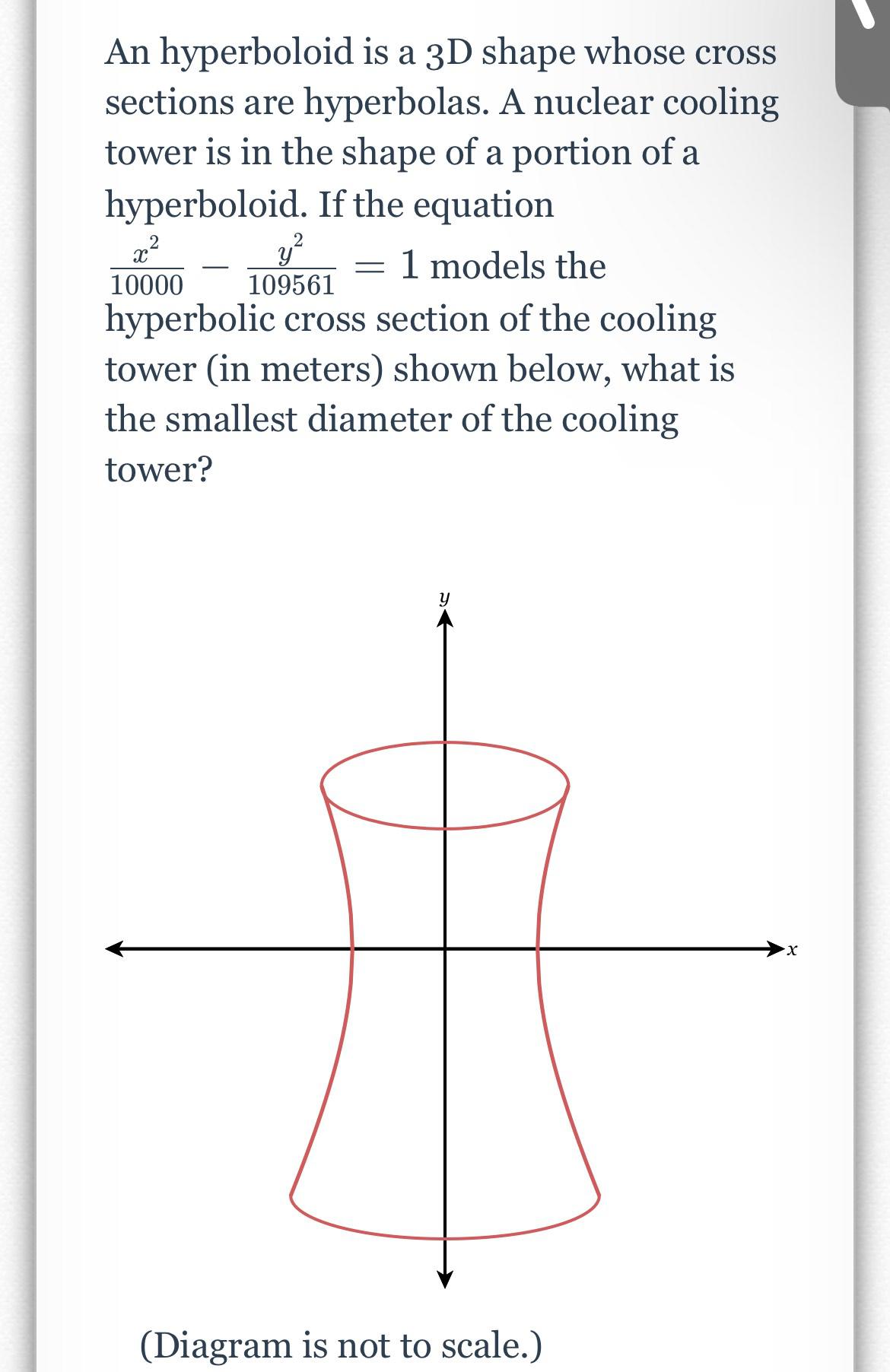
Calculus
Application of derivativesA hyperboloid is a 3D shape whose cross sections are hyperbolas. A nuclear cooling tower is in the shape of a portion of a hyperboloid. If the equation x²/10000 - y²/109561 =1 models the hyperbolic cross section of the cooling tower (in meters) shown below, what is the smallest diameter of the cooling tower?
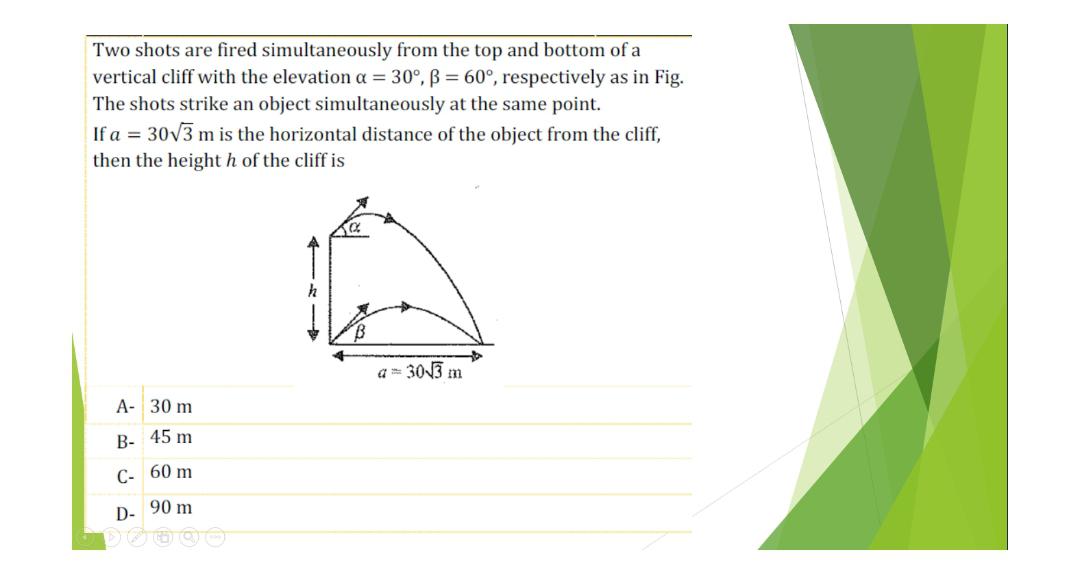
Calculus
Application of derivativesTwo shots are fired simultaneously from the top and bottom of a vertical cliff with the elevation a = 30°, ß = 60°, respectively as in Fig. The shots strike an object simultaneously at the same point. If a = 30√3 m is the horizontal distance of the object from the cliff, then the height h of the cliff is
A. 30 m
B. 45 m
C. 60 m
D. 90 m
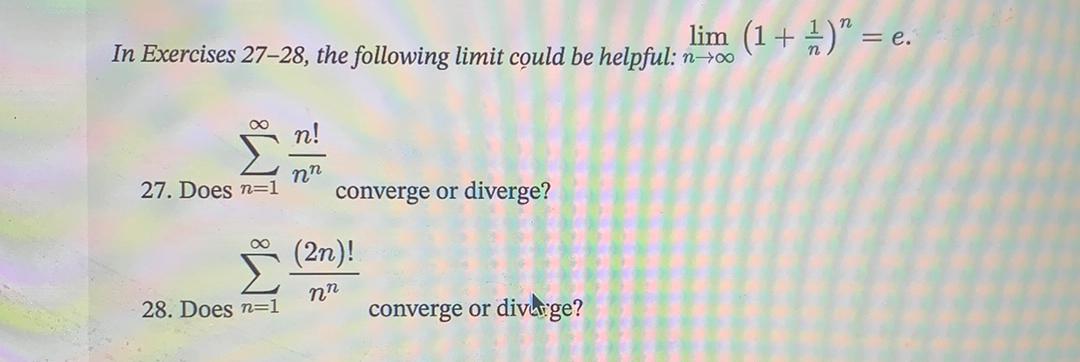
Calculus
Application of derivativesthe following limit could be helpful:
lim(1+1/n)^n=e
Does Σn!/n^n converge or diverge?
Does Σ(2n)!/n^n converge or diverge?

Calculus
Application of derivativesIn Exercises 36-41, use the Root Test to determine convergence or divergence (or state that the test is inconclusive).
Σ1/10^n
Σ1/n^n
Σ{k/(k+10)}^k

Calculus
Application of derivativesGiven the polynomial function f(x)=-4x³-x²+x+2, find:
a). Determine the maximum number of real zeros that the polynomial may have.
b). Use Decartes' Rule of Signs to determine how many positive and how many negative zeros each polynomial function may have.
Positive:_______
Negative:_______
c).List all the potential rational zeros of the polynomial function._______

Calculus
Application of derivativesConvert the parametric or polar equations to rectangular equations. Describe the shape of the graph (parabola, circle, line, etc). It may help to draw a little sketch. a. r = 5 cscθ

Calculus
Application of derivativesDuring the Apollo 14 mission, Alan Shepard hit a golf ball on the Moon. The function h(t) = 18t - 0.8t² models the height of the golf ball's trajectory on the Moon, where is the height, in metres , of the ball above the surface of the Moon and t is the time in seconds. Determine the instantaneous rate of change in the height of the ball at 5 seconds.
![Compute the average rate of change of the function f(x) = x² + 5 on the interval [0, 5].](https://media.kunduz.com/media/sug-question/raw/80185855-1660161747.8950787.jpeg?w=256)
Calculus
Application of derivativesCompute the average rate of change of the function f(x) = x² + 5 on the interval [0, 5].

Calculus
Application of derivativesJerry invests $6000 at 7.5%/a, compounded annually.
a) Determine the equation of the amount, A, after t years.
b) Estimate the instantaneous rate of change in the value at 10 years.
c) Suppose that the interest rate was compounded semi-annually instead of annually. What would the instantaneous rate of change
be at 10 years?
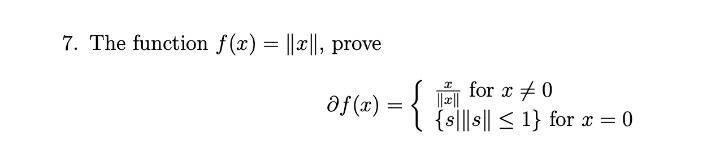
Calculus
Application of derivativesThe function f(x) = ||x||, prove
of(x) = {x/||x|| for x≠0
s|| |s||≤1 for x=0
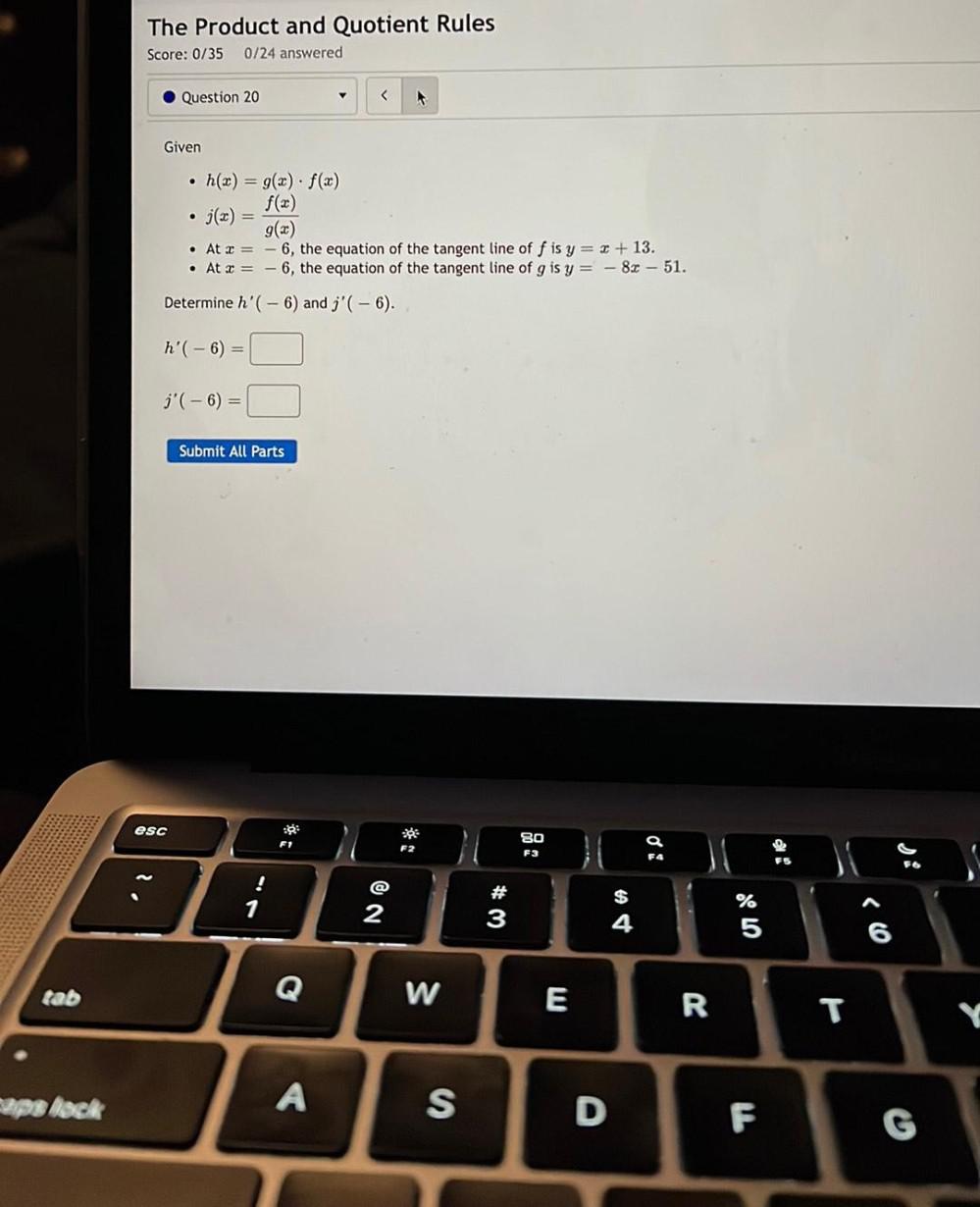
Calculus
Application of derivativesGiven
• h(x) = g(x) * f(x)
• j(x) = f(x)/g(x)
• At x = -6, the equation of the tangent line of f is y = x + 13.
• At x = -6, the equation of the tangent line of g is y=- 8x - 51.
Determine h'(- 6) and j'(-6).
h'(- 6) =
j'(- 6) =

Calculus
Application of derivatives5. Suppose that the revenue realized on the sale of company's product can be modeled by the function R(x) = 600x -0.3x² is the number of units sold and R(x) is given in dollars. (Revenue is the income a company receives from selling its goods ot services. Compute the average change in revenue, per additional item that was sold for the first 200 items.
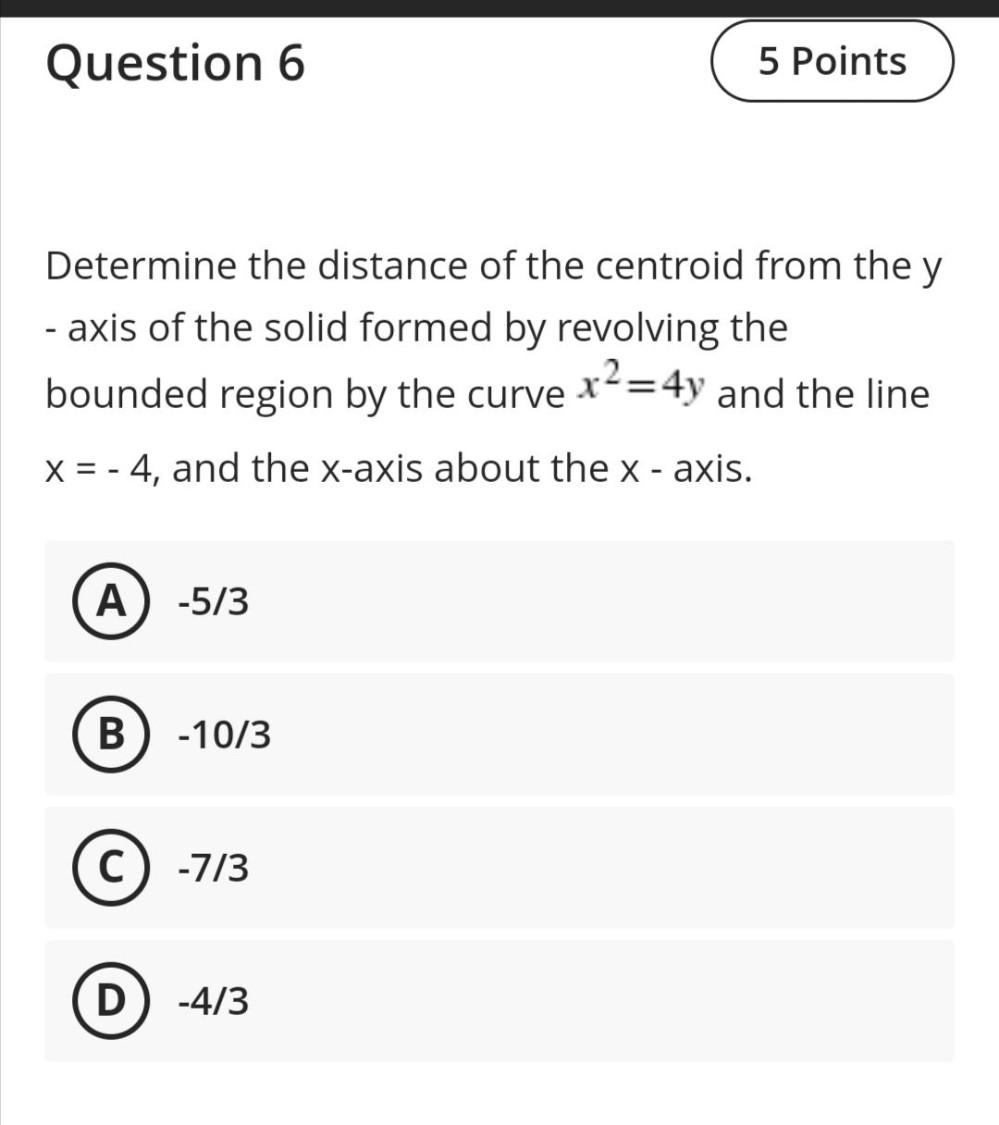
Calculus
Application of derivativesDetermine the distance of the centroid from the y- axis of the solid formed by revolving the bounded region by the curve x²=4y and the line x = - 4, and the x-axis about the x - axis.
A)-5/3
B) -10/3
C -7/3
D -4/3

Calculus
Application of derivativesThe height attained by a weight attached to a spring set in motion after t seconds is s(t)= -6cos12πt + 5 inches. Find the maximum height that the weight rises given an equilibrium position of y = 5.
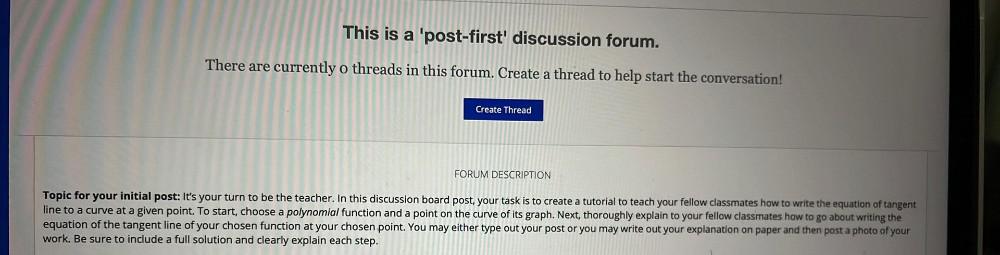
Calculus
Application of derivativesTopic for your initial post: It's your turn to be the teacher. In this discussion board post, your task is to create a tutorial to teach your line to a curve at a given point. To start, choose a polynomial function and a point on the curve of its graph. Next, thoroughly explain to your fellow classmates equation of the tangent line of your chosen function at your chosen point. You may either type out your post or you may write out your explanation on paper work. Be sure to include a full solution and clearly explain each step. fellow classmates how to write the equation of tangent how to go about writing the post a photo of your and then
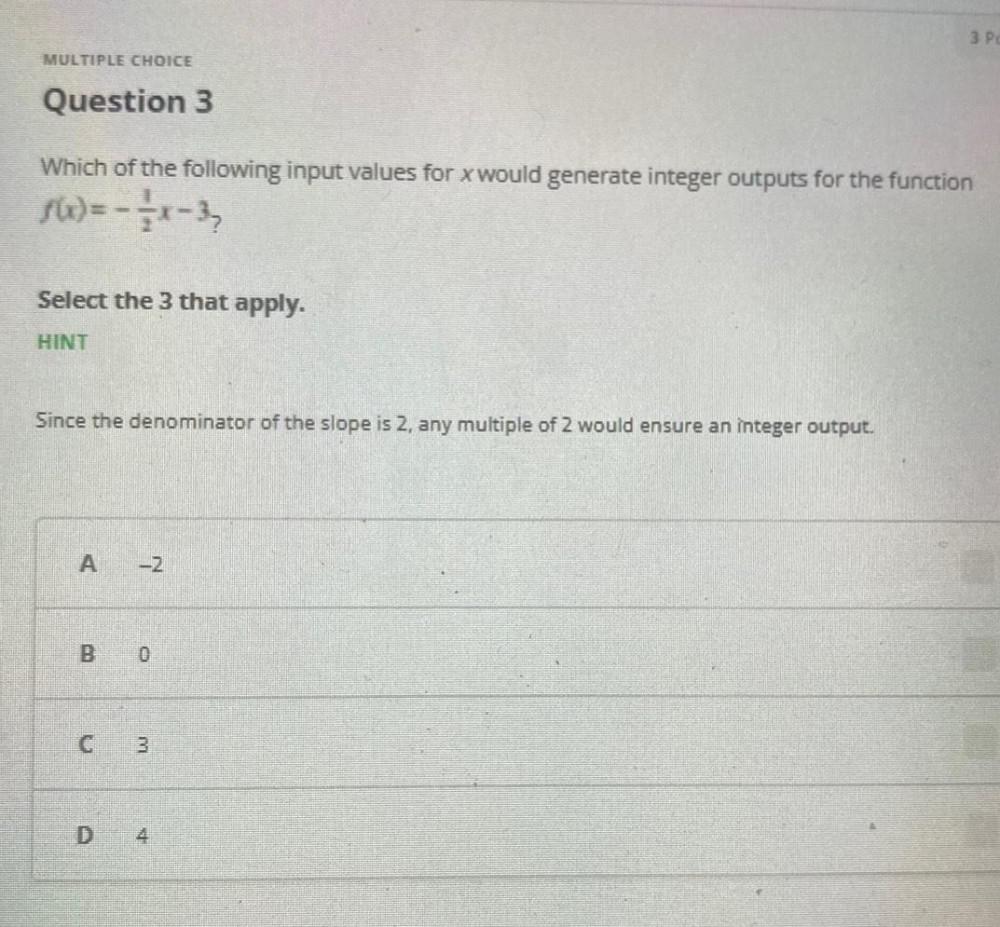
Calculus
Application of derivativesWhich of the following input values for x would generate integer outputs for the function f(x)=-1/2x-3?
Select the 3 that apply.
HINT
Since the denominator of the slope is 2, any multiple of 2 would ensure an integer output.
A. -2
B. 0
C. 3
D. 4
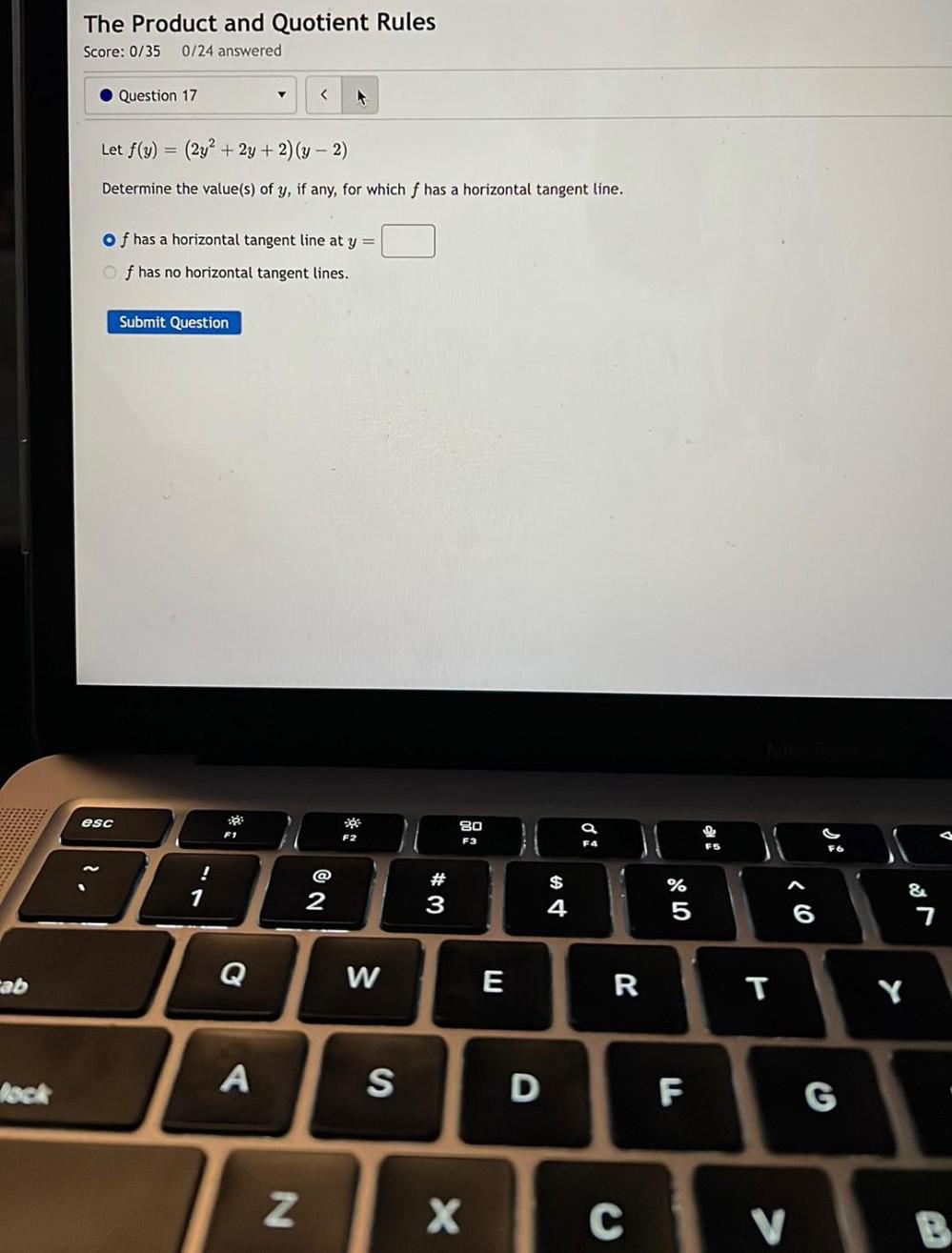
Calculus
Application of derivativesLet f(y) = (2y^2 + 2y + 2)(y-2)
Determine the value(s) of y, if any, for which f has a horizontal tangent line.
A) f has a horizontal tangent line at y =
B) f has no horizontal tangent lines.
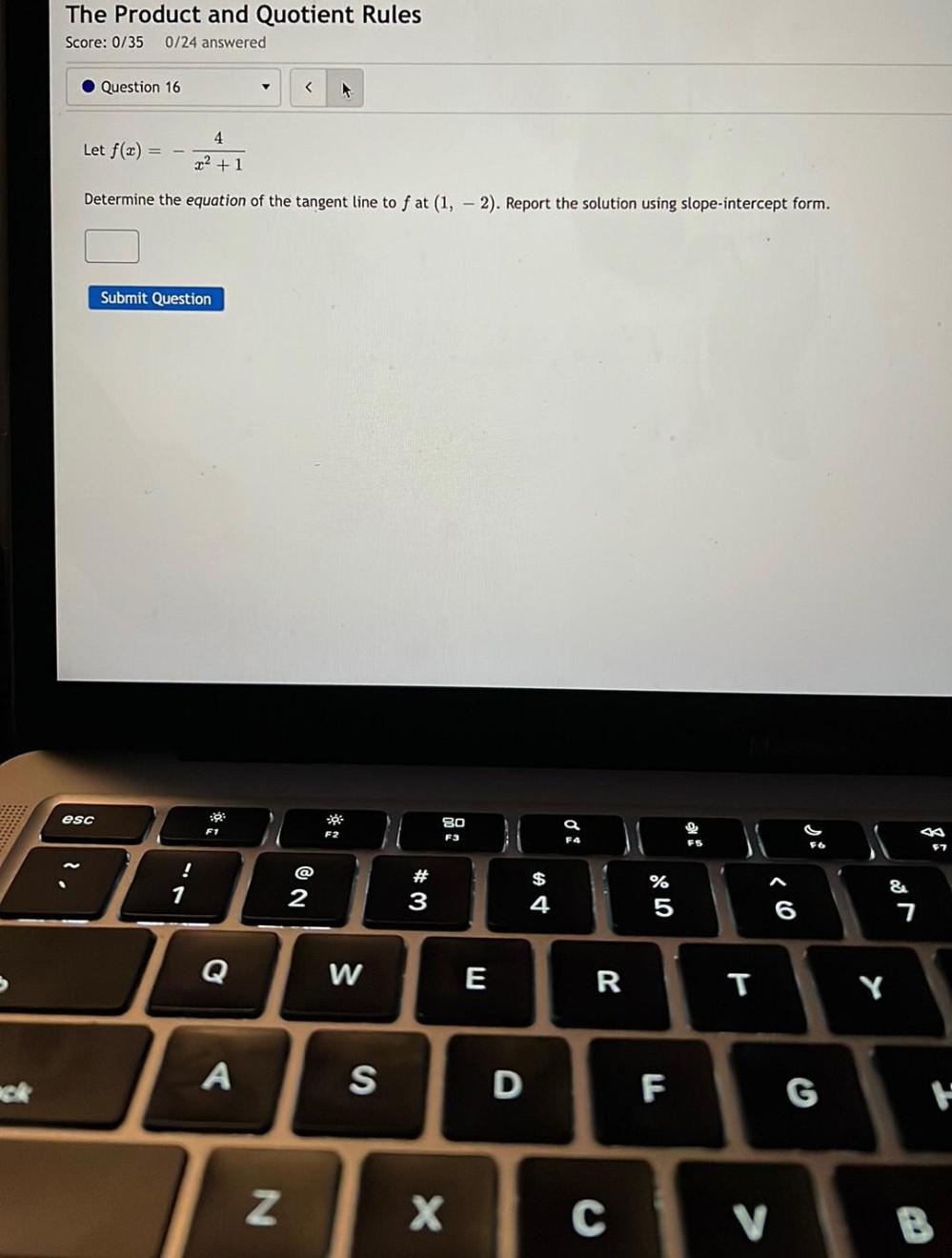
Calculus
Application of derivativesLet f(x) = 4/(x² + 1)
Determine the equation of the tangent line to f at (1, 2). Report the solution using slope-intercept form.
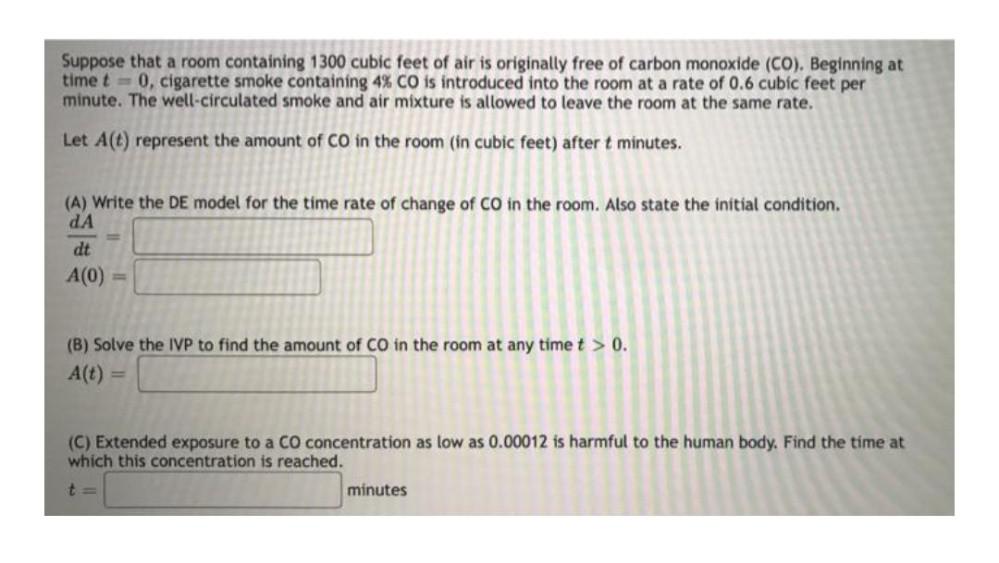
Calculus
Application of derivativesSuppose that a room containing 1300 cubic feet of air is originally free of carbon monoxide (CO). Beginning at time t= 0, cigarette smoke containing 4% CO is introduced into the room at a rate of 0.6 cubic feet per minute. The well-circulated smoke and air mixture is allowed to leave the room at the same rate.
Let A(t) represent the amount of CO in the room (in cubic feet) after t minutes.
(A) Write the DE model for the time rate of change of CO in the room. Also state the initial condition.
dA/dt= □
A(0) = □
(B) Solve the IVP to find the amount of CO in the room at any time t > 0.
A(t) = □
(C) Extended exposure to a CO concentration as low as 0.00012 is harmful to the human body. Find the time at which this concentration is reached.
t= □ minutes

Calculus
Application of derivatives7. Joey enlarged a 3-inch by 5-inch photograph on a copy machine. He enlarged it four times. The table below shows the area of the photograph after each enlargement. What is the average rate of change of the area from the original photograph to the fourth enlargement, to the nearest tenth?
a. 4.3
b. 4.5
c. 5.4
d. 6.0

Calculus
Application of derivativesA factory manufactures three products, A, B, and C. Each product requires the use of two machines, Machine I and Machine II. The total hours available, respectively, on Machine I and Machine Il per month are 6,940 and 6,930. The time requirements and profit per unit for each product are listed below.
A B C
Machine 17 10 9
Machine II 6 7 13
Profit $9 $12 $16
How many units of each product should be manufactured to maximize profit, and what is the maximum profit?
Set up the linear programming problem, with A, B, and C representing the number of units of each product that are produced.
Maximize P =
subject to:
__________ = 6,940
__________ = 6,930
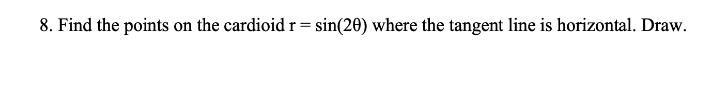
Calculus
Application of derivativesFind the points on the cardioid r = sin(2θ) where the tangent line is horizontal. Draw.

Calculus
Application of derivativesWhich integral correctly computes the length of the curve y=In(cos(x)) between x=0 and x=π/3 ?
a) π/3
∫₀tan(x) dx
b) π/3
∫₀2πln(cos(x))√(1+tan²(x)) dx
c) π/3
∫₀sec(x) dx
d)π/3
∫₀√(1 + (In(cos(x)))² )dx
Calculus
Application of derivativesJina is driving on a highway. She uses one gallon of gas every 20 miles she drives. The distance, D (in miles), she travels on g gallons of gas is given by the following function.
D(g) = 20g
How far does Jina drive if she uses 4 gallons of gas?
________ miles

Calculus
Application of derivativesSuppose that the revenue realized on the sale of company's product can be modeled by the function R(x) = 500x -0.4x² is the number of units sold and R(x) is given in dollars. (Revenue is the income a company receives from selling its goods at services. Compute the average change in revenue, per additional item that was sold for the first 50 items.

Calculus
Application of derivativesKings Dominon's opening day had 1350 people visit the park. Children under 12 paid $40, Adults under 65 paid $65 and seniors over 65 paid $50. The park had combined ticket sales of $75500. If each child was accompanied by 2 adults under the age of 65, how many of each age group were in the park?
Calculus
Application of derivativesFind the area of the sector of a circle with radius 15 feet formed by a central angle of 35°.
_______ square feet
Round your answer to two decimal places.
![Below is the function f(x) = 11 - 1/2x², together with a rectangle with one side on the x-axis, and two corners on the curve. The bottom left corner is (x, 0).
What is the area of the rectangle if x = 2.3? [Give your answer as a decimal number.]](https://media.kunduz.com/media/sug-question/raw/80431576-1660158748.7267966.jpeg?w=256)
Calculus
Application of derivativesBelow is the function f(x) = 11 - 1/2x², together with a rectangle with one side on the x-axis, and two corners on the curve. The bottom left corner is (x, 0).
What is the area of the rectangle if x = 2.3? [Give your answer as a decimal number.]
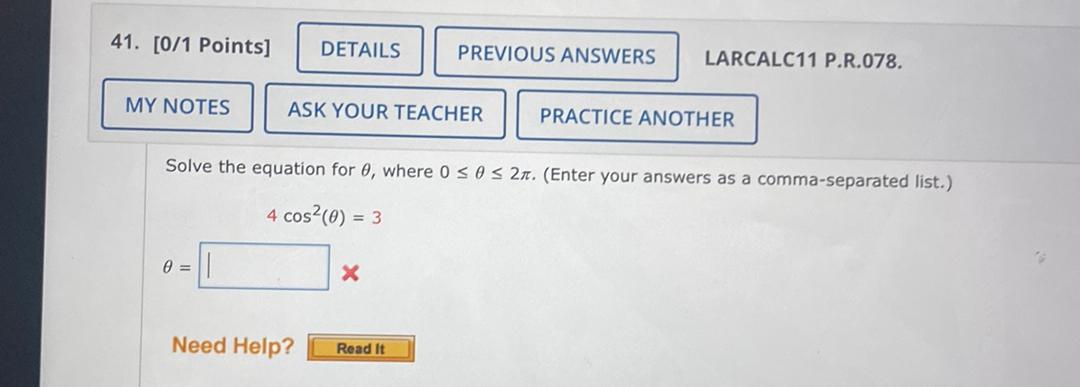
Calculus
Application of derivativesSolve the equation for θ, where 0 ≤ θ ≤ 2. (Enter your answers as a comma-separated list.)
4 cos² (θ) = 3
θ = ____

Calculus
Application of derivativesDetermine the minimum of
f(x)= (10x³ + 3x² + x + 5)²
starting at x = 3 and using a step size △ = 5.0.
Using region elimination: expanding pattern bounding plus six steps of golden section.

Calculus
Application of derivativesIn your own words, define the following.
(a) Secant line
(b). Average rate of change
(c). Tangent line
(d). Instantaneous rate of change
![Given that sin(a) = 1/3 and cos(b) = -2/6 with a and b both in the interval [ π/2, π], find the exact values of sin(a + b) and cos(a − b).](https://media.kunduz.com/media/sug-question/raw/80561844-1660154972.783678.jpeg?w=256)
Calculus
Application of derivativesGiven that sin(a) = 1/3 and cos(b) = -2/6 with a and b both in the interval [ π/2, π], find the exact values of sin(a + b) and cos(a − b).

Calculus
Application of derivatives• The volume of a cube is increasing at a rate of 10cm3/min. How fast is the surface area increasing when the length of an edge (side) is 30 cm (related rates)
•The edge of a cube was found to be 30 cm with a possible error in measurement of 0.1 cm.
a) Use differentials to estimate the maximum error in computing the volume of the cube.
b) What is the relative error? What is the percent of error?
![Given the functions f(x) = x² + 1 and g(x) = x + 1. Compute the net and the total (or absolute) area between the curves over the interval [0,2].](https://media.kunduz.com/media/sug-question/raw/80516705-1660154846.451801.jpeg?w=256)
Calculus
Application of derivativesGiven the functions f(x) = x² + 1 and g(x) = x + 1. Compute the net and the total (or absolute) area between the curves over the interval [0,2].
![6. For the function y = 30 cos[2(x + 15°)] - 60, the phase shift is
A 30° to the right
B 15° to the left
C 15° to the right
D 60° to the right](https://media.kunduz.com/media/sug-question/raw/80502917-1660154791.8234367.jpeg?w=256)
Calculus
Application of derivatives6. For the function y = 30 cos[2(x + 15°)] - 60, the phase shift is
A 30° to the right
B 15° to the left
C 15° to the right
D 60° to the right
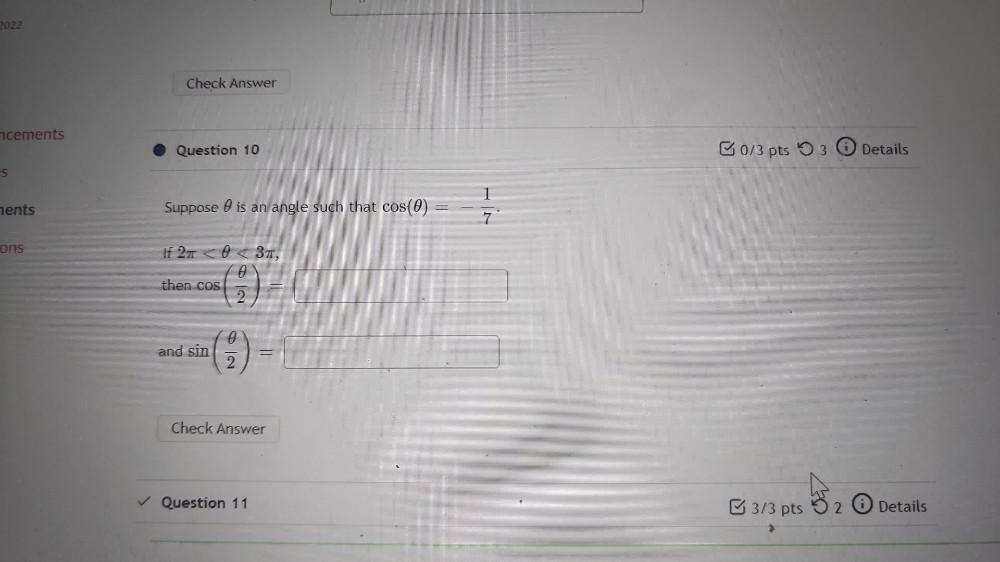
Calculus
Application of derivativesSuppose is an angle such that cos(θ)= -1/7
If 2π < 0 < 3π,
then cos(θ/2)=___
and sin(θ/2)=___
Calculus
Application of derivativesFind the θ value within [0, 2π) for function f(θ) = 7 cos(7θ) to reach its minimum value.
θ =
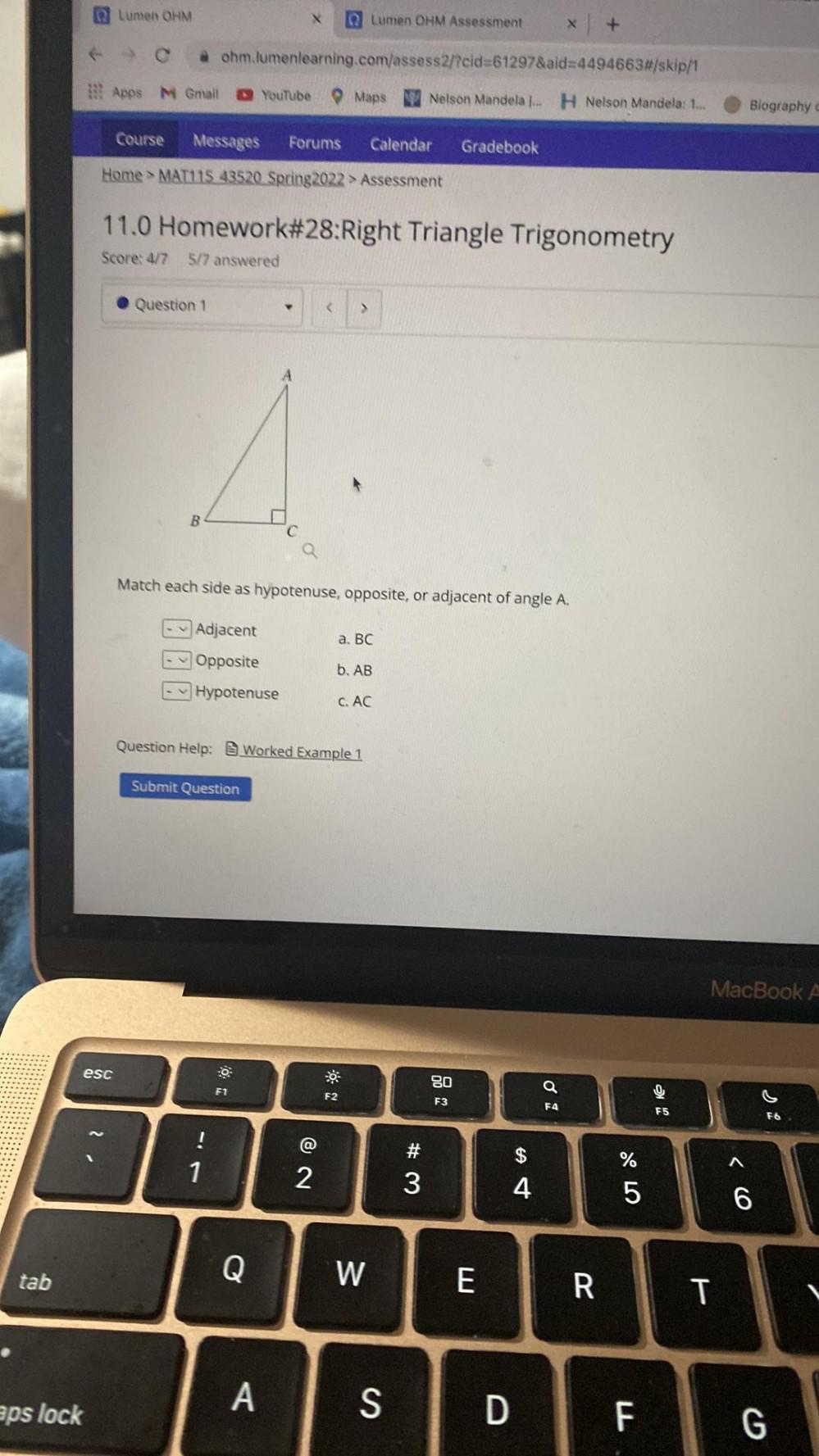
Calculus
Application of derivativesMatch each side as hypotenuse, opposite, or adjacent of angle A.
Adjacent a. BC
Opposite b. AB
Hypotenuse C. AC
Calculus
Application of derivativesDetermine the center and radius of a circle given that its equation is
(x - 1)² + (y- 8)² = 49
Center:
Radius: