Application of derivatives Questions and Answers

Calculus
Application of derivativesFlight of a Rocket The altitude (in feet) of a rocketts into flight is given by
s-f(t) =-t ³ +54t² + 470t +6 (t ≥ 0).
Find the point of inflection of the function.
(t, s)
What is the maximum velocity (in ft/s) attained by the rocket?

Calculus
Application of derivativesA ball is projected upward from the ground. Its distance in feet from the ground in t seconds is given by
s(t)=-16t^2+128t. At what times will the ball be 219 feet from the ground?
At second(s), the ball will be 219 feet from the ground
(Type an integer or decimal rounded to the nearest tenth as needed. Use a comma to separate answers as
Calculus
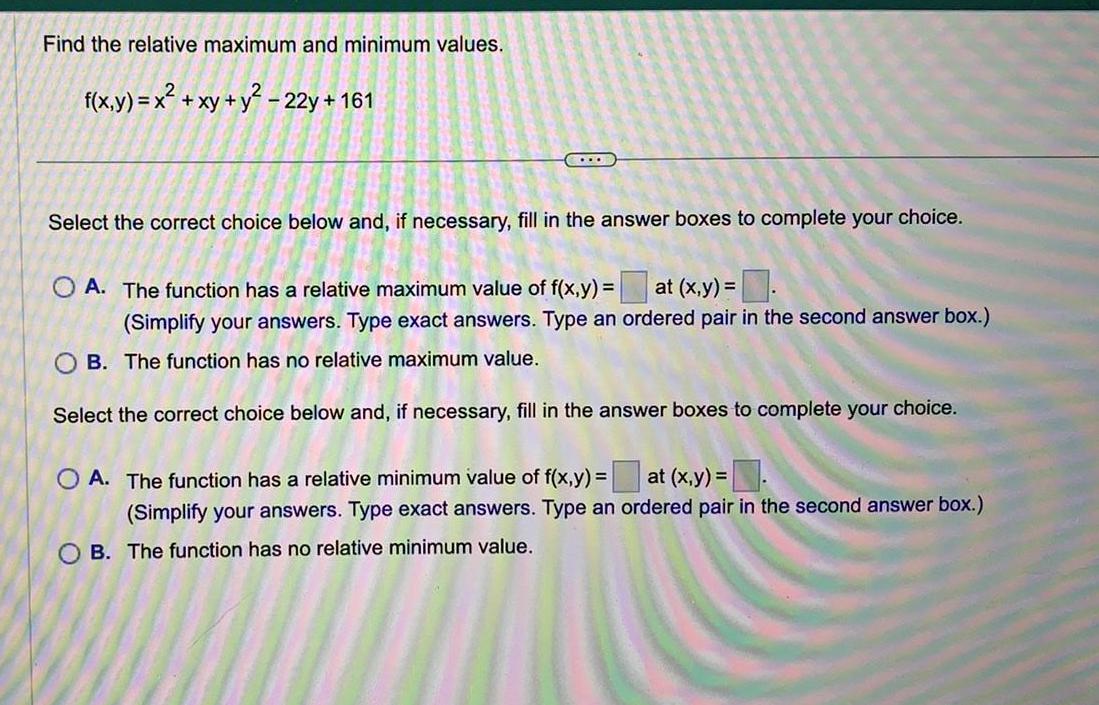
Application of derivativesFind the relative maximum and minimum values.
f(x,y) = x² + xy + y²-22y + 161
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative maximum value of f(x,y) = at (x,y) =
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative maximum value.
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
A. The function has a relative minimum value of f(x,y) = at (x,y) = .
(Simplify your answers. Type exact answers. Type an ordered pair in the second answer box.)
B. The function has no relative minimum value.

Calculus
Application of derivatives* Consider the function
f(x)=(x-9)/x²
all values of 'x' that correspond to horizontal tangent lines. Select 'None" if the function does not have any Values of x that correspond to horizontal tangent lines
Find x = o None

Calculus
Application of derivativesSuppose 0≤x≤ 2π. Find all solutions that satisfy the equation: cos(x) = -0.63
Round your answers to two places after the decimal.
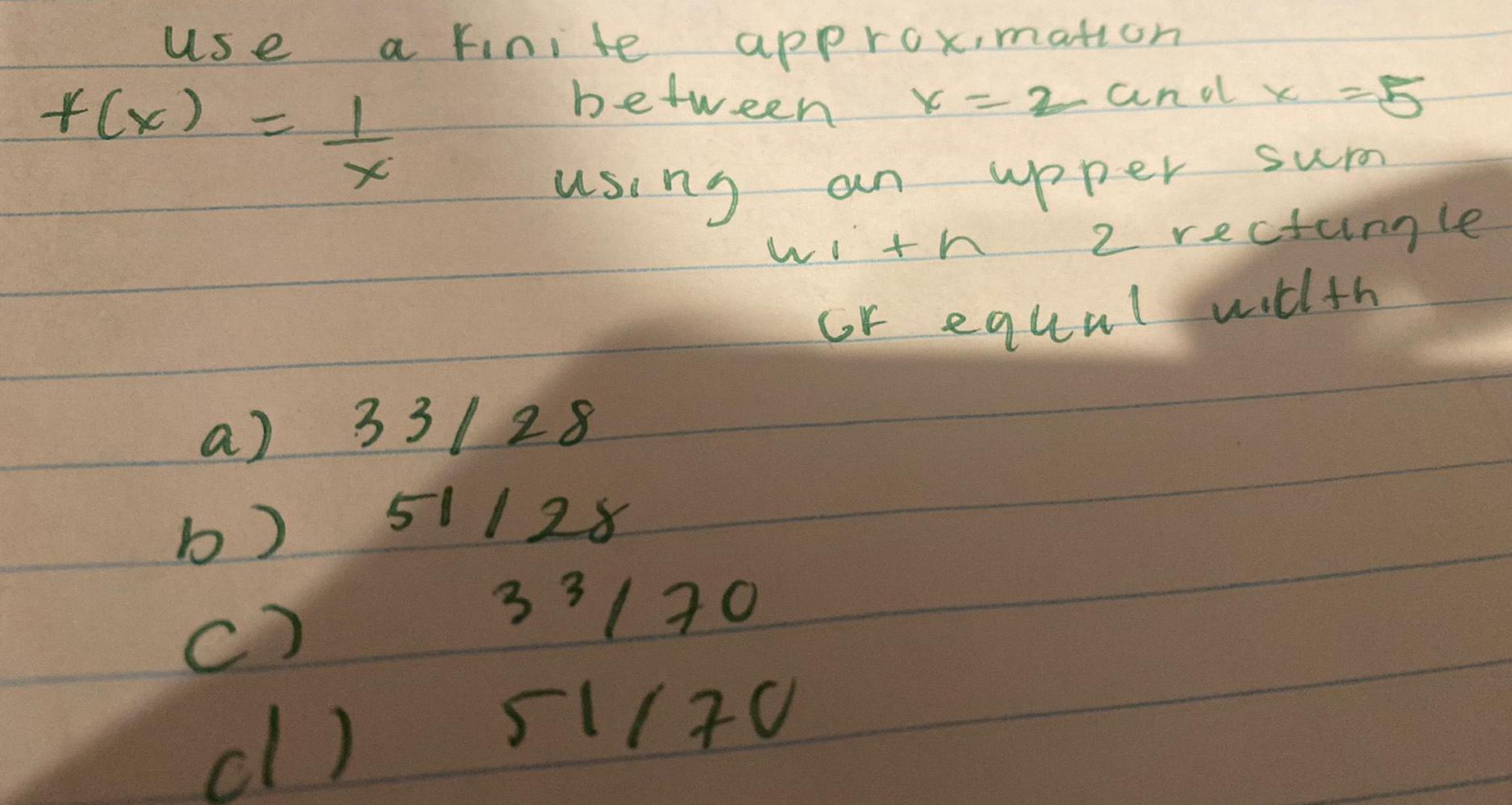
Calculus
Application of derivativesUse a finite approximation f(x)=1/x between x=2 and x=5 using an upper sum width 2 rectangles of equal width
a) 33/28
b) 51/28
c) 33/70
d) 51/70

Calculus
Application of derivativesTracy has a cell phone plan that provides 250 free minutes each month for a
flat rate of $29. For any minutes over 250, Tracy is charged $0.35 per minute.
Which of the following piecewise functions represents charges based on
Tracy's cell phone plan?
A. f(x)= {29,*> 250
29+.35x, x≤ 250}
B. f(x)={29,x≤ 250
35x, x> 250}
C. f(x)= {29,x≤ 250
35x, x> 250}
D. f(x)={29,x≤250
29+.35(x-250).x > 250}

Calculus
Application of derivativesConsider the following function.
f(x) = 4x^2/3
Find f(-8) and f(8).
f(-8)
f(8) =
Find all values c in (-8, 8) such that f'(c) = 0. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
C =
Based off of this information, what conclusions can be made about Rolle's Theorem?
This contradicts Rolle's Theorem, since f is differentiable, f(-8) = f(8), and f'(c) = 0 exists, but c is not in (-8, 8).
This does not contradict Rolle's Theorem, since f'(0) = 0, and 0 is in the interval (-8, 8).
This contradicts Rolle's Theorem, since f(-8) = f(8), there should exist a number c in (-8, 8) such that f'(c) = 0.
This does not condict Rolle's Theorem, since f'(0) does not exist, and so f is not differentiable on (-88).
Nothing can be concluded.

Calculus
Application of derivativesLet f(x) = |x-8| +2.
(a) The domain of f is
(b) List the critical number(s) of f:
(c) f'(x) > 0 for x ∈
(d) f'(x) < 0 for x ∈
(e) Local maxima of f occur at x =
(f) Local minima of f occur at x =

Calculus
Application of derivativesThe number of visitors P to a website in a given week over a 1-year period is given by P(t) = 121 + (t-89) e0.02t, where t is the week and 1≤t≤ 52.
a) Over what interval of time during the 1-year period is the number of visitors decreasing?
b) Over what interval of time during the 1-year period is the number of visitors increasing?
c) Find the critical point, and interpret its meaning.

Calculus
Application of derivativesLast week at an insurance company, Zach sold an average of 7 automobile and 5 homeowner policies per day over a 4-day period, Lisa sold an average of 9 automobile and 10 homeowner policies per day over a 4-day period, and York sold an average of 8 automobile and 6 homeowner policies per day over a 5-day period. Complete parts a and b below. a) Express this information as a sum of scalar multiples of three 2 x 1 matrices. (Type an integer or decimal for each matrix element. Do not simplify)

Calculus
Application of derivativesLast week at an insurance company, Zach sold an average of 9 automobile and 7 homeowner policies per day over a 5-day period, Elena sold an average of 6 automobile and 5 homeowner policies per day over a 4-day period, and Dakota sold an average of 8
automobile and 10 homeowner policies per day over a 5-day period. Complete parts a and b below.
a) Express this information as a sum of scalar multiples of three 2 x 1 matrices.
(Type an integer or decimal for each matrix element. Do not simplify.)
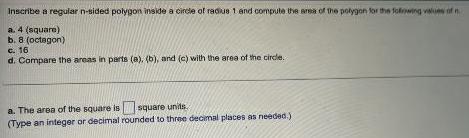
Calculus
Application of derivativesInscribe a regular n-sided polygon inside a circle of radius 1 and compute the area of the polygon for the following values of n
a. 4 (square)
b. 8 (octagon)
c. 16
d. Compare the areas in parts (a), (b), and (c) with the area of the circle.
a. The area of the square is square units
(Type an integer or decimal rounded to three decimal places as needed.)

Calculus
Application of derivativesAnswer the following.
(a) Find an angle between 0° and 360° that is coterminal with 810°.
(b) Find an angle between 0 and 2π that is coterminal with - 7π.
Give exact values for your answers.
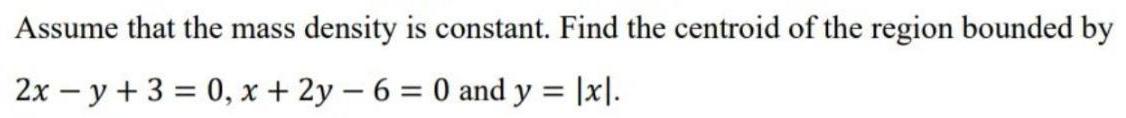
Calculus
Application of derivativesAssume that the mass density is constant. Find the centroid of the region bounded by
2x - y + 3 = 0, x + 2y - 6 = 0 and y = |x|.

Calculus
Application of derivativesThe amount of carbon-14 present in a paint after t years is given by y=y-0.00012t The paint contains 28% of its carbon-14. How old are the paintings?
The age of the paintings is years
(Round to the nearest year)

Calculus
Application of derivativesGiven z₁ = 24(cos 315° + isin 315°) and z2 = 3(cos 120° + isin 120°), what is the product of z₁ and z₂?

Calculus
Application of derivativesSuppose f(x) = 3x² and r(x) = √3x. Find and simplify the composite function r(f(x))
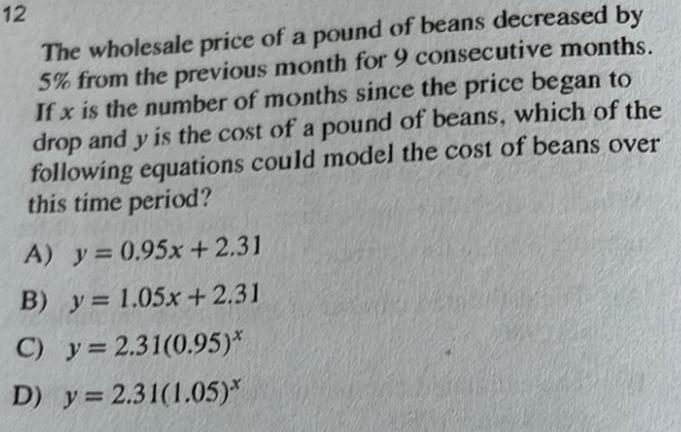
Calculus
Application of derivativesThe wholesale price of a pound of beans decreased by 5% from the previous month for 9 consecutive months. If x is the number of months since the price began to drop and y is the cost of a pound of beans, which of the following equations could model the cost of beans over
this time period?
A) y = 0.95x+2.31
B) y = 1.05x+2.31
C) y = 2.31(0.95)x
D) y = 2.31(1.05)x
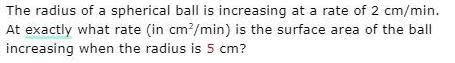
Calculus
Application of derivativesThe radius of a spherical ball is increasing at a rate of 2 cm/min. At exactly what rate (in cm²/min) is the surface area of the ball increasing when the radius is 5 cm?

Calculus
Application of derivativesThe length of a rectangle is increasing at a rate of 5 cm/s and its width is increasing at a rate of 8 cm/s. When the length is 9 cm and the width is 7 cm, how fast is the area of the rectangle increasing (in cm²/s)?

Calculus
Application of derivativesSolve the problem.
An appliance company determines that in order to sell x dishwashers, the price per dishwasher must be
p= 420- 0.4x.
It also determines that the total cost of producing x dishwashers is given by
C(x) = 5000+ 0.6x².
What is the maximum profit?
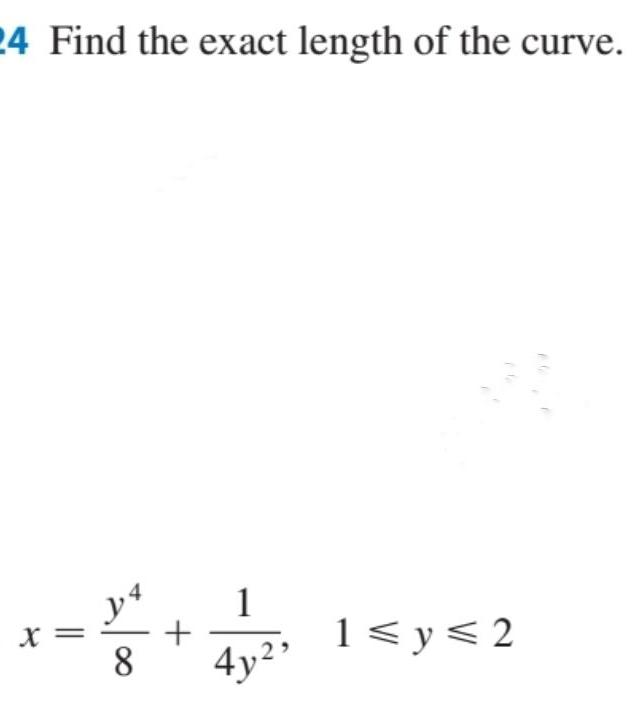

Calculus
Application of derivativesThe joint density function for random variables X, Y, and Z is f(x, y, z)= Cxyz if 0≤x≤1, 0 ≤ y ≤ 2, 0 ≤ z ≤ 2, and f(x, y, z) = 0 otherwise.
(a) Find the value of the constant C.
(b) Find P(X ≤ 1, Y ≤ 1, Z ≤ 1).
(c) Find P(X+Y+Z≤ 1).
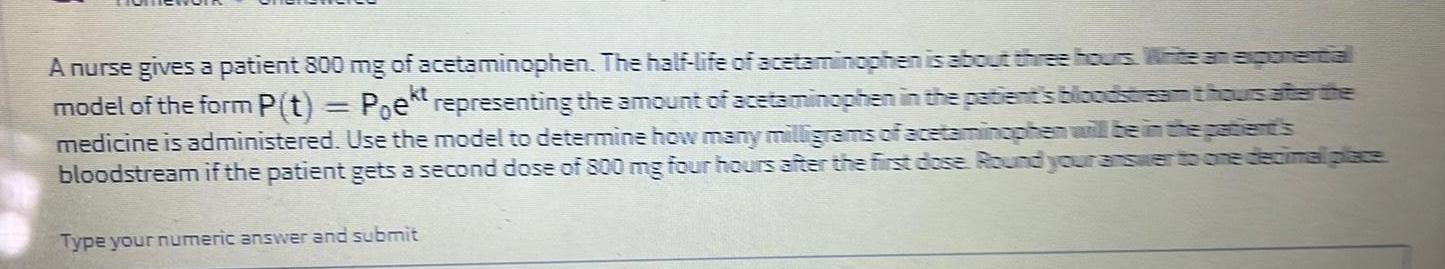
Calculus
Application of derivativesA nurse gives a patient 800 mg of acetaminophen. The half-life of acetaminophen is about the house axponential model of the form P(t) = Poet representing the amount of acetaminophen in the patient's bloodteam thousate te medicine is administered. Use the model to determine how many milligrams of acetaminophen will be in the patients
bloodstream if the patient gets a second dose of 800 mg four hours after the first dose Round your answer to one decinal place.

Calculus
Application of derivativesA cylindrical tank with a radius 3 m is being filled with water at a rate of 4 m³/min. How fast is the height of the water increasing (in m/min)?|
m/min

Calculus
Application of derivativesA company makes two types of biscuits: Jumbo and Regular. The oven can cook at most 300 biscuits per day. Each jumbo biscuit requires 2 oz of flour, each regular biscuit requires 1 oz of flour, and there is 500 oz of flour available. The income from each jumbo biscuit is $0.07 and from each regular biscuit is $0.05. How many of each size biscuit should be made to maximize income? What is the maximum income?
The company should make ( ) jumbo and regular biscuits.
(Type whole numbers.)
The maximum income is $

Calculus
Application of derivativesSolve the exact equation
(x²e^ x^2+y (2x² + 3) + 4x) dx + (x³e^ x^2+y - 12y²) dy.
The solutions are of the form F(x, y) = c, where
F(x, y)=


Calculus
Application of derivativesConsider the autonomous equation
dx/dt = (1-x²)e^x.
(a) Sketch the phase line for the equation. Label each equilibrium as a sink (stable), source (unstable), or node (neither).
b) Predict the asymptotic behavior as t→∝ of the solution satisfying x(0) = 0.
c) Predict the asymptotic behavior as t→∝ of the solution satisfying x(0) = -5.

Calculus
Application of derivativesUse the definition of a logarithm to rewrite the equation as an exponential equation. log196 (14) = 1/2

Calculus
Application of derivativesOne hour after the start of an experiment there were 105 bacteria and after five hours the count was 8505. Assuming that the population grows exponentially, that is according to the law f(x)= ae^rx, find the initial population and the population after 10 hours.
Calculus
Application of derivativesFind cif a = 2.34 mi, b 3.68 mi and ∠C= 40.7 degrees Enter crounded to 3 decimal places.

Calculus
Application of derivativesA company produces two types of solar panels per year. x thousand of type A and y thousand of type B. The revenue and cost equations, in millions of dollars, for the year are given as follows
R(x,y) = 3x + 5y
C(x,y)=x²-3xy + 8y² +11x-76y-8
Determine how many of each type of solar panel should be produced per year to maximize profit.

Calculus
Application of derivativesFind the equation of the tangent line to the graph of the given function at the specified point.
15.) y = x² + 3x + 4, at (1, 2)

Calculus
Application of derivativesAn object at the origin at time t = 0 has velocity measured in meters per second,
t 20 if 0 ≤ t ≤ 60
v(t) = {3 if 60 < t ≤ 120
9 - t 20 if 120 < t
When, if ever, does the object return to the origin? t =

Calculus
Application of derivativesA 70 lb weight stretches a spring 10 feet. The weight hangs vertically from the spring and a damping force numerically equal to 7 2√5 times the instantaneous velocity acts on the system. The weight is released from 5 feet above the equilibrium position with a downward velocity of 22 ft/s.
(a) Determine the time (in seconds) at which the mass passes through the equilibrium position.
(b) Find the time (in seconds) at which the mass attains its extreme displacement from the equilibrium position.
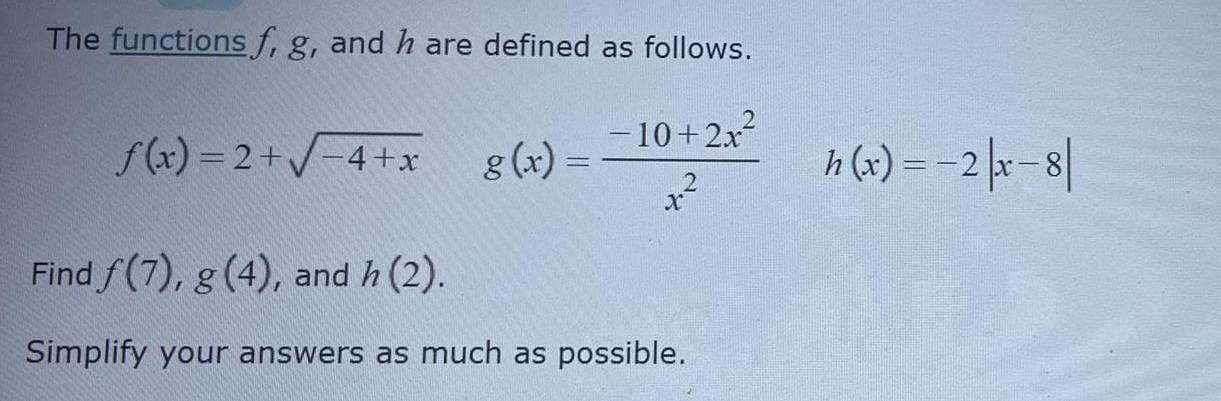
Calculus
Application of derivativesThe functions f, g, and h are defined as follows.
f(x)=2+√-4+x g(x) = −10+2x² x² h(x) = -2 |x-8|
Find f(7), g(4), and h (2).
Simplify your answers as much as possible.

Calculus
Application of derivativesThe function fis defined below.
f(x) = x² +6x-16 x²-4
Find all values of x that are NOT in the domain of f.
If there is more than one value, separate them with commas.
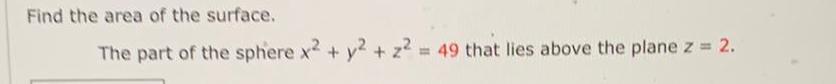
Calculus
Application of derivativesFind the area of the surface.
The part of the sphere x2 + y2 + z² = 49 that lies above the plane z = 2.
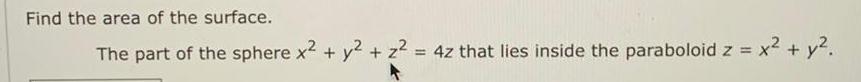
Calculus
Application of derivativesFind the area of the surface.
The part of the sphere x² + y² + z² = 4z that lies inside the paraboloid z = x² + y².

Calculus
Application of derivativesThe exposure index EI for a 35-millimeter camera is a measurement of the amount of light that hits the film. It is determined by the equation EI = log₂ (+). where f is the "f-stop" setting on the camera and t is the exposure time in seconds. Suppose the f-stop setting is 8 and the exposure time is 4 seconds. What will the resulting exposure index be?

Calculus
Application of derivativesIf f(x) is a differentiable function and f' (c) = 0 at an interior point c of f's domain, and if f" (x) > 0 for all x in the domain, must f have a local minimum at x = c? Explain.

Calculus
Application of derivativesThe function y = cotx - 2√3 3csc x has an absolute maximum value on the interval 0<x< π. Find it.

Calculus
Application of derivativesA team of engineers is testing an experimental high-voltage fuel cell with a potential application as an emergency back-up power supply in cell phone transmission towers. Unfortunately, the voltage of the prototype cell drops with time according to the equation V(t) = -0.0306t3 + 0.373t2 - 2.16t+ 15.1, where V is in volts and t is the time of operation in hours. The cell provides useful power as long as the voltage remains above <v> volts. Use Newton's method to find the useful working time of the cell to the nearest tenth of an hour (that is, solve V(t) = 6.6 volts). Use t = 7 hours as your initial guess and show all your work.


Calculus
Application of derivativesSolve the system of equations.
3x-5y-2z=2
9x-15y-6z=7
2x-3y-5z=4
Select the correct choice below and fill in any answer boxes within your choice.
A. There is one solution. The solution is
(Type exact answers in simplified form.)
B. There are infinitely many solutions. The solutions are (z), where z is any real number.
(Type exact answers in simplified form.)
C. There is no solution.

Calculus
Application of derivativesIn a certain country people own a total of about 348 million fish, cats, and dogs as pets. The number of fish owned is 14 million more than the total number of cats and dogs owned, and 17 million more cats are owned than dogs. How many of each type of pet do people in this country own?
The number of fish owned by people in this country is million, the number of cats owned by people is million, the number of dogs owned by people is million.
(Type whole numbers.)

Calculus
Application of derivativesSuppose a person 5 feet tall throws a rock vertically upward. Determine the initial velocity, vo, of the rock, if the rock reaches a maximum height of 39.52 feet. Round the solution to the nearest integer.
v0 = feet per second

Calculus
Application of derivativesSuppose you are driving along 1-95 at 134 kilometers per hour, when you notice a large board in the road ahead. You immediately begin to brake. If the large board is 52 meters ahead at the moment you begin to brake, what constant deacceleration is required in order to stop the car before striking the large board. Round the solution to the nearest hundredth, if necessary.
acceleration = meters per second squared