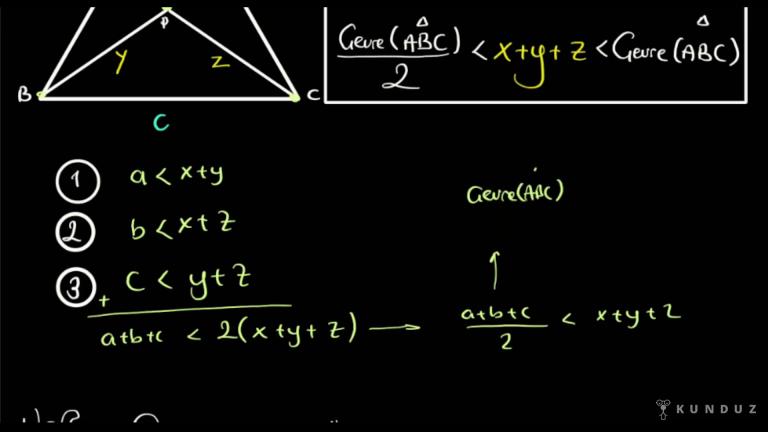Merhaba arkadaşlar, şimdi üçgende temel kavramlarda üçgen eşitsizliği konusundaysa şimdi üçgen dediğimiz şeklin nasıl oluştuğunu anlattım.
Ne gibi sınıflandırmalar sonucu oluşur?
Şimdi bunu inceleyeceğiz.
Üçgende eşitsizlik alt başlığında bu incelememiz gereken iki tane sınırlandırma vardır.
Dostlar şimdi birinci sınırlandırma ana sınırlandırma maz kenar sınırlandırması dır.
Dostlar kenar sınırlandırması dediğimiz sen herhangi üç çubukla acaba üçgen yapıyor musun yapamıyor musun?
Bunu inceler açığı ile sınırlandırma dostlar.
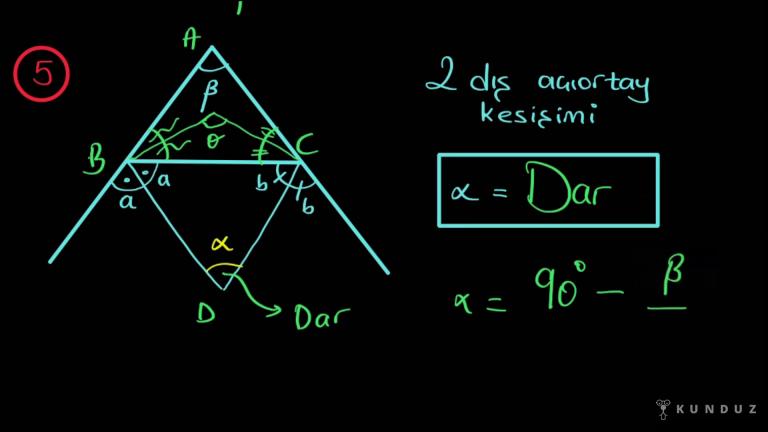
Kenar sınırlandırılmasına ek olarak der ki ben bu açıyı 90 dereceden küçük, 90 dereceden büyük, şu açıdan büyük, şu açıdan küçük diyerekten ayriyeten ekstradan bir sınırlandırma getirir.
Kenar sınırlandırması zaten yapacağım.
Bir de üstüne diyecek ki bu açığım şundan büyüktür, o zaman yeni aralıkları nelerdir diyecek.
İşte meselemiz bütün eşitsizlik konusunu Temel'i bunlara dayanmaktadır.
Üçgenin nasıl oluştuğunu, ne gibi sınıflandırmalar dahilinde olduğunu incelememiz gerekiyor.
Çünkü üçgen dediğimiz kapalı bir şekilde demek ki bunun belirli sınırları olmalı.
İşte bu konu da bunun üzerine doğmuştur.
Başlayalım.
Kenar sınırlandırması dedik.
Üçgende kenar sınırlandırması şöyledir şöyle bir kural temelinden gelmiştir bir kenar uzunluğu diğer iki kenar uzunluğunun toplamından küçüktür.
Bir üçgen de dostlar tekrar ediyorum herhangi bir kenar uzunluğu aldınız.
Herhangi bir kenar uzunluğu kesinlikle diğer iki o kenarın toplam uzunluğundan küçüktür.
Bu kadar yani siz A'ya, B'ye, C'ye göre herhangi bir kenara aldığınızda şunu bilmelisiniz ki ay aldıysanız diğer iki kenarın toplamından küçük sinüs b aldıysanız diğer iki kenar olan ABC'nin toplamından küçük bir şey bulmalısınız.
C'ye aldıysanız da diğer iki kenar olan ve beyni toplamından daha küçük bir değer olmalısınız.
Tamam, şimdi burada herhangi bir tane harfi yalnız bırakmaya çalışalım.
Bu harfler de kenar uzunlukları belirtiyor.
Bu arada burada mesela a yanlız aynı şekilde burada daha yalnız bırakalım burada daha yalnız bırakırsın.
Bırakalım bu tarafta ayağınız bırakırsam ne elde edeceğim dostlar bu tarafa yazıyorum.
B eksi c küçüktür a olur.
Şunu buraya yazsam ne elde edeceğim?
C Eksi B küçüktür a elde edeceğim.
Şimdi buradaki değerler A'nın neden büyük olduğunu gösteriyor.
Şurada ki üstteki değer de A'nın neyden küçük olduğunu gösteriyor.
İşte şimdi bir kenar için baktığınız zaman dostlar bu taraf size A'nın alabileceği minimum değeri, minimum aralığı gösterir.
Burada da A'nın alacağı maksimum değer aralığını bulmuş olursunuz.
Aslında kural sadece bunun temelinden gelişmiştir ve aslında sadece şu eşitsizlikleri ortak çözümüyle kurala ulaşabiliyoruz.
Buradaki 3 eşitsizlikten dostlar üçgen eşitsizliği elde edilir.
Gördüğünüz gibi kuralımız şu üstte gördüğünüz maksimum sınırımız olan B artı C ve şurada gördüğünüz A dediğim şey B eksi C eden ya da C eksi B eden küçük.
O zaman mutlak değer içine alırsam ki almalıyım çünkü uzunluğu mu negatif bulamam?
B Eksi c eden de mutlak değer içersinde büyük olmalı.
Baktığım uzunluk ise tamam.
Şimdi burada şuna dikkat edelim.
Mesela negatif bulunamaz dedim de 0 bulunabilir mi?
Evet bulunur.
B ve C birbirlerine eşitse atıyorum burası 3 santim, burası 3 santim ise bunlar demek ki birbirine eşit.
O zaman üç eksi üçten burası 0 olabilir mesele ama negatif olamayacağını görelim.
Dikkatli olalım burada.
Burada şunu söyleyelim artık şu denklemi sözlü olarak şöyle yorumlayabiliriz ki bir kenar uzunluğuna baktığım zaman yani ayı ele aldığım zaman farz edelim ki bu ana uzunluğu kesinlikle diğer kenarlarını yani B ve C'nin farkından büyüktür.
Diğer kenarlarının toplamı yani B artı cepheden de kesinlikle küçük olmalı.
Bakın burada eşitlik yok, burada eşitlik yok.
Diğer iki kenarın toplamına eşit olamaz.
Diğer iki kenarın farkına eşit olan maz çok önemli buralar.
Şimdi geçelim buraların nereden bulunduğuna gelelim.
Şimdi minimum değer belirttik, maksimum değer belirttik.
Nereden geldiklerine bakalım.
Şimdi ana amacımız 2 tane çocuğumuz var.
Tamam B ve C uzunlukları da bu uçları A ve B diğer uçları da ortak olacak şekilde.
Böyle birleştirdim.
Kaynaştık dım oraya.
Ana amacım şu diyorum ki A ve B birleştirmek için acaba bu uzunluk ne kadar olabilir, ne kadar olmalı?
Şimdi buradaki amacın da minimuma araştırmak tamam mı?
Siz A ve B'yi birleştirmek için minimum ne yapmalısınız?
Şimdi bunu birleştirmek için şu doğru saldığı yapıyorum da bunu minimum olması için ne yapmalıyım?
Bunların arasındaki açıyı azaltmalı.
Yani bunları birbirlerine yakınlaştırma alayım.
Yani aralarındaki açıyı azaltarak bunları birbirlerine yaklaştırıyor Rûm ve aralarındaki minimum durumu inceliyor.
Buradaki minimum durum bunların arasının 0 derece olduğu durumdur.
Dostlar bunların arasındaki açıyı 0 yaparak siz A ve B'yi birleştirmek için gereken minimum çubuk uzunluğunu hesaplamış oluyorsunuz.
Burada şu uzunluğun Bey'di, bu uzunluğu, pardon şu uzunluğu neydi?
Siz B dengeyi çıkarırsanız şurada gördüğünüz AB'ye hesaplamış olmuyor musunuz?
Evet, bu A ve B arası mesafe b, x, c eden yani aslında bizim üst üste baştan beri anlattığımız kuraldan geliyor.
E peki maksimum durum nereden geliyor?
İşte Maxxi nın durum da benzer bir şekilde ne yapacağım?
Bunların arasındaki uzunluğun maksimum olmasını istiyorum.
O zaman bu aralarındaki açıyı arttırır ki bunlar birbirlerinden uzaklaştı, arttırıyor, rom arttırıyor.
Oramar duruyorum maksimum olan 180 dereceye getiriyorum.
Maksimum olan 180 dereceye getirdiğimde.
A ve B arasındaki maksimum uzunluğu bulmuş olur.
B burasıydı.
C uzunluğu da burasıydı.
O zaman A ve B arası A ve B noktaları arasındaki mesafe bu ikisinin toplamı kadar oldu.
B artı C bu iki A ve B noktasını birleştirmek için gereken maksimum şey olur.
Dostlar B artacağı dediğim yani üste kuralda gösterdiğimiz şu b+, c altta anlattığım yerden b eksi C'yi de aynen buradan gelmekte dostlar.
Şimdi şuraya geçelim.
Burada da şunu gösterelim ki bu üç parça üçgen meydana getirebilir mi?
Diyeceğim ki üç tane çubuk aldım.
Acaba bunlar üçgen meydana getirebiliyor.
İşte ana meselemiz zaten bunu anlatmak, bunu göstermek.
Buradan dostlar herhangi bir şeyi alıp baktığınız zaman 5 metreyi seçip bunun aralığına, bunun eşitsizliğini yarattığınız zaman olup olmadığına baktığınız zaman artık diğer kenarlar için ayrı ayrı tekrar bakmanız gerekiyor.
Biri oluyorsa diğerleri de olacaktır.
Yani diyeceğim ki evet bu diğer kenar zorluklarıyla bir üçgen oluşturuyor.
O zaman diğerlerini ayrı ayrı bakmama gerek yok.
Bununla tekrar bir üçgen oluşturuyor mu diye.
Eğer oluşturmuyor ise da diğerlerine tekrar bakmama gerek yok.
Kesinlikle oluş durmayacaktır.
Yani siz ister 5'e bakarak başlayın, ister 8'de basarak bakarak başlayın, isterseniz 40 metre uzunluğuna bakarak başlayın 8'e seçelim.
Sekizi koydum ortaya.
Diyeceğim ki sekiz diğer iki kenarın farkından büyük olmalı, toplamından küçük.
Diğer uzunlukları beş ve 40 40'tan beşe çıkarırsan otuz beş eder.
Kırk ve beşi toplasan 45 sekiz.
Bu aralıkta mı dostlar?
Hayır, değil.
Demek ki ben bunlarla işte oluşturamıyor.
Gördüğünüz gibi bu 40 metre bir ucu burada kalıyor.
Siz bu ikisini bir geçirirseniz maksimum uzunluğunu.
Mesela buraya kadar gelecek işte bu iki ucu geliştirememiş olacaksınız.
Bir örnek verelim.
Çevresi 20 santim olan üçgenin kenan uzunlukları aşağıdaki sıralı uzunluk lardan hangileri olamaz dedim.
Şimdi burada ana amacımız şu çevresini biliyorum artık kenarlarının uzunlukları da biliyorum.
Buradaki meselem şu.
Nat Çubukları mı, nasıl seçmeliyiz?
Çevresini bildiğim bir üçgende.
Asıl mesele buna benziyor biraz.
Şimdi burada beş beş on üçgenine baktığım zaman ne yapacağım?
Herhangi birini seçiniz, ister beşi seçin, ister onu başlayalım, onu seçtim koydum ortaya.
Diğer iki kenarın farkı 5 ve 5'in farkı sıfır mı?
Çok güzel.
Burası uygun 0 küçüktür.
10.
Gelelim diğer tarafa 5 artı 5 yazacağım.
Diğer iki kenarın toplamı 10 küçüktür, 10 oldu.
Öyle bir şey olamaz.
10 küçüktür, 10 değil, 10 10'dan küçük değildir.
O zaman ben bunlarla yapamam.
Doğru mu?
Geldim 5 7 8'e şöyle göstereyim.
Bunun için 5, 7, 8 herhangi birini seçiyorum.
5 yi seçtim koydum ortaya.
Tamam geldim 7 ve 8 kaldı.
Diğer kenarları çıkartalım, üç toplayalım 15 5.
Bu aralıkta mı?
Evet, 5 3'ten büyük.
Evet, 5 15'ten küçük.
Tamam dostum sen olursun diyeceğim.
Gelelim diğer şıkkı mıza dostlar.
Diğer şarkımız da 2 var, 7 var, on bir var.
Seçtim 7'yi ortaya koydum.
Diğer iki kenarın farkı 11 eksi 2'den 9 mu?
Evet.
Diğer kenarlarının toplamı 13 mü?
Tamam.
On bir artı ilk yedi dediğim bu aralıkta mı?
Hayır değil.
9 küçüktür, yedi diye bir şey yapamam.
O zaman bunu da alamam dostlar.
Meselemiz böyledir.
Açı sınırlandırın, kenar sınırlandırması bize bunu anlatır.
Şimdi burada şu kuralı da göstermek istiyorum.
Bir A-B-C üçgeni içerisinde herhangi bir nokta aldıysanız ve bunu köşeler ile birleştirdi iseniz A, B, C köşeleri ile birleştirdim.
A, p uzunluğu IX, b, p uzunluğu y cephe uzunluğu Z'ye olsun dedim.
Abc'nin kenarları A-B-C olarak verilsin.
Burada kuralımız şudur.
Içerde aldığımız bu üç tane parçanın toplamı belirli bir sınırlandırma içersinde olmalı.
Çünkü üçgen kapalı bir şekil, üçgen kapalı bir şekilde.
Bunun da maksimum ve minimum değerleri vardır.
İçeride aldığım nokta ve Köselerli birleştirince.
İşte ilk startı y artı z dediğim şey ABC'nin çevre ikisinden büyük, çevresinden küçük olmalı.
Bu da şuradan geliyor dostlar şu üçgen de kenar eşitsizliği yazalım mesela aşağıya bak saydım.
Ne diyecektim?
Diğer iki kenarın toplamından küçük.
İlk jartiyer eden küçük şu üç gene bak saydım ne diyecektim?
B Uzunluğunu bakarsam şu uzunluğa bakarsan diyecektim ki ilk artı Zeydan kesinlikle küçük.
Şuraya gelseydim diyecektim ki C küçüktür kesinlikle diğer iki kenar ona y vezni toplamı.
Doğru mu?
E Burada şunlara bir taraf tarafa toplar mısınız dostlar?
A artı b artı c etti bu tarafa geldim.
2 parantezin iki tane x var, iki tane y var, iki tane Z var.
Ben iki partiyi Artı Z'yi araştırıyorum burada bir yalnız bırakayım.
O zaman A artı veya artı C bölüğü 2 küçüktür.
X artı y artı z işte zaten bu dediğim şu içerde eşitsizlik yaparak sizin bulabileceğiniz bir şey artı bir artı c dediğim neydi dostlar?
Çevre A-B-C.
Ve bunu ikiye böl demiş.
Ben de zaten onu söyledim, bakın aynı şeyi bulduk dostlar.
Tamam IX artı y, artı Z.
Bu kural buradan gelmektedir dostlar.
Ne gibi sınıflandırmalar sonucu oluşur?
Şimdi bunu inceleyeceğiz.
Üçgende eşitsizlik alt başlığında bu incelememiz gereken iki tane sınırlandırma vardır.
Dostlar şimdi birinci sınırlandırma ana sınırlandırma maz kenar sınırlandırması dır.
Dostlar kenar sınırlandırması dediğimiz sen herhangi üç çubukla acaba üçgen yapıyor musun yapamıyor musun?
Bunu inceler açığı ile sınırlandırma dostlar.
Kenar sınırlandırılmasına ek olarak der ki ben bu açıyı 90 dereceden küçük, 90 dereceden büyük, şu açıdan büyük, şu açıdan küçük diyerekten ayriyeten ekstradan bir sınırlandırma getirir.
Kenar sınırlandırması zaten yapacağım.
Bir de üstüne diyecek ki bu açığım şundan büyüktür, o zaman yeni aralıkları nelerdir diyecek.
İşte meselemiz bütün eşitsizlik konusunu Temel'i bunlara dayanmaktadır.
Üçgenin nasıl oluştuğunu, ne gibi sınıflandırmalar dahilinde olduğunu incelememiz gerekiyor.
Çünkü üçgen dediğimiz kapalı bir şekilde demek ki bunun belirli sınırları olmalı.
İşte bu konu da bunun üzerine doğmuştur.
Başlayalım.
Kenar sınırlandırması dedik.
Üçgende kenar sınırlandırması şöyledir şöyle bir kural temelinden gelmiştir bir kenar uzunluğu diğer iki kenar uzunluğunun toplamından küçüktür.
Bir üçgen de dostlar tekrar ediyorum herhangi bir kenar uzunluğu aldınız.
Herhangi bir kenar uzunluğu kesinlikle diğer iki o kenarın toplam uzunluğundan küçüktür.
Bu kadar yani siz A'ya, B'ye, C'ye göre herhangi bir kenara aldığınızda şunu bilmelisiniz ki ay aldıysanız diğer iki kenarın toplamından küçük sinüs b aldıysanız diğer iki kenar olan ABC'nin toplamından küçük bir şey bulmalısınız.
C'ye aldıysanız da diğer iki kenar olan ve beyni toplamından daha küçük bir değer olmalısınız.
Tamam, şimdi burada herhangi bir tane harfi yalnız bırakmaya çalışalım.
Bu harfler de kenar uzunlukları belirtiyor.
Bu arada burada mesela a yanlız aynı şekilde burada daha yalnız bırakalım burada daha yalnız bırakırsın.
Bırakalım bu tarafta ayağınız bırakırsam ne elde edeceğim dostlar bu tarafa yazıyorum.
B eksi c küçüktür a olur.
Şunu buraya yazsam ne elde edeceğim?
C Eksi B küçüktür a elde edeceğim.
Şimdi buradaki değerler A'nın neden büyük olduğunu gösteriyor.
Şurada ki üstteki değer de A'nın neyden küçük olduğunu gösteriyor.
İşte şimdi bir kenar için baktığınız zaman dostlar bu taraf size A'nın alabileceği minimum değeri, minimum aralığı gösterir.
Burada da A'nın alacağı maksimum değer aralığını bulmuş olursunuz.
Aslında kural sadece bunun temelinden gelişmiştir ve aslında sadece şu eşitsizlikleri ortak çözümüyle kurala ulaşabiliyoruz.
Buradaki 3 eşitsizlikten dostlar üçgen eşitsizliği elde edilir.
Gördüğünüz gibi kuralımız şu üstte gördüğünüz maksimum sınırımız olan B artı C ve şurada gördüğünüz A dediğim şey B eksi C eden ya da C eksi B eden küçük.
O zaman mutlak değer içine alırsam ki almalıyım çünkü uzunluğu mu negatif bulamam?
B Eksi c eden de mutlak değer içersinde büyük olmalı.
Baktığım uzunluk ise tamam.
Şimdi burada şuna dikkat edelim.
Mesela negatif bulunamaz dedim de 0 bulunabilir mi?
Evet bulunur.
B ve C birbirlerine eşitse atıyorum burası 3 santim, burası 3 santim ise bunlar demek ki birbirine eşit.
O zaman üç eksi üçten burası 0 olabilir mesele ama negatif olamayacağını görelim.
Dikkatli olalım burada.
Burada şunu söyleyelim artık şu denklemi sözlü olarak şöyle yorumlayabiliriz ki bir kenar uzunluğuna baktığım zaman yani ayı ele aldığım zaman farz edelim ki bu ana uzunluğu kesinlikle diğer kenarlarını yani B ve C'nin farkından büyüktür.
Diğer kenarlarının toplamı yani B artı cepheden de kesinlikle küçük olmalı.
Bakın burada eşitlik yok, burada eşitlik yok.
Diğer iki kenarın toplamına eşit olamaz.
Diğer iki kenarın farkına eşit olan maz çok önemli buralar.
Şimdi geçelim buraların nereden bulunduğuna gelelim.
Şimdi minimum değer belirttik, maksimum değer belirttik.
Nereden geldiklerine bakalım.
Şimdi ana amacımız 2 tane çocuğumuz var.
Tamam B ve C uzunlukları da bu uçları A ve B diğer uçları da ortak olacak şekilde.
Böyle birleştirdim.
Kaynaştık dım oraya.
Ana amacım şu diyorum ki A ve B birleştirmek için acaba bu uzunluk ne kadar olabilir, ne kadar olmalı?
Şimdi buradaki amacın da minimuma araştırmak tamam mı?
Siz A ve B'yi birleştirmek için minimum ne yapmalısınız?
Şimdi bunu birleştirmek için şu doğru saldığı yapıyorum da bunu minimum olması için ne yapmalıyım?
Bunların arasındaki açıyı azaltmalı.
Yani bunları birbirlerine yakınlaştırma alayım.
Yani aralarındaki açıyı azaltarak bunları birbirlerine yaklaştırıyor Rûm ve aralarındaki minimum durumu inceliyor.
Buradaki minimum durum bunların arasının 0 derece olduğu durumdur.
Dostlar bunların arasındaki açıyı 0 yaparak siz A ve B'yi birleştirmek için gereken minimum çubuk uzunluğunu hesaplamış oluyorsunuz.
Burada şu uzunluğun Bey'di, bu uzunluğu, pardon şu uzunluğu neydi?
Siz B dengeyi çıkarırsanız şurada gördüğünüz AB'ye hesaplamış olmuyor musunuz?
Evet, bu A ve B arası mesafe b, x, c eden yani aslında bizim üst üste baştan beri anlattığımız kuraldan geliyor.
E peki maksimum durum nereden geliyor?
İşte Maxxi nın durum da benzer bir şekilde ne yapacağım?
Bunların arasındaki uzunluğun maksimum olmasını istiyorum.
O zaman bu aralarındaki açıyı arttırır ki bunlar birbirlerinden uzaklaştı, arttırıyor, rom arttırıyor.
Oramar duruyorum maksimum olan 180 dereceye getiriyorum.
Maksimum olan 180 dereceye getirdiğimde.
A ve B arasındaki maksimum uzunluğu bulmuş olur.
B burasıydı.
C uzunluğu da burasıydı.
O zaman A ve B arası A ve B noktaları arasındaki mesafe bu ikisinin toplamı kadar oldu.
B artı C bu iki A ve B noktasını birleştirmek için gereken maksimum şey olur.
Dostlar B artacağı dediğim yani üste kuralda gösterdiğimiz şu b+, c altta anlattığım yerden b eksi C'yi de aynen buradan gelmekte dostlar.
Şimdi şuraya geçelim.
Burada da şunu gösterelim ki bu üç parça üçgen meydana getirebilir mi?
Diyeceğim ki üç tane çubuk aldım.
Acaba bunlar üçgen meydana getirebiliyor.
İşte ana meselemiz zaten bunu anlatmak, bunu göstermek.
Buradan dostlar herhangi bir şeyi alıp baktığınız zaman 5 metreyi seçip bunun aralığına, bunun eşitsizliğini yarattığınız zaman olup olmadığına baktığınız zaman artık diğer kenarlar için ayrı ayrı tekrar bakmanız gerekiyor.
Biri oluyorsa diğerleri de olacaktır.
Yani diyeceğim ki evet bu diğer kenar zorluklarıyla bir üçgen oluşturuyor.
O zaman diğerlerini ayrı ayrı bakmama gerek yok.
Bununla tekrar bir üçgen oluşturuyor mu diye.
Eğer oluşturmuyor ise da diğerlerine tekrar bakmama gerek yok.
Kesinlikle oluş durmayacaktır.
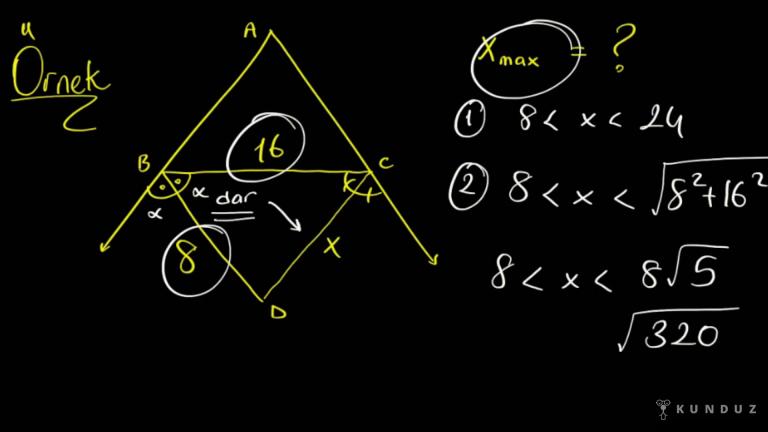
Yani siz ister 5'e bakarak başlayın, ister 8'de basarak bakarak başlayın, isterseniz 40 metre uzunluğuna bakarak başlayın 8'e seçelim.
Sekizi koydum ortaya.
Diyeceğim ki sekiz diğer iki kenarın farkından büyük olmalı, toplamından küçük.
Diğer uzunlukları beş ve 40 40'tan beşe çıkarırsan otuz beş eder.
Kırk ve beşi toplasan 45 sekiz.
Bu aralıkta mı dostlar?
Hayır, değil.
Demek ki ben bunlarla işte oluşturamıyor.
Gördüğünüz gibi bu 40 metre bir ucu burada kalıyor.
Siz bu ikisini bir geçirirseniz maksimum uzunluğunu.
Mesela buraya kadar gelecek işte bu iki ucu geliştirememiş olacaksınız.
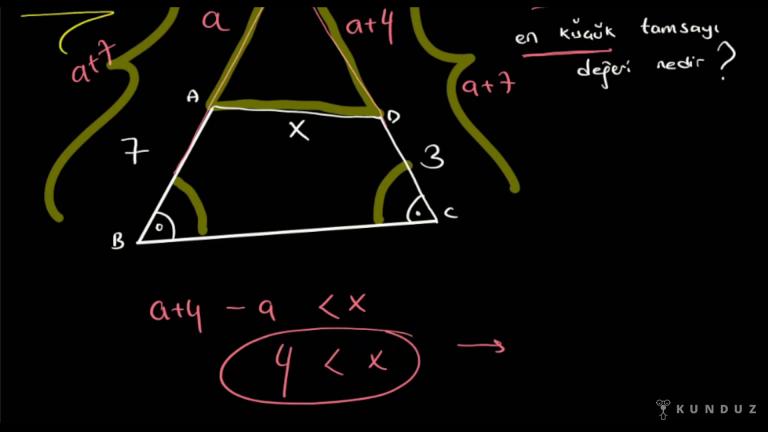
Bir örnek verelim.
Çevresi 20 santim olan üçgenin kenan uzunlukları aşağıdaki sıralı uzunluk lardan hangileri olamaz dedim.
Şimdi burada ana amacımız şu çevresini biliyorum artık kenarlarının uzunlukları da biliyorum.
Buradaki meselem şu.
Nat Çubukları mı, nasıl seçmeliyiz?
Çevresini bildiğim bir üçgende.
Asıl mesele buna benziyor biraz.
Şimdi burada beş beş on üçgenine baktığım zaman ne yapacağım?
Herhangi birini seçiniz, ister beşi seçin, ister onu başlayalım, onu seçtim koydum ortaya.
Diğer iki kenarın farkı 5 ve 5'in farkı sıfır mı?
Çok güzel.
Burası uygun 0 küçüktür.
10.
Gelelim diğer tarafa 5 artı 5 yazacağım.
Diğer iki kenarın toplamı 10 küçüktür, 10 oldu.
Öyle bir şey olamaz.
10 küçüktür, 10 değil, 10 10'dan küçük değildir.
O zaman ben bunlarla yapamam.
Doğru mu?
Geldim 5 7 8'e şöyle göstereyim.
Bunun için 5, 7, 8 herhangi birini seçiyorum.
5 yi seçtim koydum ortaya.
Tamam geldim 7 ve 8 kaldı.
Diğer kenarları çıkartalım, üç toplayalım 15 5.
Bu aralıkta mı?
Evet, 5 3'ten büyük.
Evet, 5 15'ten küçük.
Tamam dostum sen olursun diyeceğim.
Gelelim diğer şıkkı mıza dostlar.
Diğer şarkımız da 2 var, 7 var, on bir var.
Seçtim 7'yi ortaya koydum.
Diğer iki kenarın farkı 11 eksi 2'den 9 mu?
Evet.
Diğer kenarlarının toplamı 13 mü?
Tamam.
On bir artı ilk yedi dediğim bu aralıkta mı?
Hayır değil.
9 küçüktür, yedi diye bir şey yapamam.
O zaman bunu da alamam dostlar.
Meselemiz böyledir.
Açı sınırlandırın, kenar sınırlandırması bize bunu anlatır.
Şimdi burada şu kuralı da göstermek istiyorum.
Bir A-B-C üçgeni içerisinde herhangi bir nokta aldıysanız ve bunu köşeler ile birleştirdi iseniz A, B, C köşeleri ile birleştirdim.
A, p uzunluğu IX, b, p uzunluğu y cephe uzunluğu Z'ye olsun dedim.
Abc'nin kenarları A-B-C olarak verilsin.
Burada kuralımız şudur.
Içerde aldığımız bu üç tane parçanın toplamı belirli bir sınırlandırma içersinde olmalı.
Çünkü üçgen kapalı bir şekil, üçgen kapalı bir şekilde.
Bunun da maksimum ve minimum değerleri vardır.
İçeride aldığım nokta ve Köselerli birleştirince.
İşte ilk startı y artı z dediğim şey ABC'nin çevre ikisinden büyük, çevresinden küçük olmalı.
Bu da şuradan geliyor dostlar şu üçgen de kenar eşitsizliği yazalım mesela aşağıya bak saydım.
Ne diyecektim?
Diğer iki kenarın toplamından küçük.
İlk jartiyer eden küçük şu üç gene bak saydım ne diyecektim?
B Uzunluğunu bakarsam şu uzunluğa bakarsan diyecektim ki ilk artı Zeydan kesinlikle küçük.
Şuraya gelseydim diyecektim ki C küçüktür kesinlikle diğer iki kenar ona y vezni toplamı.
Doğru mu?
E Burada şunlara bir taraf tarafa toplar mısınız dostlar?
A artı b artı c etti bu tarafa geldim.
2 parantezin iki tane x var, iki tane y var, iki tane Z var.
Ben iki partiyi Artı Z'yi araştırıyorum burada bir yalnız bırakayım.
O zaman A artı veya artı C bölüğü 2 küçüktür.
X artı y artı z işte zaten bu dediğim şu içerde eşitsizlik yaparak sizin bulabileceğiniz bir şey artı bir artı c dediğim neydi dostlar?
Çevre A-B-C.
Ve bunu ikiye böl demiş.
Ben de zaten onu söyledim, bakın aynı şeyi bulduk dostlar.
Tamam IX artı y, artı Z.
Bu kural buradan gelmektedir dostlar.
Sıkça Sorulan Sorular
Üçgen eşitsizliği nedir?
Düzlemde doğrusal olmayan herhangi 3 noktanın birleştirilmesi ile oluşan geometrik şekle üçgen deriz. Fakat herhangi 3 doğru parçasının birleşimi bir üçgen oluşturmaz. Üçgenlerin kenarları arasında bir kural vardır. Üçgende herhangi bir kenarın uzunluğu diğer iki kenarın uzunluğu toplamından küçük, farkından büyük olamaz.
Örneğin ABC üçgeninde;
a kenarı için üçgen eşitsizliği : |b - c| < a < |b + c|
b kenarı için üçgen eşitsizliği: |a - c| < b < |a + c|
c kenarı için üçgen eşitsizliği: |a - b| < c < |a + b|