Merhaba.
Kunduz'un matematik dersi.
Çemberin merkezi yeri, çapı ve çapı konu anlatım videosuna hoşgeldiniz.
Düzlemde sabit bir noktadan eşit uzaklıktaki noktaların oluşturduğu geometrik şekle çember diyoruz.
Çemberi çözebilmek için çan birimizin merkezini işaretliyor arkadaşlar.
Daha sonra.
Bu noktadan eşit uzaklıktaki noktadır.
Birleştirerek çemberi oluşturuyoruz.
Şimdi merkezden çember üzerindeki bir noktaya olan uzaklığa yarıçap diyoruz arkadaşlar.
Evet şimdi buraya a dersem o a uzunluğu çam birimizin yarıçapı oluyor.
R yarıçap.
Aynı şekilde.
Çam Bilim Merkezinden 10 noktasından çember üzerindeki farklı bir noktaya bir doğru parçası çizdiğimiz de yine bu doğru parçasının uzunluğu da çemberin yarıçapı kadar oluyor arkadaşlar.
Bir de çemberin isimden bahsedebiliriz.
Çapından bahsedebiliriz arkadaşlar çapta.
Çemberin merkezinden geçen ve başlangıç ve bitiş noktaları çemberin üzerinde olan doğru parçalarıdır.
Şimdi bu şekle baktığımda CD dediğimde CD'yi doğru parçası çemberin merkezinden geçtiği için C'de doğru parçası çemberin çapı dır.
Çemberin çapı dar arkadaşlar büyüklüğü ile gösterilir ve uzunluğu çemberin merkezinden çemberin önündeki bir noktaya çizilen doğru parçaları yarı çap kadardır.
O zaman O.C.
Ve O.D doğru parçaların uzunlukları R.
Ise çapın uzunluğu 2 r dir.
Arkadaşlar.
Küçük R yeri çap büyük, r ise yarı çapın iki katı ve çap oluyor arkadaşlar şimdi.
Peki ben bu çemberi nasıl çizeceğim?
Nasıl bileceğim?
Eşit nokta uzaklıktaki noktaları da çizeceğim.
Çember çizmek için.
Arkadaşlar pergel dediğimiz aleti kullanıyoruz.
Pergelin bir tarafında kalem var, bir tarafında küçük demir bir uç var.
Bu ucu arkadaşlar çemberin merkezi olan noktayı koyup.
Kalem ile bu ucun arasını istediğim çemberin.
Yarıçapı kadar açıyorum.
R yarıçaplı yani 3 santimetre yarıçaplı bir çember çizecek isem, arada aradaki mesafe 3 santimetre olacak. 5 santimetrelik bir çember istiyorsam yarıçapı 5 santimetre olan aradaki mesafe 5 santimetre olacak.
Yani yarıçap kadar olacak.
Daha sonra.
Bu merkezi ucu merkeze getiriyorum arkadaşlar.
Evet bakın bir ucu merkezde iken.
Merkez noktasını batırıp, sabitleyerek, kalemi etrafında dolandırarak çemberi çizmiş oluyorum.
Şimdi ne demiştik arkadaşlar?
Çemberin merkezinden üzerindeki bir noktaya olan uzaklığa yarıçap diyoruz.
Başlangıç ve bitiş noktaları çemberin üzerinde olan ve çemberin merkezinden geçen doğru parçalarına BC, doğru parçasını ise çap diyoruz.
Çapı Büyük ray ile gösteriyoruz ve uzunluğu yarı çapın 2 katıdır arkadaşlar.
Çünkü o bir yarıçap dır, o bir yarıçap dır.
Behice Y.
Uzunluğunun tamamı da yarı çapın 2 katıdır.
Arkadaşlar yanda verilen çemberde yarı çap ve çap olan doğru parçalarını bulalım.
Şimdi çember mizin merkezi neresi?
Arkadaşlar o noktası yarı çapı var.
O da başlayıp çan ve iz üzerindeki noktalarda biten doğru parçaları yarıçapı vardır.
O a bir yarıçap dır.
O bey bir yarı chapter.
O odaya bir yarı yaptır.
Sonra bakıyorum o odaya bir yeri yaptır.
Sonra devam ediyorum.
O ev bir yarıçap dır ve o bir yarıçap dır arkadaşlar.
Peki çapları hangisi?
Çapları merkezden geçecek ve başlangıç ve bitiş noktaları çember üzerinde olacak.
Bakın HG doğru parçasının başlangıç ve bitiş noktaları çember üzerinde.
Ama merkezden geçmediği için ben çapı olduğunu söyleyebilir miyim?
Söyleyemem, çünkü çapın merkezden geçmesi gerekir.
O zaman A en doğru parçasına bakıyorum.
A En doğru parçasının başlangıç ve bitiş noktaları çember üzerinde ve merkezden geçiyor.
A Ey çap arkadaşlar.
Sonra bakıyorum devam eden b.
F Doğru parçası var.
B f doğru parçasının da başlangıç ve bitiş noktaları çember üzerinde ve merkezden geçiyor. A ev ve b f doğru parçaları çap dır arkadaşlar.
Yarıçapı dört birim olan bir çember çizin.
Şimdi arkadaşlar birim kredi zeminle.
Bir merkezi işaret diyorum.
Sonra pergelin ucunu.
4 1 kadar açıp.
Pergel mi?
O noktasında ser sabit değil.
Çevirerek yarıçapı dört birim olan çemberi çizmiş oluyorum.
Bakın hangi noktadan çizer isem çizdiğim.
4 birim oluyor arkadaşlar.
Çünkü merkezden çember üzerindeki hangi noktaya gidersem gideyim, yarıçap kadardır arkadaşlar.
Uçan biriminde yarıçapı dört birim olduğu için o noktasından bu çizdiğim bütün doğru parçalarının uzunlukları dört birim.
Olacak arkadaşlar.
Çemberin içerisinde kalan bölgeye iç bölge diyoruz.
İç bölge burası dışarısında kalan bölgeye dış bölge diyoruz.
Bir de arkadaşlar çemberin kendisi var.
Yani noktalar çemberin içerisinde olabilir, dışında olabilir ya da üzerinde olabilir arkadaşlar.
Bir çemberin kendisi ile iç bölgesinin birleşiminden oluşan şekli ise dahil ediyoruz.
Çemberin içi boştur arkadaşlar.
Dairenin ise içi doludur.
Mesela düşünecek olursak.
Simit nedir?
Bir çan vardir.
Ama.
Madeni parayı düşünürsek.
Madeni para.
Madeni paranın içi dolu olduğu için bir dairedir.
Simit yüzük düşünebilirsiniz.
Yüzüğü simit, yüzük gibi şeyler içi boş olduğu içi çam vardır, içi dolu olanlar dairedir arkadaşlar.
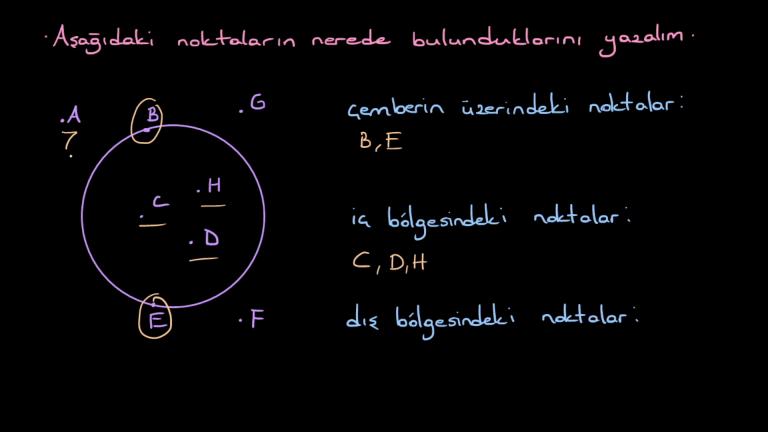
Aşağıdaki noktaların nerede bulunduklarını yazalım şimdi.
Çemberin üzerindeki noktalar hangileri?
Bakıyorum beş noktası çemberin düzeninde en noktası çemberin üzerinde.
O zaman B ve en noktaları çemberin üzerindedir.
Çemberin iç bölgesinde çemberin sınırladığı alan içerisinde kalan noktalar ise C, D ve H noktaları.
C, D ve H noktaları.
Dıştaki noktalar ise A noktası.
G noktası.
F noktası noktası.
F noktası gay noktasıdır.
Kunduz'un matematik dersi.
Çemberin merkezi yeri, çapı ve çapı konu anlatım videosuna hoşgeldiniz.
Düzlemde sabit bir noktadan eşit uzaklıktaki noktaların oluşturduğu geometrik şekle çember diyoruz.
Çemberi çözebilmek için çan birimizin merkezini işaretliyor arkadaşlar.
Daha sonra.
Bu noktadan eşit uzaklıktaki noktadır.
Birleştirerek çemberi oluşturuyoruz.
Şimdi merkezden çember üzerindeki bir noktaya olan uzaklığa yarıçap diyoruz arkadaşlar.
Evet şimdi buraya a dersem o a uzunluğu çam birimizin yarıçapı oluyor.
R yarıçap.
Aynı şekilde.
Çam Bilim Merkezinden 10 noktasından çember üzerindeki farklı bir noktaya bir doğru parçası çizdiğimiz de yine bu doğru parçasının uzunluğu da çemberin yarıçapı kadar oluyor arkadaşlar.
Bir de çemberin isimden bahsedebiliriz.
Çapından bahsedebiliriz arkadaşlar çapta.
Çemberin merkezinden geçen ve başlangıç ve bitiş noktaları çemberin üzerinde olan doğru parçalarıdır.
Şimdi bu şekle baktığımda CD dediğimde CD'yi doğru parçası çemberin merkezinden geçtiği için C'de doğru parçası çemberin çapı dır.
Çemberin çapı dar arkadaşlar büyüklüğü ile gösterilir ve uzunluğu çemberin merkezinden çemberin önündeki bir noktaya çizilen doğru parçaları yarı çap kadardır.
O zaman O.C.
Ve O.D doğru parçaların uzunlukları R.
Ise çapın uzunluğu 2 r dir.
Arkadaşlar.
Küçük R yeri çap büyük, r ise yarı çapın iki katı ve çap oluyor arkadaşlar şimdi.
Peki ben bu çemberi nasıl çizeceğim?
Nasıl bileceğim?
Eşit nokta uzaklıktaki noktaları da çizeceğim.
Çember çizmek için.
Arkadaşlar pergel dediğimiz aleti kullanıyoruz.
Pergelin bir tarafında kalem var, bir tarafında küçük demir bir uç var.
Bu ucu arkadaşlar çemberin merkezi olan noktayı koyup.
Kalem ile bu ucun arasını istediğim çemberin.
Yarıçapı kadar açıyorum.
R yarıçaplı yani 3 santimetre yarıçaplı bir çember çizecek isem, arada aradaki mesafe 3 santimetre olacak. 5 santimetrelik bir çember istiyorsam yarıçapı 5 santimetre olan aradaki mesafe 5 santimetre olacak.
Yani yarıçap kadar olacak.
Daha sonra.
Bu merkezi ucu merkeze getiriyorum arkadaşlar.
Evet bakın bir ucu merkezde iken.
Merkez noktasını batırıp, sabitleyerek, kalemi etrafında dolandırarak çemberi çizmiş oluyorum.
Şimdi ne demiştik arkadaşlar?
Çemberin merkezinden üzerindeki bir noktaya olan uzaklığa yarıçap diyoruz.
Başlangıç ve bitiş noktaları çemberin üzerinde olan ve çemberin merkezinden geçen doğru parçalarına BC, doğru parçasını ise çap diyoruz.
Çapı Büyük ray ile gösteriyoruz ve uzunluğu yarı çapın 2 katıdır arkadaşlar.
Çünkü o bir yarıçap dır, o bir yarıçap dır.
Behice Y.
Uzunluğunun tamamı da yarı çapın 2 katıdır.
Arkadaşlar yanda verilen çemberde yarı çap ve çap olan doğru parçalarını bulalım.
Şimdi çember mizin merkezi neresi?
Arkadaşlar o noktası yarı çapı var.
O da başlayıp çan ve iz üzerindeki noktalarda biten doğru parçaları yarıçapı vardır.
O a bir yarıçap dır.
O bey bir yarı chapter.
O odaya bir yarı yaptır.
Sonra bakıyorum o odaya bir yeri yaptır.
Sonra devam ediyorum.
O ev bir yarıçap dır ve o bir yarıçap dır arkadaşlar.
Peki çapları hangisi?
Çapları merkezden geçecek ve başlangıç ve bitiş noktaları çember üzerinde olacak.
Bakın HG doğru parçasının başlangıç ve bitiş noktaları çember üzerinde.
Ama merkezden geçmediği için ben çapı olduğunu söyleyebilir miyim?
Söyleyemem, çünkü çapın merkezden geçmesi gerekir.
O zaman A en doğru parçasına bakıyorum.
A En doğru parçasının başlangıç ve bitiş noktaları çember üzerinde ve merkezden geçiyor.
A Ey çap arkadaşlar.
Sonra bakıyorum devam eden b.
F Doğru parçası var.
B f doğru parçasının da başlangıç ve bitiş noktaları çember üzerinde ve merkezden geçiyor. A ev ve b f doğru parçaları çap dır arkadaşlar.
Yarıçapı dört birim olan bir çember çizin.
Şimdi arkadaşlar birim kredi zeminle.
Bir merkezi işaret diyorum.
Sonra pergelin ucunu.
4 1 kadar açıp.
Pergel mi?
O noktasında ser sabit değil.
Çevirerek yarıçapı dört birim olan çemberi çizmiş oluyorum.
Bakın hangi noktadan çizer isem çizdiğim.
4 birim oluyor arkadaşlar.
Çünkü merkezden çember üzerindeki hangi noktaya gidersem gideyim, yarıçap kadardır arkadaşlar.
Uçan biriminde yarıçapı dört birim olduğu için o noktasından bu çizdiğim bütün doğru parçalarının uzunlukları dört birim.
Olacak arkadaşlar.
Çemberin içerisinde kalan bölgeye iç bölge diyoruz.
İç bölge burası dışarısında kalan bölgeye dış bölge diyoruz.
Bir de arkadaşlar çemberin kendisi var.
Yani noktalar çemberin içerisinde olabilir, dışında olabilir ya da üzerinde olabilir arkadaşlar.
Bir çemberin kendisi ile iç bölgesinin birleşiminden oluşan şekli ise dahil ediyoruz.
Çemberin içi boştur arkadaşlar.
Dairenin ise içi doludur.
Mesela düşünecek olursak.
Simit nedir?
Bir çan vardir.
Ama.
Madeni parayı düşünürsek.
Madeni para.
Madeni paranın içi dolu olduğu için bir dairedir.
Simit yüzük düşünebilirsiniz.
Yüzüğü simit, yüzük gibi şeyler içi boş olduğu içi çam vardır, içi dolu olanlar dairedir arkadaşlar.
Aşağıdaki noktaların nerede bulunduklarını yazalım şimdi.
Çemberin üzerindeki noktalar hangileri?
Bakıyorum beş noktası çemberin düzeninde en noktası çemberin üzerinde.
O zaman B ve en noktaları çemberin üzerindedir.
Çemberin iç bölgesinde çemberin sınırladığı alan içerisinde kalan noktalar ise C, D ve H noktaları.
C, D ve H noktaları.
Dıştaki noktalar ise A noktası.
G noktası.
F noktası noktası.
F noktası gay noktasıdır.