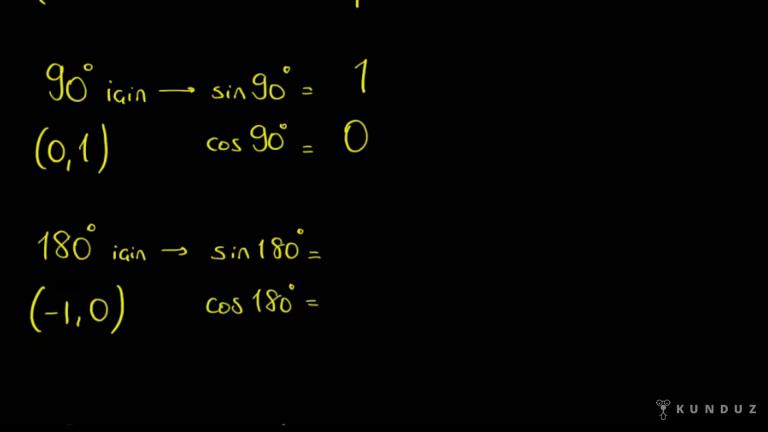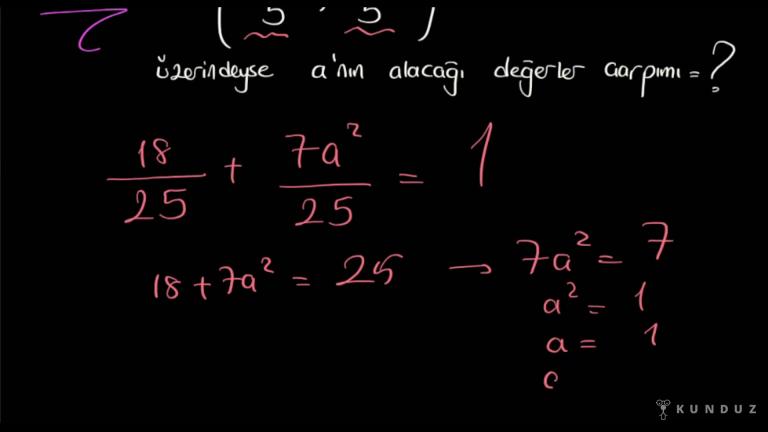Sevgili gençler, herkese merhabalar.
Bu dersimiz de trigonometrik fonksiyonların birim çember yardımıyla gösterilmesi konusuyla alakalı sorular çözmeye çalışacağız.
İsterseniz vakit kaybetmeden ilk sorumuz da başlayalım.
Diyor ki örnek 1'de şekilde verilen o merkezli birim çemberde AB'nin karesi, artı BBC'nin karesi toplamı kaçtır?
Şimdi burada tabii birim çember lafı bizim için önemli.
Neden?
Çünkü A o beynin, diğer taraftan çemberin, diğer taraflardan ölçülen yarıçap bağlarının hep bir olduğunu söylüyor bu bize.
Dolayısıyla gördüğünüz gibi şu ağaca uzunluğu bir artı birden iki birim olmuş oldu ve biliyorsunuz çember de her zaman çapı gören çevre açı doksan derecedir.
Yani buradaki c, b, a açısı.
Çapı gördüğü için hangi çapı acıya çapını gördüğü için kendisi 90 derecedir.
Dolayısıyla dikkat ederseniz eğer a bc üçgenin de 1 bir Pisagor bağıntısı yazarsak nedir o dik kenarlar?
Abe'nin karesi artı.
Diğer taraftan B.
Nin Karesi eşittir.
Hipotez 3'ün yani ikinin karesine.
Bu da benden istediği toplamıdır.
Arkadaşlar ikinin karesinden 4 olarak bulunmuş olur diyelim ve devam edelim.
Sıradaki sorumuza geçmiş olalım.
Diyor ki aşağıda o merkezli birim çember gösterilmiştir.
Buradaki t b o açısı.
Geçmiş derece ve P.
Hash O.
A'ya dik olduğuna göre A hash uzunluğunun çeşidini bulunuz demiş.
Evet, şimdi aslında yapacağımız şey şu hemen burada yine birim çember olduğunu bize söylemiş.
Ne yapacağız biz?
Hemen O ve P uzunluğunu birleştireceğiz.
Buranın da yine 1.
Olduğunu biliyorum değil mi?
Hemen bakın şurada İkiz Ken ağırlıklar var.
Burada 70 yetmiş açılar da yazılabilir.
Yani şu açı boyu yorum hemen içinde 70 derece imiş.
Dolayısı 70 yetmiş topladık, 140 yaptı.
D parçası şurası 180'den çıkardığımızda üst 40'ı 40 derece olarak bulmuş olduk.
Hemen 40'ı aşağıya ne yapıyorum türlerini alıyorum.
Yani onu 90 dereceyle tamamlıyorum.
50 derece olarak yazdım, bitti.
Bundan sonrası biliyorsunuz.
Neydi?
İlk 80 aynı zamanda kutusunu 87.
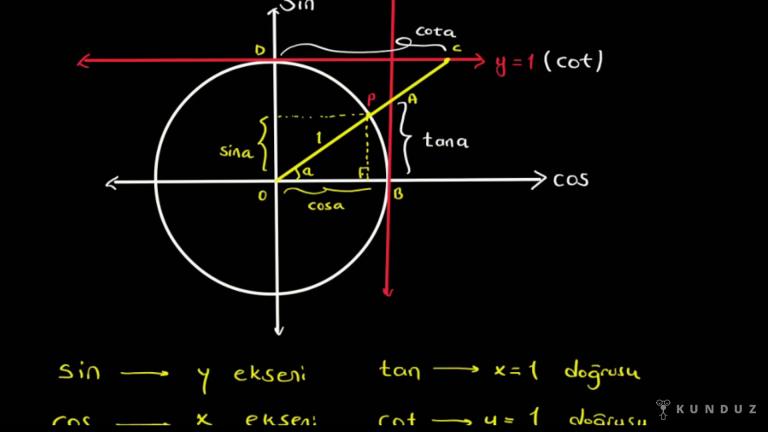
Yer ekseni de sinüs ekseni diyen.
Aslında şunu demeye çalışıyorum Bu 50 derecenin şu aşının bitim kolunu ilk 80 üzerine düşündüğümüzde o hash karşılığı aslında kolunuz 50 derece demektir.
Bizim işimiz verecek olan kısım burası.
Bu soruda belki yaramaz ama paylaş.
Eğer istemiş olsaydı da biz buna ne diyecektik?
Eee sinüs 50 diyecektik.
Neden?
Çünkü bu da karşıya baktığımızda şuraya yani y eksenine, yani sinüs eksenine bunun yansıması olmuş olacaktı.
Peki şimdi o zaman bakın şunu görmüş olduk.
Buranın yine tamamının bir olduğunu biliyorum.
Aslında bana sorulan A hash uzunluğu ile yanındaki o hash yani kolunuz 50 derece ifadesini topladığımızda 1 veriyormuş.
O halde nedir biz aha şu uzunluğunu yerine bir eksi koysan 150 yazabiliriz.
Böylelikle aha uzunluğunun eşiğinde bulmuş oluruz.
Sevgili arkadaşlar diyelim ve sıradaki sorumuza geçelim.
Aşağıda koordinatları verilen noktalardan hangisi birim çember üzerinde bulunur diye sorulmuş.
Şimdi birim çember üzerinde olması demek 1.
Noktaları nedir?
Apsis ve oradan hatlarının karelerinin topladığımızda 1 etmesi demektir.
Dolayısıyla hemen A seçeneğine bakıyorum.
Eksi bir bölü ikinin karesiyle bir bölü ikinin karesini topladığımızda her ikisi de birbirine dört yapan iki tane bir bölü dört nedir?
Bir bölü ikidir.
Dolayısıyla bu noktası birim çember üzerinde değildir.
Sonucu bir çıkmadığı için b ye bakalım.
B diyor ki eksi birin karesi 1 olur.
Diğer taraftaki eksi birin karesi de 1 olur.
Toplarsanız 2 olur.
Yine sonuç 1 çıkmadığı birim çember üzerinde değil.
C şıklığıyla devam ediyorum.
Isterseniz karesini yazayım direk eksi 1 bölü kök 3.
Bunun karesi nedir 1.
Böyle 3'tür artı 2 bölü kök 3 o da 4 bölü 3'tür.
Toplarsak burası da 5 bölü 3 olmuş oldu.
Bu da birim çember üzerinde değil de seçeneğini yazıyorum.
1 in karesi 2'nin karesi topladık ne yapar 5 yapar.
Yine sonuç 1 çıkmadı.
Birim çember üzerinde değildir.
Eeee seçeneğine geldim.
Karelerin yazabilir isterseniz.
Eksi 3 bölü beşin karesi artı 9 bölü 25 yaptı.
Artı 4 bölü beşin karesi ise 16 biri 25 yaptı.
Paydalar aynı 25 üst tarafı topluyorum 9 artı 16, o da 25 yaptı.
Bakın 25 bölü 25'ten 1.
Dolayısıyla en seçeneğinde verilen eksi üç, bölü beş, dört bölü beş noktası.
Bu noktaların hepsi sitelerinin ve İşte sesin karesi artı orijinal karesi.
Bu toplam değeri 1 geldiği için noktamız birim çember üzerindedir diyebiliriz sevgili gençler.
Ve gelelim bir sonraki soruya.
Şimdi diyor ke kar eşittir bir artı kos karakız çarpı iki artı single olduğuna göre kanun verici tam sayı değerleri kaç tanedir?
Şimdi aslında buradaki temel mantık şu.
Az önce de ifade etmiştik ilk sekseni ve y ekseni.
Neydi bunlar sırasıyla eee komünist ve sözünü 80'leri.
Şimdi birim çember üzerinde biz bunları gösterdiğimiz için o zaman sinüs ix ifadesi de sevgili arkadaşlar, komünün IX ifadesi de yani burada IX olmak zorundadır.
Alfa da olabilir.
Hangi sorudan bağımsız olsun, içinde ne yazarsa yazsın eksi birle artı bir arasında değer alır.
Ben bunu zaten biliyorum.
O halde şimdi burada ııı.
Tam sayı değerleri kaç tanedir?
Bunu bulmanın yolu aslında şuradan geçiyor.
Bir en büyük değerini bulmamız gerekiyor Max değerini bulabilmek için.
Şimdi burada Koç'un üstün en büyük değeri nedir?
1'dir.
Bir artı birin karesi ııı komünist ise.
1 değerini verdim.
Diğer taraftan yine senin başına da artı var, sorun yok.
O da ifadeyi büyütmeye çalışıyor.
Ona da bir değerini verelim.
Hani şöyle bir de durum yok.
Koçun uzun bir olduğu yerde sen üstü biri olamaz.
Hayır, açılar farklı olduğu için olabilir.
Yani Koç'un üstte biri olur, sinüs de bir olur.
Çünkü bir dikkat açısı 1 2 açısı.
Dolayısıyla çarpı koyuyorum oraya, iki artı da 1 yazdım.
Sevgili gençler.
Dolayısıyla ne oldu?
Bakınız bir artı birden.
Şurası iki, şurası da üç yaptı.
Bunun en büyük değeri kan, en büyük değeri altyapı.
Şimdi geldik bir de minimum değerini bulalım.
Karıştır diyorum minimumda.
Şimdi komünist için alabileceği en küçük değer eksi 1.
Ama şimdi burada karesini alıyorum ya yine büyüyecek.
Dolayısıyla Koç'un sükse ne verelim sıfır verelim burada sinsice.
Bu ifadeye de yine en küçük değeri eksi bir verebiliriz.
Burda problem yok.
Eee ne olur?
Hemen yazıyorum.
1 artı sıfırın karesi 1 oldu burası diğer taraftan 2.
Artı eksi 1 ki eksi 1 diye yazayım.
Burası da 1 oldu.
1 çarpı birden 1 oldu.
Bu da nedir?
En küçük değeridir sevgili arkadaşlar.
Şimdi burada kendisi bu aralıkta değer alacak kanun.
Birden büyük ve eşit, alttan küçük ve eşit, dolayısıyla birden altıya kadar olan birikmiş 4-5-6 sayıların hepsini alabilir.
Dolayısıyla kaç tanedir?
Diye soruyordu bize.
6 tanedir deyip sorumuzu bitirmiş oluruz.
Sevgili arkadaşlar.
Şimdi gelelim bir sonraki soruya.
Buradaki sorunun mantığı bir öncekine göre biraz farklı.
Neden şimdi burada da yine alabileceği kaç tam sayı değeri vardır?
Artık bunu anladınız.
1 En küçük değeri, bir de en büyük değeri bulacağız.
Bu aralıktaki bütün değerdir, alır diyeceğiz sonrasında.
Ama burada dikkat ederseniz bir önceki sorudaki gibi değil.
Neden açıların her ikisi de aynı.
Yani şimdi burada mantık şudur aslında kaosun üstüne yapmak lazım.
Artı bir ise eksi yapalım.
Başında eksi var yedi olsun ama olmaz işte.
Neden ıı o sürünsün biri olduğu yerde zaten sinsi otomatikman ne olacaktır.
Sıfır olacaktır.
O halde bu aradığımız ifadenin en büyük değerini, yani ilk adımda başlarken en büyük değerini bulamamış olacağız.
Burada şöyle bir yol var sevgili arkadaşlar, eğer bu açılar birbirinin aynısı ise kat sayılara bakıyoruz.
Bizim önemli olan katsayılar.
Bu ifadeye biz ne diyelim?
Yine isterseniz işte a büyük a diyelim.
Buradaki anın yine en büyük maksimum değerini bulurken şöyle yapıyoruz kat sayılarına bakıyoruz.
3'ün karesi, artı x 4'ün karesi.
Kat sayıların, karların topluyoruz, kök içerisine alıyoruz zaten.
Tabii şurası 9 artı 16 25 kök 25'ten ne olur?
Artı 5 geldi en büyük değer, minimum değer de yine buna çok benziyor.
En küçük değeri sadece başında eksisi var arkadaşlar.
Yine katsayıları alıyorum.
Eee karelerini topluyorum şu şekilde bu sefer en küçük değerini de eksi 5 bulmuş olduk.
Bu aralıktaki tüm değerleri alabilir.
A dediğimiz ifade o halde kaçmış.
Bu değerler 5 tane negatif, 5 tane pozitif var 10 bir de 0 var.
Bu aralıkta on bir tane değeri vardır diyebiliriz sevgili gençler.
Tabi bunu karıştırmamak lazım.
Tekrar söylüyorum eğer şu açılar birbirinin aynısı ise şu verdiğim formülü kullanacağız.
Bir önceki sorudaki gibi açılar birbirinden farklıysa.
İşte değer en büyük değer sorulduğunda +1 en küçük değer olduğunu eksi 1 olarak değerlerimizi seçeceğiz diyelim ve bu soruyla birlikte dersimizi noktalamış olalım.
Bir sonraki dersi görüşmek üzere kendinize çok iyi bakın.
Birim Çember Yeni Nesil Sorular
Dik Üçgen
Birim Çember 4 / 4
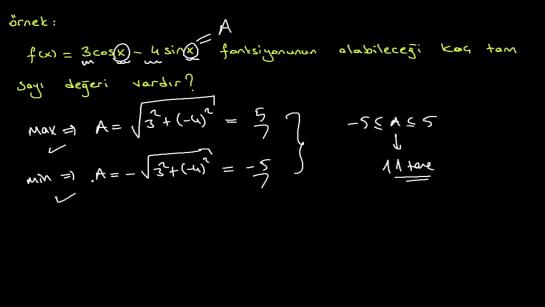
Birim Çember Yeni Nesil Sorular