Merhabalar iç açıortay konusundayız.
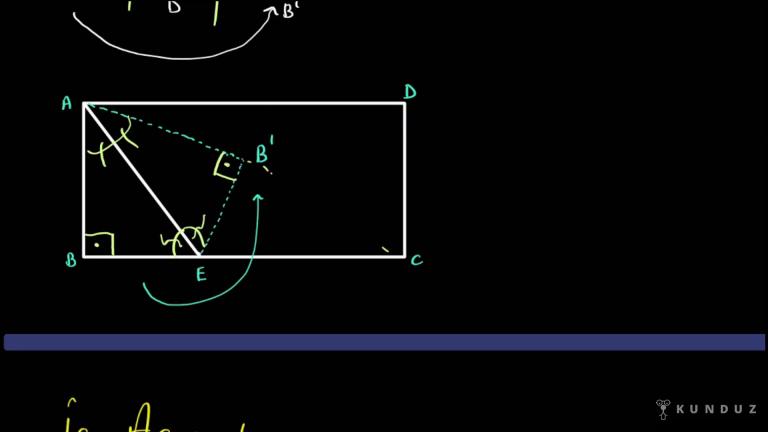
Şimdi soruda bir ABC üçgeni verdim B'den bir açıortay, C'den bir açıortay ve AD'yi de birleştirdim.
Şimdi D dediğim yerde BD ve CD'nin kesişimi tamam.
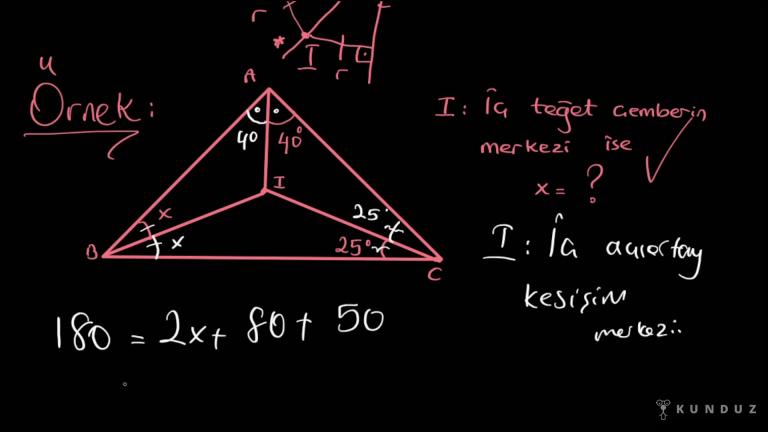
Şimdi burada D açısını 126 olarak verdim, a açısını bulalım.
Şimdi burada bir üçgen içerisinde iki tane iç açıortayın kesiştiği yer iç teğet çemberin merkezidir ve aynı zamanda iç açıortayların kesişim merkezidir.
Yani siz 2 tane açıortay çizdiniz bir yerde kesişti ya üçüncü çizdiğiniz açı ortay da oradan geçer.
Yani siz köşe ile kesişim noktasını birleştirir iseniz kesinlikle bir açıortay elde etmelisiniz.
Yani burada D dediğim yer iç teğet çemberin merkezi ya da iç açıortayların kesişim merkezidir.
Yani siz B'den ve C'den çizince açıortay elde ettiyseniz A'dan D'ye çizince de açıortay elde ediyorsunuz.
Tamam bu açıortaydı yazdık.
Şimdi diğer bilmediğim açıları da harfler vereyim ki bir denklem sistemi oluşturabileyim.
Tamam onları da yazdım.
Şimdi büyük üçgene bakınca ABC üçgeni içerisinde iç açılar toplamı eşitliğinden yola çıkarak şu denklemi yazabilirim.
180 derece eşittir 2a artı 2b artı 2c.
Büyük üçgeni baktım ve bunu yazabildim.
Tamam, ikinci olarak bakmam gereken yer ne bana verilen ile gideceğim yoldur.
Bana neresi verilmiş, 126 derece.
O zaman bunun olduğu üçgen içerisinde gitmeliyim.
Yani 180 derece eşittir.
Yani BDC üçgenin içerisindeki iç açılar toplamı eşittir 126 derece artı b artı c.
Ben buradan b artı c'yi çekebiliyorum.
54 derece eşittir b artı c etti.
b artı c'yi de burada kullanabiliyorum.
Çok güzel 180 derece eksi 2b eksi 2c eşittir 2a.
a'yı yalnız bıraktım, a'yı soruyor soru bana.
Burada 180 derece eksi 2 parantezinde b artı c oldu burası.
Bölü 2 size direk a'yı veriyor.
Şu bölü iki direkt buraya attım.
b artı c'yi buraya yazıyorum.
180 eksi iki tane 54 108 mi etti?
Yüksek 180'den direk 108'i çıkarırsan 72 derece mi etti.
72 bölü 2 size a'yı mı verdi?
A dediğim şeyi 36 derece buluyoruz dostlar.
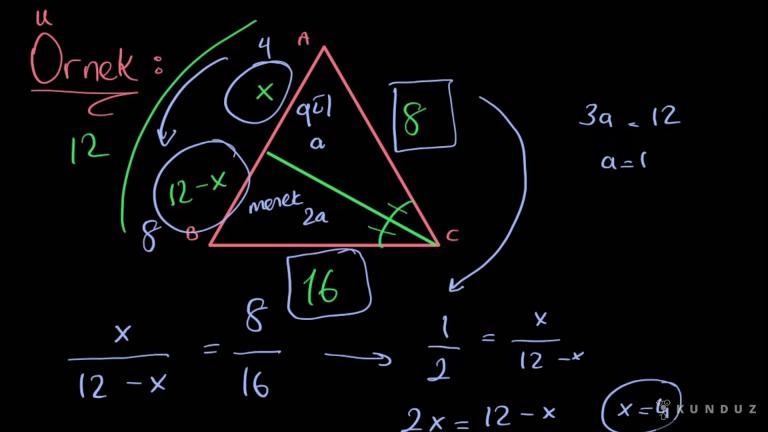
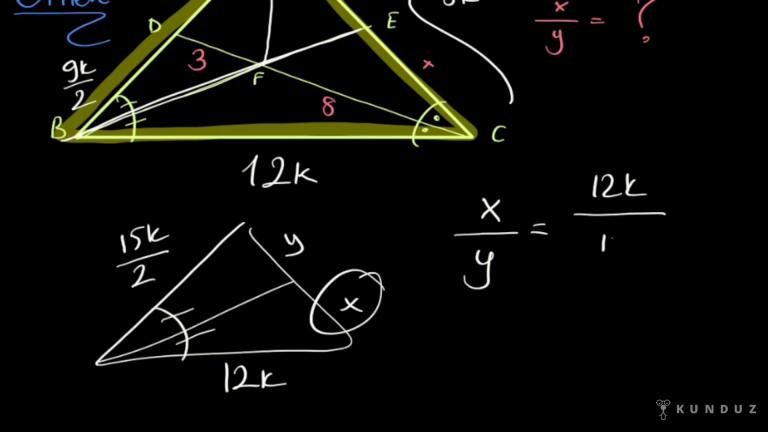
Devam edelim şimdi bir ABC üçgeni verdim.
BE açıortay, CE açıortay, DF arası 3,FC arası 8 santimetre olsun.
AE y, EC x ise x bölü y'nin oranını istiyorum.
Bu arada BC eşittir 4 AD eşitliğini de vermiş olalım.
Şimdi burada ilk başlamam gereken şey şudur.
2 tane açıortay çizmiştim.
BE ve CD'yi çizmiştim.
Bunlar F'de kesişmiş, çok güzel.
Demek ki F noktası iç teğet çemberin merkezidir ya da iç açıortayların kesişim merkezidir.
Yani bu bana demek istiyor ki sen A köşesiyle de F'yi birleştirince açıortay elde etmelisin.
Burası da burasına eşit olmalı.
Burada da bir açıortay bulmalısınız.
Şimdi burada şunu diyebilmeliyim.
Artık ADC üçgeninde şu 3 ve 8 oranlı kullanabiliyorum.
Çünkü A ve F'yi birleştirince burası açıortay oldu.
O zaman buradaki oranı buradaki yan kenarlara yansıtabilirim.
Ne demek istiyorum?
3'e 3k gelirse gelsin diyorum.
3'e 3k gelsin, 3'e 3k gelirse sekize ne gelir?
Sekize 8k gelir dostlar.
AC uzunluğu 8k, AD uzunluğu 3k yazdık.
Tamam şimdi başka buradaki işlemimiz bitti, başka neler yapmalıyım?
Şimdi ben AD'yi buldum mu?
Buldum.
Şimdi soruda bana AD ile alakalı bir şey verdi.
4 çarpı AD o zaman 12k eşittir BC oldu.
BC yerine 12k'yi yapıştıralım.
Şimdi geçelim başka bir yerde şu açıortayı kullanırım.
Üç tane açıortayım var.
Bir yerlerden bakalım.
Şu üçgene bakmanızı istiyorum.
BDC üçgeni.
Buradaki üçgendeyim.
Şimdi burada şu açıortayım var.
Doğru mu bu açıortay?
O zaman şununla şu arasındaki oranlar bu yandaki kenarlara da yansımalı.
Demeliyim ki sekize 12k geldiyse 3'e acaba kaç gelir?
Çünkü ben burayı bilmiyorum.
Burayı bulmaya çalışıyorum zaten.
Ne dedim sekize 12k geldiyse üçe kaç gelir, bunu araştırıyorum.
İçler dışlarımı yapıyorum.
Soru işaretini yalnız bırakmaya çalışıyorum.
36k bölü sekiz geldi.
Bölün dörde 9k bölü iki etti.
Yani burada gördüğünüz BD uzunluğu 9k bölü iki ya da dört buçuk k'de diyebilirsiniz.
Şimdi buradaki açıortayı da kullandım, burayı kullandım, burayı kullandım.
Çok güzel, bayağı yaklaştık.
Şimdi burada son bir yere bakmanızı istiyorum.
Şurada en büyük üçgende.
En büyük üçgen de yine buradaki B köşesindeki açıortayı kullanacağım.
Şimdi burada x bölü y'yi araştırdığım için bu açıortayı seçtim dostlar.
Tamam büyük üçgene baktığınız zaman şöyle bir üçgenim var.
Buradan açıortayı çizdim.
Bunu çizince burası y oldu, burası x oldu.
Burası komple kaç oldu?
Dört buçuk, üç daha yedi buçuk.
Yani 15k bölü iki diyebilirim.
Alt tarafa geçersem burası 12k verilmiş.
Buranın açıortay olduğunu zaten soru bana söyledi.
x bölü y2ye geçiş yapabiliyorum artık.
x bölü y 12k bölü x'e gelen uzunluk bölü y'ye gelen uzunluk, 15 bölü iki.
Burayı üst tarafa atarsanız 24 bölü 15 eder.
Üçe bölerseniz sekiz bölü beş bulursunuz dostlar.
Şimdi soruda bir ABC üçgeni verdim B'den bir açıortay, C'den bir açıortay ve AD'yi de birleştirdim.
Şimdi D dediğim yerde BD ve CD'nin kesişimi tamam.
Şimdi burada D açısını 126 olarak verdim, a açısını bulalım.
Şimdi burada bir üçgen içerisinde iki tane iç açıortayın kesiştiği yer iç teğet çemberin merkezidir ve aynı zamanda iç açıortayların kesişim merkezidir.
Yani siz 2 tane açıortay çizdiniz bir yerde kesişti ya üçüncü çizdiğiniz açı ortay da oradan geçer.
Yani siz köşe ile kesişim noktasını birleştirir iseniz kesinlikle bir açıortay elde etmelisiniz.
Yani burada D dediğim yer iç teğet çemberin merkezi ya da iç açıortayların kesişim merkezidir.
Yani siz B'den ve C'den çizince açıortay elde ettiyseniz A'dan D'ye çizince de açıortay elde ediyorsunuz.
Tamam bu açıortaydı yazdık.
Şimdi diğer bilmediğim açıları da harfler vereyim ki bir denklem sistemi oluşturabileyim.
Tamam onları da yazdım.
Şimdi büyük üçgene bakınca ABC üçgeni içerisinde iç açılar toplamı eşitliğinden yola çıkarak şu denklemi yazabilirim.
180 derece eşittir 2a artı 2b artı 2c.
Büyük üçgeni baktım ve bunu yazabildim.
Tamam, ikinci olarak bakmam gereken yer ne bana verilen ile gideceğim yoldur.
Bana neresi verilmiş, 126 derece.
O zaman bunun olduğu üçgen içerisinde gitmeliyim.
Yani 180 derece eşittir.
Yani BDC üçgenin içerisindeki iç açılar toplamı eşittir 126 derece artı b artı c.
Ben buradan b artı c'yi çekebiliyorum.
54 derece eşittir b artı c etti.
b artı c'yi de burada kullanabiliyorum.
Çok güzel 180 derece eksi 2b eksi 2c eşittir 2a.
a'yı yalnız bıraktım, a'yı soruyor soru bana.
Burada 180 derece eksi 2 parantezinde b artı c oldu burası.
Bölü 2 size direk a'yı veriyor.
Şu bölü iki direkt buraya attım.
b artı c'yi buraya yazıyorum.
180 eksi iki tane 54 108 mi etti?
Yüksek 180'den direk 108'i çıkarırsan 72 derece mi etti.
72 bölü 2 size a'yı mı verdi?
A dediğim şeyi 36 derece buluyoruz dostlar.
Devam edelim şimdi bir ABC üçgeni verdim.
BE açıortay, CE açıortay, DF arası 3,FC arası 8 santimetre olsun.
AE y, EC x ise x bölü y'nin oranını istiyorum.
Bu arada BC eşittir 4 AD eşitliğini de vermiş olalım.
Şimdi burada ilk başlamam gereken şey şudur.
2 tane açıortay çizmiştim.
BE ve CD'yi çizmiştim.
Bunlar F'de kesişmiş, çok güzel.
Demek ki F noktası iç teğet çemberin merkezidir ya da iç açıortayların kesişim merkezidir.
Yani bu bana demek istiyor ki sen A köşesiyle de F'yi birleştirince açıortay elde etmelisin.
Burası da burasına eşit olmalı.
Burada da bir açıortay bulmalısınız.
Şimdi burada şunu diyebilmeliyim.
Artık ADC üçgeninde şu 3 ve 8 oranlı kullanabiliyorum.
Çünkü A ve F'yi birleştirince burası açıortay oldu.
O zaman buradaki oranı buradaki yan kenarlara yansıtabilirim.
Ne demek istiyorum?
3'e 3k gelirse gelsin diyorum.
3'e 3k gelsin, 3'e 3k gelirse sekize ne gelir?
Sekize 8k gelir dostlar.
AC uzunluğu 8k, AD uzunluğu 3k yazdık.
Tamam şimdi başka buradaki işlemimiz bitti, başka neler yapmalıyım?
Şimdi ben AD'yi buldum mu?
Buldum.
Şimdi soruda bana AD ile alakalı bir şey verdi.
4 çarpı AD o zaman 12k eşittir BC oldu.
BC yerine 12k'yi yapıştıralım.
Şimdi geçelim başka bir yerde şu açıortayı kullanırım.
Üç tane açıortayım var.
Bir yerlerden bakalım.
Şu üçgene bakmanızı istiyorum.
BDC üçgeni.
Buradaki üçgendeyim.
Şimdi burada şu açıortayım var.
Doğru mu bu açıortay?
O zaman şununla şu arasındaki oranlar bu yandaki kenarlara da yansımalı.
Demeliyim ki sekize 12k geldiyse 3'e acaba kaç gelir?
Çünkü ben burayı bilmiyorum.
Burayı bulmaya çalışıyorum zaten.
Ne dedim sekize 12k geldiyse üçe kaç gelir, bunu araştırıyorum.
İçler dışlarımı yapıyorum.
Soru işaretini yalnız bırakmaya çalışıyorum.
36k bölü sekiz geldi.
Bölün dörde 9k bölü iki etti.
Yani burada gördüğünüz BD uzunluğu 9k bölü iki ya da dört buçuk k'de diyebilirsiniz.
Şimdi buradaki açıortayı da kullandım, burayı kullandım, burayı kullandım.
Çok güzel, bayağı yaklaştık.
Şimdi burada son bir yere bakmanızı istiyorum.
Şurada en büyük üçgende.
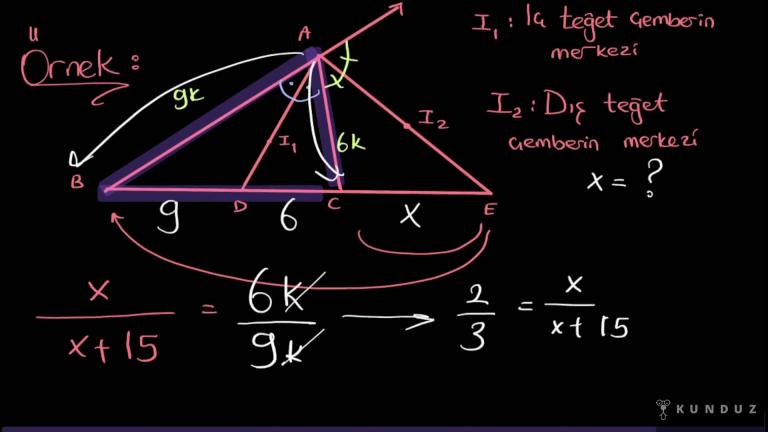
En büyük üçgen de yine buradaki B köşesindeki açıortayı kullanacağım.
Şimdi burada x bölü y'yi araştırdığım için bu açıortayı seçtim dostlar.
Tamam büyük üçgene baktığınız zaman şöyle bir üçgenim var.
Buradan açıortayı çizdim.
Bunu çizince burası y oldu, burası x oldu.
Burası komple kaç oldu?
Dört buçuk, üç daha yedi buçuk.
Yani 15k bölü iki diyebilirim.
Alt tarafa geçersem burası 12k verilmiş.
Buranın açıortay olduğunu zaten soru bana söyledi.
x bölü y2ye geçiş yapabiliyorum artık.
x bölü y 12k bölü x'e gelen uzunluk bölü y'ye gelen uzunluk, 15 bölü iki.
Burayı üst tarafa atarsanız 24 bölü 15 eder.
Üçe bölerseniz sekiz bölü beş bulursunuz dostlar.