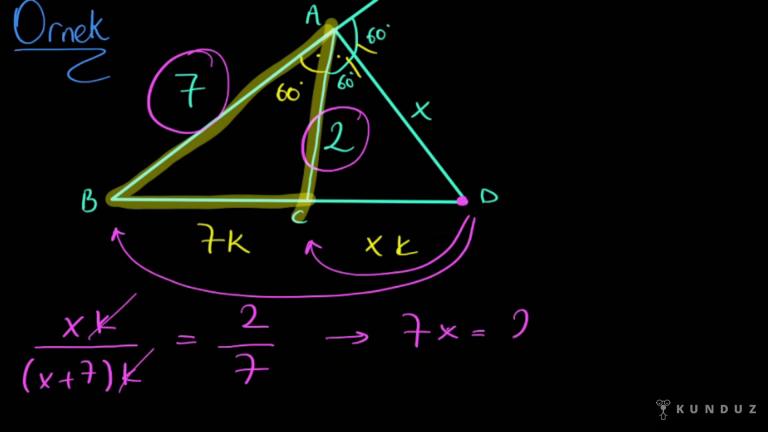Üçgende Açıortay Yeni Nesil Sorular

Sevgili konusu izleyenleri herkese merhabalar.
Bu dersimiz de üçgende aç ortaya konusuyla ilgili örnek sorular çözmeye devam edeceğiz.
Ilk sorumuz la başlayalım.
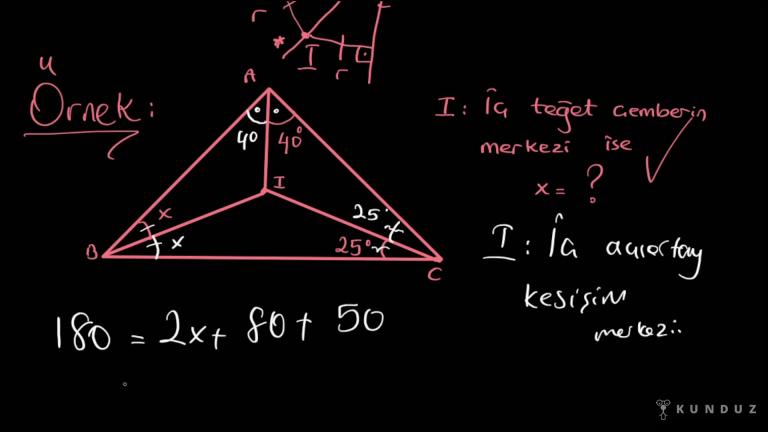
Şekildeki A BC üçgeninde de ale ve legacy açıları birbirine eşit.
Acaba karşısı kaç açısına eşit?
A b 12 santim aka 6 santim kale 8 santim olduğuna göre BC artı CL toplamı kaç santimetre?
Diye sorulmuş.
İlk sorumuz üçgenin hem iç açı ortay hem dışa uç orta bilgisi barındıran bir soru.
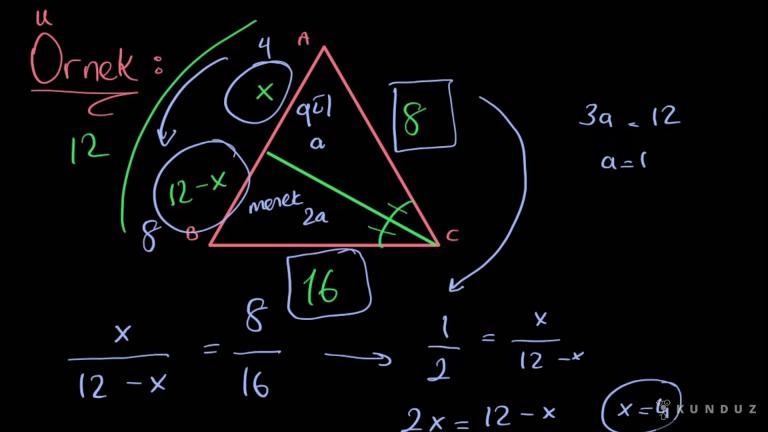
Öncelikle bakınız, acele üçgenine dikkat edelim.
Burada C köşesinden çizilen bir iç açı ortay var.
Yani biz bu durumda ne diyorduk?
İşte AC IE'nin 6'ya oranı.
Diğer taraftan CL nin 8 oranı birbirine eşittir.
Yani sevgili arkadaşlar, aslında A.C.
Bölü CL ya da derece fark etmez.
Neymiş 6 bölü 8'den üç bölü dörde eşittir.
O halde hemen gelin buraya 3k k da 4 k yazalım.
Şimdi bu 3 3 ortayı tamamladık.
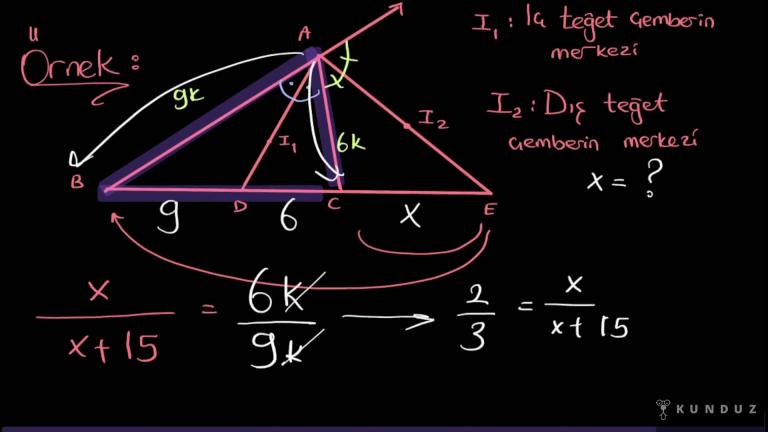
Ab önce üçgenin A köşesinden 1 de dışa 3 orta çizilmiş.
Dışa çık ortayla şöyle yapıyordum Bakın neşe ortayı takip ediyorum.
Kırıldığı yerde duruyorum.
Sonra açığa geri döneceğim işte.
L Ece'nin L.
Bey oranı devam ediyorum.
A Ece'nin AB oranına eşittir.
Hatta hilal taktiği demiştik.
Ay yıldız demiştik buna değil mi?
Yani 4.
K bölü BL.
4.
Kabulü BL.
Eşittir 3 kabül.
12 Hemen bunu yazdım.
Dağlar kısaldı.
Şu üçlü 12 saat eleştirdim.
4 içler dışlar çarpımı yapıyorum.
Böyle eşittir 4 kere 4'ten 10 6 santimetre bulduk için.
Şura 10 60.
Bakın dikkat edersiniz BC artı CL yi soruyor şimdi burada.
Zaten bunları tek tek bulmak şu anki verilerle imkansız.
Çünkü bu sadece oranlarını biliyorum.
Kanalları, sayıları bilmiyorum ama sorduğu istediği yer BBC artı CL şu toplam zaten nedir sevgili arkadaşlar böyledir.
Dolayısıyla 16 santimetre olarak o ikisinin toplamı bulunmuş olur diyelim.
Sıradaki sorumuza geçelim.
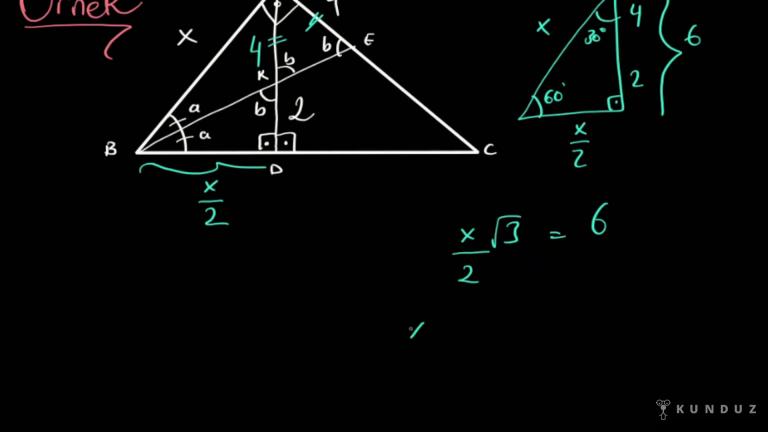
Şekildeki Ale?
N A.T.
Açısının aç ortağıdır.
B.k, anne cl, anne K.D, A.T.
Ve L.
Ate bunlar birbirilerine dikmiş arkadaşlar şekilde gözüküyor.
B k kart 8 kd 2 k artı 3 cl ise 3 K artı 2 brom ve l 4 em artı 5 birim olduğuna göre bize em kaçtır diye sorulmuş.
Tamam, hemen şurada ne dedik, burası aç oradaymış, aç ortan örnek k noktasından iki kola çizdiğimiz dilimler birbirine eşit oluyordu.
Yani hemen kad sekizi gelin iki artı üç eşit diyelim.
Buradan K aş 5 olduğunu bulalım.
Şimdi kaçtır 5'i hemen C'yi bulmak için kullanıyorum.
Üç kere beş, beş, iki ekledim.
17 diyorum buraya.
Lc de L.
E'ye eşittir sonuçta.
Hani dedik ya kollar üzerinden çizilen dikmişler eşit.
Bu sefer L noktası için bu özelliği kullanacağız.
Dört hem artı beşi.
17'ye eşit dersek 4 them eşittir 12, em eşittir üç birim olarak bulunmuş olur.
Sevgili gençler diyelim hemen bir sonraki sorumuza geçmiş olalım.
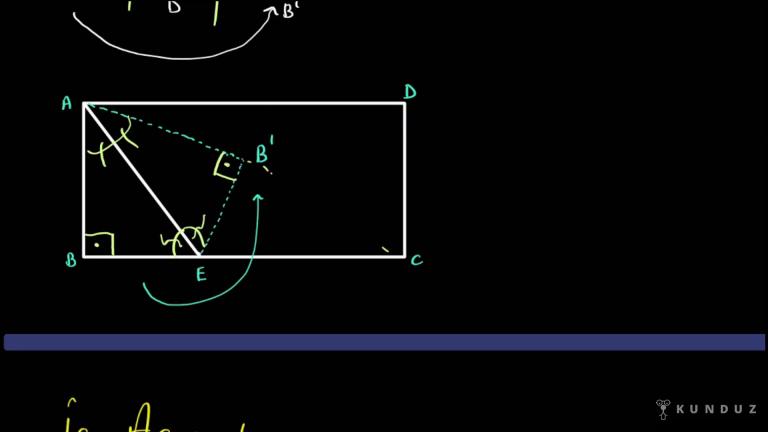
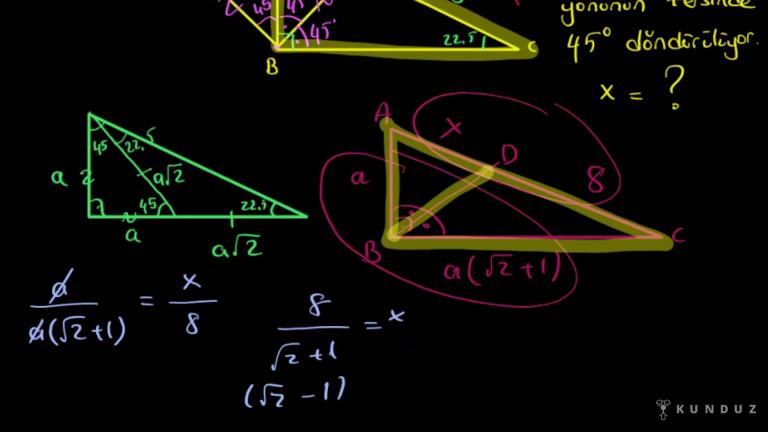
Diyor ki birinci şekildeki bir gecede üç kere B, C boyunca A, B üçgenin üzerine katlandığını da D noktası ikinci şekildeki gibi deyiş noktasıyla çakışıyor muş.
Cd ve B'de birbirine dikkat!
Şurası 90 derece imiş.
Sevgili gençler, şurada da katlama olduğunu bize göstermeye çalışmış.
Ya Şura yine doksan.
Sonrasında CD 3 B, 7 a, b 10 santim olduğuna göre b acı açısının ölçüsü kaç derecedir diye soruluyor.
Şimdi hemen bakın ben birini şekil üzerinde yapayım, bütün şekilde gösterdiği şeyi de noktasına öbür tarafa kattığımızda ne yapıyormuş?
Şu şekilde bir buradaki tabii ki döndüğünde de yine bu buraya geldiğinde doksan derece olmaya devam eder de üst noktasıyla çalışmıştı.
Ama bu katlama sonucu biliyorsunuz burası ne olur aç orta olur.
Yani şurası üçgen CD, CD üstü de 3 olur.
Aynı şekilde B de 7 iken B de üste 7 olur.
Yani şuraya kadar 10 dediği yer tamamıyla sevgili gençler.
Yine 10 eksi 7'den şurası da gördüğünüz gibi 3 santim olmuş olacak.
Sonrasında bize sorulan açı şu açı bakın dikkat edin burası ikiz kenarı deki üçgen olmuş oldu.
Yani aslında buralar alfa alfa dır.
O halde 90 artı iki alfa eşittir 180'den, iki alfa eşittir 90 derece olur.
Yine bunların hepsi derece sevgili gençler.
Dolayısıyla bize sunulan ve isteyen alfa dedik biz ona 45 derece olarak bulunmuş olur.
Sevgili gençler diyelim hemen bir sonraki sorumuza geçelim.
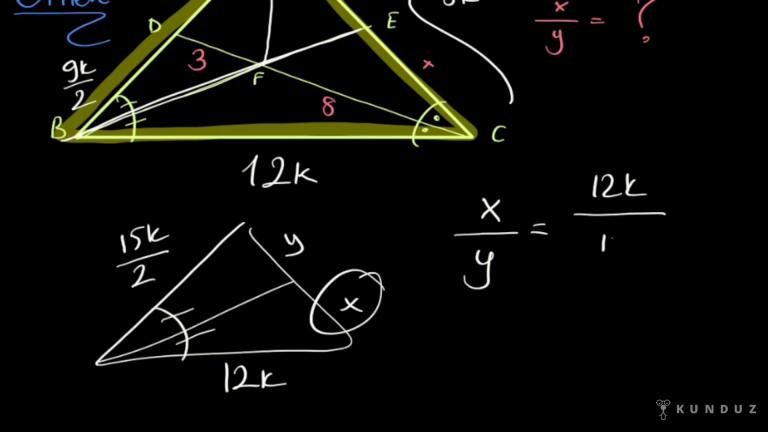
Şekilde ABD üçgeni biçiminde.
Bu döllenmiş bir tarlanın B ve C köşelerinden bağlanan iki ipin.
Diğer uçları bahçenin içinde bir de noktasına bağlanmıştır.
Yani şurda bebeğe bir ip bağlamış, diğer ucu D'ye bağlamış, aynı şekilde C'ye başka bir ip bağlamış, aynı ucu yani C'nin C noktasına bağladığı ipin ucunu aynı şekilde yine de noktasına bağlamış.
Diyor ki B de ipi üzerindeki noktalar A.B ve BC kenarlarına, CD 200 önündeki noktalar ise ACE ve BC kenarlarına eşit uzaklıktadır.
Yani bu ne demek?
Bakınız burası açı oradaymış arkadaşlar burada içi oradaymış değil mi?
Noktanın uzaklıkları dik ölçülür.
Örnek mesela d noktasına bakalım.
İşte H ve diğer tarafa çizdiğimiz şekilde de k eşit uzaklıkta ise burası aç ortaya olmalı.
Yani şunlar da tabii ki birbirine eşittir.
Aynı şekilde sevgili gençler.
Şöyle düşünelim tabii ki bu b d, k doğrusal olmak zorunda değil değil mi yani?
O ne zaman olur işte ağaca eşittir BC 2 ya da üçgen eşkenar üçgen olur.
Buradaki noktalar doğrusu olmak zorunda.
Aynı şekilde bakın şimdi c, d, e yani c aç.
Orta üstünden bir de nokta seçilmiş dereceye indirilmiş.
Ben de aynı şekilde Ağca'yı bir dik indireceğim.
Bu da bakın yuvarlakla gösterilecek.
Örneğin bu noktaya ne diyelim?
S noktası diyelim.
Aynı şekilde B dese de doğru olmak zorunda değil.
Yani lütfen çizme, aldatmayalım, öyleymiş gibi duruyor.
Aslında yapmamaya da çalıştım ama doğrusu olmak zorunda değil.
Pek diyor ki D noktasının kenarına uzak diyen de 3 metre imiş.
Dolayısıyla burası 3, bakın burası da 3 değil mi?
Şurası da 3.
Bunlar hep birbirine eşit imiş.
Ab artı A.C.
Yani ona X diyelim, şuraya da Y diyelim, toplamları 8 metre demiş.
Taraflı alan o yeşille boyalı alan kaç metrekaredir diye soruluyor.
Şimdi şöyle düşünelim.
Bakınız burada eğer siz AB'yi de birleştirmiş olsaydınız, yine aynı şekilde doğru su olmak zorunda değil ama burası da aç ortaya olmuş olurdu.
Bize sorulan oradaki tuğralı alan şu şekilde bulunur.
Iki tane üçgenin toplamı oldu.
Aslında o adede alan.
Aaa D B üçgeni artı sağ tarafta kalan alan DC üçgeni şeklinde ifade edilebilir.
Şimdi Ade Bey'e dikkat edin lütfen.
Tabanı IX.
Ona inen yükseklik 3 bölü 2.
Aynı şekilde ad dc ye bakalım bu sefer tabanımız y yükseklik 3.
Bölü 2.
Arkadaşlar burayı 3 1 2 parantezine alıyorum iki tartıya geliyor ix tartıya.
O iki kenarının uzunluk toplamı zaten bana 8 metre olarak verilmişti.
Yani hemen bunu yerine yazıyorum.
Şöyle üç bölü iki çarpı sekiz sekiz ikiye bölüm 4 üç kere 4'ten 12 metrekare olarak bize sorulan paralı bölgenin alanı bulunmuş olur sevgili gençler diyelim.
Umarım faydalı bir ders olmuştur.
Bu soruyla birlikte dersimizi bitiriyorum.
Bir sonraki dersi görüşmek üzere kendinize çok iyi bakın.