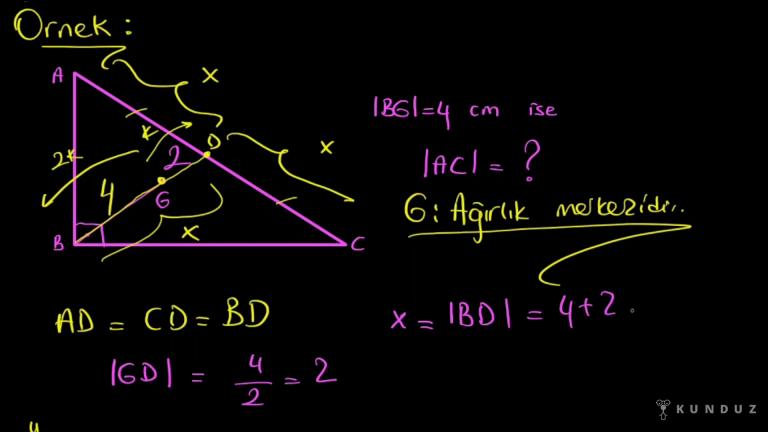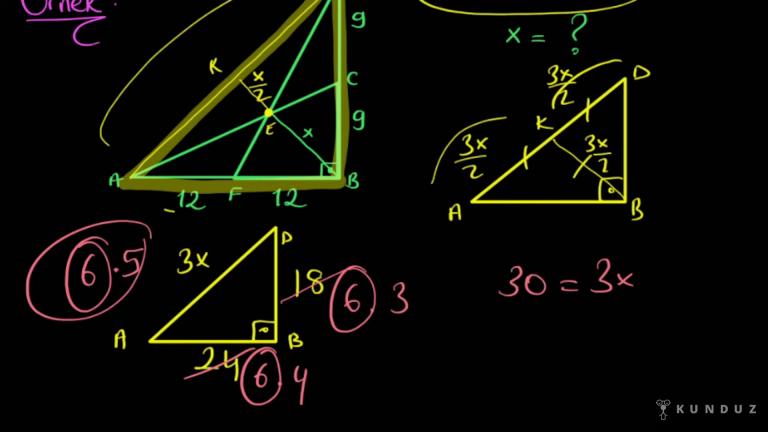Bir başka özel durum.
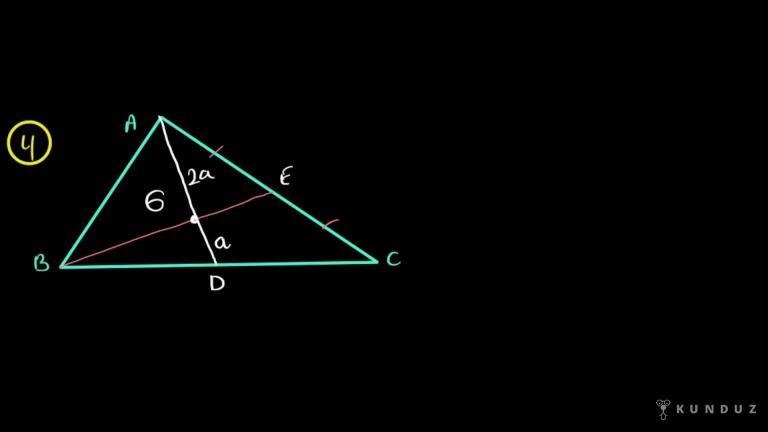
Yine dik bir üçgende 90 dereceden hipotenüse inen kenarortayın uzunluğu hipotenüsün uzunluğunun yarısıdır.
Yani eşit böldüğü parçalara eşittir.
Yani siz dik olan üçgende dik köşeden eğer karşı tarafa kenarortay inerseniz, tamam buralar eşit bölündü de işte AD uzunluğunu da hesaplayabiliyoruz.
AD uzunluğu bu eşit böldüğümüz parçalarla aynı uzunluktadır. Yani hipotenüsün yarısı konumundadır.
Yani üçgenimizin şeklinin değişmesi fark etmez dik üçgen olması zorunludur, dik köşeden karşı kenara kenarortay iniyorum işte kenarortayımın uzunluğu hipotenüsün yarısı oluyor.
O zaman burada muhteşem üçlü dememizin sebebi AD eşittir BD eşittir CD eşitliğinin yaşanmış olması arkadaşlar.
Dikten indiğini unutmayınız rica ediyorum dik bir üçgende bu kuralı gerçekleştirebiliyoruz.
Burada minik bir ekleme yapmak istiyorum arkadaşlar.
Şimdi dikten indiğimiz zaman dik bir üçgende kenarortay indiğimiz zaman kenarortayı uzunluğunun burada gördüğünüz BC kenarının yarısı yani A bölü 2 kadar olduğunu gösterdik.
Muhteşem üçlü dedik buna da. Peki ya o üçgen dar açılı bir üçgense, dar açılı köşeden inersem buradaki özel noktam şu açım dar tamam ama BC uzunluğum sabit yani buradaki A bölü 2-A bölü 2 oranım değişmeyecek A bölü 2-A bölü 2 uzunluğumda değişmeyecek yani.
BC sabit duruyor, ben bu açıyı daraltırsam acaba Va ne olur demek istiyorum onu göstermek istiyorum.
İşte siz bu Vc'yi sabit tutup buradaki Va uzunluğunu bulmak istiyorsanız eğer açıyı daraltırsanız Va'yı uzatmış olursunuz arkadaşlar.
Size lastik örneği vermiştim üçgende eşitsizlik konusunda arkadaşlar.
Bir lastiği böyle çekerseniz uzar demiştim.
İşte aynen onun gibi bir mantık.
Açım daralır o yüzden de bu uzar arkadaşlar gördüğünüz gibi.
Yani bunu göstermek istedim size.
Tam tersi açım genişlerse yani gördüğünüz gibi 90 derecede böyleydi dar açıda böyleydi, şuraya dar yazalım Burası 90° dar açıda uzundu, 90 derecede eşitti, geniş açıda ne olacak peki?
Geniş açıda işte A bölü yaptığımız A bölü 2 uzunluğunu değiştirmedim. Yani BC'yi sabit tutarak bir kıyaslama yaptık. BC'yi sabit tutarak A köşesinin açısını dik dar ve geniş olarak inceledim.
İlk başta zaten size dikken anlattım A bölü 2 eşittir dedim.
Muhteşem üçlü kuralı dedik ona.
BC sabit tutup bu açıyı daraltırsam Va'nın uzadığını gösterdim.
Aynı şekilde açıyı genişletip yine BC'yi sabit tutarsam arkadaşlar A bölü 2 Va'dan daha uzun olmuş oluyor arkadaşlar.
Bunları aktarmak istedim.
Şimdi şöyle küçük bir örnek yapalım.
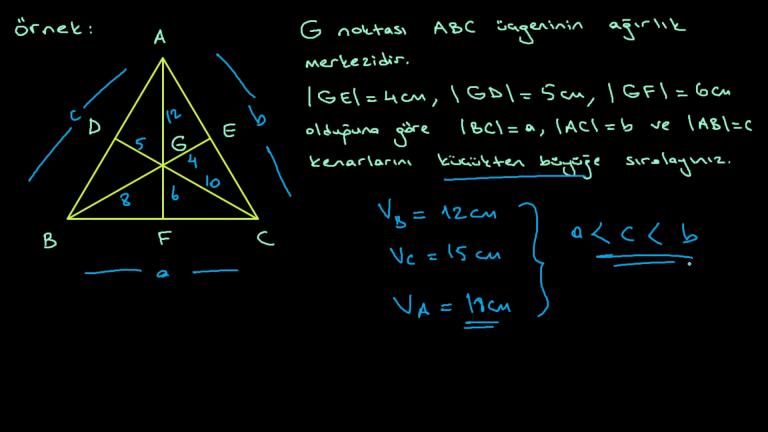
Dik bir üçgen verdim size demiş ki BG 4 santim yazalım.
Tamam AC uzunluğunu soruyu soruyor.
Şimdi size muhteşem üçlü anlattım aklınızda kalması bakımından bunu göstermek istiyorum.
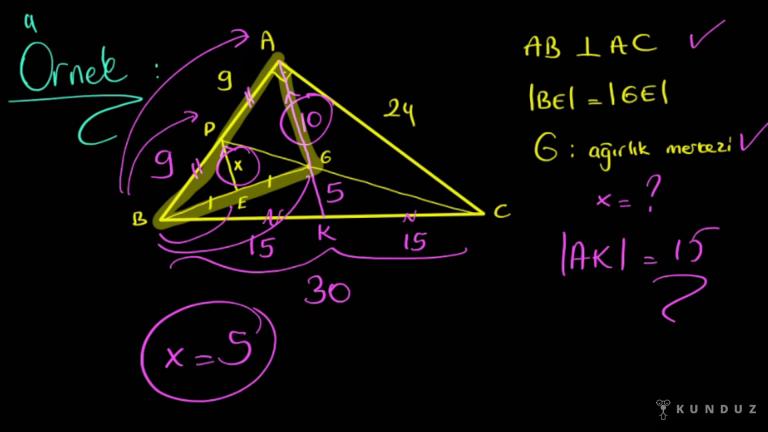
Şimdi bir burada ekleyelim G ağırlık merkezi olsun, ağırlık merkezidir.
Şimdi G ağırlık merkezi olmasaydı soru bomboş havadaydı. Yani G noktasını bana niye vermiş herhangi bir nokta Şurada da olabilir.
Yani demek istediğim şu önemlidir arkadaşlar.
Yani soruyu okumanın önemi vardır, G ağırlık merkezi demeseydi işlem yapamayacaktım.
G'nin ağırlık merkezi olması ve bunun köşeye birleşmiş olması ben bunu uzatırsam eğer değdiği nokta kenarın ortası olacaktır.
Yani AC'nin ortasını bulmuş olacaktı.
Şimdi ben dik bir köşeden kenarortay mı indim?
Evet indik.
Demek ki burada bir muhteşem üçlü kuralı yapmış olduk. Burası eşittir, burası eşittir, burası demeliyim. Yani D harfi verirsen AD eşittir CD eşittir BD olmalı, tamam.
Şimdi burası güzeldi zaten buraları bulmak istiyorum da nasıl bulacağım burayı?
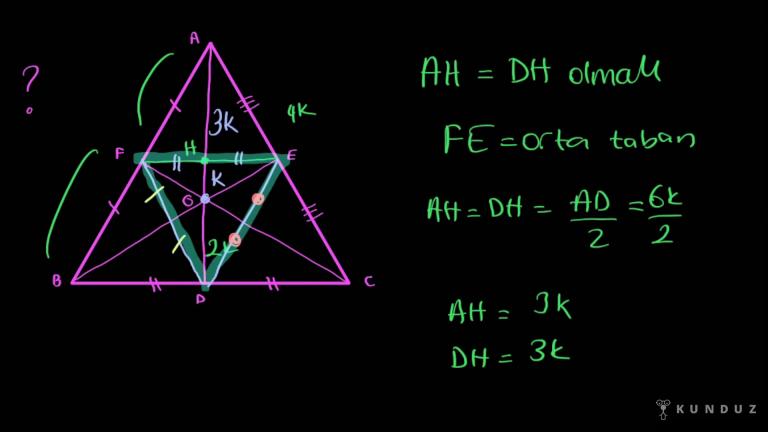
Şimdi burada da kenarortayın başta anlattığım kuralı yani ağırlık merkezinin kuralı.
Ağırlık merkezi kenara bir birim köşeye iki birim uzaklıkta olacak şekilde yerleşir.
Yani bir kenarortayı üzerinde kenara bir birim şuraya hatta yazalım 2k ve k olarak verelim.
Kenara bir birim köşeye iki birim olacak şekilde uzaklık alır.
Yani burada 2k'ye Yani burada GD uzunluğunu şöyle buluyorum: 4/2 eşittir 2 diyorum.
Teker teker yazmak istedim. Yani nasıl bulduğumu görmeniz açısından.
Ben 2x'i araştırıyordum, buradan BD dediğim şey x midir; şurada BD dediğim BD uzunluğu x'e eşit.
O zaman x dediğimde 4+2 midir, eşittir 6.
Benden AC istiyordu, AC uzunluğu iki tane x, iki tane 6, 12 santimetre buluruz.
Yine dik bir üçgende 90 dereceden hipotenüse inen kenarortayın uzunluğu hipotenüsün uzunluğunun yarısıdır.
Yani eşit böldüğü parçalara eşittir.
Yani siz dik olan üçgende dik köşeden eğer karşı tarafa kenarortay inerseniz, tamam buralar eşit bölündü de işte AD uzunluğunu da hesaplayabiliyoruz.
AD uzunluğu bu eşit böldüğümüz parçalarla aynı uzunluktadır. Yani hipotenüsün yarısı konumundadır.
Yani üçgenimizin şeklinin değişmesi fark etmez dik üçgen olması zorunludur, dik köşeden karşı kenara kenarortay iniyorum işte kenarortayımın uzunluğu hipotenüsün yarısı oluyor.
O zaman burada muhteşem üçlü dememizin sebebi AD eşittir BD eşittir CD eşitliğinin yaşanmış olması arkadaşlar.
Dikten indiğini unutmayınız rica ediyorum dik bir üçgende bu kuralı gerçekleştirebiliyoruz.
Burada minik bir ekleme yapmak istiyorum arkadaşlar.
Şimdi dikten indiğimiz zaman dik bir üçgende kenarortay indiğimiz zaman kenarortayı uzunluğunun burada gördüğünüz BC kenarının yarısı yani A bölü 2 kadar olduğunu gösterdik.
Muhteşem üçlü dedik buna da. Peki ya o üçgen dar açılı bir üçgense, dar açılı köşeden inersem buradaki özel noktam şu açım dar tamam ama BC uzunluğum sabit yani buradaki A bölü 2-A bölü 2 oranım değişmeyecek A bölü 2-A bölü 2 uzunluğumda değişmeyecek yani.
BC sabit duruyor, ben bu açıyı daraltırsam acaba Va ne olur demek istiyorum onu göstermek istiyorum.
İşte siz bu Vc'yi sabit tutup buradaki Va uzunluğunu bulmak istiyorsanız eğer açıyı daraltırsanız Va'yı uzatmış olursunuz arkadaşlar.
Size lastik örneği vermiştim üçgende eşitsizlik konusunda arkadaşlar.
Bir lastiği böyle çekerseniz uzar demiştim.
İşte aynen onun gibi bir mantık.
Açım daralır o yüzden de bu uzar arkadaşlar gördüğünüz gibi.
Yani bunu göstermek istedim size.
Tam tersi açım genişlerse yani gördüğünüz gibi 90 derecede böyleydi dar açıda böyleydi, şuraya dar yazalım Burası 90° dar açıda uzundu, 90 derecede eşitti, geniş açıda ne olacak peki?
Geniş açıda işte A bölü yaptığımız A bölü 2 uzunluğunu değiştirmedim. Yani BC'yi sabit tutarak bir kıyaslama yaptık. BC'yi sabit tutarak A köşesinin açısını dik dar ve geniş olarak inceledim.
İlk başta zaten size dikken anlattım A bölü 2 eşittir dedim.
Muhteşem üçlü kuralı dedik ona.
BC sabit tutup bu açıyı daraltırsam Va'nın uzadığını gösterdim.
Aynı şekilde açıyı genişletip yine BC'yi sabit tutarsam arkadaşlar A bölü 2 Va'dan daha uzun olmuş oluyor arkadaşlar.
Bunları aktarmak istedim.
Şimdi şöyle küçük bir örnek yapalım.
Dik bir üçgen verdim size demiş ki BG 4 santim yazalım.
Tamam AC uzunluğunu soruyu soruyor.
Şimdi size muhteşem üçlü anlattım aklınızda kalması bakımından bunu göstermek istiyorum.
Şimdi bir burada ekleyelim G ağırlık merkezi olsun, ağırlık merkezidir.
Şimdi G ağırlık merkezi olmasaydı soru bomboş havadaydı. Yani G noktasını bana niye vermiş herhangi bir nokta Şurada da olabilir.
Yani demek istediğim şu önemlidir arkadaşlar.
Yani soruyu okumanın önemi vardır, G ağırlık merkezi demeseydi işlem yapamayacaktım.
G'nin ağırlık merkezi olması ve bunun köşeye birleşmiş olması ben bunu uzatırsam eğer değdiği nokta kenarın ortası olacaktır.
Yani AC'nin ortasını bulmuş olacaktı.
Şimdi ben dik bir köşeden kenarortay mı indim?
Evet indik.
Demek ki burada bir muhteşem üçlü kuralı yapmış olduk. Burası eşittir, burası eşittir, burası demeliyim. Yani D harfi verirsen AD eşittir CD eşittir BD olmalı, tamam.
Şimdi burası güzeldi zaten buraları bulmak istiyorum da nasıl bulacağım burayı?
Şimdi burada da kenarortayın başta anlattığım kuralı yani ağırlık merkezinin kuralı.
Ağırlık merkezi kenara bir birim köşeye iki birim uzaklıkta olacak şekilde yerleşir.
Yani bir kenarortayı üzerinde kenara bir birim şuraya hatta yazalım 2k ve k olarak verelim.
Kenara bir birim köşeye iki birim olacak şekilde uzaklık alır.
Yani burada 2k'ye Yani burada GD uzunluğunu şöyle buluyorum: 4/2 eşittir 2 diyorum.
Teker teker yazmak istedim. Yani nasıl bulduğumu görmeniz açısından.
Ben 2x'i araştırıyordum, buradan BD dediğim şey x midir; şurada BD dediğim BD uzunluğu x'e eşit.
O zaman x dediğimde 4+2 midir, eşittir 6.
Benden AC istiyordu, AC uzunluğu iki tane x, iki tane 6, 12 santimetre buluruz.