Merhaba dostlar, Öklid kuralındayız şimdi öklid kuralıyla alakalı birkaç örnek bakalım.
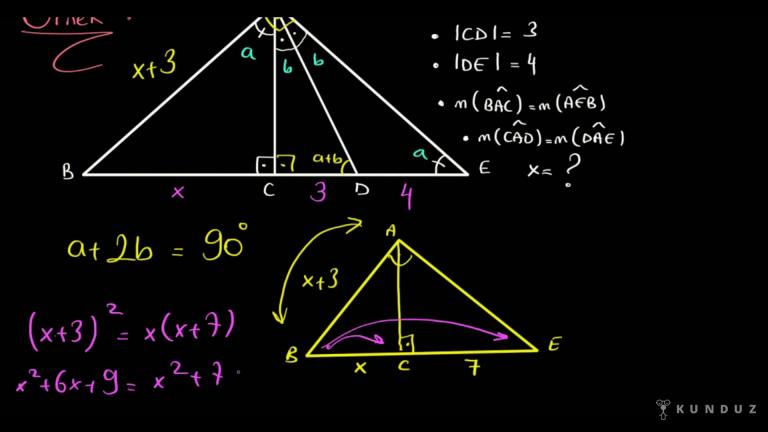
Şimdi örnekte ABC büyük üçgeni görüyorsunuz.
A noktasından yola başlayan koşucu şekildeki yol izleyerek C noktasına geliyor.
Ne kadar yol koşar diyorum.
Önce A'dan B'ye sonra B'den D'ye, sonra D'den E'ye sonra E'den C'ye gelerek yolunu bitiriyor.
Şimdi soruda verilene bakalım AB diktir BC.
BE diktir AC.
DE diktir BC tamam.
AD uzunluğu üç birim, CD uzunluğu 6 birim.
Tamam verilenler bitti.
Şimdi burada bilmem gereken neler var, görmem gereken neler var?
ABC bir dik üçgen ve dik köşeden dikilmiş BD diktir AC var çok güzel, BDC bir dik üçgendir ve dik olan D köşesinden D diktir BC çizilmiş çok güzel.
O zaman bu iki gösterdiğim şekilde de Öklid bağlantısını yazabilir.
Öklid bağıntısı neydi?
Tekrar bir hatırlatmak adına şuraya yazalım dikten dik indiğiniz durumda dostlar.
H, p, k hipotenüse ait yüksekliğin karesi eşittir altta ayrılan hipotenüste ayrılan parçaların çarpımı idi.
P çarpı k ya da şuralara da c dersem şuraya c dersem C'nin karesi eşittir.
p çarpı p artı k.
Tabiki de parantez içerisinde.
Şuraya b dersem b kare eşittir.
Bu sefer burdan geliyorum.
C çarpı p artı k oluyor dostlar şurayı temizleyeyim karışmasın.
Öklid teoremim buydu.
Tamam şimdi burada nasıl ilerlemeliyim peki ilk yolum ne olmalı?
İlk yolum büyük üçgende hep Öklid kuralı yapmak dostlar.
Çünkü burada gördüğünüz gibi dikten dik indi.
BD dik denilen bir dikme.
O zaman h kare yani hipotenüse ait yüksekliğin karesi eşittir hipotenüse ayrılan parçaların çarpımı.
O zaman b'nin karesi eşittir.
3 çarpı 6 18 kök 18.
Nedir?
Üç kök ikidir çok güzel.
Şimdi burada başka göstermek istediğim bir şey daha var.
Şimdi şunu biliyorum ki BDC üçgeninde dikten dik inme var.
Bir Öklid kuralı var.
Çok güzel ama işime yarayacak bir yer görüyorum.
Nedir o da dostlar?
Ab diktir BC, DE diktir BC.
Bu ne demektir dostlar, bu iki parça birbirine paraleldir, AB ve de BC'ye dik oldukları için birbirlerine paraleldir.
Şu paralelliği nasıl göstereyim bilmiyorum yazıyorum en iyisi.
Çünkü burada yol gösterme işaretleriyle karışmasın.
AB paraleldir DE oluyor dostlar.
Bu bana ne anlatmalı bana ne bu paralellikten hocam demeyiniz.
Çünkü burada şurada gördüğünüz 3 ve 6'yı boşuna vermedim, aslında üçe x geliyor derseniz x dediğim yer BE.
6'ya 2 x gelir, 3'e ise 6'ya 2 x gelir, 3'ün 2 katı olmuş, x'in de iki katı oluyor.
Tamam.
Şimdi bunu da yazdıktan sonra artık buraların hangi oranda ayrıldıklarını bildiğim için Pisagor teoremini yapabilirim.
BDC üçgeninde nasıl yaparım?
BDC üçgeninde bildiğim yer neresi?
6 ya da 3 kök iki ya da 6.
B ya da C.
Demek ki şu formüllerden birini kullanacağım.
Şu 3 kök 2'yi kullanıyorum.
Ne diyelim?
3 kök 2'nin karesi eşittir x çarpı hepsi yani x Şu oklar da gitsin çarpı 3x.
3x kare 18 eşittir 3x kare.
X eşittir kök 6 geldi dostlar.
Şimdi ben halen yoluma, yolumu hesaplamadan şöyle şu yolları bir değiştirelim.
Kök 6 bulduk doğru mu?
Burası kök 6 burası iki kök 6 etti.
Şimdi şurada Pisagor şimdi ben geldiği bu yoldan şurayı hesaplayabilir miyim?
Öncelikle hesaplarım nasıl hesaplarım?
Şurada Pisagor yaparak üçün karesi 9 3 kök 2'nin karesi 18 topladım 27 etti bana.
Üç kök 3 tamam 1.
AB yolunu buldum.
BD yolunu zaten biliyorum.
DE yolunu nasıl hesaplarım burada gördüğünüz Pisagorla, burada gördüğünüz Pisagorla ya da büyük üçgendeki Öklid mantığıyla hesaplayabilirim.
18'den 6 çıkardım 12 Pisagorla hesap alıyorum şu anda.
BDE üçgeninde on sekiz karesi eksi üç kök 2'nin karesi eksi kök altının karesi 12 etti.
Burası iki kök üç etti.
Bu yolu da hesapladım bu yolu da biliyorum artık gittiği yollu tamamiyle hesaplayabilirim.
AB yolum üç kök üç artı BD yolum üç kök iki artı DE yolum iki kök üç artı EC yolum iki kök altı.
Sonunda ne üç kök, üç beş kök, üç artı, üç kök, iki artı iki kök altı koşucunun gittiği toplam yol miktarı.
Evet, devam edelim.
Yine bir dik ABC üçgeni verdim, dik a köşesinden bir dikme indim.
Diktir BC.
Tamam.
Sonra dik ABE üçgeninde dik olan E köşesinden ED'yi indim.
Yine dikme olarak.
ED diktir AB tamam dikmeleri gösterdik.
AD 4 birim.
BD bir birim uzaklığında.
EC x birim ne kadardır diye soruyorum.
Şimdi burada dikilen dikme inmeleri bol.
Maşallah bir sürü çizdik ama geçişini öğrenmek lazım yani şimdi burada ABE üçgeninde siz bu ikisinin yardımıyla şuraya geçiyorsunuz.
Buradan sonra Pisagorla şuraya geçiyorsunuz.
Daha sonra aynı şekilde PisagorLa şuraya geçiş yapabiliyorsunuz.
Aynı şekilde bu sefer Öklid bağıntısı ile şurayı biliyorum burayı biliyorum x'e geçiş yapabiliyorum.
Yani yaptığım şey aslında biraz yapboza benziyor atlaya atlaya.
Yavaş yavaş doldura doldura geliyorum.
Şimdi ilk yapacağım şey.
Şurayı silelim ABE üçgeninde Öklid nedir?
Gördüğünüz gibi E dik köşesinden dikme inmiş.
O zaman hipotenüse ait yüksekliğin karesi şuraya h edersem h kare eşittir bir çarpı 4.
O zaman h dediğim şey iki oldu.
Buraya iki yazdım.
Sonra iki dört.
Buraya gelen uzunluk Pisagorla iki kök beş.
Bir dik kenar diğer dik yandan iki katı ise hipotenüs kısa dik kenarın kök beş katı tamam.
Aynı şekilde burada da bir dik kenar diğer dik kenarın iki katı.
O zaman kısanın kök 5 katı.
1, kök 5 katı kök 5 etti.
Tamam şurayı temizliyorum.
Şimdi büyük üçgende Öklid bağlantısına bakıyorum.
Hipotenüse ait yükseklik burası mı?
Evet, 2 kök beşin karesi eşittir kök 5 çarpı x.
Aşağıda gördüğünüz hipotenüse ait parçalar 20.
20 bölü kök 5 mi etti.
20 bölü kök 5 eşittir x.
O zaman 20 kök 5 bölü 5 aşağı kök 5'le genişlettik.
Şöyle gösterelim buradan 4 kök 5 bulunur dostlar.
Şimdi örnekte ABC büyük üçgeni görüyorsunuz.
A noktasından yola başlayan koşucu şekildeki yol izleyerek C noktasına geliyor.
Ne kadar yol koşar diyorum.
Önce A'dan B'ye sonra B'den D'ye, sonra D'den E'ye sonra E'den C'ye gelerek yolunu bitiriyor.
Şimdi soruda verilene bakalım AB diktir BC.
BE diktir AC.
DE diktir BC tamam.
AD uzunluğu üç birim, CD uzunluğu 6 birim.
Tamam verilenler bitti.
Şimdi burada bilmem gereken neler var, görmem gereken neler var?
ABC bir dik üçgen ve dik köşeden dikilmiş BD diktir AC var çok güzel, BDC bir dik üçgendir ve dik olan D köşesinden D diktir BC çizilmiş çok güzel.
O zaman bu iki gösterdiğim şekilde de Öklid bağlantısını yazabilir.
Öklid bağıntısı neydi?
Tekrar bir hatırlatmak adına şuraya yazalım dikten dik indiğiniz durumda dostlar.
H, p, k hipotenüse ait yüksekliğin karesi eşittir altta ayrılan hipotenüste ayrılan parçaların çarpımı idi.
P çarpı k ya da şuralara da c dersem şuraya c dersem C'nin karesi eşittir.
p çarpı p artı k.
Tabiki de parantez içerisinde.
Şuraya b dersem b kare eşittir.
Bu sefer burdan geliyorum.
C çarpı p artı k oluyor dostlar şurayı temizleyeyim karışmasın.
Öklid teoremim buydu.
Tamam şimdi burada nasıl ilerlemeliyim peki ilk yolum ne olmalı?
İlk yolum büyük üçgende hep Öklid kuralı yapmak dostlar.
Çünkü burada gördüğünüz gibi dikten dik indi.
BD dik denilen bir dikme.
O zaman h kare yani hipotenüse ait yüksekliğin karesi eşittir hipotenüse ayrılan parçaların çarpımı.
O zaman b'nin karesi eşittir.
3 çarpı 6 18 kök 18.
Nedir?
Üç kök ikidir çok güzel.
Şimdi burada başka göstermek istediğim bir şey daha var.
Şimdi şunu biliyorum ki BDC üçgeninde dikten dik inme var.
Bir Öklid kuralı var.
Çok güzel ama işime yarayacak bir yer görüyorum.
Nedir o da dostlar?
Ab diktir BC, DE diktir BC.
Bu ne demektir dostlar, bu iki parça birbirine paraleldir, AB ve de BC'ye dik oldukları için birbirlerine paraleldir.
Şu paralelliği nasıl göstereyim bilmiyorum yazıyorum en iyisi.
Çünkü burada yol gösterme işaretleriyle karışmasın.
AB paraleldir DE oluyor dostlar.
Bu bana ne anlatmalı bana ne bu paralellikten hocam demeyiniz.
Çünkü burada şurada gördüğünüz 3 ve 6'yı boşuna vermedim, aslında üçe x geliyor derseniz x dediğim yer BE.
6'ya 2 x gelir, 3'e ise 6'ya 2 x gelir, 3'ün 2 katı olmuş, x'in de iki katı oluyor.
Tamam.
Şimdi bunu da yazdıktan sonra artık buraların hangi oranda ayrıldıklarını bildiğim için Pisagor teoremini yapabilirim.
BDC üçgeninde nasıl yaparım?
BDC üçgeninde bildiğim yer neresi?
6 ya da 3 kök iki ya da 6.
B ya da C.
Demek ki şu formüllerden birini kullanacağım.
Şu 3 kök 2'yi kullanıyorum.
Ne diyelim?
3 kök 2'nin karesi eşittir x çarpı hepsi yani x Şu oklar da gitsin çarpı 3x.
3x kare 18 eşittir 3x kare.
X eşittir kök 6 geldi dostlar.
Şimdi ben halen yoluma, yolumu hesaplamadan şöyle şu yolları bir değiştirelim.
Kök 6 bulduk doğru mu?
Burası kök 6 burası iki kök 6 etti.
Şimdi şurada Pisagor şimdi ben geldiği bu yoldan şurayı hesaplayabilir miyim?
Öncelikle hesaplarım nasıl hesaplarım?
Şurada Pisagor yaparak üçün karesi 9 3 kök 2'nin karesi 18 topladım 27 etti bana.
Üç kök 3 tamam 1.
AB yolunu buldum.
BD yolunu zaten biliyorum.
DE yolunu nasıl hesaplarım burada gördüğünüz Pisagorla, burada gördüğünüz Pisagorla ya da büyük üçgendeki Öklid mantığıyla hesaplayabilirim.
18'den 6 çıkardım 12 Pisagorla hesap alıyorum şu anda.
BDE üçgeninde on sekiz karesi eksi üç kök 2'nin karesi eksi kök altının karesi 12 etti.
Burası iki kök üç etti.
Bu yolu da hesapladım bu yolu da biliyorum artık gittiği yollu tamamiyle hesaplayabilirim.
AB yolum üç kök üç artı BD yolum üç kök iki artı DE yolum iki kök üç artı EC yolum iki kök altı.
Sonunda ne üç kök, üç beş kök, üç artı, üç kök, iki artı iki kök altı koşucunun gittiği toplam yol miktarı.
Evet, devam edelim.
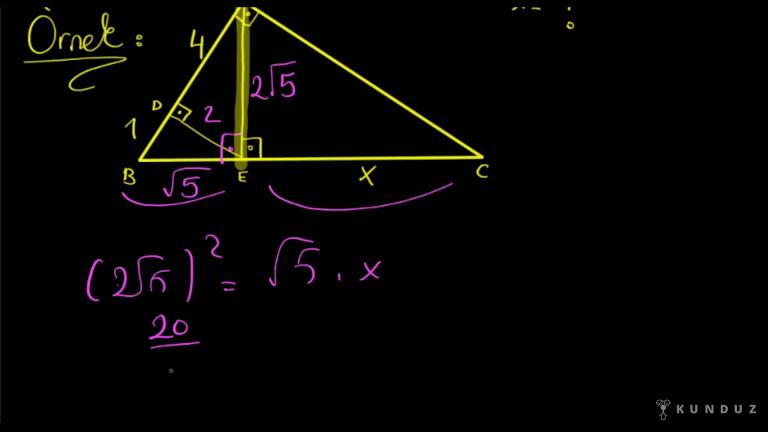
Yine bir dik ABC üçgeni verdim, dik a köşesinden bir dikme indim.
Diktir BC.
Tamam.
Sonra dik ABE üçgeninde dik olan E köşesinden ED'yi indim.
Yine dikme olarak.
ED diktir AB tamam dikmeleri gösterdik.
AD 4 birim.
BD bir birim uzaklığında.
EC x birim ne kadardır diye soruyorum.
Şimdi burada dikilen dikme inmeleri bol.
Maşallah bir sürü çizdik ama geçişini öğrenmek lazım yani şimdi burada ABE üçgeninde siz bu ikisinin yardımıyla şuraya geçiyorsunuz.
Buradan sonra Pisagorla şuraya geçiyorsunuz.
Daha sonra aynı şekilde PisagorLa şuraya geçiş yapabiliyorsunuz.
Aynı şekilde bu sefer Öklid bağıntısı ile şurayı biliyorum burayı biliyorum x'e geçiş yapabiliyorum.
Yani yaptığım şey aslında biraz yapboza benziyor atlaya atlaya.
Yavaş yavaş doldura doldura geliyorum.
Şimdi ilk yapacağım şey.
Şurayı silelim ABE üçgeninde Öklid nedir?
Gördüğünüz gibi E dik köşesinden dikme inmiş.
O zaman hipotenüse ait yüksekliğin karesi şuraya h edersem h kare eşittir bir çarpı 4.
O zaman h dediğim şey iki oldu.
Buraya iki yazdım.
Sonra iki dört.
Buraya gelen uzunluk Pisagorla iki kök beş.
Bir dik kenar diğer dik yandan iki katı ise hipotenüs kısa dik kenarın kök beş katı tamam.
Aynı şekilde burada da bir dik kenar diğer dik kenarın iki katı.
O zaman kısanın kök 5 katı.
1, kök 5 katı kök 5 etti.
Tamam şurayı temizliyorum.
Şimdi büyük üçgende Öklid bağlantısına bakıyorum.
Hipotenüse ait yükseklik burası mı?
Evet, 2 kök beşin karesi eşittir kök 5 çarpı x.
Aşağıda gördüğünüz hipotenüse ait parçalar 20.
20 bölü kök 5 mi etti.
20 bölü kök 5 eşittir x.
O zaman 20 kök 5 bölü 5 aşağı kök 5'le genişlettik.
Şöyle gösterelim buradan 4 kök 5 bulunur dostlar.