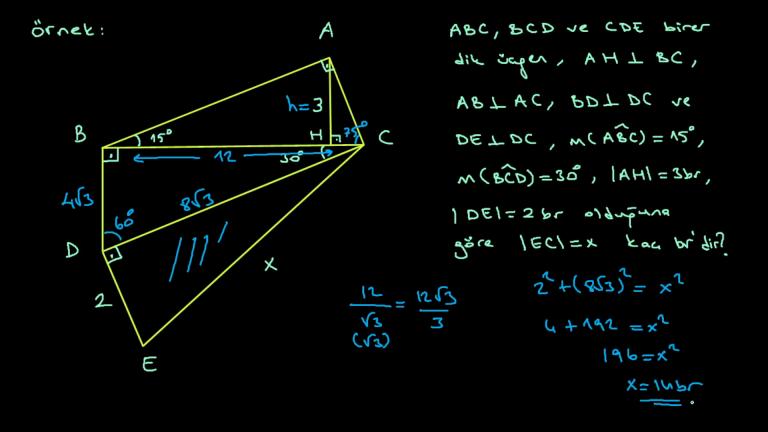Evet Pisagor, devam ediyoruz dostlar.
Yeni bir AB CD'yi dört yeni verdim.
Iki birim 7 8 birim.
Evcen'in BBC'ye eşit olduğunu AB'nin BBC'ye yedik.
Abd'nin ödeyeceği dik olduğunu verdik.
Ab'nin Hicks'in uzunluğunu bulmanızı istiyorum.
Şimdi burada ne yapmalıyım?
Dostlar ilk yapacağım hamle ne olmalı?
B ve Ege'yi birleştirmek doğru mu?
Çünkü Ece ve B C ikiz kenar.
Hayır.
Ama burada ikiz kentler var, doğru.
Ama siz bu 90 dereceyi neden görüyorsunuz?
Böyle birşey yapmamalıyız, ilk amirimiz boğulmamak.
Ben bu 90 dereceyi dönersem neden bu 90 dereceyi kullanmamış olayım ki?
Boşuna mı vermiş oldum?
Hayır.
Demek ki hamle böyle değil.
Demek ki başka bir yeri birleştirmeliyiz.
Şimdi bu 90 dereceye bakıyorum da bu 90 dereceyi barındıran, şu 90 dereceyi barındıran bir üçgen yok.
Demek ki ilki işlemin bu 90 dereceyi barındıran bir üçgen yaratmak, bir dik üçgen bulabilmek.
Yani A ve C köşelerini birleştirir.
Hem bu 90 derece üçgen içerisine koyuyorum.
A ve C yi birleştirdim.
Şimdi burada eşitlik var.
Sağ tarafta bir eye DC üçgeni, dik üçgen A, DC üçgeni dik üçgen.
Şu büyük üç kentten bahsediyorum.
Bu tarafa geliyorum.
A A-B-C bir dik üçgen, üç tane dik üçgenin var dostlar.
Buradan demek ki 3 tane denklem yazabiliyorum ve aslında iki tane de birbirine eşit kenar uzunluğu var.
Bu çok güzel.
Demek ki bu bana şunu ifade ediyor ki kenar uzunlukları harf vererek denklem sistemlerini çözmemiz gerekiyor.
İşte burada harf vererek dinleyeceksiniz.
Harf vermekten korkmayınız.
Ağca'ya A.
Diyorum, A.
Aceh dedim buraya yazdım.
Ağca'ya a.
Diyorum, Ece'ye B.
Diyorum.
B dersem burası da B.
Etti.
Şu dereceyi de C ediyorum.
Tamam devam diyorum, ikisi bulmaya çalışıyorum.
İlk yapacağım Pisagor şurada olsun tamam mı?
Buradaki Pisagor yapıyorum.
B, C ve 8'in olduğu ede C üçgeninde hipotezin üssün karesi bekar eşittir C kare artı 64 8'in karesi tamam.
İkinci Pisagor korum de C7 üçgeninde dostlar.
Bu dik üçgenin bu kenarı on santim on biri mi?
Evet, o zaman hippi dönüşsün karesi nedir?
Akare eşittir onun karesi yüz artı diğer dik kenarın c ckd.
Şimdi burada iki tarafta da C kare var.
Görüyorsunuz doğru mu?
Eşitliğin sağ tarafında iki tarafta da C karı var.
Şu bir kareyi tekrar bu alt tarafa yazmak istiyorum.
C kare artı 64 şurayı temizleyelim.
Şimdi burada şuradan şunu çıkarırsan akare eksi b kare eşittir.
C Kareler birbirini götürdü mü?
100 x 64 yani 30 6'yı elde etmiş olduk.
Şimdi işte miz Suriye kaldı.
Nedir buraya kaldı.
A, B, C üçgenin de Pisagor yapıyorum.
Akare eşittir IX kare artı bekarı.
Sen bu tarafa gel bakalım.
Ankara eksi B kare eşittir IX kare oldu.
Bana kare art akare eksi b kareyi buldum.
Burası otuz altı eşittir.
Ix kare IX.
O zaman 6 birim bulunuyor dostla.
Evet, devam edelim dostlar, şimdi burada bir ABC'de 4 yeni verdim size AB uzunluğunu a diyelim.
O zaman C7 uzunluğunu 2 a vermişiz.
Ay uzunluğu 2, Beyce uzunluğu 5, EPD uzunluğu 4 ABC'de 4 yeni.
İçersinde ACE köşe geni ve B de köşelerini dik kesilmekte.
Şimdi burada anın uzunluğunu bulmamız isteniyor.
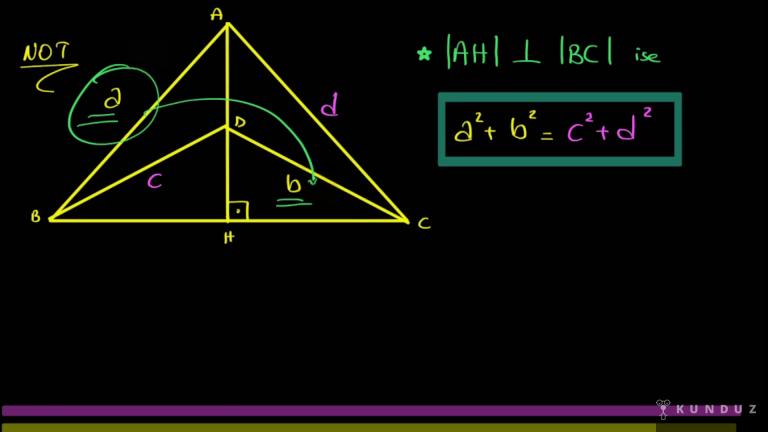
Bu tarz soruları hem üçgen de hem de dörtgen de anlatmıştık.
Köşe genleri dik kesişen şöyle dörtgen gördüğünüz zaman karşılıklı kenar uzunlukları, kollarının kareleri, toplamı, toplamları birbirlerine eşittir.
Ne demek istiyorum?
Şurada gördüğünüz AB ve DC'nin uzunlukları kareleri toplamı eşittir.
Burada gördüğünüz Beyce ve Aden'in kenar uzunlukları kareleri toplamına eşittir.
Ben şu taraftan ağılı denklemi elde edeceğim biliyorum.
Bu tarafta 5 var.
Bu tarafta da zaten Pisagor elde edebileceğim bir uzunluk var.
Bu kuralı hatırlatmak babında çözdüm.
Şimdi şu anda 3 günde Pisagor yaparsam 2 4 buraya gelecek.
Uzunluk nedir?
2 kök 5.
Nasıl buldun böyle hızlıca bir dik kenar diğer dik kenarın iki katını?
Evet 4 2'nin iki katı.
O zaman patroniçesi uzunluğu küt kısa olan dik kenar uzunluğunun kök 5 kat oluyordu.
2 kök 5 tamam.
Şimdi burada burayı biliyorum, burayı biliyorum.
Şurada şurada denklem olarak yazabiliyorum.
Akare artı iki anın karesi eşittir beşin karesi artı 2 kök beşin karesi.
Buradan gelecek denklem nedir?
Şurada 4 akare bir akare da 5 tane akare eşittir 25.
Artı buradan da 20 geliyor.
45 5.
Şuradan akare eşittir 9 oldu a eşittir 3 bulunur dostlar.
Evet, son soruyla devam edelim.
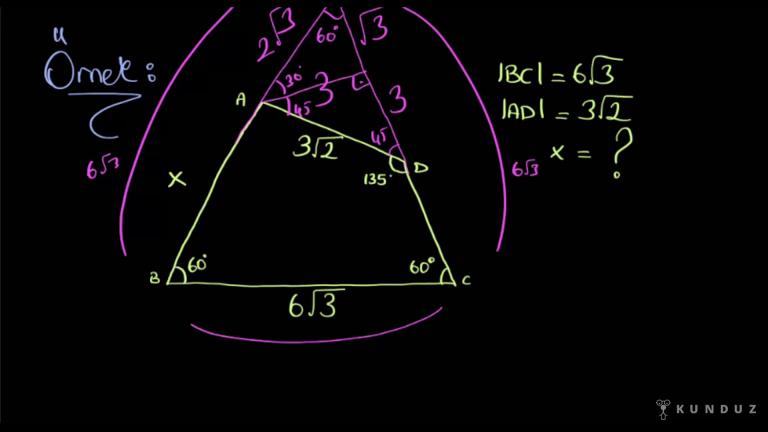
Bir A-B-C dik üçgeni verdim, AB'ye diktir, acÄ aceba açısını 15 derece olarak verdik.
Ağacı uzunluğunu da iki kök 3 artı 4 olarak verelim.
Şimdi buradan AB uzunlu yani İLKSAN ne kadar olduğunu bulalım.
Şimdi bu 15 75, 93 yeni doğru mu?
Tamam, şimdi bu 15 75 90 üçgeninde size şunu göstermiştim dedik.
Yani iPod dönüşse ait yüksekliğin uzunluğu hipotezin tenisin dörtte biridir.
Yani buraya aslında beyce biri 4 diyelim adet PC bölüğü 4.
Bunu anlatmıştım da burada göstermek istediğim şey bu değil.
İşte bunu anlatmıştım.
Şimdi bu göstermek istediğim şey 15, 75, 90 üçgenini güzel bir hale getirmek.
15, 75, 90 ülkenin de bildiğim, rahatça bildiğim bir trigonometrik değer yok.
O zaman bunu rahatça trigonometrik değerlerini bildiğim üçgenler haline getirmem lazım.
Neden bahsediyorum?
45, 45, 90 ülkenin trigonometrik değerlerini rahatlıkla hesap duyabiliyor.
30 60, 90 üçgenine getirmeliyiz.
30, 60, 90 ülkenin trigonometrik değerlerini rahatlıkla bulabiliyorum ve biliyorum.
Peki ben bu 15 üçgenini 15 dereceyi, 15 üçgenini 15 dereceyi ne hale getirmeli?
45 derece haline mi getirmeliyiz?
30 derece annemi getirmeyelim, 60 derece haline mi getirmeliyiz?
Kullanarak.
İşte burada 30 derece haline getirmek daha önemlidir.
Neden?
Çünkü 30 derecenin getirmem için ikinci bir 15 derece daha gerekecektir.
Şekil üstünde göstererek anlatayım.
Burada B, C parçasından 15 derece ayrılacak şekilde bir parça çiziyorum dostlar.
Şu şekilde görelim 15 derece derken BBC'den 15 derece şuradan söz ediyorum, 15 derece böyle oldu.
Şuraya da dev noktası diyelim.
Şimdi burada şuranın 2 kök, 3 artı 4 birim olduğunu biliyorum.
2 kök, 3 artı 4 birim tamam.
Şimdi siz aşağıda B.
Dc'de bir ikiz kenar lık yapmadınız mı?
Hem 15 hem 15.
İşte bahsettiğim mesele buydu.
Siz 30 dereceyi tamamlamaya çalışınca 15 artı 15 30 olduğu için bir ikiz kenar yaratmış oluyorsunuz.
Böylelikle şöyle ikiz ken aldığımızda gösterelim b de eşittir C7 oldu.
İki tane iç saçımın toplamı kendilerine komşu olmayan dış açı eşit midir?
15, 15, 30 etti.
Ademi açım 30 derece oldu.
30 90 burası 60 derece, ABD açısı 60 derece oldu.
Şimdi işlemin daha kolay.
Çünkü üst tarafta bir 30, 60, 90 üçgenin trigonometrik değerlerini rahatlıkla biliyorum.
Alt tarafta da bir ikiz kenar üçgen yaratmış oluyorum.
Ilerleyebilir.
30 derecenin karşısı içse ABD üçgeni içerisinde 90 derecenin karşılığı bunun iki katı 60 derecenin karşısında bunun kökü 3 katı olur.
Ciksin kökü üç katı olur.
Ix kök 3.
E Alt tarafta ikiz kenar lık yer atmıştım.
Burası eşittir burası yani P7 eşittir CED dedim.
E B de iki içse burada CD'ye de 2 X olur.
İşte sorun burada bitti.
Ace uzunluğun 2 x artı IX kök 3 mü?
Evet bu aynı zamanda şu diyelim değilmidir?
2 kök üç artı 4 isimli çıkıyor dostlar iki ilk seneki koyarsanız zaten bu değerleri şu değer zaten eşit olması gerektiği için iki kök üç eşittir x kökü 3 x eşittir iki bulunur dostlar.
Yeni bir AB CD'yi dört yeni verdim.
Iki birim 7 8 birim.
Evcen'in BBC'ye eşit olduğunu AB'nin BBC'ye yedik.
Abd'nin ödeyeceği dik olduğunu verdik.
Ab'nin Hicks'in uzunluğunu bulmanızı istiyorum.
Şimdi burada ne yapmalıyım?
Dostlar ilk yapacağım hamle ne olmalı?
B ve Ege'yi birleştirmek doğru mu?
Çünkü Ece ve B C ikiz kenar.
Hayır.
Ama burada ikiz kentler var, doğru.
Ama siz bu 90 dereceyi neden görüyorsunuz?
Böyle birşey yapmamalıyız, ilk amirimiz boğulmamak.
Ben bu 90 dereceyi dönersem neden bu 90 dereceyi kullanmamış olayım ki?
Boşuna mı vermiş oldum?
Hayır.
Demek ki hamle böyle değil.
Demek ki başka bir yeri birleştirmeliyiz.
Şimdi bu 90 dereceye bakıyorum da bu 90 dereceyi barındıran, şu 90 dereceyi barındıran bir üçgen yok.
Demek ki ilki işlemin bu 90 dereceyi barındıran bir üçgen yaratmak, bir dik üçgen bulabilmek.
Yani A ve C köşelerini birleştirir.
Hem bu 90 derece üçgen içerisine koyuyorum.
A ve C yi birleştirdim.
Şimdi burada eşitlik var.
Sağ tarafta bir eye DC üçgeni, dik üçgen A, DC üçgeni dik üçgen.
Şu büyük üç kentten bahsediyorum.
Bu tarafa geliyorum.
A A-B-C bir dik üçgen, üç tane dik üçgenin var dostlar.
Buradan demek ki 3 tane denklem yazabiliyorum ve aslında iki tane de birbirine eşit kenar uzunluğu var.
Bu çok güzel.
Demek ki bu bana şunu ifade ediyor ki kenar uzunlukları harf vererek denklem sistemlerini çözmemiz gerekiyor.
İşte burada harf vererek dinleyeceksiniz.
Harf vermekten korkmayınız.
Ağca'ya A.
Diyorum, A.
Aceh dedim buraya yazdım.
Ağca'ya a.
Diyorum, Ece'ye B.
Diyorum.
B dersem burası da B.
Etti.
Şu dereceyi de C ediyorum.
Tamam devam diyorum, ikisi bulmaya çalışıyorum.
İlk yapacağım Pisagor şurada olsun tamam mı?
Buradaki Pisagor yapıyorum.
B, C ve 8'in olduğu ede C üçgeninde hipotezin üssün karesi bekar eşittir C kare artı 64 8'in karesi tamam.
İkinci Pisagor korum de C7 üçgeninde dostlar.
Bu dik üçgenin bu kenarı on santim on biri mi?
Evet, o zaman hippi dönüşsün karesi nedir?
Akare eşittir onun karesi yüz artı diğer dik kenarın c ckd.
Şimdi burada iki tarafta da C kare var.
Görüyorsunuz doğru mu?
Eşitliğin sağ tarafında iki tarafta da C karı var.
Şu bir kareyi tekrar bu alt tarafa yazmak istiyorum.
C kare artı 64 şurayı temizleyelim.
Şimdi burada şuradan şunu çıkarırsan akare eksi b kare eşittir.
C Kareler birbirini götürdü mü?
100 x 64 yani 30 6'yı elde etmiş olduk.
Şimdi işte miz Suriye kaldı.
Nedir buraya kaldı.
A, B, C üçgenin de Pisagor yapıyorum.
Akare eşittir IX kare artı bekarı.
Sen bu tarafa gel bakalım.
Ankara eksi B kare eşittir IX kare oldu.
Bana kare art akare eksi b kareyi buldum.
Burası otuz altı eşittir.
Ix kare IX.
O zaman 6 birim bulunuyor dostla.
Evet, devam edelim dostlar, şimdi burada bir ABC'de 4 yeni verdim size AB uzunluğunu a diyelim.
O zaman C7 uzunluğunu 2 a vermişiz.
Ay uzunluğu 2, Beyce uzunluğu 5, EPD uzunluğu 4 ABC'de 4 yeni.
İçersinde ACE köşe geni ve B de köşelerini dik kesilmekte.
Şimdi burada anın uzunluğunu bulmamız isteniyor.
Bu tarz soruları hem üçgen de hem de dörtgen de anlatmıştık.
Köşe genleri dik kesişen şöyle dörtgen gördüğünüz zaman karşılıklı kenar uzunlukları, kollarının kareleri, toplamı, toplamları birbirlerine eşittir.
Ne demek istiyorum?
Şurada gördüğünüz AB ve DC'nin uzunlukları kareleri toplamı eşittir.
Burada gördüğünüz Beyce ve Aden'in kenar uzunlukları kareleri toplamına eşittir.
Ben şu taraftan ağılı denklemi elde edeceğim biliyorum.
Bu tarafta 5 var.
Bu tarafta da zaten Pisagor elde edebileceğim bir uzunluk var.
Bu kuralı hatırlatmak babında çözdüm.
Şimdi şu anda 3 günde Pisagor yaparsam 2 4 buraya gelecek.
Uzunluk nedir?
2 kök 5.
Nasıl buldun böyle hızlıca bir dik kenar diğer dik kenarın iki katını?
Evet 4 2'nin iki katı.
O zaman patroniçesi uzunluğu küt kısa olan dik kenar uzunluğunun kök 5 kat oluyordu.
2 kök 5 tamam.
Şimdi burada burayı biliyorum, burayı biliyorum.
Şurada şurada denklem olarak yazabiliyorum.
Akare artı iki anın karesi eşittir beşin karesi artı 2 kök beşin karesi.
Buradan gelecek denklem nedir?
Şurada 4 akare bir akare da 5 tane akare eşittir 25.
Artı buradan da 20 geliyor.
45 5.
Şuradan akare eşittir 9 oldu a eşittir 3 bulunur dostlar.
Evet, son soruyla devam edelim.
Bir A-B-C dik üçgeni verdim, AB'ye diktir, acÄ aceba açısını 15 derece olarak verdik.
Ağacı uzunluğunu da iki kök 3 artı 4 olarak verelim.
Şimdi buradan AB uzunlu yani İLKSAN ne kadar olduğunu bulalım.
Şimdi bu 15 75, 93 yeni doğru mu?
Tamam, şimdi bu 15 75 90 üçgeninde size şunu göstermiştim dedik.
Yani iPod dönüşse ait yüksekliğin uzunluğu hipotezin tenisin dörtte biridir.
Yani buraya aslında beyce biri 4 diyelim adet PC bölüğü 4.
Bunu anlatmıştım da burada göstermek istediğim şey bu değil.
İşte bunu anlatmıştım.
Şimdi bu göstermek istediğim şey 15, 75, 90 üçgenini güzel bir hale getirmek.
15, 75, 90 ülkenin de bildiğim, rahatça bildiğim bir trigonometrik değer yok.
O zaman bunu rahatça trigonometrik değerlerini bildiğim üçgenler haline getirmem lazım.
Neden bahsediyorum?
45, 45, 90 ülkenin trigonometrik değerlerini rahatlıkla hesap duyabiliyor.
30 60, 90 üçgenine getirmeliyiz.
30, 60, 90 ülkenin trigonometrik değerlerini rahatlıkla bulabiliyorum ve biliyorum.
Peki ben bu 15 üçgenini 15 dereceyi, 15 üçgenini 15 dereceyi ne hale getirmeli?
45 derece haline mi getirmeliyiz?
30 derece annemi getirmeyelim, 60 derece haline mi getirmeliyiz?
Kullanarak.
İşte burada 30 derece haline getirmek daha önemlidir.
Neden?
Çünkü 30 derecenin getirmem için ikinci bir 15 derece daha gerekecektir.
Şekil üstünde göstererek anlatayım.
Burada B, C parçasından 15 derece ayrılacak şekilde bir parça çiziyorum dostlar.
Şu şekilde görelim 15 derece derken BBC'den 15 derece şuradan söz ediyorum, 15 derece böyle oldu.
Şuraya da dev noktası diyelim.
Şimdi burada şuranın 2 kök, 3 artı 4 birim olduğunu biliyorum.
2 kök, 3 artı 4 birim tamam.
Şimdi siz aşağıda B.
Dc'de bir ikiz kenar lık yapmadınız mı?
Hem 15 hem 15.
İşte bahsettiğim mesele buydu.
Siz 30 dereceyi tamamlamaya çalışınca 15 artı 15 30 olduğu için bir ikiz kenar yaratmış oluyorsunuz.
Böylelikle şöyle ikiz ken aldığımızda gösterelim b de eşittir C7 oldu.
İki tane iç saçımın toplamı kendilerine komşu olmayan dış açı eşit midir?
15, 15, 30 etti.
Ademi açım 30 derece oldu.
30 90 burası 60 derece, ABD açısı 60 derece oldu.
Şimdi işlemin daha kolay.
Çünkü üst tarafta bir 30, 60, 90 üçgenin trigonometrik değerlerini rahatlıkla biliyorum.
Alt tarafta da bir ikiz kenar üçgen yaratmış oluyorum.
Ilerleyebilir.
30 derecenin karşısı içse ABD üçgeni içerisinde 90 derecenin karşılığı bunun iki katı 60 derecenin karşısında bunun kökü 3 katı olur.
Ciksin kökü üç katı olur.
Ix kök 3.
E Alt tarafta ikiz kenar lık yer atmıştım.
Burası eşittir burası yani P7 eşittir CED dedim.
E B de iki içse burada CD'ye de 2 X olur.
İşte sorun burada bitti.
Ace uzunluğun 2 x artı IX kök 3 mü?
Evet bu aynı zamanda şu diyelim değilmidir?
2 kök üç artı 4 isimli çıkıyor dostlar iki ilk seneki koyarsanız zaten bu değerleri şu değer zaten eşit olması gerektiği için iki kök üç eşittir x kökü 3 x eşittir iki bulunur dostlar.