Merhabalar, üçgende açılarda son olarak bazı özel üçgen türleri ve açı özellikleri hakkında bilgi verelim.
İkiz kenar la başlayabiliriz arkadaşlar.
İkiz kenar üçgen adı üstünde zaten iki tane eşit kenar lazım bana.
Yani bir A-B-C üçgenin de AB eşittir a c verildiyse bu bir ikiz kenar üçgen dir diyeceğim.
Burada beyce kenarı yani eşit olmayan son kenar ım taban kenar dır.
Arkadaşlar A köşesi yani tabanı gören taraf da tepe olarak adlandırılabilir.
Arkadaşlar burada eğer a b eşittir acı eşitliği yani bir kenar eşitliği verdiyse biz de açı eşitliği yazabiliriz.
Yani sol alttaki tabana alf edersek sanattaki taban açısına da alfa yazacağız arkadaşlar.
2.
İskender üçgen deki açı özelliğimiz bu şekilde gelişir arkadaşlar.
Şimdi burada anlatmak istediğim son bir kural da arkadaşlar ikiz kenarda tepe köşeden inen dikme açı ortay özelliği taşır.
Ne demek istiyorum Ağa'dan bir dik inerse ki arkadaşlar.
Bu bir açı ortay arkadaşlar.
İkiz olmayan tabanı gören.
Bir köşeden yani A köşesinden eğer siz dikmeyi yerseniz o hem açı ortadır hem de kenar ortay dır.
Arkadaşlar bunun tersini ya da karıştığını da söylemek mümkün.
Ne demek istiyorum?
Tepeden inen kenar ortay aynı zamanda aç orta aydır.
Yani burada aç Ortaylı'ya bize vermeseydi arkadaşlar sadece kenar orta aylığı verseydi, ağdan inen bir kenar ortay ikiz kenar olmayan yere indiği için arkadaşlar bu hem diktir diyecektim hem de buraya eşit açıya böldü diyecektim.
Aynı şekilde açı ortay olarak verdiyse de yani bize bu kenar orta aylığı da vermediyse sadece dediki tepe açıdan bir açı ortay indirdim.
O zaman buranın dik olduğunu ve buraların eşit bölüneceğini biz yazacağız.
Arkadaşlar önemli olan parça burasıydı ilerleyelim.
Eşkenar üçgeni geçelim, eski arkadaşlar eşkenar ile şöyle devam edelim, kenarları eşit, iç ve dış açıları da eşit.
İç açıları 60.
Dış açıları 120 derece olacan olan üçgen eşkenar ikiz kenar gibidir aslında.
Arkadaşlar burada ama herhangi bir köşeden inen dik hem açı orta hem de kenar orta aydır.
Herhangi bir köşeden dedim arkadaşlar burası önemli.
İsterseniz Ağa'dan inin, isterseniz B eden C'den inin hem aç ortağı hem kenar ortay oluyor.
Dik inilen açı 30 30 bölünüyor, 60'ı açı ortay böler.
Eğer 30 30 bölecek ve buradan mesela şuradan bir örneklem yaparsam hem açı ortay hem kenar orta yollu için böyle bölünecek arkadaşlar.
60 eşit bölüp otuz otuz yaratıyorum.
Soldaki üçgen ya da sağdaki üçgen de 30, 60, 90 üçgenler oluşur.
Arkadaşlar eşkenar da dikkat etmemiz gereken yer bir şekilde kenar eşitliğini kullanabileceğimizi unutmamak olur.
Bu sorularda tavsiyem eşit olan kenarları tarama hızıdır.
Yani bir eşkenar verildiği kadar şu şekilde taramalı sın diyorum sana.
Gözünüzden başka ikiz veya eşkenar üçgenler kaçırmamanızı önler arkadaşlar.
Devam edelim.
İkiz kenar, dik üçgen.
İkiz kenar da küçükken aslında isminden gayet belli arkadaşlar dik bir üçgen ele alıyoruz ve üçgenin miz ikiz olduğu için de taban açıları da eşit oluyor.
Yani alfa alfa olarak verdiğim yerler 90 derece olması gerektiği için iki tane Alfa'nın bir alfa am 45 derece oluyor.
Burada dik olan kenarları da görmek deseniz.
Burada tabii 90 derecenin karşısına Hypo Tenis diyoruz.
Kenarı mıza Hypo Tenis diyoruz arkadaşlar bunu da belirtelim.
Muhteşem üçlü kuralımız var.
Dik bir üçgen içerisinde bunu da açıklamak gerekiyor.
Dik bir üçgen içerisinde arkadaşlar dik açıdan inen kenar ortay uzunluğu buradaki dik dik çok önemli.
Buradaki dik dik olmazsa bahsettiğim şeyi yaratamıyor.
Düz dik açıdan inen kenar orta uzunluğu hipotezin üssün yarısıdır.
Yani siz ağa'dan neden?
Çünkü dik liğin olduğu köşeden hipotezin ise bir kenar orta iner iseniz hipotezin üssün yarısını elde edersiniz.
Mesele bu kadar yani adÄ eşittir B de eşittir CD'yi buluyoruz.
Burada şöyle bir yeri kaçırmamak lazım.
Eğer bir diskten inen adÄ eşittir dCi eşitliği görüyorsanız.
Bey'di eşitliğinde siz yaza bilmelisiniz arkadaşlar, önemli bir nokta burada ikiz kenar yıllıklar oluştuğu için mesela şu açı, şu açı eşit olduğu için, bu açı, bu açı eşit olduğu için açı sorularında kullanılabilen bir özellik.
Bunu da aktaralım.
Son olarak orta tabandan bahsetmek istiyorum.
Arkadaşlar buradaki paralelliği açıklamak istiyorum.
Ne demek istiyorum?
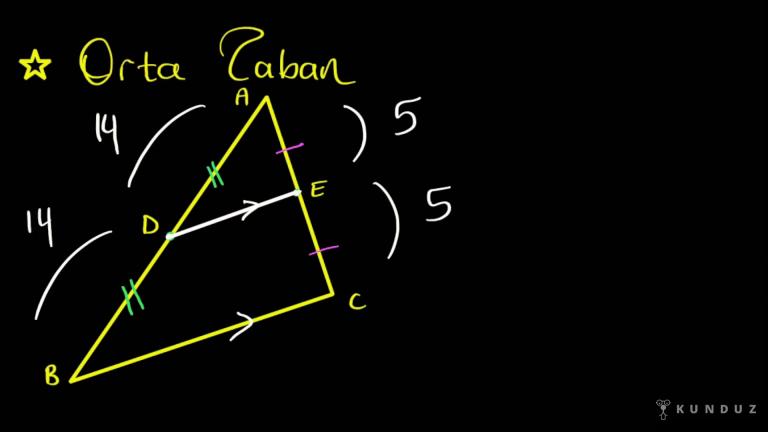
Bir üçgen de kenarları ın orta noktaları birleştirilir ise oluşan parça.
Diğer kenara parelel olur.
Ne demek istiyorum?
Ab aldım dedim ki bunun orta noktası dev ağacı aldım.
Dedim ki bunun orta noktası ee.
İşte burada ana meselem şudur ki deveyi iyi birleştiriyoruz ve diyorum ki de paraleldir BC olmalı arkadaşlar.
Çünkü sağ ve soldaki oran aynı olduğu için arkadaşlar kenarlar paraleldir.
Burada gördüğünüz oran bir bir, burada gördüğünüz oran bir bir uzunlukları farklı da olsa fark etmez.
Isterseniz buraya 5'e 5, buraya on, dörde 14 deyin 5 bölü beşte birdir.
14 veli 14 de birdir.
Buradaki oranın aynı olması önemli arkadaşlar.
Bu paralelliği işte açı taşımada kullana bildiğimiz için aktarmak isterim.
Dikkatli olmakta fayda var arkadaşlar.
İkizkenar üçgende açı özellikleri nelerdir?
En az iki kenar uzunluğu eşit olan üçgenlere ikizkenar üçgen denir.
İkizkenar üçgenlerin aynı zamanda en az iki açısı da birbirine eşittir. Yani iki açısı birbirine eşit bir üçgen için ikizkenar üçgendir diyebiliriz.
Verilen ikizkenar üçgende;
|AB| = |AC|
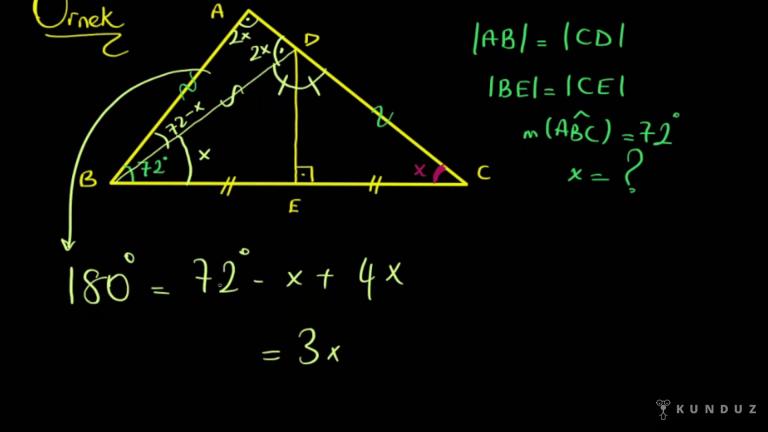
İkizkenar üçgenlerde tepe noktasından çizilen açıortay üçgenin yüksekliğini verir. Aynı zamanda tabanı da iki eşit parçaya ayırır. Bu yüzden ikizkenar üçgenlerde tepe noktasından çizilen açıortay, aynı zamanda kenarortay ve yüksekliktir diyebiliriz.
Eşkenar üçgende açı özellikleri nelerdir?
Tüm kenarları eşit üçgenlere eşkenar üçgen denir. Eşkenar üçgenlerin aynı zamanda tüm iç açı ölçüleri de eşittir ve dir.
|AB| = |AC| = |BC|
Eşkenar üçgenlerde tüm köşelerden çizilen açıortay aynı zamanda yükseklik ve kenarortaydır.
Muhteşem üçlü nedir?
Dik üçgende den hipotenüse inen kenarortayın uzunluğu hipotenüsün yarısına eşittir.