Merhaba dostlar Üçgende Açılar konusundayız şimdi birkaç örnek bakalım sizlerle beraber.
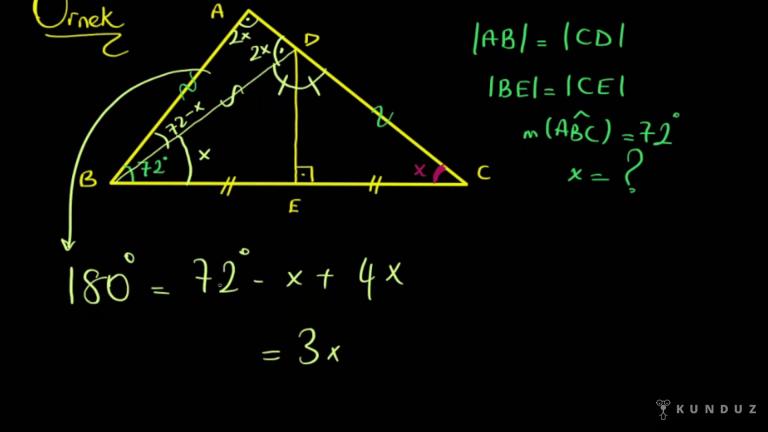
Gördüğünüz gibi çizgili açılar birbirine eşit, noktalı aşçılar birbirine eşit, şurası yani DEB aşçısı 30 derece, bizden EAC yani x açısının kaç derece olduğunu bulmamız isteniyor.
Şimdi böyle soru tarzları bellidir.
Bunlar denklem çözme sistemleridir.
Siz büyük üçgenine bakıp, küçük üçgenine bakıp denklemler oluşturup bu denklemleri çözebilmelisiniz.
Asıl mesele zaten bu büyük üçgeni ya da küçük üçgeni bakabilip oraların içerisinde yer alan denklemleri çözebilmek.
Madem denklem çözme sorulara diyoruz bunlara denklem haline getirebileceğine harfler vermeyeyim, yani nokta ve açıları böyle bırakmamalıyız.
Harf vermekten kaçınmayınız korkmayınız.
Buradaki noktalı aşılara a diyelim.
Çizgili açılara b diyelim.
Şimdi bakacağım belirli üçgenler olmalı ki belirli bir eşitlik elde edebileyim.
Birinci bakacağımız yer şurası olsun dostlar.
Şu üçüne bakarsanız iki tane iç açının toplamı yani b ve otuzdan bahsediyorum kendini komşu olmayan bir dış açı.
b ve 30'u toplarsam demek ki a açısını vermek zorunda.
O zaman burada bir eşitlik yakaladım.
a eşittir b+30 tamam.
Şimdi ikinci bakmamız gereken yer neresidir?
Şurada bir ilerleme yapabilirim, bir yer bulamıyorum ama şu açıyı a'lı cinsten tanımlayabilirim.
Hangi üçgen içerisinde konuşuyorum?
Şu gördüğünüz ADE.
Burada a var.
O zaman şuraya kalan 180-2a oluyor.
Tamam bu açıyı da tanımadım.
Şimdi bakmam gereken yerlerle bu işi halletmeyim.
Nereye bakayım dostlar?
Büyük üçgen içerisine bakmanızı istiyorum.
Büyük üçgen derken en büyük üçgenden bahsediyorum.
Şöyle şuraya da çizelim.
ABC üçgeni.
Şu açı nedir?
a açısı 180-2a+x tamam bu aşağısı b bu aşağısı b.
Ben burada iç açılar toplamı yazabilirim.
İç açılar toplamı dediğim şöyle.
2 bu tarafa biraz da yaklaştıralım 180 derece.
Bunun iç açıları toplamı kesinlikle 180 olmalı.
Topluyorum b var b var 2b artı üstteki gördüğün.
180- 2a+x.
Şu 180'leri bir gönderelim eşitliğin farklı tarafındalar.
2a ve 2b'yi bu tarafa atalım ki x burada yalnız kalsın.
Tamam 2a buraya artı 2a diye geldi.
Bu 2b de eksi 2b diye geldi.
Şurayı 2 parantezine alalım mı?
a-b=x oldu.
Şuraya bakar mısınız dostlar?
Şurada da 30'u yalnız bırakıyorum.
30 derece eşittir b buraya eksi diye gitti eksi b.
Şimdi bunu getirin buraya yazın dostlar şöyle.
İki çarpı 30 derece eşittir x eşittir 60 derece bulunur.
Evet, ikinci sorumuzdayız.
Burada yine ABC büyük üçgenini vermiş, B köşesinden açıortay, C köşesinden açıortayı çizmiş.
Bu açıortayların kesişim açısına 4x-10 üst tarafta A açısına da 3x+20 derece yazdık.
Şimdi dedik ki x derecesini hesaplayınız.
Şimdi burada konu anlatımında da söylediğim gibi iki tane bir üçgen içerisinde iki tane iç açıortayın kesişim açısı şurada harf vermeden rahatlıkla bulunabiliyordu.
Normalde büyük üçgende şuralarda harfler vererek a veya b olarak ilerleyerek bulabilirsiniz.
Ama kısa yolumuz var.
Neydi arkadaşlar, iki tane iç açıortayın kesişim açısı eşittir, şuraya da yazalım konuşurken 4x-10 derece eşittir 90 derece artı açı ortay çizgi dediğimiz bu A açısının yarısı.
Yani şöyle yazalım (3x+20)/2.
Ben buradan x'i bulabilir miyim?
Bulurum.
Bir eşitlik sistemim var ve sadece x var.
O zaman bulabilirim.
Şöyle 4x+10 derece eşittir 90.
Şuraya her tarafı ikiyle çarpıyoruz ki rahatlıkla işleminiz yapalım.
8x-20=180 + 3x+ 20 dostlar.
Burada ilerlersem 3x'i bu tarafa attım.
5x oldu bu 20 buraya artı 20 olarak geçti, 40 oldu, 220 etti.
x dediğim şey 44 derece bulunur.
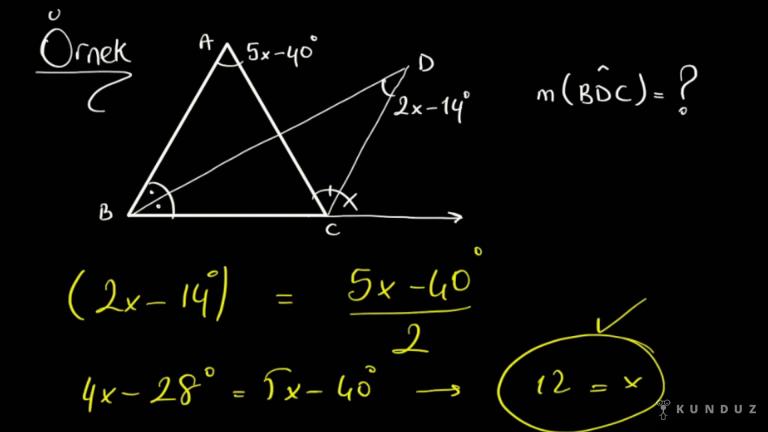
Şimdiki sorumuzda dostlar bir ABC üçgeni verilmiş, B köşesinden bir iç açıortay, C köşesinden de bir dış açıortay çizilmiş.
Bunların kesişim açısı 2x-14 derece olarak verilmiş.
Burada A köşesini de 5x-40 derece olarak verdik.
Bizden istenen BDC yani şurada gördüğünüz bu kesişim açısını hesaplamamız isteniyor.
Şimdi bunu konular konusunda da üçgende açılar konusunda da göstermiştim.
Bir açı iç açıortay ve bir dış açıortayın kesişim açısı yani 2x-14 eşittir bu hiç açıortay çizmediğimiz yerin yarısıdır.
5x- 40 bu a ölçüsünün yarısı olmalıdır.
Burada gördüğünüz kesişim açısı bu gördüğünüz a açısının yani hiç iç açıortay dış açıortay çizmediğim bu açının yarısı olmalı ve burada hemen içler dışlar yapalım.
4x-28 derece eşittir 5x-40 derece.
x bu tarafa gelsin.
Sağ tarafta x kaldı.
40'ı buraya atarsam artı diye gider.
O zaman -12 derece olarak buluyorum dostlar ama sadece x'i istemiyor bizden BDC açısı yani buradaki 2x-14 deniyor.
2 çarpı 12 eksi 14 eşittir 10 derece bulunur.
Gördüğünüz gibi çizgili açılar birbirine eşit, noktalı aşçılar birbirine eşit, şurası yani DEB aşçısı 30 derece, bizden EAC yani x açısının kaç derece olduğunu bulmamız isteniyor.
Şimdi böyle soru tarzları bellidir.
Bunlar denklem çözme sistemleridir.
Siz büyük üçgenine bakıp, küçük üçgenine bakıp denklemler oluşturup bu denklemleri çözebilmelisiniz.
Asıl mesele zaten bu büyük üçgeni ya da küçük üçgeni bakabilip oraların içerisinde yer alan denklemleri çözebilmek.
Madem denklem çözme sorulara diyoruz bunlara denklem haline getirebileceğine harfler vermeyeyim, yani nokta ve açıları böyle bırakmamalıyız.
Harf vermekten kaçınmayınız korkmayınız.
Buradaki noktalı aşılara a diyelim.
Çizgili açılara b diyelim.
Şimdi bakacağım belirli üçgenler olmalı ki belirli bir eşitlik elde edebileyim.
Birinci bakacağımız yer şurası olsun dostlar.
Şu üçüne bakarsanız iki tane iç açının toplamı yani b ve otuzdan bahsediyorum kendini komşu olmayan bir dış açı.
b ve 30'u toplarsam demek ki a açısını vermek zorunda.
O zaman burada bir eşitlik yakaladım.
a eşittir b+30 tamam.
Şimdi ikinci bakmamız gereken yer neresidir?
Şurada bir ilerleme yapabilirim, bir yer bulamıyorum ama şu açıyı a'lı cinsten tanımlayabilirim.
Hangi üçgen içerisinde konuşuyorum?
Şu gördüğünüz ADE.
Burada a var.
O zaman şuraya kalan 180-2a oluyor.
Tamam bu açıyı da tanımadım.
Şimdi bakmam gereken yerlerle bu işi halletmeyim.
Nereye bakayım dostlar?
Büyük üçgen içerisine bakmanızı istiyorum.
Büyük üçgen derken en büyük üçgenden bahsediyorum.
Şöyle şuraya da çizelim.
ABC üçgeni.
Şu açı nedir?
a açısı 180-2a+x tamam bu aşağısı b bu aşağısı b.
Ben burada iç açılar toplamı yazabilirim.
İç açılar toplamı dediğim şöyle.
2 bu tarafa biraz da yaklaştıralım 180 derece.
Bunun iç açıları toplamı kesinlikle 180 olmalı.
Topluyorum b var b var 2b artı üstteki gördüğün.
180- 2a+x.
Şu 180'leri bir gönderelim eşitliğin farklı tarafındalar.
2a ve 2b'yi bu tarafa atalım ki x burada yalnız kalsın.
Tamam 2a buraya artı 2a diye geldi.
Bu 2b de eksi 2b diye geldi.
Şurayı 2 parantezine alalım mı?
a-b=x oldu.
Şuraya bakar mısınız dostlar?
Şurada da 30'u yalnız bırakıyorum.
30 derece eşittir b buraya eksi diye gitti eksi b.
Şimdi bunu getirin buraya yazın dostlar şöyle.
İki çarpı 30 derece eşittir x eşittir 60 derece bulunur.
Evet, ikinci sorumuzdayız.
Burada yine ABC büyük üçgenini vermiş, B köşesinden açıortay, C köşesinden açıortayı çizmiş.
Bu açıortayların kesişim açısına 4x-10 üst tarafta A açısına da 3x+20 derece yazdık.
Şimdi dedik ki x derecesini hesaplayınız.
Şimdi burada konu anlatımında da söylediğim gibi iki tane bir üçgen içerisinde iki tane iç açıortayın kesişim açısı şurada harf vermeden rahatlıkla bulunabiliyordu.
Normalde büyük üçgende şuralarda harfler vererek a veya b olarak ilerleyerek bulabilirsiniz.
Ama kısa yolumuz var.
Neydi arkadaşlar, iki tane iç açıortayın kesişim açısı eşittir, şuraya da yazalım konuşurken 4x-10 derece eşittir 90 derece artı açı ortay çizgi dediğimiz bu A açısının yarısı.
Yani şöyle yazalım (3x+20)/2.
Ben buradan x'i bulabilir miyim?
Bulurum.
Bir eşitlik sistemim var ve sadece x var.
O zaman bulabilirim.
Şöyle 4x+10 derece eşittir 90.
Şuraya her tarafı ikiyle çarpıyoruz ki rahatlıkla işleminiz yapalım.
8x-20=180 + 3x+ 20 dostlar.
Burada ilerlersem 3x'i bu tarafa attım.
5x oldu bu 20 buraya artı 20 olarak geçti, 40 oldu, 220 etti.
x dediğim şey 44 derece bulunur.
Şimdiki sorumuzda dostlar bir ABC üçgeni verilmiş, B köşesinden bir iç açıortay, C köşesinden de bir dış açıortay çizilmiş.
Bunların kesişim açısı 2x-14 derece olarak verilmiş.
Burada A köşesini de 5x-40 derece olarak verdik.
Bizden istenen BDC yani şurada gördüğünüz bu kesişim açısını hesaplamamız isteniyor.
Şimdi bunu konular konusunda da üçgende açılar konusunda da göstermiştim.
Bir açı iç açıortay ve bir dış açıortayın kesişim açısı yani 2x-14 eşittir bu hiç açıortay çizmediğimiz yerin yarısıdır.
5x- 40 bu a ölçüsünün yarısı olmalıdır.
Burada gördüğünüz kesişim açısı bu gördüğünüz a açısının yani hiç iç açıortay dış açıortay çizmediğim bu açının yarısı olmalı ve burada hemen içler dışlar yapalım.
4x-28 derece eşittir 5x-40 derece.
x bu tarafa gelsin.
Sağ tarafta x kaldı.
40'ı buraya atarsam artı diye gider.
O zaman -12 derece olarak buluyorum dostlar ama sadece x'i istemiyor bizden BDC açısı yani buradaki 2x-14 deniyor.
2 çarpı 12 eksi 14 eşittir 10 derece bulunur.