Merhaba dostlar üçgende açılar devam.
ABC üçgeni verdik.
AH diktir BC verdik.
BH eşittir DH.
Tamam şu gördüğünüz çizgili açılar birbirine eşit.
ABC açısına x dedik DAC açısı da 24 derece olarak verildi.
x açısını bulalım şimdi.
Şimdi burada size bu uzunlukları neden verdim?
Bu eşitliği neden verdim?
Bu dikliği neden verdim?
Bunun bir sebebi var.
Gördüğünüz gibi ABD üçgenine bakarsanız bu üçgen içerisinde A'dan indim.
Bir dik aynı zamanda kenarortay olmuş.
Bu bir ikizkenar özelliği idi.
Dostlar bir köşeden indiğiniz dik aynı zamanda kenarortay ise bu bir ikizkenar üçgendir ve bu kenarortay bu yükseklik aynı zamanda açıortay idi.
Şimdi ikiz kenarlık dedik de ikizkenarlık nasıl ikizkenarlık?
Bu üçgen için konuştum.
Unutmayın bu kenar bu kenara eşit bölünmüş o zaman A'dan A dediğim yer tepe olmuş.
Demek ki burası taban olmuş o zaman AB eşittir AC'dır.
Bu eşitliği görelim tamam.
Buradaki yükseklik aynı zamanda kenarortay ve açı ortaydır.
Yani BAH açısı DAH açısına eşittir.
Yani buralara harfler verirsem burası A idi ikiz kenarlıkla burayı da A derece bulduk.
Bundan bahsetmeye çalışıyorum.
İkizkenarlık varsa taban açıları da eşittir.
Sol tarafta x varsa sağ tarafa da ben x yazabilirim.
O zaman şurada biraz daha küçük diyelim.
Çok büyük oldu.
Tamam şimdi burada bir bişeyler yazmam lazım.
Ne yazmam lazım?
Şu üçgene bakarsanız artı 24 yani iki tane iç açının toplamı kendilerine komşu olmayan bir dış açıya eşit.
A artı 24 derece eşittir x.
Bunu yazabiliriz.
Tamam, ikinci yazmam gereken ne?
Şu üçgene bakabilirsiniz mesela bu üçgene baktığınız zaman da A artı x eşittir kesinlikle 90 derece.
Ben buraya bakarak sistemi çözebilirim.
Üst tarafa bakarsan şu üst tarafta 24 derece yalnız bırakıyorum.
Karşı tarafa attım.
Yani 24 derece eşittir x eksi a.
Alt tarafa baktığım zaman artı X var.
Yani x artı a'yı da aşağı yazarsam şöyle 90 derece olduğunu biliyorum.
Şunları bir taraf tarafa toplayalım bakalım a'lar gitti bu tarafta 2x kaldı.
Bu tarafta 24 ve 90'nın toplamı 114 etti.
x dediğim değer 57 derece olarak bulunur.
Şimdi ikinci sorumuzdayız.
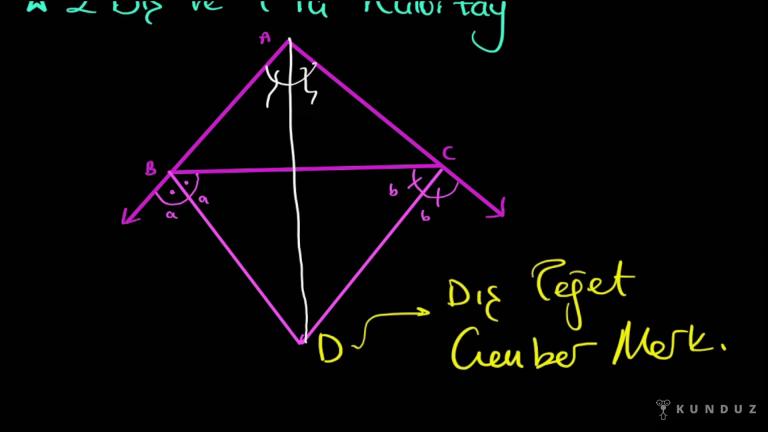
Büyük bir ABC üçgeni verdik.
AD eşittir AB aynı zamanda DE eşittir CE eşitliğini görüyoruz.
Bu aradaki ADE açısını 40 derece verdik.
BAC açısı ne kadardır diye soruyorum.
Şimdi buradaki büyük açıyı bulmamız isteniyor.
Şimdi ben bu açıyı geçmem için şimdi soruya bakıyorum.
Hiçbir şey verilmemiş.
İki tane kenar eşitliği var ortada.
Bir tane 40 derece var burada.
Lütfen rica ediyorum harf vermekten çekinmeyin.
İkizlik verdim.
Bu ikizliği açılara yansıttım.
Kenar eşitliği verdim de bunu siz de açı eşitliğini yazdım.
Bu kenar bu kenara eşitse demek ki ABD üçgeninde şu açı, şu açı eşittir.
DEC üçgeninde de bu kenar, bu kenar eşitse burada gördüğüm açı, burada gördüğüm taban açısına eşittir.
Harf verin dedik.
O zaman A'ya A, B'ye B yazabilirim.
Şimdi buraya baktığım zaman şurada bir eşitlik anlayabiliyorum.
Burada 180 derece.
Burası bir doğrusal olduğu için BDC doğrusal olduğu için burasının 180 derece olduğunu biliyorum.
Doğrusal açı 180.
O zaman bu 3 açının toplamı A artı B artı 40 180 olmalı.
Buradan A artı B çekebiliyorum 140 derece çok güzel.
A artı b'yi buldum da a artı b istenmiyor ki bende büyük üçgende şuradaki değer isteniyor.
Şimdi ben bir büyük üçgen çizersem eğer böyle bir üçgenden söz ediyorum.
Burası A kadardı, burası B kadar.
ABC üçgenini çiziyorum dostlar.
Tamam nereyi isteniyor?
Şuradaki tepe açısını bul dendi bana.
Şimdi bu üçgen içerisinde iç açılar toplamını yazsaydım 180 derece eşittir A artı B artı X yazacaktım.
Şurasını alfa dedik de X diyelim.
Tamam ben A artı B'yi biliyorum buraya kopyala yapıştır 180 derece 140 artı x ise X dediğim şey 40 derece bulunur.
Evet, bu sorumuzda yine bir ABC üçgeni verdik.
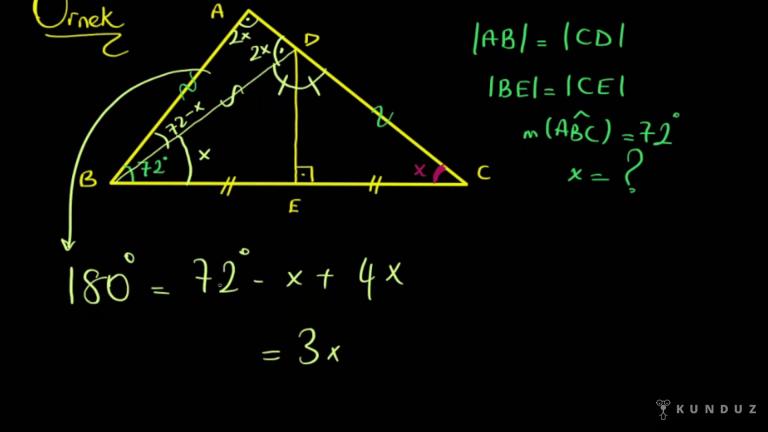
Gördüğünüz gibi AB eşittir CD, BE eşittir CE.
Buradaki açıyı 72 olarak verdim.
x derecesinin kaç olduğunu bulalım şimdi.
Şimdi bu soruya baktığımız zaman yine bir dik inmişim ve indiği tabana eşit bölmüş.
Şimdi bunu biliyorum ki bir üçgen içerisinde inen köşeden inen bir dik aynı zamanda kenarortaysa bu uzunluk diye dediğim şey DE dediğim parça aynı zamanda açıortaydır ve o üçgen bir ikizkenar üçgendir.
Şimdi buraya bakıyorum da D'nin olduğu köşe bir üçgene dahil değil.
Demek ki onu bir köşe ile birleştirip üçgen haline getirmeliyiz.
Taban burasıysa demek ki B ve D'yi birleştirmeliyiz.
Şuradaki işlemim ilk olarak bu.
Şimdi BDC üçgenine baktığınız zaman şu üçgene baktığınız zaman D'den inen dik aynı zamanda kenarortay.
O zaman burası kesinlikle bir ikizkenar üçgendir ve bu DE aynı zamanda açıortaydır.
Şurada şu eşitliği ben yazabilirim.
Şu eşitlik de ikiz kenarlıktan gelmekte.
Yani DC eşittir DB olmalı.
Şuraya da bu işareti koyabilirim.
İkizkenarlıktan geldi burası.
Buna dik ise ve inen dik eşit böldüyse ikizkenardır, açıortaydır.
Sadece bunları yazdık dostlar.
Şimdi burada yazmanız gereken şey bu taban açısı x ise burada gördüğünüz taban açısı da x'dir.
Yani şurası eşittir şurası ise bu açı eşittir burada gördüğünüz x açısı.
x'i buraya taşımış olduk.
Burası komple 72 idi.
Şuraya kalan yetmiş iki eksi x oldu.
Çok güzel.
Şimdi büyük üçgene bakarsanız hangi üçgenden bahsediyorum?
Büyük üçgen derken şu DBC üçgene bakarsanız iki tane iç açının toplamı yani x ve x'in toplamı kendilerine komşu olmayan bir dış açıya eşittir.
Yani ADB açısı.
x artı x'ten 2 x gelmekte dostlar.
Sadece buraya yazıyorum.
Şurası da 2 x etti.
Şimdi ben şu üçgene bakarsam, ABD üçgeninde bakarsam bu kenar eşittir bu kenar.
O zaman A açısı eşittir, D açısı yazabilmeliyiz.
Yani burası 2x ise şurası da 2x'dir.
Şimdi şu üçgene bakıp, şurada gördüğünüz üçgene bakıp iç açılar toplamı yazıyorum.
Bu ABD üçgeninde iç açılar toplamı 180 olacak.
72 eksi x artı, 2x artı 2x daha 4 tane x etti ve burası 3 x etti.
180 72'yi de diğer tarafa attım.
72 çıkarırsan 108 derece kalır.
Buradan x'e ulaşabilirim.
108 bölü 3'ten 36 derece buluruz.
ABC üçgeni verdik.
AH diktir BC verdik.
BH eşittir DH.
Tamam şu gördüğünüz çizgili açılar birbirine eşit.
ABC açısına x dedik DAC açısı da 24 derece olarak verildi.
x açısını bulalım şimdi.
Şimdi burada size bu uzunlukları neden verdim?
Bu eşitliği neden verdim?
Bu dikliği neden verdim?
Bunun bir sebebi var.
Gördüğünüz gibi ABD üçgenine bakarsanız bu üçgen içerisinde A'dan indim.
Bir dik aynı zamanda kenarortay olmuş.
Bu bir ikizkenar özelliği idi.
Dostlar bir köşeden indiğiniz dik aynı zamanda kenarortay ise bu bir ikizkenar üçgendir ve bu kenarortay bu yükseklik aynı zamanda açıortay idi.
Şimdi ikiz kenarlık dedik de ikizkenarlık nasıl ikizkenarlık?
Bu üçgen için konuştum.
Unutmayın bu kenar bu kenara eşit bölünmüş o zaman A'dan A dediğim yer tepe olmuş.
Demek ki burası taban olmuş o zaman AB eşittir AC'dır.
Bu eşitliği görelim tamam.
Buradaki yükseklik aynı zamanda kenarortay ve açı ortaydır.
Yani BAH açısı DAH açısına eşittir.
Yani buralara harfler verirsem burası A idi ikiz kenarlıkla burayı da A derece bulduk.
Bundan bahsetmeye çalışıyorum.
İkizkenarlık varsa taban açıları da eşittir.
Sol tarafta x varsa sağ tarafa da ben x yazabilirim.
O zaman şurada biraz daha küçük diyelim.
Çok büyük oldu.
Tamam şimdi burada bir bişeyler yazmam lazım.
Ne yazmam lazım?
Şu üçgene bakarsanız artı 24 yani iki tane iç açının toplamı kendilerine komşu olmayan bir dış açıya eşit.
A artı 24 derece eşittir x.
Bunu yazabiliriz.
Tamam, ikinci yazmam gereken ne?
Şu üçgene bakabilirsiniz mesela bu üçgene baktığınız zaman da A artı x eşittir kesinlikle 90 derece.
Ben buraya bakarak sistemi çözebilirim.
Üst tarafa bakarsan şu üst tarafta 24 derece yalnız bırakıyorum.
Karşı tarafa attım.
Yani 24 derece eşittir x eksi a.
Alt tarafa baktığım zaman artı X var.
Yani x artı a'yı da aşağı yazarsam şöyle 90 derece olduğunu biliyorum.
Şunları bir taraf tarafa toplayalım bakalım a'lar gitti bu tarafta 2x kaldı.
Bu tarafta 24 ve 90'nın toplamı 114 etti.
x dediğim değer 57 derece olarak bulunur.
Şimdi ikinci sorumuzdayız.
Büyük bir ABC üçgeni verdik.
AD eşittir AB aynı zamanda DE eşittir CE eşitliğini görüyoruz.
Bu aradaki ADE açısını 40 derece verdik.
BAC açısı ne kadardır diye soruyorum.
Şimdi buradaki büyük açıyı bulmamız isteniyor.
Şimdi ben bu açıyı geçmem için şimdi soruya bakıyorum.
Hiçbir şey verilmemiş.
İki tane kenar eşitliği var ortada.
Bir tane 40 derece var burada.
Lütfen rica ediyorum harf vermekten çekinmeyin.
İkizlik verdim.
Bu ikizliği açılara yansıttım.
Kenar eşitliği verdim de bunu siz de açı eşitliğini yazdım.
Bu kenar bu kenara eşitse demek ki ABD üçgeninde şu açı, şu açı eşittir.
DEC üçgeninde de bu kenar, bu kenar eşitse burada gördüğüm açı, burada gördüğüm taban açısına eşittir.
Harf verin dedik.
O zaman A'ya A, B'ye B yazabilirim.
Şimdi buraya baktığım zaman şurada bir eşitlik anlayabiliyorum.
Burada 180 derece.
Burası bir doğrusal olduğu için BDC doğrusal olduğu için burasının 180 derece olduğunu biliyorum.
Doğrusal açı 180.
O zaman bu 3 açının toplamı A artı B artı 40 180 olmalı.
Buradan A artı B çekebiliyorum 140 derece çok güzel.
A artı b'yi buldum da a artı b istenmiyor ki bende büyük üçgende şuradaki değer isteniyor.
Şimdi ben bir büyük üçgen çizersem eğer böyle bir üçgenden söz ediyorum.
Burası A kadardı, burası B kadar.
ABC üçgenini çiziyorum dostlar.
Tamam nereyi isteniyor?
Şuradaki tepe açısını bul dendi bana.
Şimdi bu üçgen içerisinde iç açılar toplamını yazsaydım 180 derece eşittir A artı B artı X yazacaktım.
Şurasını alfa dedik de X diyelim.
Tamam ben A artı B'yi biliyorum buraya kopyala yapıştır 180 derece 140 artı x ise X dediğim şey 40 derece bulunur.
Evet, bu sorumuzda yine bir ABC üçgeni verdik.
Gördüğünüz gibi AB eşittir CD, BE eşittir CE.
Buradaki açıyı 72 olarak verdim.
x derecesinin kaç olduğunu bulalım şimdi.
Şimdi bu soruya baktığımız zaman yine bir dik inmişim ve indiği tabana eşit bölmüş.
Şimdi bunu biliyorum ki bir üçgen içerisinde inen köşeden inen bir dik aynı zamanda kenarortaysa bu uzunluk diye dediğim şey DE dediğim parça aynı zamanda açıortaydır ve o üçgen bir ikizkenar üçgendir.
Şimdi buraya bakıyorum da D'nin olduğu köşe bir üçgene dahil değil.
Demek ki onu bir köşe ile birleştirip üçgen haline getirmeliyiz.
Taban burasıysa demek ki B ve D'yi birleştirmeliyiz.
Şuradaki işlemim ilk olarak bu.
Şimdi BDC üçgenine baktığınız zaman şu üçgene baktığınız zaman D'den inen dik aynı zamanda kenarortay.
O zaman burası kesinlikle bir ikizkenar üçgendir ve bu DE aynı zamanda açıortaydır.
Şurada şu eşitliği ben yazabilirim.
Şu eşitlik de ikiz kenarlıktan gelmekte.
Yani DC eşittir DB olmalı.
Şuraya da bu işareti koyabilirim.
İkizkenarlıktan geldi burası.
Buna dik ise ve inen dik eşit böldüyse ikizkenardır, açıortaydır.
Sadece bunları yazdık dostlar.
Şimdi burada yazmanız gereken şey bu taban açısı x ise burada gördüğünüz taban açısı da x'dir.
Yani şurası eşittir şurası ise bu açı eşittir burada gördüğünüz x açısı.
x'i buraya taşımış olduk.
Burası komple 72 idi.
Şuraya kalan yetmiş iki eksi x oldu.
Çok güzel.
Şimdi büyük üçgene bakarsanız hangi üçgenden bahsediyorum?
Büyük üçgen derken şu DBC üçgene bakarsanız iki tane iç açının toplamı yani x ve x'in toplamı kendilerine komşu olmayan bir dış açıya eşittir.
Yani ADB açısı.
x artı x'ten 2 x gelmekte dostlar.
Sadece buraya yazıyorum.
Şurası da 2 x etti.
Şimdi ben şu üçgene bakarsam, ABD üçgeninde bakarsam bu kenar eşittir bu kenar.
O zaman A açısı eşittir, D açısı yazabilmeliyiz.
Yani burası 2x ise şurası da 2x'dir.
Şimdi şu üçgene bakıp, şurada gördüğünüz üçgene bakıp iç açılar toplamı yazıyorum.
Bu ABD üçgeninde iç açılar toplamı 180 olacak.
72 eksi x artı, 2x artı 2x daha 4 tane x etti ve burası 3 x etti.
180 72'yi de diğer tarafa attım.
72 çıkarırsan 108 derece kalır.
Buradan x'e ulaşabilirim.
108 bölü 3'ten 36 derece buluruz.