Üçgende Açılar Yeni Nesil Sorular

Sevgili Kunduz, izleyenleri herkese merhabalar.
Bu dersimiz de üçgende açılar konusuyla ilgili örnek sorular çözeceğiz.
Hazırsanız ilk sorumuz da başlayalım.
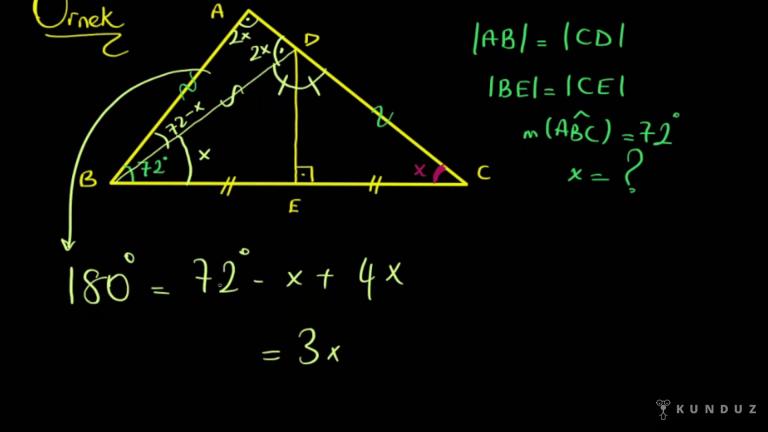
A BC üçgenin iç açıları arasında yedi çarpı a x iki çarpı b küçüktür, iki çarpı C bağıntısı olduğuna göre ağasının alabileceği en büyük tam sayı değeri kaçtır diye sorulmuş.
Şimdi hemen şuradaki x 2-B ifadesini karşıya atalım.
Hatta onu da şöyle yazayım artık 7 tane açısı bakın kimden küçük oluyor.
Iki parantezinde b açısı artı c açısından daha küçükmüş.
Şimdi biliyorsunuz.
A BC eğer bir üçgen ise iç açılarının toplamı yani a artı B artı C toplamı 180 derece olmalıdır.
Burada B artacağı yalnız başına bırakırsak eğer.
Eee ne olur?
B artı C toplamı.
180 eksi a.
Olarak yazılabilir.
Hemen gidelim bunu yerine yazalım.
Bakın şuradaki b artacağı yerine yani 7 tane a küçükmüş iki çarpımı da 180 eksi ağdan net.
Bunu da atıyorum içeri ya da küçüktür.
360 derece yine 360 derece ile çarptım.
Yine eksi iki AAA oldu orası da.
Eksi iki ay, öbür tarafı artı iki adliye attım.
Yedi ayla topladım arkadaşlar.
Dokuz tane ağaç.
Kimden küçükmüş?
360 dereceden küçükmüş.
9'la her tarafı sade eleştirirsiniz.
Her açısı 360 bölü 9, yani 40'tan daha küçük bir değer alabileceği en büyük tam sayı değerini sormuş.
Em a yazalım artık onun yerine 40 dereceden küçük verebileceğimiz en büyük tam sayı değeri 30 9'dur.
Sevgili gençler diyelim, bir sonraki sorumuza geçelim.
Diyor ki kaleme bir üçgen miş.
Kale, ln, nt, ts ve sevmem.
Hepsi birbirine eşit.
Kale me açısı 130 derece imiş.
Hemen bakın suçu öylece.
130 derece olduğuna göre ln t açısı bize sorulmuş.
Tamam.
Hemen şuradaki en küçük ikiz kenar üçgen den x ix diye açıları isim vermeye başlayalım.
Biliyorsunuz iki çatının toplamı bunlara komşu olmayan bir dış açı eder.
Dolayısıyla buralar iki ikisidir.
Yine ikiz kenardan şimdi n tl ye bakınız bu sefer iç maçlarımız 2 ix ve x topladım 3 x oldu ikisi kenardan.
Bakın burası da 3 ikiz.
Şimdi şu dış açıya bakalım bu da l m n üçgenin de iç açımız 3 x diğer iç açımız.
X topladım bunları 4 x yaptı.
Dolayısıyla x kenardan şurası da nedir arkadaşlar?
Eee 4 fikstür tamam.
Şimdi kale mi?
En büyük 3 gene bakacak olursanız eğer 4 IX var, bir IX var, bir de 130 derece var.
Bunların toplamı 180 derece olacak.
Hemen karşıya attım, 5 x eşittir 50 derece, dolayısıyla x eşittir 10 derece olarak bulundu.
Şimdi bana sorulan Açı le ne teydi yani şurası soruluyor aslında.
Şimdi iki senenin 10 yazarsak bakın burası üç eksen 30 30 oldu.
Bana sorulan açı yı bulabilmek için soru işareti dedim.
Bunu artı 30 artı 30 yani 60 derece bu toplamında 180 derece olması gerekir.
Sorulan ln tersi 180 x 60'tan 120 derece olarak hesaplanmış olur.
Sevgili arkadaşlar diyelim vakit kaybetmeden sıradaki sorumuza geçelim şekilde kabaca üçgenin de adeta açısı 90 derece imiş.
Ace de B, C, D ve B ede.
Üçü birbirine eşit olduğuna göre bir, iki, üç, dört, beş ifadelerinden hangileri kesinlikle doğrudur diye sorulmuş.
Evet.
Şimdi arkadaşlar şöyle bir durum var bunlara isimler verelim.
Alfa alfa.
Yani acısı 2 arif olmuş oldu.
Şimdi şu kısımda nedir?
90 artı alfa olmuş oldu.
Şimdi çizgiyi arif demiştik ya, şurası sayfaydı.
90 artı arif olmuş oldu.
Şimdi bakın bu ne zaman geçerliydi?
Hatırlayın lütfen.
Eğer şu kadar aç orta aysa değil mi buralara?
Çoğu orta aysa tepedeki açı.
Eee neyse.
Bu iki açı orta arasında oluşan açı doksan artı onun yarısıydı.
Dolayısıyla gerçekten 90 artı 2 arif, iki yani 90 artı Alf olarak buradaki açı bulundu.
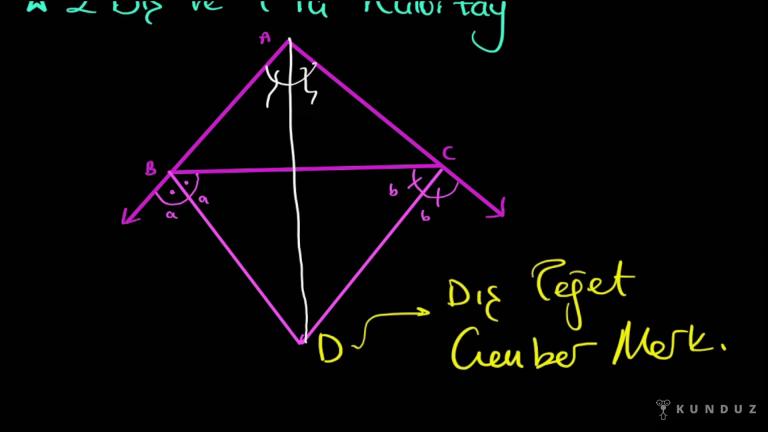
O halde yaşadıkları kesinlikle açı orta aydır.
Yani aslında noktası üçgenin iç içe, orta aylarının kesim noktasıdır.
Buna içte çemberinin merkez de denir.
Şimdi bir bakalım ifadeleri yorumlamaya çalışalım.
Bunlar ışığında bize ne yaptırıyor?
Diyor ki b, a.d açısı ve a, c, d açısı birbirine eşit.
Bakıyorum b.
Ağ da dediğimiz yere biz nokta demişiz değil mi?
Diğer taraftan arcade dediğimiz her çizgi farklı bir açı.
Bunlar birbirlerine eşit değil.
Devam ediyorum ABD açısıyla.
Cb açısı her iki çizgiyle gösterilmiş.
Gerçekten koçlar birbirine eşittir.
A bc açısıyla b açı açısı.
Evet bunların eşit olacak ııı durumları.
Iıı şu anda ııı kesin değildir değil mi yani?
Hani elimizde böyle bir bir yok olabilir ama kesinlikle sol için bu ifadeye doğru diyemeyiz.
Diyor ki diyalogda sağ BC 3'ün.
İşte çemberin merkezde kesinlikle bu ifade doğrudur.
İç açı orta ayların kesim noktası olduğu için iç de çemberin merkezidir.
Gelelim beşinci ifademizi.
Diyor ki.
A derece açısı.
Yani bakın şu aç diyor ki doksan artı a bc yani şu tepedeki b açısının yarısıdır.
Evet kesinlikle öyledir arkadaşlar.
Eee ağdan vc eden aç ortayla bir çeşit orta gelip kesişir.
Dilerse.
Arada aç ortada arasında oluşan bu açığı nasıl buluyorduk?
90 artı tepedeki açının yarısı diyorduk.
Dolayısıyla bu ifadede doğrudur.
O halde hangileri?
Kesinlikle doğruymuş.
İki, dört ve beş kesinlikle doğrudur.
Diğerleri kesindir diyemeyiz.
Sevgili gençler diyelim, sıradaki sorumuza geçelim.
Diyor ki, iç açıları sırasıyla 2, 3 ve 6 sayıları ile orantılı olan bir AB hece üçgenin dış açıları hangi sayılarla sırasıyla orantılıdır?
Peki şimdi küçük bir üçgen hemen çizmeye çalışalım.
Bunun iç ve dış açılarını da şöyle gösterelim bakın kenarlarını uzatıyorum.
Diyor ki A, B, C üçgen olsun bu.
Neymiş?
Sırasıyla Adam başlıyorum.
İşte iki alfa.
Sonrasında üç alfa ve altı alfa.
Şimdi burada şunu yaparsanız doğru sonuca ulaşma ihtimaliniz biraz düşük olur.
Şimdi iç açı ortayla iç şartların toplamı 180 olacak.
İşte İki üç, beş topladım altı daha.
Yani iki alfa, artı üç alfa, artı altı.
Alfa ne yaptı burası on bir alfa eşittir 180 derece desek hocam buradan alfa tam gelmiyor.
Evet doğru.
Zaten sizden alfa idi isteyen yok.
Sevgili arkadaşlar burada alfa bulmanıza gerek de yok.
Eee dış açıları bulacağız.
Mesela A köşesinde oluşan şu dış açı nasıl bulunur?
Buna komşu olmayan iki tane iç açıyı toplarsanız, üç alfa ve altı halifeyi toplarsanız buna 9 alfa olur.
Bakın aynı şeyi yapalım.
B doluşan nasıl bulacağız iki iç bunlara.
Komşu olmayan dışa eşittir.
Yani iki halife ile Alt Alfa'nın toplamı.
Bu sefer burası nedir?
Sekiz sayfadır.
Son olarak C7 oluşan dış açı iki alfa ile üç alfa.
Bunlara komşu olmayan iki tane iç açılır.
Dolayısıyla beş alfa dır.
O halde sırasıyla hemen yazalım.
Ağdaki dokuz, B deki sekiz de beş.
Bu sayılarla dış ağaçlarımız da orantılıdır.
Sevgili gençler, dediğim gibi yukarıdaki yönteme başvurmanız da hiç ama hiç gerek yok diyelim.
Bu soruyla birlikte de dersimizi bitirelim.
Umarım faydalı bir soru çözüm videosu olmuştur.
Bir sonraki dersimizi de görüşmek üzere kendinize çok iyi bakın.