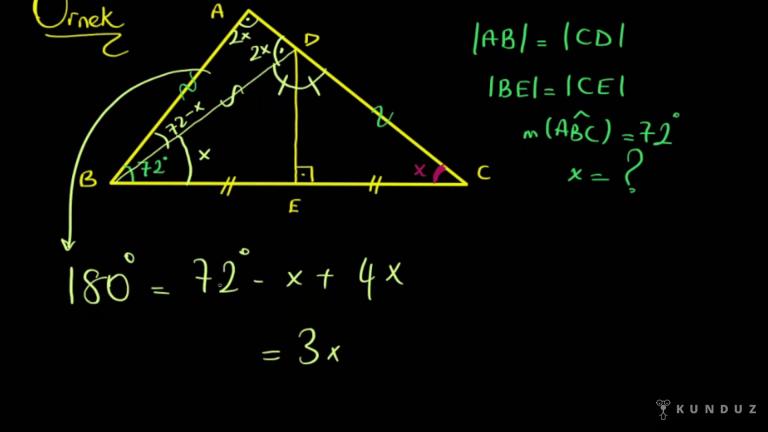
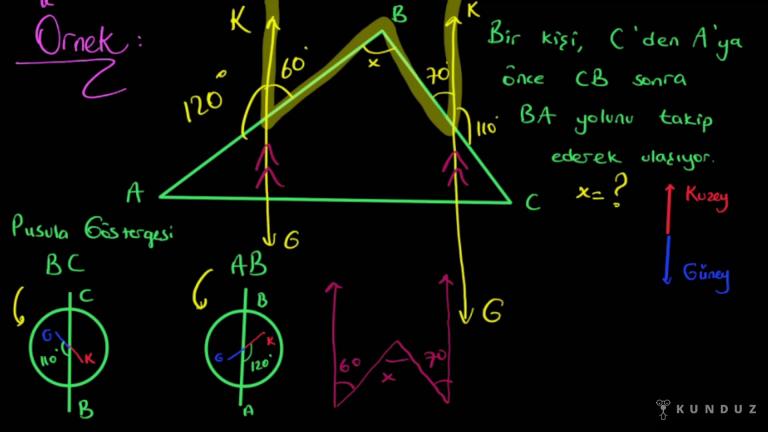
Merhabalar, hepinize şimdi üçgende aşçılar konusunda Aç Orta Ay'dan kaynaklı bazı özel durumları aktarmak istiyorum.
Başlayalım.
Önce bir bakalım bir üçgen daha ortay nedir?
Beraber ne yaparlar?
Açı ortay dediğimiz belli bir açıyı ortadan ikiye yaran yani tam eşit olacak şekilde bölen, doğru parçası doğru ya da işine verilen isim.
Şimdi üçgen de ama her köşeden çıkan özel bir durum olarak anlatıyorum.
Her köşeden çıkan açı taylar bir noktada kesişir.
Her biri bu kesişim noktasından geçer.
Mecbur.
Peki nedir bu önemli kesişim noktası?
Bu noktaya içte çemberin merkezi adı veriniz.
Yani biz bir üçgen de iç açı tayları çekilince içten tüm kenarlara teğet olan bu çemberin merkezinden geçecekler.
Ya da tersten gitsen mesela soru bana iç teğet çemberini verirse ne yapacağım?
O zaman demeliyim ki bu noktayı ve herhangi bir köşeyi birleştirirsek.
Köşede açı ortay yaratır.
Önemli bir noktadır.
Bazı soru tarzlarında sıklıkla danışılan bir özelliktir.
Ilerleyelim şimdi.
İşte iç ortaklarımızın yarattığı bazı özel durumlara bakalım, bu özel durum demem aslında tamamen bir çıkarım dır.
Vay aman tanrım!
Gibisinden bir formül düşünmediniz.
Zaman kazanmamız için önemlidir tabii.
Bir üçgende iki tane iç açı ortamın kesişmesi durumunda bu kesişim açısını hızlıca hesaplayan biliyoruz.
Çünkü bu formülde açı ortaları bu açı ortay açılarını hesaplı almamıza gerek yok.
Burada gördüğünüz işlemler de iki tane iç açı ortay verilirse eğer ben buradaki şuralarda harfler verecek olursam aşçılara ayağa bhp dersem burada ayı ya da Bey'i hesaplamaya gerek kalmayacak.
Direk formül üzerinden hızlıca gidebilirim.
Bu bana zaman tasarrufu sağlıyor.
Ne güzel.
Tabii ki bileyim bunu.
Ama hatırlamaz olsanız da formülü hemencecik nereden geldiğimizi, nereden geldiğini bunun anlatayım.
Burada gördüğünüz arkadaşlar büyük üçgen de yani A-B-C üçgenin de iç açılar toplamı yazıyoruz.
Nedir?
İki artı iki ve artı ye eşittir 180.
Diğer üçgenine belediyece 3G'li.
Şimdi ilk başta büyük üçgende yani ciksin olmadığı üçgende işlem yaptım.
Şimdi de küçük üç kene yani Hicks'in olduğu yani araştırmak istediğim açı.
Çünkü iki tane iç açı ortanın kesiştiği açı IX açısı iyi açısı değil.
Geldim bu üç kene bakıyorum A artı B artı IX eşittir 180.
İşte burada arkadaşlar ortak çözüm yapıyoruz ve bu A ve B leri yok ediyoruz.
Ben buraya ikiyle çarpar burayı çıkarırsan arkadaşlar 2 aydan 2 aya çıkaracağım.
2 beyden 2 B çıkaracağım.
Sadece ilk ve yaya kalacak.
Bilinmeyen 2 tane kalacak ve buradan şu formülünü elde etmiş olacak.
Formülün nereden geldiğini anlattım.
Hızlıca yol almamız bakımından artık bunları bilmeme gerek kalmayacak.
Bana bir soru verildiğinde iki tane iç açı ortanın kesişim açısını burada gördüğünüz açı ortay çizme dediğim açıyı bilerek bulabiliyorum.
Onu anlatmaya çalışıyorum.
Daha hızlı gitmeli iyi mi aktarmaya çalışıyorum.
Peki ilerleyelim, şimdi iki dış açı ortay kesilirse ne olur bunu inceleyelim, kuralımız şu burada gördüğünüz iki tane dış açı orta in kesişim açısı A mı?
Evet, ben demek ki bunu araştırıyorum.
Aaa eşittir 90 eksi b ölü iki b dediğimde dış açı ortay çizgi dediğim köşe varya oradaki iç açı 90 eksi b.
İyi ki burada gördüğünüz A açısını verecektir.
Yani burada da üstte anlattığım gibi arkadaşlar buralar harf versem ilk s ix açısı gayeye açısı desem burası ne olacak 180 x 2x.
Buradaki iç açım ne olacak?
180 eksi 2'ye alacak.
İlk önce beynin olduğu üçgende işlem yapıyorum, iç açılar toplamı eşittir.
Şuuru da kağıtçı buradaki açı burada kerç edeceğim.
İkinci 3 önemli anın olduğu üçgen anın olduğu üçgen de ilk Sariye var a var.
Yine 2 tane denklem buluyorum.
Buradaki X ve Y bilinmeyenlerini yok edip taraf tarafa çözerek elimde sadece ağlı beyli 2 tane bilinmeyen kalıyor.
Bunu da formülde çekerse meğer 2 tane dışa çekirdeğin kesişim açısı 90 derece eksi ve bölü 2 oluyor arkadaşlar.
Şimdi ilerleyelim, bir iç ve bir dış aç ortağın kesişim açısı nedir peki?
Gördüğünüz gibi A-B-C üçgeni içinde B de iç açı ortay CD de A-B-C üçgeninde bir dış açı ortadır.
Şimdi diyoruz ki bir iç ve bir dış açı in kesişim açısı yani A kaç derecedir yani nasıl hesaplanıyor bu?
Buradaki formül mü şudur?
Yine burada hiç aç ortay falan çizme edeyim.
Bu yalnız köşe ile işlem yapıp bu yalnız köşeyi ikiye bölüyor Rum ve A derecesini elde ediyorum.
Ya da diyeceğim ki B'yi bulmak istiyorum.
O zaman diyeceğim ki A2 ile çarparsa değerdedir.
Tersten de gidebilir mi?
Yani tabiki de illa burayı vergi vermek zorunda değil.
Ağa'dan da B'ye geçiş yapabiliriz.
Mantığımız o kesişim açısını hesaplamak istiyorum ama ben kuralım onun üstüne geliştirilmiş A açısı eşittir bu açı ortay çizme diyeyim aşının derecesinin yarısı bu kadar.
Buradan aynı şekilde yapacağımız formül arkadaşlar.
A ve B dedik buralara IX İKSV'ye, Y harflerini verirsek arkadaşlar şunu söylemiştim.
İki tane iç açının toplamı kendilerine komşu olmayan bir dış açığa eşittir.
Yani burada ikisi artı beğeniye eşit olacak iki tane iç açıyı topladım.
A ve B köşelerini.
A-b-c üçgenin de bunların dış açısı burası mı iki?
Şimdi bakmanızı istediğim üçgen B de C üçgeni B, DC üçgeni de A ve eksi toplasan bunların dış açısı nedir?
B Sadece üçgenin de bunlara komşu olmayan dış açı yani Eyyyy eşittir.
İşte buradan gelen kural şudur Arkadaşlar yine İKSV'ye iyi taraf tarafa iptal ediyorum.
Onları yazmıyorum tabiki de birbirini yok ediyorum ki Ağlı Beyliği iki tane bilinmeyen kalsın.
Elimde birbirleriyle ilişkisini ölçeğin kuralım.
Bu A eşittir B bölüğü.
2.
Son olarak.
Dış çemberi açıklayayım.
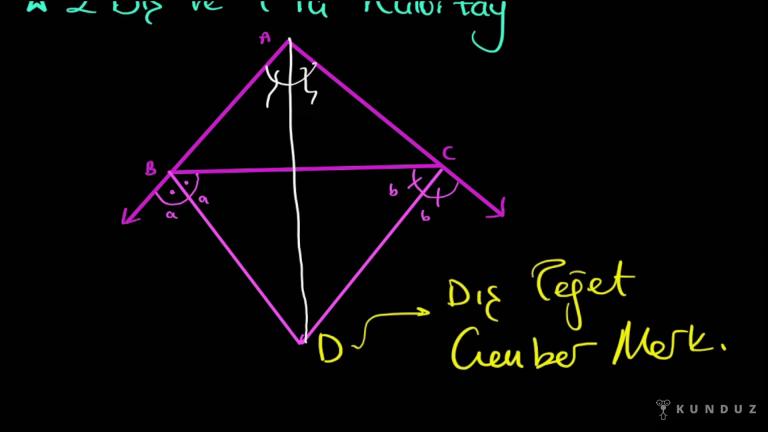
Bir üçgen de nasıl iç açı ortaya dar bir noktada kesişiyor, İsa şimdi komşu iki dış açı da bir noktada kesişir ve bu noktaya dış çemberin merkezi adı veriniz.
Burada gördüğünüz gibi A-B-C üçgenin iki tane dış açısı bir noktada kesişir ve bu nokta dış çemberin merkezidir.
Burada dev noktası dış çemberin merkezi ama bir şey daha eklemek istiyorum.
Burada sadece dış açı ortayla alakalı bir şey düşünmenizi istemiyorum.
Ben ABD'yi birleştirir isem.
Adiye dediğim şey iç açı ortay olmalıdır, arkadaşlar şurası şuraya eşit olmak zorundadır.
Bu dış heyeti bunu çözemedim.
Biraz büyük oldu da şurada bütün kenarlara ve uzantılarına teğet olan bir çember düşününüz.
Çemberi böyle devam etmekte.
İşte burada aktarmak istediğim sizlere iki tane dış açı orta kesişimi aynı zamanda diğer açı orta çizgi dediğim köşe ile de iç açı ortay olarak kesişir arkadaşlar.
B ve c eden dış açı ortakları burada kesiştiği değilseniz ağa'dan da iç açı ortay çözeceksiniz.
Bazı soru tarzları bunun üstüne geliştirilmiştir.
Yani ben B ve c den gelen bir dış iç dış açı ortay kesişimi biliyorsam orayla diğer köşeyi birleştirirsek.
Buranın da bir iç açı ortayı olacağını bilmeliyiz.
Başlayalım.
Önce bir bakalım bir üçgen daha ortay nedir?
Beraber ne yaparlar?
Açı ortay dediğimiz belli bir açıyı ortadan ikiye yaran yani tam eşit olacak şekilde bölen, doğru parçası doğru ya da işine verilen isim.
Şimdi üçgen de ama her köşeden çıkan özel bir durum olarak anlatıyorum.
Her köşeden çıkan açı taylar bir noktada kesişir.
Her biri bu kesişim noktasından geçer.
Mecbur.
Peki nedir bu önemli kesişim noktası?
Bu noktaya içte çemberin merkezi adı veriniz.
Yani biz bir üçgen de iç açı tayları çekilince içten tüm kenarlara teğet olan bu çemberin merkezinden geçecekler.
Ya da tersten gitsen mesela soru bana iç teğet çemberini verirse ne yapacağım?
O zaman demeliyim ki bu noktayı ve herhangi bir köşeyi birleştirirsek.
Köşede açı ortay yaratır.
Önemli bir noktadır.
Bazı soru tarzlarında sıklıkla danışılan bir özelliktir.
Ilerleyelim şimdi.
İşte iç ortaklarımızın yarattığı bazı özel durumlara bakalım, bu özel durum demem aslında tamamen bir çıkarım dır.
Vay aman tanrım!
Gibisinden bir formül düşünmediniz.
Zaman kazanmamız için önemlidir tabii.
Bir üçgende iki tane iç açı ortamın kesişmesi durumunda bu kesişim açısını hızlıca hesaplayan biliyoruz.
Çünkü bu formülde açı ortaları bu açı ortay açılarını hesaplı almamıza gerek yok.
Burada gördüğünüz işlemler de iki tane iç açı ortay verilirse eğer ben buradaki şuralarda harfler verecek olursam aşçılara ayağa bhp dersem burada ayı ya da Bey'i hesaplamaya gerek kalmayacak.
Direk formül üzerinden hızlıca gidebilirim.
Bu bana zaman tasarrufu sağlıyor.
Ne güzel.
Tabii ki bileyim bunu.
Ama hatırlamaz olsanız da formülü hemencecik nereden geldiğimizi, nereden geldiğini bunun anlatayım.
Burada gördüğünüz arkadaşlar büyük üçgen de yani A-B-C üçgenin de iç açılar toplamı yazıyoruz.
Nedir?
İki artı iki ve artı ye eşittir 180.
Diğer üçgenine belediyece 3G'li.
Şimdi ilk başta büyük üçgende yani ciksin olmadığı üçgende işlem yaptım.
Şimdi de küçük üç kene yani Hicks'in olduğu yani araştırmak istediğim açı.
Çünkü iki tane iç açı ortanın kesiştiği açı IX açısı iyi açısı değil.
Geldim bu üç kene bakıyorum A artı B artı IX eşittir 180.
İşte burada arkadaşlar ortak çözüm yapıyoruz ve bu A ve B leri yok ediyoruz.
Ben buraya ikiyle çarpar burayı çıkarırsan arkadaşlar 2 aydan 2 aya çıkaracağım.
2 beyden 2 B çıkaracağım.
Sadece ilk ve yaya kalacak.
Bilinmeyen 2 tane kalacak ve buradan şu formülünü elde etmiş olacak.
Formülün nereden geldiğini anlattım.
Hızlıca yol almamız bakımından artık bunları bilmeme gerek kalmayacak.
Bana bir soru verildiğinde iki tane iç açı ortanın kesişim açısını burada gördüğünüz açı ortay çizme dediğim açıyı bilerek bulabiliyorum.
Onu anlatmaya çalışıyorum.
Daha hızlı gitmeli iyi mi aktarmaya çalışıyorum.
Peki ilerleyelim, şimdi iki dış açı ortay kesilirse ne olur bunu inceleyelim, kuralımız şu burada gördüğünüz iki tane dış açı orta in kesişim açısı A mı?
Evet, ben demek ki bunu araştırıyorum.
Aaa eşittir 90 eksi b ölü iki b dediğimde dış açı ortay çizgi dediğim köşe varya oradaki iç açı 90 eksi b.
İyi ki burada gördüğünüz A açısını verecektir.
Yani burada da üstte anlattığım gibi arkadaşlar buralar harf versem ilk s ix açısı gayeye açısı desem burası ne olacak 180 x 2x.
Buradaki iç açım ne olacak?
180 eksi 2'ye alacak.
İlk önce beynin olduğu üçgende işlem yapıyorum, iç açılar toplamı eşittir.
Şuuru da kağıtçı buradaki açı burada kerç edeceğim.
İkinci 3 önemli anın olduğu üçgen anın olduğu üçgen de ilk Sariye var a var.
Yine 2 tane denklem buluyorum.
Buradaki X ve Y bilinmeyenlerini yok edip taraf tarafa çözerek elimde sadece ağlı beyli 2 tane bilinmeyen kalıyor.
Bunu da formülde çekerse meğer 2 tane dışa çekirdeğin kesişim açısı 90 derece eksi ve bölü 2 oluyor arkadaşlar.
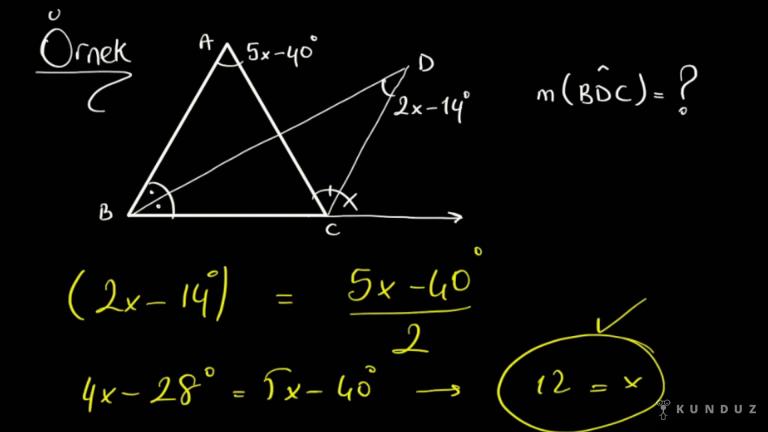
Şimdi ilerleyelim, bir iç ve bir dış aç ortağın kesişim açısı nedir peki?
Gördüğünüz gibi A-B-C üçgeni içinde B de iç açı ortay CD de A-B-C üçgeninde bir dış açı ortadır.
Şimdi diyoruz ki bir iç ve bir dış açı in kesişim açısı yani A kaç derecedir yani nasıl hesaplanıyor bu?
Buradaki formül mü şudur?
Yine burada hiç aç ortay falan çizme edeyim.
Bu yalnız köşe ile işlem yapıp bu yalnız köşeyi ikiye bölüyor Rum ve A derecesini elde ediyorum.
Ya da diyeceğim ki B'yi bulmak istiyorum.
O zaman diyeceğim ki A2 ile çarparsa değerdedir.
Tersten de gidebilir mi?
Yani tabiki de illa burayı vergi vermek zorunda değil.
Ağa'dan da B'ye geçiş yapabiliriz.
Mantığımız o kesişim açısını hesaplamak istiyorum ama ben kuralım onun üstüne geliştirilmiş A açısı eşittir bu açı ortay çizme diyeyim aşının derecesinin yarısı bu kadar.
Buradan aynı şekilde yapacağımız formül arkadaşlar.
A ve B dedik buralara IX İKSV'ye, Y harflerini verirsek arkadaşlar şunu söylemiştim.
İki tane iç açının toplamı kendilerine komşu olmayan bir dış açığa eşittir.
Yani burada ikisi artı beğeniye eşit olacak iki tane iç açıyı topladım.
A ve B köşelerini.
A-b-c üçgenin de bunların dış açısı burası mı iki?
Şimdi bakmanızı istediğim üçgen B de C üçgeni B, DC üçgeni de A ve eksi toplasan bunların dış açısı nedir?
B Sadece üçgenin de bunlara komşu olmayan dış açı yani Eyyyy eşittir.
İşte buradan gelen kural şudur Arkadaşlar yine İKSV'ye iyi taraf tarafa iptal ediyorum.
Onları yazmıyorum tabiki de birbirini yok ediyorum ki Ağlı Beyliği iki tane bilinmeyen kalsın.
Elimde birbirleriyle ilişkisini ölçeğin kuralım.
Bu A eşittir B bölüğü.
2.
Son olarak.
Dış çemberi açıklayayım.
Bir üçgen de nasıl iç açı ortaya dar bir noktada kesişiyor, İsa şimdi komşu iki dış açı da bir noktada kesişir ve bu noktaya dış çemberin merkezi adı veriniz.
Burada gördüğünüz gibi A-B-C üçgenin iki tane dış açısı bir noktada kesişir ve bu nokta dış çemberin merkezidir.
Burada dev noktası dış çemberin merkezi ama bir şey daha eklemek istiyorum.
Burada sadece dış açı ortayla alakalı bir şey düşünmenizi istemiyorum.
Ben ABD'yi birleştirir isem.
Adiye dediğim şey iç açı ortay olmalıdır, arkadaşlar şurası şuraya eşit olmak zorundadır.
Bu dış heyeti bunu çözemedim.
Biraz büyük oldu da şurada bütün kenarlara ve uzantılarına teğet olan bir çember düşününüz.
Çemberi böyle devam etmekte.
İşte burada aktarmak istediğim sizlere iki tane dış açı orta kesişimi aynı zamanda diğer açı orta çizgi dediğim köşe ile de iç açı ortay olarak kesişir arkadaşlar.
B ve c eden dış açı ortakları burada kesiştiği değilseniz ağa'dan da iç açı ortay çözeceksiniz.
Bazı soru tarzları bunun üstüne geliştirilmiştir.
Yani ben B ve c den gelen bir dış iç dış açı ortay kesişimi biliyorsam orayla diğer köşeyi birleştirirsek.
Buranın da bir iç açı ortayı olacağını bilmeliyiz.
Sıkça Sorulan Sorular
Açıortay nedir?
Geometride bir açıyı iki eş parçaya bölen doğru parçasına açıortay denir.
Açıortay özellikleri nelerdir?
Üçgende açılar konusunda açıortaydan kaynaklı bazı özel durumlar ve kurallar mevcuttur. Bu açıortay kurallarına iç teğet çember ile giriş yapalım.
Üçgenin iç açıortaylarının kesişim noktasına iç teğet çemberin merkezidir. İç teğet çember bir üçgende çizilebilecek en büyük çaplı çembere verilen isimdir.
İki iç açıortayın kesişim açısını formülü ile bulunabilir.