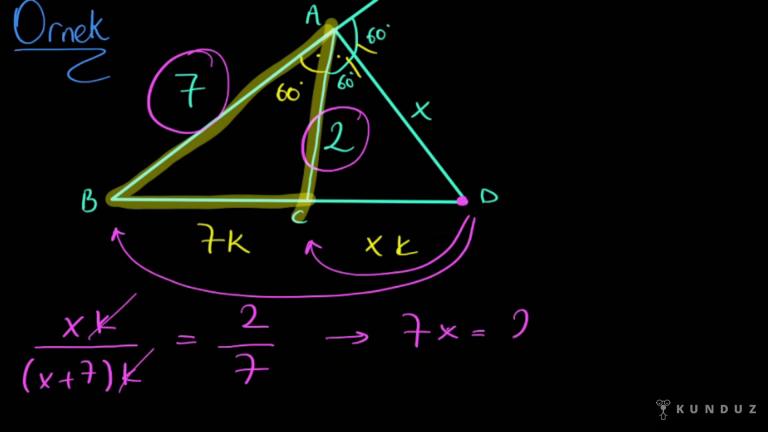Merhabalar şimdi iç açı orta teoremini aktarayım.
Teorem falan böyle süslü kelimeler kullandırma, bakmayın yine benzerlik ile doğmuş bir kural anlatacağım şekilde.
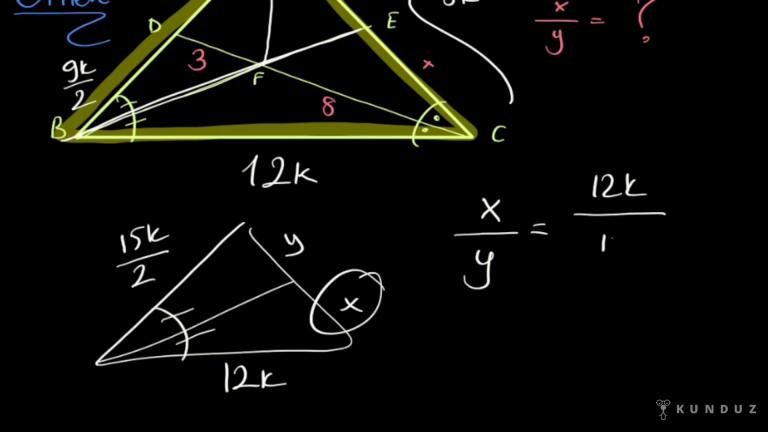
Gördüğünüz gibi bir üçgen de eğer açı ortay çizilir ise ilk bölünmenin oranı Y bölümlerinin oranına eşit oluyor.
Yani işçiler dişler de yapabilirsin yani alış şeklini de değiştirebilirsiniz asıl yani ix bölgeyi de or anlayıp m bölüne y de diyebilirsiniz.
Yani burada Y.
Ve M.
Nin yerini değiştirir.
Hem yine aynı sonuç aynı oranı sağlamak zorundayım.
İlk bölge eşittir meye bölüne ya da ilk bölünme eşittir y bölü ne yapmak zorundayım?
Şimdi neden böyle benzerlikten geliyor dedim.
Onu aktarmaya çalışayım.
Yine 3 kelime aldım.
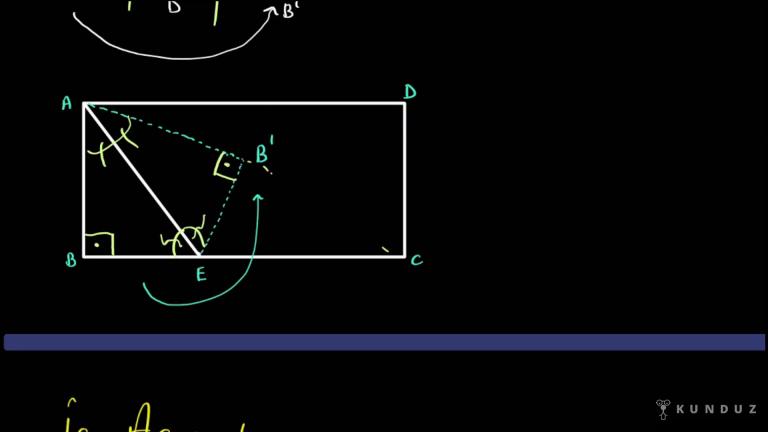
Dedim ki a, b, c 3 kelime aldım b eden açı.
Ortayı çizdim acaba neden iki bölüme eşittir?
Y Bölünmeye buluyoruz.
Şimdi buradan size tavsiyem bu gördüğünüz açı ortaya uzattığımız.
Uzatıyorum, uzatıyorum gitti böyle uzadı.
Sonra diyorum ki C köşesinden A, B kenarına bir paralel çizdiniz.
Yani A, B kenarı böyleyse galiba çizeceğim şekil böyle bir şey olacak.
Tamam bu paralelliği de göstermek istiyorum.
Şimdi burada paralellik yarattıysa bu paraleli kullanmalıyız.
Bu paralelliği yaratmanın bir sebebi var.
Nedir bu sebep?
Şurada gördüğünüz iç ters açılar.
Buradaki açım ne ise yani şuradaki an için ne ise buradaki açım da o değil midir?
İç ters açılar, Z kuralı ne derseniz deyin.
Demek ki ben o açıyı taşıyan biliyorum.
Buradaki açımı noktayla gösterdim.
Buraya da aynı şekilde geldim.
Şimdi ikinci bakmanızı istediğim yer bir üçgen.
Şurada gördüğünüz üçgen den bahsediyorum.
Şu gördüğünüz açı ve bu gördüğünüz açı birbirine eşit bulduk.
Demek ki burada bir ikiz kenar lık yarattık biz arkadaşlar.
Yani bu kenar ne ise bu kenar da aynı olmalı.
Çünkü üçgen de bu kenar bu, açı bu.
Açı eşitse bu kenar bu kenara eşittir.
Burasını yere vermiş.
O zaman ben buraya ye yazabilirim.
Tamam şimdi son olarak bakmanızı istediğim yine paralelliği dönerek del şuradaki tatlı mı tatlı kelebeği görmek burada.
Peki kelebek kuralımız neydi?
İsterseniz böyle başlayın.
Yani ilk bölü ye eşittir.
Şöyle gösterelim onda m bölüne.
Içler dışlar mı yaptınız zaten üstte anlattığım yere getiriyor aynı şey.
Yani benzerlikten geldiği neden bir çıkarım dediğim.
Bundan dolayıdır arkadaşlar.
Bir parelel çekerek bu kuralın aslını aslında göstermiş oluruz.
İşte açı ortay özel bir durum oluyor.
Böylelikle eşit derecede böldüğü için o açıyı taşıdığım yerlerde bazı kullanma imkanı sunuyor ve ben özellikle böyle bir kural oluşturabiliriz.
Ilerleyelim mesela, şu da aklınızda oturması için yine bir sözlü anlatım göstermek istiyorum.
Mesela A-B-C üçgeninde de yine ade aç ordayım, indim.
Buralar 8, buralar yedi olarak verilsin.
Burada sözlü olarak aklıma şöyle bir orantı oturtmamız lazım.
Diyeceğim ki sekize 8, köye gelirse 7'ye 7 okey gelmeli.
Sekize 24 kere mi geldi?
3 köye katı doğru mu?
O zaman 7'nin de üç köye katı, yirmi 21 köye gelmeli.
Demeliyim.
Aklın oturması gereken mantık bu.
Buradaki örneğe dönelim.
Bey'den bir aç orta indim.
Şurası 13 olsun, burası yedi olsun.
Ab'ye 90 bir diyelim.
Şimdi burada açı ortay varsa oran vardır, oranı yapmam lazım ama yani formüle girmeden demeliyim ki 13'e 91 geldiyse yediye kaç gelecek 13'e 91 yedi katı mı gelmiş, yedi yedi yedi katı gelecek 49 gelir diyeceğiz.
Yani sözlü olarak bunları söyleyebilir, pek daha hızlı ilerleme sağlayabiliriz.
Şimdi bir örnekle böyle bir pekiştirme yapalım, bunu bir deneyelim.
Yani bu anlattıklarım şundan önemli.
Size üç kenarı verilen bir üçgen olabilir, bir köşeden çıkan açı atayın karşı kenarı hangi uzunlukta keseceğini bileceksiniz.
Mesela bu örnekte öyle bir soru çözelim.
Üçgen şeklinde bir inşaat alanını plan olsun ne ise aç.
Ortaç'ın ayırdığı parçaların uzunluğunu hesaplamak gerekirse işleme.
Selahi Bu ayrılan parçalardan bir tarafa gül ekmek istiyorum.
Bir tarafa menekşe ekmek istiyorum.
Olsun bunların uzunlukları ne?
Hesaplama maç ortay sayesinde hesap kolay açı ortay teoremi sayesinde kolay olabilir.
Yani buralara kaç tane gül gerekeceğini, kaç tane menekşe gerekeceğini ona göre sipariş vereceğimi bulabilir.
Bundan bahsediyorum.
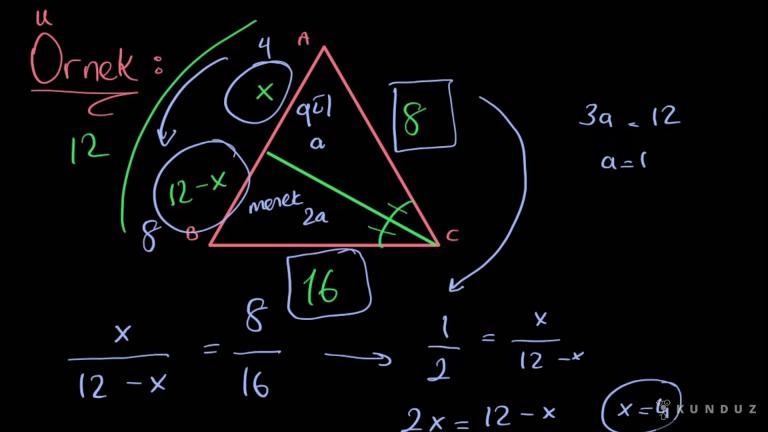
Mesela kenar uzunlukları 12 olsun, burası 8 olsun, şuraya da 16 verelim.
Diyelim ki CHP'den çıkan açı ortay ayırdığı parçaların uzunlukları bulalım.
Mesela ona göre gül ve menekşe siparişi vereceğim.
Diyorum ki CHP'den çiziyorum açı ortayı mı böyle bir açı ortay olsun.
Tamam şimdi burası komple 12 12 metre diyelim.
Şimdi ben burayı biliyor muyum?
Hayır ilk dedim.
O zaman burası 12 eksik demekti, toplamının 12 olması için.
İşte diyorum ki ben bu tarafa gül çekeceğim, bu tarafa menekşe ekeceğiz.
O yüzden buranın ve buranın kaç metre olduğunu bileyim ki ona göre siparişi vereyim.
O yüzden bu hesapta bana iç açı ortay teoremi oldukça yardımcı olacak.
Ne diyebilirsiniz?
İsterseniz şu bölü şu şu görüşü deyin, isterseniz şu böyle, şu eşittir şu beri şu değil.
Yapmak istediğiniz şey aynı olacaktır.
Ix Bölüğü 12 x IX eşittir şu böyle şu yaptım.
Şimdi de bu böyle.
Bu yapmam lazım.
Bakın ilk böyle 12 eksi IX dedikten sonra 16 58 diyemezsiniz.
Birinci de böyle geldiyseniz ikincide de böyle gitmelisiniz.
Yani böyle tersten giderseniz ilk böyle 12 eksi eşittir 16 böyle 8 derseniz yanlış yaparsınız.
Demek istediğimi tekrar söylüyorum ilk kez böyle 12 izlediyseniz, buradan buraya geldiyseniz aynı şekli takip edip 8 bölü 16 demelisiniz.
8 bölü 16 buraya geldim.
8 böyle 16 bir bölü 2'dir.
Bir böyle iki eşittir IX böyle 12 eksi IX çarpar öz 2 x eşittir 12 eksi IX, IX bu tarafa attım üç x eşittir on iki x eşittir 4 metre bulunur.
Yani 4 metrelik bir gül alanı var.
Küre de yazalım.
12'den 4 çıkarırsan 8 metre.
8 metrelik de bir menekşe alanım var zaten.
İlk başta kafamda oturması gereken sözlü mantıktan da öyle gitmeliydi.
Sekize ne gelirse 16 onun iki katı gelmeli demeliydi.
Yani buraya A deseydim buraya İ.K.
Demeliydim mesela başta.
O zaman ne diyecektim?
3 ağanın toplamı, toplam uzunluğu neydi?
12 metre etmeli̇ o zaman.
A dedim şeyi 4'te bulabilirdi.
Yani buraya yine 4, buraya 8 yazacaktım.
Sonuç değişmeyecekti tabii ki.
Yani sözlü olarak da yine hızlı bir şekilde ilerlemesi açısından yardımcı olacaktı bu.
Teorem falan böyle süslü kelimeler kullandırma, bakmayın yine benzerlik ile doğmuş bir kural anlatacağım şekilde.
Gördüğünüz gibi bir üçgen de eğer açı ortay çizilir ise ilk bölünmenin oranı Y bölümlerinin oranına eşit oluyor.
Yani işçiler dişler de yapabilirsin yani alış şeklini de değiştirebilirsiniz asıl yani ix bölgeyi de or anlayıp m bölüne y de diyebilirsiniz.
Yani burada Y.
Ve M.
Nin yerini değiştirir.
Hem yine aynı sonuç aynı oranı sağlamak zorundayım.
İlk bölge eşittir meye bölüne ya da ilk bölünme eşittir y bölü ne yapmak zorundayım?
Şimdi neden böyle benzerlikten geliyor dedim.
Onu aktarmaya çalışayım.
Yine 3 kelime aldım.
Dedim ki a, b, c 3 kelime aldım b eden açı.
Ortayı çizdim acaba neden iki bölüme eşittir?
Y Bölünmeye buluyoruz.
Şimdi buradan size tavsiyem bu gördüğünüz açı ortaya uzattığımız.
Uzatıyorum, uzatıyorum gitti böyle uzadı.
Sonra diyorum ki C köşesinden A, B kenarına bir paralel çizdiniz.
Yani A, B kenarı böyleyse galiba çizeceğim şekil böyle bir şey olacak.
Tamam bu paralelliği de göstermek istiyorum.
Şimdi burada paralellik yarattıysa bu paraleli kullanmalıyız.
Bu paralelliği yaratmanın bir sebebi var.
Nedir bu sebep?
Şurada gördüğünüz iç ters açılar.
Buradaki açım ne ise yani şuradaki an için ne ise buradaki açım da o değil midir?
İç ters açılar, Z kuralı ne derseniz deyin.
Demek ki ben o açıyı taşıyan biliyorum.
Buradaki açımı noktayla gösterdim.
Buraya da aynı şekilde geldim.
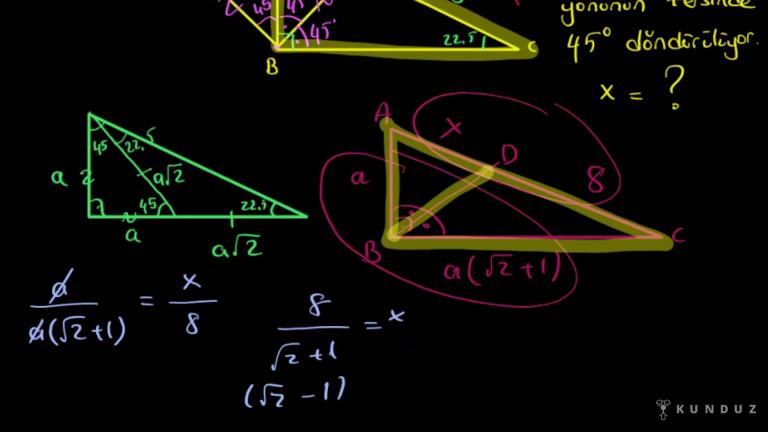
Şimdi ikinci bakmanızı istediğim yer bir üçgen.
Şurada gördüğünüz üçgen den bahsediyorum.
Şu gördüğünüz açı ve bu gördüğünüz açı birbirine eşit bulduk.
Demek ki burada bir ikiz kenar lık yarattık biz arkadaşlar.
Yani bu kenar ne ise bu kenar da aynı olmalı.
Çünkü üçgen de bu kenar bu, açı bu.
Açı eşitse bu kenar bu kenara eşittir.
Burasını yere vermiş.
O zaman ben buraya ye yazabilirim.
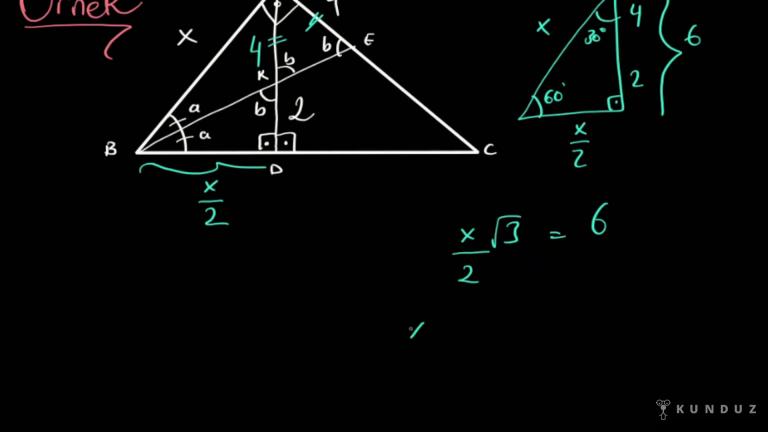
Tamam şimdi son olarak bakmanızı istediğim yine paralelliği dönerek del şuradaki tatlı mı tatlı kelebeği görmek burada.
Peki kelebek kuralımız neydi?
İsterseniz böyle başlayın.
Yani ilk bölü ye eşittir.
Şöyle gösterelim onda m bölüne.
Içler dışlar mı yaptınız zaten üstte anlattığım yere getiriyor aynı şey.
Yani benzerlikten geldiği neden bir çıkarım dediğim.
Bundan dolayıdır arkadaşlar.
Bir parelel çekerek bu kuralın aslını aslında göstermiş oluruz.
İşte açı ortay özel bir durum oluyor.
Böylelikle eşit derecede böldüğü için o açıyı taşıdığım yerlerde bazı kullanma imkanı sunuyor ve ben özellikle böyle bir kural oluşturabiliriz.
Ilerleyelim mesela, şu da aklınızda oturması için yine bir sözlü anlatım göstermek istiyorum.
Mesela A-B-C üçgeninde de yine ade aç ordayım, indim.
Buralar 8, buralar yedi olarak verilsin.
Burada sözlü olarak aklıma şöyle bir orantı oturtmamız lazım.
Diyeceğim ki sekize 8, köye gelirse 7'ye 7 okey gelmeli.
Sekize 24 kere mi geldi?
3 köye katı doğru mu?
O zaman 7'nin de üç köye katı, yirmi 21 köye gelmeli.
Demeliyim.
Aklın oturması gereken mantık bu.
Buradaki örneğe dönelim.
Bey'den bir aç orta indim.
Şurası 13 olsun, burası yedi olsun.
Ab'ye 90 bir diyelim.
Şimdi burada açı ortay varsa oran vardır, oranı yapmam lazım ama yani formüle girmeden demeliyim ki 13'e 91 geldiyse yediye kaç gelecek 13'e 91 yedi katı mı gelmiş, yedi yedi yedi katı gelecek 49 gelir diyeceğiz.
Yani sözlü olarak bunları söyleyebilir, pek daha hızlı ilerleme sağlayabiliriz.
Şimdi bir örnekle böyle bir pekiştirme yapalım, bunu bir deneyelim.
Yani bu anlattıklarım şundan önemli.
Size üç kenarı verilen bir üçgen olabilir, bir köşeden çıkan açı atayın karşı kenarı hangi uzunlukta keseceğini bileceksiniz.
Mesela bu örnekte öyle bir soru çözelim.
Üçgen şeklinde bir inşaat alanını plan olsun ne ise aç.
Ortaç'ın ayırdığı parçaların uzunluğunu hesaplamak gerekirse işleme.
Selahi Bu ayrılan parçalardan bir tarafa gül ekmek istiyorum.
Bir tarafa menekşe ekmek istiyorum.
Olsun bunların uzunlukları ne?
Hesaplama maç ortay sayesinde hesap kolay açı ortay teoremi sayesinde kolay olabilir.
Yani buralara kaç tane gül gerekeceğini, kaç tane menekşe gerekeceğini ona göre sipariş vereceğimi bulabilir.
Bundan bahsediyorum.
Mesela kenar uzunlukları 12 olsun, burası 8 olsun, şuraya da 16 verelim.
Diyelim ki CHP'den çıkan açı ortay ayırdığı parçaların uzunlukları bulalım.
Mesela ona göre gül ve menekşe siparişi vereceğim.
Diyorum ki CHP'den çiziyorum açı ortayı mı böyle bir açı ortay olsun.
Tamam şimdi burası komple 12 12 metre diyelim.
Şimdi ben burayı biliyor muyum?
Hayır ilk dedim.
O zaman burası 12 eksik demekti, toplamının 12 olması için.
İşte diyorum ki ben bu tarafa gül çekeceğim, bu tarafa menekşe ekeceğiz.
O yüzden buranın ve buranın kaç metre olduğunu bileyim ki ona göre siparişi vereyim.
O yüzden bu hesapta bana iç açı ortay teoremi oldukça yardımcı olacak.
Ne diyebilirsiniz?
İsterseniz şu bölü şu şu görüşü deyin, isterseniz şu böyle, şu eşittir şu beri şu değil.
Yapmak istediğiniz şey aynı olacaktır.
Ix Bölüğü 12 x IX eşittir şu böyle şu yaptım.
Şimdi de bu böyle.
Bu yapmam lazım.
Bakın ilk böyle 12 eksi IX dedikten sonra 16 58 diyemezsiniz.
Birinci de böyle geldiyseniz ikincide de böyle gitmelisiniz.
Yani böyle tersten giderseniz ilk böyle 12 eksi eşittir 16 böyle 8 derseniz yanlış yaparsınız.
Demek istediğimi tekrar söylüyorum ilk kez böyle 12 izlediyseniz, buradan buraya geldiyseniz aynı şekli takip edip 8 bölü 16 demelisiniz.
8 bölü 16 buraya geldim.
8 böyle 16 bir bölü 2'dir.
Bir böyle iki eşittir IX böyle 12 eksi IX çarpar öz 2 x eşittir 12 eksi IX, IX bu tarafa attım üç x eşittir on iki x eşittir 4 metre bulunur.
Yani 4 metrelik bir gül alanı var.
Küre de yazalım.
12'den 4 çıkarırsan 8 metre.
8 metrelik de bir menekşe alanım var zaten.
İlk başta kafamda oturması gereken sözlü mantıktan da öyle gitmeliydi.
Sekize ne gelirse 16 onun iki katı gelmeli demeliydi.
Yani buraya A deseydim buraya İ.K.
Demeliydim mesela başta.
O zaman ne diyecektim?
3 ağanın toplamı, toplam uzunluğu neydi?
12 metre etmeli̇ o zaman.
A dedim şeyi 4'te bulabilirdi.
Yani buraya yine 4, buraya 8 yazacaktım.
Sonuç değişmeyecekti tabii ki.
Yani sözlü olarak da yine hızlı bir şekilde ilerlemesi açısından yardımcı olacaktı bu.