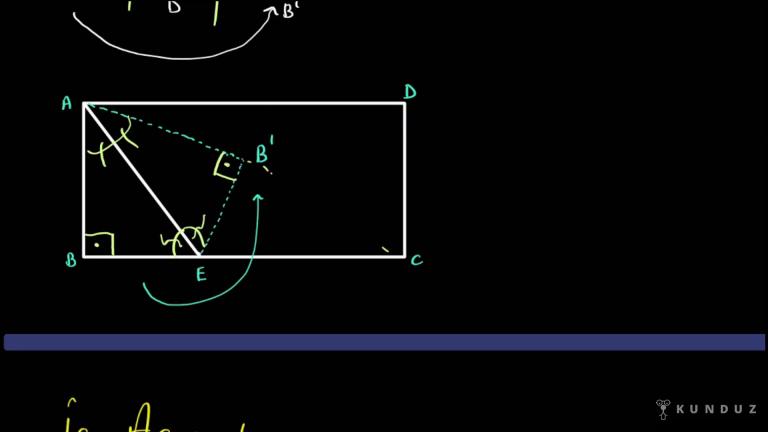
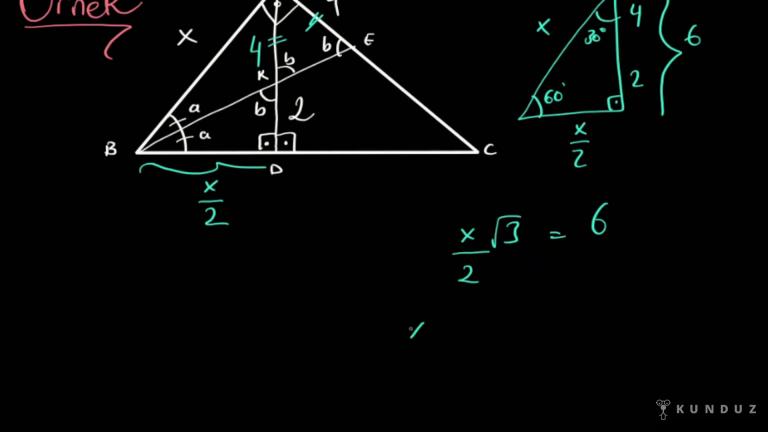
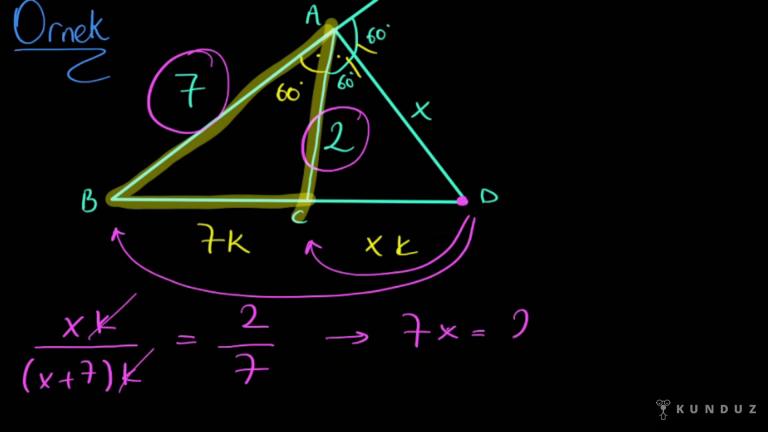Merhabalar, açıortaya devam ediyoruz, gördüğünüz gibi bir ABD üçgeni verdim.
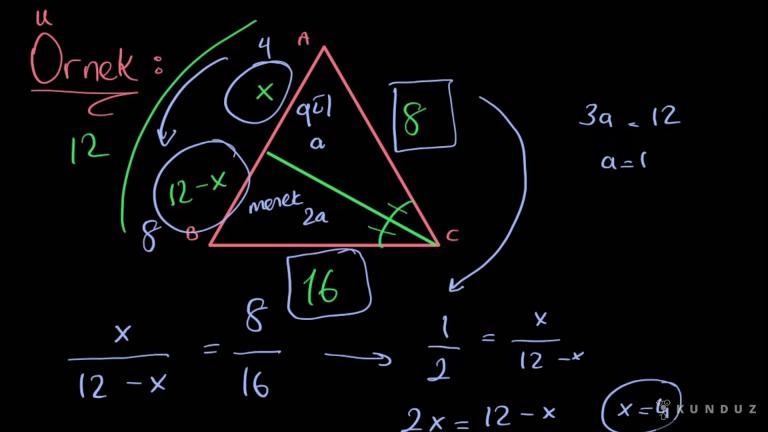
ACB açısı 2a, BAC açısı a kadar.
BC on iki uzunluğunda, AD eşittir CD eşittir 4 uzunluğunda.
AC uzunluğunu istiyorum.
Şimdi burada açıortay anlatıyorum da bu verdiklerinde bir açıortaylık yok.
Şimdi burada ne yapacağım peki?
2a'yı eşit bölecek şekilde yani burada a'ya a yapacak şekilde ilerlemeli miyim acaba?
Hayır.
Çünkü ben öyle yapsam bile yani şurada bir açıortaylık oluştursa bile burayı biliyor muyum?
Hayır.
Burayı biliyor muyum?
Hayır.
Burayı biliyor muyum?
Onu da hayır.
O zaman buradan ilerlememeliyim.
Demek ki bana bunu söylüyor bu yol.
Buraları temizliyorum.
E buradan gitmeyeceksem ne yapacağım şimdi?
Size şuradaki çizgiyi vermesinin bir sebebi vardır.
Bu bir soru tarzıdır dostlar.
Burada ilerlerseniz burası 2a ise şurası 180 eksi 2a eder mi?
Bu kenar bu kenara eşitse bunların taban açıları eşit değil midir?
O zaman bu açı bu açıya eşittir.
180 eksi 2a aynı zamanda buraya eşittir.
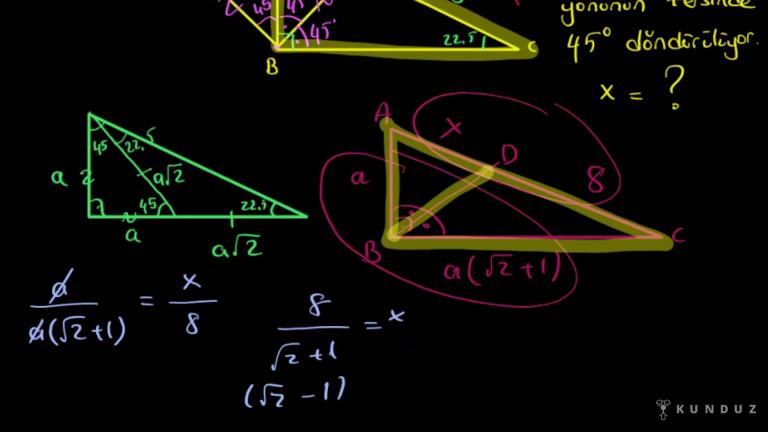
Tamam, şimdi bu soru tarzlarında dediğim gibi şurayı uzatmalısınız dostlar.
Şöyle şurayı uzattığını farz edin.
Tamam buraya uzatırsa 180 eksi 2a, a ile topladım, burası 180 eksi a etti.
180 olması için buraya kaç kaldı?
a kaldı.
a a 2a etti.
Şu 2a'yı götürdü.
Evet toplamda 180 kaldı.
Şimdi burada görmem gereken burada mis gibi bir dış açıortayı yakaladık dostlar.
Aslında buradaki işlemlerin hepsi şuradaki dış açıortaylığı görmek içindi.
Yani burada gizlemişler.
Bu bir gizlenmiş sorudur dostlar.
Yani şuradaki işlemlerin şu anda yapacakları için hiçbir önemi kalmadı.
Sıraları siliyor çünkü ben dış açıortay olduğunu bilmiyordum ama araştırarak buldum.
Demek ki bunu kullanmalıyız.
Bunu kullanacağım.
Nasıl kullanacağım?
Bu dış açıortay şu gördüğünüz ACD üçgenine aittir.
O zaman yapacağım kural şu şekilde olacaktır.
12 bölü 12 artı 4 on altı eşittir x bölü 4, x bölü 4.
O zaman 16'yı dörde bölelim, 12'yi dörde bölelim, x eşittir 3 buluruz.
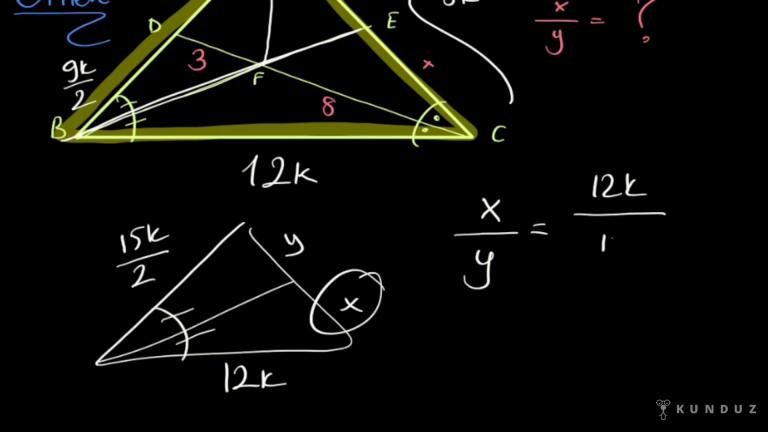
Evet, diğer sorumuzda yine bir üçgen verdim.
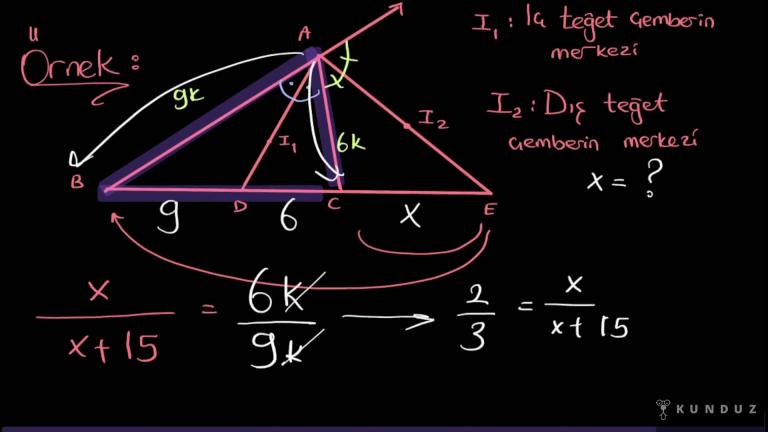
ABE üçgenin hem dış açıortayı hem de iç açıortayı çizdim aynı köşeye ait.
Şimdi burada CD 2, DE 7, BC x olarak verdim.
Siz soruyorum hadi x'i bulalım.
Şimdi burada x'i bulmamızın yolu nedir?
Şimdi burada dış açıortayı, iç açıortayı nasıl kullanmalıyız?
Bu açılara harfler verip a, a, b, b deyip bu ikisini toplayıp 180'e eşitleyip buranın 90 derece olduğunu bilmek midir?
Çözüm yolu burada değil.
Burası rahat.
Neden rahat?
Şimdi şu üçgen içerisinde siz iç açıortay teoremi ile ikiye 2k k gelsin derseniz düzeltelim 2'ye 2k, o zaman 7'ye 7k gelsin dersiniz, istediğiniz gibi söylersiniz.
2'ye 2k gelsin diyorum.
O zaman 7'ye de 7k gelmeli.
Tamam şimdi iç açıortayı kullandım, ikinci şeyim ne?
Dış açıortayı kullanmak.
Dış açıortay da bu üçgene ait dostlar.
Şimdi o zaman kuralım nasıl olacak?
Burası böyle.
Burası yani BC bölü BE, x bölü x artı 2 artı 7.
x artı 9'a eşittir.
Şurada gördüğünüz oranlar 2 k bölü 7 k yapılmalı.
Dostlar burayı anlayabiliyorum, iki bölü yedi içler dışlar yapalım.
Burası 7x eder, şimdi ikiyle burayı çarpıyorum.
Şu köşeleri sadeleştirdim.
Göstereyim 2x artı on sekiz 5x eşittir on sekiz ise x eşittir on sekiz bölü beş ya da üç virgül altı.
Ne yazarsanız artık.
Şimdi üçüncü sorumuzdayız.
ABD üçgeni verdim.
İçeride bir AC parçası iki, AB parçası yedi, AD x uzunluğunda.
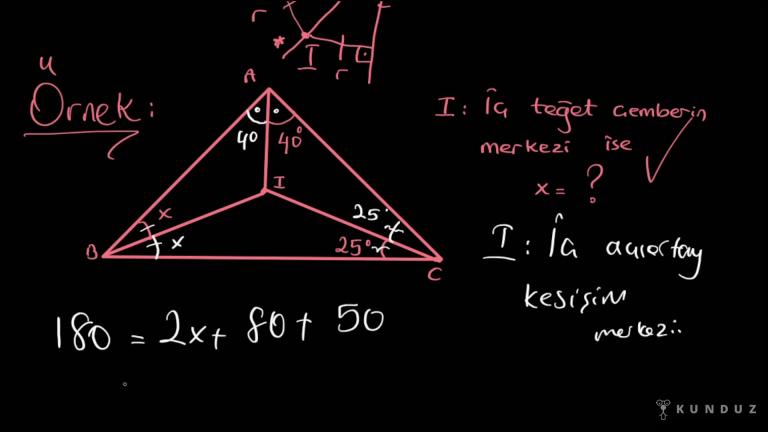
Bu açılar gördüğünüz gibi 60'ar derece.
Şimdi soru da tam tamamlanmamış gibi.
Burası 60, burası 60.
Burası kaç hesaplayamıyor muyuz?
Hesaplarız tabii ki de burası da 60 derece.
Şimdi gizlemeye çalışmış biraz ama açıkta kalmış biraz.
60, 60, 60.
Şimdi şöyle baksam iç açıortay görüyorum.
Şöyle baksam dış açıortay görüyorum.
İç açıortay ama iç açıortay bu üçgen için dış açıortay.
Bu üçgen için arkadaşlar şimdi soruda bakalım şimdi iç açıortaylığı bir kullanalım.
Şurada ABD üçgeninde büyük üçgende iç açıortay var.
O zaman hatta şöyle gösterelim şu üçgende iç açıortay var.
İç açıortay dediğim de şurası.
O zaman 7'ye 7 k gelirse diyelim x'e ne gelir?
xk gelir bunu diyebilirim.
7'ye 7k gelsin o zaman x'e de xk gelir diyoruz.
Tamam şimdi şurayı temizleyelim, rahatça ilerleyelim.
Şuraları verdim şimdi ikinci olarak dış açıortayı kullanmam lazım.
Dış açı ortay da şu üçgene ait.
ABC'de A açısının dışına ait bir dış açıortay çizmiştim.
O da buymuş.
Bunun formülünü nasıl yapardım peki?
Şu noktayı alıyorduk, şu şekil aklınızda kalsın diye sürekli oklarla gösteriyorum.
Buradaki işlemi yapınca da şu bölü şu eşittir 2 bölü 7 diyecektim.
Yani xk bölü xk artı 7 k.
K parantezine alsam x artı 7 k etmeyecek mi?
Tamamı x artı 7 k.
Tamam eşittir bölü ne diyecektim?
2 bölü yedi, iki bölü yedi dedik ve burada k'ler sadeleşti, şurada içler dışlar yapıyorum.
Yedi tane X eşittir 2x artı 14.
5 tane X eşittir 14 ise x dediğim şey 14 bölü 5 ya da iki bölü 8 olarak elde edilir dostlar.
ACB açısı 2a, BAC açısı a kadar.
BC on iki uzunluğunda, AD eşittir CD eşittir 4 uzunluğunda.
AC uzunluğunu istiyorum.
Şimdi burada açıortay anlatıyorum da bu verdiklerinde bir açıortaylık yok.
Şimdi burada ne yapacağım peki?
2a'yı eşit bölecek şekilde yani burada a'ya a yapacak şekilde ilerlemeli miyim acaba?
Hayır.
Çünkü ben öyle yapsam bile yani şurada bir açıortaylık oluştursa bile burayı biliyor muyum?
Hayır.
Burayı biliyor muyum?
Hayır.
Burayı biliyor muyum?
Onu da hayır.
O zaman buradan ilerlememeliyim.
Demek ki bana bunu söylüyor bu yol.
Buraları temizliyorum.
E buradan gitmeyeceksem ne yapacağım şimdi?
Size şuradaki çizgiyi vermesinin bir sebebi vardır.
Bu bir soru tarzıdır dostlar.
Burada ilerlerseniz burası 2a ise şurası 180 eksi 2a eder mi?
Bu kenar bu kenara eşitse bunların taban açıları eşit değil midir?
O zaman bu açı bu açıya eşittir.
180 eksi 2a aynı zamanda buraya eşittir.
Tamam, şimdi bu soru tarzlarında dediğim gibi şurayı uzatmalısınız dostlar.
Şöyle şurayı uzattığını farz edin.
Tamam buraya uzatırsa 180 eksi 2a, a ile topladım, burası 180 eksi a etti.
180 olması için buraya kaç kaldı?
a kaldı.
a a 2a etti.
Şu 2a'yı götürdü.
Evet toplamda 180 kaldı.
Şimdi burada görmem gereken burada mis gibi bir dış açıortayı yakaladık dostlar.
Aslında buradaki işlemlerin hepsi şuradaki dış açıortaylığı görmek içindi.
Yani burada gizlemişler.
Bu bir gizlenmiş sorudur dostlar.
Yani şuradaki işlemlerin şu anda yapacakları için hiçbir önemi kalmadı.
Sıraları siliyor çünkü ben dış açıortay olduğunu bilmiyordum ama araştırarak buldum.
Demek ki bunu kullanmalıyız.
Bunu kullanacağım.
Nasıl kullanacağım?
Bu dış açıortay şu gördüğünüz ACD üçgenine aittir.
O zaman yapacağım kural şu şekilde olacaktır.
12 bölü 12 artı 4 on altı eşittir x bölü 4, x bölü 4.
O zaman 16'yı dörde bölelim, 12'yi dörde bölelim, x eşittir 3 buluruz.
Evet, diğer sorumuzda yine bir üçgen verdim.
ABE üçgenin hem dış açıortayı hem de iç açıortayı çizdim aynı köşeye ait.
Şimdi burada CD 2, DE 7, BC x olarak verdim.
Siz soruyorum hadi x'i bulalım.
Şimdi burada x'i bulmamızın yolu nedir?
Şimdi burada dış açıortayı, iç açıortayı nasıl kullanmalıyız?
Bu açılara harfler verip a, a, b, b deyip bu ikisini toplayıp 180'e eşitleyip buranın 90 derece olduğunu bilmek midir?
Çözüm yolu burada değil.
Burası rahat.
Neden rahat?
Şimdi şu üçgen içerisinde siz iç açıortay teoremi ile ikiye 2k k gelsin derseniz düzeltelim 2'ye 2k, o zaman 7'ye 7k gelsin dersiniz, istediğiniz gibi söylersiniz.
2'ye 2k gelsin diyorum.
O zaman 7'ye de 7k gelmeli.
Tamam şimdi iç açıortayı kullandım, ikinci şeyim ne?
Dış açıortayı kullanmak.
Dış açıortay da bu üçgene ait dostlar.
Şimdi o zaman kuralım nasıl olacak?
Burası böyle.
Burası yani BC bölü BE, x bölü x artı 2 artı 7.
x artı 9'a eşittir.
Şurada gördüğünüz oranlar 2 k bölü 7 k yapılmalı.
Dostlar burayı anlayabiliyorum, iki bölü yedi içler dışlar yapalım.
Burası 7x eder, şimdi ikiyle burayı çarpıyorum.
Şu köşeleri sadeleştirdim.
Göstereyim 2x artı on sekiz 5x eşittir on sekiz ise x eşittir on sekiz bölü beş ya da üç virgül altı.
Ne yazarsanız artık.
Şimdi üçüncü sorumuzdayız.
ABD üçgeni verdim.
İçeride bir AC parçası iki, AB parçası yedi, AD x uzunluğunda.
Bu açılar gördüğünüz gibi 60'ar derece.
Şimdi soru da tam tamamlanmamış gibi.
Burası 60, burası 60.
Burası kaç hesaplayamıyor muyuz?
Hesaplarız tabii ki de burası da 60 derece.
Şimdi gizlemeye çalışmış biraz ama açıkta kalmış biraz.
60, 60, 60.
Şimdi şöyle baksam iç açıortay görüyorum.
Şöyle baksam dış açıortay görüyorum.
İç açıortay ama iç açıortay bu üçgen için dış açıortay.
Bu üçgen için arkadaşlar şimdi soruda bakalım şimdi iç açıortaylığı bir kullanalım.
Şurada ABD üçgeninde büyük üçgende iç açıortay var.
O zaman hatta şöyle gösterelim şu üçgende iç açıortay var.
İç açıortay dediğim de şurası.
O zaman 7'ye 7 k gelirse diyelim x'e ne gelir?
xk gelir bunu diyebilirim.
7'ye 7k gelsin o zaman x'e de xk gelir diyoruz.
Tamam şimdi şurayı temizleyelim, rahatça ilerleyelim.
Şuraları verdim şimdi ikinci olarak dış açıortayı kullanmam lazım.
Dış açı ortay da şu üçgene ait.
ABC'de A açısının dışına ait bir dış açıortay çizmiştim.
O da buymuş.
Bunun formülünü nasıl yapardım peki?
Şu noktayı alıyorduk, şu şekil aklınızda kalsın diye sürekli oklarla gösteriyorum.
Buradaki işlemi yapınca da şu bölü şu eşittir 2 bölü 7 diyecektim.
Yani xk bölü xk artı 7 k.
K parantezine alsam x artı 7 k etmeyecek mi?
Tamamı x artı 7 k.
Tamam eşittir bölü ne diyecektim?
2 bölü yedi, iki bölü yedi dedik ve burada k'ler sadeleşti, şurada içler dışlar yapıyorum.
Yedi tane X eşittir 2x artı 14.
5 tane X eşittir 14 ise x dediğim şey 14 bölü 5 ya da iki bölü 8 olarak elde edilir dostlar.