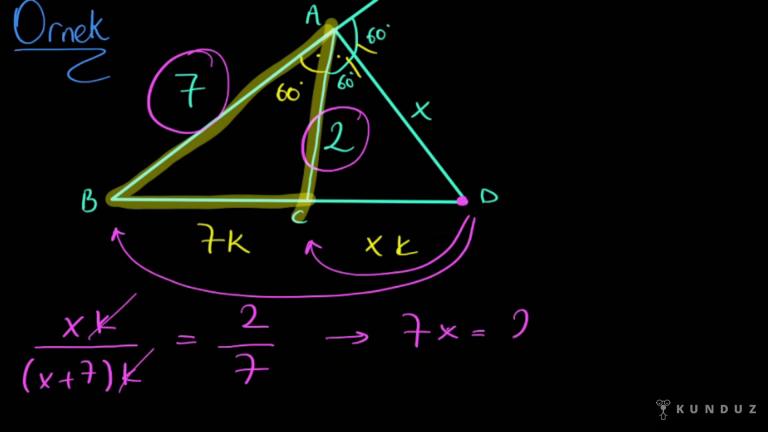Merhabalar, dış açıortay konusundayız.
İç açıortay bir üçgenin iç açısını eşit bölerek oluşuyorsa dış açıortay da dış açısını eşit bölerek oluşur.
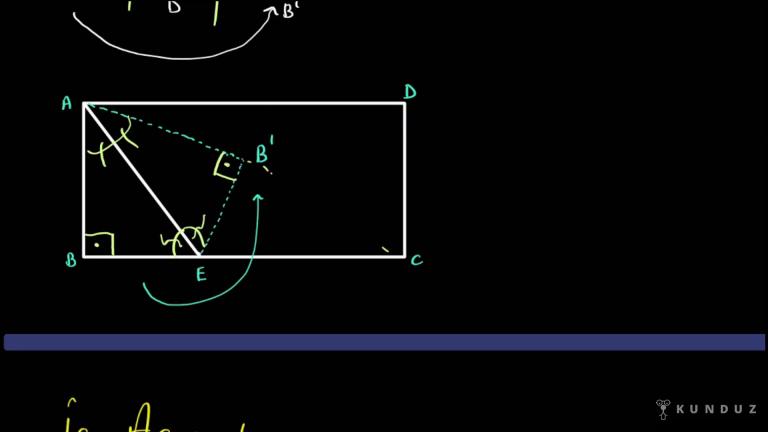
Arkadaşlar ABC üçgenini görüyorsunuz.
A köşesinin dış açı ortayını çiziyorum ve bunu ortalayacak şekilde çıkacak ışınım A köşesine ait dış açı ortayım oluyor.
Yine aynı şekilde C'yi uzatın dış açıortay içi ortalayacak şekilde ışın yapıştırın.
Bu gördüğünüz C'ye ait dış açıortay demektir.
Aynı şekilde B'ye de yapabilirsiniz.
Tabiki de şimdi iç açıortay da iç teğet çemberin merkezini anlattık.
Şimdi sıra dış teğet çemberin merkezini anlatmakta.
Bir üçgenin iki tane dış açıortayı bir noktada kesişir.
Bu nokta aynı zamanda dış teğet çemberin merkezi olmaktadır.
Gördüğünüz gibi dış teğet dememin sebebi çember dışarıda ve kenarlara direkt ya da dolaylı olarak teğet yani BC kenarına direk teğet.
Gördüğünüz gibi teğet noktamız burası.
AB ya da BC kenarına dokunmuyor ama bunların uzantılarına da teğet işte.
Dış teğet çemberin merkezi dediğimiz yer de I noktası oluyor ve bu nokta bir dış açıortay için çok özel bir noktadır.
Çünkü iki tane dış açı ortayım bu noktada kesişmektedir.
Yani B'den ve C'den çıkartacağım dış açı ortaylar I noktasında kesişecektir arkadaşlar.
Yani bana soru da dış çemberin merkezi verilirse ben oradan bir açıortay elde edebilirim diye düşünüyorum.
B noktası, B köşesi ve merkezini birleştirir.
Buradan bir dış açıortay C ve I'yı birleştirir.
Ama aynı şekilde buradan da bir başka dış açıortay elde edebileceğimi bilmem gerekir.
Peki dış açıortay teoremi nedir?
Dış açıortay teoremi.
Burada gördüğünüz gibi ABC üçgeninin A köşesinin dış açıortayını çiziyorum.
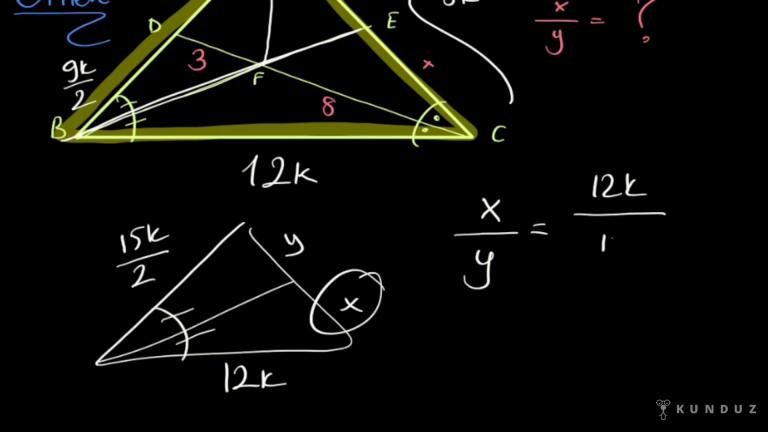
Burada kalan parça x, y ve c olarak isimlendiriliyor.
Buradaki kuralımız şudur x bölü x artı y eşittir b bölü c kural bu kadar.
Yine teorem falan deyip de havalı kelimelerime takılmayın benzerliktir bu işin aslı arkadaşlar.
Açıların eşit bölünmesi bize benzer olabilecek üçgenler yaratmaktadır.
O yüzden özel durumdur ve iç açıortayıydı.
Açıortay diye kurallar, konular anlatıyoruz sizlere.
Peki bu nereden geliyor arkadaşlar hemen onu gösterelim.
Kalemimizi aldık diyor ki şimdi bu kuralı ispatla diyoruz değil mi?
A'nın dış açıortayını çizdim.
Diyorum ki bu teorem nereden geldi?
Bu terimi bulabilmek için arkadaşlar c köşesinden AB'ye bir paralel çiziyoruz.
C köşesinden AB'ye bir paralel çizersem buna benzerdir.
Tamam şu paralelliği gösteriyorum.
Sonra dedim ki madem burada paralellik var, şurada benim bildiğim bir z kuralı var.
Nedir bu Z kuralı arkadaşlar?
İç ters açılar yani buradaki açı alfaysa iç ters açılardan burası da alfa olur.
Burası zaten alfa olarak verilmiş.
Şimdi şu üçgene bakmanızı istiyorum.
Bu üçgende iki tane iki tane eş açım var.
O zaman kesinlikle burada bir ikizkenarlık vardır.
Tabanları eşitse bu iki kenarlar eşittir arkadaşlar.
Yani şuraya da harf verirsek, k dersek CK eşittir CA olur arkadaşlar.
Yani şuranın uzunluğunu b yazabilirim, CK eşittir CA eşittir b yazdık arkadaşlar.
Şimdi paralelliği kullanmamız bitmedi arkadaşlar.
Şöyle şöyle şu üçgene bakmanızı istiyorum.
Şuraya da dahil edebilirim.
Tekrar çizeyim şurayı rahat görelim.
Şöyle şöyle bir üçgenim var.
Dedim ki C noktası buradaydı.
Buradan diğer kenara bir paralel çizdim.
Ben tekrar harflerimi veriyorum ki rahatça görebilirim arkadaşlar.
KCB.
Burası C uzunluğunda.
Burasını B buldum.
KC'yi CA'ya eşit B buldum onu da yazdım.
X ve Y burada paralellik varsa istediğin benzerliği yazabilir miyim?
Artık yazabilirim.
Nedir?
x bölü x artı y eşittir b bölü C.
Üstte anlattığım kuralın ispatını yaptık arkadaşlar, nereden geldiğini bilin diye diyorum.
Yani mesele bundan ibaret.
Bir örnekle devam edelim.
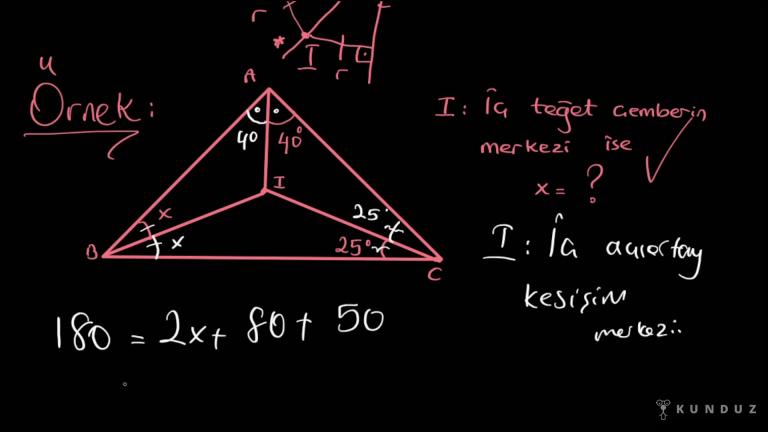
Mesela şimdi ABC üçgeni verilsin.
ABC üçgeni için I1 iç t çemberin merkezi.
I2 dış teğet çemberin merkezi olarak verilsin.
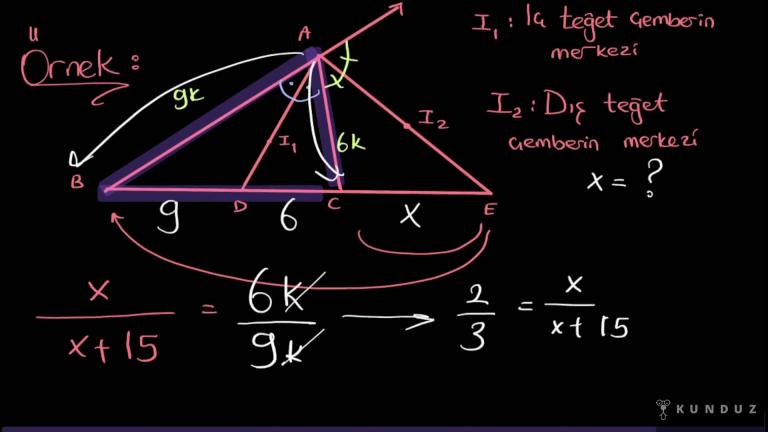
9, 6 ve x uzunlukları da verilsin, x'in ne kadar olduğu sorulsun.
Şimdi bana iç teğet çemberi ve dış teğet çemberin merkezini boşuna vermediler.
Şimdi bunlar ne demekti?
Bana açıortayla alakalı hiçbir bilgi vermemiş ama dolaylı olarak vermiş.
Aslında I1 dediğim şey iç teğet çemberin merkezi ise iç açıortayların kesişim merkezidir.
Yani ben A ve I1'i birleştirdiğimiz zaman oluşacak bir açıortay olduğunu bilmeli.
Aynı şekilde ı2.
ı2 dediğim de demek ki 2 tane de dış açıortayın kesişim merkezidir.
Yani ben buradan a köşesinden ı2 birleştirirsem buradan bir dış açıortay geleceğini bilmeli idim.
Ya da C'yi birleştirirseydiniz burada da oluşacak şey bir dış açıortay olacaktı arkadaşlar.
Yani buralara harf vermeme gerek yok.
Birinin iç açıortay, birinin dış açıortay olduğunu görüyorum ABC üçgeni için.
Tamam şimdi bana verilenler kullanayım bana uzunluk vermiş uzunluk soruyor.
Demek ki uzunlukta işlemler yapacağım iç açıortay dış açıortayı da gördüm.
Demek ki bunların teoremlerini kullanarak sonuca ulaşacak.
Şimdi buradaki sözlü anlatımlarıma ilerlemek istiyorum.
Ne diyelim?
6'ya 6k gelirse 9'a 9k gelir.
Ne yaptın peki hocam?
Şöyle ABC üçgenini aldım.
Dedim ki ABC üçgeninde iç açıortay var.
O zaman diyeceğim ki tabandaki oran kenardaki oranlara yansır.
Yani altıya altı k derseniz dokuza da dokuz k gelir diyebilirsiniz.
Mesele bundan ibaret.
Bunu yaptım, bunu göstermeye çalıştım.
Şimdi bunu kullandık da dışaçıortayı kullanmadık, hemen kullanalım, kalemimizi alıyoruz, dış açıortay teoremini yazıyorum.
x bölü alt tabanın hepsi x artı 15 eşittir.
Geldim buraya yine kalemi değiştirelim.
Şurası bölü şurası şöyle tekrar okları gösteririm yani 6 k bölü 9 k.
Bunu yazıyorum arkadaşlar.
6 k bölü 9 k sadeleşir, k'ler zaten gitti.
6 bölü 9, 2 bölü 3 tür.
Bölü x artı 15.
Buradan sadeleştirme yapalım, içler dışlar yapıyoruz, 2 x artı 30 eşittir 3 x.
X eşittir 30 çıktı arkadaşlar bundan ibaret.
İç açıortay bir üçgenin iç açısını eşit bölerek oluşuyorsa dış açıortay da dış açısını eşit bölerek oluşur.
Arkadaşlar ABC üçgenini görüyorsunuz.
A köşesinin dış açı ortayını çiziyorum ve bunu ortalayacak şekilde çıkacak ışınım A köşesine ait dış açı ortayım oluyor.
Yine aynı şekilde C'yi uzatın dış açıortay içi ortalayacak şekilde ışın yapıştırın.
Bu gördüğünüz C'ye ait dış açıortay demektir.
Aynı şekilde B'ye de yapabilirsiniz.
Tabiki de şimdi iç açıortay da iç teğet çemberin merkezini anlattık.
Şimdi sıra dış teğet çemberin merkezini anlatmakta.
Bir üçgenin iki tane dış açıortayı bir noktada kesişir.
Bu nokta aynı zamanda dış teğet çemberin merkezi olmaktadır.
Gördüğünüz gibi dış teğet dememin sebebi çember dışarıda ve kenarlara direkt ya da dolaylı olarak teğet yani BC kenarına direk teğet.
Gördüğünüz gibi teğet noktamız burası.
AB ya da BC kenarına dokunmuyor ama bunların uzantılarına da teğet işte.
Dış teğet çemberin merkezi dediğimiz yer de I noktası oluyor ve bu nokta bir dış açıortay için çok özel bir noktadır.
Çünkü iki tane dış açı ortayım bu noktada kesişmektedir.
Yani B'den ve C'den çıkartacağım dış açı ortaylar I noktasında kesişecektir arkadaşlar.
Yani bana soru da dış çemberin merkezi verilirse ben oradan bir açıortay elde edebilirim diye düşünüyorum.
B noktası, B köşesi ve merkezini birleştirir.
Buradan bir dış açıortay C ve I'yı birleştirir.
Ama aynı şekilde buradan da bir başka dış açıortay elde edebileceğimi bilmem gerekir.
Peki dış açıortay teoremi nedir?
Dış açıortay teoremi.
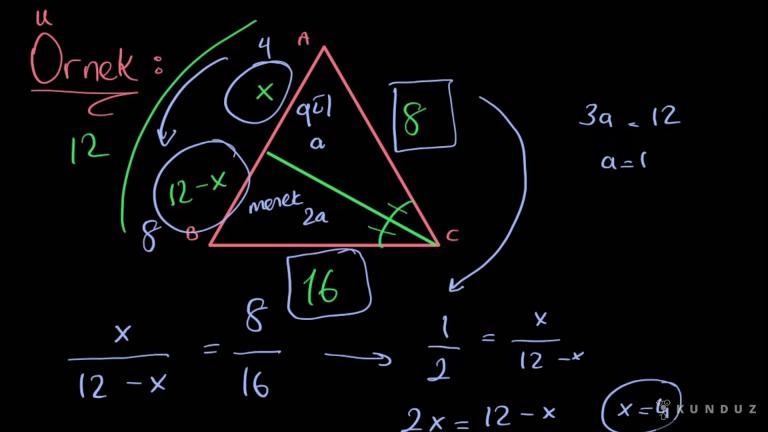
Burada gördüğünüz gibi ABC üçgeninin A köşesinin dış açıortayını çiziyorum.
Burada kalan parça x, y ve c olarak isimlendiriliyor.
Buradaki kuralımız şudur x bölü x artı y eşittir b bölü c kural bu kadar.
Yine teorem falan deyip de havalı kelimelerime takılmayın benzerliktir bu işin aslı arkadaşlar.
Açıların eşit bölünmesi bize benzer olabilecek üçgenler yaratmaktadır.
O yüzden özel durumdur ve iç açıortayıydı.
Açıortay diye kurallar, konular anlatıyoruz sizlere.
Peki bu nereden geliyor arkadaşlar hemen onu gösterelim.
Kalemimizi aldık diyor ki şimdi bu kuralı ispatla diyoruz değil mi?
A'nın dış açıortayını çizdim.
Diyorum ki bu teorem nereden geldi?
Bu terimi bulabilmek için arkadaşlar c köşesinden AB'ye bir paralel çiziyoruz.
C köşesinden AB'ye bir paralel çizersem buna benzerdir.
Tamam şu paralelliği gösteriyorum.
Sonra dedim ki madem burada paralellik var, şurada benim bildiğim bir z kuralı var.
Nedir bu Z kuralı arkadaşlar?
İç ters açılar yani buradaki açı alfaysa iç ters açılardan burası da alfa olur.
Burası zaten alfa olarak verilmiş.
Şimdi şu üçgene bakmanızı istiyorum.
Bu üçgende iki tane iki tane eş açım var.
O zaman kesinlikle burada bir ikizkenarlık vardır.
Tabanları eşitse bu iki kenarlar eşittir arkadaşlar.
Yani şuraya da harf verirsek, k dersek CK eşittir CA olur arkadaşlar.
Yani şuranın uzunluğunu b yazabilirim, CK eşittir CA eşittir b yazdık arkadaşlar.
Şimdi paralelliği kullanmamız bitmedi arkadaşlar.
Şöyle şöyle şu üçgene bakmanızı istiyorum.
Şuraya da dahil edebilirim.
Tekrar çizeyim şurayı rahat görelim.
Şöyle şöyle bir üçgenim var.
Dedim ki C noktası buradaydı.
Buradan diğer kenara bir paralel çizdim.
Ben tekrar harflerimi veriyorum ki rahatça görebilirim arkadaşlar.
KCB.
Burası C uzunluğunda.
Burasını B buldum.
KC'yi CA'ya eşit B buldum onu da yazdım.
X ve Y burada paralellik varsa istediğin benzerliği yazabilir miyim?
Artık yazabilirim.
Nedir?
x bölü x artı y eşittir b bölü C.
Üstte anlattığım kuralın ispatını yaptık arkadaşlar, nereden geldiğini bilin diye diyorum.
Yani mesele bundan ibaret.
Bir örnekle devam edelim.
Mesela şimdi ABC üçgeni verilsin.
ABC üçgeni için I1 iç t çemberin merkezi.
I2 dış teğet çemberin merkezi olarak verilsin.
9, 6 ve x uzunlukları da verilsin, x'in ne kadar olduğu sorulsun.
Şimdi bana iç teğet çemberi ve dış teğet çemberin merkezini boşuna vermediler.
Şimdi bunlar ne demekti?
Bana açıortayla alakalı hiçbir bilgi vermemiş ama dolaylı olarak vermiş.
Aslında I1 dediğim şey iç teğet çemberin merkezi ise iç açıortayların kesişim merkezidir.
Yani ben A ve I1'i birleştirdiğimiz zaman oluşacak bir açıortay olduğunu bilmeli.
Aynı şekilde ı2.
ı2 dediğim de demek ki 2 tane de dış açıortayın kesişim merkezidir.
Yani ben buradan a köşesinden ı2 birleştirirsem buradan bir dış açıortay geleceğini bilmeli idim.
Ya da C'yi birleştirirseydiniz burada da oluşacak şey bir dış açıortay olacaktı arkadaşlar.
Yani buralara harf vermeme gerek yok.
Birinin iç açıortay, birinin dış açıortay olduğunu görüyorum ABC üçgeni için.
Tamam şimdi bana verilenler kullanayım bana uzunluk vermiş uzunluk soruyor.
Demek ki uzunlukta işlemler yapacağım iç açıortay dış açıortayı da gördüm.
Demek ki bunların teoremlerini kullanarak sonuca ulaşacak.
Şimdi buradaki sözlü anlatımlarıma ilerlemek istiyorum.
Ne diyelim?
6'ya 6k gelirse 9'a 9k gelir.
Ne yaptın peki hocam?
Şöyle ABC üçgenini aldım.
Dedim ki ABC üçgeninde iç açıortay var.
O zaman diyeceğim ki tabandaki oran kenardaki oranlara yansır.
Yani altıya altı k derseniz dokuza da dokuz k gelir diyebilirsiniz.
Mesele bundan ibaret.
Bunu yaptım, bunu göstermeye çalıştım.
Şimdi bunu kullandık da dışaçıortayı kullanmadık, hemen kullanalım, kalemimizi alıyoruz, dış açıortay teoremini yazıyorum.
x bölü alt tabanın hepsi x artı 15 eşittir.
Geldim buraya yine kalemi değiştirelim.
Şurası bölü şurası şöyle tekrar okları gösteririm yani 6 k bölü 9 k.
Bunu yazıyorum arkadaşlar.
6 k bölü 9 k sadeleşir, k'ler zaten gitti.
6 bölü 9, 2 bölü 3 tür.
Bölü x artı 15.
Buradan sadeleştirme yapalım, içler dışlar yapıyoruz, 2 x artı 30 eşittir 3 x.
X eşittir 30 çıktı arkadaşlar bundan ibaret.
Sıkça Sorulan Sorular
Dış açıortay teoremi nedir? Dış açıortay özellikleri nelerdir?