Üçgende İçaçıortay Giriş

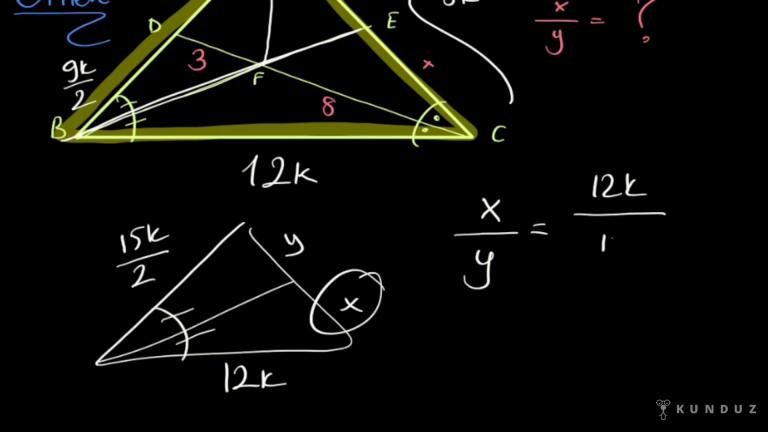
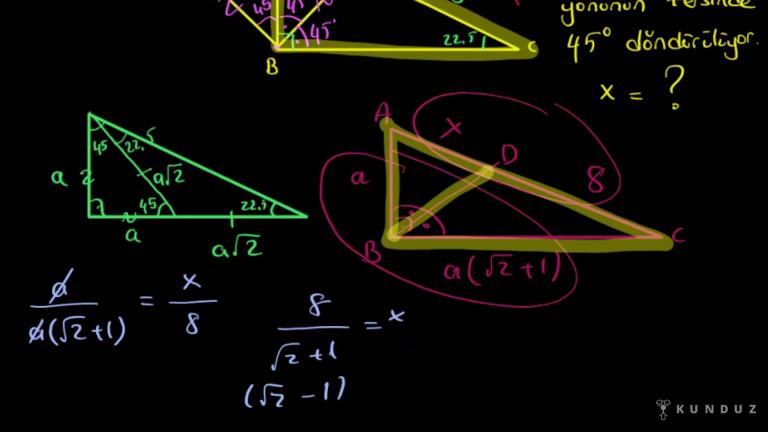
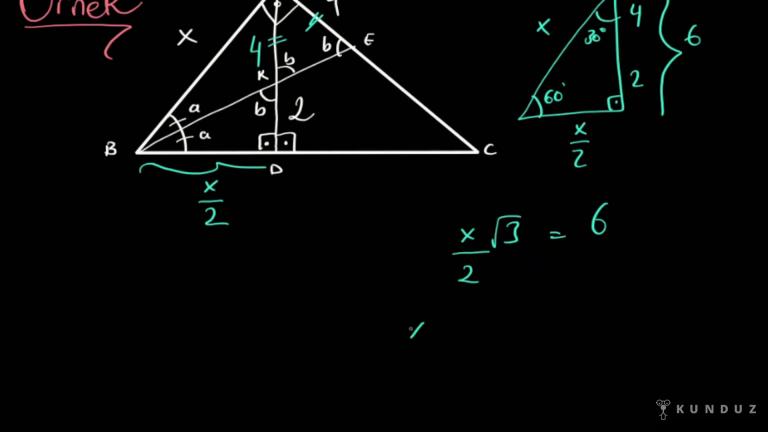
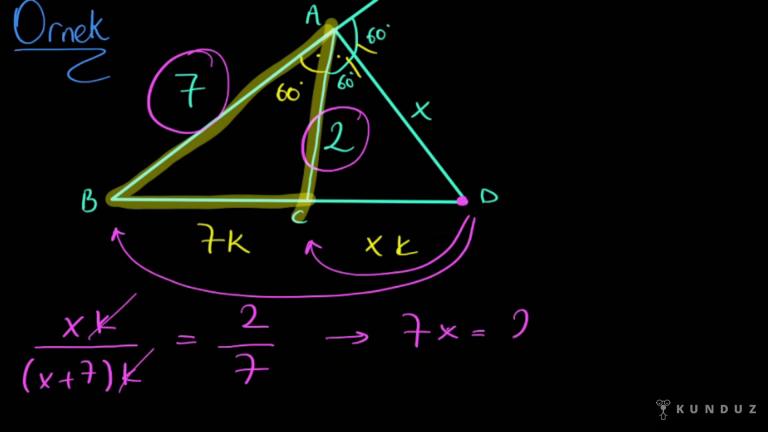Merhabalar üçgende açı ortay konumundayız, açı ortay dediğimiz adı üstünde bir açıyı İtalyan doğru doğru parçası veya içindir.
Yani burada gördüğünüz a b açısını ortalanan bu ışın OGC ışını yani bir açı ortay dir.
Arkadaşlar açımı çizdim, eşit bölecek şekilde ortadan belirledim ve şu köşeli birleştirip götürdüm.
İşte bu sizin açı ortağınız oluyor arkadaşlar.
Açı orta in tanımı basit.
Yani bu aşamada benzerliğin bu konuya katmış olduğu bir özellik var.
Ondan bahsetmek istiyorum.
Arkadaşlar nedir bu özellik?
Yine gördüğünüz gibi bir bir açı yaptım.
Dedim ki o şuralarda harp verelim o AB olsun açı ortay olacak şekilde C.
Yi çıkarttım.
Dedim ki bu açı orta üzerinde aldığınız bir nokta ve bu noktaları bu noktadan gördüğünüz bu kollara dik meler içerseniz kuralımız diyor ki bu indiğiniz dik nelerin uzunlukları birbirine eşittir.
Yani demek istediğim şu oralara da harp verelim de diyelim.
Ee diyelim.
Bu uzunlukları bir birine eşittir diyor.
Aynı zamanda diyor ki bu kolların, bu kolların uzunlukları da, bu parçaların uzunlukları da, kol parçaların uzunlukları da birbirine eşittir.
Yani o de eşittir, o ediyor.
Bir şuraya da hak verelim ke diyelim üstünden herhangi bir nokta aldınız ve bundan kollara dikmeleri indiğiniz istediğiniz yerden alabilirsiniz.
Arkadaşlar buradan aldığıma bakmayın.
Buradan mı aldınız?
Buradan dikin diniz bir buradan dikin.
Deniz iki kuralımız diyor ki burası buraya eşittir ve aynı zamanda buradan buraya.
Yani bu kol parçaları da birbirlerine eşittir.
Şimdi bu kuralımız neden var ve neden ben başta benzerlik ile alakalı dedim.
Şimdi burada açıları isimler vermek istiyorum.
Arkadaşlar şurada mesela göstermek istiyorum.
Yani neden buradan geldiğini anlatmak istiyorum.
Açımı çizdim.
Alfa halife olacak şekilde açık ortamı da yazdım.
Sonra dedim ki bir de nokta sağlıyorum ve bu dev noktasından kollarına dikmeleri iniyorum de noktasından indim.
B dedim de noktasından bu kola indim.
C noktası dedim.
Sonra dedim ki burada kalan açım alfa 90 ise burası kesinlikle 90 x sayfadır.
Alttaki üç gene bakıyorum 90 alfa.
O zaman burası da 90 x sayfadır.
Şimdi üstteki üç gene bakınız.
Yani ABD üçgenine bakınız.
Alfa 90 x alfa.
Yoksa alttaki üçgen yani arcade üçgenine bakınız.
Alfa doksan eksi alfa doksan iç açıları eşit ve eşit.
O zaman bu iki üçgende kesinlikle iç açılar eşit olduğu için benzerlik vardır diyebilir miyim?
Evet diyebilirim.
Peki bu iki üçgen de acaba 90 derecelik karşısı eşit uzunlukta mı?
Evet, çünkü aynı kenarı görüyorlar.
O zaman bir iç açıları karşılıklı eşit ve iki açıların gördüğü kenarlar karşılıklı olarak eşit olduğu için bu iki üçgen kesinlikle şu etkenlerdir.
Yani burada 90'nın karşısı adÄ, alttaki üçgen de 90'nı karşısı, adÄ, iç açıları eşit.
Ve aynı açı ölçüsünü gördü, kenar uzunlukları da eşit olduğu için bu üçgenler eşittir diyoruz.
O zaman Alfa'nın gördüğü kenar uzunlukları da eşittir diyeceğim ve 90 x Alfa'nın gördüğü kenar uzunlukları da eşit diyeceğim.
Kural bundan ibaretti.
Açı ortay doğru sundan ya da parçasından aynı noktadan yan kenarlara, o doğrulara inen yükseklikleri eşittir ve ayrılan bu kol parçaları da eşittir diyeceğim.
Yani Alpha'nın parçası burada kеrе kadarsa burada da 2'ye kadardır.
O yüzden bunlar eşit dedim.
Burada 90 eksi Alfa'nın karşısı m'ye kadarsa burada da 90 eksi Alfa'nın karşısı eşittir ve m'ye kadardır.
Benzerlikten geldiğinin kanıtı işte buradadır.
Arkadaşlar bunu bilirsek üstteki anlattığım şeyi zaten aklımızdan tutabiliriz.
Peki doğru olarak incelemeyi bırakıp ta kapalı bir şekil olan üçgen içerisine yerleştirilecek açı ortay ne olur acaba?
Üçgen de köşelere ait iki açı ortay çeşidi vardır.
Köşenin iç açısı iç açısını orta varsanız iç açı ortay dış açı orta ortalar masanızda dış açı orta elde edersiniz.
Burada unutmamanız istediğim bir nokta var katlama soruları.
Katlama sorularında bu şekli unutmayınız.
Burada gösterdim bu şekil gerçekten çok önemli.
Katlama soruları açı ortay oluşturur.
Ne demek istiyorum?
Siz bir açı yaptınız ve buradan ortadan bir açı ortay doğrusu olarak diyorsunuz ki bunun etrafından katlama yapınız harf verilen A, B, C, A-B-C üçgenin de şu gördüğünüz ABD üçgenini ade etrafında katlayın izliyor.
Buraya da göstermeye çalıştım.
Siz bu solda gördüğünüz şu üçgen den bahsediyorum.
Burayı katarsanız arkadaşlar katlama doğrusuyla yan olan bu komşu olan yerlerde açı ortay oluşur.
Yani burası bu açı kat açı ortay doğrusuyla yan açımı evet o zaman burada bir açı ortay oluşur.
Yani burası alfa ise burası da alfa olur.
Burası beta ise burası da beton olur.
Şunları farklı şeylerle gösterelim.
Burası beta, oysa burası da beta oldu.
Aynı şekilde iç tarafta da bundan bahsedebiliriz.
Yani burası TED.
Oysa burası da TED adır.
Neden?
Çünkü bunlar gördüğünüz gibi aç ortayla komşuya komşu.
Oysa burası TED.
Oysa bu tarafa da TED alacak.
Ben kutladım diye açım değişmeyecek.
Bu tarafta Alfa mı?
Bu tarafa da gelse alfa olacak.
Bu tarafta beta mı görüyorum?
Buraya gitse de beta olacak.
Ted mi gördüm?
Burada da TED olacak.
Kutladım diye açı değişmez.
Kutladım diye uzunluk da değişmez.
Ab uzunluğu burada ne ise burada da odur.
Ben katılıyorum.
Kısaltma yorumu yorum çekmiyorum.
Tamam mı?
Aynı şekilde burada beye de uzunlu burada neyse burada da odur.
Katmıyorum, değişmeyecek.
İşte bu şekli aklımıza oturtmamız lazım.
Yani burada çok düzgün çizdiğim için öyle aklınızda kalmasın.
Üçgen şöyle bir şey de olabilirdi.
Ben bunu katlar.
Nasıl olacak böyle bir şekil elde edeceğim.
Buna benzer bir şekil doğru mu?
Yani burada aklımda kalması gereken yer hop burası açı ortay oldu.
Hoop burada da gördüğünüz gibi açılar eşit bölündü.
Aynı şekilde şunları tekrardan farklı gösterelim, şöyle şöyle burada gördüğünüz ve burada gördüğünüz açılar da birbirine eşittir.
Bu gördüğüm uzunluk ne ise bu gördüğümüz aynıdır.
Bu gördüğüm ne ise bu gördüğüm de aynıdır.
Açı ortay konusunda bunu göstermek istiyorum.
Bazı soru tarzları bunun üzerine gelişmiştir.
Mesela şöyle ilerleyelim.
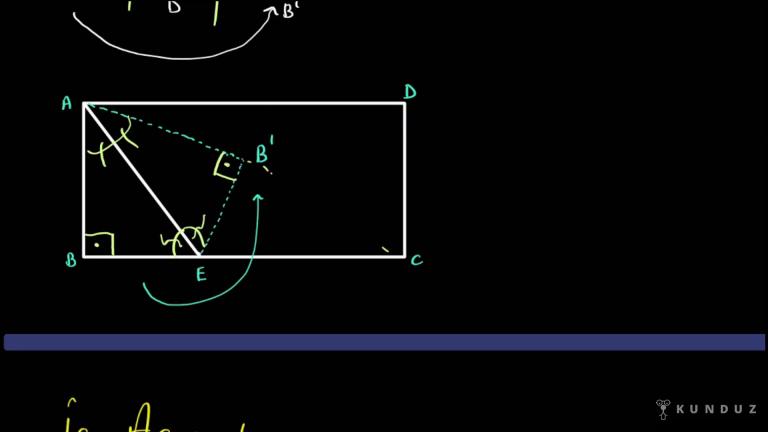
Üçgen içerisinde bir kenarı bir verilen doğru parçası etrafında katlama soruları mesela.
Böyle sorular gelebiliyor.
Böyle sorularda ne yapacağım?
Katlama doğrusu burası mı?
Evet, o zaman burada ben bir açı ortay oluşmuş mesela bunu yazmam lazım.
Burası Alfa mıydı?
Evet kutladım.
Buraya geldi.
Alfa değişecek mi?
Hayır.
İşte o zaman bu A ve B yüzü üçgeninde A, B, B üstü şöyle göstereyim.
Hatta kötü gösterdik.
Şöyle şöyle, şöyle bu üçgen içerisinde bir açı ortay yarattık.
Gördüğünüz gibi aynı düşünceyle burası ve burası da açı ortay olmadı mı arkadaşlar?
Açı ortay demeyelim de buna yani eşit derecede oldu demeyelim.
Burası ve burası birbirine eşit oldu.
Peki burada aynı derecede buraya gelecek arkadaşlar?
B Üstündeki açı b.
Köşesindeki açıya eşit olacak katladığını bir uzunluk değişti mi?
Hayır.
Katladığını diye uzunluk değişti mi?
Hayır.
Alt taraflarda eşittir.
Yani burada işte şurada gördüğünüz açı ortay bize bazı yardımlarda bulunacaktır.
Soruyu çözerken ya da dikdörtgen içerisinde yer alan kaplama soruları da olabiliyor.
Burada da açı ortay oluşabiliyor arkadaşlar.
Neden bahsediyorum?
Şu gördüğünüz üçgeni AB'ye üçgenini ay etrafında katlayın diyorlar.
Yani böyle bir patlamadan bahsediyoruz.
Bu köşe köşedeki açım değişecek mi?
Hayır.
B deki ne ise B isimdeki de o şurada gördüğünüz açı değişecek mi?
Hayır.
Hop aynı açın buraya da gelecek.
Buradaki açım değişecek mi peki?
Hayır.
Buradaki ölçüm ne ise burada karşımda olacak.
Yani şuraya uzatmış olsaydım, mesela şuraya gelseydi şu gördüğünüz üçgen de bir açı ortay görecektik biz.
Yani Şûra'nın uzatıldığını varsayın.
Yani şurada gördüğünüz açı ortayı soru içerisinde kullanabilir dedik.
Misal olarak gösterdim sadece bunu yani.
Aç Ortaç'ın nasıl, nerelerde, ne gibi soru tarzlarında kullanıldığını görmeniz açısından açıklıyorum.
Böyle soru tarzlarında işleyeceğiz birazdan.
Yani bu tarz sorular uzunluk soruları da olabilir.
Açı sorusu da olabilir.
Aklımız da aç.
Ortaya nasıl bir durum yarattığını tutmamız gerekiyor.
Bilgilendirmek için ekledim bunları.
Soru çözümünde de göstereceğim zaten arkadaşlar.