Application of derivatives Questions and Answers

Calculus
Application of derivativesFind the θ value within [0, 2π) for function f(θ) = 9 sin(10 θ) to reach its maximum value.
θ =?

Calculus
Application of derivativesThe cost, in dollars, to produce a vats of ice cream is C(x) = 9x + 14. When selling them to ice cream shops, the price-demand function, in dollars per vat, is p(x) = 87 - 3x
Find the profit function.
P(x) =
How many vats of ice cream need to be sold maximize the profit.
Find the maximum profit.
Find the price to charge per vat to maximize profit.

Calculus
Application of derivativesFind the θ value within [0, 2π) for function f(θ) = 9 sin(10θ) to reach its maximum value.
θ =


Calculus
Application of derivativesIn Exercises 57-62, write the slope-intercept equations of the lines through the given point (a) parallel to the given line and (b) perpendicular to the given line.
Point
57. (2, 1)
62. (-4,1)
Line
4x - 2y = 3
x+y=7
y +2=0

Calculus
Application of derivativesA true-false test consists of 16 questions.
a) In how many ways can the test be completed, selecting true or false for each question?
b) What is the probability that a test is randomly answered perfectly?
a) In how many ways can the test be completed, selecting true or false for each question?
The test can be completed in ways.
(Type a whole number.)
b) What is the probability that a test is randomly answered perfectly?
The probability is
(Type an integer or a simplified fraction.)

Calculus
Application of derivativesSuppose E and F are events such that n(E) = 12, n(F) = 16, and n(ENF) = 3.
a) Find P(EIF).
b) Find P(FIE).
a) P(EIF) =
b) P(FIE) =
(Type an integer or a simplified fraction.)
(Type an integer or a simplified fraction.)

Calculus
Application of derivativesComplete the parametric equations for the line where the planes -2x-4y-4z=-8 and -15x-y-10z=-29 intersect.
x(t) = 36t:
y(t) = _______________________
z(t) = _______________________
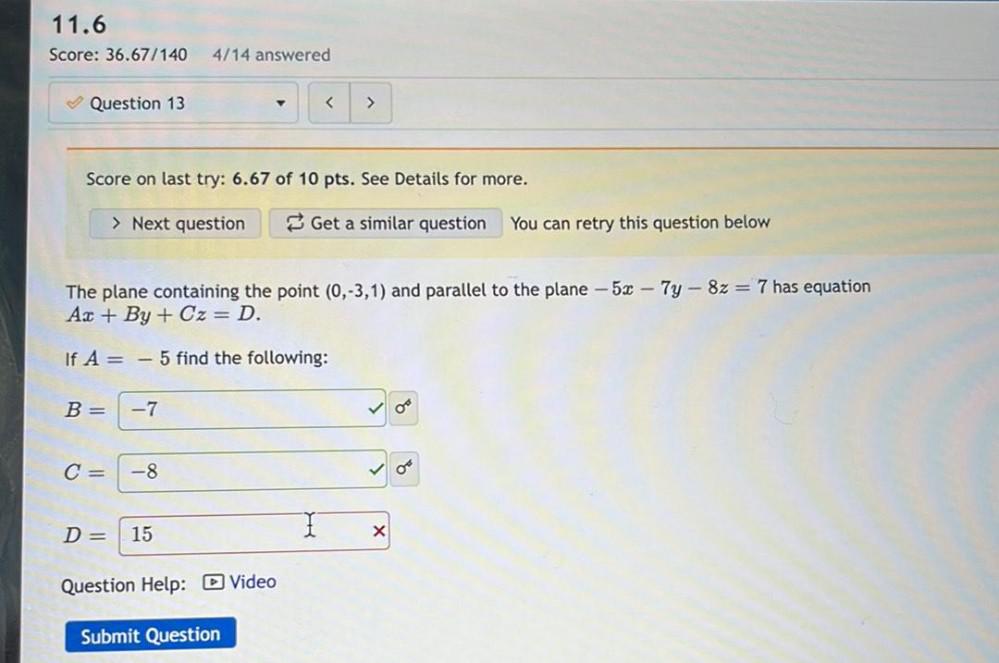
Calculus
Application of derivativesThe plane containing the point (0,-3,1) and parallel to the plane
-5x-7y-8z=7 has equation Ax+By+Cz= D.
If A=-5 find the following:
B = -7
C=-8
D=15

Calculus
Application of derivativesIndicate whether the table specifies a function.
Domain Range
- 14 4
-11 -11
17 2
-3 15
The table is a function.
The table is not a function.
![1)Find the slope of the secant line for the function f(x) = (-1/2)(x²-3x - 10) passing through (1, 6) and (4,3).
2). Find the average rate of change off(x) = x² over the interval [-1,1].](https://media.kunduz.com/media/sug-question/raw/82123073-1660035154.959921.jpeg?w=256)
Calculus
Application of derivatives1)Find the slope of the secant line for the function f(x) = (-1/2)(x²-3x - 10) passing through (1, 6) and (4,3).
2). Find the average rate of change off(x) = x² over the interval [-1,1].


Calculus
Application of derivativesWrite the first three terms in the binomial expansion, expressing the result in simplified form.
(3x+2y)7

Calculus
Application of derivativesFind the center, foci, and vertices of the ellipse. Graph the equation.
4x²+36y²-24x+288y +468 = 0

Calculus
Application of derivativesIn an experiment on social interaction, 6 people will sit in 6 seats in a row. In how many ways can this be done?
There are ___ ways.

Calculus
Application of derivativesCharles and Bernice ("Ray") Eames were American designers who made major contributions to modern architecture and furniture design. Suppose that a manufacturer wants to make an Eames elliptical coffee table 78 in long and 62 in wide out of an 8 ft by 4 ft piece of birch plywood. If the center of a piece of plywood is positioned at (0, 0), determine the distance from the center at which the foci should be located to draw the ellipse. Express numbers in exact, simplest form.

Calculus
Application of derivativesOf the entering class at a college, 69% attended public high school, 25% attended private high school, and 6% were home schooled. Of those who attended public high school, 19% made the Dean's list, 18% of those who attended private high school made the Dean's list, and 17% of those who were home schooled made the Dean's list. A student is randomly chosen.
a) Find the probability that the student made the Dean's list.
b) Find the probability that the student came from a public high school, given that the student made the Dean's list.
c) Find the probability that the student was not home schooled, given that the student did not make the Dean's list.
a) The probability that the student made the Dean's list is ___
(Do not round until the final answer: Then round to four decimal places as needed.)
b) The probability that the student came from a public high school, given that the student made the Dean's list, is ___
(Do not round until the final answer. Then round to four decimal places as needed.)
c) The probability that the student was not home schooled, given that the student did not make the Dean's list, is ___
(Do not round until the final answer. Then round to four decimal places as needed.)
BICEERD

Calculus
Application of derivativesFor (y-6)²/25-(x+5)²/16=1
(a) Identify the center.
(b) Identify the vertices.
(c) Identify the foci.
(d) Write equations for the asymptotes.
(e) Graph the hyperbola.
Give exact answers. Express numbers in simplest form using integers, fractions, or radicals.
Part: 1 / 5
(a) The center is ( , ).
Part 2 of 5
(b) The vertices are ( , ) and ( , ).

Calculus
Application of derivativesKevin wants to build a rectangular pen for his animals. One side of the pen will be against the barn; the other three sides will be enclosed with wire fencing. If Kevin has 850 feet of fencing, what dimensions would maximize the area of the pen?
a) Let ω be the length of the pen perpendicular to the barn. Write an equation to model the area of the pen in terms of ω.
Area = ______________
b) What width ω would maximize the area?
ω = ______________

Calculus
Application of derivativesA person on earth is observing the moon, which is 238,860 miles away. The moon has a diameter of 2160 miles. What is the angle in degrees spanned by the moon in the eye of the beholder? Note, consider the diameter of the moon as an arc length for this question. Give your solution rounded to 3 places after the decimal.

Calculus
Application of derivativesA telephone company determines that the duration t, in minutes, of a phone call is an exponentially distributed random variable with a probability density function f(t) = 3 e 3t, 0≤t<∞o. Find the probability that a phone call will last no more than 1.5 min. The probability is __

Calculus
Application of derivativesSolve ΔABC subject to the given conditions, if possible. Round the measures of the angles (in degrees) to 1 decimal place if necessary.
a=2.8, b=4, c = 14.2
The triangle with these conditions does not exist.
The triangle with these conditions does exist.
A≈_
B≈_
C≈_

Calculus
Application of derivativesFind the maximum value of f(x, y) = 4x² - 6y² + 15 on the disk
x² + y² ≤ 1

Calculus
Application of derivativesA hot brick is removed from a kiln at 225° C above room temperature. Over time, the brick cools off. After 2 hours have elapsed, the brick is 30° C above room temperature. Let t be the time in hours since the brick was removed from the kiln. Let y = H(t) be the difference between the brick's and the room's temperature at time t: Assume that H(t) is an exponential function.
Interpret the physical meaning of the horizontal asymptote of H(t).

Calculus
Application of derivativesConsider the following curve.
F(X)=X-6/X2
Find the local minimum and maximum values of f. (Enter your answers as comma-separated lists.
local minimum values____
local maximum values_____

Calculus
Application of derivativesIf a tank holds 3500 gallons of water, which drains from the bottom of the tank in 50 minutes, then Toricelli's Law gives the volume V of water remaining in the tank after t minutes as - 3500 (1-¹² 50 V = (b) 10 min (c) 20 m Find the rate (in gal/min) at which water is draining from the tank after the following amounts of time. (Remember that the rate must be negative because the amount of water in the tank is decreasing.) (a) 5 min (d) 50 min gal/min t = gal/min gal/min 2 gal/min 0 ≤ t ≤ 50. At what time (in min) is the water flowing out the fastest? t = min At what time (in min) is the water flowing out the slowest? min
![Let h(x)=-7+ 5/x
Determine the average value, h(c), of h over [6, 8].
h(c) =
Determine the value(s) of c in [6, 8] guaranteed by the Mean Value Theorem.
c=](https://media.kunduz.com/media/sug-question/raw/84711500-1659806745.0810807.jpeg?w=256)
Calculus
Application of derivativesLet h(x)=-7+ 5/x
Determine the average value, h(c), of h over [6, 8].
h(c) =
Determine the value(s) of c in [6, 8] guaranteed by the Mean Value Theorem.
c=

Calculus
Application of derivativesA population is growing according to the exponential model given by P (t) = 500e0.25t, where t is measured in years. How many years will it take for the population to reach 1000? (Round your answer to one decimal place.)

Calculus
Application of derivativesThe population of trout in a pond is given by P = 0.4P(1 - P 10,000) -f, where f trout are caught per year.
Consider the case where a certain number of fish are added to the pond, or f = -300. What are the nonnegative equilibria and their stabilities? (Round your answer to two decimal places.)
![4. Solve the initial-value problem
y"(t)- y'(t)- 6y(t) = 0, y(0) = 2, and y'(0) = 1.
[Hint: First determine the solution by computing the roots of the associated quadratic equation, then determine the values of the constants using the given initial conditions]](https://media.kunduz.com/media/sug-question/raw/79832882-1659640522.6361883.jpeg?w=256)
Calculus
Application of derivatives4. Solve the initial-value problem
y"(t)- y'(t)- 6y(t) = 0, y(0) = 2, and y'(0) = 1.
[Hint: First determine the solution by computing the roots of the associated quadratic equation, then determine the values of the constants using the given initial conditions]

Calculus
Application of derivativesFind the general power series solution centered at Xo= 0 for the differential equation
y' - 2xy = 0

Calculus
Application of derivativesConsider the first-order equation with initial condition
dy/dt=-y+t² y(0) = 1
Use a value of Ax = h = 1.0 to find y(1) by the third-order Runge-Kutta (RK) method, showing all equations and work.

Calculus
Application of derivativesDetermine the open intervals on which the graph of f(x) = 3x² +7x-3 is concave
downward or concave upward.
concave downward on (-∞,∞)
concave upward on (-∞,0); concave downward on (0,∞)
concave upward on (-∞,1); concave downward on (1,∞)
concave upward on (-∞,∞)
concave downward on (-∞,0); concave upward on (0,∞)

Calculus
Application of derivativesDetermine all solutions to the equation -√2sin 2x = sin² x + cos²x on the interval [0, 2π).
x= 5π/8,7π/8
x=5π/4,7π/4
x=5π/8,7π/8,13π/8,15π/8
x=5π/4,7π/4,9π/4,11π/4

Calculus
Application of derivativesSuppose the position equation for a moving object is given by s(t) = 3t² + 2t + 5, where s is measured in meters and t is measured in seconds. Find the velocity of the object when t=2 seconds.
13 m/s
14 m/s
10 m/s
6 m/s
None of these
![Locate the absolute extrema of the function f(x) = x³-12x on the closed interval [0, 4].
absolute max: (2, -16); absolute min: (4, 16)
no absolute max; absolute min: (4, 16)
absolute max: (4, 16); absolute min: (2, -16)
absolute max: (4,16); no absolute min
no absolute max or min](https://media.kunduz.com/media/sug-question/raw/84692056-1659620283.6129649.jpeg?w=256)
Calculus
Application of derivativesLocate the absolute extrema of the function f(x) = x³-12x on the closed interval [0, 4].
absolute max: (2, -16); absolute min: (4, 16)
no absolute max; absolute min: (4, 16)
absolute max: (4, 16); absolute min: (2, -16)
absolute max: (4,16); no absolute min
no absolute max or min

Calculus
Application of derivativesSuppose the monthly total revenue for the manufacture of golf balls is R(x) = 1.78x, where x is the number of golf balls sold each month.
a. What is the slope of the graph of the total revenue function?
b. What is the marginal revenue for the product?
c. Interpret the marginal revenue of this product.
a. What is the slope of the graph of the total revenue function?
b. What is the marginal revenue (rate of change of the revenue function) for the product?
$
c. Choose the correct interpretation of the marginal revenue of this product.
i) The revenue will decrease by $1.78 for each additional golf ball sold in a month.
ii) Each month the revenue is increased by $1.78 a day.
iii) The revenue will increase by $1.78 for each additional golf ball sold in a month.
iv) Each month the revenue is decreased by $1.78 a day.

Calculus
Application of derivativesGraph the function. Estimate the intervals on which the function is increasing or
decreasing and any relative maxima or minima.
f(x)=7-lx|
Determine on which interval(s) f(x) is increasing. Select the correct choice below and, if
necessary, fill in the answer box to complete your choice.
A. The function f is increasing on the interval
(Type your answer in interval notation. Use a comma to separate answers as
needed.)
B. There is no interval on which the function f(x) is increasing.
Determine on which interval(s) f(x) is decreasing. Select the correct choice below and,
if necessary, fill in the answer box to complete your choice.
A. There is no interval on which the function f(x) is decreasing.
B. The function f is decreasing on the interval
(Type your answer in interval notation. Use a comma to separate answers as
needed.)

Calculus
Application of derivativesFind an equation of the tangent plane to the surface z = ln(x - 2y) at the point (3, 1,0).

Calculus
Application of derivativesThe population of a certain city was 170000 in 1998, and the observed relative growth rate is 3 percent per year. Hint: This model is similar to A=Pe^(rt).
(a) Find a function that models the population after t years.
(b) Find the projected population in the year 2004.
Your answer is
(c) In what year will the population reach 2758827
Your answer is

Calculus
Application of derivativesConsider the function f(x) = -4 ln(x + 3) - 7. Show all work to answer the following:
a) What is the parent function?
b) List all transformations.
c) What is the equations of the asymptote?
d) What is the domain?
e) What is the range?

Calculus
Application of derivativesIf you deposit $4000 into an account earning 3% interest per year compounded continuously, how long will it take to triple your investment?
Show all work and leave your answer EXACT -- DO NOT ROUND.

Calculus
Application of derivativesSketch the slope field of y' = y and sketch the solution with initial condition y(0) = -1.
![The height h in centimeters of Shuntaro's pogo stick from the ground as he jumps on it since s seconds have passed is roughly modelled by the equation
h(s) = sin2 4x + 2sin4x + 1.
a. How many times does Shuntaro hit the ground in the first 5 seconds? [A2]
b. How many centimeters is Shuntaro off the ground after 2 seconds? [A2]
c. During the first second, when is Shuntaro 2.5cm to two decimal places? [A3]](https://media.kunduz.com/media/sug-question/raw/84675727-1659133147.8027494.jpeg?w=256)
Calculus
Application of derivativesThe height h in centimeters of Shuntaro's pogo stick from the ground as he jumps on it since s seconds have passed is roughly modelled by the equation
h(s) = sin2 4x + 2sin4x + 1.
a. How many times does Shuntaro hit the ground in the first 5 seconds? [A2]
b. How many centimeters is Shuntaro off the ground after 2 seconds? [A2]
c. During the first second, when is Shuntaro 2.5cm to two decimal places? [A3]

Calculus
Application of derivativesAn open rectangular box having a volume of 108 in.3 is to be constructed from a tin sheet. Find the dimensions of such a box if the amount of material used in its construction is to be minimal. Hint: Let the dimensions of the box be x x y x z. Then xyz = 108, and the amount of material used is given by S = xy + 2yz + 2xz. Show that the following is true and minimize f(x, y).

Calculus
Application of derivativesThe Ace Novelty company produces two souvenirs: Type A and Type B. The number of Type A souvenirs, x, and the number of Type B souvenirs, y, that the company can produce weekly are related by the equation 8x² + y - 4 = 0, where x and y are measured in units of a thousand. The profits for a Type A souvenir and a Type B souvenir are $16 and $8, respectively. How many of each type of souvenirs should the company produce to maximize its profit?
Type A
Type B

Calculus
Application of derivativesSolve the linear programming problem.
Maximize
P=7x+7y
Subject to
2x+y ≤ 20
x + 2y ≤ 16
x, y ≥0
Select the correct choice below and fill in any answer boxes present in your choice. What
is the maximum value of P?
A. P=
(Type an integer or a fraction.)
B. There is no maximum value of P.

Calculus
Application of derivativesProduction Function for a Company: Suppose the production output of a certain country is given by
f(x, y) = 100x^3/5.y^2/5
billion dollars if x billion dollars are spent for labor and y billion dollars are spent on capital. Find the output if the country spent $243 billion on labor and $32 billion on capital.
$________ billion

Calculus
Application of derivativesFor the function shown in the figure below, find the average rate of change from (-3, 10) to (1, -6).
The average rate of change is (Simplify your answer.)

Calculus
Application of derivativesUse the method of Lagrange multipliers to maximize the function subject to the given constraint.
Maximize the function f(x, y) =√ y² - x^2 subject to the constraint x + 2y - 5 = 0.
maximum of
at (x, y) =