Application of derivatives Questions and Answers

Calculus
Application of derivativesFind the common ratio for the geometric sequence.
-1 3, -1 15, -1 75, - 1 375, -1 1875,...
Common ratio:

Calculus
Application of derivativesFind the domain of the function. (Enter your answers using interval notation.)
g(r, s) = √rs
The domain of g is the set of all ordered pairs (r, s) such that r ∈ , s ∈ , and rs ∈

Calculus
Application of derivativesIf f(x) and g(x) are differentiable functions for 0≤x≤1 such that f(0) = 2, g(0)=0, f(1) = 6, g(1)=2, then which of the following are true for some 0 <c<1(c in one options may be different from c in another)?
(a) f'(c)-f(0) = g'(c) (b) f'(c)-g(0)=2g'(c)
(c) f'(c) + f(1) =3g'(c) (d) f'(c)+2g(1) = 4g'(c)
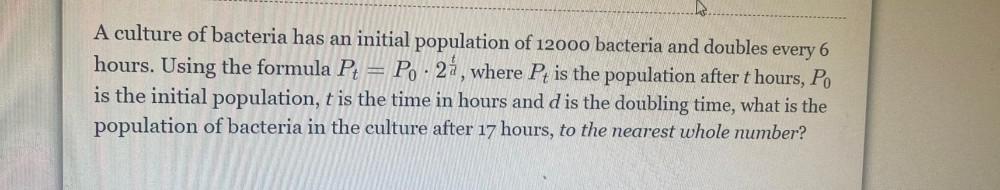
Calculus
Application of derivativesA culture of bacteria has an initial population of 12000 bacteria and doubles every 6 hours. Using the formula Pₜ = P₀ * 2ᵗ/ᵈ, where Pₜ is the population after t hours, P₀ is the initial population, t is the time in hours and d is the doubling time, what is the population of bacteria in the culture after 17 hours, to the nearest whole number?
Calculus
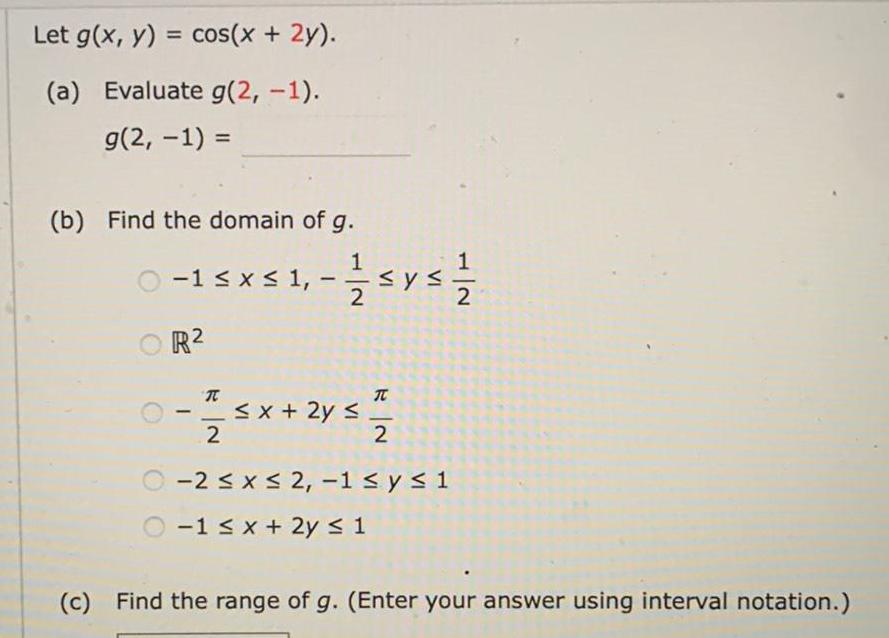
Application of derivativesLet g(x, y) = cos(x + 2y).
(a) Evaluate g(2, -1).
g(2, -1) =
(b) Find the domain of g.
-1 ≤ x ≤ 1, -1 2 ≤ y ≤ 1 2
R²
-π 2 ≤ x + 2y ≤ π 2
-2 ≤ x ≤ 2, -1 ≤ y ≤ 1
-1 ≤ x + 2y ≤ 1
(c) Find the range of g. (Enter your answer using interval notation.)
![Calculate the Taylor polynomial T3 centered at a = a for the given function and values of a and Estimate the accuracy of the 3th degree Taylor approximation, f(x) 73(x), centered at x = a on the given interval.
f(x) = ex/2, a = 2, and [2, 4]](https://media.kunduz.com/media/sug-question/raw/84656142-1658958862.7131405.jpeg?w=256)
Calculus
Application of derivativesCalculate the Taylor polynomial T3 centered at a = a for the given function and values of a and Estimate the accuracy of the 3th degree Taylor approximation, f(x) 73(x), centered at x = a on the given interval.
f(x) = ex/2, a = 2, and [2, 4]


Calculus
Application of derivativesDifferentiate f and find the domain of f. (Enter the domain in interval notation.)
f(x) = In(x² - 6x)
derivative f'(x) =
domain

Calculus
Application of derivativesThe governing differential equation is the 1-D heat equation:
∂T/∂t = α(∂²T/∂x²)
Using the explicit and implicit methods, determine the finite difference approximations of the differential equation of 1-D heat equation using the forward finite difference for time and the central finite difference for position and discuss the stability condition for the two methods.
Calculus
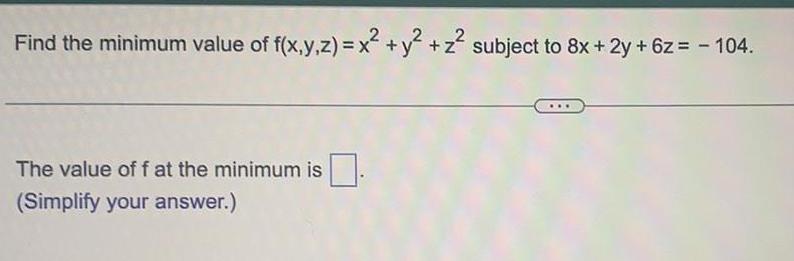
Application of derivativesFind the minimum value of f(x,y,z) = x² + y² + z² subject to 8x + 2y + 6z = - 104.
The value of f at the minimum is .
(Simplify your answer.)

Calculus
Application of derivativesWarning: Questions 2 and 3 below are asking for the taylor polynomials centered at x = 1. This means you are plugging x = 1 into the derivatives and including powers of (x - 1) in your answer. Refer to the definition from question 1 as a guide.
2. Find the first three Taylor polynomials, po, P₁, and p2 for the function f(x): ln x at x = 1.
Calculus
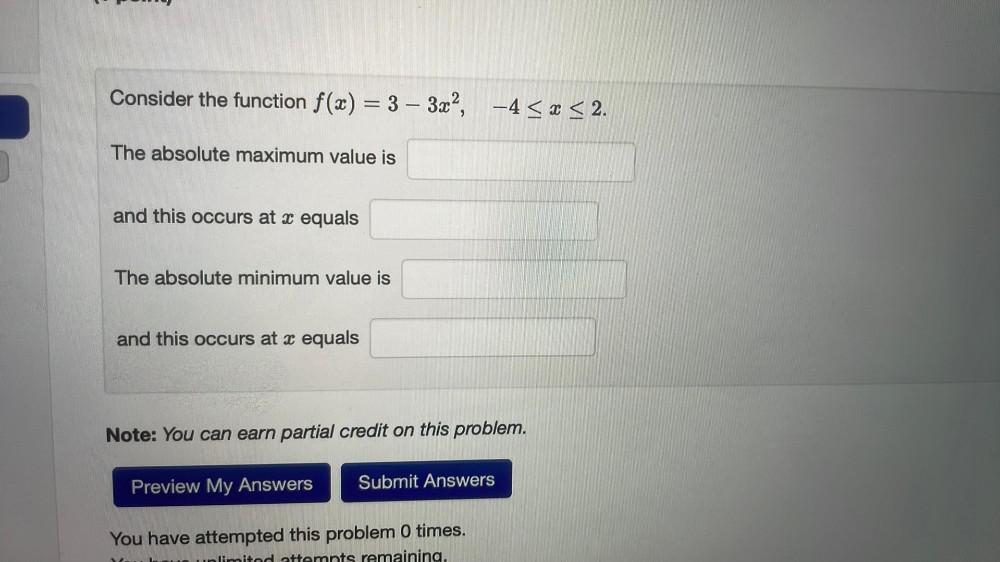
Application of derivativesConsider the function f(x) = 3 - 3x², -4 ≤ x ≤ 2.
The absolute maximum value is
and this occurs at x equals
The absolute minimum value is
and this occurs at x equals
![Let f(x) = x⁴(x - 1)³.
(a) Find the critical numbers of the function f. (Enter your answers from smallest to largest.)
smallest value x₁=
x₂=
largest value x₃=
(b) What does the Second Derivative Test tell you about the behavior of fat these critical numbers?
At x₁ the second derivative test [ is inconclusive]
At x₂ the second derivative test [indicates a local minimum]
At x₃ the second derivative test [is inconclusive]
(c) What does the First Derivative Test tell you? Note what the First Derivative Test tells you that Second Derivative Test does not.
At x₁ the first derivative test [indicates a local maximum]
At x₂ the first derivative test [indicates a local minimum]
At x₃ the first derivative test [indicates neither a minimum nor a maximum]](https://media.kunduz.com/media/sug-question/raw/82851195-1658667119.8497024.jpeg?w=256)
Calculus
Application of derivativesLet f(x) = x⁴(x - 1)³.
(a) Find the critical numbers of the function f. (Enter your answers from smallest to largest.)
smallest value x₁=
x₂=
largest value x₃=
(b) What does the Second Derivative Test tell you about the behavior of fat these critical numbers?
At x₁ the second derivative test [ is inconclusive]
At x₂ the second derivative test [indicates a local minimum]
At x₃ the second derivative test [is inconclusive]
(c) What does the First Derivative Test tell you? Note what the First Derivative Test tells you that Second Derivative Test does not.
At x₁ the first derivative test [indicates a local maximum]
At x₂ the first derivative test [indicates a local minimum]
At x₃ the first derivative test [indicates neither a minimum nor a maximum]
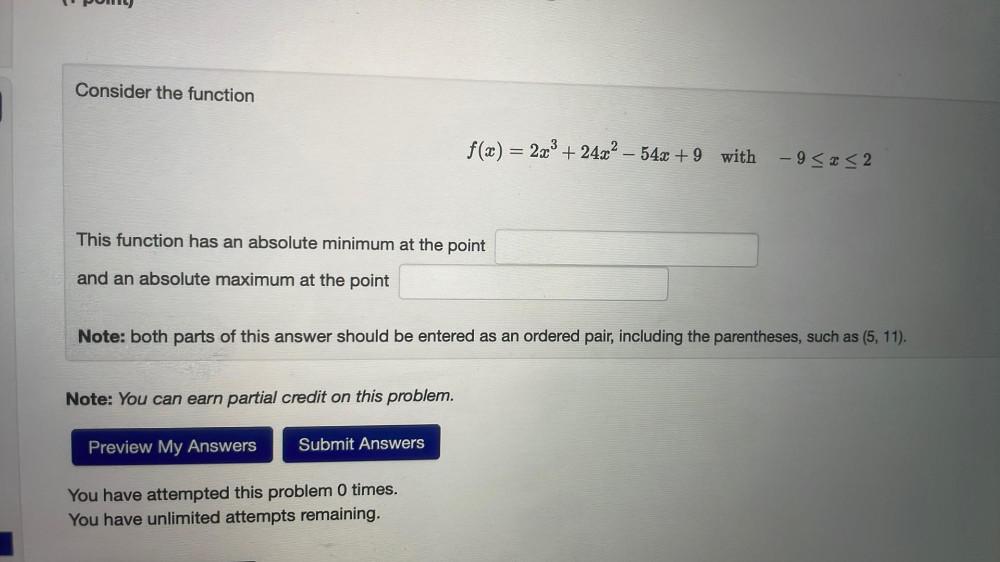
Calculus
Application of derivativesConsider the function
f(x) = 2x³ + 24x² - 54x +9 with -9 ≤ x ≤ 2
This function has an absolute minimum at the point
and an absolute maximum at the point
![Consider the function f(x) = 12x⁵ + 30x⁴ - 300x³ + 2.
f(x) has inflection points at (reading from left to right) x = D, E, and F
where D is
and E is
and F is
For each of the following intervals, tell whether f(x) is concave up (type in CU) or concave down (type in CD).
(-∞, D):
[D, E]:
[E, F]:
[F, ∞):](https://media.kunduz.com/media/sug-question/raw/82682353-1658667071.2856834.jpeg?w=256)
Calculus
Application of derivativesConsider the function f(x) = 12x⁵ + 30x⁴ - 300x³ + 2.
f(x) has inflection points at (reading from left to right) x = D, E, and F
where D is
and E is
and F is
For each of the following intervals, tell whether f(x) is concave up (type in CU) or concave down (type in CD).
(-∞, D):
[D, E]:
[E, F]:
[F, ∞):
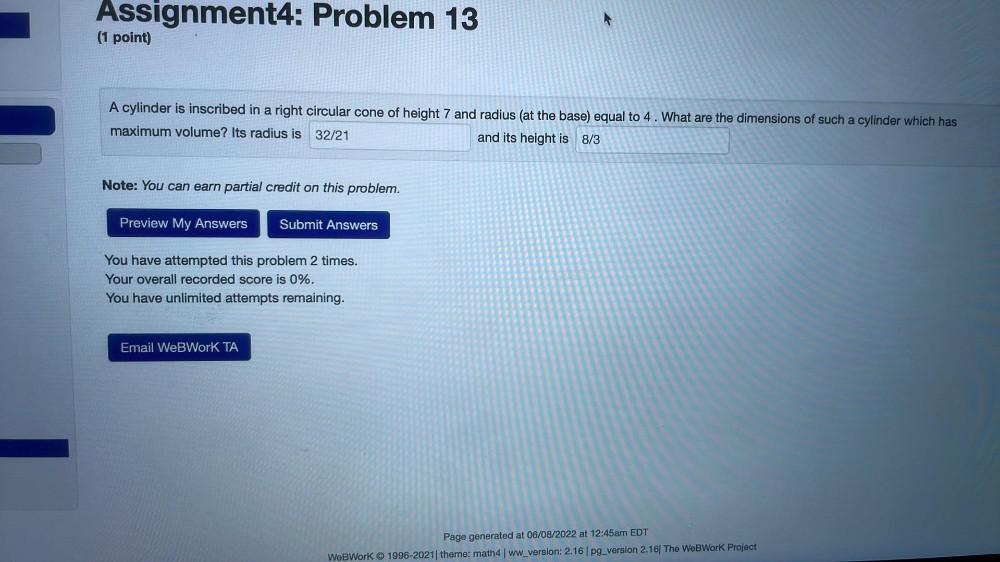
Calculus
Application of derivativesA cylinder is inscribed in a right circular cone of height 7 and radius (at the base) equal to 4. What are the dimensions of such a cylinder which has
maximum volume? Its radius is 32/21 and its height is 8/3 Note: You can earn partial credit on this problem.
Preview My Answers Submit Answers You have attempted this problem 2 times. Your overall recorded score is 0%. You have unlimited attempts remaining.

Calculus
Application of derivativesf(x) = 4x/ x² - 49
(A) List all critical numbers of f. If there are no critical numbers, enter 'NONE'.
Critical numbers =
(B) Use interval notation to indicate where f(x) is decreasing.
Note: Use 'INF' for ∞, '-INF' for -∞, and use 'U' for the union symbol.
Decreasing:
(C)List the x-values of all local maxima of f. If there are no local maxima, enter 'NONE'.
x values of local maxima =
(D) List the x-values of all local minima of f. If there are no local minima, enter 'NONE'.
x values of local minima =
(E) List the values of all inflection points of f. If there are no inflection points, enter 'NONE'.
Inflection points=
(F) Use interval notation to indicate where f(x) is concave up.
Concave up:
(G) Use interval notation to indicate where f(x) is concave down.
Concave down:
(H) List all horizontal asymptotes of f. If there are no horizontal asymptotes, enter 'NONE'.
Horizontal asymptotes y =
(I) List all vertical asymptotes of f.
If there are no vertical asymptotes, enter 'NONE'.
vertical asymptotes x =
(J) Use all of the preceding information to sketch a graph of f. When you're finished, enter a "1" in the box below.
Graph Complete:
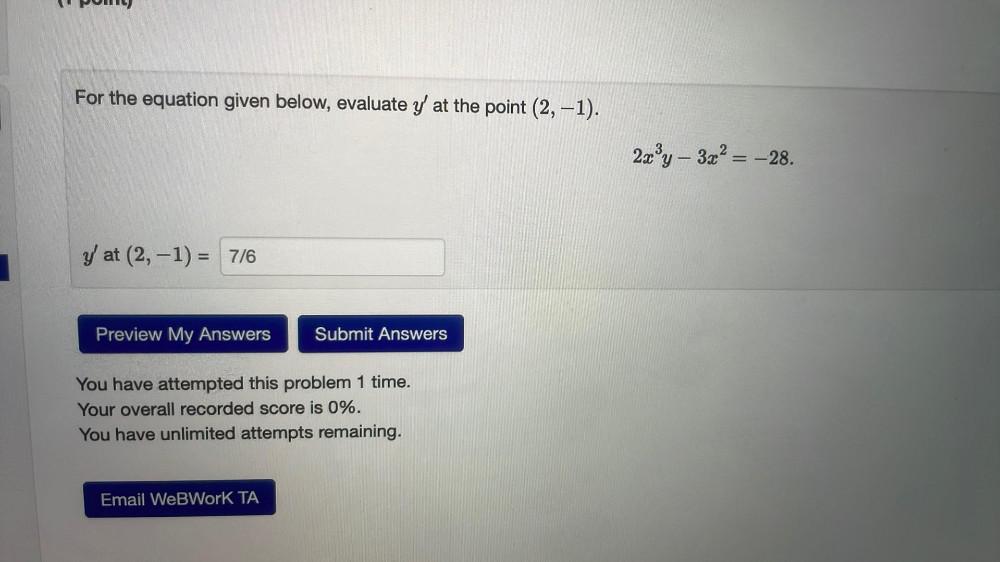
Calculus
Application of derivativesFor the equation given below, evaluate y' at the point (2, -1).
2x³y - 3x² = -28.
y' at (2, -1) = 7/6
![Here is a graph of the function h. Use the graph to find the following.
If there is more than one answer, separate them with commas.
(a) All values at which h has a local maximum:[]
(b) All local maximum values of h:[]](https://media.kunduz.com/media/sug-question/raw/82851499-1658666856.9453695.jpeg?w=256)
Calculus
Application of derivativesHere is a graph of the function h. Use the graph to find the following.
If there is more than one answer, separate them with commas.
(a) All values at which h has a local maximum:[]
(b) All local maximum values of h:[]
![Suppose the temperature at a point in a metal cube is given by T(u, v, w) = 90 - 55e ^[-1/20(u²+v² +w²)] where the centre of the cube is taken to be at (1, 0, -2). Find the rate of change of temperature at the origin in the direction of the unit vector. r=(1/√7)(-2,1,-3).](https://media.kunduz.com/media/sug-question/raw/82685659-1658666697.2938864.jpeg?w=256)
Calculus
Application of derivativesSuppose the temperature at a point in a metal cube is given by T(u, v, w) = 90 - 55e ^[-1/20(u²+v² +w²)] where the centre of the cube is taken to be at (1, 0, -2). Find the rate of change of temperature at the origin in the direction of the unit vector. r=(1/√7)(-2,1,-3).
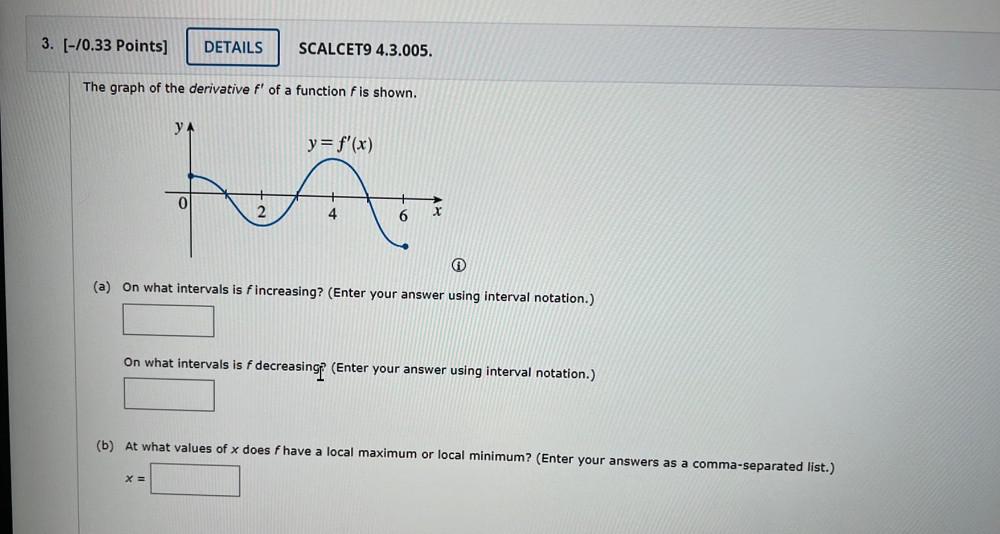
Calculus
Application of derivativesThe graph of the derivative f' of a function f is shown.
(a) On what intervals is f increasing? (Enter your answer using interval notation.)
On what intervals is f decreasing? (Enter your answer using interval notation.)
(b) At what values of x does f have a local maximum or local minimum? (Enter your answers as a comma-separated list.)
X =

Calculus
Application of derivativesAt what rate is the shadow of a 6-ft tall man shortening as he walks at 8 ft/s on a level path toward the streetlight that is 20 ft above the pavement? Also, find the rate at which his head is receding from the light when he is 20 ft from the post.
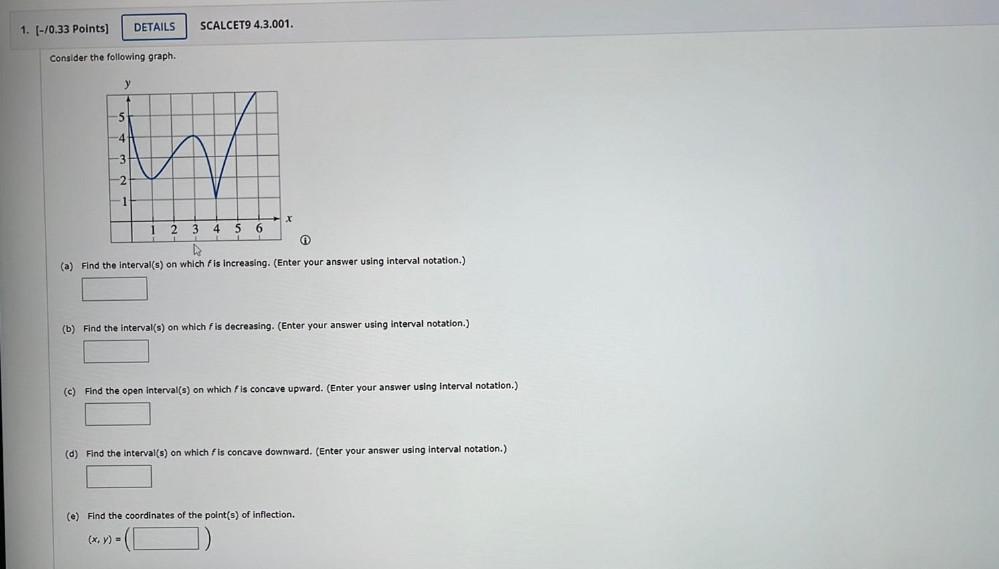
Calculus
Application of derivativesconsider the following graph
(a) Find the interval(s) on which f is increasing. (Enter your answer using interval notation.)
(b) Find the interval(s) on which f is decreasing.(Enter your answer using interval notation.)
(c) Find the open interval(s) on which f is concave upward. (Enter your answer using interval notation.)
(d) Find the interval(s) on which f is concave downward. (Enter your answer using interval notation.)
(e) Find the coordinates of the point(s) of inflection. (x, y) =

Calculus
Application of derivativesUse the Taylor series to estimate f(x) =(x-1) e^-x at xi+1=1 for Xi = 0.5. Use the 3rd order approximation and calculate the percentage relative true error for each step.
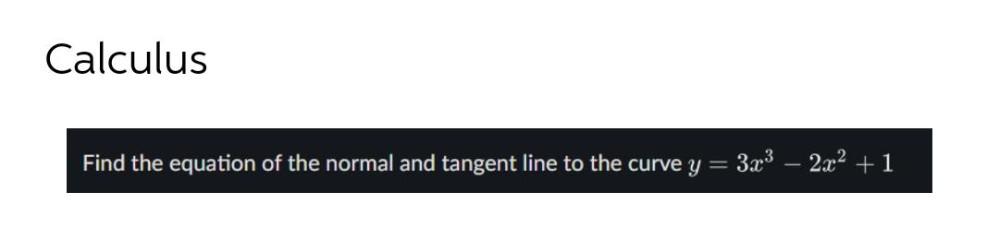
Calculus
Application of derivativesFind the equation of the normal and tangent line to the curve y = 3x³ - 2x² + 1

Calculus
Application of derivativesA 2 m tall woman is running at a rate of 2 m/s when she spots a bird in a tree 6 m off off the ground.
How fast is the angle of elevation to the bird increasing when she is 3 m from the base of the tree?
a) 0.32 rad/s
b) 0.16 rad/s
c) 0.64 rad/s
d) 0.5 rad/s

Calculus
Application of derivativesEnzo needs to construct two electrical poles 30 m apart. The first pole is 28 m tall, while the second is 12 m tall. In order to support the weight of the poles, a stake is to be planted at ground level. Then, a tension wire will be attached from each of the poles onto the stake. If Enzo wants to minimize the amount of tension wire used, how far from the 12 m tall post should he plant the stake?
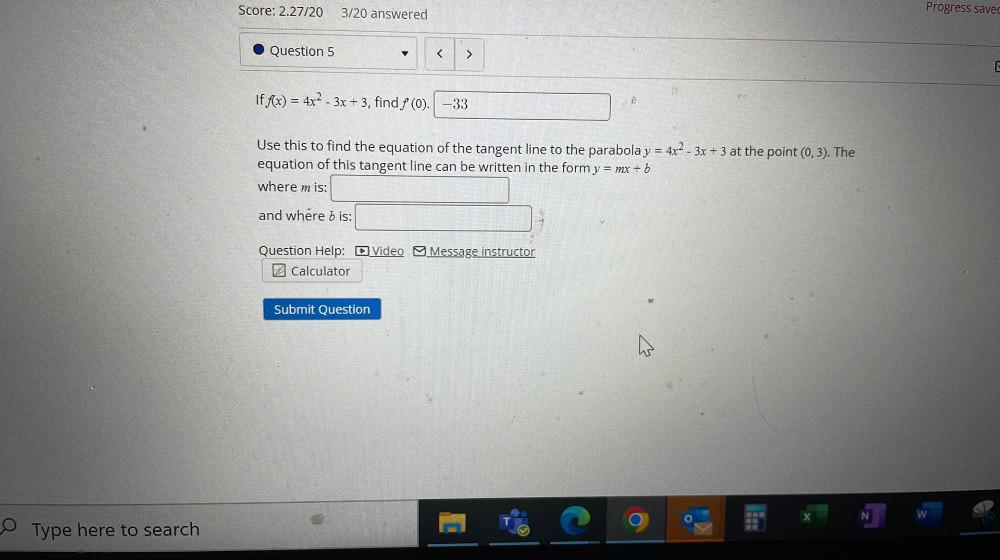
Calculus
Application of derivativesIf f(x) = 4x²-3x + 3, find f '(0).
Use this to find the equation of the tangent line to the parabola y = 4x² - 3x + 3 at the point (0, 3).The equation of this tangent line can be written in the form y =mx+b
where m is:
and where b is:

Calculus
Application of derivativesFinance. Suppose that $2,300 is invested at 3.6% annual interest rate, compounded monthly. How much money will be in the account in (A) 6 months? (B) 7 years?
(A) Amount after 6 months: $____ (Round to the nearest cent.)
(B) Amount after 7 years: $____ (Round to the nearest cent.)
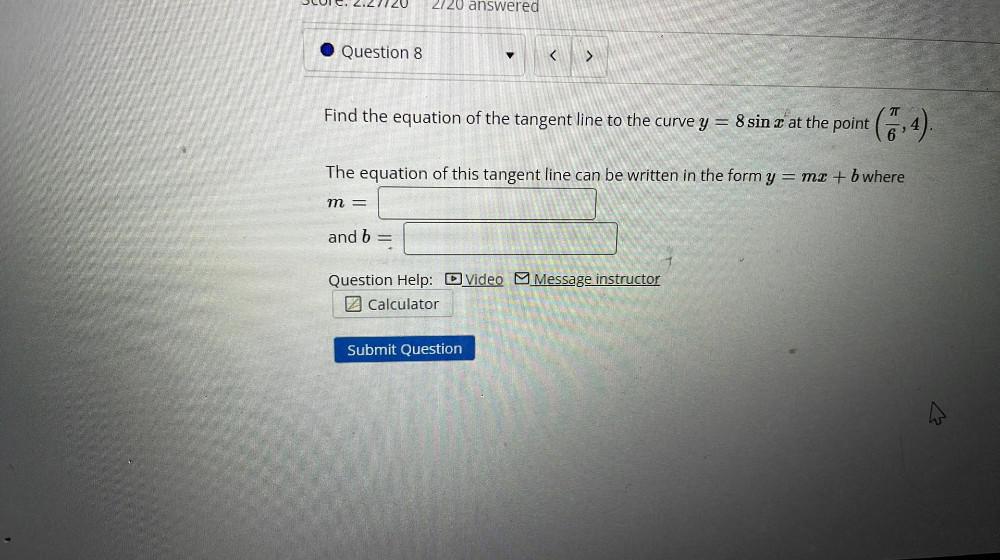
Calculus
Application of derivativesFind the equation of the tangent line to the curve y = 8 sinx at the point (π/6,4).
The equation of this tangent line can be written in the form y = mx + b where
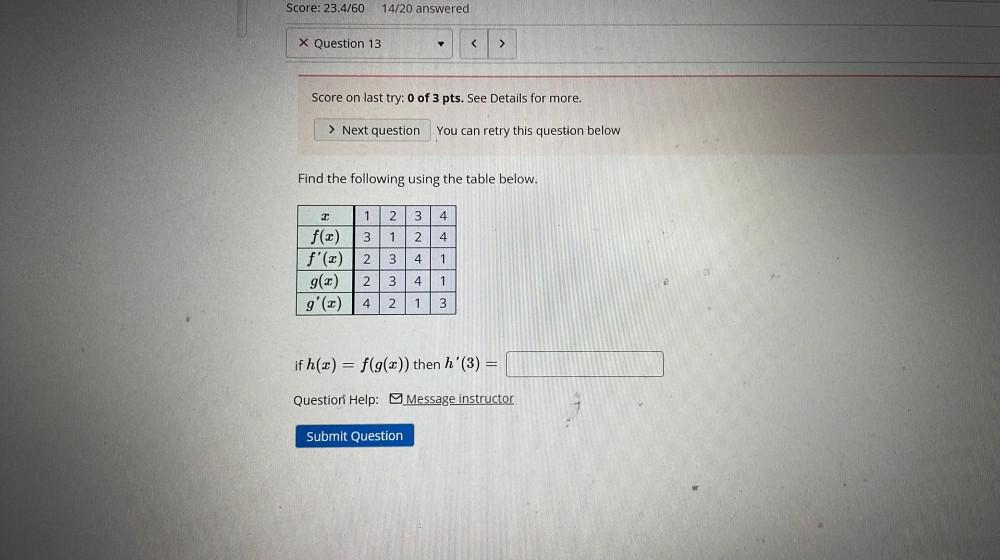
Calculus
Application of derivativesFind the following using the table below.
if h(x) = f(g(x)) then h'(3) =

Calculus
Application of derivativesDetermine the global minima and maxima of the function:
ƒ (x, y, z) = e^x⁴ +z⁴
under the set:
A := {(x, y, z) ∈ R³ : x⁴ + (y² + z²)² = 1
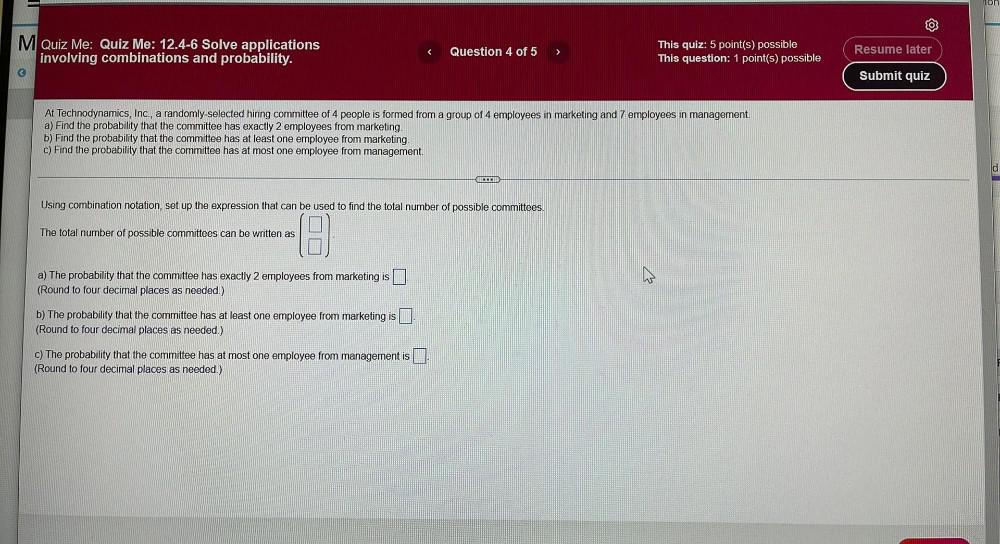
Calculus
Application of derivativesAt Technodynamics, Inc., a randomly-selected hiring committee of 4 people is formed from a group of 4 employees in marketing and 7 employees in management.
a) Find the probability that the committee has exactly 2 employees from marketing.
b) Find the probability that the committee has at least one employee from marketing.
c) Find the probability that the committee has at most one employee from management.
Using combination notation, set up the expression that can be used to find the total number of possible committees.
The total number of possible committees can be written as
a) The probability that the committee has exactly 2 employees from marketing is
b) The probability that the committee has at least one employee from marketing is
c) The probability that the committee has at most one employee from management is
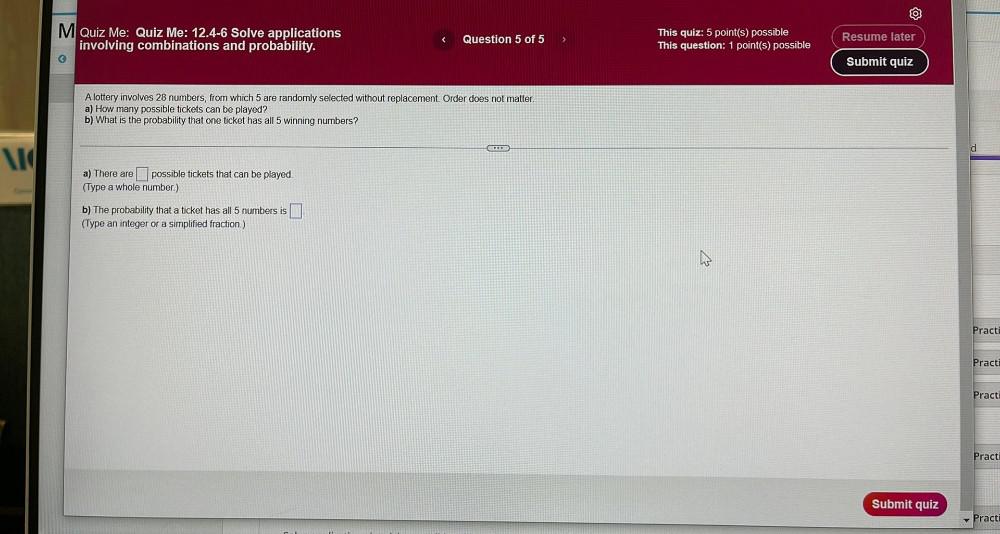
Calculus
Application of derivativesA lottery involves 28 numbers, from which 5 are randomly selected without replacement. Order does not matter.
a) How many possible tickets can be played?
b) What is the probability that one ticket has all 5 winning numbers?
a) There are possible tickets that can be played.
b) The probability that a ticket has all 5 numbers is
![The table provides various values, including all zeros, of a tangent function f (x) on the interval [-π, π].
What is the period of the function?](https://media.kunduz.com/media/sug-question/raw/83704233-1658665674.6178904.jpeg?w=256)
Calculus
Application of derivativesThe table provides various values, including all zeros, of a tangent function f (x) on the interval [-π, π].
What is the period of the function?
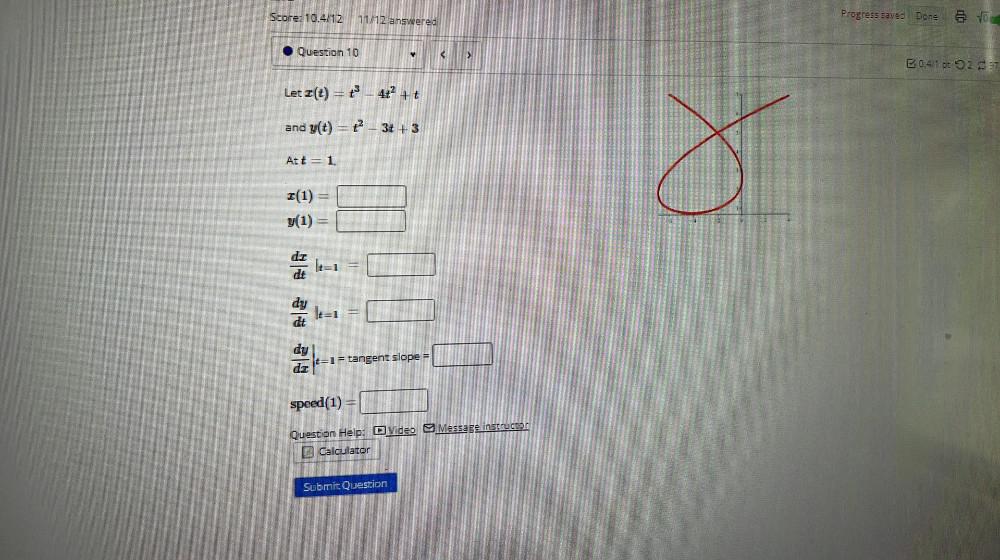
Calculus
Application of derivativesLet I(t) = t³ - 4t² + t
and y(t) = t² - 3t + 3
At t = 1.
x(1) =
y(1) =
dx/dt |t=1 =
dy/dt |t=1 =
dy/dt |t=1= tangent slope =
speed (1) =

Calculus
Application of derivativesIf two lines have no points of intersection and the same direction vector, they are:
a. intersecting lines
b. skew lines
c. parallel lines
d. coincident lines
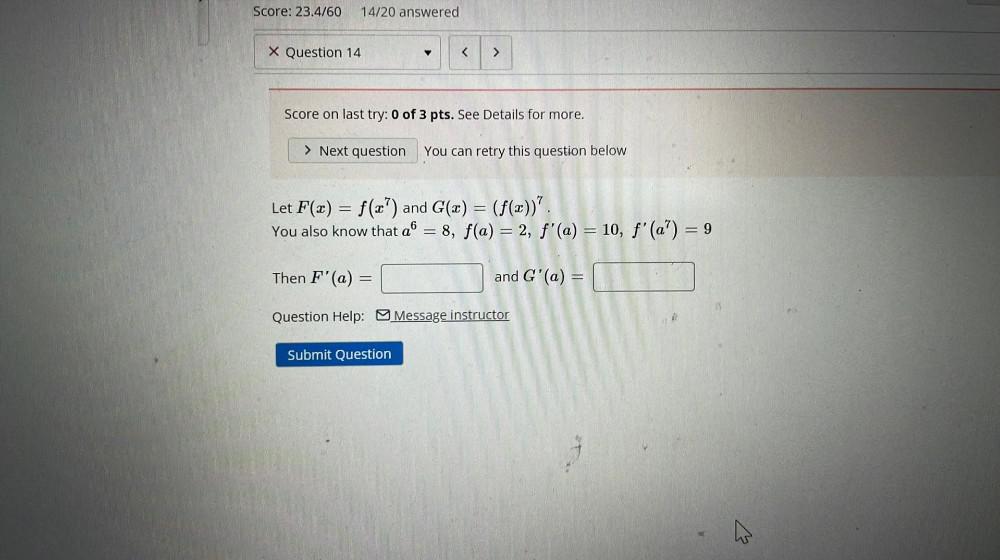
Calculus
Application of derivativesLet F(x) = f(x⁷) and G(x) = (f(x))⁷.
You also know that a⁶ = 8, f(a) = 2, ƒ'(a) = 10, f'(a⁷) = 9
Then F'(a) =
and G'(a) =
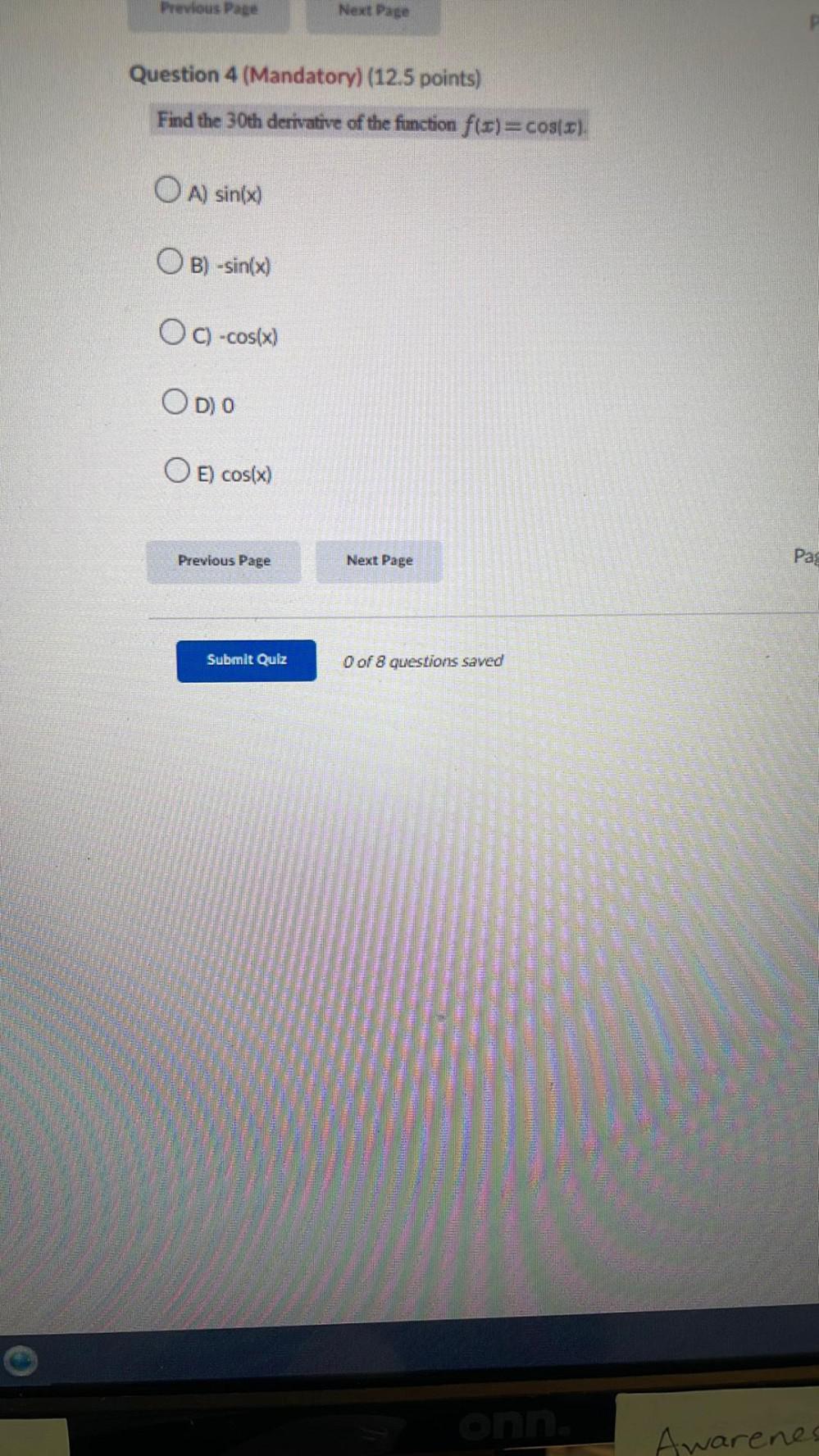
Calculus
Application of derivativesFind the 30th derivative of the function f(x) = cos(x).
A) sin(x)
B) -sin(x)
c)-cos(x)
D) 0
E) cos(x)
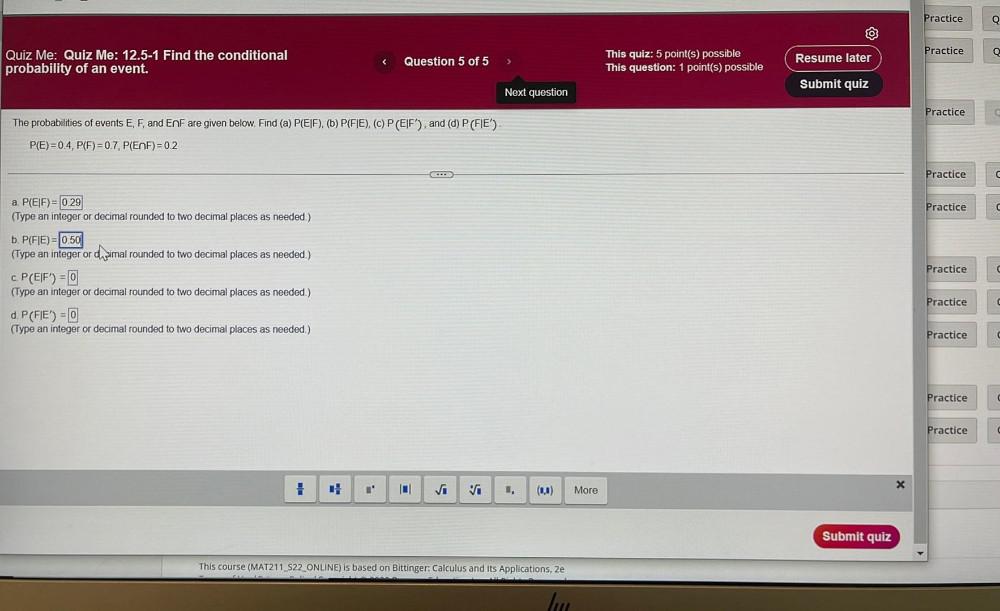
Calculus
Application of derivativesThe probabilities of events E, F, and E⋂F are given below. Find (a) P(EIF), (b) P(FIE), (c) P (EIF'), and (d) P (FIE').
P(E) = 0.4, P(F) = 0.7, P(E⋂F) = 0.2
a. P(EIF) =
(Type an integer or decimal rounded to two decimal places as needed.)
b. P(FIE) =
(Type an integer or decimal rounded to two decimal places as needed.)
c. P (EIF') =
(Type an integer or decimal rounded to two decimal places as needed.)
d. P (FIE') =
(Type an integer or decimal rounded to two decimal places as needed.)
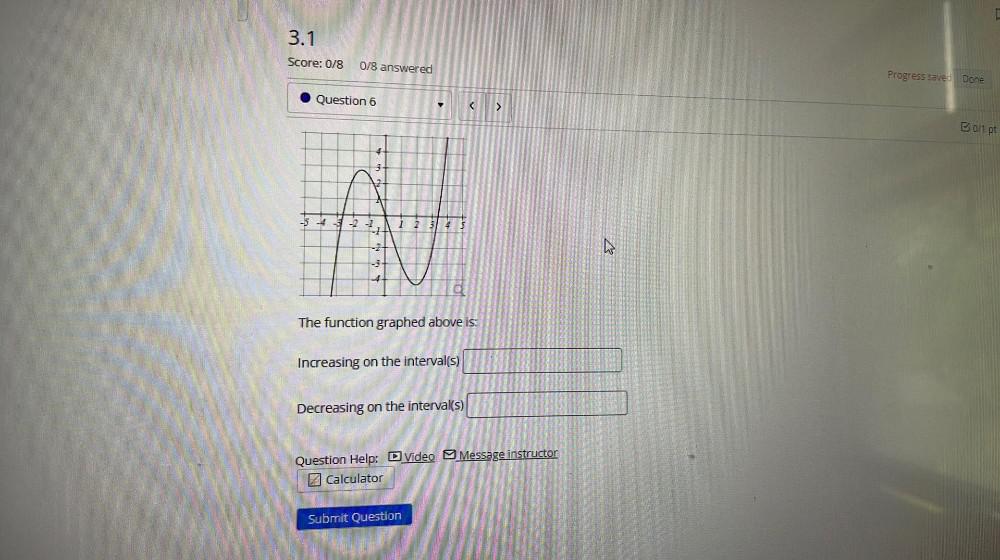
Calculus
Application of derivativesThe function graphed above is:
Increasing on the interval(s)
Decreasing on the interval(s)
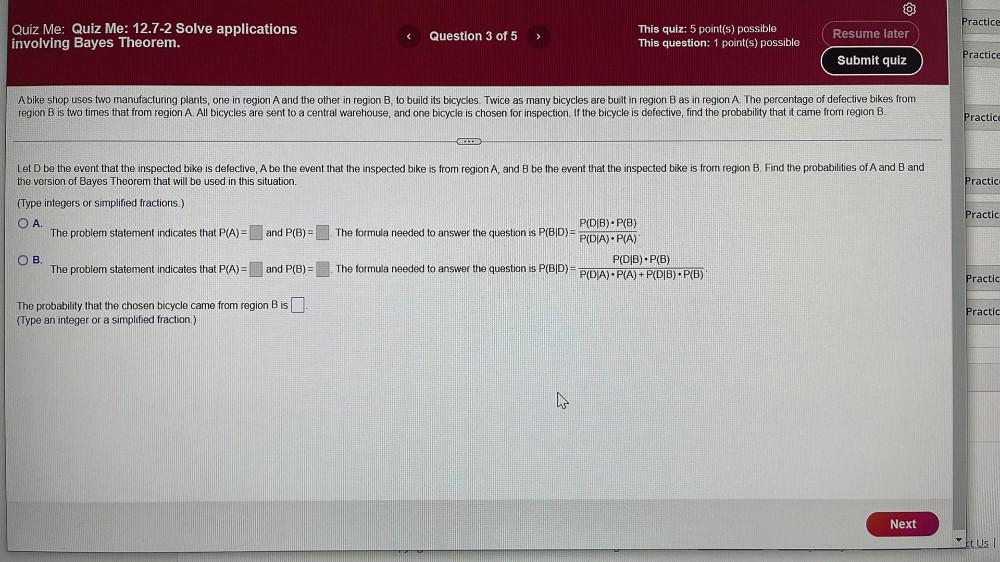
Calculus
Application of derivativesA bike shop uses two manufacturing plants, one in region A and the other in region B, to build its bicycles. Twice as many bicycles are built in region B as in region A. The percentage of defective bikes from region B is two times that from region A. All bicycles are sent to a central warehouse, and one bicycle is chosen for inspection. If the bicycle is defective, find the probability that it came from region B.
Let D be the event that the inspected bike is defective, A be the event that the inspected bike is from region A, and B be the event that the inspected bike is from region B. Find the probabilities of A and B and the version of Bayes Theorem that will be used in this situation.
A. The problem statement indicates that P(A) = and P(B) = The formula needed to answer the question is P(BID)= P(DIB).P(B) / P(DIA).P(A)
B. The problem statement indicates that P(A) = and P(B) = The formula needed to answer the question is P(BID)= P(DIB).P(B) / P(DIA).P(A) + P(DIB).P(B)
The probability that the chosen bicycle came from region B is
(Type an integer or a simplified fraction.)
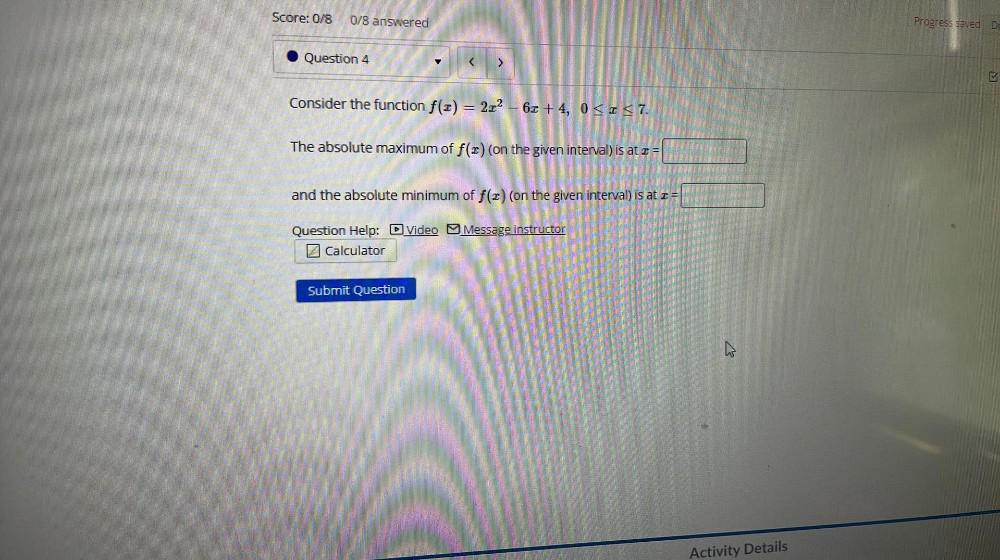
Calculus
Application of derivativesConsider the function f(x) = 2x² - 6x +4, 0 ≤ x ≤ 7.
The absolute maximum of f(x) (on the given interval) is at x =
and the absolute minimum of f(x) (on the given interval) is at x =
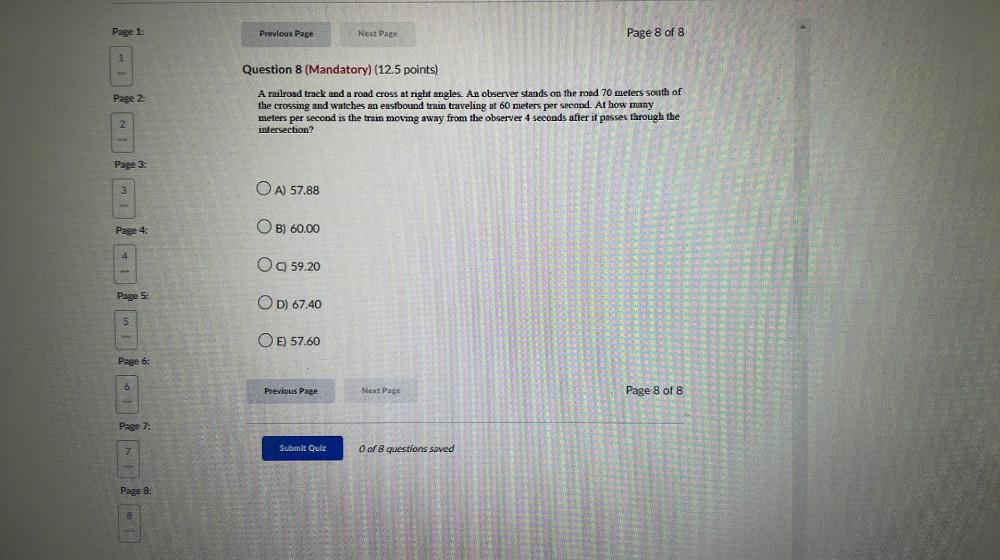
Calculus
Application of derivativesA railroad track and a road cross at right angles. An observer stands on the road 70 meters south of the crossing and watches an eastbound train traveling at 60 meters per second. At how many
meters per second is the train moving away from the observer 4 seconds after it passes through the intersection?
A) 57.88
B) 60.00
C) 59.20
D) 67.40
E) 57.60
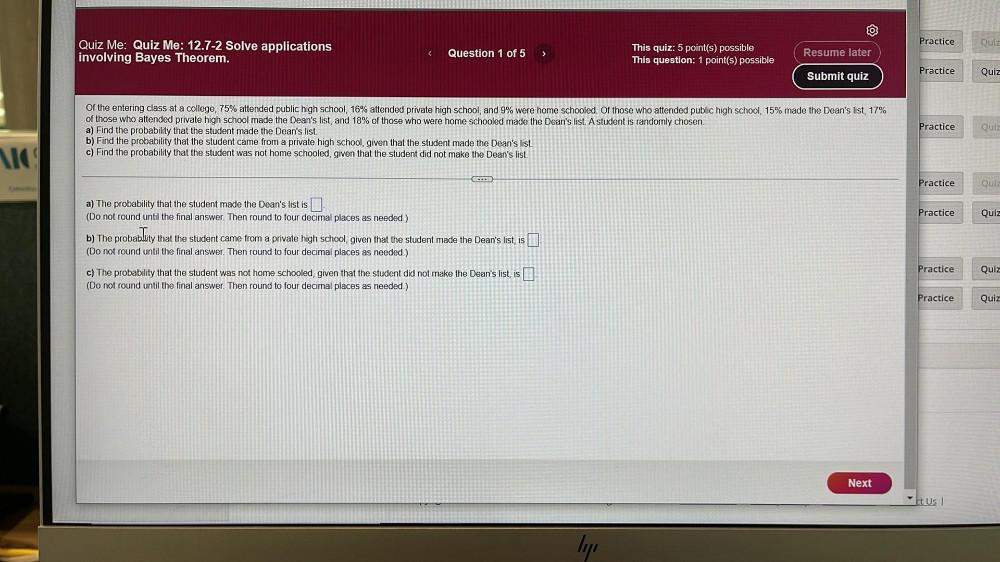
Calculus
Application of derivativesOf the entering class at a college, 75% attended public high school, 16% attended private high school, and 9% were home schooled. Of those who attended public high school, 15% made the Dean's list, 17% of those who attended private high school made the Dean's list, and 18% of those who were home schooled made the Dean's list. A student is randomly chosen.
a) Find the probability that the student made the Dean's list.
b) Find the probability that the student came from a private high school, given that the student made the Dean's list.
c) Find the probability that the student was not home schooled, given that the student did not make the Dean's list.
a) The probability that the student made the Dean's list is.
(Do not round until the final answer. Then round to four decimal places as needed.)
b) The probability that the student came from a private high school, given that the student made the Dean's list, is
(Do not round until the final answer. Then round to four decimal places as needed.)
c) The probability that the student was not home schooled, given that the student did not make the Dean's list, is
(Do not round until the final answer. Then round to four decimal places as needed.)

Calculus
Application of derivativesFind the equation of the tangent line to the graph of f(x) = 1/x⁹ when x = 1.
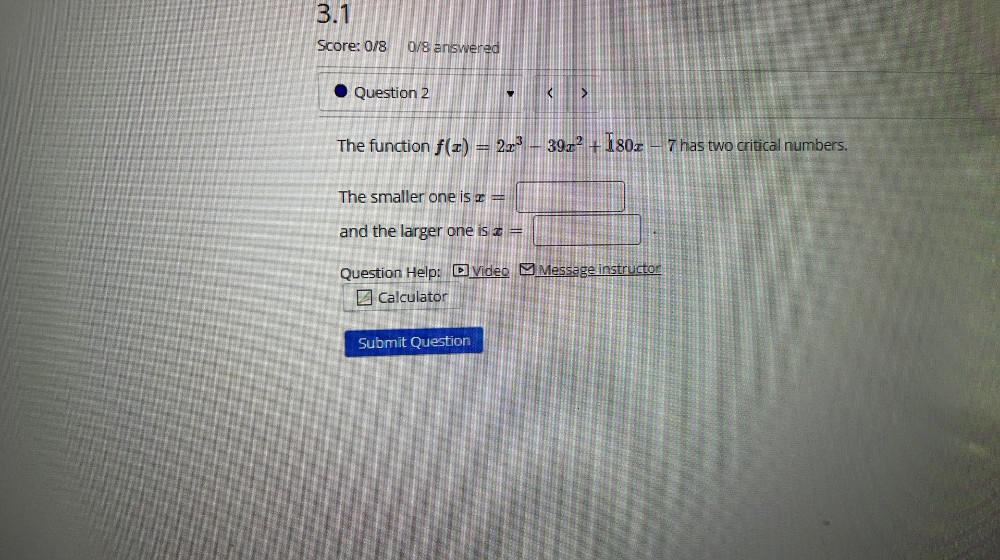
Calculus
Application of derivativesThe function f(z) = 2x³ – 39x² + 180x – 7 has two critical numbers.
The smaller one is x =
and the larger one is x =
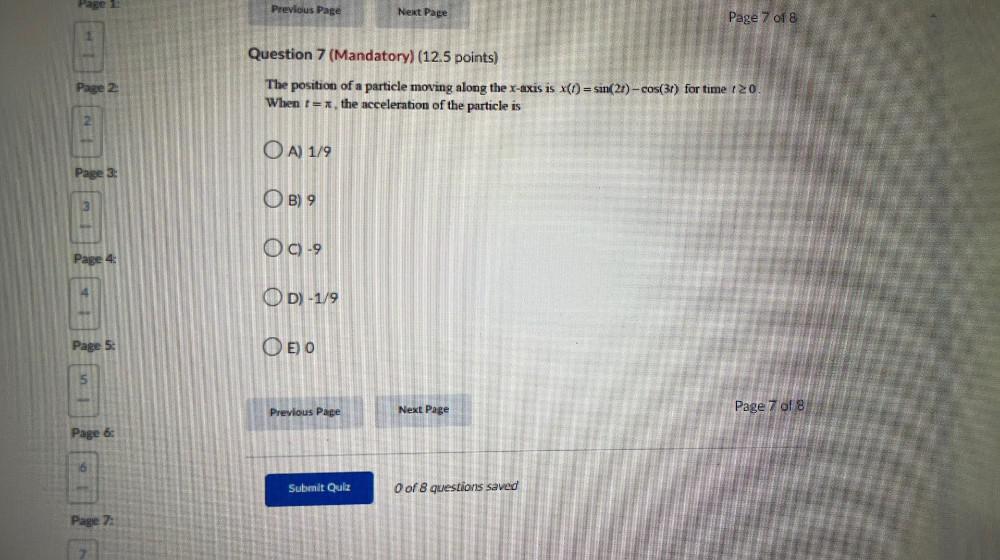
Calculus
Application of derivativesThe position of a particle moving along the x-axis is x(t)=sin(2t)-cos(3t) for time t≥0.
When t=π, the acceleration of the particle is
A) 1/9
B) 9
C) -9
D) -1/9
E) 0

Calculus
Application of derivativesGiven the vector field F(x, y) = (ye^sinx cosx, e^sinx) and the curve C with equation y² -√ysin x = 0
a) Show that F is conservative and find a potential f (x, y) of F
b) Compute the work done by force F along C from (π/2,1) to (π,0)

Calculus
Application of derivativesDetermine the point(s) at which the function f(x) = 2x³ - 15x² + 36x has a horizontal tangent line.