Application of derivatives Questions and Answers

Calculus
Application of derivatives2 ex 4r 2r 2 r V Part 3 of 3 From the previous step we have ex 42 2r 2 0 Since ex is never 0 then we know 4 2r2 0 Solving the above equation gives the solutions to the quadratic equation smaller value larger value L 11 47 2r 2

Calculus
Application of derivativesFind the arc length of the graph of the function f x over 0 1 0 2 2 1 OM 6 1

Calculus
Application of derivativest up a definite integral for the volume of the solid generated by revolving the plane region bounded by y x y 0 x out the x axis You must show your work to receive full credit Edit Format Table

Calculus
Application of derivativesSet up a definite integral for the area of the region bounded by the graphs of y x y x in the first quadrant You must show your work to receive full credit Edit Format Table

Calculus
Application of derivativesFind the area of the region bounded by the graphs of y x y in the first quadrant O 6 4 2 3 0 4 2 6 3 0 1 O
Calculus
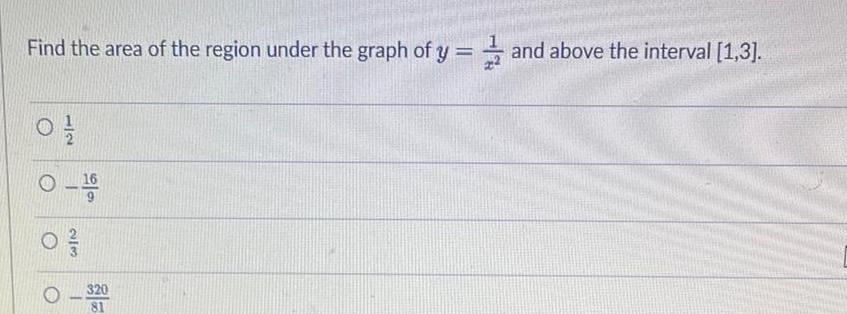
Application of derivativesFind the area of the region under the graph of y and above the interval 1 3 223 320 81
Calculus
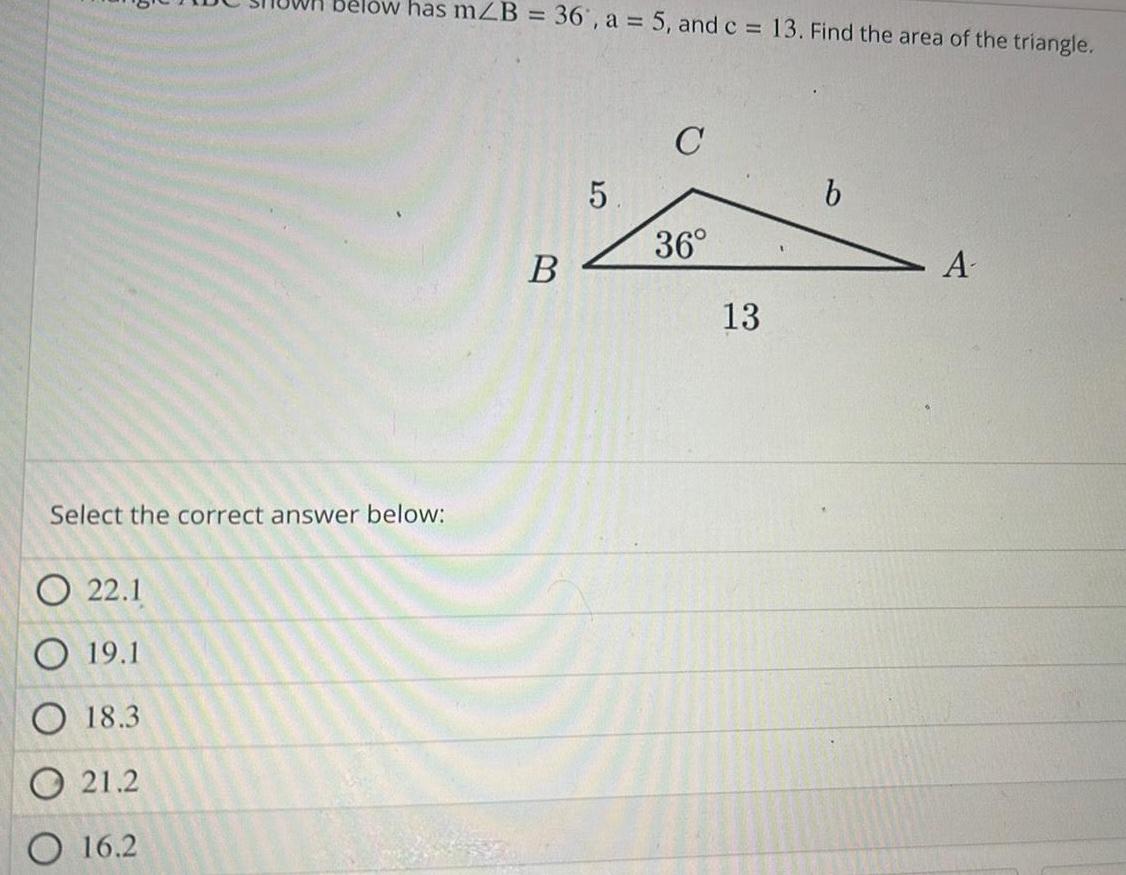
Application of derivativeslow has mZB 36 a 5 and c 13 Find the area of the triangle Select the correct answer below O 22 1 O 19 1 O 18 3 21 2 O 16 2 B 5 C 36 13 b A
Calculus
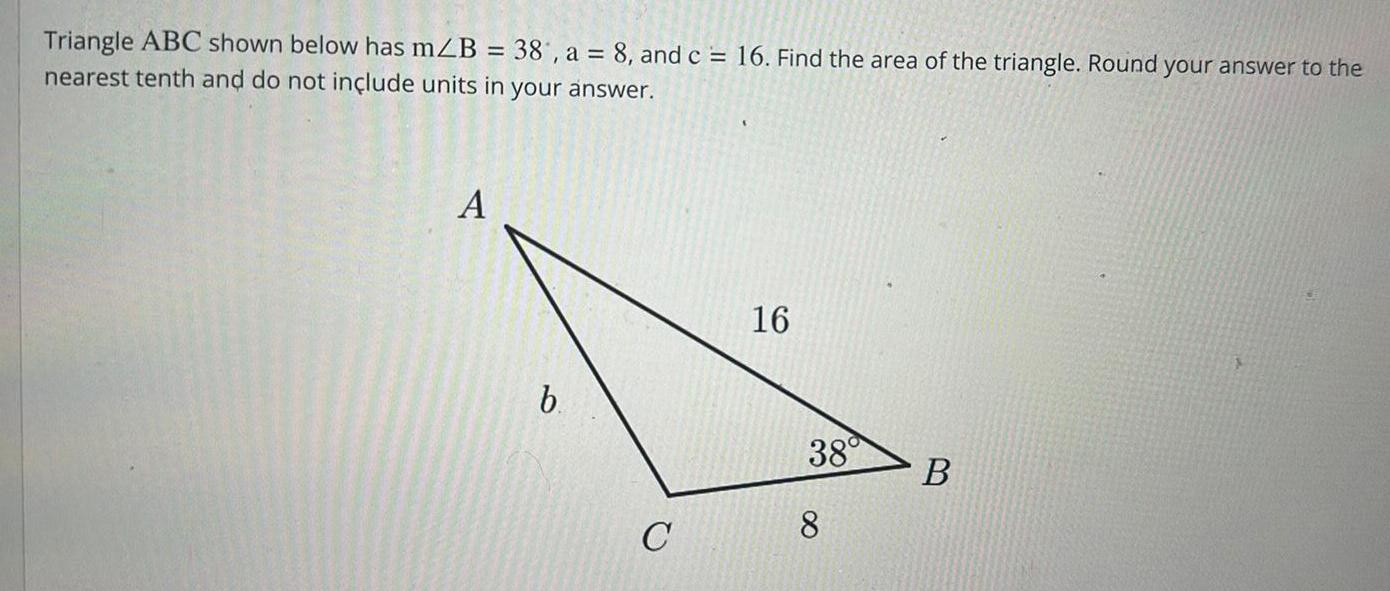
Application of derivativesTriangle ABC shown below has mZB 38 a 8 and c 16 Find the area of the triangle Round your answer to the nearest tenth and do not include units in your answer A b C 16 38 8 B
Calculus
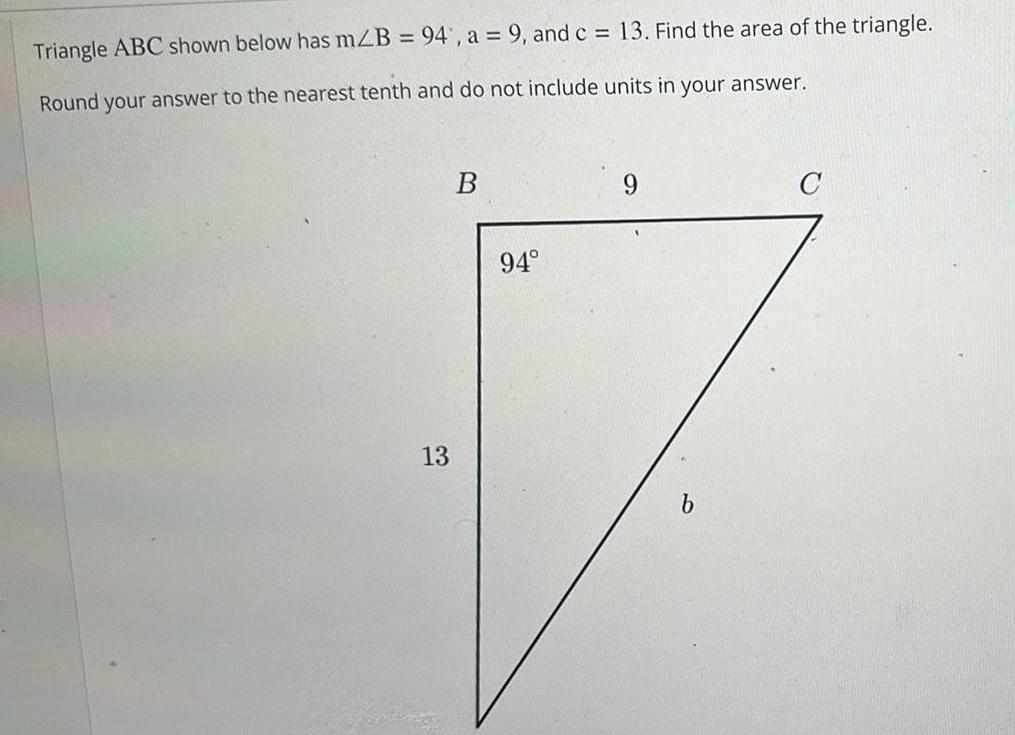
Application of derivativesTriangle ABC shown below has mZB 94 a 9 and c 13 Find the area of the triangle Round your answer to the nearest tenth and do not include units in your answer 13 B 94 b C
Calculus
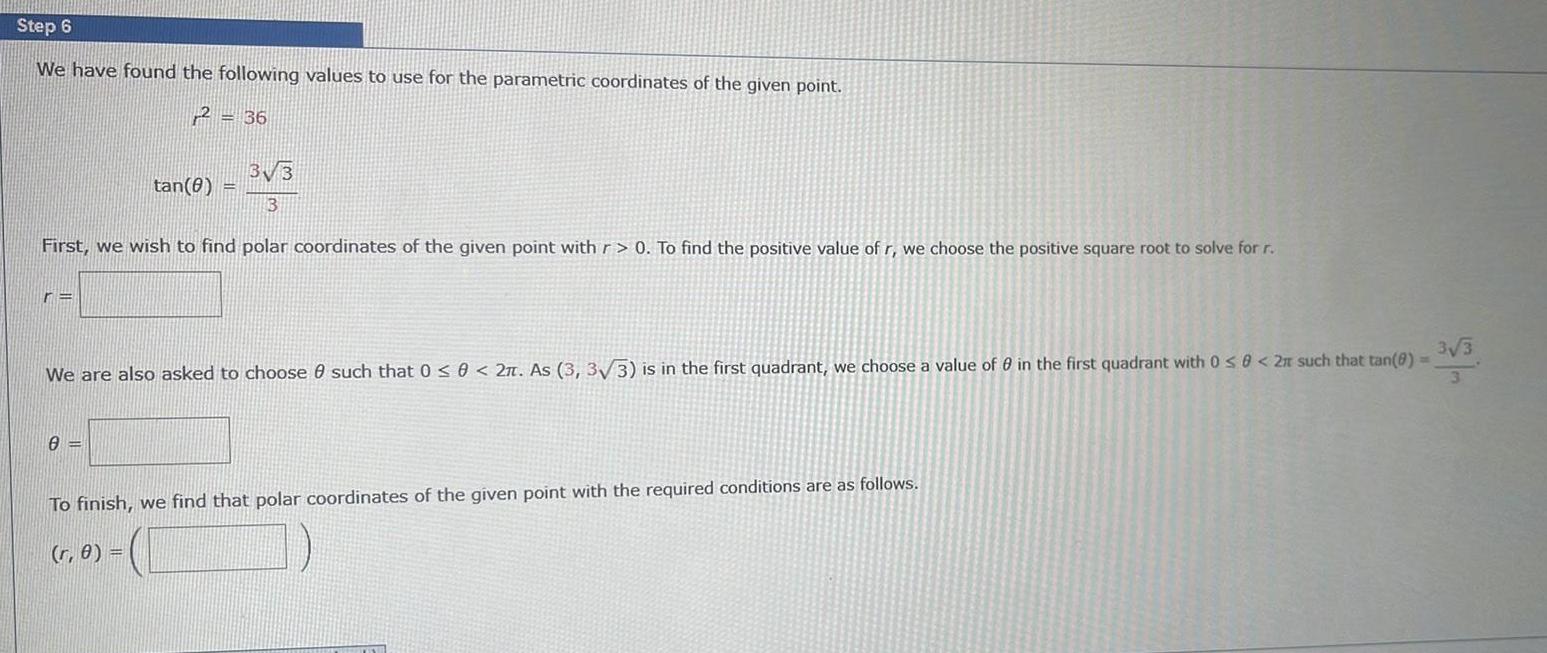
Application of derivativesStep 6 We have found the following values to use for the parametric coordinates of the given point 2 36 3 3 3 First we wish to find polar coordinates of the given point with r 0 To find the positive value of r we choose the positive square root to solve for r re tan 8 We are also asked to choose 0 such that 0 0 2 As 3 3 3 is in the first quadrant we choose a value of 0 in the first quadrant with 0 8 2r such that tan 0 3 3 3 0 To finish we find that polar coordinates of the given point with the required conditions are as follows r 0 VISIE
Calculus
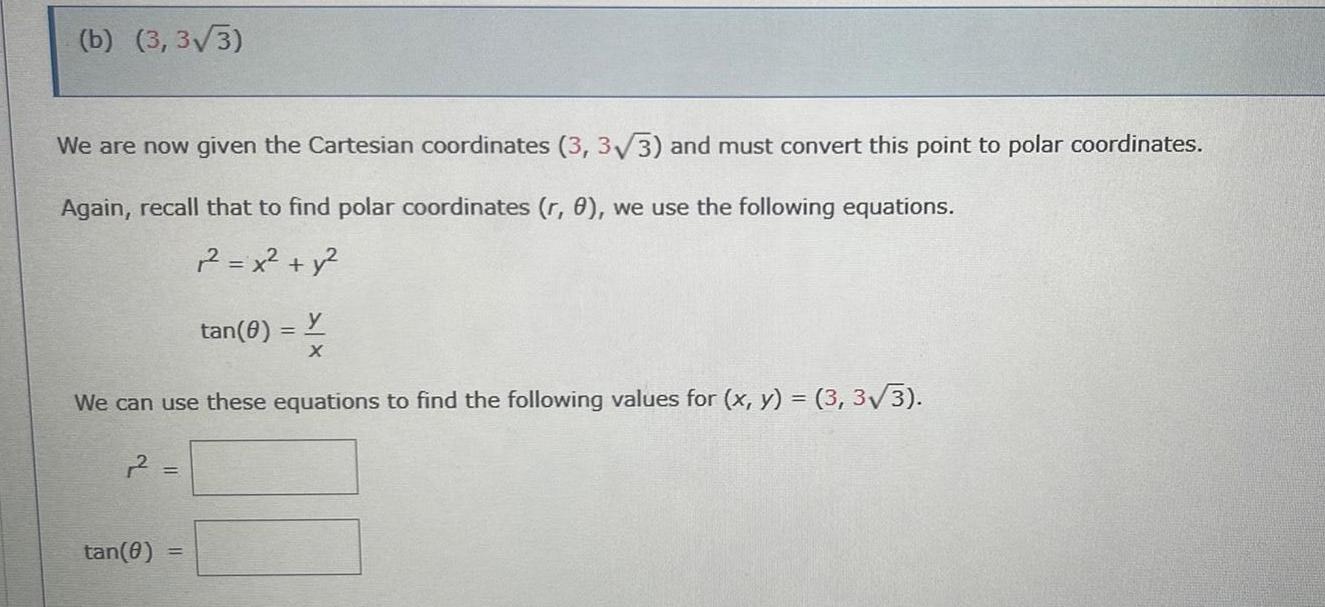
Application of derivativesb 3 3 3 We are now given the Cartesian coordinates 3 3 3 and must convert this point to polar coordinates Again recall that to find polar coordinates r 0 we use the following equations 2 x y y X We can use these equations to find the following values for x y 3 3 3 tan 0 tan 0
Calculus
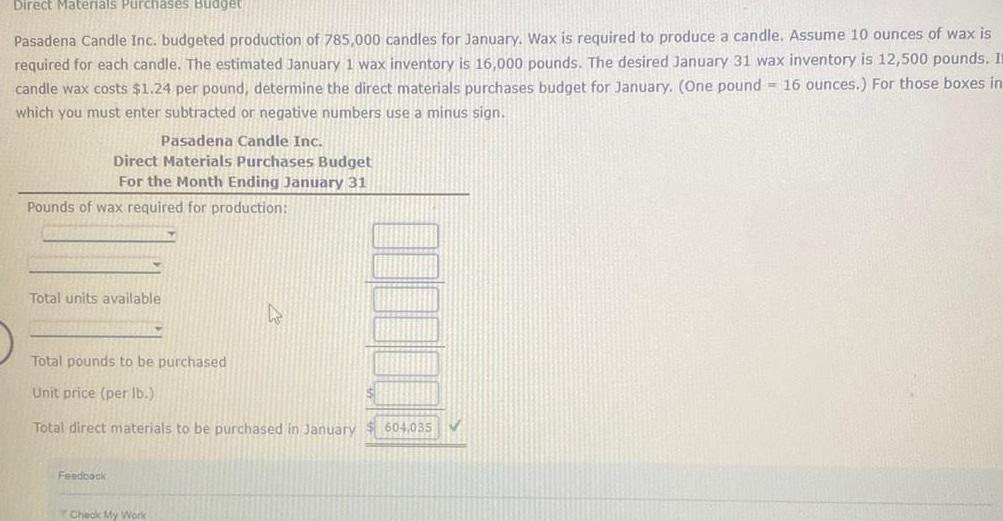
Application of derivativesDirect Materials Purchases Budget Pasadena Candle Inc budgeted production of 785 000 candles for January Wax is required to produce a candle Assume 10 ounces of wax is required for each candle The estimated January 1 wax inventory is 16 000 pounds The desired January 31 wax inventory is 12 500 pounds It candle wax costs 1 24 per pound determine the direct materials purchases budget for January One pound 16 ounces For those boxes in which you must enter subtracted or negative numbers use a minus sign Pasadena Candle Inc Direct Materials Purchases Budget For the Month Ending January 31 Pounds of wax required for production Total units available Total pounds to be purchased Unit price per lb Total direct materials to be purchased in January 604 035 Feedback Check My Work

Calculus
Application of derivativesFind an equation of the parabola with focus 3 1 and directrix x 5 0 0 0
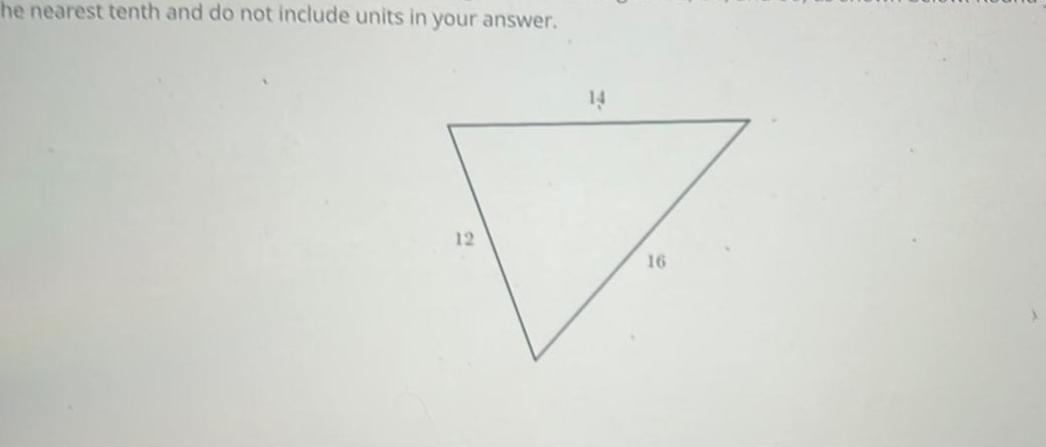
Calculus
Application of derivativesA circle has a radius of 4 5yd A sector of the circle has a central angle of 2 9 radians Find the area of the sector Do not round any intermediate computations Round your answer to the nearest tenth yd X S

Calculus
Application of derivativesA vector is described Express the vector in terms of i and j A quarterback releases a football with a speed of 38 feet per second at an angle of 30 with the horizontal V Simplify your answer Type an exact answer using radicals as needed Use integers or fractions for any numbers in the expression Type your answer in the form Rationalize all denominators
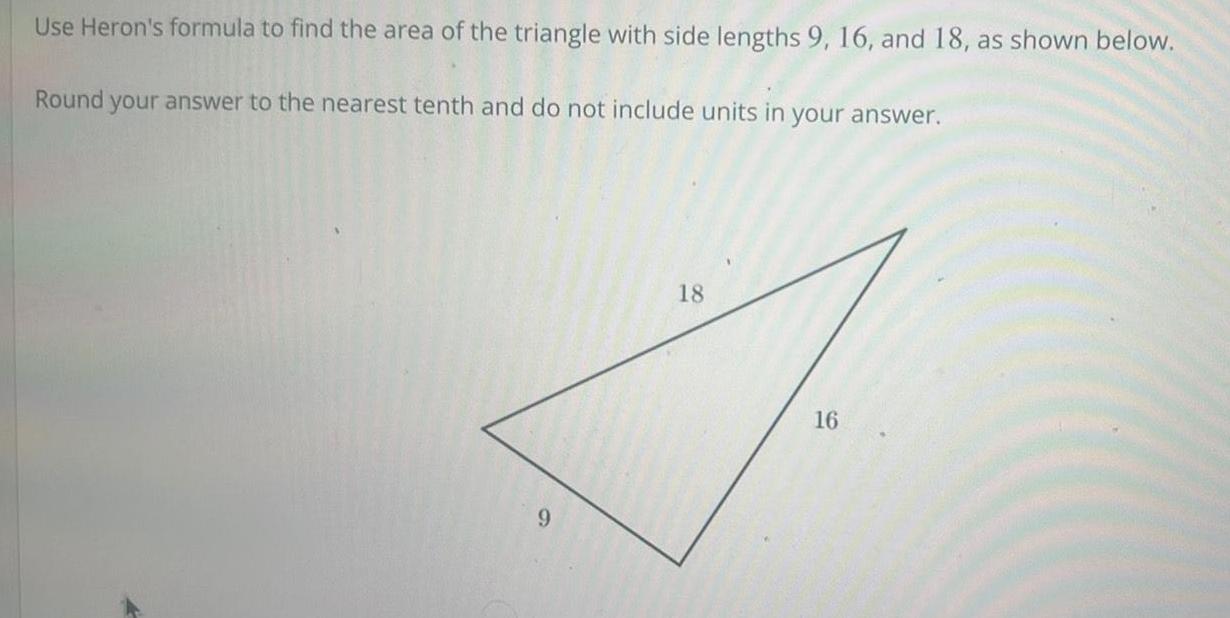
Calculus
Application of derivativesUse Heron s formula to find the area of the triangle with side lengths 9 16 and 18 as shown below Round your answer to the nearest tenth and do not include units in your answer 9 18 16
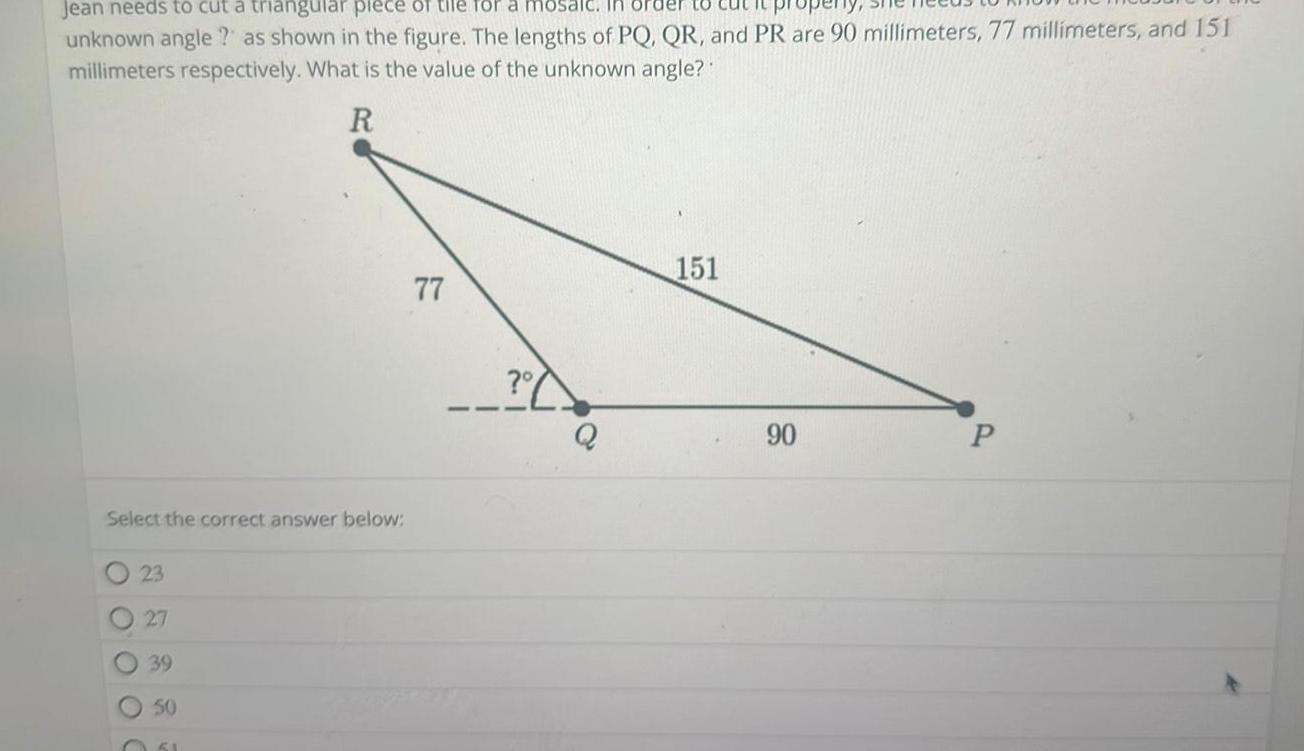
Calculus
Application of derivativesJean needs to cut a triangular piece of tile for a mosaic In unknown angle as shown in the figure The lengths of PQ QR and PR are 90 millimeters 77 millimeters and 151 millimeters respectively What is the value of the unknown angle R Select the correct answer below 23 27 39 50 051 77 Q 151 90 P
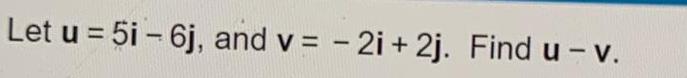
Calculus
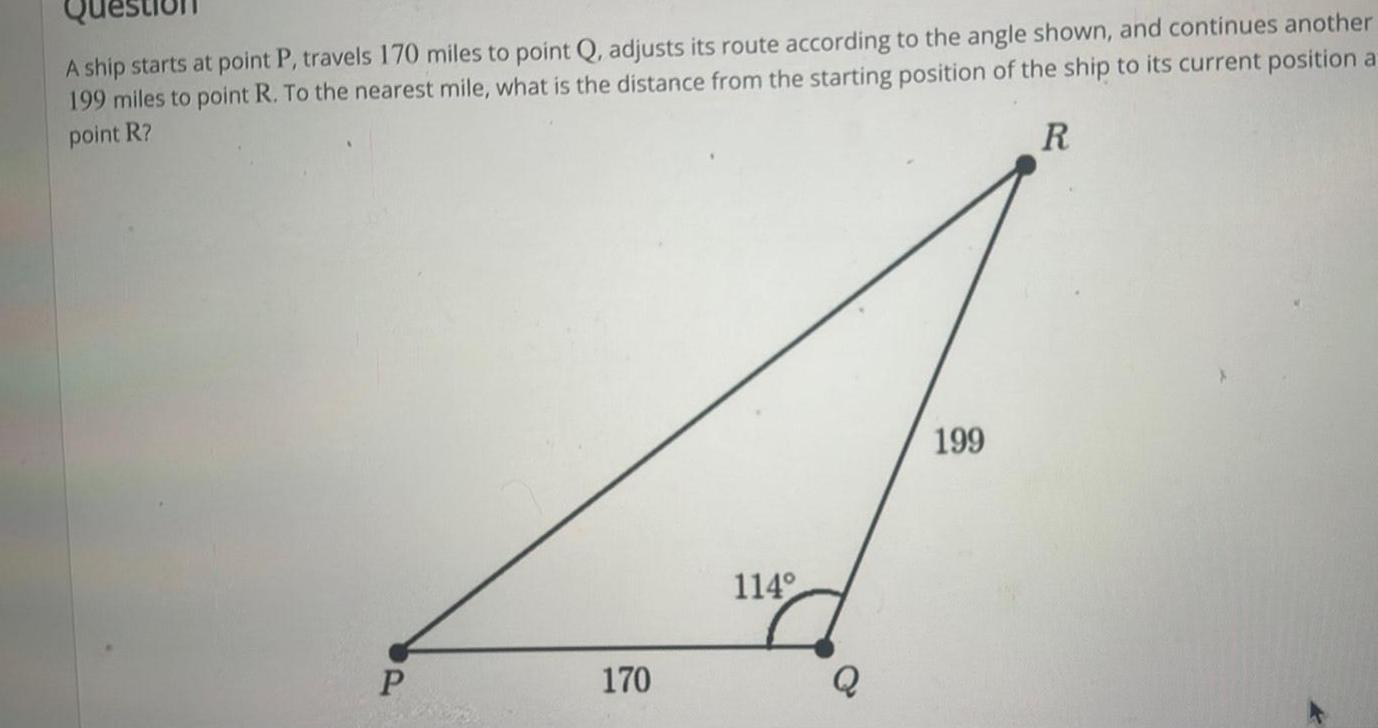
Application of derivativesA ship starts at point P travels 170 miles to point Q adjusts its route according to the angle shown and continues another 199 miles to point R To the nearest mile what is the distance from the starting position of the ship to its current position a point R R P 170 114 Q 199

Calculus
Application of derivativesTwo ships leave a harbor at the same time One ship travels on a bearing 15 W at 18 miles per hour The other ship travels on a bearing N75 E at 9 miles per hour How far apart will the ships be after 2 hours accom The distance is approximately miles Round to the nearest tenth as needed
Calculus
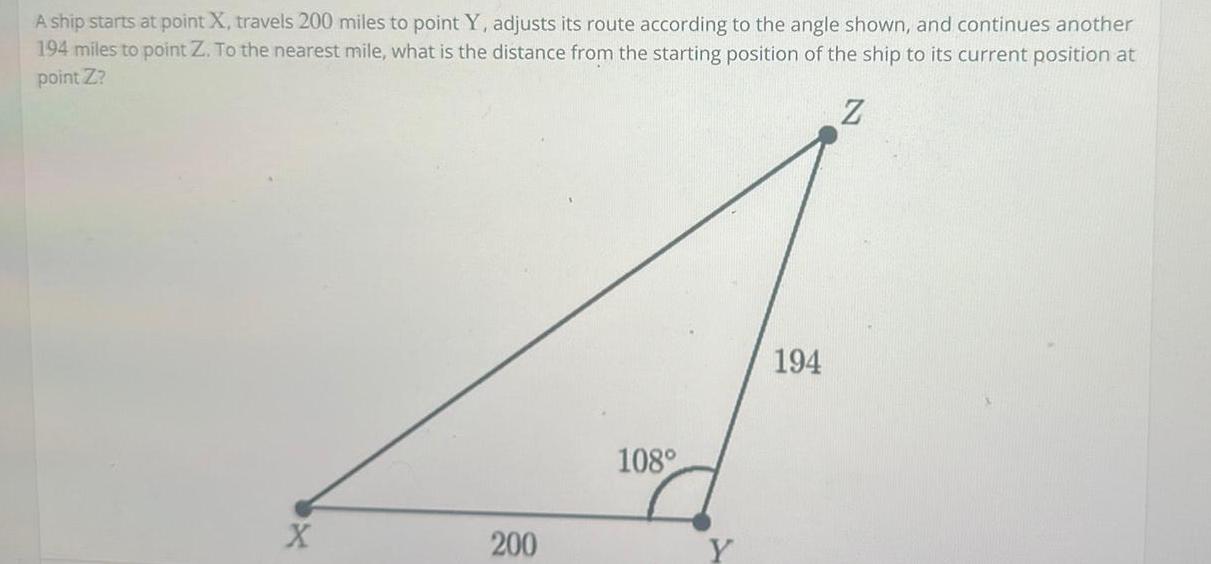
Application of derivativesA ship starts at point X travels 200 miles to point Y adjusts its route according to the angle shown and continues another 194 miles to point Z To the nearest mile what is the distance from the starting position of the ship to its current position at point Z Z X 200 108 194
Calculus
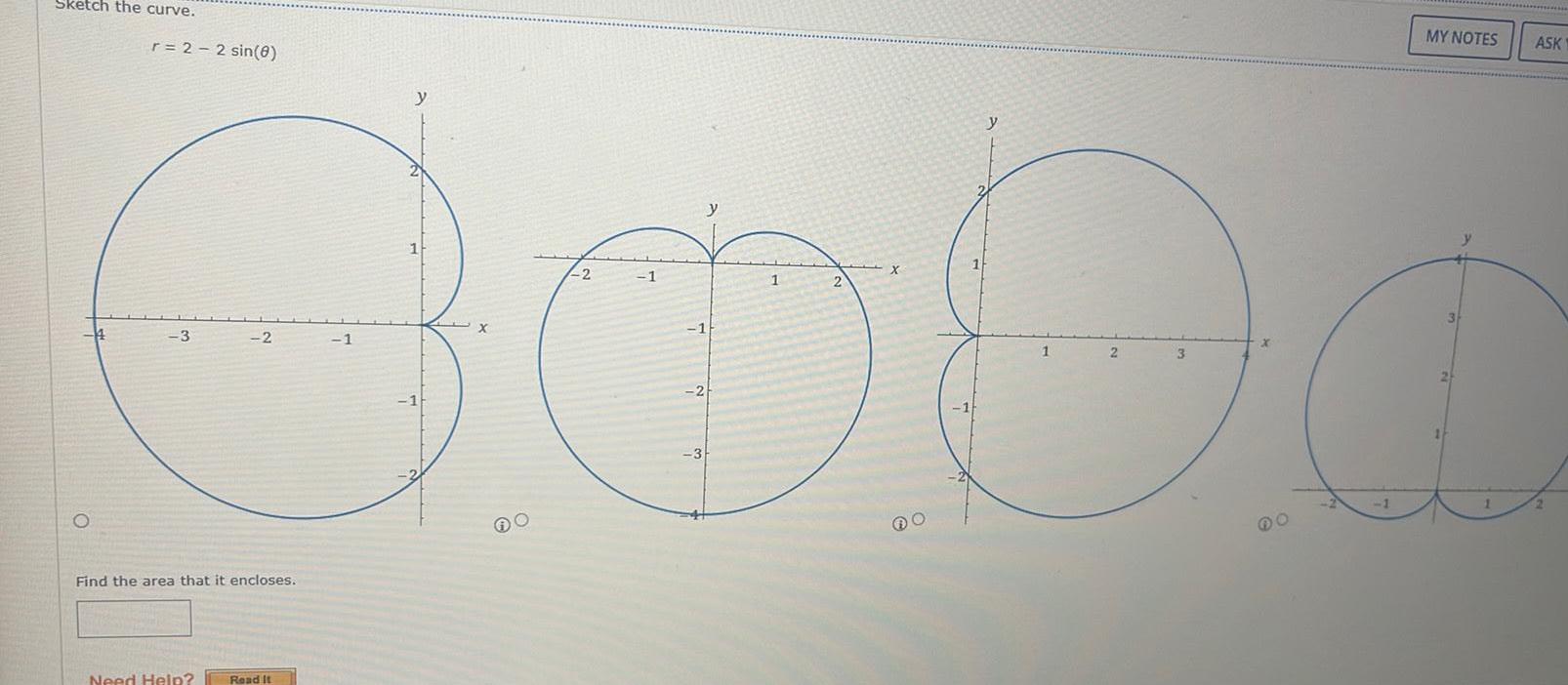
Application of derivativesSketch the curve r 2 2 sin 8 O y 1 X Co90 1 3 2 Find the area that it encloses Need Help Read It 1 y 2 y 1 2 MY NOTES 3 3 ASK 2
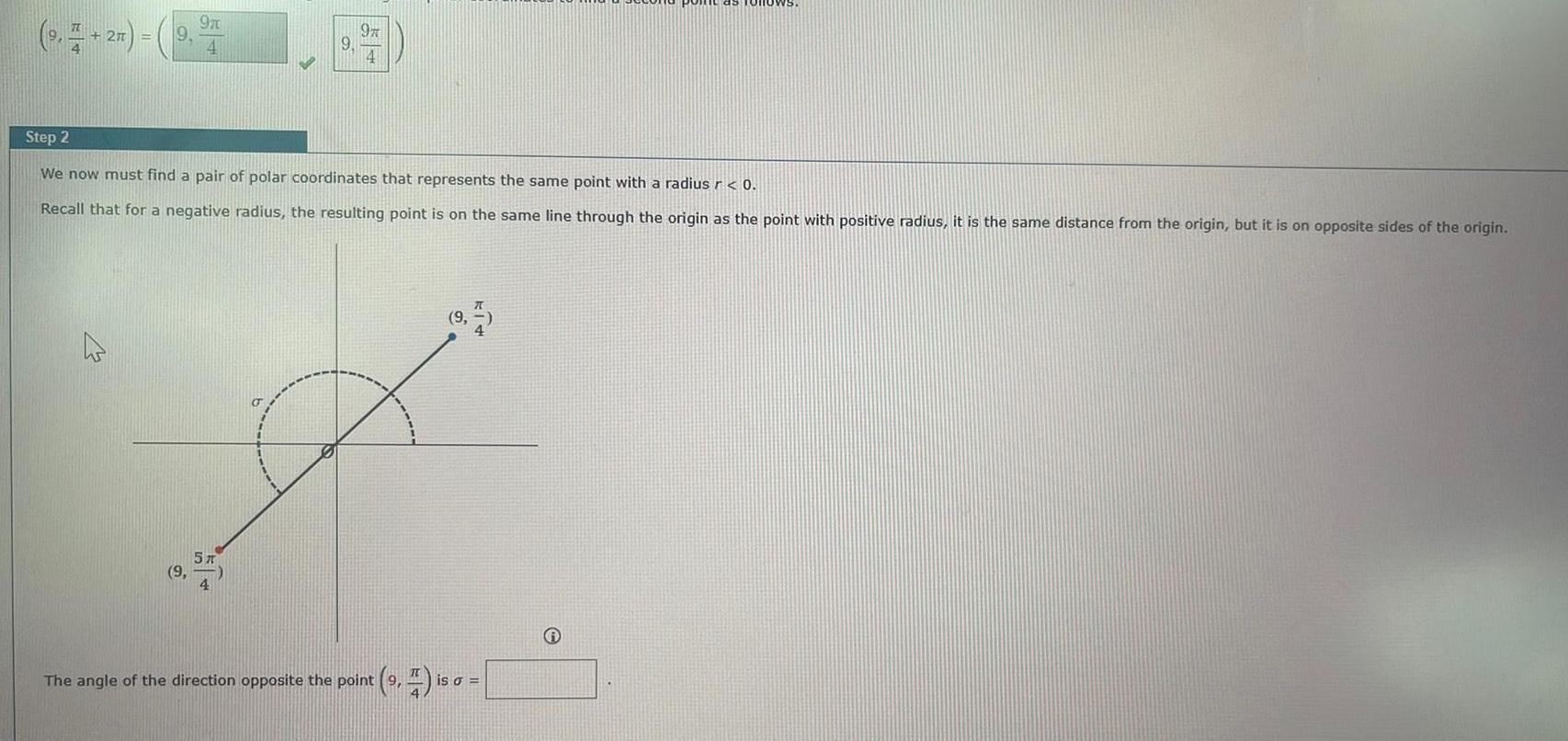
Calculus
Application of derivatives970 9 2m 9 4 I 97 4 Step 2 We now must find a pair of polar coordinates that represents the same point with a radius r 0 Recall that for a negative radius the resulting point is on the same line through the origin as the point with positive radius it is the same distance from the origin but it is on opposite sides of the origin 5 T 9 The angle of the direction opposite the point is 50
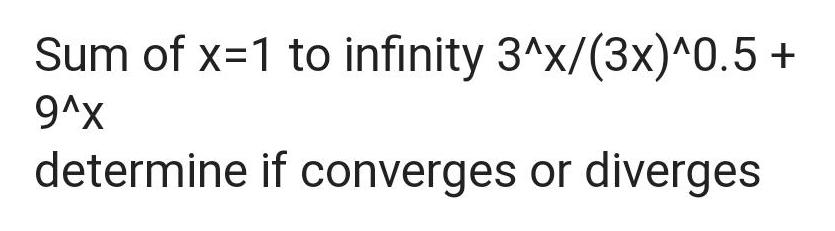
Calculus
Application of derivativesSum of x 1 to infinity 3 x 3x 0 5 9 x determine if converges or diverges
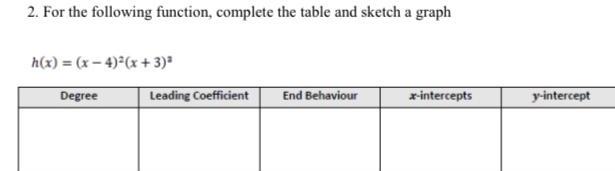
Calculus
Application of derivatives2 For the following function complete the table and sketch a graph h x x 4 x 3 Degree Leading Coefficient End Behaviour x intercepts y intercept
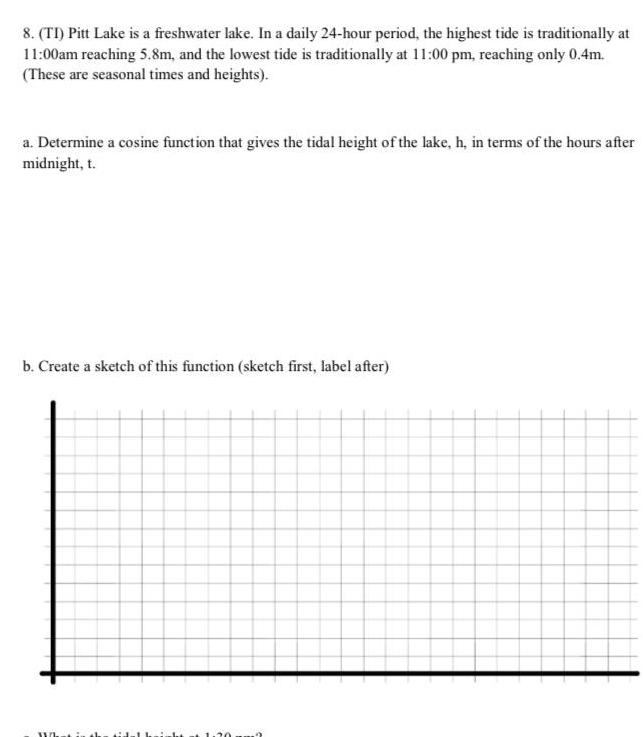
Calculus
Application of derivatives8 TI Pitt Lake is a freshwater lake In a daily 24 hour period the highest tide is traditionally at 11 00am reaching 5 8m and the lowest tide is traditionally at 11 00 pm reaching only 0 4m These are seasonal times and heights a Determine a cosine function that gives the tidal height of the lake h in terms of the hours after midnight t b Create a sketch of this function sketch first label after What is th 20

Calculus
Application of derivatives81 Christina travels on one street for 1 750 meters She then turns and travels on another street for 1 821 meters This route is represented in the figure by the sequence of points X Y Z According to the angle shown in the figure and the given information what is the distance to the nearest meter from Christina s house to school represented by the line from X to Z in the figure Provide your answer below X 1750 129 Y 1821 Z
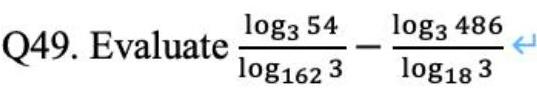

Calculus
Application of derivativesse Newton s method with the specified initial approx ation x to find x3 the third approxim x 1 0 X 2 X X3 1 53912 2

Calculus
Application of derivativesIf 19 200 cm2 of material is available to make a box with a square base and an open top find the largest possible volume of the box Step 1 We are given that the box has a square base and an open top Let b represent the length of the box s base and let h represent the height of the box each measured in cm Let V represent volume of the box measured in cm Writing an equation for Vin terms of b and h gives us the following V 256000 cm3 X Let S represent the surface area of the box measured in cm2 Writing an equation for S in terms of b and h gives us the following s b 4bh cm

Calculus
Application of derivativesGraph the following iction f x Label the vertical asymptote State the domain and range of the function f x log x Graph the given function f x Label the vertical asymptote Choose the correct graph The domain of this logarithmic function is Type your answer in interval notation The range of this logarithmic function is Type your answer in interval notation COL A O C f x f x B O D Af x G E G C E G

Calculus
Application of derivativesFind two numbers whose difference is 54 and whose product is a minimum Step 1 If two numbers have a difference of 54 and we let x represent the smaller of these two numbers then the larger of these two numbers is given by the foll 27 X
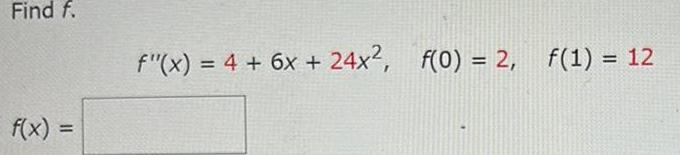
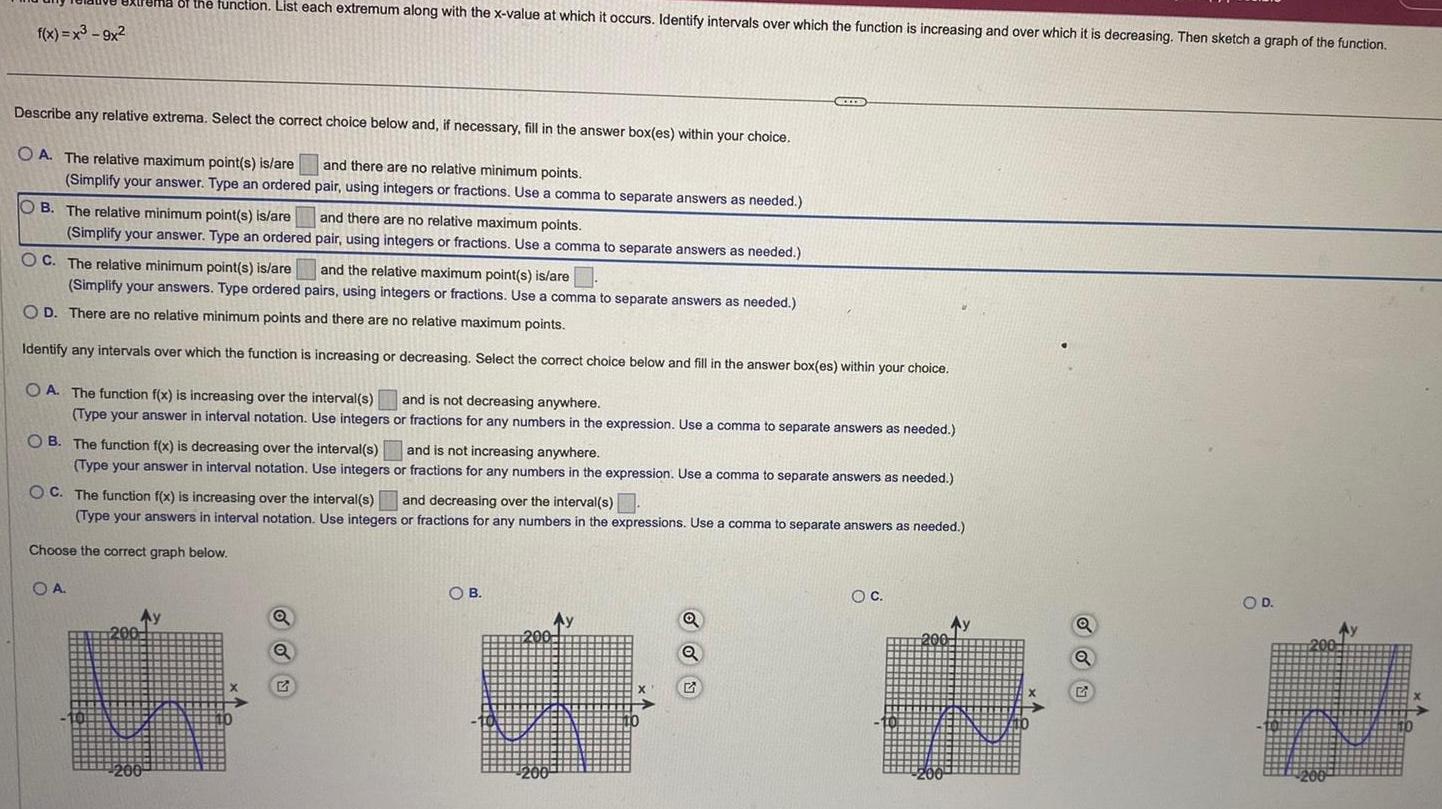
Calculus
Application of derivativesf x x 9x Tema of the function List each extremum along with the x value at which it occurs Identify intervals over which the function is increasing and over which it is decreasing Then sketch a graph of the function Describe any relative extrema Select the correct choice below and if necessary fill in the answer box es within your choice and there are no relative minimum points pair using integers or fractions Use a comma to separate answers as needed OA The relative maximum point s is are Simplify your answer Type an ordered OB The relative minimum point s is are Simplify your answer Type an ordered OC The relative minimum point s is are and there are no relative maximum points pair using integers or fractions Use a comma to separate answers as needed and the relative maximum point s is are Simplify your answers Type ordered pairs using integers or fractions Use a comma to separate answers as needed OD There are no relative minimum points and there are no relative maximum points Identify any intervals over which the function is increasing or decreasing Select the correct choice below and fill in the answer box es within your choice OA OA The function f x is increasing over the interval s and is not decreasing anywhere Type your answer in interval notation Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed OB The function f x is decreasing over the interval s and is not increasing anywhere Type your answer in interval notation Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed OC The function f x is increasing over the interval s and decreasing over the interval s Type your answers in interval notation Use integers or fractions for any numbers in the expressions Use a comma to separate answers as needed Choose the correct graph below 200 Ay Q OB Ay 200 200 Q Q G O C 200 Ay N Q O D 7

Calculus
Application of derivativesAssume that the equation exyz sin x y z implicitly defines z as a function of x y We will find using two methods z x a Go through and implicitly take partial derivatives with respect to x on both sides of the given equation treating z as a function of x and treating y as constant and remembering to use the chain rule when necessary Then solve for This is the method you learned in Calc I x b i Ignore the above equation for a moment and consider the general case where some equation F x y z 0 implicitly defines z as a function of x y Use the multivariable chain rule to find a general formula for x z ii Now use the formula you found to find az for the above example x

Calculus
Application of derivativesTwo artillery bases are located at the points P and R represented in the figure Each of the bases locates an enemy airplane at point Q and measures the angles of elevation to the airplane Given the elevation angles in the figure and the fact that the two bases are 662 meters apart what is the distance in meters from the base at point R to the airplane Round your answer to the nearest tenth if necessary
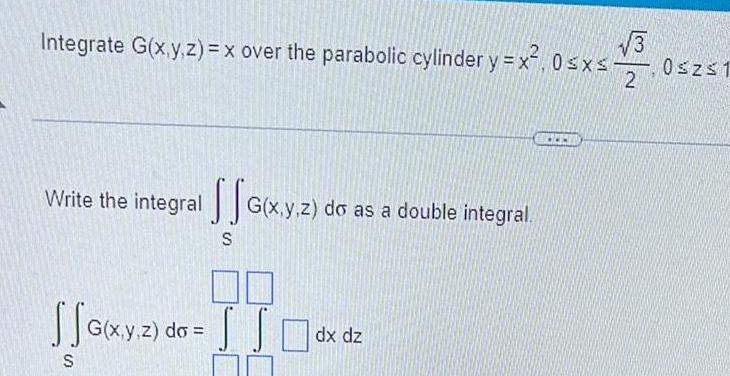
Calculus
Application of derivatives3 Integrate G x y z x over the parabolic cylinder y x 0 x 2 Write the integral G x y z do as a double integral S SS G x y z do SSO dx dz S 0 z 1
Calculus
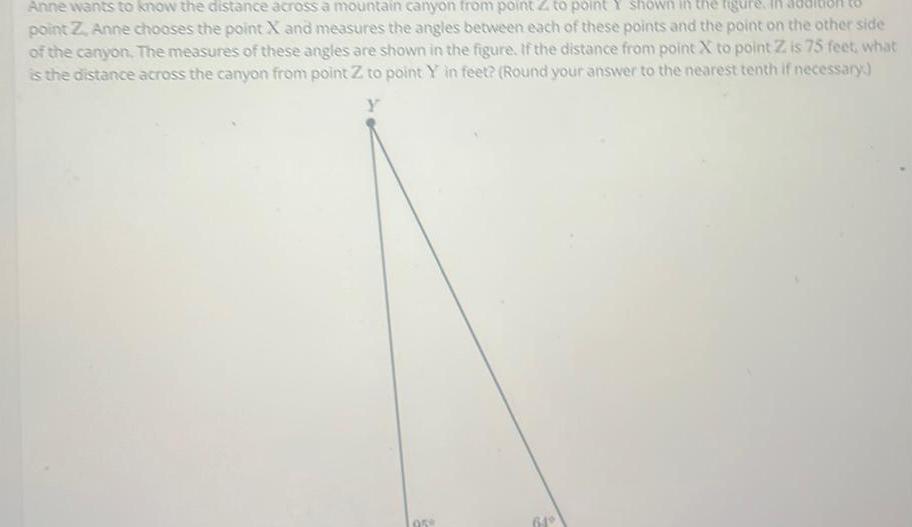
Application of derivativesAnne wants to know the distance across a mountain canyon from point Z to point Y shown in the figure point Z Anne chooses the point X and measures the angles between each of these points and the point on the other side of the canyon The measures of these angles are shown in the figure If the distance from point X to point Z is 75 feet what is the distance across the canyon from point Z to point Y in feet Round your answer to the nearest tenth if necessary Y 958

Calculus
Application of derivativesIn AABC sin B sin C and b 12 Find the side length c Select the correct answer below O c 1 2 Oc 2 4 O c 9 O c 42 c 24

Calculus
Application of derivativesTwo artillery bases are located at the points K and M represented in the figure Each of the bases locates an enemy airplane at point L and measures the angles of elevation to the airplane Given the elevation angles in the figure and the fact that the two bases are 485 meters apart what is the distance in meters from the base at point M to the airplane L
Calculus
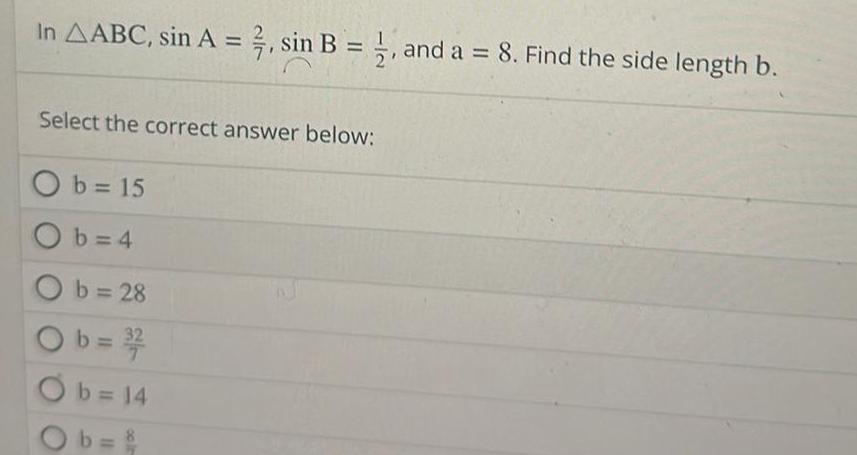
Application of derivativesIn AABC sin A 2 sin B 1 and a 8 Find the side length b Select the correct answer below Ob 15 Ob 4 Ob 28 b 3 7 Ob 14 Ob

Calculus
Application of derivativesConsider the autonomous differential equation Critical Point 1 Critical Point 2 Critical Point 3 Use a computer system of graphics calculator to plot a slope field and or enough solution curves to indicate the stability or instability of each critical point of the differential equation Some of these critical points may be semistable List the critical points in increasing order is is is dx dt x x 4

Calculus
Application of derivativesdy Let y t be the solution to d 7te satisfying y 0 3 dt a Use Euler s Method with time step h 0 2 to approximate y 0 2 y 0 4 y 1 0 ktk 00 10 2 20 4 30 6 40 8 51 0 Yk 3 b Use separation of variables to find y t exactly y t c Compute the error in the approximations to y 0 2 y 0 6 and y 1 y 0 2 Y y 0 6 Y3 ly 1 ys

Calculus
Application of derivativesdy Let y t be the solution to dr y satisfying y 0 2 dt Use Euler s Method with time step h 0 2 to approximate y 0 2 y 0 4 y 1 0 f tn yn Ay ntn 00 10 2 20 4 30 6 40 8 51 0 Yn 2 h 0 2 0 2 0 2 0 2 0 2

Calculus
Application of derivativesUse Green s Theorem to find the counterclockwise circulation and outward flux for the field F y 2x i 2x y j and curve C the triangle bounded by y 0 x 3 a The flux is Simplify your answer
Calculus
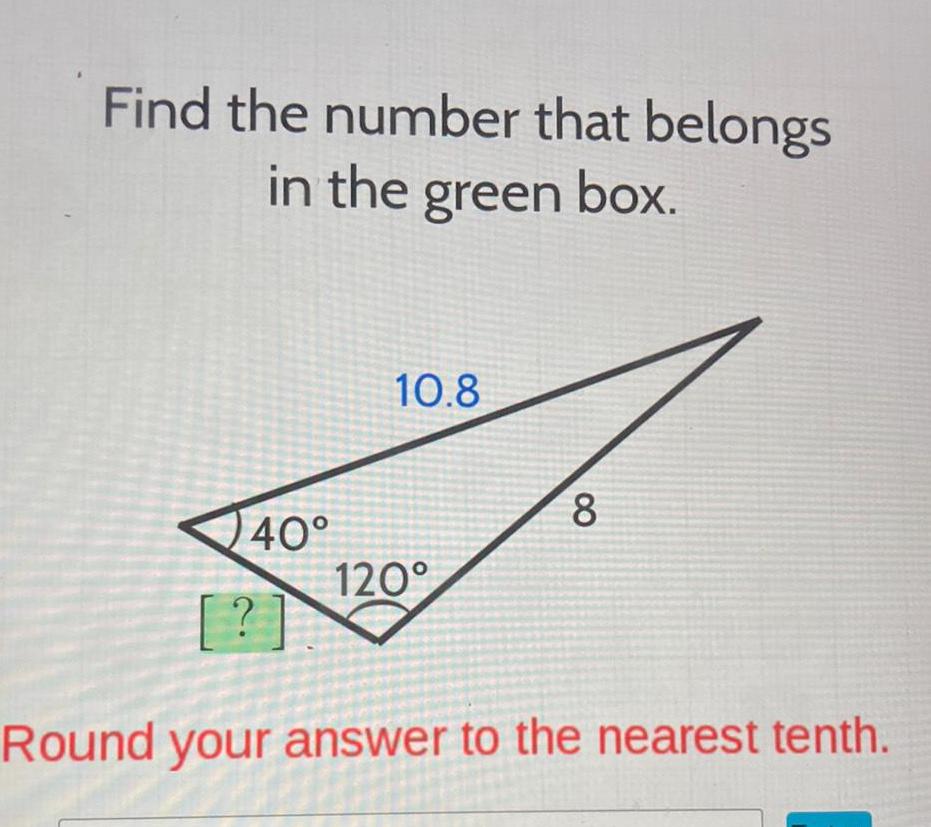
Application of derivativesFind the number that belongs in the green box 40 10 8 120 8 Round your answer to the nearest tenth
Calculus
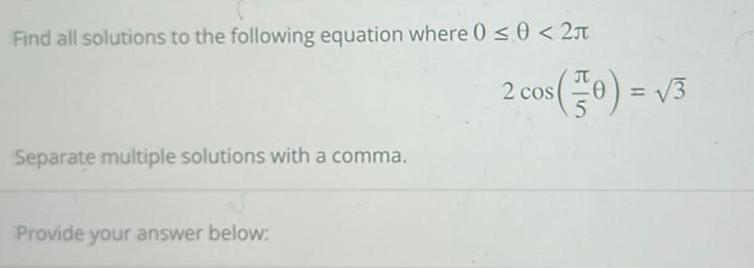
Application of derivativesFind all solutions to the following equation where 0 0 2 Separate multiple solutions with a comma Provide your answer below 2 cos 0 3
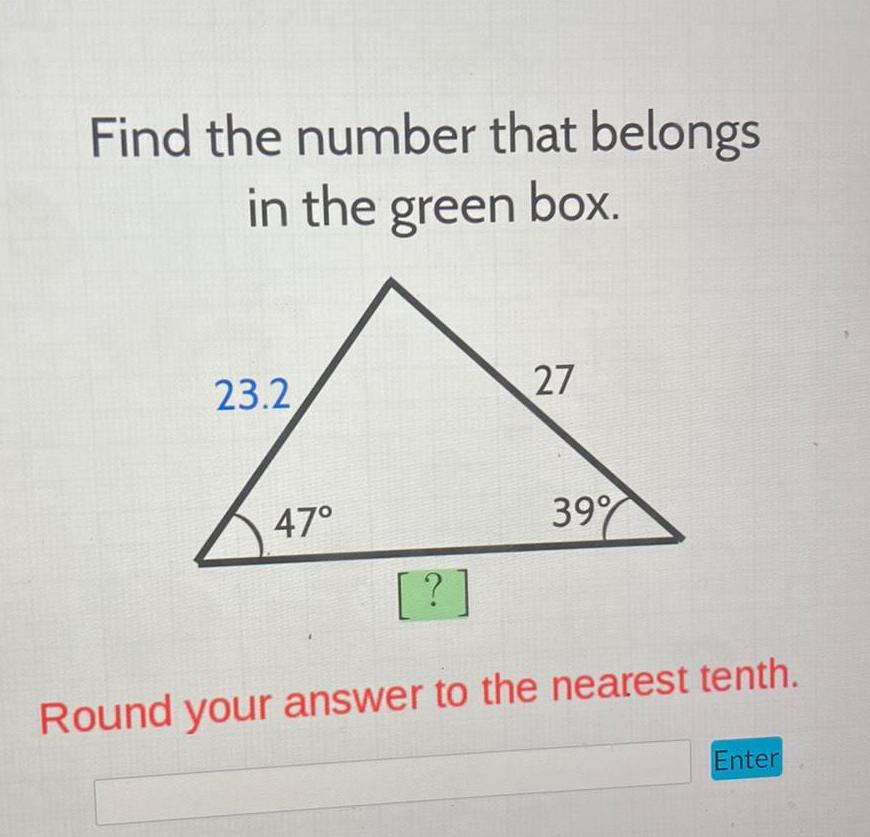
Calculus
Application of derivativesFind the number that belongs in the green box 23 2 47 27 39 Round your answer to the nearest tenth Enter