Application of derivatives Questions and Answers
Calculus
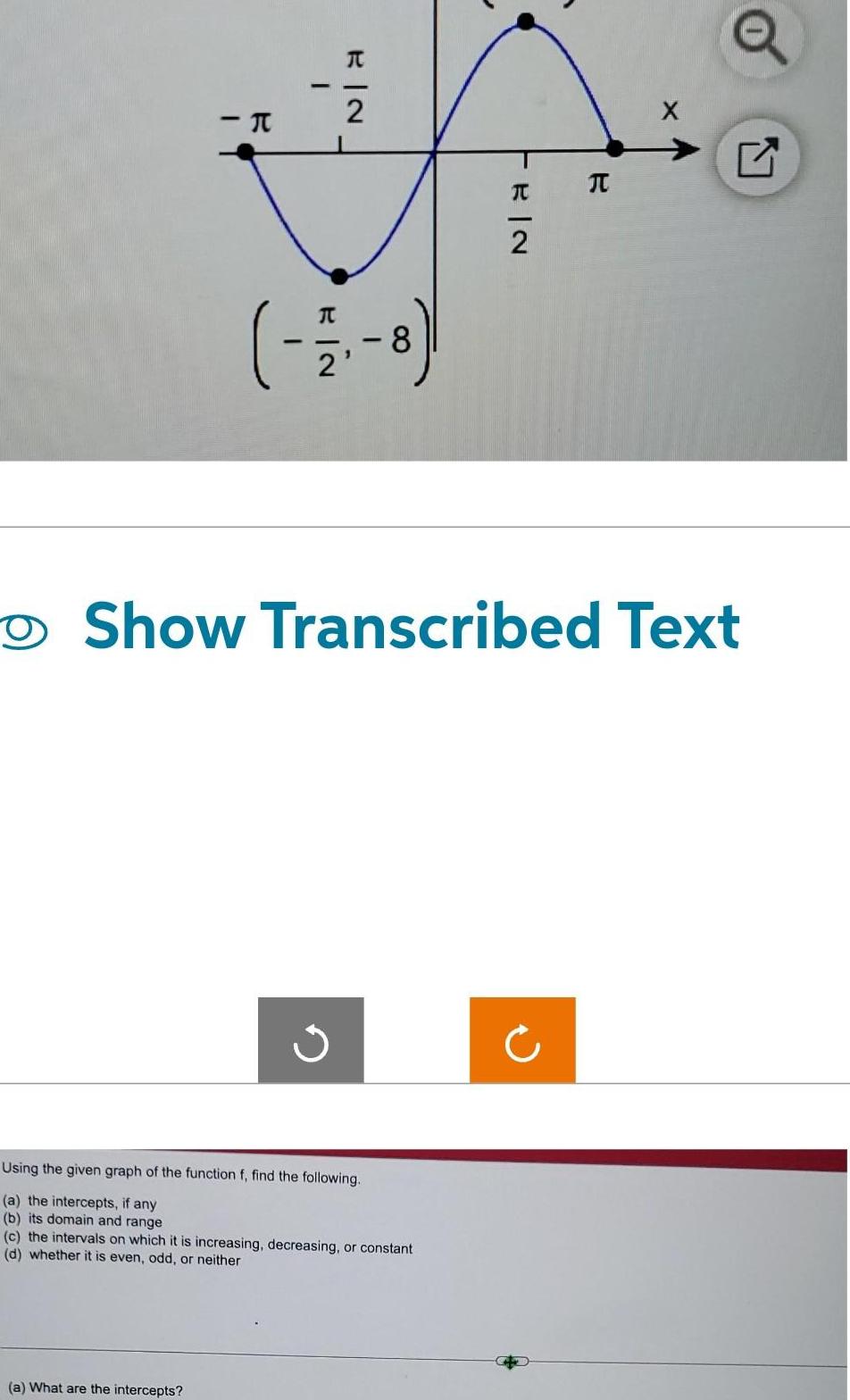
Application of derivativesI H I a What are the intercepts RIN 2 17 8 Using the given graph of the function f find the following a the intercepts if any b its domain and range c the intervals on which it is increasing decreasing or constant d whether it is even odd or neither FEIN 2 Show Transcribed Text R Q

Calculus
Application of derivativesC 2 Before drawing any more graphs let s see what members of this family have in common Since 3 lim x x 2x c for any value of c they all have the x axis as a horizontal asymptote A vertical asymptote will occur when c 1 there is no vertical asymptote the top graph above When c 1 the graph has a single vertical asymptote x 1 because 3 lim x 1 x 2x 1 0 f x Now we compute the derivative When c 1 there are two vertical asymptotes x 1 3 lim x 1 x 1 x 2x c This shows that f x 0 when x maximum value f 1 0 For c 1 this means that f increases on the interval in interval notation if c 1 f x 0 when x 1 and f x 0 when x 1 the bottom graph above For c 1 f 1 0 Solving this equation we get x 1 and decreases on the interval in interval notation For c 1 there is an absolute is a local maximum value and the intervals of increase and decrease are interrupted at the vertical asymptotes When The figures below are a slide show displaying five members of the family all graphed in the viewing rectangle 5 4 by 6 6 As predicted c 1 is a value at which a transition takes place from 0 as c co As c decreases two vertical asymptotes to one and then to none As c increases from 1 we see that the maximum point becomes lower this is explained by the fact that c 1 1

Calculus
Application of derivativesQuestion Solve the equation 3tan a 3tan a given that Separate your answers with commas

Calculus
Application of derivativesFind the antiderivative F off that satisfies the given condition Check your answer by comparing the graphs of f and F f x 2e 8x F 0 5 F x
Calculus
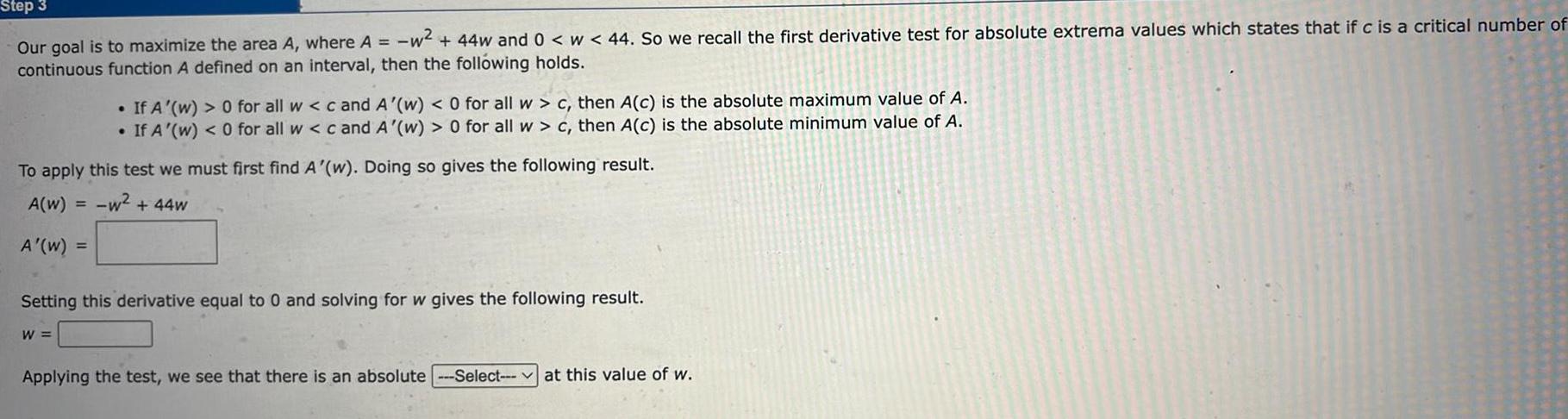
Application of derivativesStep 3 our goal is to maximize the area A where A w 44w and 0 w 44 So we recall the first derivative test for absolute extrema values which states that if c is a critical number of continuous function A defined on an interval then the following holds To apply this test we must first find A w Doing so gives the following result A W w 44w A W W If A w 0 for all w c and A w 0 for all w c then A c is the absolute maximum value of A If A w 0 for all w c and A w 0 for all w c then A c is the absolute minimum value of A Setting this derivative equal to 0 and solving for w gives the following result Applying the test we see that there is an absolute Select at this value of w

Calculus
Application of derivativesWe are given that the perimeter of the rectangle is 88 m Therefore P 88 We substitute this value into the perimeter equation determined in the previous step P 21 2w 88 2 2w We then solve the resulting equation for I 88 2 2w 1 Next we substitute this expression for into the area equation determined in the previous step and expand the result A lw A w Recalling that area must be greater 0 we note that this equation is valid when 0 W

Calculus
Application of derivativesWe have determined that the absolute minimum of f x occurs at x 28 where x is the smaller of the two numbers whose product we wish to minimize Recall that the other number is given by x 56 Thus the two numbers whose difference is 56 and whose product is a minimum are as follows smaller number larger number

Calculus
Application of derivativesWe wish to minimize this function so we recall the first derivative test for absolute extrema values which states that if c is a critical number of a continuous function f defined on an interv then the following holds If f x 0 for all x c and f x 0 for all x c then f c is the absolute maximum value of f If f x 0 for all x c and f x 0 for all x c then f c is the absolute minimum value of f To apply this test we must first find f x Doing so gives the following result f x x 56x f x Setting this derivative equal to 0 and solving for x gives the following result X Applying the test we see that there is an absolute Select at this value of x

Calculus
Application of derivativesIf C x is the cost of producing x units of a commodity then the average cost per unit is c x C x 3 000 110x 6x 2 a Find the total cost in dollars at a production level of 1 000 units b Find the average cost in dollars per unit at a production level of 1 000 units per unit c Find the marginal cost in dollars per unit at a production level of 1 000 units per unit d Find the production level in units that will minimize the average cost units e What is the minimum average cost in dollars per unit per unit C x X Consider the cost function C x given below Round your answers to the nearest cent

Calculus
Application of derivativesIf 30 000 cm of material is available to make a box with a square base and an open top find the largest possible volume in cm of the box 3 cm

Calculus
Application of derivativesConsider the following problem a farmer with 750 feet of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle What is largest possible total area of the four pens a Draw several diagrams illustrating the situation some with shallow wide pens and some with deep narrow pens Find the total areas of these configurations Does it appear that there is maximum area If so estimate it b Draw a diagram illustrating the general situation Let x denote the length of each of two sides and three dividers Let y denote the length of the other two sides c Write an expression for the total area A in terms of both x and y A d Use the given information to write an equation that relates the variables e Use part d to write the total area as a function of one variable A x f Finish solving the problem by finding the largest area in ft ft
Calculus
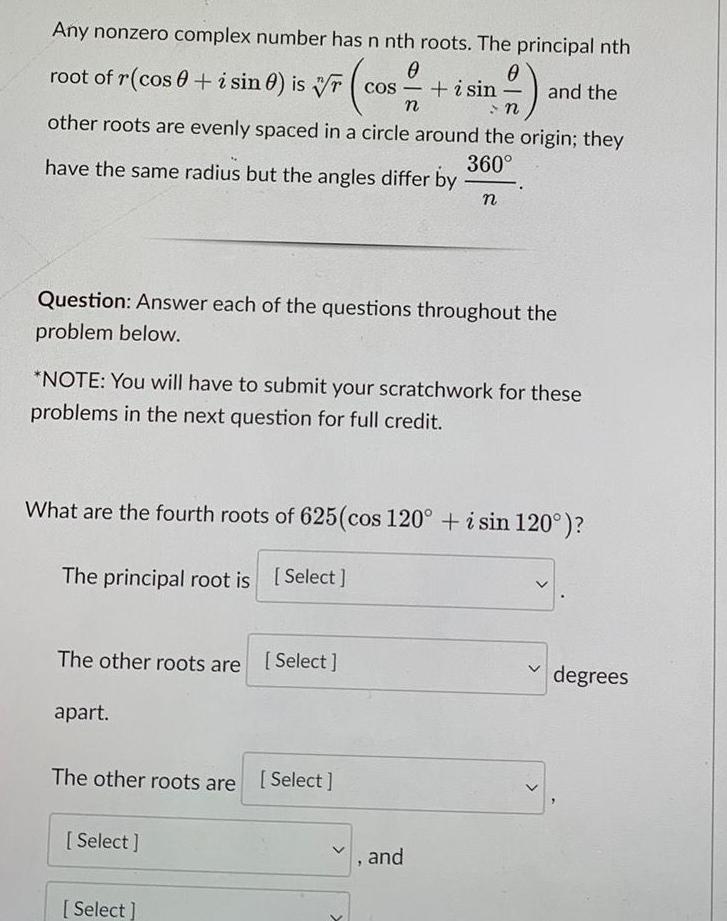
Application of derivativesAny nonzero complex number has n nth roots The principal nth root of r cos i sin 0 is rcos i sin 0 cos n other roots are evenly spaced in a circle around the origin they have the same radius but the angles differ by 360 Question Answer each of the questions throughout the problem below NOTE You will have to submit your scratchwork for these problems in the next question for full credit The other roots are Select apart What are the fourth roots of 625 cos 120 i sin 120 The principal root is Select The other roots are Select Select and the n Select 7 and degrees
Calculus
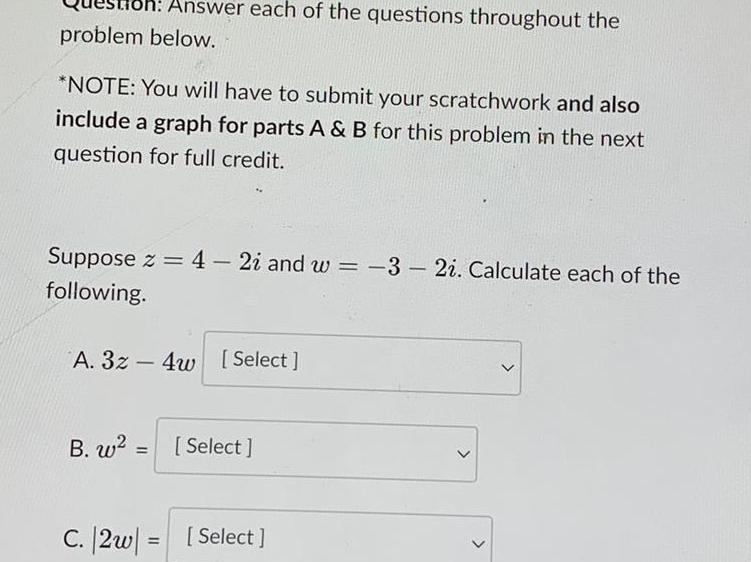
Application of derivativesoh Answer each of the questions throughout the problem below NOTE You will have to submit your scratchwork and also include a graph for parts A B for this problem in the next question for full credit Suppose z 4 2i and w 3 2i Calculate each of the following A 3z4w Select B w Select C 2w Select

Calculus
Application of derivativesSuppose oil spills from a ruptured tanker and spreads in a circular pattern If the radius of the oil increases at a constant rate of 2cm sec how fast is the area of the spill increasing when the radius is 30cm 607T 120 T 900TT
Calculus
Application of derivativesLet g be the function given by g x x At what value of x on the closed interval 1 1 does g have an absolute maximum O 1 0 1 04 3
Calculus
Application of derivativesHow many points of inflection are on the graph of the function f x 12x 14x 7x 9 Select the correct answer O O O O 0 1 2 3 4

Calculus
Application of derivativesFind the values of a for which y ea satisfies the equation y 4y 8 a 1 and a 1 a 3 and a 3 a 1 and a 3 a 1 and a 3

Calculus
Application of derivativesDifferentiate the function Y O e e e e O2e 2e 2 ez e O 4 e e 0 4 O ez e z x ete ex e

Calculus
Application of derivativesCalculate the derivatives of the following function sin 1 x x Ocos x x 1 sin O 1 2 3 ONA 2 1 x 3 x 1 1 x 2

Calculus
Application of derivativesf x 13 0 1 02 3 5 17 28 41 Selected values of a differentiable function f are given in the table above What is the fewest possible number of values of c in the interval 0 11 for which the Mean Value Theorem guarantees that f c 4
Calculus
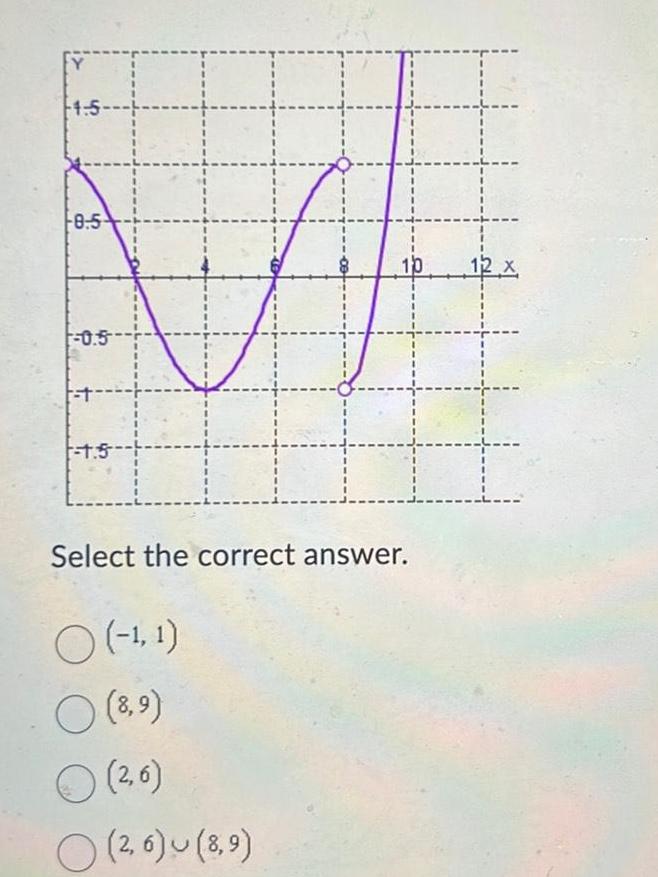
Application of derivatives4 5 8 5 0 5 1 5 10 Select the correct answer O 1 1 8 9 2 6 O 26 u 8 9 12 x

Calculus
Application of derivativesFind the critical numbers of f x x x 3 Select the correct answer 27 7 20 O 0 2 O 0 3 0 3 22 1 7 2 2 2 O 0 2 0 2 1 1 12 2 7 0 2 12
Calculus
Application of derivativesFind the inflection points for the function given f x 8x 2 sinx 0 x 3x Select the correct answer 8x 2x 16x 2 x 2 2 16x 2 x 8x 2 2x 16x 2 x 8x 2x 16x x 8x 2 2 16x
Calculus
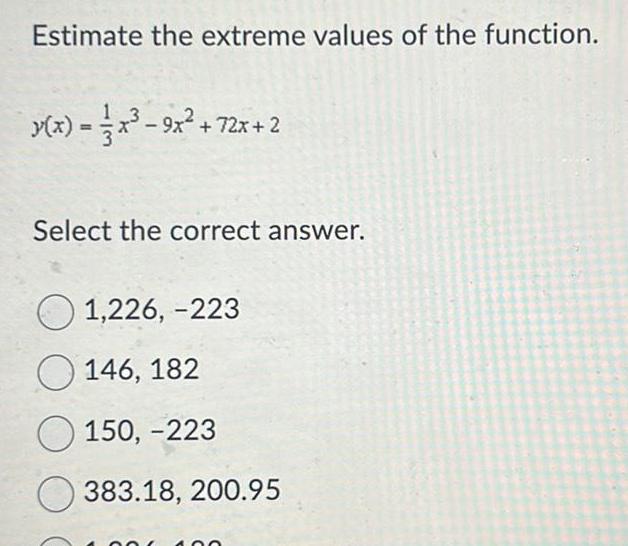
Application of derivativesEstimate the extreme values of the function y x x 9x 72x 2 Select the correct answer 1 226 223 146 182 150 223 383 18 200 95 O

Calculus
Application of derivativesFind the number c that satisfies the conclusion of the Mean Value Theorem on the given interval f x 2 x 0 9 Select the correct answer Oc 914 c 0 Oc 1 4 Oc s none of these

Calculus
Application of derivatives1 point Use the Wronskian to show that the functions y e x and y ex are linearly independent Wronskian det These functions are linearly independent because the Wronskian Choose zero for all x
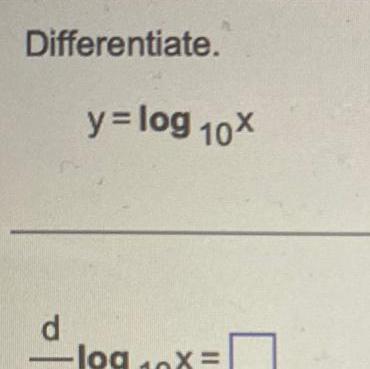

Calculus
Application of derivativesidentify a1 r and n for the sum of the geometric series 1 2 38 9 32 27 128 81 512
Calculus
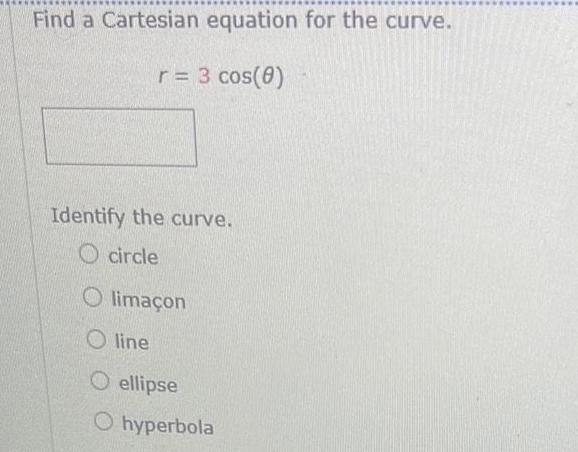
Application of derivativesFind a Cartesian equation for the curve r 3 cos 0 Identify the curve circle Olima on Oline O ellipse Ohyperbola

Calculus
Application of derivativesStudents in a zoology class took a final exam They took equivalent forms of the exam at monthly intervals thereafter After t months the average score S t as a percentage was found to be given by the following equation where t20 Complete parts a through e below S t 81 15 In t 1 Osts80 a What was the average score when they initially took the test The average score was Round to one decimal place as needed b What was the average score after 4 months The average score after 4 months was Round to one decimal place as needed c What was the average score after 24 months The average score after 24 months was Round to one decimal place as needed d Find S t S t e Find S 4 and S 24 and interpret the meaning of these numbers S 4 which means that after 4 months the average score is Type integers or decimals by points a month and S 24 which means that after 24 months the average score is by points a month


Calculus
Application of derivativesFind the length of the minor axis of an ellipse if the vertices are located at 5 7 and 5 3 and the foci are at 5 6 and 5 2 Thanks
Calculus
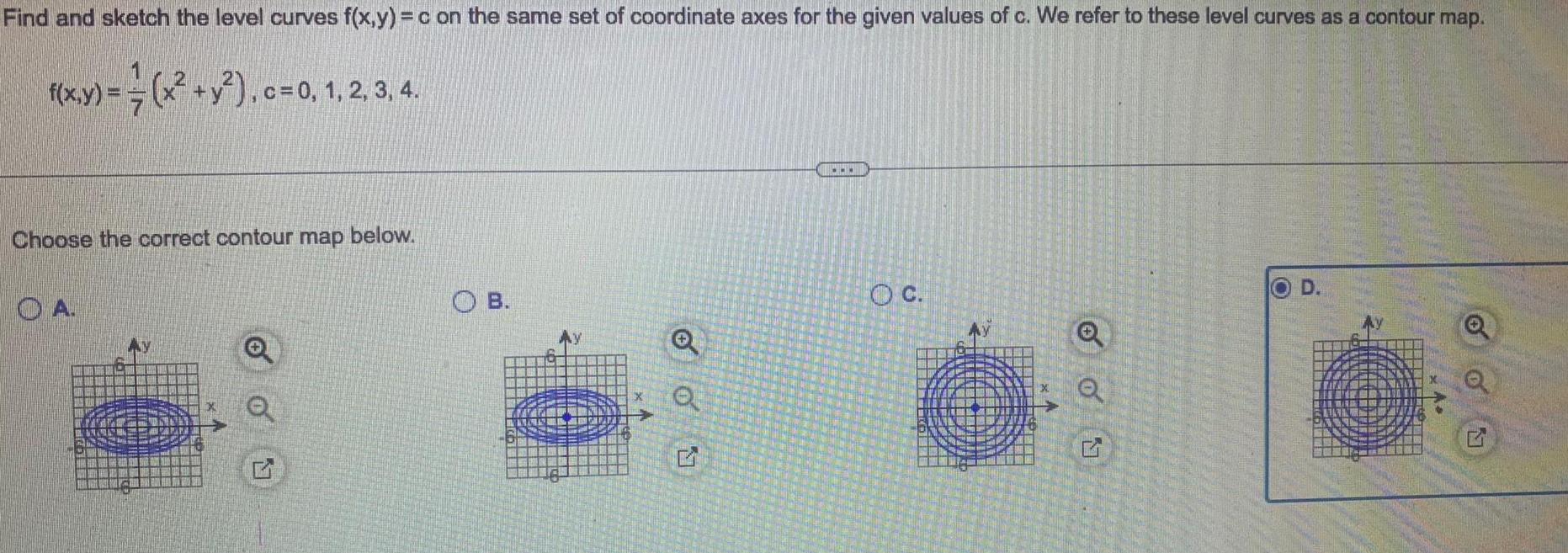
Application of derivativesFind and sketch the level curves f x y c on the same set of coordinate axes for the given values of c We refer to these level curves as a contour map 1 x y c 0 1 2 3 4 Choose the correct contour map below OA 00 1 OB OON e OC 6 Q G OD
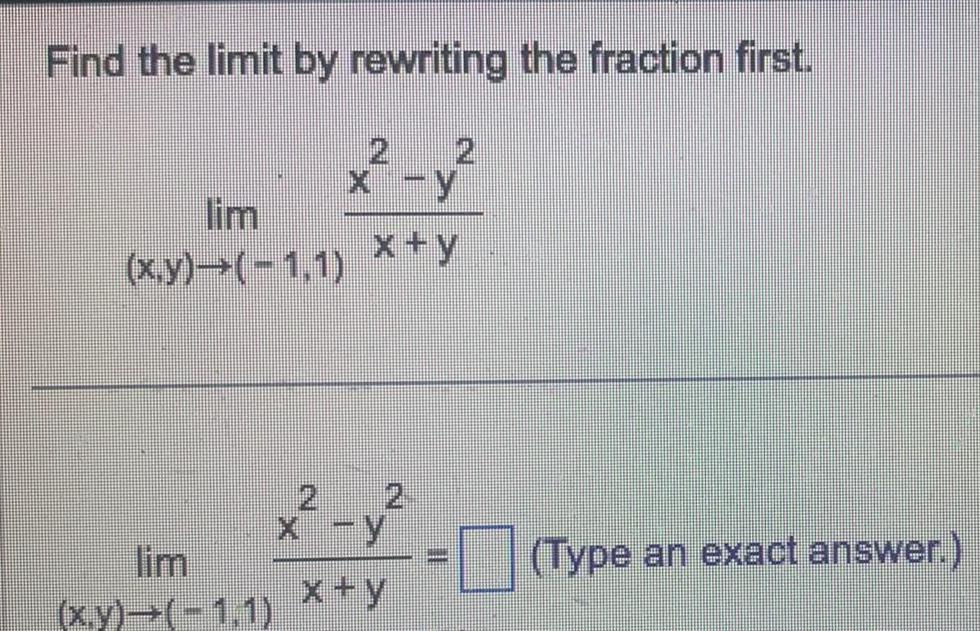
Calculus
Application of derivativesFind the limit by rewriting the fraction first lim x y 1 1 lim x y 1 1 y x y x y x y III Type an exact answer
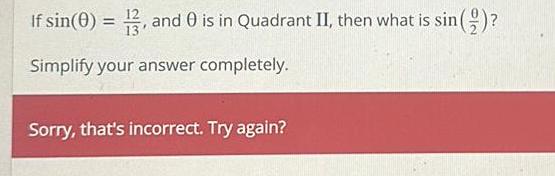
Calculus
Application of derivativesIf sin 0 13 and 0 is in Quadrant II then what is sin Simplify your answer completely Sorry that s incorrect Try again

Calculus
Application of derivativesConsidering only the values of 0 for which sec 0cos 20 is defined sec 0cos 20 Select the correct answer below 2sin 0 tan 0 csc 0 2 O2 sec 0

Calculus
Application of derivativesCalculate f 8x 6 dx given the following 7 7 7 8 7 x dx 93 1x dx 100 xcx 20 169 33 3 2 7 7 4 8x 6 dx

Calculus
Application of derivativesCalculate 5x x dx given the following 9 9 5 5 x cx 804 3 10 Sx dx 271 3 9 5 5x x dx Type an integer or a simplified fraction xdx 28

Calculus
Application of derivativesGiven that sin 0 213 and is in Quadrant II what is cos 20 2 13 Provide your answer below 20

Calculus
Application of derivativesConsidering only the values of for which csc cos 23 is defined which of the following expressions is equivalent to csc cos 23 Select the correct answer below 2 O2 sec O2sin tan 2sin 6 O cor B 1
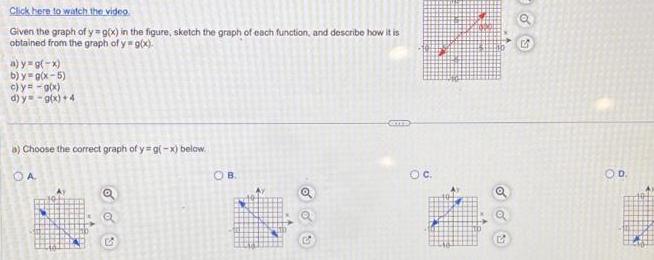
Calculus
Application of derivativesClick here to watch the video Given the graph of y g x in the figure sketch the graph of each function and describe how it is obtained from the graph of y g x a y g x b y g x 5 c y g x d y g x 4 a Choose the correct graph of y g x below OA OOS OB M GYES a OD
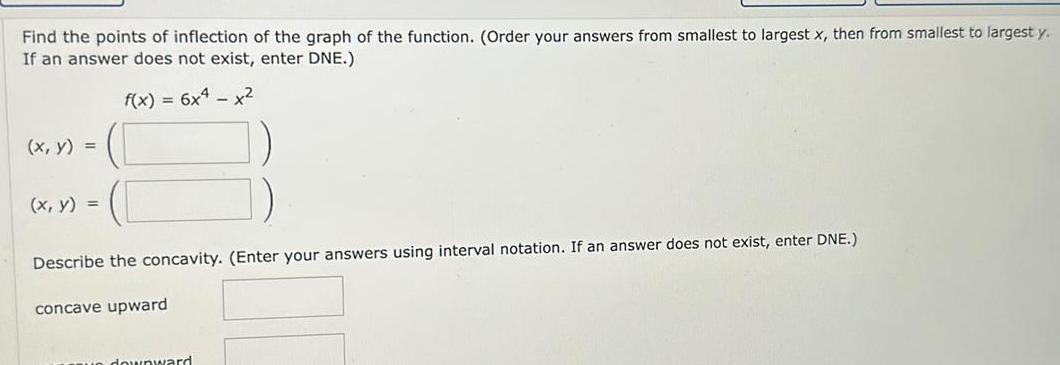
Calculus
Application of derivativesFind the points of inflection of the graph of the function Order your answers from smallest to largest x then from smallest to largest y If an answer does not exist enter DNE f x 6x4 x x y x y Describe the concavity Enter your answers using interval notation If an answer does not exist enter DNE concave upward downward
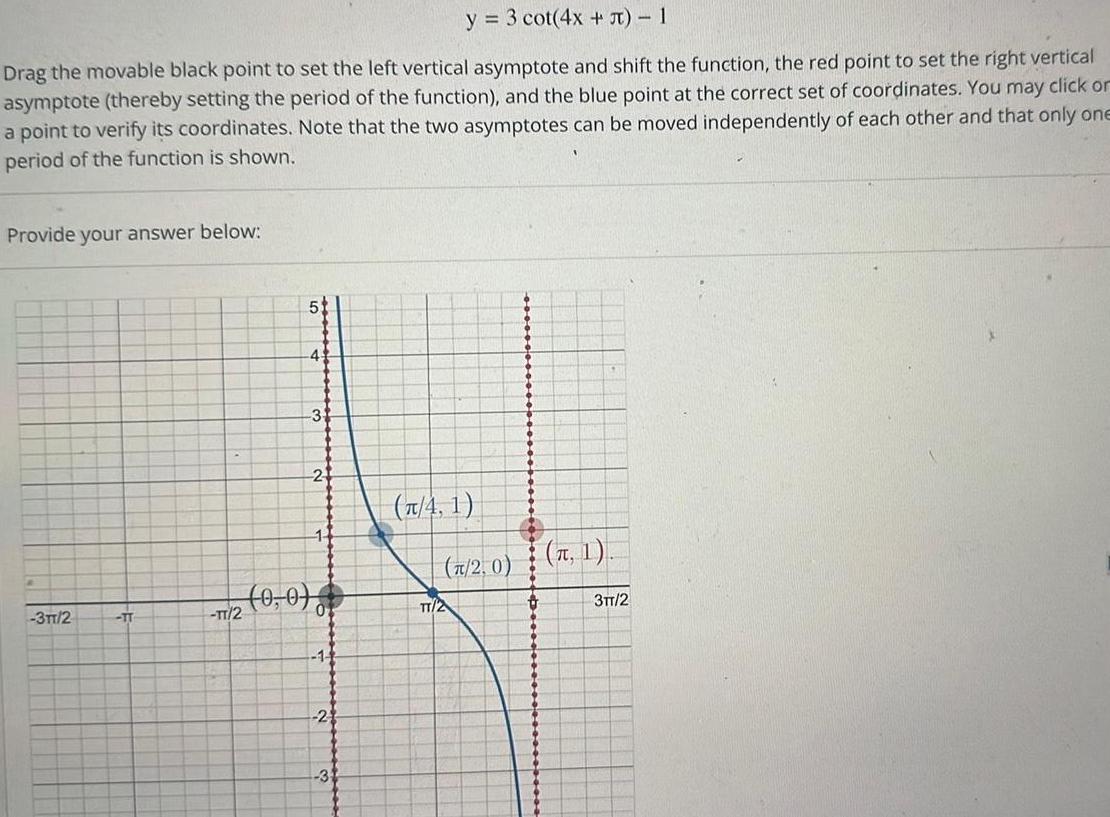
Calculus
Application of derivativesy 3 cot 4x 1 Drag the movable black point to set the left vertical asymptote and shift the function the red point to set the right vertical asymptote thereby setting the period of the function and the blue point at the correct set of coordinates You may click or a point to verify its coordinates Note that the two asymptotes can be moved independently of each other and that only one period of the function is shown Provide your answer below 3TT 2 TT 5 4 3 2 1 1 72 0 0 1 2 3 4 1 2 0 TT 2 6 D 1 3TT 2

Calculus
Application of derivativesFind the extrema and points of inflection if any exist of the function Use a graphing utility to graph the function and confirm your results If an answer does not exist enter DNE f x x 1 e x x y minimum maximum point of inflection x y x y
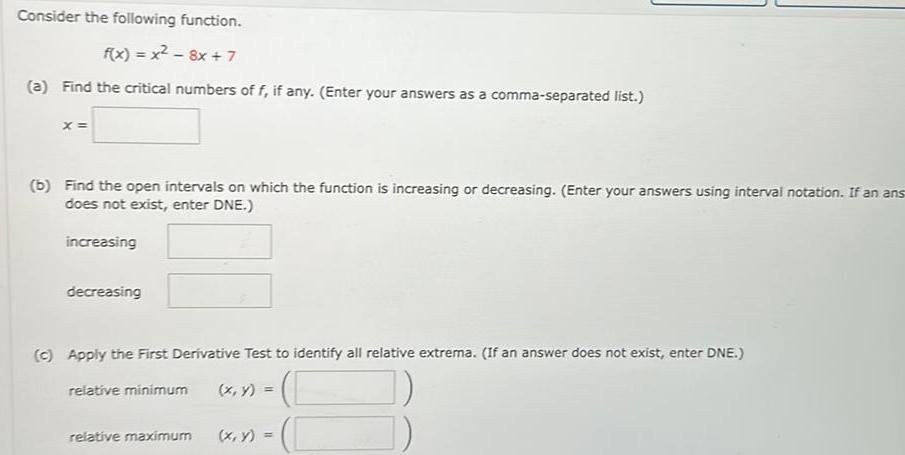
Calculus
Application of derivativesConsider the following function f x x 8x 7 a Find the critical numbers of f if any Enter your answers as a comma separated list X b Find the open intervals on which the function is increasing or decreasing Enter your answers using interval notation If an ans does not exist enter DNE increasing decreasing c Apply the First Derivative Test to identify all relative extrema If an answer does not exist enter DNE relative minimum x y relative maximum x y

Calculus
Application of derivativesThe radius r of a circle is increasing at a rate of 7 centimeters per minute Find the rate of change of the area when r 35 centimet cm min

Calculus
Application of derivatives1 point Let S 1 represent the amount of a chemical reactant present at time t where i 20 Assume that S t can be determined by solving the initial value problem S aS K S and S 0 So where a K and So are positive constants Obtain an implicit solution of the initial value problem The differential equation often referred to as the Michaelis Menten equation arises in the study of biochemical reactions Enter the constant So as SO with a zero not the letter O help equations

Calculus
Application of derivativesSolve sin 5x cos 8x cos 5x sin 8x 0 8 for the smallest positive solution X Give your answer accurate to two decimal places

