Application of derivatives Questions and Answers

Calculus
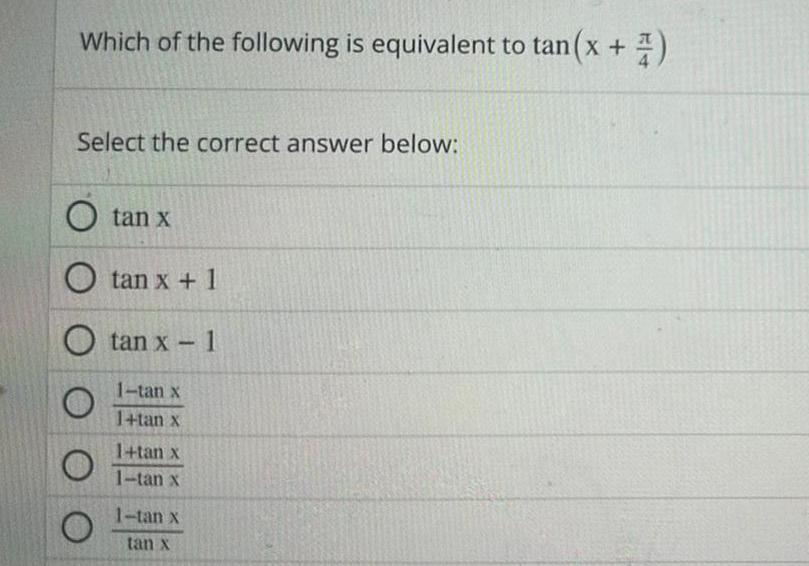
Application of derivativesWhich of the following is equivalent to tan x 2 Select the correct answer below O tan x O tan x 1 O tan x 1 1 tan x 1 tan x O 1 tan x 1 tan x 1 tan x tan x
Calculus
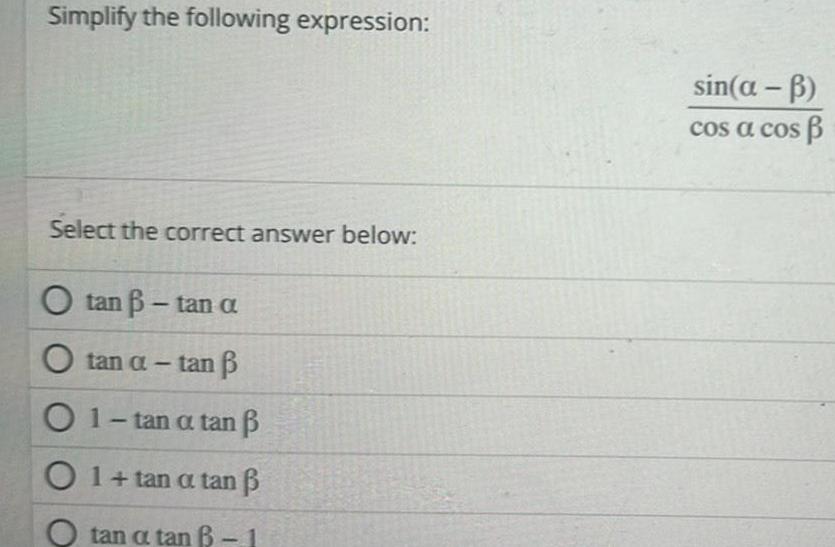
Application of derivativesSimplify the following expression Select the correct answer below O tan tan a tan a tan 01 tan a tan p O 1 tan a tan tan a tan B 1 sin a b cos a cos p

Calculus
Application of derivativesSimplify the following expression using the sum and difference identities 5 Cos 7 COS Select the correct answer below cos 3 O sin 3 COS 11 O sin 1 4 O sin 4 COS COS sin 5 57 sin 7

Calculus
Application of derivativesPrevi 1 point A spaceship is traveling directly away from earth with speed 412 4 km s At time t 0 s it is 500 km from earth How far is it from earth on minute after time t 0 s Include units in your answer Distance help units

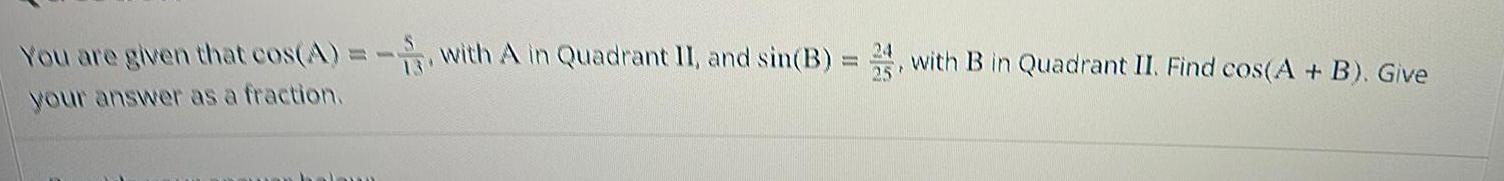
Calculus
Application of derivativesYou are given that cos A with A in Quadrant II and sin B 2 with B in Quadrant II Find cos A B Give your answer as a fraction

Calculus
Application of derivativesThe population of deer in a forest can be modeled with the sinusoidal function p 6000cos 1 51000 where t is the number of years after 1976 To the nearest whole number what was the population in the year 1994 NOTE The angle is in radians Provide your answer below
Calculus
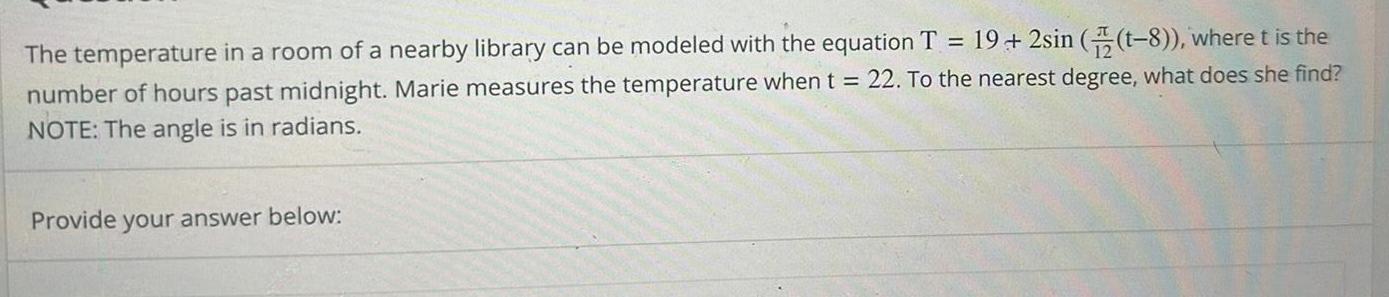
Application of derivatives19 2sin t 8 where t is the The temperature in a room of a nearby library can be modeled with the equation T number of hours past midnight Marie measures the temperature when t 22 To the nearest degree what does she find NOTE The angle is in radians Provide your answer below

Calculus
Application of derivativesQuestion You are given that cos A 3 with A in Quadrant I and sin B answer as a fraction answer below 2 with B in Quadrant I Find sin A 1
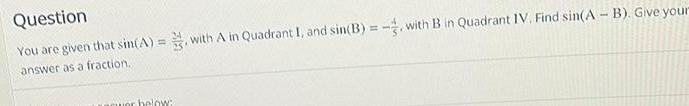
Calculus
Application of derivativesQuestion You are given that sin A with A in Quadrant I and sin B with B in Quadrant IV Find sin A B Give your answer as a fraction aquer below
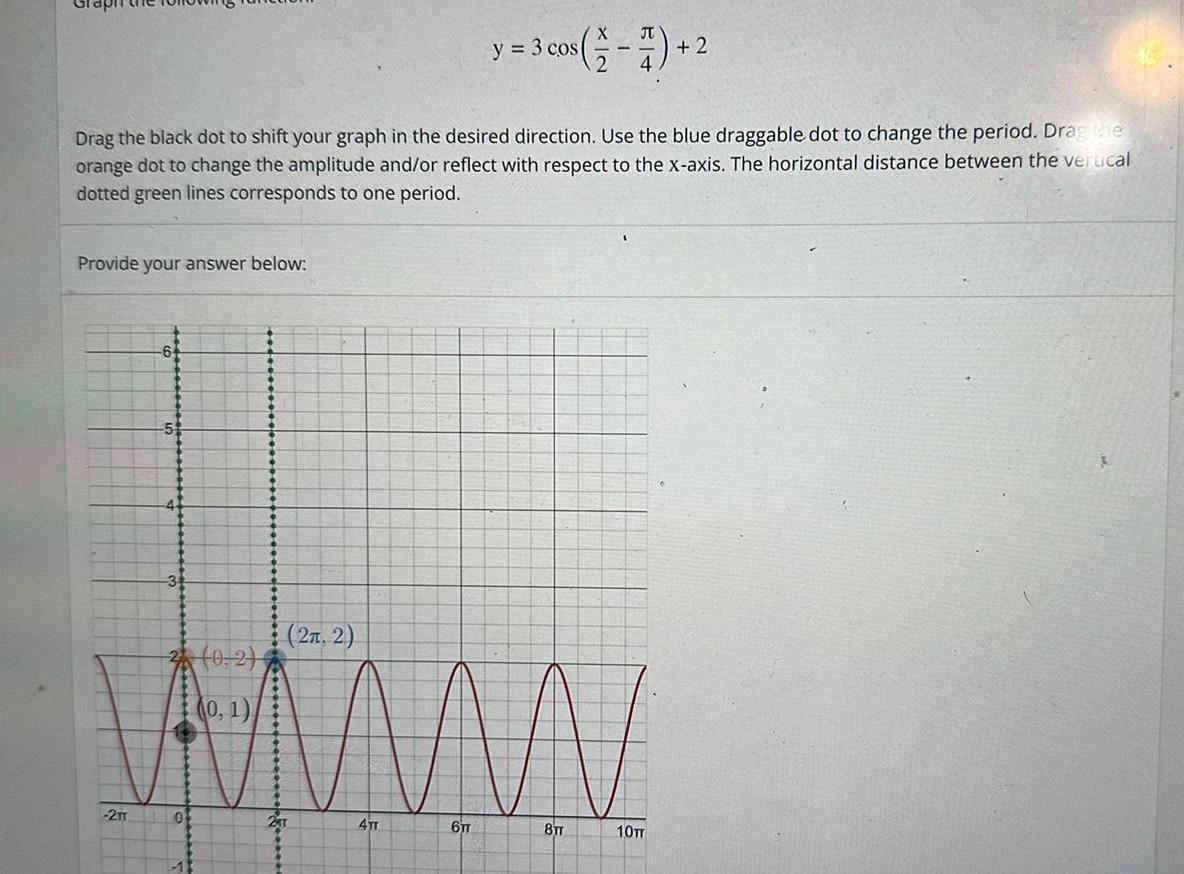
Calculus
Application of derivativesy 3 cos 2 Drag the black dot to shift your graph in the desired direction Use the blue draggable dot to change the period Drag the orange dot to change the amplitude and or reflect with respect to the x axis The horizontal distance between the vertical dotted green lines corresponds to one period Provide your answer below 2TT 6 5 4 3 2 0 2 0 1 0 13 2 2 4TT 6TT 8TT 10TT
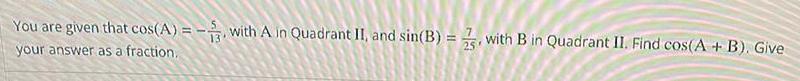
Calculus
Application of derivativesYou are given that cos A with A in Quadrant II and sin B 13 your answer as a fraction with B in Quadrant II Find cos A B Give
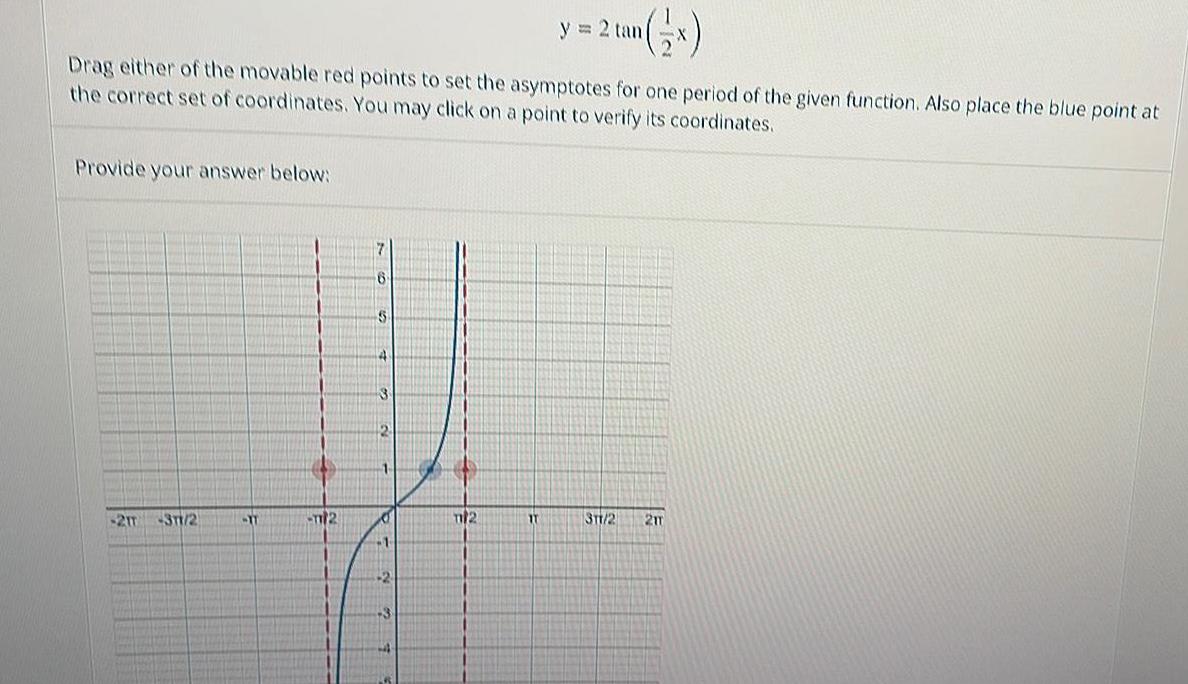
Calculus
Application of derivativesProvide your answer below Drag either of the movable red points to set the asymptotes for one period of the given function Also place the blue point at the correct set of coordinates You may click on a point to verify its coordinates 21T 31 2 IT T2 6 3 2 6 1 1 2 2 tan x IT y 2 tan 311 2 2m
Calculus
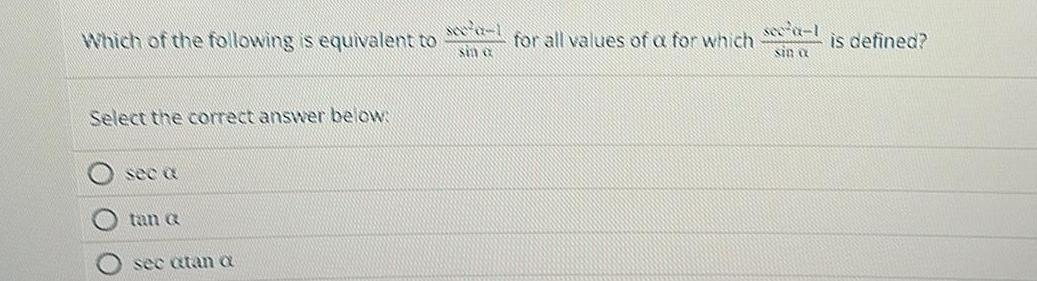
Application of derivativesWhich of the following is equivalent to for all values of a for which Select the correct answer below see a tan a sec atan a sce a 1 sin a is defined
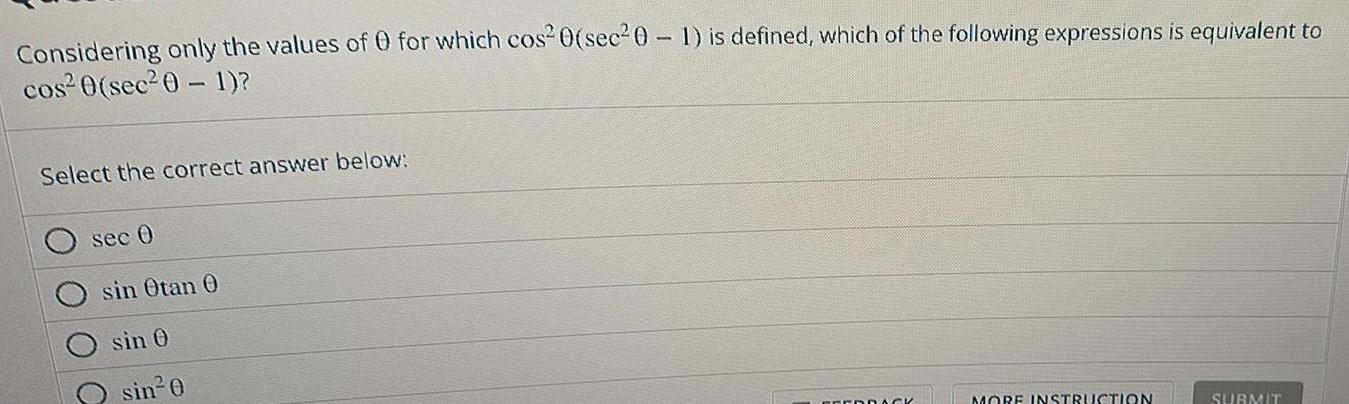
Calculus
Application of derivativesConsidering only the values of 0 for which cos 0 sec 0 1 is defined which of the following expressions is equivalent to cos 0 sec 0 1 Select the correct answer below sec 0 sin Otan 0 sin 0 sin 0 FEEDRACK MORE INSTRUCTION SUBMIT

Calculus
Application of derivativesWhich of the following is equivalent to csc 0 sec 0 1 sec 0 1 for all values of 0 for which csc 0 sec 0 1 sec 0 1 is defined Select the correct answer below Otan 0 Osec 0 O cot 0
Calculus
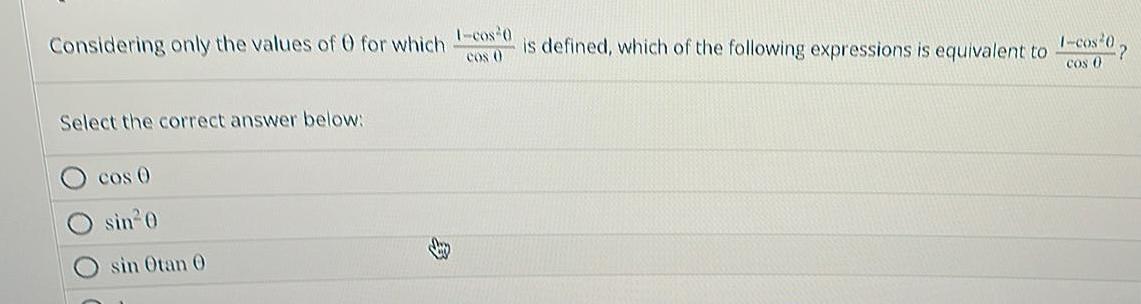
Application of derivativesConsidering only the values of 0 for which I cos 0 is defined which of the following expressions is equivalent to I cos 07 Cos 0 Select the correct answer below cos sin 0 sin Otan 0
Calculus
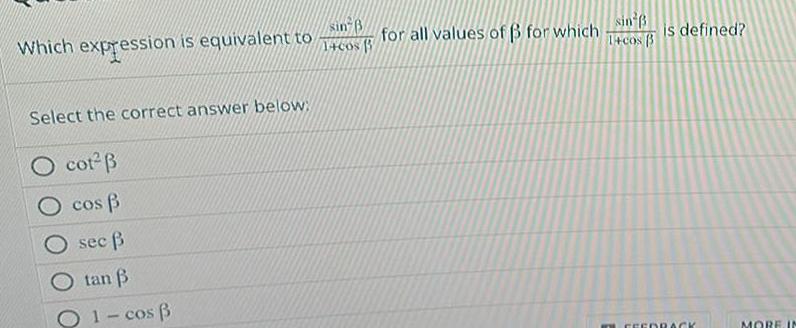
Application of derivativesWhich expression is equivalent to Select the correct answer below O cot B O cos B sec O tan 01 cos B sin B 1 cos B for all values of B for which sin 1 cos B is defined FEEDBACK MORE IN
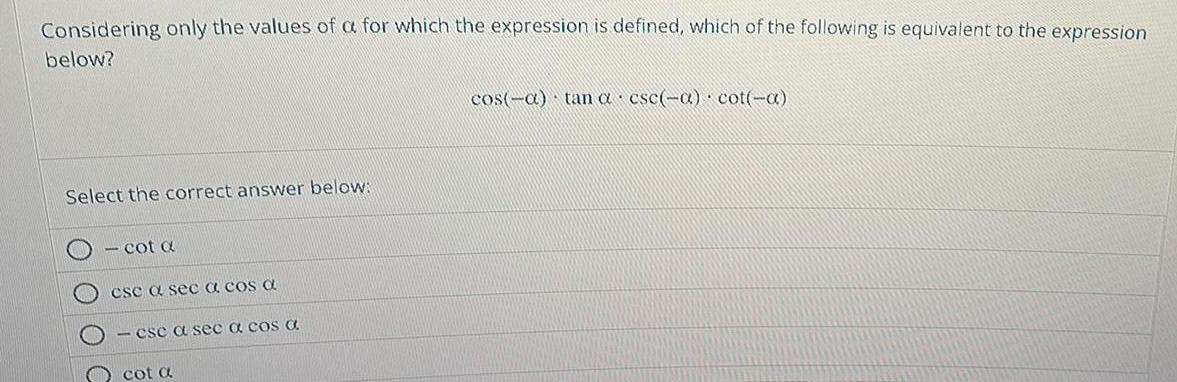
Calculus
Application of derivativesConsidering only the values of a for which the expression is defined which of the following is equivalent to the expression below Select the correct answer below cot a cse a sec a cos a csc a sec a cos C cot a cos a tan a cse a cot a
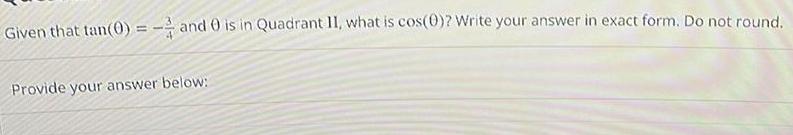
Calculus
Application of derivativesGiven that tan 0 and 0 is in Quadrant II what is cos 0 Write your answer in exact form Do not round Provide your answer below
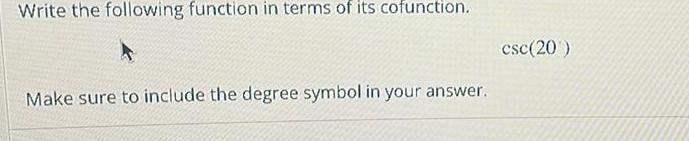
Calculus
Application of derivativesWrite the following function in terms of its cofunction Make sure to include the degree symbol in your answer csc 20

Calculus
Application of derivatives11 Test the series for convergence using the Root Test 00 n 1 6n 5n 4 n
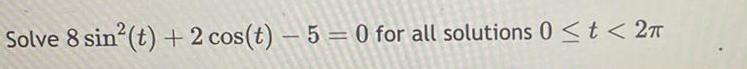


Calculus
Application of derivativesA fence is to be built to enclose a rectangular area of 1800 square feet The fence along three sides is to be made of material that costs 5 per foot The material for the fourth side costs 15 per foot Find the dimensions of the rectangle that will allow for the most economical fence to be built The short side is 300 ft and the long side is 600 ft

Calculus
Application of derivativesA parcel delivery service will deliver a package only if the length plus girth distance around does not exceed 120 inches A Find the dimensions of a rectangular box with square ends that satisfies the delivery service s restriction and has maximum volume What is the maximum volume B Find the dimensions radius and height of a cylindrical container that meets the delivery service s restriction and has maximum volume What is the maximum volume A The dimensions of the rectangular box are Use a comma to separate answers as needed in COLLE

Calculus
Application of derivativesOf all numbers whose difference is 2 find the two that have the minimum product What are the two numbers Use a comma to separate answers as needed

Calculus
Application of derivativesFind the dimensions of a rectangle with a perimeter of 184 feet that has the maximum area The side lengths are feet Use a comma to separate answers as needed
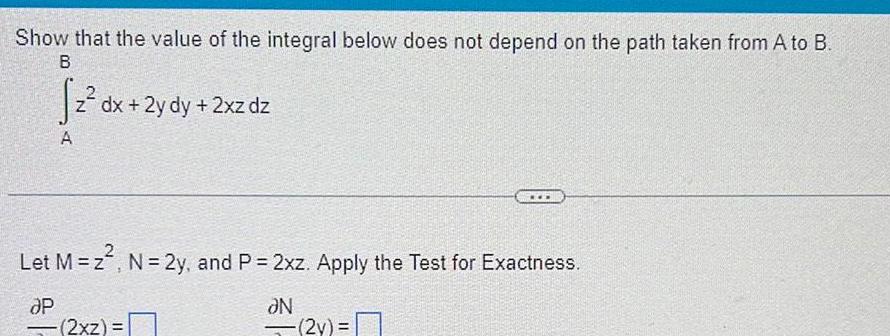
Calculus
Application of derivativesShow that the value of the integral below does not depend on the path taken from A to B B dx A dx 2y dy 2xz dz Let M z N 2y and P 2xz Apply the Test for Exactness P N 2xz 2y
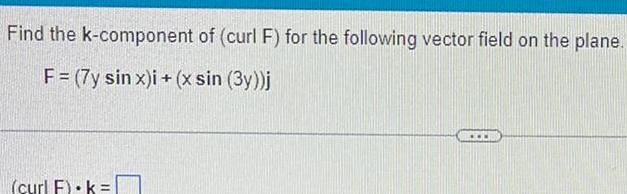
Calculus
Application of derivativesFind the k component of curl F for the following vector field on the plane F 7y sin x i x sin 3y j curl F k www
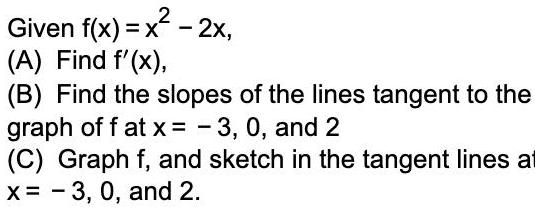
Calculus
Application of derivativesGiven f x x 2x A Find f x B Find the slopes of the lines tangent to the graph off at x 3 0 and 2 C Graph f and sketch in the tangent lines at x 3 0 and 2
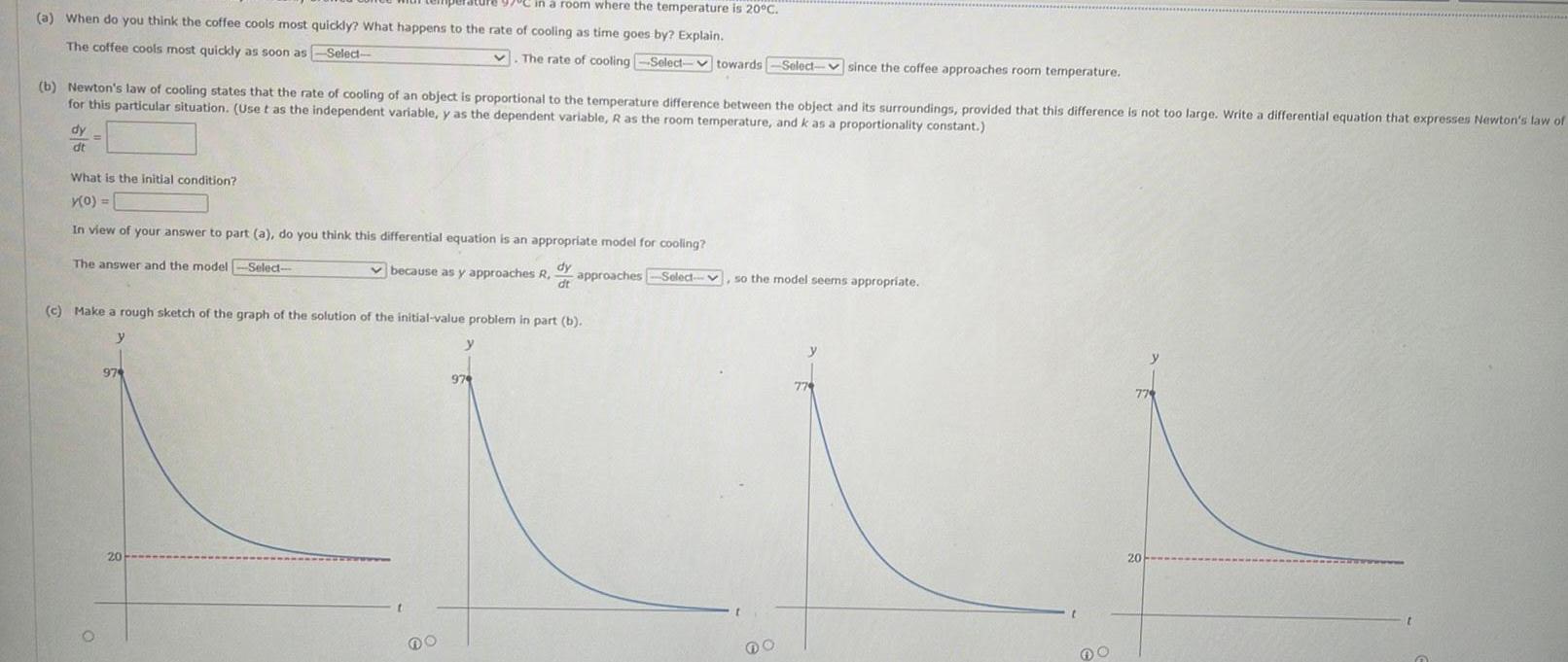
Calculus
Application of derivativesin a room where the temperature is 20 C a When do you think the coffee cools most quickly What happens to the rate of cooling as time goes by Explain The coffee cools most quickly as soon as Select b Newton s law of cooling states that the rate of cooling of an object is proportional to the temperature difference between the object and its surroundings provided that this difference is not too large Write a differential equation that expresses Newton s law of for this particular situation Use t as the independent variable y as the dependent variable R as the room temperature and k as a proportionality constant dy dt What is the initial condition y 0 In view of your answer to part a do you think this differential equation is an appropriate model for cooling Select dy dt approaches Select The answer and the model 974 c Make a rough sketch of the graph of the solution of the initial value problem in part b y 20 because as y approaches R The rate of cooling Select towards Select since the coffee approaches room temperature t DO y 979 so the model seems appropriate o 774 779 20
Calculus
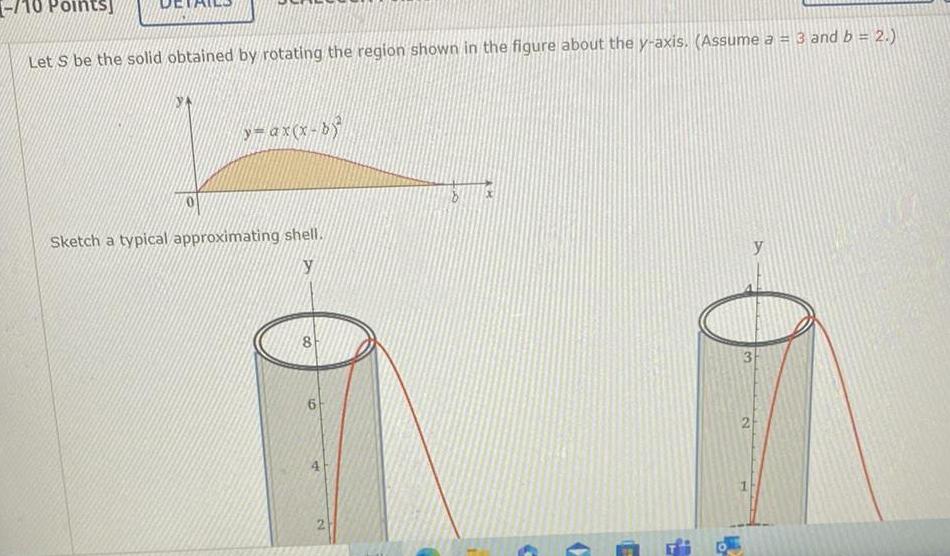
Application of derivativesPoints Let S be the solid obtained by rotating the region shown in the figure about the y axis Assume a 3 and b 2 y axx b Sketch a typical approximating shell y 8 6 4 x Fi 3 N y

Calculus
Application of derivativesFind the solution of the differential equation that satisfies the given initial condition dA Ab2 cos br A 0 b dr
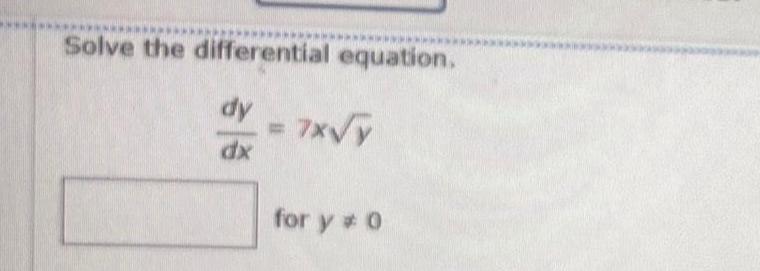

Calculus
Application of derivativesWrite a differential equation that models the given situation The stated rate of change is with respect to time t Use k for the proportionality constant For a car with maximum velocity M the rate of change of the velocity v of the car is proportional to the difference between M and v dv dt Need Help Read
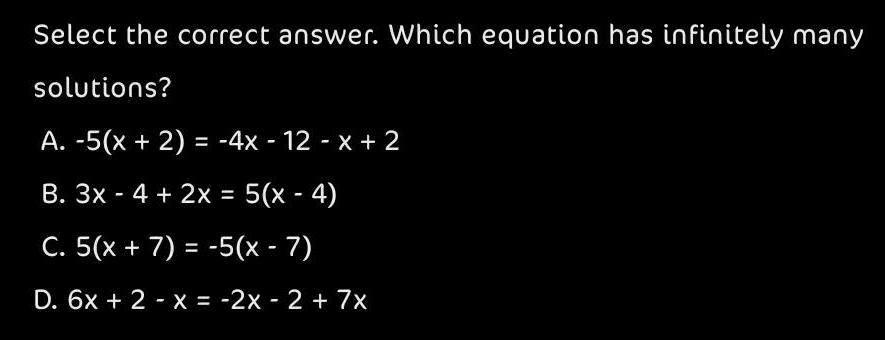
Calculus
Application of derivativesSelect the correct answer Which equation has infinitely many solutions A 5 x 2 4x 12 x 2 B 3x 4 2x 5 x 4 C 5 x 7 5 x 7 D 6x 2 x 2x 2 7x

Calculus
Application of derivatives3 Solve the following system of non linear equations by using the fi x y x x 1 2y 18 0 Newton Raphson method Start with xo 2 and yo 11 and carry out the first two iterations Firstly write the general formula of this method f2 x y x 1 y 6 25 C for solving system of non linear equations and analyse the convergence criteria of this method olution 3 Solution by the Newton Raphson method
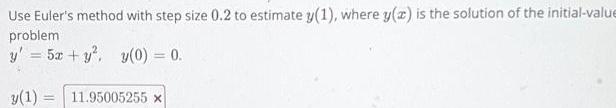
Calculus
Application of derivativesUse Euler s method with step size 0 2 to estimate y 1 where y a is the solution of the initial value problem y 5x y y 0 0 y 1 11 95005255 x

Calculus
Application of derivatives1 point Initially 10 grams of salt are dissolved into 40 liters of water Brine with concentration of salt 4 grams per liter is added at a rate of 2 liters per minute The tank is well mixed and drained at 2 liters per minute a Let x be the amount of salt in grams in the solution after 1 minutes have elapsed Find a formula for the incremental change in the amount of salt Ax in terms of the amount of salt in the solution x and the incremental change in time At Enter At as Deltat Ax grams b Find a formula for the amount of salt in grams after t minutes have elapsed x t grams c How long must the process continue until there are exactly 20 grams of salt in the tank minutes
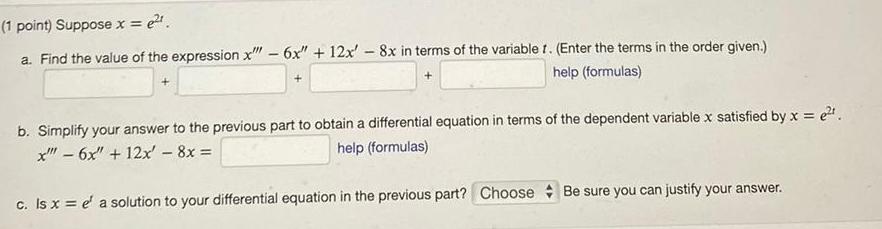
Calculus
Application of derivativese 1 point Suppose x a Find the value of the expression x 6x 12x 8x in terms of the variable r Enter the terms in the order given help formulas b Simplify your answer to the previous part to obtain a differential equation in terms of the dependent variable x satisfied by x e x 6x 12x 8x help formulas c Is x e a solution to your differential equation in the previous part Choose Be sure you can justify your answer

Calculus
Application of derivativesSimplify the trigonometric expression below considering only the values of for which the expression is defined cos B tan B esc B cot B Remember to put parentheses around the argument of any trigonometric function

Calculus
Application of derivativesConsidering only the values of 0 for which the expression is defined which of the following is equivalent to the expression below Select the correct answer below sin 0 01 sin 0 O 1 cos 0 tan 0 csc 0
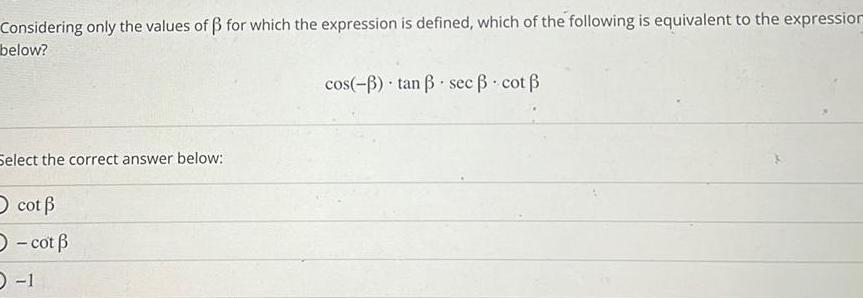
Calculus
Application of derivativesConsidering only the values of for which the expression is defined which of the following is equivalent to the expression below Select the correct answer below O cot cot 0 1 cos tan sec cot
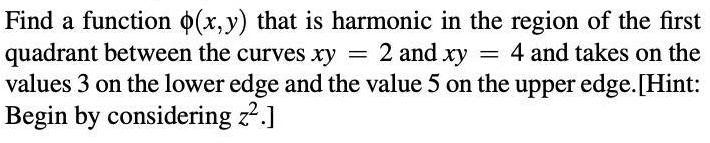
Calculus
Application of derivativesFind a function x y that is harmonic in the region of the first quadrant between the curves xy 2 and xy 4 and takes on the values 3 on the lower edge and the value 5 on the upper edge Hint Begin by considering z
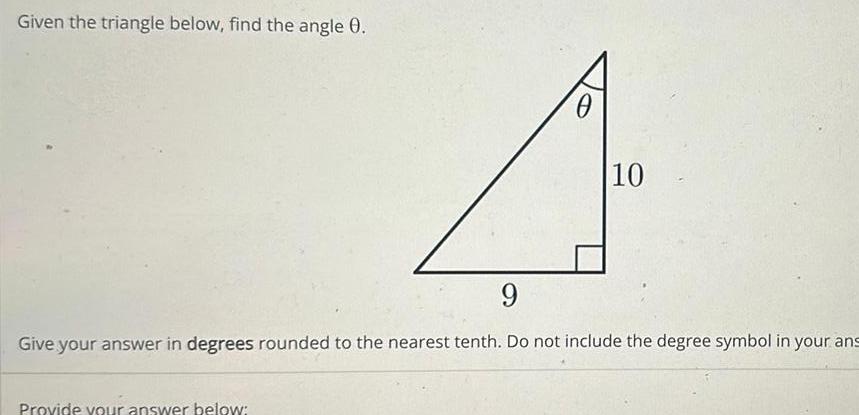
Calculus
Application of derivativesGiven the triangle below find the angle 0 0 Provide your answer below 10 9 Give your answer in degrees rounded to the nearest tenth Do not include the degree symbol in your ans
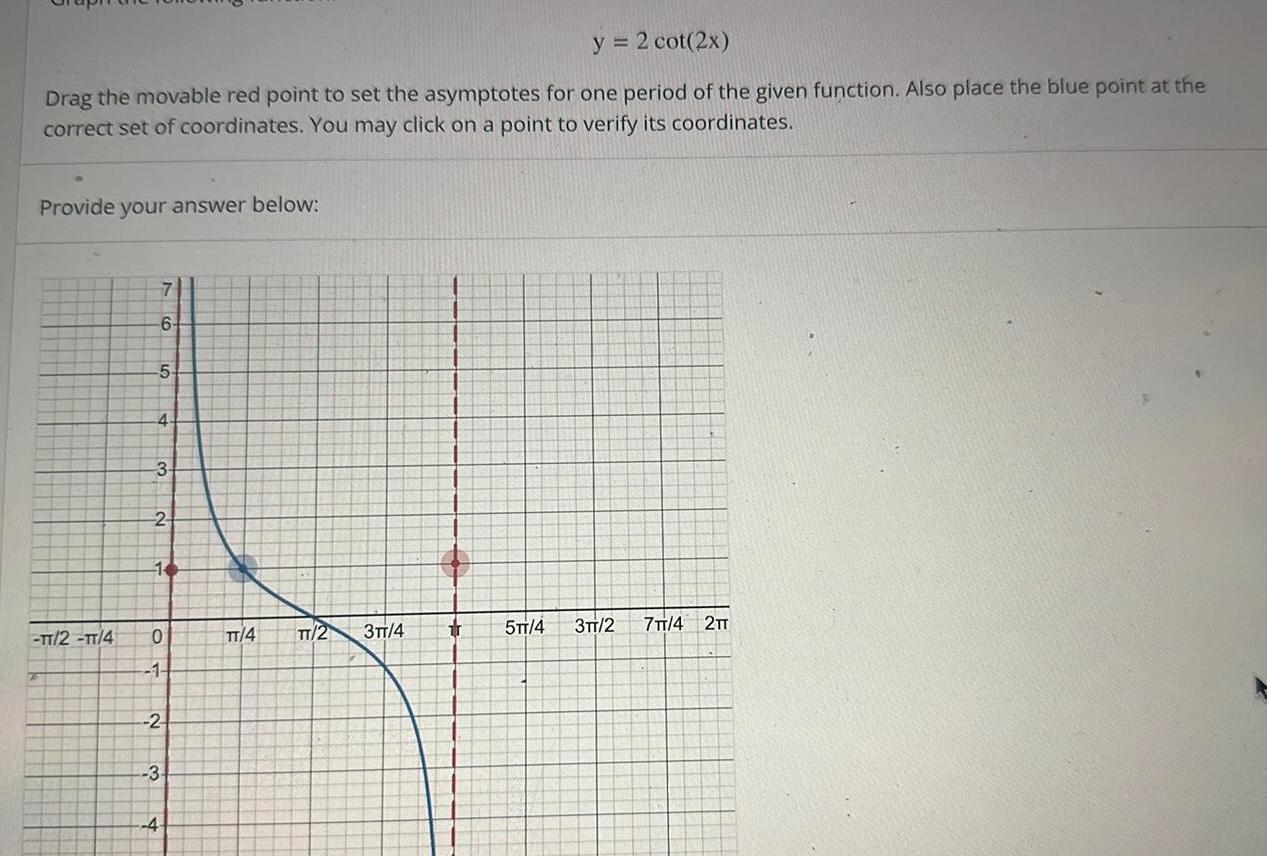
Calculus
Application of derivativesy 2 cot 2x Drag the movable red point to set the asymptotes for one period of the given function Also place the blue point at the correct set of coordinates You may click on a point to verify its coordinates Provide your answer below TT 2 TT 4 6 5 4 3 2 16 0 1 2 3 4 TT 4 TT 2 3TT 4 3 5TT 4 3TT 2 7TT 4 2TT
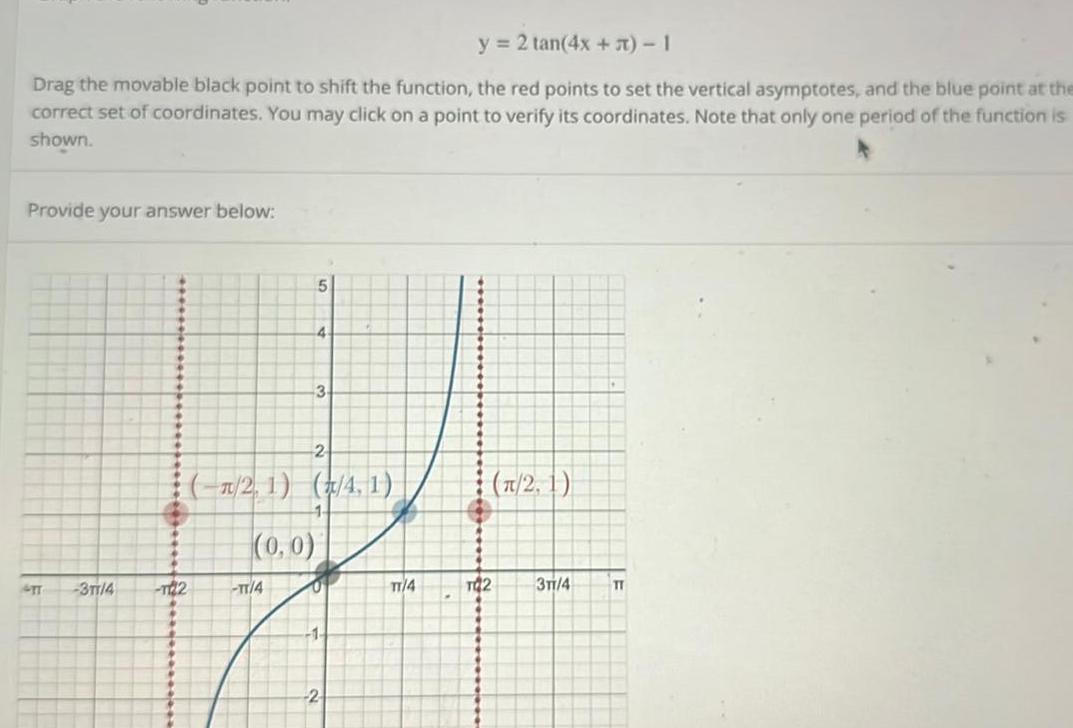
Calculus
Application of derivativesy 2 tan 4x 1 Drag the movable black point to shift the function the red points to set the vertical asymptotes and the blue point at the correct set of coordinates You may click on a point to verify its coordinates Note that only one period of the function is shown Provide your answer below 3TT 4 122 5 TT 4 4 2 2 1 4 1 0 0 3 1 2 TT 4 2 1 TQ2 3TT 4 TT
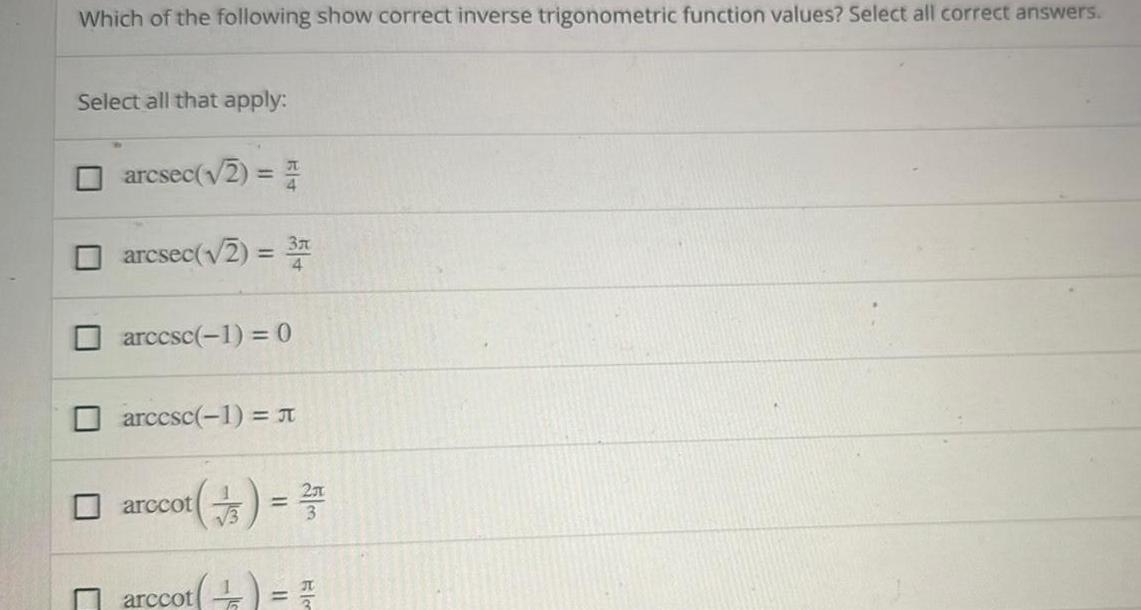
Calculus
Application of derivativesWhich of the following show correct inverse trigonometric function values Select all correct answers Select all that apply arcsec 2 4 arcsec 2 3 arccsc 1 0 arcesc 1 arccot 4 3 3 10 3 T arccot